1 Introduction

Squeeze film dampers (SFDs) are simple configurations mounted on aircraft engines to suppress vibrations of rotors and promote system stability. The system with SFDs is nonlinear, which means the nonlinear forces caused by oil film will lead to undesired unbalance responses in some operation conditions. These nonlinear characteristics of squeeze film damper have provided plenty of material for research since Cooper’s work in 1963 [1], and many researchers reported jump phenomenon and non-synchronous motion in SFD-rotor system by theoretical analysis [2,3,4] and experimental validation [5, 6]. Furthermore, sub-harmonic motions, which contain fractional frequency components in system responses, were observed by Holmes et al. [7,8,9] in their experimental works.

With the appearance of more detailed research work based on different computational methods, more nonlinear characters alternating with parameters variation are revealed. Zhao [10, 11] used the trigonometric collocation method embedding arc-length continuation algorithm to investigate the stability and bifurcation of an eccentric SFD-rotor system, in which the period motion, sub-harmonic motion and quasi-periodic motion transforming into each other with the variation of rotor speed were observed, and these results were compared with those of a concentric system. Zhu [12] compared the slow acceleration method with synchronous circular centered-orbit motion solution and numerical integration method in the study of a flexible rotor supported by SFDs, in which three forms of the multiple-solution responses due to saddle-node bifurcation were obtained. Sundararajan [13] presented a shooting scheme along with arc-length continuation algorithm for periodically forced rotor systems, as an example, an eccentric SFD system was solved by this method. Besides, the similar results to Zhao’s work [11], this system exists another multiple-solution range, in which a stable period-3 solution coexists with a period-1 solution. Furthermore, the system has the evolution route: period-3, period-6, chaos, period-3, with rotor speed running up. Based on a numerical continuation method, Inayat-Hussain [14, 15] also obtained a period-3 motion which coexists with a chaotic motion due to period-doubling bifurcation in a rigid rotor supported by SFDs without centering springs. This period-3 motion has two evolution routes to chaos: period-doubling bifurcation and boundary crisis. Comparing with the preceding results in SFDs without centering springs, the system supported by centering springs has the following two routes to chaos: period-doubling cascades and type 3 intermittency. Bonello [16] presented an integrated approach containing receptance harmonic balance method and time marching techniques to analyze the period solution and aperiodic solution of a multiple SFDs system, in which the sub-harmonic motion and quasi-period motion were verified by simulations and experiments. In conclusion, since each single method has its advantage and drawback, the development of hybrid method is a general tendency applied to reveal more detailed characteristics of nonlinear system.

Similar to the research works of SFDs with simple structure, complex nonlinear dynamic behaviors also have been found in some other SFDs with sophisticated structure. In the study of a porous squeeze film damper system lubricated by micropolar fluid, Cai-Wan [17] showed the wide ranges of quasi-period motion and chaotic motion with varying rotor speed. In rotor systems with full-floating ring bearings, containing two serial SFDs separated by a rotatable floating ring, the undesired symmetry-breaking effect and total instability phenomenon caused by self-excited vibrations were reported by Schweizer [18]. Further, the sub-synchronous oscillations and the critical limit cycle were reported in the semi-floating ring bearings [19], the floating ring of which is not rotatable. Zhou [20] analyzed the nonlinear responses of rotor with ball bearing and floating ring squeeze film dampers by discussing the effects of out-ring mass, bearing stiffness and supports stiffness on the non-synchronous response, and it was concluded that the floating ring SFD can effectively prevent bistable responses of the system.

All these research works mentioned above focus on the responses with a single-frequency excitation. However, there remains a need for the studies of responses caused by two-frequency excitations which comes from dual-rotor systems such as aircraft engines. To simulate on a twin-spool aero-engine system with a real size, Bonello and Pham [21, 22] introduced the impulsive receptance method (IRM) and compared it with reformulation of the Newmark-beta method and receptance harmonic balance method (RHBM) in order to choose proper methods for analyzing large-order nonlinear systems. Furthermore, these selected methods [23] were used to achieve an insight into the effect of the ratio between two rotor’s speeds on the vibration response. It was shown that the responses are particularly sensitive to the initial phase angle between the rotors, especially when the speed ratio was a ratio of two low integers. Obviously, affected by two unbalanced excitations of different frequencies, a nonlinear system shows some interesting complex characteristics which need to be investigated in detail.

The motivation of this paper is to detect the nonlinear characteristics of a flexible rotor supported by squeeze film damper excited by two different frequencies. By using harmonic balance method matching fourth Runge–Kutta method and Hsu method, the periodic solutions containing combined frequencies and quasi-period solutions are obtained, and stability of the periodic solutions affected by parameters, such as ratio of excitation frequencies, oil viscosity and clearance, are also analyzed.

2 Model of SFD-rotor system

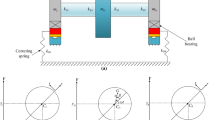
As outlined in Fig. 1, the low-pressure rotor of aircraft engine is simplified as an asymmetric, linear-elastic rotor, the left end is supported by a SFD in parallel with linear spring, and the right end is supported by a linear spring. The dotted line disk represents a simplified high-pressure rotor, which provides a high-frequency excitation to the system. The rotor model is comprised of a disk of mass \(m_\mathrm{o}\), left journal of mass \(m_{\mathrm{a}}\), right journal of mass \(m_{\mathrm{b}}\) and massless flexible shaft. The left journal is supported by a linear spring of stiffness \(k_{\mathrm{a}}\) and a SFD of clearance c. The right journal is supported by a linear spring of stiffness \(k_{\mathrm{b}}\). Hence, considering the short bearing approximation of oil film [12], the motion equations of the rotor system can be written as:

Fig. 1
figure 1

Simplified model of low-pressure rotor

Full size image
$$\begin{aligned} \left\{ {\begin{array}{l} m_{\mathrm{o}} {\ddot{x}}+c_1 \left( {{\dot{x}}-{\dot{x}}_1 } \right) -c_2 \left( {{\dot{\theta }}_{\mathrm{y}} -{\dot{\theta }}_{\mathrm{y}1} } \right) +k_{\mathrm{rr}} \left( {x-x_1 } \right) \\ \qquad \,\, -\,k_{\mathrm{r}{\upvarphi } } \left( {\theta _{\mathrm{y}} -\theta _{\mathrm{y}1} } \right) =\delta _1 \Omega _1 ^{ 2 }\hbox {cos}\Omega _1 t+\delta _2 \Omega _2^2 \cos \Omega _2 t \\ m_{\mathrm{o}} {\ddot{y}}+c_1 \left( {{\dot{y}}-{\dot{y}}_1 } \right) +c_2 \left( {{\dot{\theta }}_{\mathrm{x}} -{\dot{\theta }}_{\mathrm{x}1} } \right) +k_{\mathrm{rr}} \left( {y-y_1 } \right) \\ \qquad \,\,+\,k _{\mathrm{r}{\upvarphi } } \left( {\theta _{\mathrm{x}} -\theta _{\mathrm{x}1} } \right) =\delta _1 \Omega _1 ^{ 2 }\hbox {sin}\Omega _1 t+\delta _2 \Omega _2^2 \sin \Omega _2 t \\ J_{\mathrm{d}} {\ddot{\theta }}_{\mathrm{x}} +J_{\mathrm{p}} \Omega _1 {\dot{\theta }}_{\mathrm{y}} +c_3 \left( {{\dot{y}}-{\dot{y}}_1 } \right) +c_4 \left( {{\dot{\theta }}_{\mathrm{x}} -{\dot{\theta }}_{\mathrm{x}1} } \right) \\ \qquad \,\,+k_{{\upvarphi } \mathrm{r}} \left( {y-y_1 } \right) +k_{{{\upvarphi } {\upvarphi } }} \left( {\theta _{\mathrm{x}} -\theta _{\mathrm{x1}} } \right) =\delta _2 \Omega _2^2 l_3 \sin \Omega _2 t \\ J_{\mathrm{d}} {\ddot{\theta }}_{\mathrm{y}} -J_{\mathrm{p}} \Omega _1 {\dot{\theta }}_{\mathrm{x}} -c_3 \left( {{\dot{x}}-{\dot{x}}_1 } \right) +c_4 \left( {{\dot{\theta }}_{\mathrm{y}} -{\dot{\theta }}_{\mathrm{y}1} } \right) \\ \qquad \,\, -k_{{\upvarphi } \mathrm{r}} \left( {x-x_1 } \right) +k_{{{\upvarphi } {\upvarphi } }} \left( {\theta _{\mathrm{y}} -\theta _{\mathrm{y}1} } \right) =-\delta _2 \Omega _2^2 l_3 \cos \Omega _2 t \\ m_{\mathrm{a}} {\ddot{x}}_{\mathrm{a}} -\gamma _2 c_1 \left( {{\dot{x}}-{\dot{x}}_1 } \right) +\gamma _2 c_2 \left( {{\dot{\theta }}_{\mathrm{y}} -{\dot{\theta }}_{\mathrm{y}1} } \right) -\gamma _2 k_{\mathrm{rr}} \left( {x-x_1 } \right) \\ \qquad \quad +\,\gamma _2 k_{\mathrm{r}{\upvarphi } } \left( {\theta _{\mathrm{y}} -\theta _{\mathrm{y}1} } \right) +c_5 {\dot{x}}_{\mathrm{a}} +k_{\mathrm{a}} x_{\mathrm{a}} +F_{\mathrm{cx}} =0 \\ m_{\mathrm{a}} {\ddot{y}}_{\mathrm{a}} -\gamma _2 c_1 \left( {{\dot{y}}-{\dot{y}}_1 } \right) -\gamma _2 c_2 \left( {{\dot{\theta }}_{\mathrm{x}} -{\dot{\theta }}_{\mathrm{x}1} } \right) -\gamma _2 k_{\mathrm{rr}} \left( {y-y_1 } \right) \\ \quad \qquad -\,\gamma _2 k_{\mathrm{r}{\upvarphi } } \left( {\theta _{\mathrm{x}} -\theta _{\mathrm{x1}} } \right) +c_5 {\dot{y}}_{\mathrm{a}} +k_{\mathrm{a}} y_{\mathrm{a}} +F_{\mathrm{cy}} =0 \\ m_{\mathrm{b}} {\ddot{x}}_{\mathrm{b}} -\gamma _1 c_1 \left( {{\dot{x}}-{\dot{x}}_1 } \right) +\gamma _1 c_2 \left( {{\dot{\theta }}_{\mathrm{y}} -{\dot{\theta }}_{\mathrm{y}1} } \right) -\gamma _1 k_{\mathrm{rr}} \left( {x-x_1 } \right) \\ \quad \qquad +\,\gamma _1 k_{\mathrm{r}{\upvarphi } } \left( {\theta _{\mathrm{y}} -\theta _{\mathrm{y}1} } \right) +c_6 {\dot{x}}_{\mathrm{b}} +k_{\mathrm{b}} x_{\mathrm{b}} =0 \\ m_{\mathrm{b}} {\ddot{y}}_{\mathrm{b}} -\gamma _1 c_1 \left( {{\dot{y}}-{\dot{y}}_1 } \right) -\gamma _1 c_2 \left( {{\dot{\theta }}_{\mathrm{x}} -{\dot{\theta }}_{\mathrm{x1}} } \right) -\gamma _1 k_{\mathrm{rr}} \left( {y-y_1 } \right) \\ \quad \qquad -\,\gamma _1 k_{\mathrm{r}{\upvarphi } } \left( {\theta _{\mathrm{x}} -\theta _{\mathrm{x}1} } \right) +c_6 {\dot{y}}_{\mathrm{b}} +k_{\mathrm{b}} y_{\mathrm{b}} =0 \\ \end{array}} \right. \end{aligned}$$
(1)

in which, \(l=l_1 +l_2 \), \(\gamma _1 =l_1 /l\) and \(\gamma _2 =l_2 /l\) are used to define the length and ratio parameters, \(x_1 =\gamma _2 x_{\mathrm{a}} +\gamma _1 x_{\mathrm{b}} \), \(y_1 =\gamma _2 y_{\mathrm{a}} +\gamma _1 y_{\mathrm{b}} \), \(\theta _{\mathrm{x}1} =\left( {y_{\mathrm{a}} -y_{\mathrm{b}} } \right) /l\) and \(\theta _{\mathrm{y}1} =\left( {x_{\mathrm{b}} -x_{\mathrm{a}} } \right) /l\) are rigid body displacements of disk center, \(k_{\mathrm{rr}} \), \(k_{\mathrm{r}{\upvarphi } } \) and \(k_{{{\upvarphi }{\upvarphi } }} \) represent stiffness parameters of the shaft, \(c_{1}\sim c_{6}\) represent damper parameters, \(J_{\mathrm{p}} \) and \(J_{\mathrm{d}} \) represent polar moment of inertia and equatorial moment of inertia, \(\delta _1 \) and \(\delta _2 \) are equivalent unbalance values, \(\omega _1 \) and \(\omega _2 \) are rotational speeds of low-pressure rotor and high-pressure rotor, \(F_{\mathrm{cx}} =F_{\mathrm{r}} x_{\mathrm{a}} /r-F_{{{\uptau } }} y_{\mathrm{a}} /r\) and \(F_{\mathrm{cy}} =F_{\mathrm{r}} y_{\mathrm{a}} /r+F_{{{\uptau } }} x_{\mathrm{a}} /r\) are components of oil film force in x-coordinate and y-coordinate, \(F_{\mathrm{r}} =\mu RL^{3}/c^{3}\left( {I_3^{02} {\dot{r}}+I_3^{11} r{\dot{\psi }}} \right) \) and \(F_{{{\uptau } }} =\mu RL^{3}/c^{3}\left( {I_3^{11} {\dot{r}}+I_3^{20} r{\dot{\psi }}} \right) \) are the oil film forces of radial direction and tangential direction, \(r=\sqrt{x_{\mathrm{a}}^2 +y_{\mathrm{a}}^2 }\) and \(\psi =\arctan \left( {y_{\mathrm{a}} /x_{\mathrm{a}} } \right) \) are the displacements of radial direction and tangential direction, \(\mu \) is the viscosity coefficient of oil, R is the radius of journal, L is the length of SFD, and the integral parameters are defined as \(I_n^{lm} =\int _{\theta _1 }^{\theta _2 } {\frac{\sin ^{l}\theta \cos ^{m}\theta d\theta }{(1+r\cos \theta /c)^{n}}} \) [24].

The dimensionless parameters are introduced as follows:

$$\begin{aligned}&\tau =\Omega _1 t, \quad q_1 =\frac{x}{c}, \quad q_2 =\frac{y}{c}, \quad q_3 =\frac{\theta _{\mathrm{x}} l}{c}, \quad \\&q_4 =\frac{\theta _{\mathrm{y}} l}{c}, q_5 =\frac{x_{\mathrm{a}} }{c}, \quad q_6 =\frac{y_{\mathrm{a}} }{c}, \quad q_7 =\frac{x_{\mathrm{b}} }{c}, \quad q_8 =\frac{y_{\mathrm{b}} }{c}. \end{aligned}$$

Thus, the motion equation (1) can be rewritten as:

$$\begin{aligned}&\left\{ \begin{array}{l} q^{\prime \prime }_1 + {\zeta _1}{q^{\prime }_1} - {\zeta _2}{q^{\prime }_4} - \left( {{\zeta _2} + {\zeta _1}{\gamma _2}} \right) {q^{\prime }_5} \\ \quad \,\,\, +\, \left( {{\zeta _2} - {\gamma _1}{\zeta _1}} \right) {q^{\prime }_7} + {\kappa _1}{q_1} - {\kappa _2}{q_4} - \left( {{\kappa _2} + {\kappa _1}{\gamma _2}} \right) {q_5} \\ \quad \,\,\, +\, \left( {{\kappa _2} - {\gamma _1}{\kappa _1}} \right) {q_7} = {U_1}\mathrm{{cos}}\tau + {\xi ^2}{U_2}\cos \xi \tau \\ {q^{\prime \prime }_2} + {\zeta _1}{q^{\prime }_2} + {\zeta _2}{q^{\prime }_3} - \left( {{\zeta _2} + {\zeta _1}{\gamma _2}} \right) {q^{\prime }_6} \\ \quad \,\,\,+\, \left( {{\zeta _2} - {\gamma _1}{\zeta _1}} \right) {q^{\prime }_8} + {\kappa _1}{q_2} + {\kappa _2}{q_3} - \left( {{\kappa _2} + {\kappa _1}{\gamma _2}} \right) {q_6} \\ \quad \,\,\,+ \,\left( {{\kappa _2} - {\gamma _1}{\kappa _1}} \right) {q_8} = {U_1}\mathrm{{sin}}\tau + {\xi ^2}{U_2}\sin \xi \tau \\ {\alpha _0}{q^{\prime \prime }_3} + {\alpha _\mathrm{{0}}}\eta {q^{\prime }_4} + {\zeta _3}{q^{\prime }_2} + {\zeta _4}{q^{\prime }_3} - \left( {{\zeta _4} + {\zeta _3}{\gamma _2}} \right) {q^{\prime }_6} \\ \qquad \quad + \,\left( {{\zeta _4} - {\gamma _1}{\zeta _3}} \right) {q^{\prime }_8} + {\kappa _3}{q_2} + {\kappa _4}{q_3} - \left( {{\kappa _4} + {\kappa _3}{\gamma _2}} \right) {q_6} \\ \qquad \quad +\, \left( {{\kappa _4} - {\gamma _1}{\kappa _3}} \right) {q_8}\mathrm{{ = }}{\xi ^2}{U_3}\sin \xi \tau \\ {\alpha _0}{q^{\prime \prime }_4} - {\alpha _\mathrm{{0}}}\eta {q^{\prime }_3} - {\zeta _3}{q^{\prime }_1} + {\zeta _4}{q^{\prime }_4} + \left( {{\zeta _4} + {\zeta _3}{\gamma _2}} \right) {q^{\prime }_5} \\ \qquad \quad - \,\left( {{\zeta _4} - {\gamma _1}{\zeta _3}} \right) {q^{\prime }_7} - {\kappa _3}{q_1} + {\kappa _4}{q_4} + \left( {{\kappa _4} + {\kappa _3}{\gamma _2}} \right) {q_5} \\ \qquad \quad - \,\left( {{\kappa _4} - {\gamma _1}{\kappa _3}} \right) {q_7} = - {\xi ^2}{U_3}\cos \xi \tau \\ {\alpha _1}{q^{\prime \prime }_5} - {\gamma _2}{\zeta _1}{q^{\prime }_1} + {\gamma _2}{\zeta _2}{q^{\prime }_4} + {\gamma _2}\left( {{\zeta _2} + {\gamma _2}{\zeta _1}} \right) {q^{\prime }_5} \\ \qquad \quad - \,{\gamma _2}\left( {{\zeta _2} - {\gamma _1}{\zeta _1}} \right) {q^{\prime }_7} + {\zeta _5}{q^{\prime }_5} - {\gamma _2}{\kappa _1}{q_1} + {\gamma _2}{\kappa _2}{q_4} \\ \qquad \quad +\, {\gamma _2}\left( {{\kappa _2} + {\gamma _2}{\kappa _1}} \right) {q_5} - {\gamma _2}\left( {{\kappa _2} - {\gamma _1}{\kappa _1}} \right) {q_7} + {\kappa _5}{q_5} \\ \qquad \quad + \,B{{\bar{F}}_{\mathrm{{cx}}}} = 0\\ {\alpha _1}{q^{\prime \prime }_6} - {\gamma _2}{\zeta _1}{q^{\prime }_2} - {\gamma _2}{\zeta _2}{q^{\prime }_3} + {\gamma _2}\left( {{\zeta _2} + {\gamma _2}{\zeta _1}} \right) {q^{\prime }_6}\\ \qquad \quad -\, {\gamma _2}\left( {{\zeta _2} - {\gamma _1}{\zeta _1}} \right) {q^{\prime }_8} + {\zeta _5}{q^{\prime }_6} - {\gamma _2}{\kappa _1}{q_2} - {\gamma _2}{\kappa _2}{q_3} \\ \qquad \quad +\, {\gamma _2}\left( {{\kappa _2} + {\gamma _2}{\kappa _1}} \right) {q_6} - {\gamma _2}\left( {{\kappa _2} - {\gamma _1}{\kappa _1}} \right) {q_8} + {\kappa _5}{q_6} \\ \qquad \quad + \,B{{\bar{F}}_{\mathrm{{cy}}}} = 0\\ {\alpha _2}{q^{\prime \prime }_7} - {\gamma _1}{\zeta _1}{q^{\prime }_1} + {\gamma _1}{\zeta _2}{q^{\prime }_4} + {\gamma _1}\left( {{\zeta _2} + {\gamma _2}{\zeta _1}} \right) {q^{\prime }_5}\\ \qquad \quad - \,{\gamma _1}\left( {{\zeta _2} - {\zeta _1}{\gamma _1}} \right) {q^{\prime }_7} + {\zeta _6}{q^{\prime }_7} - {\gamma _1}{\kappa _1}{q_1} + {\gamma _1}{\kappa _2}{q_4} \\ \qquad \quad + \,{\gamma _1}\left( {{\kappa _2} + {\gamma _2}{\kappa _1}} \right) {q_5} - {\gamma _1}\left( {{\kappa _2} - {\kappa _1}{\gamma _1}} \right) {q_7} \\ \qquad \quad + \,{\kappa _6}{q_7} = 0\\ {\alpha _2}{q^{\prime \prime }_8} - {\gamma _1}{\zeta _1}{q^{\prime }_2} - {\gamma _1}{\zeta _2}{q^{\prime }_3} + {\gamma _1}\left( {{\zeta _2} + {\gamma _2}{\zeta _1}} \right) {q^{\prime }_6} \\ \qquad \quad - \,{\gamma _1}\left( {{\zeta _2} - {\zeta _1}{\gamma _1}} \right) {q^{\prime }_8} + {\zeta _6}{q^{\prime }_8} - {\gamma _1}{\kappa _1}{q_2} - {\gamma _1}{\kappa _2}{q_3} \\ \qquad \quad +\, {\gamma _1}\left( {{\kappa _2} + {\gamma _2}{\kappa _1}} \right) {q_6} - {\gamma _1}\left( {{\kappa _2} - {\kappa _1}{\gamma _1}} \right) {q_8} + {\kappa _6}{q_8} = 0 \end{array} \right. \nonumber \\ \end{aligned}$$
(2)

in which, the other dimensionless parameters are defined as: \(\zeta _1 =\frac{c_1 }{m_{\mathrm{o}} \Omega _1 }\), \(\zeta _2 =\frac{c_2 }{m_{\mathrm{o}} l\Omega _1 }\), \(\zeta _3 =\frac{c_3 }{m_{\mathrm{o}} l\Omega _1 }\), \(\zeta _4 =\frac{c_4 }{m_{\mathrm{o}} l^{2}\Omega _1 }\), \(\zeta _5 =\frac{c_5 }{m_{\mathrm{o}} \Omega _1 }\), \(\zeta _6 =\frac{c_6 }{m_{\mathrm{o}} \Omega _1 }\), \(\kappa _1 =\frac{k_{\mathrm{rr}} }{m_{\mathrm{o}} \Omega _1^2 }\), \(\kappa _2 =\frac{k_{\mathrm{r}{\upvarphi } } }{m_{\mathrm{o}} l\Omega _1^2 }\), \(\kappa _3 =\frac{k_{\mathrm{r}{\upvarphi } } }{m_{\mathrm{o}} l\Omega _1^2 }\), \(\kappa _4 =\frac{k_{{{\upvarphi }{\upvarphi } }} }{m_{\mathrm{o}} l^{2}\Omega _1^2 }\), \(\kappa _5 =\frac{k_{\mathrm{a}} }{m_{\mathrm{o}} \Omega _1^2 }\), \(\kappa _6 =\frac{k_{\mathrm{b}} }{m_{\mathrm{o}} \Omega _1^2 }\), \(\eta =\frac{J_{\mathrm{p}} }{J_{\mathrm{d}} }\), \(\alpha _0 =\frac{J_{\mathrm{d}} }{m_{\mathrm{o}} l^{2}}\), \(\alpha _1 =\frac{m_{\mathrm{a}} }{m_{\mathrm{o}} }\), \(\alpha _2 =\frac{m_{\mathrm{b}} }{m_{\mathrm{o}} }\), \(U_1 =\frac{\delta _1 }{cm_{\mathrm{o}} }\), \(U_2 =\frac{\delta _2 }{cm_{\mathrm{o}} }\), \(U_3 =\frac{\delta _2 l_3 }{m_{\mathrm{o}} lc}\), \(\xi =\frac{\Omega _2 }{\Omega _1 }\), \(\varepsilon =\frac{r}{c}\), \(B=\frac{\mu RL^{3}}{m_{\mathrm{o}} c^{3}\Omega _1 }\), \(\bar{{F}}_{\mathrm{cx}} =\bar{{F}}_{\mathrm{r}} \frac{q_5 }{\varepsilon }-\bar{{F}}_{{{\uptau } }} \frac{q_6 }{\varepsilon }\), \(\bar{{F}}_{\mathrm{cy}} =\bar{{F}}_{\mathrm{r}} \frac{q_6 }{\varepsilon }+\bar{{F}}_{{{\uptau } }} \frac{q_5 }{\varepsilon }\), \(\bar{{F}}_{\mathrm{r}} =I_3^{02} {\varepsilon }^{\prime }+I_3^{11} \varepsilon {\psi }^{\prime }\), \(\bar{{F}}_{{{\uptau } }} =I_3^{11} {\varepsilon }^{\prime }+I_3^{20} \varepsilon {\psi }^{\prime }\).

3 Method of solution and stability analysis

3.1 Multiple harmonic balance method

Equation (2) describes a nonlinear system with external two-frequency excitations, in which the responses may contain two incommensurable frequencies and a series of combination frequencies of them. To analyze the system with multiple-frequency excitation, a multiple harmonic balance method proposed by Kim [25] in a study on internal resonance problem of incommensurable frequencies is chosen. The discrete time solution of Eq. (2) can be assumed as:

$$\begin{aligned} q_j \left( {m,n} \right)= & {} \sum _{k=-M}^M \sum _{l=-M}^M a_{j,k,l} \cos \frac{2\pi }{N}\left( {mk+nl} \right) \nonumber \\&+\,b_{j,k,l} \sin \frac{2\pi }{N}\left( {mk+nl} \right) \nonumber \\= & {} \sum _{k=-M}^M \sum _{l=-M}^M a_{j,k,l} \cos \left( {k\tau _1 +l\tau _2 } \right) \nonumber \\&+\,b_{j,k,l} \sin \left( {k\tau _1 +l\tau _2 } \right) \end{aligned}$$
(3)

The substitution variables \(\tau _1 =\tau ,\tau _2 =\xi \tau \) represent independent time dimension, both of them vary from 0 to \(2\pi \), and m, n varying from 0 to \(N-1\).

Correspondingly, the nonlinear forces are expressed as:

$$\begin{aligned} \left\{ \!\!{\begin{array}{l} \bar{{F}}_{\mathrm{cx}} \left( {q_5 ,q_6 ,{q}^{\prime }_5 ,{q}^{\prime }_6 } \right) \left( {m,n} \right) =\sum _{k=-M}^M \sum _{l=-M}^M\\ \quad \times {\left( {c_{5,k,l} \cos \frac{2\pi }{N}\left( {mk+nl} \right) +d_{5,k,l} \sin \frac{2\pi }{N}\left( {mk+nl} \right) } \right) }\\ \bar{{F}}_{\mathrm{cy}} \left( {q_5 ,q_6 ,{q}^{\prime }_5 ,{q}^{\prime }_6 } \right) \left( {m,n} \right) =\sum _{k=-M}^M \sum _{l=-M}^M\\ \quad \times {\left( {c_{6,k,l} \cos \frac{2\pi }{N}\left( {mk+nl} \right) +d_{6,k,l} \sin \frac{2\pi }{N}\left( {mk+nl} \right) } \right) }\\ \end{array}} \right. \end{aligned}$$
(4)
Table 1 Parameters of rotor and squeeze film damper system
Full size table
Fig. 2
figure 2

Frequency–Amplitude results of two numerical algorithms (\(\xi =1.30)\). a center of disk \(q_{1}\), b journal of SFD \(q_{5}\)

Full size image

Substituting Eqs. (3) and (4) into Eq. (2), and considering the differential operator \(\frac{d}{d\tau }=\frac{\partial }{\partial \tau _1 }+\xi \frac{\partial }{\partial \tau _2 }\), rearranging the terms with the same trigonometric elements leads to the following equations:

$$\begin{aligned} g_{1,k,l}= & {} \left[ {\kappa _1 -\left( {k+l\xi } \right) ^{2}} \right] a_{1kl} +\zeta _1 \left( {k+l\xi } \right) b_{1kl} \nonumber \\&-\,\kappa _2 a_{4kl} -\zeta _2 \left( {k+l\xi } \right) b_{4kl} -\left( {\kappa _2 +\gamma _2 \kappa _1 } \right) a_{5kl} \nonumber \\&-\,\left( {\zeta _2 +\gamma _2 \zeta _1 } \right) \left( {k+l\xi } \right) b_{5kl} +\left( {\kappa _2 -\gamma _1 \kappa _1 } \right) a_{7kl} \nonumber \\&+\,\left( {\zeta _2 -\gamma _1 \zeta _1 } \right) \left( {k+l\xi } \right) b_{7kl} -U_1 \phi _1 -\xi ^{2}U_2 \phi _2 =0 \nonumber \\ g_{2,k,l}= & {} -\zeta _1 \left( {k+l\xi } \right) a_{1kl} +\left[ {\kappa _1 -\left( {k+l\xi } \right) ^{2}} \right] b_{1kl}\nonumber \\&+\,\zeta _2 \left( {k+l\xi } \right) a_{4kl} -\kappa _2 b_{4kl} +\left( {\zeta _2 +\gamma _2 \zeta _1 } \right) \nonumber \\&\left( {k+l\xi } \right) a_{5kl} - \left( {\kappa _2 +\gamma _2 \kappa _1 } \right) b_{5kl} - \left( {\zeta _2 -\gamma _1 \zeta _1 } \right) \nonumber \\&\left( {k+l\xi } \right) a_{7kl} +\left( {\kappa _2 -\gamma _1 \kappa _1 } \right) b_{7kl} =0 \nonumber \\&\vdots \nonumber \\ g_{15,k,l}= & {} -\gamma _1 \zeta _1 \left( {k+l\xi } \right) b_{2kl} -\gamma _1 \kappa _2 a_{3kl} \nonumber \\&-\,\gamma _1 \zeta _2 \left( {k+l\xi } \right) b_{3kl} +\gamma _1 \left( {\kappa _2 +\gamma _2 \kappa _1 } \right) a_{6kl} \nonumber \\&+\,\gamma _1 \left( {\zeta _2 +\gamma _2 \zeta _1 } \right) \left( {k+l\xi } \right) b_{6kl} -\gamma _1 \kappa _1 a_{2kl} \nonumber \\&+\,\left[ {\left( {\kappa _6 -\gamma _1 \kappa _2 +\gamma _1^2 \kappa _1 } \right) -\alpha _2 \left( {k+l\xi } \right) ^{2}} \right] a_{8kl} \nonumber \\&+\,\left[ {\gamma _1 \left( {\gamma _1 \zeta _1 -\zeta _2 } \right) +\zeta _6 } \right] \left( {k+l\xi } \right) b_{8kl} =0 \nonumber \\ g_{16,k,l}= & {} \gamma _1 \left( {\kappa _2 +\gamma _2 \kappa _1 } \right) b_{6kl} \nonumber \\&+\,\left[ {\left( {\kappa _6 -\gamma _1 \kappa _2 +\gamma _1^2 \kappa _1 } \right) -\alpha _2 \left( {k+l\xi } \right) ^{2}} \right] b_{8kl} \nonumber \\&-\,\left[ {\gamma _1 \left( {\gamma _1 \zeta _1 -\zeta _2 } \right) +\zeta _6 } \right] \left( {k+l\xi } \right) a_{8kl} \nonumber \\&\gamma _1 \zeta _1 \left( {k+l\xi } \right) a_{2kl} -\gamma _1 \kappa _1 b_{2kl} +\gamma _1 \zeta _2 \left( {k+l\xi } \right) a_{3kl} \nonumber \\&-\,\gamma _1 \kappa _2 b_{3kl} -\gamma _1 \left( {\zeta _2 +\gamma _2 \zeta _1 } \right) \left( {k+l\xi } \right) a_{6kl} =0\nonumber \\ \end{aligned}$$
(5)

in which, \(\phi _1 =\left\{ {\begin{array}{ll} 1&{}\left( {k=1,l=0} \right) \\ 0&{}\hbox {others} \\ \end{array}} \right. \), \(\phi _2 =\left\{ {\begin{array}{ll} 1&{}\left( {k=0,l=1} \right) \\ 0&{}\hbox {others} \\ \end{array}} \right. \), the other terms are shown in Appendix 2. Equation (5) can be expressed as:

$$\begin{aligned} G\left( {P,Q} \right)= & {} \left[ g_{1,k,l} \left( {P,Q} \right) ,g_{2,k,l} \left( {P,Q} \right) ,\right. \nonumber \\&\quad \left. \ldots ,g_{16,k,l} \left( {P,Q} \right) \right] ^\mathrm{T}=0 \end{aligned}$$
(6)
$$\begin{aligned} \left[ {{\begin{array}{c} P \\ Q \\ \end{array} }} \right] ^\mathrm{T}= & {} \left[ {{\begin{array}{ccccccc} {a_{1,k,l} }&{} {b_{1,k,l} }&{} {a_{2,k,l} }&{} {b_{2,k,l} }&{} \ldots &{} {a_{8,k,l} }&{} {b_{8,k,l} } \\ {c_{1,k,l} }&{} {d_{1,k,l} }&{} {c_{2,k,l} }&{} {d_{2,k,l} }&{} \ldots &{} {c_{8,k,l} }&{} {d_{8,k,l} } \\ \end{array} }} \right] ^\mathrm{T}\nonumber \\ \end{aligned}$$
(7)
Fig. 3
figure 3

Time responses of \(q_{1}\) in different resonance region. a \(\lambda =0.762\), b \(\lambda =4.013\)

Full size image

Equation (6) contains a series of algebraic equations about unknown coefficients P and Q. The coefficients Q can be expressed by using the coefficients P by Eq. (3) and the relationships as follows:

$$\begin{aligned} \left[ {{\begin{array}{c} {c_{5,k,l} } \\ {c_{6,k,l} } \\ \end{array} }} \right]= & {} \frac{2}{N^{2}}\sum _{m=0}^{N-1} \sum _{n=0}^{N-1} \left[ {{\begin{array}{c} {\bar{{F}}_{\mathrm{cx}} \left( {q_5 ,q_6 ,{q}^{\prime }_5 ,{q}^{\prime }_6 } \right) \left( {m,n} \right) } \\ {\bar{{F}}_{\mathrm{cy}} \left( {q_5 ,q_6 ,{q}^{\prime }_5 ,{q}^{\prime }_6 } \right) \left( {m,n} \right) } \\ \end{array} }} \right] \nonumber \\&\times \cos \frac{2\pi }{N} \left( {mk+nl} \right) \nonumber \\ \left[ {{\begin{array}{c} {d_{5,k,l} } \\ {d_{6,k,l} } \\ \end{array} }} \right]= & {} \frac{2}{N^{2}}\sum _{m=0}^{N-1} \sum _{n=0}^{N-1} \left[ {{\begin{array}{c} {\bar{{F}}_{\mathrm{cx}} \left( {q_5 ,q_6 ,{q}^{\prime }_5 ,{q}^{\prime }_6 } \right) \left( {m,n} \right) } \\ {\bar{{F}}_{\mathrm{cy}} \left( {q_5 ,q_6 ,{q}^{\prime }_5 ,{q}^{\prime }_6 } \right) \left( {m,n} \right) } \\ \end{array} }} \right] \nonumber \\&\times \sin \frac{2\pi }{N} \left( {mk+nl} \right) \end{aligned}$$
(8)

Finally, Eq. (6) only contains unknown coefficients P which can be solved by iterative method such as Newton-Rapson algorithm:

$$\begin{aligned} J^{\left( i \right) }\left( {P^{\left( {i+1} \right) }-P^{\left( i \right) }} \right) +G^{\left( i \right) }=0 \end{aligned}$$
(9)

The Jacobian matrix is expressed as:

$$\begin{aligned} J=\frac{dG\left( {P,Q} \right) }{dP}=\frac{\partial G\left( {P,Q} \right) }{\partial P}+\frac{\partial G\left( {P,Q} \right) }{\partial Q}\cdot \frac{dQ}{dP} \end{aligned}$$
(10)

Based on the relationships of P and Q which revealed in Eqs. (3) and (8), term \(\frac{dQ}{dP}\) can be derived. Therefore, by giving an proper initial value \(P^{\left( 0 \right) }\), the convergence solution can be obtained.

3.2 Pseudo-arc-length continuation

Generally, the convergence of Newton-Rapson algorithm depends on the selection of initial value, the improper initial value will lead to faults of the algorithm, especially at the neighborhood of some bifurcation points such as saddle-node bifurcation points [26]. To overcome the limitation of the algorithm, a pseudo-arc-length continuation is embedded in the Newton-Rapson algorithm as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{\partial G}{\partial P}\frac{dP}{ds}+\frac{\partial G}{\partial \lambda }\frac{{\hbox {d}}\lambda }{{\hbox {d}}s}=0 \\ \frac{{\hbox {d}}P^{T}}{{\hbox {d}}s}\frac{{\hbox {d}}P}{{\hbox {d}}s}+\left( {\frac{{\hbox {d}}\lambda }{{\hbox {d}}s}} \right) ^{2}=1 \\ \end{array}} \right. \end{aligned}$$
(11)
Fig. 4
figure 4

Bifurcation diagram of center of disk \(q_{1}\)

Full size image
Fig. 5
figure 5

Frequency spectrogram, Poincare section and phase diagram of three different frequencies. a \(\lambda =4.01\), b \(\lambda =4.053\), c \(\lambda =4.147\)

Full size image

in which, \(\lambda =\frac{\Omega _1 }{\Omega _0 }\) is a variable of frequency, \(\Omega _0 \) is a constant selected for convenience. The new initial value can be estimated by:

$$\begin{aligned} \left[ {{\begin{array}{cc} {P^{\left( 1 \right) }}&{} {\lambda ^{\left( 1 \right) }} \\ \end{array} }} \right] ^\mathrm{T}=\left[ {{\begin{array}{cc} {P^{\left( 0 \right) }}&{} {\lambda ^{\left( 0 \right) }} \\ \end{array} }} \right] ^\mathrm{T}+\delta \left[ {{\begin{array}{cc} {\frac{dP}{ds}}&{} {\frac{d\lambda }{ds}} \\ \end{array} }} \right] ^\mathrm{T} \end{aligned}$$
(12)

where

$$\begin{aligned}&\left\{ {\begin{array}{l} \frac{dP_i }{ds}=\left( {-1} \right) ^{i}C\left( {P,\lambda } \right) \cdot \det \left[ {DH_{\left[ {-i} \right] } \left( {P,\lambda } \right) } \right] \\ \frac{d\lambda }{ds}=\left( {-1} \right) ^{N+1}C\left( {P,\lambda } \right) \cdot \det \left[ {DH_{\left[ {-\left( {N+1} \right) } \right] } \left( {P,\lambda } \right) } \right] \\ \end{array}} \right. \nonumber \\ \end{aligned}$$
(13)
$$\begin{aligned}&DH\left( {P,\lambda } \right) =\left[ {{\begin{array}{cc} {\frac{\partial G}{\partial P}}&{} {\frac{\partial G}{\partial \lambda }} \\ \end{array} }} \right] \end{aligned}$$
(14)
$$\begin{aligned}&C\left( {P,\lambda } \right) =\frac{\left( {-1} \right) ^{N+1}\mathrm{sgn}\left[ {G_P \left( {P^{\left( 0 \right) },\lambda ^{\left( 0 \right) }} \right) } \right] }{\sqrt{\mathop {\sum }\nolimits _{i=1}^{N+1} {\left( {\det \left[ {DH_{\left[ {-i} \right] } } \right] } \right) ^{2}} }} \end{aligned}$$
(15)

in which, the operator notation \(DH_{\left[ {-i} \right] } \) means matrix DH subtract by the i throw.

According to the new initial value \(\left[ {{\begin{array}{cc} {P^{\left( 1 \right) }}&{} {\lambda ^{\left( 1 \right) }} \\ \end{array} }} \right] ^\mathrm{T}\), the solution can be obtained by the iterative formula derived from Eq. (11) as follows:

$$\begin{aligned} \left[ {{\begin{array}{c} {P^{\left( {i+1} \right) }} \\ {\lambda ^{\left( {i+1} \right) }} \\ \end{array} }} \right]= & {} \left[ {{\begin{array}{c} {P^{\left( i \right) }} \\ {\lambda ^{\left( i \right) }} \\ \end{array} }} \right] -\left[ {{\begin{array}{cc} {G_P \left( {P^{\left( i \right) },\lambda ^{\left( i \right) }} \right) } &{} {G_\lambda \left( {P^{\left( i \right) },\lambda ^{\left( i \right) }} \right) } \\ {\frac{dP^{T}}{ds}}&{} {\frac{d\lambda }{ds}} \\ \end{array} }} \right] ^{-1}\nonumber \\&\cdot \left[ {{\begin{array}{c} {G\left( {P^{\left( i \right) },\lambda ^{\left( i \right) }} \right) } \\ {\frac{dP^{T}}{ds}\left( {P^{\left( i \right) }-P^{\left( 1 \right) }} \right) +\frac{d\lambda }{ds}\left( {\lambda ^{\left( i \right) }-\lambda ^{\left( 1 \right) }} \right) } \\ \end{array} }} \right] .\nonumber \\ \end{aligned}$$
(16)

3.3 Floquet stability analysis and Hsu’s method

The Floquet multipliers are useful indexes to reflect the stability of the system. If all the Floquet multipliers are within the unit circle in the complex plane, the period solution is stable, or else the period solution is unstable. There are three ways that a periodic solution loses stability [13]:

  1. (1)

    One of the multipliers cross the unit circle through (\(+1\), 0), the period solution loses stability by saddle-node bifurcation, or pitchfork bifurcation or symmetry-breaking bifurcation.

  2. (2)

    One of the multipliers cross the unit circle through (\(-1\), 0), the period solution loses stability by period-doubling bifurcation.

  3. (3)

    A pair of conjugate multipliers cross the unit circle, the period solution loses stability by secondary Hopf bifurcation.

Hsu [27] proposed a numerical scheme to obtain Floquet multipliers, which is carried out by discretizing one period into a number of intervals and multiplying constant coefficient matrices over each interval one by one. This scheme is used here, and its procedures are list as follows:

Firstly, rewrite the motion Eq. (2) into the state equation:

$$\begin{aligned}&U=\left[ {{\begin{array}{ccccc} {q_1 }&{{q}^{\prime }_1 }&\cdots&{q_8 }&{{q}^{\prime }_8 } \end{array} }} \right] ^\mathrm{T} \end{aligned}$$
(17)
$$\begin{aligned}&{U}^{\prime }\left( {\hat{{\tau }}} \right) =F\left( U \right) \end{aligned}$$
(18)

Then, deduce the perturbation equation about \(\Delta U\):

$$\begin{aligned} \left( {U^{*}\left( {\hat{{\tau }}} \right) +\Delta U} \right) ^{\prime }= & {} F\left( {\hat{{\tau }},U^{*}\left( {\hat{{\tau }}} \right) +\Delta U} \right) \end{aligned}$$
(19)
$$\begin{aligned} \Delta {U}^{\prime }= & {} \left. {\frac{\partial F\left( {\hat{{\tau }},U\left( {\hat{{\tau }}} \right) } \right) }{\partial U\left( {\hat{{\tau }}} \right) }} \right| _{U=U^{*}} \nonumber \\&\cdot \Delta U=A\left( {\hat{{\tau }},U^{*}\left( {\hat{{\tau }}} \right) } \right) \Delta U \end{aligned}$$
(20)

where \(U^{*}\left( {\hat{{\tau }}} \right) \) is the period solution, thus matrix A is a period matrix.

Finally, compute monodromy matrix D:

$$\begin{aligned} D= & {} \prod _{n=N}^1 {\exp \left( {\Delta T\cdot A\left( {U^{*}\left( {\hat{{\tau }}_n } \right) ,\hat{{\tau }}_n } \right) } \right) }\nonumber \\\approx & {} \prod _{n=N}^1 {\left( {I+\sum _j^{N_j } {\frac{\left( {\Delta T\cdot A\left( {U^{*}\left( {\hat{{\tau }}_n } \right) ,\hat{{\tau }}_n } \right) } \right) ^{j}}{j!}} } \right) } \end{aligned}$$
(21)

in which \(\Delta T=T/N\) represents the time interval, \(\hat{{\tau }}_n \) represents the end time of n th interval.

The eigenvalues of monodromy matrix D are the Floquet multipliers of the corresponding periodic solution.

Fig. 6
figure 6

Frequency–Amplitude curves of resonance region of the rigid body translation

Full size image
Table 2 Floquet multipliers nearby bifurcation point
Full size table
Fig. 7
figure 7

Amplitude curves for different response frequency components

Full size image
Fig. 8
figure 8

Amplitude curves for different response frequency components

Full size image
Fig. 9
figure 9

Frequency–amplitude curves of resonance region of first bending mode (\(\xi =1.3\))

Full size image
Table 3 Floquet multipliers nearby bifurcation point
Full size table
Fig. 10
figure 10

Poincare sections and phase diagrams of two periodic solutions and a quasi-periodic solution at \(\lambda =4.179\) (\(\xi =1.3\))

Full size image

4 Results and discussions

The numerical analysis is carried out by using both harmonic balance method and fourth order Runge-Kutta method. The physical parameters of the system are listed in Table 1.

4.1 Period solution and quasi-periodic solution

Choosing the maximal harmonic parameter \(M=5\) and constant frequency \(\varOmega _{0}=300\,\hbox { rad/s}\), the relationships between dimensionless amplitude and dimensionless frequency are shown in Fig. 2. It is clear that there are three pairs of resonant peaks in Fig. 2b from low frequency to high frequency, which are, respectively, corresponding to the vibration modes of rigid body translation and rigid body rotation, and the first bending mode. Each pair of peaks represents the resonant peaks excited by low-frequency \(\omega _{1}\) and high-frequency \(\omega _{2}\). The influence on the rigid body rotation is not obvious in Fig. 2a. Thus, the nonlinear characteristics of system are concentrated on the rigid body translation mode and the first bending mode. Moreover, the solutions from the harmonic balance method agree well with that from the Runge-Kutta method in most of the frequency region. The displacement responses of \(q_{1 }\) on two frequencies of resonant peaks \(\lambda =0.762\) and \(\lambda =4.013\) are shown in Fig. 3, which means the choice of harmonic parameter is applicable.

Besides, there is a region that two results are not fit nearby \(\lambda =4.2\). To explain the difference, the bifurcation diagram between \(\lambda =3.95\) and \(\lambda =4.30\) is shown in Fig. 4. Since there are two periods \(2\pi \) and \(2 \pi /\xi \) in this two-frequency excited system, the period \(2\nu \pi \) is chosen as the period of Poincare mapping to ensure the correctness of calculation. The integer \(\nu \) should satisfy the condition that \(\xi \nu \) is an integer, thus the period \(2\nu \pi \) can be a common period of the two excitations. Based on this definition, the meaning of Poincare section needs to be redefined: a single point means the periodic solutions contain all \(k\omega _{1}+l\omega _{2}\) frequencies, some independent points mean the solutions contain fractional ratio of \(k\omega _{1}+l\omega _{2}\) frequencies, and a closed circle means that there is a quasi-periodic solution which belongs to neither \(k\omega _{1}+l\omega _{2}\) nor their fractional ratio. It is clear to see the system gets into aperiodic motion at \(\lambda =4.02\), and the amplitude of the motion increase dramatically at \(\lambda =4.089\), finally at \(\lambda =4.27\), the motion returns back to periodic solution. The frequency spectrogram, Poincare section and phase diagram corresponding to the three motions are given in Fig. 5. In the case of \(\lambda =4.01\), the motion of the system is periodic, and the major response frequencies are dimensionless excitation frequencies \(\omega _{1}=1.00, \omega _{2}=1.30\) and their combined frequencies \(2 \omega _{1}-\omega _{2}=0.70\), \(3\omega _{1}-2 \omega _{2}=0.40\). In the case of \(\lambda =4.053\), besides the frequencies \(\omega _{1}\), \(\omega _{2}\) and their combined frequencies, there is a frequency \(\omega _{\mathrm{a}}=0.275\), which cannot be expressed as integral multiple combination of \(\omega _{1}\) and \(\omega _{2}\). The amplitude of \(\omega _{\mathrm{a}}\) is lower than that of \(\omega _{1}\) and \(\omega _{2}\), and the system motion is quasi-periodic motion with a low amplitude. Different from the former two, in the case of \(\lambda =4.147\), the dominating frequencies are no longer \(\omega _{1}\) and \(\omega _{2}\), but a new frequency \(\omega _{\mathrm{b}}=0.195\), which differs from \(\omega _{\mathrm{a}}\) and also cannot be expressed as integral multiple combination of excitation frequencies. And, the motion of system is a quasi-periodic motion with high amplitude, and a jump phenomenon, harmful to the safety of the system, occurs when the frequency \(\lambda \) increases. The difference of results obtained by harmonic balance method and Runge–Kutta method reflects the limitation of the harmonic balance method: since the frequency of quasi-periodic solution cannot be expressed by the assumptive frequencies \(k\omega _{1}+l\omega _{2}\), the difference of magnitude is caused by the amplitude value of quasi-periodic frequency component \(\omega _{\mathrm{a}}\) in Fig. 5(b-1) and \(\omega _{\mathrm{b}}\) in Fig. 5(c-1). More discussions about the relationship between periodic solution and quasi-periodic solution will be given in Sect. 4.3 in this paper.

Fig. 11
figure 11

Frequency–amplitude curves of resonance region with different frequency ratios. a \(\xi =1.25\), b \(\xi =1.28\), c \(\xi =1.30\), d \(\xi =1.33\). Straight line Harmonic balance (stable solution), Dashed line Harmonic balance (unstable solution), Opencircle Runge–Kutta (periodic solution), +Runge–Kutta (quasi-periodic solution)

Full size image
Fig. 12
figure 12

Frequency–amplitude curves of resonance region with ratio \(\xi =1.36\)

Full size image
Fig. 13
figure 13

Frequency spectrogram, Poincare section and phase diagram of two kinds of quasi-periodic solution at \(\lambda =4.25\) ( \(\xi =1.36\))

Full size image

4.2 Resonance region of rigid body translation mode

As mentioned before, the resonance of the rigid body translation is a region where the response amplitude is large and the nonlinear characteristic is outstanding. In Fig. 6, the two resonant peaks from left to right are corresponding to the primary resonant peaks caused by the high excitation frequency \(\omega _2 \) and the low excitation frequency \(\omega _1 \) respectively. The dotted line represents the unstable solution, and points A, B, C, D are saddle–node bifurcation points judged by Floquet multiplier, as listed in Table 2. The jump phenomenon will occur when the rotor speed goes up through point A, C or goes down through point B, D. The result is similar to that of rotor-SFD system with single excitation frequency [12]. Besides this nonlinear characteristic, the responses of the system also contain components of the two excitation frequencies and their combined frequencies, as shown in Fig. 7. It is clear to see that there are two dominating frequencies \(\omega _1 \) and \(\omega _2 \), corresponding to the two resonant peaks. When \(\lambda \) runs near 0.55, the resonant peak is aroused by the excitation of higher-frequency \(\omega _2 \), and with the increase in the frequency \(\omega _2 \), the amplitude of frequency component \(\omega _1 \) decreases; meanwhile, the amplitude of combined frequency \(2\omega _2 -\omega _1 \) ascends sharply to reach the magnitude of amplitude of frequency \(\omega _1 \). When \(\lambda \) goes near 0.75, the resonant peak is motivated by excitation of lower-frequency \(\omega _1 \), and with the increase in the frequency \(\omega _1 \), the amplitude of fundamental frequencies \(\omega _1 \), \(\omega _2 \) and combined frequency \(2\omega _1 -\omega _2 \) all increase. Out of the resonance region, the combined frequencies are all inconspicuous.

4.3 Resonance region of first bending mode

According to Fig. 2, the resonance region of first bending mode is another region which is worth analyzing the nonlinear characteristic. The response frequencies are shown in Fig. 8, it is obvious that the fundamental frequencies \(\omega _{1}\) and \(\omega _{2}\) are dominated and others combined frequencies are inconspicuous except frequencies \(2\omega _{1}- \omega _{2}\) and \(3\omega _{1}-2\omega _{2}\).

As mentioned in Sect. 4.1, there exists quasi-periodic solutions in the resonance region, and Fig. 9 shows the solutions obtained by harmonic balance method and Runge-Kutta method. The points A, B are second Hopf bifurcation points, and the points C, D are saddle-node bifurcation points which are judged by the Floquet multipliers listed in Table 3, thus there are two unstable regions A-B and C-D on the periodic solution branch. The independent quasi-periodic solution E-F exists in region from \(\lambda =4.040\) to \(\lambda =4.265\), coexisting with periodic solution, while quasi-periodic solution A-G comes from the unstable periodic solution. In the region between point C and point D, there are three solutions corresponded to one value of \(\lambda \), for instance, Fig. 10 shows the comparison of the three solutions at \(\lambda =4.179\), ordered by amplitude from low to high, the first two solutions are periodic solutions, but the third one is a quasi-periodic solution.

Fig. 14
figure 14

Frequency–amplitude curves of resonance region with ratio \(\xi =1.37\)

Full size image
Fig. 15
figure 15

Frequency–amplitude curves of resonance region with different parameters combination. a \(c=0.19\,\hbox { mm}\), \(\mu =1.562\times 10^{-2}\,\hbox { N s/m}^{ 2 }\), b \(c=0.18\,\hbox { mm}\), \(\mu =1.562\times 10^{-2}\,\hbox {Ns/m}^{ 2 }\), c \(c=0.20\,\hbox { mm}\), \(\mu =1.708\times 10^{-2}\,\hbox { Ns/m}^{ 2 }\), d \(c=0.20\,\hbox { mm}\), \(\mu =1.855\times 10^{-2}\,\hbox { Ns/m}^{ 2 }\). Straight line Harmonic balance (stable solution), Dashed line Harmonic balance (unstable solution), opencircle Runge-Kutta (periodic solution), +Runge-Kutta (quasi-periodic solution)

Full size image

The unstable solutions may lead to three different kinds of jump phenomena with the rotor speed going up or going down: between one quasi-periodic solution and another quasi-periodic solution, between quasi-periodic solution and periodic solution, and between two periodic solutions. When the rotor speed goes up through point A, the periodic solution loses stability entering the quasi-periodic motion, and with the increasing speed, the quasi-periodic motion on section A-G will jump up to the quasi-periodic section E-F, then jump down to the periodic solution. If the rotor speed goes up from point B, the periodic motion will go from point B to point C, and then jump up to another stable periodic solution with a small amplitude. When the rotor speed goes down, the periodic motion will jump down form point D and lose stability on point B resulting into periodic section E-F, the amplitude will become higher and higher until the computational divergence as the speed goes down. In this system, the resonant peak has the ‘soft stiffness’ characteristic, moreover, the multiple stable state solutions cause the large amplitude jump. The unstable section A-B is a main reason for the jump phenomenon, and the quasi-periodic solution E-F is an essential condition.

The unstable solution near the resonant peak of first bending mode was early reported by McLean and Hahn [28] in their study about a symmetry flexible rotor supported by squeeze film dampers under single excitation, and then Zhao [10] explained that the periodic solution loses stability through second Hopf bifurcation. In the study of single excitation system, Hussain [29] and Zhu [12], respectively, obtained the low amplitude quasi-periodic solution and the high amplitude quasi-periodic solution near the resonant peak of first bending mode, which are corresponding to the section AG and the section EF in this paper. Moreover, in this paper the resonant peak in the local figure of Fig. 9 forms a cross structure, and this characteristic was also reported in Zhu’s work [12], thus it is a basic characteristic of nonlinear system consisted of SFD and flexible rotor.

The nonlinear characteristic such as second Hopf bifurcation, quasi-periodic solution and cross structure in this paper also can be obtained in flexible rotor-squeeze film dampers system with single excitation system, and the bifurcation mechanism and the region of quasi-periodic solution are agreed with the other researchers’ results mentioned above.

4.4 Effect of parameters

The amplitude jump is a harmful effect on the system, and the unstable solution is an important factor of this phenomenon, so the effect of parameters on the unstable region should be analyzed.

Figure 11 shows the effect of ratio of excitation frequencies on unstable region and resonant peak. It is obvious that the quasi-periodic solution and unstable region are not distinct with the increase of the frequency ratio \(\xi \), but the resonant peak shows the irregular change between ‘soft spring characteristic’ (\(\xi =1.25, \xi =1.30, \xi =1.33\)) and a kind of ‘cross characteristic’ (\(\xi =1.28\)).

Moreover, as shown in Fig. 12, when \(\xi =1.36\), besides the unstable region A-B and quasi-periodic solution G-H mentioned above, there is another unstable region E-F with quasi-periodic solution J-K. The points A, B, E, F are secondary Hopf bifurcation points, and points C, D are saddle-node bifurcation points. The jump phenomenon can occur from periodic solution to quasi-periodic solution or from quasi-periodic solution to quasi-periodic solution. Figure 13 shows the comparison of the two kinds of quasi-periodic solutions at \(\lambda =4.25\), it is clear to see the differences in the frequency spectrograms (\(\omega _{\mathrm{m}}=0.195, \omega _{\mathrm{n}}=0.177\)), Poincare sections and phase diagrams.

Figure 14 shows an interesting result in the case of \(\xi =1.37\), there are still two kinds of quasi-periodic solutions, but unlike the results for \(\xi =1.36\), there are only two secondary Hopf bifurcation points C and D, and the unstable region at the left of resonant peak vanish. The resonant peak has the ‘hard spring characteristic’, but the periodic solution will jump from point A to the quasi-periodic solution E-F when the rotor speed goes up. Since the jump point A is beyond the unstable region C-D, the points B, C are saddle-node bifurcation points

The effects of the different ratios of excitation frequencies show abundant nonlinear phenomenon and multiple-solution conditions, and the system nonlinear characteristics are sensitive to the frequency ratio. The unstable solution caused by saddle-node bifurcation makes the cross structure of solution express the ‘soft’ or ‘cross’ characteristic: If the cross point is crossed by a unstable solution and a stable solution, the resonant peak has ‘soft’ characteristic; if the cross point is crossed by two stable solutions, the resonant peak has ‘cross’ characteristic. Moreover, the system also can express ‘hard’ characteristic in some other conditions.

The effects of clearance c and kinetic viscosity coefficient \(\mu \) under the same ratio \(\xi =1.3\) are shown in Fig. 15. Compared with Figs. 9 and 15a, b describe the effects of varying clearances on the system. The decrease of the clearance makes the cross structure vanish, makes the unstable region gradually disappear and leads to the periodic solutions of the region all be stable. Meanwhile, the quasi-periodic motions still exist, which may cause the jump phenomenon when the system receives some disturbance. Similarly, the increase in the viscosity can also attenuate the nonlinear characteristic as shown in Fig. 15c, d.

Summing up the above analysis, the basic nonlinear characteristic of flexible rotor combined with squeeze film damper under two-frequency excitations is similar to the system under single-frequency excitation, for instance, the jump phenomena and hard stiffness effect on the resonant peak of rigid body translation mode caused by saddle-node bifurcation, the jump phenomena nearby the resonant peak of the first bending mode caused by second Hopf bifurcation and independent quasi-periodic solution, and the cross structure on the resonant peak of the first bending mode caused by saddle-node bifurcation. The influence of SFD parameter is also similar to the single-frequency excitation system. However, the system with two-frequency excitations has its particular characteristic: The jump phenomena can exhibit different stiffness characteristics, i.e., ‘soft’, ‘cross’ and ‘hard’ due to different frequency ratio, and another unstable region and quasi-periodic solution could appear in certain frequency ratios; therefore, the frequency ratio is an important parameter in a two-frequency excited nonlinear system. Finally, the response of the combination frequencies is also a characteristic of two-frequency excited nonlinear system.

5 Conclusions

In this paper, the nonlinear characteristics of a flexible rotor with squeeze film damper excited by two-frequency excitation have been investigated via harmonic balance method and Runge-Kutta method. The nonlinear characteristics have been focused mainly on two resonance regions corresponding to the rigid body translation and first bending mode, respectively. It has been concluded that the responses in resonance region of rigid body translation perform jump phenomenon and show ‘hard spring’ nonlinear characteristic. Besides the excitation frequencies, the response contains primary combination frequencies of \(2\omega _{2}-\omega _{1}\) and \(2\omega _{1}-\omega _{2}\). The response in resonance region of first bending mode has abundant nonlinear characteristic, for instance, jump phenomena caused by saddle-node bifurcation, second Hopf bifurcation and quasi-periodic solution, and the response contains primary combination frequencies of \(2\omega _{1}- \omega _{2}\) and \(3\omega _{1}-2\omega _{2}\). The unstable solution caused by saddle-node bifurcation on the cross structure makes the resonant peak show ‘soft’ or ‘cross’ characteristics under different ratios of frequencies; moreover, the resonant peak also shows ‘hard’ characteristic in the case of \(\xi =1.37\). The unstable solution caused by secondary Hopf bifurcation makes the system perform quasi-periodic motions and jump up to other independent quasi-periodic motions with large amplitudes. In some conditions (\(\xi =1.36,\xi =1.37\)), there are two independent quasi-periodic solutions, the system shows more complex jump phenomenon. The number of unstable regions and the nonlinear characteristics are sensitive to the ratio of excitation frequencies. The decrease in clearance or increase in viscosity could attenuate the nonlinear characteristics of resonant peak. The results in the paper will contribute to a better understanding of the nonlinear dynamic behaviors of the SFD-rotor systems with two excitations and provide a theoretical foundation for optimization of the system parameters.