1 Introduction

Genetic regulatory networks (GRNs) are biologically dynamic systems which describe the interactions of genes in living cells. Many researches have been carried out, which aims at understanding the process of gene regulation and explaining the biological phenomena. Synthetic genetic networks have been designed and implemented to explore the interactions among genes [1].

Dynamic behaviors (such as stability, bifurcation, period oscillations and chaos) have been a significant research aspect which contributes to analyzing the biological functions. Many literatures have reported the dynamic properties of GRNs. Mathematically, equilibria exist when concentrations of the gene products are constants while bifurcations often occur when the equilibria are destabilized [2–4]. The period or amplitude of oscillations may change as biological parameters vary [5, 6]. Complex mechanisms of the gene expression can even induce chaos [7, 8]. Having a deep knowledge of the system dynamics contributes to the analysis and design of schemes in the fields of biology and control [9–12].

To inquire into the capability of genetic regulatory systems to take on complex dynamic activities, Smolen et al. [13] proposed a simple kinetic model which included autoregulation, positive and negative feedback loops of transcription factors (TFs). Concretely speaking, it can be described as one gene is an activator that activates the transcription of itself and that of the other. In turn, the latter represses the transcription of both of them [14]. The authors found that the genetic system manifested multiple steady states, and they studied the oscillatory regions by numerical simulations. As an easy-implemented genetic oscillator that is robust and period tunable, it receives much attention in engineering [15]. On the other hand, different mathematical models were also developed based on its topology architecture, and relevant works have been extensively done. Hasty et al. [16] developed a model and considered coupling the oscillator to a cellular process. They showed the amplification effect of protein oscillations by the oscillator. Liu and Jia [17] considered a stochastic model. In the case of correlated and uncorrelated noises, they investigated how fluctuations in the degradation rate and synthesis rate of TFs in a genetic system yielded switching processes. Since the research by Smolen et al. [18], some works have been done to deal with the model that incorporates delay. Stability and bifurcation analysis were carried out, and the delay-induced oscillations were studied [19–21]. Due to the features and advantages in the field of synthetic biology, the theoretical research based on the genetic circuit in [13] still develops forward.

Although quite a few results have been reported on the dynamics of GRNs, most of them are based on continuous-time models, and the dynamic analysis is mainly about stability, bifurcation or the resulting period solution [22]. Nevertheless, when a continuous-time model is implemented for computer simulation, it inevitably needs to be discretized [23]. Recently, there is an interest in the discrete-time dynamics analysis of biological systems [24, 25]. For example, the bifurcation and chaos have been studied in a discrete Ricardo–Malthus model [26]. The discrete-time version can retain biological function similarities and dynamic characteristics of the continuous-time model when the step size is small enough. In addition, it may also present new dynamics which is not observed in the continuous-time model [27]. Therefore, it is meaningful to consider the dynamics of discrete-time genetic regulatory networks (DGRNs). The fold bifurcation and flip bifurcation in a discrete genetic system were studied in [28], and it was shown that the system presented chaotic behaviors. The bifurcation conditions on the step size were derived. For a DGRN, when the true concentrations of gene products are not available, the observer needs to be designed to make an estimation [29]. Based on determined DGRN models, different stability conditions are derived [30–32]. When the delay is introduced, bifurcations may occur. In [33], the Neimark–Sacker bifurcation was investigated in a delayed DGRN. Choosing the delay as a bifurcation parameter, the authors derived the bifurcation condition and the properties of the bifurcating periodic solution. Most of these researches are about stability or onefold bifurcation, but more interesting dynamic phenomena such as diverse bifurcations and chaotic behaviors are not fully studied.

Motivated by the above discussions, a discrete-time genetic model that is established based on the topological structure first discussed in [13] is presented. Three bifurcations are investigated by using theories of bifurcation [34, 35] and center manifold [36]. Moreover, numerical simulations exhibit richer dynamics of the discrete-time model than that of the continuous-time model. This paper is organized as follows. In Sect. 2, the existence and stability of the fixed points of the genetic model are discussed. In Sect. 3, the parameter conditions under which fold bifurcation, flip bifurcation and Neimark–Sacker bifurcation occur are reported. In Sect. 4, numerical simulations are shown to illustrate our theoretical results and to exhibit rich dynamic behaviors such as period-7, -14, -5, -10 orbits and chaos. Finally, conclusion and discussion are given in Sect. 5.

2 Existence and stability of the positive fixed points

In this section, we shall first develop a mathematical model of a genetic regulatory network, whose schematic can be found in [13]. Here, protein concentrations are considered as the only variables. The dynamic relationships between two regulators are formulated as

$$\begin{aligned} {{\dot{p}}_1}( t )= & {} - {k_1}{p_1}( t ) + \frac{{{a_{11}}{{\left( {\frac{{{p_1}( t )}}{{{b_{11}}}}} \right) }^h} + {a_{12}}}}{{1 + {{\left( {\frac{{{p_1}( t )}}{{{b_{11}}}}} \right) }^h} + {{\left( {\frac{{{p_2}( t )}}{{{b_{12}}}}} \right) }^h}}},\nonumber \\ {{\dot{p}}_2}( t )= & {} - {k_2}{p_2}( t ) + \frac{{{a_{21}}{{\left( {\frac{{{p_1}(t)}}{{{b_{21}}}}} \right) }^h} + {a_{22}}}}{{1 + {{\left( {\frac{{{p_1}( t )}}{{{b_{21}}}}} \right) }^h} + {{\left( {\frac{{{p_2}( t )}}{{{b_{22}}}}} \right) }^h}}}, \end{aligned}$$
(2.1)

where \({p_i}\) denotes the concentration of protein i and \({k_i}\) stands for the degradation rate of it. \({a_{ij}}\) and \({b_{ij}}\) are transcription rate and transcription coefficient of protein j to gene i, respectively. h is the Hill coefficient. For specific analysis, we consider \(h=2, {a_{ii}} = {a_{ji}} = {a_{i}}\) and \({b_{ii}} = {b_{ji}} = {b_{i}}\) throughout this paper, which are general and rational premises [37]. It should be paid attention that \(i,j = 1,2\). The Hill coefficient \(h=2\) indicates that two monomers are needed to form a homodimer [38], and TFs regulate the transcription of a gene in the form of a homodimer. \(h=1\) and \(h > 2\) mean that TFs act in the form of a monomer and a multimer (the degree is larger than 2), respectively. Since homodimers (or dimers) are initially generated when TFs are polymerized, the homodimer is an elementary and essential form of TFs to regulate the gene expression.

For conciseness, we introduce the rescaled parameters

$$\begin{aligned}&\frac{{{p_1}( t )}}{{{b_1}}} = x( t ), \quad {\frac{{{p_2}( t )}}{{{b_2}}} = y( t ),}\\&\frac{{{a_1}}}{{{b_1}}} = {\alpha _1}, \quad {\frac{{{a_2}}}{{{b_1}}} = {\alpha _2},} \quad {\frac{{{b_1}}}{{{b_2}}} = \beta .} \end{aligned}$$

Then, system (2.1) can be rewritten as

$$\begin{aligned} \dot{x}( t )= & {} - {k_1}x( t ) + \frac{{{\alpha _1}{x^2}( t ) + {\alpha _2}}}{{1 + {x^2}( t ) + {y^2}( t )}},\nonumber \\ \dot{y}( t )= & {} - {k_2}y( t ) + \frac{{{\alpha _1}\beta {x^2}( t ) + {\alpha _2}\beta }}{{1 + {x^2}( t ) + {y^2}( t )}}, \end{aligned}$$
(2.2)

where x and y are transformed concentrations of node 1 and node 2. \({\alpha _1}\) and \({\alpha _2}\) are transformed synthesis rate affected by two nodes, respectively. \(\beta \) is a positive constant. \({k_1}\) and \({k_2}\) have the same meanings as those in (2.1). The above continuous-time model can be discretized to yield the corresponding discrete-time form. Applying the Euler method to system (2.2), we get the following formulations

$$\begin{aligned} x( {n + 1} )= & {} x( n ) - {k_1}\delta x( n ) + \frac{{\delta ( {{\alpha _1}{x^2}( n ) + {\alpha _2} } )}}{{1 + {x^2}(n) + {y^2}(n)}},\nonumber \\ y( {n + 1} )= & {} y( n ) - {k_2}\delta y( n ) + \frac{{\beta \delta ( {{\alpha _1}{x^2}( n ) + {\alpha _2} } )}}{{1 + {x^2}( n ) + {y^2}( n )}},\nonumber \\ \end{aligned}$$
(2.3)

where \(\delta \) is the discretization step size, x( n ) and y( n ) are approximate values of \(x( {n\delta } )\) and \(y( {n\delta } )\). Note that the above equation is not only an approximation of the original model but also a new dynamic system. It could reflect the dynamics of system (2.2) in some degree and may present new dynamic characteristics as well. In the following, we will consider the dynamics of system (2.3).

Suppose that \(E( {{x^{*}},{y^{*}}} )\) is a fixed point of system (2.3), it should satisfy

$$\begin{aligned} {{k_1}{x^{*}}=\frac{{{\alpha _1}{x^{{*^2}}} + {\alpha _2}}}{{1 + {x^{{*^2}}} + {y^{{*^2}}}}},} \quad {{y^{*}}= \frac{{\beta {k_1}}}{{{k_2}}}{x^{*}}.} \end{aligned}$$
(2.4)

Then, \({x^{*}}\) is a root of the following cubic function

$$\begin{aligned} f(z)= & {} {k_1}\left( 1 + {\left( \frac{{\beta {k_1}}}{{{k_2}}}\right) ^2}\right) {z^3} - {\alpha _1}{z^2}\nonumber \\&+\,{k_1}z-{\alpha _2}. \end{aligned}$$
(2.5)

To determine the number of fixed points, we define the related function and variables as

$$\begin{aligned} {\varphi ( {{\alpha _1}} )}= & {} \frac{{4{\alpha _2}\alpha _1^3 - k_1^2\alpha _1^2 - 18{\alpha _2}k_1^2\left( 1 + {{\left( {\frac{{\beta {k_1}}}{{{k_2}}}} \right) }^2} \right) {\alpha _1} + k_1^2\left( 1 + {{\left( {\frac{{\beta {k_1}}}{{{k_2}}}} \right) }^2} \right) \left[ 27\alpha _2^2\left( {\mathrm{{1}} + {{\left( {\frac{{\beta {k_1}}}{{{k_2}}}} \right) }^2}} \right) \mathrm{{ + 4}}k_1^2 \right] }}{{108k_1^4{{\left( 1 + {{\left( {\frac{{\beta {k_1}}}{{{k_2}}}} \right) }^2} \right) }^4}}},\\ p= & {} \frac{{3k_1^2\left( 1 + {{\left( {\frac{{\beta {k_1}}}{{{k_2}}}} \right) }^2} \right) - \alpha _1^2}}{{3k_1^2{{\left( 1 + {{\left( {\frac{{\beta {k_1}}}{{{k_2}}}} \right) }^2} \right) }^2}}}\quad \mathrm {and} \nonumber \\ q= & {} \frac{{ - 2\alpha _1^3 + 9k_1^2\left( {1 + {{\left( {\frac{{\beta {k_1}}}{{{k_2}}}} \right) }^2}} \right) {\alpha _1}} - 27{\alpha _2}k_1^2{{\left( {1 + {{\left( {\frac{{\beta {k_1}}}{{{k_2}}}} \right) }^2}} \right) }^2} }{{27k_1^3{{\left( {1 + {{\left( {\frac{{\beta {k_1}}}{{{k_2}}}} \right) }^2}} \right) }^3}}}.\nonumber \end{aligned}$$
(2.6)

In view of the biochemical mechanism, we only consider the positive roots of Eq. (2.5). We denote \({\varphi ( {{\alpha _1}} )}\) by \(\varphi \) for simplicity. Based on the Cardan formula [39] and the above expressions, the results about the existence and number of the positive fixed points are explicitly given.

Lemma 2.1

  1. (i)

    If \(\varphi > 0\), or \(\varphi = 0\) and \(p,q = 0,\) then system (2.3) has a unique positive fixed point \({E_{11}}( {x_{11}^{*},y_{11}^{*}})\), where \(x_{11}^{*} = \frac{{{\alpha _1}}}{{3{k_1}\left( {1 + {{\left( {\frac{{\beta {k_1}}}{{{k_2}}}} \right) }^2}} \right) }} + \root 3 \of {{ - \frac{q}{2} + \sqrt{\varphi }}} + \root 3 \of {{ - \frac{q}{2} - \sqrt{\varphi }}}\);

  1. (ii)

    if \(\varphi = 0, p < 0\) and \(q \ne 0,\) then system (2.3) has two positive fixed points \({E_{21}}( {x_{21}^{*},y_{21}^{*}} )\) and \({E_{22}}( {x_{22}^{*},y_{22}^{*}} )\), where \(x_{21}^{*} = \frac{{{\alpha _1}}}{{3{k_1}\left( 1 + {{\left( \frac{{\beta {k_1}}}{{{k_2}}}\right) }^2}\right) }} - 2\root 3 \of {{\frac{q}{2}}}, x_{22}^{*} = \frac{{{\alpha _1}}}{{3{k_1}\left( {1 + {{\left( {\frac{{\beta {k_1}}}{{{k_2}}}} \right) }^2}} \right) }} + \root 3 \of {{\frac{q}{2}}};\)

  2. (iii)

    if \(\varphi < 0,\) then system (2.3) has three positive fixed points \({E_{31}}( {x_{31}^{*},y_{31}^{*}} ), {E_{32}}( {x_{32}^{*},y_{32}^{*}} )\) and \({E_{33}}( {x_{33}^{*},y_{33}^{*}} )\), where \(x_{31}^{*}< x_{32}^{*} < x_{33}^{*}.\)

Remark 2.1

From Eq. (2.4), we know that \(E( {{x^{*}},{y^{*}}} )\) is an equilibrium of continuous system (2.2) if and only if it is a fixed point of discrete system (2.3). Thus, Lemma 2.1 also gives the existence conditions of the equilibria of system (2.2).

It is noted that when \(\varphi > 0, x_{11}^{*}\) is a simple root of Eq. (2.5). When \(\varphi = 0\) and \(p,q = 0,\) it is a triple root. We only consider the first case in the context below. For an arbitrary positive fixed point \(E( {{x^{*}},{y^{*}}} )\), the Jacobian matrix of system (2.3) is

$$\begin{aligned}&J({x^{*}},{y^{*}})\\&\quad = \left( {\begin{array}{cc} {1 - {k_1}\delta + \frac{{2\delta {x^{*}}\left( {\alpha _1} + {\alpha _1}{y^{{*^2}}} - {\alpha _2}\right) }}{{{{\left( 1 + {x^{{*^2}}} + {y^{{*^2}}}\right) }^2}}}}&{}{ - \frac{{2\delta {y^{*}}\left( {\alpha _1}{x^{{*^2}}} + {\alpha _2}\right) }}{{{{\left( 1 + {x^{{*^2}}} + {y^{{*^2}}}\right) }^2}}}}\\ {\frac{{2\delta \beta {x^{*}}\left( {\alpha _1} + {\alpha _1}{y^{{*^2}}} - {\alpha _2}\right) }}{{{{\left( 1 + {x^{{*^2}}} + {y^{{*^2}}}\right) }^2}}}}&{}{1 - {k_2}\delta - \frac{{2\delta \beta {y^{*}}\left( {\alpha _1}{x^{{*^2}}} + {\alpha _2}\right) }}{{{{\left( 1 + {x^{{*^2}}} + {y^{{*^2}}}\right) }^2}}}} \end{array}} \right) . \end{aligned}$$

Correspondingly, the characteristic equation can be expressed as

$$\begin{aligned} {\lambda ^2} + {R_1}\lambda + {R_2} = 0, \end{aligned}$$
(2.7)

where

$$\begin{aligned} {R_1}= & {} \delta \left[ {k_1} + {k_2} - \frac{{2{x^{*}}\left( {{\alpha _1} + {\alpha _1}{y^{{*^2}}} - {\alpha _2}} \right) }}{{{{\left( {1 + {x^{{*^2}}} + {y^{{*^2}}}} \right) }^2}}} \right. \\&\left. + \frac{{2\beta {y^{*}}\left( {{\alpha _1}{x^{{*^2}}} + {\alpha _2}} \right) }}{{{{\left( {1 + {x^{{*^2}}} + {y^{{*^2}}}} \right) }^2}}} \right] - 2, \\ {R_2}= & {} {\delta ^2}\left[ {k_1}{k_2} + \frac{{2\beta {k_1}{y^{*}}\left( {{\alpha _1}{x^{{*^2}}} + {\alpha _2}} \right) }}{{{{\left( {1 + {x^{{*^2}}} + {y^{{*^2}}}} \right) }^2}}}\right. \\&\left. - \frac{{2{k_2}{x^{*}}\left( {{\alpha _1} + {\alpha _1}{y^{{*^2}}} - {\alpha _2}} \right) }}{{{{\left( {1 + {x^{{*^2}}} + {y^{{*^2}}}} \right) }^2}}} \right] \\&- \delta \left[ {{k_1} + {k_2} - \frac{{2{x^{*}}\left( {{\alpha _1} + {\alpha _1}{y^{{*^2}}} - {\alpha _2}} \right) }}{{{{\left( {1 + {x^{{*^2}}} + {y^{{*^2}}}} \right) }^2}}}} \right. \\&\left. { + \frac{{2\beta {y^{*}}\left( {{\alpha _1}{x^{{*^2}}} + {\alpha _2}} \right) }}{{{{\left( {1 + {x^{{*^2}}} + {y^{{*^2}}}} \right) }^2}}}} \right] + 1. \end{aligned}$$

Let

$$\begin{aligned} {S_1}= & {} {k_1} + {k_2} - \frac{{2{x^{*}}\left( {{\alpha _1} + {\alpha _1}{y^{{*^2}}} - {\alpha _2}} \right) }}{{{{\left( {1 + {x^{{*^2}}} + {y^{{*^2}}}} \right) }^2}}}\\&+ \frac{{2\beta {y^{*}}\left( {{\alpha _1}{x^{{*^2}}} + {\alpha _2}} \right) }}{{{{\left( {1 + {x^{{*^2}}} + {y^{{*^2}}}} \right) }^2}}},\\ {S_2}= & {} {k_1}{k_2} + \frac{{2\beta {k_1}{y^{*}}\left( {{\alpha _1}{x^{{*^2}}} + {\alpha _2}} \right) }}{{{{\left( {1 + {x^{{*^2}}} + {y^{{*^2}}}} \right) }^2}}} \\&- \frac{{2{k_2}{x^{*}}\left( {{\alpha _1} + {\alpha _1}{y^{{*^2}}} - {\alpha _2}} \right) }}{{{{\left( {1 + {x^{{*^2}}} + {y^{{*^2}}}} \right) }^2}}}. \end{aligned}$$

Then, Eq. (2.7) can be rewritten as

$$\begin{aligned} {\lambda ^2} + ({S_1}\delta - 2)\lambda + {S_2}{\delta ^2} - {S_1}\delta + 1 = 0. \end{aligned}$$

Based on Eq. (2.4), we have

$$\begin{aligned} {S_2}= & {} \frac{{{k_1}{k_2}{{\left( {1 + {x^{{*^2}}} + {y^{{*^2}}}} \right) }^2} + 2\frac{{{{( {\beta {k_1}} )}^2}}}{{{k_2}}}{x^{*}}\left( {{\alpha _1}{x^{{*^2}}} + {\alpha _2}} \right) - 2{k_2}{x^{*}}\left[ {{\alpha _1}\left( {1 + {x^{{*^2}}} + {y^{{*^2}}}} \right) - \left( {{\alpha _1}{x^{{*^2}}} + {\alpha _2}} \right) } \right] }}{{{{\left( {1 + {x^{{*^2}}} + {y^{{*^2}}}} \right) }^2}}}\\= & {} \frac{{{k_2}\left[ {{k_1}{{\left( {1 + {x^{{*^2}}} + {y^{{*^2}}}} \right) }^2} + 2{k_1}{{\left( {\frac{{\beta {k_1}}}{{{k_2}}}} \right) }^2}{x^{{*^2}}}\left( {1 + {x^{{*^2}}} + {y^{{*^2}}}} \right) - 2{x^{*}}\left( {{\alpha _1} - {k_1}{x^{*}}} \right) \left( {1 + {x^{{*^2}}} + {y^{{*^2}}}} \right) } \right] }}{{{{\left( {1 + {x^{{*^2}}} + {y^{{*^2}}}} \right) }^2}}} \\= & {} \frac{{{k_2}\left\{ {{k_1}\left[ {1 + \left( {1 + {{\left( {\frac{{\beta {k_1}}}{{{k_2}}}} \right) }^2}} \right) {x^{{*^2}}}} \right] + 2{k_1}{{\left( {\frac{{\beta {k_1}}}{{{k_2}}}} \right) }^2}{x^{{*^2}}} - 2{x^{*}}\left( {{\alpha _1} - {k_1}{x^{*}}} \right) } \right\} }}{{1 + \left( {1 + {{\left( {\frac{{\beta {k_1}}}{{{k_2}}}} \right) }^2}} \right) {x^{{*^2}}}}} \\= & {} \frac{{{k_2}\left[ {3{k_1}\left( {1 + {{\left( {\frac{{\beta {k_1}}}{{{k_2}}}} \right) }^2}} \right) {x^{{*^2}}} - 2{\alpha _1}{x^{*}} + {k_1}} \right] }}{{1 + \left( {1 + {{\left( {\frac{{\beta {k_1}}}{{{k_2}}}} \right) }^2}} \right) {x^{{*^2}}}}}. \end{aligned}$$

From Eq. (2.5), one has \({S_2} = \frac{{{k_2}f^{\prime }({x^{*}})}}{{1 + \left( {1 + {{\left( {\frac{{\beta {k_1}}}{{{k_2}}}} \right) }^2}} \right) {x^{{*^2}}}}}\). Denote that \(\Delta (\lambda ) = {\lambda ^2} + ({S_1}\delta - 2)\lambda + {S_2}{\delta ^2} - {S_1}\delta + 1.\) It is obvious that \(\Delta ( 1 ) = {S_2}{\delta ^2}, \Delta ( -1 ) ={S_2}{\delta ^2} - 2{S_1}\delta + 4\). From the geometric properties of \(f^{\prime }( z )\), we have \({S_2} > 0\) for the fixed points \({E_{11}}\left( {x_{11}^{*},y_{11}^{*}} \right) , {E_{21}}\left( {x_{21}^{*},y_{21}^{*}}\right) , {E_{31}}\left( {x_{31}^{*},y_{31}^{*}} \right) \) and \({E_{33}}\left( {x_{33}^{*},y_{33}^{*}} \right) \). For \({E_{22}}\left( {x_{22}^{*},y_{22}^{*}} \right) \) and \({E_{32}}\left( {x_{32}^{*},y_{32}^{*}} \right) \), we have \({S_2} = 0\) and \({S_2} < 0\), respectively. Then, \(\Delta ( 1 ) = 0\) and \(\Delta ( 1 ) < 0\) hold for the fixed points \({E_{22}}\left( {x_{22}^{*},y_{22}^{*}} \right) \) and \({E_{32}}\left( {x_{32}^{*},y_{32}^{*}} \right) \). One has \(\Delta ( 1 ) > 0\) for other fixed points. Thus, one of the eigenvalues at the fixed point \({E_{22}}\left( {x_{22}^{*},y_{22}^{*}}\right) \) is 1, which indicates that \({E_{22}}\left( {x_{22}^{*},y_{22}^{*}}\right) \) may be a saddle-node fixed point. As to the fixed point \({E_{32}}\left( {x_{32}^{*},y_{32}^{*}}\right) \), when \(\Delta ( -1 ) = 0\), system (2.3) may present a flip bifurcation there.

Based on Lemma 2.2 in [40], we discuss the stability of the fixed points which satisfy \({S_2} \ge 0\). When \({S_2} > 0\) and \({S_1} \le 0\), we have \(\Delta ( -1 )>0\), which indicates that \(\left| {{\lambda _1}} \right| > 1\) and \(\left| {{\lambda _2}} \right| > 1\). It is shown that none of these fixed points is stable. Hence, it is stable only when \({S_1} > 0\). In the following, we give the local dynamic analysis.

Lemma 2.2

Let \(E( {{x^{*}},{y^{*}}} )\) be a fixed point of system (2.3),

  1. (i)

    It is locally asymptotically stable if one of the following conditions holds:

  2. (i1)

    \({S_2} > 0, 2\sqrt{S_2} < {S_1}\) and \(0< \delta < \frac{{{S_1} - \sqrt{{{S_1}^2} - 4{S_2}} }}{{S_2}};\)

  3. (i2)

    \({S_2} > 0, 0 < {S_1} \le 2\sqrt{{S_2}}\) and \( 0< \delta < \frac{{S_1}}{{S_2}};\)

  4. (ii)

    It is unstable if one of the following conditions holds:

  5. (ii1)

    \({S_2} > 0, {S_1} \le 0;\)

  6. (ii2)

    \({S_2} > 0, 2\sqrt{S_2} < {S_1}\) and \(\frac{{{S_1} - \sqrt{{{S_1}^2} - 4{S_2}} }}{{S_2}}< \delta < \frac{{{S_1} + \sqrt{{{S_1}^2} - 4{S_2}} }}{{S_2}}\) or \(\delta > \frac{{{S_1} + \sqrt{{{S_1}^2} - 4{S_2}} }}{{S_2}};\)

  7. (ii3)

    \({S_2} > 0, 0 < {S_1} \le 2\sqrt{{S_2}}\) and \(\delta > \frac{{S_1}}{{S_2}};\)

  8. (iii)

    It may undergo a bifurcation if one of the following conditions holds:

  9. (iii1)

    \({S_2} = 0, {S_1} \ne 0\) and \( {S_1} \ne \frac{{2}}{{\delta }}\);

  10. (iii2)

    \({S_2} > 0, 2\sqrt{S_2} < {S_1}, \delta = \frac{{{S_1} \pm \sqrt{{{S_1}^2} - 4{S_2}} }}{{S_2}}\) and \(\delta \ne \frac{2}{{S_1}},\frac{4}{{S_1}}\);

  11. (iii3)

    \({S_2} > 0, 0< {S_1} < 2\sqrt{{S_2}}\) and \(\delta = \frac{{S_1}}{{S_2}}\).

Remark 2.2

It is known that in continuous system (2.2), if both eigenvalues have negative real parts, the equilibrium is locally asymptotically stable. Lemma 2.2 indicates the difference of local stability between the equilibria in system (2.2) and the fixed points in system (2.3). Moreover, a saddle-node bifurcation occurs in system (2.2) when the system has a simple eigenvalue 0, and a Hopf bifurcation may appear when the system has a pair of simple pure imaginary eigenvalues. Thus, Lemma 2.2 also implies the differentia of bifurcations between system (2.2) and system (2.3).

3 Bifurcation analysis

In this section, we shall analyze the fold bifurcation, flip bifurcation and Neimark–Sacker bifurcation of system (2.3). Parameter conditions under which bifurcations occur are derived by using theories of bifurcation and center manifold.

Based on the analysis in the above section, we first consider the fold bifurcation at the fixed point \({E_{22}}\left( x_{22}^{*},y_{22}^{*}\right) \) and take \({\alpha _1}\) as a bifurcation parameter. Since \(x_{22}^{*}\) is a root of Eq. (2.5), we should guarantee that \({\alpha _1}\) satisfies (ii) of Lemma 2.1, from which the critical bifurcation value of \({\alpha _1}\) can be computed. The explicit conditions of \({\alpha _1}\) will be derived.

Let

$$\begin{aligned} \phi= & {} \frac{{k_1^4\left( {1 + {{\left( {\frac{{\beta {k_1}}}{{{k_2}}}} \right) }^2}} \right) {{\left[ {27\alpha _2^2\left( {1 + {{\left( {\frac{{\beta {k_1}}}{{{k_2}}}} \right) }^2}} \right) - k_1^2} \right] }^3}}}{{1728\alpha _2^4}}, \\ g= & {} \frac{{k_1^2\left[ {5832\alpha _2^4{{\left( {1 + {{\left( {\frac{{\beta {k_1}}}{{{k_2}}}} \right) }^2}} \right) }^2} + 540\alpha _2^2k_1^2\left( {1 + {{\left( {\frac{{\beta {k_1}}}{{{k_2}}}} \right) }^2}} \right) - k_1^4} \right] }}{{864\alpha _2^3}}. \end{aligned}$$

From \(\varphi ^{\prime }({\alpha _1}) = \frac{{6{\alpha _2}\alpha _1^2 - k_1^2{\alpha _1} - 9{\alpha _2}k_1^2\left( {1 + {{\left( {\frac{{\beta {k_1}}}{{{k_2}}}}\right) }^2}}\right) }}{{54k_1^4{{\left( {1 + {{\left( {\frac{{\beta {k_1}}}{{{k_2}}}} \right) }^2}} \right) }^4}}},\) we have \(\varphi ^{\prime }({0}) =- \frac{{{\alpha _2}}}{{6k_1^2{{\left( {1 + {{\left( {\frac{{\beta {k_1}}}{{{k_2}}}}\right) }^2}}\right) }^3}}} <0\). \(\varphi \) first increases and then decreases in the left half plane of the rectangular coordinate system, and it has opposite monotonicities in the right half plane. Based on the variation of \(\varphi \), we can analyze the critical value of \({\alpha _1}\). In view of the biological meaning, we only focus on the positive values. When \(\phi > 0\), Eq. (2.6) has a unique negative root. When \(\phi = 0\) and \(g \ne 0,\) Eq. (2.6) has two real roots, one of which is positive and the other is negative. The positive one is a double root, and it is denoted by

$$\begin{aligned} {\alpha _{{1_{11}}}} = \frac{{k_1^2}}{{12{\alpha _2}}} + \root 3 \of {{\frac{g}{2}}}. \end{aligned}$$
(3.1)

When \(\phi < 0,\) Eq. (2.6) has three real roots, two of which are positive and another is negative. For convenience, we define \({e_1} = {\mathrm{Re}} \left( {\root 3 \of {{ - \frac{g}{2} + i\sqrt{ - \phi } }}} \right) , {e_2} = {\mathrm{Im}} \left( {\root 3 \of {{ - \frac{g}{2} + i\sqrt{ - \phi } }}} \right) \ne 0\). Then, three roots are denoted by \({r_1} = \frac{{k_1^2}}{{12{\alpha _2}}} + 2{e_1}, {r_2} = \frac{{k_1^2}}{{12{\alpha _2}}} - {e_1} - \sqrt{3} {e_2}\) and \({r_3} = \frac{{k_1^2}}{{12{\alpha _2}}} - {e_1} + \sqrt{3} {e_2}\). We define two sets \({D_1} = \{ {i_1}:{i_1} = \arg {\mathop {\max }\nolimits _{{\bar{i}} \in \left\{ {1,2,3} \right\} }} {r_{\bar{i}}}\},\) \({D_2} = \{ {i_2}:{i_2} = \arg {\mathop {\min }\nolimits _{{\bar{i}} \in \left\{ {1,2,3} \right\} }} {r_{\bar{i}}}\}\). Since three roots are not equal to each other, \({D_1}\) and \({D_2}\) both contain a unique element which can be simply denoted as \(i_1\) and \(i_2\), respectively. Let \({i_3} = 6 - {i_1} - {i_2}\). Two values of \({\alpha _1}\) are given by

$$\begin{aligned} {\alpha _{{1_{21}}}}= & {} {r_{{i_1}}},\end{aligned}$$
(3.2)
$$\begin{aligned} {\alpha _{{1_{22}}}}= & {} {r_{{i_3}}}. \end{aligned}$$
(3.3)

In order to avoid confusion, we use \({\bar{\alpha }_1}\) to replace \({\alpha _{{1_{11}}}}, {\alpha _{{1_{21}}}}\) and \({\alpha _{{1_{22}}}}\). From (ii) of Lemma 2.1, we also require

$$\begin{aligned}&{\bar{\alpha }_1} > {k_1}\sqrt{3\left( 1 + {{\left( \frac{{\beta {k_1}}}{{{k_2}}}\right) }^2}\right) },\end{aligned}$$
(3.4)
$$\begin{aligned}&2\bar{\alpha }_1^3 - 9k_1^2\left( 1 + {\left( \frac{{\beta {k_1}}}{{{k_2}}}\right) ^2}\right) {\bar{\alpha }_1} \nonumber \\&\quad +\,27{\alpha _2}k_1^2{\left( 1 + {\left( \frac{{\beta {k_1}}}{{{k_2}}}\right) ^2}\right) ^2}\ne 0. \end{aligned}$$
(3.5)

Let \({\alpha _1}={\bar{\alpha }_1}\), system (2.3) can be described as

$$\begin{aligned} \left( {\begin{array}{c} x\\ y \end{array}} \right) \mapsto \left( {\begin{array}{c} x-\delta {k_1}x+\frac{{\delta \left( {{{\bar{\alpha }}_1}{x^2} + {\alpha _2}}\right) }}{{1+{x^2}+{y^2}}}\\ y-\delta {k_2}y + \frac{{\delta \beta \left( {{{\bar{\alpha }}_1}{x^2} + {\alpha _2}}\right) }}{{1 + {x^2} + {y^2}}} \end{array}} \right) . \end{aligned}$$
(3.6)

Then, the eigenvalues of system (3.6) at the fixed point \({E_{22}}\left( {x_{22}^{*},y_{22}^{*}}\right) \) are \({\lambda _1}=1,{{\lambda _2}=1-{S_1}\delta }\). The condition (iii1) in Lemma 2.2 is equivalent to \(\left| {{\lambda _2}} \right| \ne 1\), and it leads to

$$\begin{aligned} {\bar{\alpha }_1}\ne & {} \frac{{( {{k_1} + {k_2}} )\left( {1 + x_{22}^{{*^2}} + y_{22}^{{*^2}}}\right) }}{{2x_{22}^{*}}}\nonumber \\&+\,{k_1}\left( {x_{22}^{*}+ \beta y_{22}^{*}}\right) \end{aligned}$$
(3.7)

and

$$\begin{aligned} {\bar{\alpha }_1} \ne \frac{{\left( {1 + x_{22}^{{*^2}} + y_{22}^{{*^2}}} \right) \left[ {( {{k_1} + {k_2}} )\delta - 2} \right] + 2\delta {k_1}x_{22}^{*}\left( {x_{22}^{*} + \beta y_{22}^{*}}\right) }}{{2\delta x_{22}^{*}}}.\nonumber \\ \end{aligned}$$
(3.8)

Remark 3.1

Conditions (3.1)–(3.5) ensure the existence of the fixed point \({E_{22}}\left( {x_{22}^{*},y_{22}^{*}}\right) \). In (3.7) and (3.8), it seems that \({\bar{\alpha }_1}\) is related to \({E_{22}}\left( {x_{22}^{*},y_{22}^{*}}\right) \). Nevertheless, since \({x_{22}^{*}}\) is a root of Eq. (2.5), it actually means that (3.7) and (3.8) are conditions on biological parameters.

Let \(X = x - x_{22}^{*}, Y = y - y_{22}^{*}\) and \(\alpha _1^{*} = {\alpha _1}-{\bar{\alpha }_1}\), where \(\alpha _1^{*} \) is a new dependent variable. We shift the fixed point \({E_{22}}\left( x_{22}^{*},y_{22}^{*}\right) \) to the origin and expand the right-hand side of system (2.3) in Taylor series; then, system (2.3) becomes

(3.9)

where

$$\begin{aligned}&{c_{11}} = 1 - {k_1}\delta + \frac{{2\delta x_{22}^{*}\left( {{{\bar{\alpha }}_1} + {{\bar{\alpha }}_1}y_{22}^{{*^2}} - {\alpha _2}} \right) }}{{{{\left( {1 + x_{22}^{{*^2}} + y_{22}^{{*^2}}} \right) }^2}}}, \\&{c_{12}} = \frac{{\delta x_{22}^{{*^2}}}}{{1 + x_{22}^{{*^2}} + y_{22}^{{*^2}}}}, \\&{c_{13}} = - \frac{{2\delta y_{22}^{*}\left( {{{\bar{\alpha }}_1}x_{22}^{{*^2}} + {\alpha _2}} \right) }}{{{{\left( {1 + x_{22}^{{*^2}} + y_{22}^{{*^2}}} \right) }^2}}},\\&{c_{31}} = \frac{{2\delta \beta x_{22}^{*}\left( {{{\bar{\alpha }}_1} + {{\bar{\alpha }}_1}y_{22}^{{*^2}} - {\alpha _2}} \right) }}{{{{\left( {1 + x_{22}^{{*^2}} + y_{22}^{{*^2}}} \right) }^2}}}, \\&{c_{32}} = \frac{{\delta \beta x_{22}^{{*^2}}}}{{1 + x_{22}^{{*^2}} + y_{22}^{{*^2}}}}, \\&{c_{33}} = 1 - {k_2}\delta - \frac{{2\delta \beta y_{22}^{*}\left( {{{\bar{\alpha }}_1}x_{22}^{{*^2}} + {\alpha _2}} \right) }}{{{{\left( {1 + x_{22}^{{*^2}} + y_{22}^{{*^2}}} \right) }^2}}}, \end{aligned}$$
$$\begin{aligned} F\left( {X,\alpha _1^{*},Y} \right)= & {} {u_{200}}{X^2} + {u_{101}}XY + {u_{110}}X\alpha _1^{*} \\&+\, {u_{002}}{Y^2} + {u_{011}}Y\alpha _1^{*} + {u_{300}}{X^3} \\&+\, {u_{201}}{X^2}Y + {u_{210}}{X^2}\alpha _1^{*} + {u_{102}}X{Y^2}\\&+\, {u_{111}}XY\alpha _1^{*} + {u_{003}}{Y^3} + {u_{012}}{Y^2}\alpha _1^{*}\\&+\, O\left( {{{\left( {\left| {{X}} \right| + \left| {\alpha _1^{*}} \right| + \left| {{Y}} \right| }\right) }^4}} \right) , \end{aligned}$$

and \({u_{200}}, {u_{101}}, {u_{110}}, {u_{002}}, {u_{011}}, {u_{300}}, {u_{201}}, {u_{210}}, {u_{102}}\), \({u_{111}}, {u_{003}}, {u_{012}}\) are given in “Appendix”.

From the expressions in system (3.9), we have \({c_{32}}( {1 - {c_{11}}} ) + {c_{31}}{c_{12}} = \frac{{\beta {k_1}{\delta ^2}x_{22}^{{*^2}}}}{{1 + x_{22}^{{*^2}} + y_{22}^{{*^2}}}} > 0\) and \({S_1}\delta =2-{c_{11}}-{c_{33}}\), which leads to \({\lambda _2} = {c_{11}}+{c_{33}}-1\). From \({\lambda _1} = 1,\) one gets \({c_{13}}{c_{31}} - ( {1 - {c_{11}}} )( {1 - {c_{33}}} ) = 0.\) If \({c_{11}} \ne 1,\) we can define an invertible matrix

$$\begin{aligned} {T_1} = \left( {\begin{array}{ccc} c_{13}&{}{\frac{{{c_{12}}( {1 - {\lambda _2}} )}}{{{c_{32}}(1 - {c_{11}}) + {c_{31}}{c_{12}}}}}&{}c_{13}\\ 0&{}{\frac{{( {1 - {\lambda _2}} )( {1 - {c_{11}}} )}}{{{c_{32}}( {1 - {c_{11}}} ) + {c_{31}}{c_{12}}}}}&{}0\\ 1-c_{11}&{}1&{}\lambda _{2}-c_{11} \end{array}} \right) . \end{aligned}$$

Under the transformation

$$\begin{aligned} \left( \begin{array}{l} X\\ \alpha _1^{*}\\ Y \end{array} \right) = {T_1}\left( \begin{array}{l} {X_1}\\ \hat{\alpha } _1^{*}\\ {Y_1} \end{array} \right) , \end{aligned}$$

system (3.9) becomes

$$\begin{aligned} \left( \begin{array}{l} {X_1}\\ \hat{\alpha } _1^{*}\\ {Y_1} \end{array} \right)\mapsto & {} \left( {\begin{array}{ccc} 1&{}1&{}0\\ 0&{}1&{}0\\ 0&{}0&{}{{\lambda _2}} \end{array}} \right) \left( \begin{array}{l} {X_1}\\ \hat{\alpha } _1^{*}\\ {Y_1} \end{array} \right) \nonumber \\&+\,\left( {\begin{array}{c} {\frac{{( {{\lambda _2} - {c_{11}} - \beta {c_{13}}} )\tilde{F}\left( {X_1},\hat{\alpha } _1^{*},{Y_1}\right) }}{{{c_{13}}( {{\lambda _2} - 1} ){{\left( {1 + x_{22}^{{*^2}} + y_{22}^{{*^2}}} \right) }^3}}}}\\ 0\\ {\frac{{( {{c_{11}} - 1 + \beta {c_{13}}} )\tilde{F}\left( {X_1},\hat{\alpha } _1^{*},{Y_1}\right) }}{{{c_{13}}( {{\lambda _2} - 1} ){{\left( {1 + x_{22}^{{*^2}} + y_{22}^{{*^2}}} \right) }^3}}}} \end{array}} \right) , \end{aligned}$$
(3.10)

where

$$\begin{aligned}&\tilde{F}\left( {{X_1},\hat{\alpha } _1^{*},{Y_1}} \right) = F\left( {X,\alpha _1^{*},Y} \right) , \nonumber \\&X = {c_{13}}( {{X_1} + {Y_1}} ) + \frac{{{c_{12}}( {1 - {\lambda _2}} )\hat{\alpha } _1^{*}}}{{{c_{32}}( {1 - {c_{11}}} ) + {c_{31}}{c_{12}}}},\nonumber \\&\alpha _1^{*} = \frac{{( {1 - {\lambda _2}} )( {1 - {c_{11}}} )\hat{\alpha } _1^{*}}}{{{c_{32}}( {1 - {c_{11}}} ) + {c_{31}}{c_{12}}}}, \nonumber \\&Y = ( {1 - {c_{11}}} ){X_1} + ( {{\lambda _2} - {c_{11}}} ){Y_1} + \hat{\alpha } _1^{*}. \end{aligned}$$
(3.11)

Based on the center manifold theorem, the center manifold of system (3.10) can be written as

$$\begin{aligned} {W^c}( {0,0,0} )= & {} \Big \{ \left( {{X_1},\hat{\alpha } _1^{*},{Y_1}} \right) \in {R^3}, \\&{Y_1}= M_1^{*}\left( {{X_1},\hat{\alpha } _1^{*}}\right) ,M_1^{*}( {0,0} )=0,\\&DM_1^{*}( {0,0} ) = 0 \Big \}. \end{aligned}$$

We assume that \(M_1^{*}({X_1},\hat{\alpha } _1^{*})\) has the following form:

$$\begin{aligned} M_1^{*}\left( {{X_1},\hat{\alpha } _1^{*}} \right)= & {} {\varpi _1}X_1^2 + {\varpi _2}{X_1}\hat{\alpha } _1^{*} + {\varpi _3}\hat{\alpha } _1^{{*^2}} \nonumber \\&+ O\left( {{{\left( {\left| {{X_1}} \right| + \left| {\hat{\alpha } _1^{*}} \right| }\right) }^3}} \right) . \end{aligned}$$
(3.12)

It follows from (3.10) that

$$\begin{aligned}&M_1^{*}\left( {{X_1} + \hat{\alpha } _1^{*} + \frac{{( {{\lambda _2} - {c_{11}} - \beta {c_{13}}} )\tilde{F}\left( {{X_1},\hat{\alpha } _1^{*},M_1^{*}\left( {{X_1},\hat{\alpha } _1^{*}}\right) } \right) }}{{{c_{13}}( {{\lambda _2} - 1} ){{\left( {1 + x_{22}^{{*^2}} + y_{22}^{{*^2}}} \right) }^3}}},\hat{\alpha } _1^{*}} \right) \nonumber \\&\quad -\, {\lambda _2}M_1^{*}\left( {{X_1},\hat{\alpha } _1^{*}} \right) - \frac{{( {{c_{11}} - 1 + \beta {c_{13}}} )\tilde{F}\left( {{X_1},\hat{\alpha } _1^{*},M_1^{*}\left( {{X_1},\hat{\alpha } _1^{*}}\right) }\right) }}{{{c_{13}}( {{\lambda _2} - 1} ){{\left( {1 + x_{22}^{{*^2}} + y_{22}^{{*^2}}}\right) }^3}}}\nonumber \\&\quad = 0. \end{aligned}$$
(3.13)

Substituting (3.11) and (3.12) into (3.13), we get

$$\begin{aligned} {\varpi _1}= & {} {\varpi _{01}}, \quad {\varpi _2} = \frac{{2{\varpi _{01}}}}{{{\lambda _2} - 1}} + {\varpi _{02}}, \\ {\varpi _3}= & {} \frac{{{\varpi _{01}} + {\varpi _{02}}}}{{{\lambda _2} - 1}} +{\varpi _{03}}, \end{aligned}$$

where

$$\begin{aligned} {\varpi _{01}}= & {} - \frac{{( {{c_{11}} - 1 + \beta {c_{13}}} )\left[ c_{13}^2{u_{200}} + {c_{13}}(1 - {c_{11}}){u_{101}} + {{(1 - {c_{11}})}^2}{u_{002}}\right] }}{{{c_{13}}{{( {{\lambda _2} - 1} )}^2}{{\left( {1 + x_{22}^{{*^2}} + y_{22}^{{*^2}}} \right) }^3}}},\\ {\varpi _{02}}= & {} \frac{{{c_{11}} - 1 + \beta {c_{13}}}}{{{c_{13}}({\lambda _2} - 1){{\left( {1 + x_{22}^{{*^2}} + y_{22}^{{*^2}}}\right) }^3}}}\left\{ - \frac{{{c_{13}}{u_{101}} + 2(1 - {c_{11}}){u_{002}}}}{{{\lambda _2} - 1}} \right. \\&\left. { + \frac{{2{c_{12}}{c_{13}}{u_{200}} + (1 - {c_{11}})[{c_{12}}{u_{101}} + {c_{13}}{u_{110}}] + {{(1 - {c_{11}})}^2}{u_{011}}}}{{{c_{32}}(1 - {c_{11}}) + {c_{31}}{c_{12}}}}} \right\} , \\ {\varpi _{03}}= & {} - \frac{{{c_{11}} - 1 + \beta {c_{13}}}}{{{c_{13}}{{\left( 1 + x_{22}^{{*^2}} + y_{22}^{{*^2}}\right) }^3}}}\left\{ {\frac{{{u_{002}}}}{{{{({\lambda _2} - 1)}^2}}}} - \frac{{{c_{12}}{u_{101}} + (1 - {c_{11}}){u_{011}}}}{{({\lambda _2} - 1)[{c_{32}}(1 - {c_{11}}) + {c_{31}}{c_{12}}]}} \right. \\&\left. { + \frac{{c_{12}^2{u_{200}} + {c_{12}}(1 - {c_{11}}){u_{110}}}}{{{{[{c_{32}}(1 - {c_{11}}) + {c_{31}}{c_{12}}]}^2}}}} \right\} . \end{aligned}$$

Therefore, the system restricted to the center manifold is expressed as

$$\begin{aligned}&{F^{*}}:{X_1} \mapsto {X_1} + \hat{\alpha } _1^{*} + {\sigma _1}X_1^2 + {\sigma _2}{X_1}\hat{\alpha } _1^{*} + {\sigma _3}\hat{\alpha } _1^{{*^2}}\nonumber \\&\quad +\,( {{\sigma _{{4_0}}} + {\sigma _{{4_1}}}{\varpi _1}} )X_1^3 + ( {{\sigma _{{5_0}}} + {\sigma _{{5_1}}}{\varpi _1} + {\sigma _{{5_2}}}{\varpi _2}} )X_1^2\hat{\alpha } _1^{*} \nonumber \\&\quad +\,( {{\sigma _{{6_0}}} + {\sigma _{{6_2}}}{\varpi _2} + {\sigma _{{6_3}}}{\varpi _3}} ){X_1}\hat{\alpha } _1^{{*^2}} + ( {{\sigma _{{7_0}}} + {\sigma _{{7_3}}}{\varpi _3}} )\hat{\alpha } _1^{{*^3}} \nonumber \\&\quad +\,O\left( {{{\left( {\left| {{X_1}} \right| + \left| {\hat{\alpha } _1^{*}} \right| }\right) }^4}} \right) , \end{aligned}$$
(3.14)

where \({\sigma _1}, {\sigma _2}, {\sigma _3}, {\sigma _{{4_0}}}, {\sigma _{{4_1}}}, {\sigma _{{5_0}}}, {\sigma _{{5_1}}}, {\sigma _{{5_2}}}, {\sigma _{{6_0}}}, {\sigma _{{6_2}}}, {\sigma _{{6_3}}}, {\sigma _{{7_0}}}, {\sigma _{{7_3}}}\) are given in “Appendix”. It is obvious that \({F^{*}}( {0,0} ) = 0, {\left. {\frac{{\partial {F^{*}}}}{{\partial {X_1}}}} \right| _{_{(0,0)}}} = 1, {\left. {\frac{{{\partial ^2}{F^{*}}}}{{\partial {X_1}^2}}} \right| _{(0,0)}} = 2{\sigma _1}.\)

Hence, based on the above analysis, we give the following theorem.

Theorem 3.1

System (2.3) undergoes a fold bifurcation at the fixed point \({E_{22}}(x_{22}^{*},y_{22}^{*})\), if one of conditions (3.1), (3.2) and (3.3) holds, conditions (3.4), (3.5), (3.7) and (3.8) are satisfied, and \({c_{11}} \ne 1, {\sigma _1}\ne 0 \). Moreover, if \({\sigma _1} < 0\) (resp., \({\sigma _1} > 0\)), then two fixed points bifurcate from \({E_{22}}(x_{22}^{*},y_{22}^{*})\) for \({\alpha _1} < {\bar{\alpha }_1}\) (resp., \({\alpha _1} > {\bar{\alpha }_1}\)), coalesce as \({E_{22}}(x_{22}^{*},y_{22}^{*})\) at \({\alpha _1} = {\bar{\alpha }_1}\) and disappear for \({\alpha _1} > {\bar{\alpha }_1}\) (resp., \({\alpha _1} < {\bar{\alpha }_1}\)).

Theorem 3.1 shows the creation and destruction of fixed points in the vicinity of a saddle-node fixed point. The fixed points mean that the concentrations of TFs are constants. We know that the existence of a saddle-node fixed point is dependent on the synthesis rate \({\alpha _1}\). In Theorem 3.1, the value of \({\alpha _1}\) not only guarantees that \({E_{22}}(x_{22}^{*},y_{22}^{*})\) exists, but also ensures that the condition of the eigenvalues is satisfied. The center manifold theorem enables us to only analyze the flow on the center manifold. \({\sigma _1} \ne 0\) is the nondegenerate condition, which indicates the type of the bifurcation, namely the fold bifurcation. When the nondegenerate condition is satisfied, whether two fixed points appear or disappear is decided by the value of \({\alpha _1}\), which is related to other biological parameters. It is shown that once \({\alpha _1}\) crosses the critical value, the number of fixed points changes, and the sign of \({\sigma _1}\) determines the direction of the variation. System (2.3) has at most three fixed points, and it may present bistability, that is, the concentration of TFs keeps at either of the two constant values.

Note that a saddle-node bifurcation that occurs in continuous system (2.2) corresponds to a fold bifurcation that appears in discrete system (2.3). Thus, the fold bifurcation in Theorem 3.1 also shows how the number of the equilibria of system (2.2) varies.

Remark 3.2

In [13], the authors investigated the multiple equilibria using bifurcation diagrams, which are obtained by changing the parameters in certain ranges. For system (2.3), which is established based on the genetic circuit in [13], we present the quantitative relationship between the biochemical parameter \({\alpha _1}\) and the variation of the number of fixed points. Our result provides an analytic proof for the fold bifurcation.

Remark 3.3

When a system undergoes a fold bifurcation, it could have multiple fixed points and present multistability. The stimulation of TFs may switch the system from one fixed point to another. Chronical exposure to chemicals makes the gene expression change [41], which corresponds to the variation of steady states in genetic systems. The analysis of fold bifurcation helps us to investigate the gene expression of different phenotype traits.

At the fixed points \({E_{11}}\left( {x_{11}^{*},y_{11}^{*}}\right) , {E_{21}}\left( {x_{21}^{*},y_{21}^{*}}\right) \), \({E_{31}}\left( {x_{31}^{*},y_{31}^{*}}\right) \) and \({E_{33}}( {x_{33}^{*},y_{33}^{*}} )\), we consider the flip bifurcation and Neimark–Sacker bifurcation of system (2.3). For simplicity, we only give the theoretical analysis for the fixed point \({E_{11}}\left( x_{11}^{*},y_{11}^{*}\right) \). Similar derivations can be obtained for other fixed points. Different from the situation of fold bifurcation, the existence of \(x_{11}^{*}\) is not related to the bifurcation parameter \(\delta \). Thus, we analyze the flip bifurcation and Neimark–Sacker bifurcation based on (iii2) and (iii3) of Lemma 2.2, respectively. The flip bifurcation is first considered. Let \({\delta _1} = \frac{{{S_1} - \sqrt{{{S_1}^2} - 4{S_2}} }}{{S_2}}.\) We only focus on the case \(\delta = {\delta _1}\), and the other case where \(\delta = \frac{{{S_1} + \sqrt{{{S_1}^2} - 4{S_2}} }}{{S_2}}\) can be similarly certified. When parameters satisfy (iii2) of Lemma 2.2, system (2.3) can be rewritten as

$$\begin{aligned} \left( \begin{array}{c} x\\ y \end{array} \right) \mapsto \left( \begin{array}{c} x - {k_1}{\delta _1}x + \frac{{{\delta _1}\left( {\alpha _1}{x^2} + {\alpha _2}\right) }}{{1 + {x^2} + {y^2}}}\\ y - {k_2}{\delta _1}x + \frac{{{\delta _1}\beta \left( {\alpha _1}{x^2} + {\alpha _2}\right) }}{{1 + {x^2} + {y^2}}} \end{array} \right) . \end{aligned}$$
(3.15)

The eigenvalues at the fixed point \({E_{11}}\left( x_{11}^{*},y_{11}^{*}\right) \) are \({\lambda _1} = - 1,{\lambda _2} = 3 - {S_1}{\delta _1}.\) Let \(X = x - x_{11}^{*}, Y = y - y_{11}^{*}\) and \({\delta ^{*}}=\delta -{\delta _1}\). System (2.3) becomes

$$\begin{aligned} \left( \begin{array}{l} X\\ {\delta ^{*}}\\ Y \end{array} \right)\mapsto & {} \left( {\begin{array}{ccc} {\bar{c}}_{11}&{}0&{}{{{\bar{c}}_{13}}}\\ 0&{} 1&{}0\\ {\bar{c}}_{31}&{}0&{}{\bar{c}}_{33} \end{array}} \right) \left( \begin{array}{c} X\\ {\delta ^{*}}\\ Y \end{array} \right) \nonumber \\&+\left( {\begin{array}{c} {\frac{{G(X, {\delta ^{*}},Y)}}{{{{(1 + x_{11}^{{*^2}} + y_{11}^{{*^2}})}^3}}} - {k_1}X{\delta ^{*}}}\\ 0\\ {\frac{{\beta G(X, {\delta ^{*}},Y)}}{{{{(1 + x_{11}^{{*^2}} + y_{11}^{{*^2}})}^3}}} - {k_2}Y{\delta ^{*}}} \end{array}} \right) , \end{aligned}$$
(3.16)

where

$$\begin{aligned}&{{\bar{c}}_{11}} = 1 - {k_1}{\delta _1} + \frac{{2{\delta _1}x_{11}^{*}\left( {\alpha _1} + {\alpha _1}y_{11}^{{*^2}} - {\alpha _2}\right) }}{{{{\left( 1 + x_{11}^{{*^2}} + y_{11}^{{*^2}}\right) }^2}}},\\&{{\bar{c}}_{13}} = - \frac{{2{\delta _1}y_{11}^{*}\left( {\alpha _1}x_{11}^{{*^2}} + {\alpha _2}\right) }}{{{{\left( 1 + {x^{{*^2}}} + {y^{{*^2}}}\right) }^2}}},\nonumber \\&{{\bar{c}}_{31}} = \frac{{2{\delta _1}\beta x_{11}^{*}\left( {\alpha _1} + {\alpha _1}y_{11}^{{*^2}} - {\alpha _2}\right) }}{{{{\left( 1 + x_{11}^{{*^2}} + y_{11}^{{*^2}}\right) }^2}}}, \\&{{\bar{c}}_{33}} = 1 - {k_2}{\delta _1} - \frac{{2{\delta _1}\beta y_{11}^{*}\left( {\alpha _1}x_{11}^{{*^2}} + {\alpha _2}\right) }}{{{{\left( 1 + x_{11}^{{*^2}} + y_{11}^{{*^2}}\right) }^2}}}, \end{aligned}$$
$$\begin{aligned} G(X,{\delta ^{*}},Y)= & {} {v_{200}}{X^2} + {v_{101}}XY + {v_{110}}X{\delta ^{*}} + {v_{002}}{Y^2}\\&+ {v_{011}}Y{\delta ^{*}} + {v_{300}}{X^3}+ {v_{201}}{X^2}Y \\&+ {v_{210}}{X^2}{\delta ^{*}} + {v_{102}}X{Y^2} + {v_{111}}XY{\delta ^{*}}\\&+ {v_{003}}{Y^3} + {v_{012}}{Y^2}{\delta ^{*}}\\&+ O\left( {{{\left( {\left| {{X}} \right| + \left| {\delta ^{*}} \right| + \left| {{Y}} \right| } \right) }^4}} \right) , \end{aligned}$$

and \({v_{200}}, {v_{101}}, {v_{110}}, {v_{002}}, {v_{011}}, {v_{300}}\), \({v_{201}}, {v_{210}}, {v_{102}}, {v_{111}}, {v_{003}}, {v_{012}}\) are given in “Appendix”.

From the expressions in system (3.16), we have \({S_1}{\delta _1} =2-{{{{\bar{c}}_{11}}}-{{{\bar{c}}_{33}}}}\), which indicates that \({\lambda _2} = {{{{\bar{c}}_{11}}}+{{{\bar{c}}_{33}}}}+1\). From \({\lambda _1} = -1\), one has \({{{\bar{c}}_{13}}}{{{\bar{c}}_{31}}} - ( {1 + {{{\bar{c}}_{11}}}} )( {1 + {{{\bar{c}}_{33}}}} ) = 0.\) The condition \(\left| {{\lambda _2}} \right| \ne 1\) leads to \({\bar{c}_{11}} + {\bar{c}_{33}} \ne - 2,0.\) Then, we introduce an invertible matrix

$$\begin{aligned} {T_2} = \left( {\begin{array}{ccc} {\bar{c}}_{13}&{}0&{}{\bar{c}}_{13}\\ 0&{}1&{}0\\ -({\bar{c}}_{11} + 1)&{} 0&{}\lambda _{2}-{\bar{c}}_{11} \end{array}} \right) . \end{aligned}$$

Under the transformation

$$\begin{aligned} \left( \begin{array}{l} X\\ {\delta ^{*}}\\ Y \end{array} \right) = {T_2}\left( \begin{array}{l} {X_2}\\ {{\hat{\delta } }^{*}}\\ {Y_2} \end{array} \right) , \end{aligned}$$

system (3.16) becomes

$$\begin{aligned} \left( \begin{array}{l} {X_2}\\ {{\hat{\delta } }^{*}}\\ {Y_2} \end{array} \right)\mapsto & {} \left( {\begin{array}{ccc} -1&{}0&{}0\\ 0&{}1&{}0\\ 0&{}0&{}\lambda _2 \end{array}} \right) \left( {\begin{array}{c} {{X_2}}\\ {{{\hat{\delta } }^{*}}}\\ {{Y_2}} \end{array}} \right) \nonumber \\&+\left( {\begin{array}{c} \bar{G}_{1}\left( {X_2},{{\hat{\delta }}^{*}},{Y_2}\right) \\ 0\\ {\bar{G}}_{2}\left( {X_2},{{\hat{\delta } }^{*}},{Y_2}\right) \end{array}} \right) , \end{aligned}$$
(3.17)

where

$$\begin{aligned}&{{\bar{G}}_1}\left( {{X_2},{{\hat{\delta } }^{*}}},{Y_2} \right) = \frac{{{k_2}}}{{{{\bar{c}}_{11}} + 2 + {{\bar{c}}_{33}}}}Y{\delta ^{*}}\\&\quad - \frac{{{k_1}( {1 + {{\bar{c}}_{33}}} )}}{{{{\bar{c}}_{13}}( {{{\bar{c}}_{11}} + 2 + {{\bar{c}}_{33}}} )}}X{\delta ^{*}} \\&\quad + \frac{{( {1 + {{\bar{c}}_{33}} - \beta {{\bar{c}}_{13}}} )G( {X,{\delta ^{*}}},Y )}}{{{{\bar{c}}_{13}}( {{{\bar{c}}_{11}} + 2 + {{\bar{c}}_{33}}} ){{\left( 1 + x_{11}^{{*^2}} + y_{11}^{{*^2}}\right) }^3}}},\\&{{\bar{G}}_2}\left( {{X_2},{{\hat{\delta } }^{*}}},{Y_2}\right) = - \frac{{{k_2}}}{{{{\bar{c}}_{11}} + 2 + {{\bar{c}}_{33}}}}Y{\delta ^{*}}\\&\quad - \frac{{{k_1}( {1 + {{\bar{c}}_{11}}} )}}{{{{\bar{c}}_{13}}( {{{\bar{c}}_{11}} + 2 + {{\bar{c}}_{33}}} )}}X{\delta ^{*}} \\&\quad + \frac{{( {1 + {{\bar{c}}_{11}} + \beta {{\bar{c}}_{13}}} )G( {X,{\delta ^{*}}},Y )}}{{{{\bar{c}}_{13}}( {{{\bar{c}}_{11}} + 2 + {{\bar{c}}_{33}}} ){{\left( 1 + x_{11}^{{*^2}} + y_{11}^{{*^2}}\right) }^3}}},\\&{X = {{\bar{c}}_{13}}( {{X_2} + {Y_2}} )}, \quad {{\delta ^{*}} = {{\hat{\delta } }^{*}}}, \\&Y = - ( {{{\bar{c}}_{11}} + 1} ){{X_2}} + ( {{\lambda _2} - {{\bar{c}}_{11}}} ){Y_2}. \end{aligned}$$

Using the center manifold theorem, we can describe the center manifold of system (3.17) as

$$\begin{aligned} M_2^{*}({X_2},{\hat{\delta } ^{*}})= & {} {\mu _1}X_2^2 + {\mu _2}{X_2}{\hat{\delta } ^{*}} + {\mu _3}{\hat{\delta } ^{{*^2}}} \\&+ O\left( {{{\left( {\left| {{X_2}} \right| + \left| {{{\hat{\delta } }^{*}}} \right| } \right) }^3}} \right) , \end{aligned}$$

which satisfies \(M_2^{*}( {0,0} ) = 0, DM_2^{*}( {0,0} ) = 0.\) From system (3.17), one has

$$\begin{aligned}&M_2^{*}\left( { - {X_2} + {{\bar{G}}_1}\left( {{X_2},{{\hat{\delta } }^{*}}},M_2^{*}\left( {{X_2},{{\hat{\delta } }^{*}}} \right) \right) , {{\hat{\delta } }^{*}}} \right) \\&\quad - {\lambda _2}M_2^{*}\left( {{X_2},{{\hat{\delta } }^{*}}} \right) - {\bar{G}_2}\left( {{X_2},{{\hat{\delta } }^{*}}},M_2^{*}\left( {{X_2},{{\hat{\delta } }^{*}}}\right) \right) = 0. \end{aligned}$$

Similar to the analysis of fold bifurcation, it is easy to get

$$\begin{aligned} {\mu _1}= & {} \frac{{(1 + {{\bar{c}}_{11}} + \beta {{\bar{c}}_{13}})\left[ \bar{c}_{13}^2{v_{200}} - {{\bar{c}}_{13}}\left( {1 + {{\bar{c}}_{11}}} \right) {v_{101}} + {{\left( {1 + {{\bar{c}}_{11}}} \right) }^2}{v_{002}}\right] }}{{{{\bar{c}}_{13}}\left( {1 - {\lambda _2}} \right) \left( {{{\bar{c}}_{11}} + 2 + {{\bar{c}}_{33}}} \right) {{\left( {1 + x_{11}^{{*^2}} + y_{11}^{{*^2}}} \right) }^3}}},\\ {\mu _2}= & {} \frac{{({k_1} - {k_2})({{\bar{c}}_{11}} + 1)}}{{(1 + {\lambda _2})({{\bar{c}}_{11}} + 2 + {{\bar{c}}_{33}})}} \\&\quad - \frac{{(1 + {{\bar{c}}_{11}} + \beta {{\bar{c}}_{33}})[{{\bar{c}}_{13}}{v_{110}} - (1 + {{\bar{c}}_{11}}){v_{011}}]}}{{{{\bar{c}}_{13}}(1 + {\lambda _2})({{\bar{c}}_{11}} + 2 + {{\bar{c}}_{33}}){{\left( 1 + x_{11}^{{*^2}} + y_{11}^{{*^2}}\right) }^3}}},\\ {\mu _3}= & {} 0. \end{aligned}$$

Therefore, the system restricted to the center manifold can be expressed as

$$\begin{aligned}&{G^{*}}:{X_2} \mapsto - {X_2} + {\vartheta _1}X_2^2 + {\vartheta _2}{X_2}{{\hat{\delta } }^{*}}\\&\quad +\,( {{\vartheta _{{3_0}}} +{\vartheta _{{3_1}}}{\mu _1}} )X_2^3 + ( {{\vartheta _{{4_0}}} + {\vartheta _{{4_1}}}{\mu _1} + {\vartheta _{{4_2}}}{\mu _2}} )X_2^2{{\hat{\delta } }^{*}} \\&\quad +\,{\vartheta _{{5_2}}}{\mu _2}{X_2}{{\hat{\delta } }^{{*^2}}} + O\left( {{{\left( {\left| {{X_2}} \right| + \left| {{{\hat{\delta } }^{*}}} \right| } \right) }^4}} \right) , \end{aligned}$$

where \({\vartheta _1}, {\vartheta _2}, {\vartheta _{{3_0}}}, {\vartheta _{{3_1}}}, {\vartheta _{{4_0}}}, {\vartheta _{{4_1}}}, {\vartheta _{{4_2}}}, {\vartheta _{{5_2}}}\) are given in “Appendix”.

To determine the existence of flip bifurcation, the following two quantities are required to be nonzero:

$$\begin{aligned} {\rho _1}= & {} {{\left. {\left( {\frac{{{\partial ^2}{G^{^{*}}}}}{{\partial {X_2}\partial {{\hat{\delta } }^{*}}}} + \frac{1}{2}\frac{{\partial {G^{^{*}}}}}{{\partial {{\hat{\delta } }^{*}}}}\frac{{{\partial ^2}{G^{^{*}}}}}{{\partial X_2^2}}} \right) } \right| }_{(0,0)}} = {\vartheta _2},\\ {\rho _2}= & {} {{\left. {\left( {\frac{1}{6}\frac{{{\partial ^3}{G^{^{*}}}}}{{\partial X_2^3}} + {{\left( {\frac{1}{2}\frac{{{\partial ^2}{G^{^{*}}}}}{{\partial X_2^2}}} \right) }^2}} \right) } \right| }_{(0,0)}} \\= & {} \vartheta _1^2 + {{\vartheta _{{3_0}}} + {\vartheta _{{3_1}}}{\mu _1}}. \end{aligned}$$

Based on the above analysis, the following result can be obtained.

Theorem 3.2

System (2.3) undergoes a flip bifurcation at the fixed point \({E_{11}}(x_{11}^{*},y_{11}^{*})\), if \(\delta = {\delta _1}\) and other conditions in (iii2) of Lemma 2.2 are satisfied, and \({\rho _1}, {\rho _2} \ne 0\). Moreover, if \({\rho _2} > 0\) (resp., \({\rho _2} < 0\)), then the period-2 orbit bifurcating from \({E_{11}}(x_{11}^{*},y_{11}^{*})\) is stable (resp., unstable).

Theorem 3.2 shows the loss of stability of a fixed point and the creation of a period-2 orbit. When the discretization step size \(\delta \) varies, the stability of the fixed point may change, and TFs’ concentrations deviate from the original constant values. When \(\delta \) crosses the critical value \({\delta _1}, {E_{11}}(x_{11}^{*},y_{11}^{*})\) loses the stability, and the bifurcation induces a stable or unstable period-2 orbit, which means that the time that the transcription factor needs to return to a certain concentration is twice as much as it needs before the bifurcation occurs. Although the value of \({E_{11}}(x_{11}^{*},y_{11}^{*})\) is independent on \(\delta \), the variation of \(\delta \) affects the eigenvalues of system (2.3). Thus, the value of \(\delta \) determines the occurrence of flip bifurcation, and the quantity \({\rho _2}\) affects the stability of the periodic orbit.

Note that the value of the fixed point in system (2.3) is not related to \(\delta \). Thus, compared with the conditions of \({\alpha _1}\) in Theorem 3.1, the condition of \(\delta \) is relatively simple. The flip bifurcation is generated without destroying the properties of the original system.

Remark 3.4

Some dynamic behaviors have been studied for the model which is developed based on the genetic circuit in [13]. However, to the best of our knowledge, the flip bifurcation has not been reported yet. The occurrence of a flip bifurcation is theoretically proved in Theorem 3.2 and will be illustrated by the numerical simulation. Thus, our result enriches the dynamics that could be presented by the circuit in [13].

Remark 3.5

The transcription often keeps at a steady level, or it may present a periodic rhythm. Affected by some factors, the period doubling of transcriptional activities occurs, and the gene expression changes, which leads to phenotypic changes [42], such as cell differentiation. The flip bifurcation helps us to probe into the underlying reason for the changes of phenotypes from the perspective of dynamics.

In what follows, we will investigate the Neimark–Sacker bifurcation, when \({\delta _2} = \frac{{{S_1}}}{{{S_2}}}\) and other conditions in (iii3) of Lemma 2.2 hold. System (2.3) can be written as

$$\begin{aligned} \left( \begin{array}{c} x\\ y \end{array} \right) \mapsto \left( \begin{array}{c} x - {k_1}{\delta _2}x + \frac{{{\delta _2}( {{\alpha _1}{x^2} + {\alpha _2}} )}}{{1 + {x^2} + {y^2}}}\\ y - {k_2}{\delta _2}y + \frac{{\beta {\delta _2}( {{\alpha _1}{x^2} + {\alpha _2}} )}}{{1 + {x^2} + {y^2}}} \end{array} \right) . \end{aligned}$$
(3.18)

Let \(X = x - x_{11}^{*},Y = y - y_{11}^{*}\). System (3.18) becomes

$$\begin{aligned} \left( \begin{array}{c} X\\ Y \end{array} \right)\rightarrow & {} \left( {\begin{array}{cc} {{{\tilde{c}}_{11}}}&{}{{{\tilde{c}}_{12}}}\\ {{{\tilde{c}}_{21}}}&{}{{{\tilde{c}}_{22}}} \end{array}} \right) \left( \begin{array}{l} X\\ Y \end{array} \right) \nonumber \\&+\left( \begin{array}{l} \frac{{H(X,Y)}}{{{{\left( 1 + x_{11}^{{*^2}} + y_{11}^{{*^2}}\right) }^3}}}\\ \frac{{\beta H(X,Y)}}{{{{\left( 1 + x_{11}^{{*^2}} + y_{11}^{{*^2}}\right) }^3}}} \end{array} \right) , \end{aligned}$$
(3.19)

where

$$\begin{aligned} H(X,Y)= & {} {w_{20}}{X^2} + {w_{11}}XY + {w_{02}}{Y^2} + {w_{30}}{X^3}\\&+\,{w_{21}}{X^2}Y + {w_{12}}X{Y^2} + {w_{03}}{Y^3}\\&+\,O\left( {{{\left( {\left| {{X}} \right| + \left| {{Y}} \right| } \right) }^4}} \right) , \end{aligned}$$

and \({{\tilde{c}}_{11}}, {{\tilde{c}}_{12}}, {{\tilde{c}}_{21}}, {{\tilde{c}}_{22}}, {w_{20}}, {w_{11}}, {w_{02}}, {w_{30}}, {w_{21}}, {w_{12}}, {w_{03}}\) are given in “Appendix”.

Note that the eigenvalues at the fixed point \({E_{11}}(x_{11}^{*},y_{11}^{*})\) are complex conjugate, and they can be given by

$$\begin{aligned} {\lambda _{1,2}} = {\upsilon _1} \pm i{\upsilon _2}, \end{aligned}$$

where \({{\upsilon _1} = \frac{{2 - {S_1}{\delta _2}}}{2}}, {{\upsilon _2} = \frac{{{\delta _2}\sqrt{4{S_2} - S_1^2} }}{2}.}\) Besides, we have \({\left| {{\lambda _{1,2}}} \right| = \sqrt{{R_2}} }\) and \({l = {{\left. {\frac{{d\left| {{\lambda _{1,2}}} \right| }}{{d\delta }}} \right| }_{\delta = {\delta _2}}} = \frac{{{S_1}}}{2} > 0}\), where \({{R_2} = {S_2}\delta _2^2 - {S_1}{\delta _2} + 1.}\) If \({R_1} = - 2 + {S_1}{\delta _2}\ne 0,1\), we get \({\delta _2} \ne \frac{2}{{{S_1}}},\frac{3}{{{S_1}}}\), which indicates that \(S_1^2 \ne 2{S_2},3{S_2}\). Then one has \(\lambda _{1,2}^n \ne 1, n = 1,2,3,4.\)

Let

$$\begin{aligned} {T_3} = \left( {\begin{array}{cc} {{\tilde{c}}_{12}}&{} 0\\ {\upsilon _1} - {{\tilde{c}}_{11}}&{} - {\upsilon _2} \end{array}} \right) . \end{aligned}$$

Under the transformation

$$\begin{aligned} \left( \begin{array}{c} X\\ Y \end{array} \right) = {T_3}\left( \begin{array}{c} {X_3}\\ {Y_3} \end{array} \right) , \end{aligned}$$

system (3.19) becomes

$$\begin{aligned} \left( \begin{array}{l} {X_3}\\ {Y_3} \end{array} \right)\rightarrow & {} \left( {\begin{array}{*{20}{c}} {{\upsilon _1}}&{}{ - {\upsilon _2}}\\ {{\upsilon _2}}&{}{{\upsilon _1}} \end{array}} \right) \left( \begin{array}{l} {X_3}\\ {Y_3} \end{array} \right) \nonumber \\&+\left( {\begin{array}{c} {\frac{{\tilde{H}({X_3},{Y_3})}}{{{{\tilde{c}}_{12}}}}}\\ {\frac{{\left( {{\upsilon _1} - {{\tilde{c}}_{11}} - \beta {{\tilde{c}}_{12}}} \right) \tilde{H}({X_3},{Y_3})}}{{{{\tilde{c}}_{12}}{\upsilon _2}}}} \end{array}} \right) , \end{aligned}$$
(3.20)

where \(\tilde{H}\left( {{X_3},{Y_3}} \right) = \frac{{H(X,Y)}}{{{{( {1 + x_{11}^{{*^2}} + y_{11}^{{*^2}}} )}^3}}},\) \({X = {{\tilde{c}}_{12}}{X_3}}\) and \({Y = ( {{\upsilon _1} - {{\tilde{c}}_{11}}} ){X_3} - {\upsilon _2}{Y_3}.}\)

To guarantee the occurrence of a Neimark–Sacker bifurcation in system (3.20), we require that the following quantity cannot be zero:

$$\begin{aligned} \xi= & {} - {\mathrm{Re}} \left( {\frac{{(1 - 2{\lambda _1})\lambda _2^2}}{{1 - {\lambda _1}}}{\eta _{20}}{\eta _{11}}} \right) - \frac{1}{2}{\left| {{\eta _{11}}} \right| ^2} - {\left| {{\eta _{02}}} \right| ^2} \\&+\,{\mathrm{Re}} ({\lambda _2}{\eta _{21}}), \end{aligned}$$

where

$$\begin{aligned} {\eta _{20}}= & {} \frac{{{\upsilon _2}\left( {{\tilde{H}}_{{X_3}{X_3}}} - {{\tilde{H}}_{{Y_3}{Y_3}}}\right) + 2\left( {\upsilon _1} - {{\tilde{c}}_{11}} - \beta {{\tilde{c}}_{12}}\right) {{\tilde{H}}_{{X_3}{Y_3}}} + i\left[ {\left( {\upsilon _1} - {{\tilde{c}}_{11}} - \beta {{\tilde{c}}_{12}}\right) \left( {{\tilde{H}}_{{X_3}{X_3}}} - {{\tilde{H}}_{{Y_3}{Y_3}}}\right) - 2{{\upsilon _2}{\tilde{H}}_{{X_3}{Y_3}}}}\right] }}{{8{{\tilde{c}}_{12}}{\upsilon _2}}},\\ {\eta _{11}}= & {} \frac{{{\upsilon _2}\left( {{\tilde{H}}_{{X_3}{X_3}}} + {{\tilde{H}}_{{Y_3}{Y_3}}}\right) + i\left[ \left( {\upsilon _1} - {{\tilde{c}}_{11}} - \beta {{\tilde{c}}_{12}}\right) \left( {{\tilde{H}}_{{X_3}{X_3}}} + {{\tilde{H}}_{{Y_3}{Y_3}}}\right) \right] }}{{4{{\tilde{c}}_{12}}{\upsilon _2}}}, \\ {\eta _{02}}= & {} \frac{{{\upsilon _2}\left( {{\tilde{H}}_{{X_3}{X_3}}} - {{\tilde{H}}_{{Y_3}{Y_3}}}\right) - 2\left( {\upsilon _1} - {{\tilde{c}}_{11}} - \beta {{\tilde{c}}_{12}}\right) {{\tilde{H}}_{{X_3}{Y_3}}} + i\left[ \left( {\upsilon _1} - {{\tilde{c}}_{11}} - \beta {{\tilde{c}}_{12}}\right) \left( {{\tilde{H}}_{{X_3}{X_3}}} - {{\tilde{H}}_{{Y_3}{Y_3}}}\right) + 2{\upsilon _2}{{\tilde{H}}_{{X_3}{Y_3}}}\right] }}{{8{{\tilde{c}}_{12}}{\upsilon _2}}},\\ {\eta _{21}}= & {} \frac{1}{{16{{\tilde{c}}_{12}}{\upsilon _2}}}\left\{ {\upsilon _2}\left( {{\tilde{H}}_{{X_3}{X_3}{X_3}}} + {{\tilde{H}}_{{X_3}{Y_3}{Y_3}}}\right) \right. +\, \left( {\upsilon _1} - {{\tilde{c}}_{11}} - \beta {{\tilde{c}}_{12}}\right) \left( {{\tilde{H}}_{{X_3}{X_3}{Y_3}}} + {{\tilde{H}}_{{Y_3}{Y_3}{Y_3}}}\right) \\&+\, i\left[ {\left( {\upsilon _1} - {{\tilde{c}}_{11}} - \beta {{\tilde{c}}_{12}}\right) \left( {{\tilde{H}}_{{X_3}{X_3}{X_3}}} - {{\tilde{H}}_{{X_3}{Y_3}{Y_3}}}\right) }\left. -\, {{\upsilon _2} \left( {{\tilde{H}}_{{Y_3}{Y_3}{Y_3}}}+{\tilde{H}}_{{X_3}{X_3}{Y_3}}\right) } \right] \right\} , \end{aligned}$$

and \({{\tilde{H}}_{{X_3}{X_3}}}, {{\tilde{H}}_{{Y_3}{Y_3}}}, {{\tilde{H}}_{{X_3}{Y_3}}}, {{\tilde{H}}_{{X_3}{X_3}{X_3}}}, {{\tilde{H}}_{{X_3}{X_3}{Y_3}}}\),\({{\tilde{H}}_{{X_3}{Y_3}{Y_3}}}, {{\tilde{H}}_{{Y_3}{Y_3}{Y_3}}}\) are high-order partial derivatives of \(\tilde{H}\left( {{X_3},{Y_3}} \right) \) and they are given in “Appendix”.

Theorem 3.3

System (2.3) undergoes a Neimark–Sacker bifurcation at the fixed point \({E_{11}}(x_{11}^{*},y_{11}^{*})\), if \(\delta = {\delta _2}\) and other conditions in (iii3) of Lemma 2.2 are satisfied, and \(S_1^2 \ne 2{S_2},3{S_2}, \xi \ne 0\). Moreover, if \(\xi < 0\) (resp., \(\xi > 0\)), then an attracting (resp., repelling) closed invariant curve bifurcates from \({E_{11}}(x_{11}^{*},y_{11}^{*})\) for \(\delta > {\delta _2}\) (resp., \(\delta < {\delta _2}\)).

Theorem 3.3 gives another way in which the fixed point of system (2.3) loses the stability. The concentrations of TFs change. When the system undergoes a Neimark–Sacker bifurcation, it generates a unique closed invariant curve around the fixed point. TFs’ concentrations present oscillations near the original concentration values, and they present a cyclic behavior. Similar to the situation of flip bifurcation, the step size \(\delta \) has no effect on the existence of the fixed point, but it could change the local stability of the fixed point. \(\xi \ne 0\) is the nondegenerate condition, and the sign of \(\xi \) determines the stability of the closed curve and the direction from which it arises. For a stable (attracting) closed curve, an arbitrary neighboring trajectory tends to it as time approaches infinity.

Remark 3.6

In [20, 21], for the model established in [13], the authors reported the Hopf bifurcation. In Theorem 3.3, the occurrence of a Neimark–Sacker bifurcation is demonstrated in system (2.3), which is developed based on the genetic circuit in [13]. Although a Neimark–Sacker bifurcation can be seen as an analogue of a Hopf bifurcation in the continuous system, it is actually a different bifurcation. Thus, our result extends the capability of the circuit in [13] to generate multiple bifurcations.

Remark 3.7

When the time interval between two transcriptional activities is short, the gene expression level is steady. When the gap grows to a certain extent, the concentrations of TFs oscillate, but they can present recurrent behaviors. For example, for the dormice, the circadian rhythm of a locomotor activity persists throughout the hibernation season [43]. The Neimark–Sacker bifurcation gives an explanation for this cyclic behavior and helps us to explore this biological phenomenon.

Fig. 1
figure 1

Bifurcation diagram in \(({\alpha _1},x)\) plane for \(9.75 \le {\alpha _1} \le 10.098\) with initial values \(({x_0},{y_0}) = (0.15,0.12)\)

Full size image

4 Numerical simulations

In this section, we will show bifurcation diagrams, phase portraits and maximum Lyapunov exponents to illustrate the theoretical results. Moreover, it is shown that system (2.3) can also exhibit richer dynamic phenomena than those derived by the theoretical analysis. The bifurcation parameters are given as follows: (i) Varying \({\alpha _1}\) in range \(9.75 \le {\alpha _1} \le 10.098\), and fixing \({k_1} = 5, {k_2} = 10, {\alpha _2} = 5, \beta = 1, \delta =0.05\). (ii) Varying \(\delta \) in range \(0.3 \le \delta \le 0.3895,\) and fixing \({k_1} = 2, {k_2} = 2.4, {\alpha _1} = 2, {\alpha _2} = 5, \beta = 6\). (iii) Varying \(\delta \) in range \(0.93 \le \delta \le 1.139,\) and fixing \({k_1} = \frac{{50}}{{11}}, {k_2} = \frac{{93}}{{55}}, {\alpha _1} = \frac{{225}}{{22}}, {\alpha _2} = \frac{{6}}{{11}}, \beta = \frac{{93}}{{500}}\).

Fig. 2
figure 2

a Bifurcation diagram in \((\delta ,x)\) plane for \(0.3 \le \delta \le 0.3895\) with initial values \(({x_0},{y_0}) = (0.6,0.55)\). b Maximum Lyapunov exponents corresponding to (a). c Phase portrait of period-1 orbit for \(\delta = 0.305\). d Phase portrait of period-2 orbit for \(\delta = 0.35\)

Full size image
Fig. 3
figure 3

a Bifurcation diagram in \((\delta ,x)\) plane for \(0.93 \le \delta \le 1.139\) with initial values \(({x_0},{y_0}) = (1,0.5)\). b Local amplification corresponding to (a) for \(1.049 \le \delta \le 1.0979\). c Bifurcation diagram in \((\delta ,y)\) plane. d Local amplification corresponding to (c)

Full size image
Fig. 4
figure 4

Phase portraits for different values of \(\delta \) corresponding Fig. 3. a \(\delta =0.933\), b \(\delta =0.94\), c \(\delta =0.95\), d \(\delta =1.019\), e \(\delta =1.05\), f \(\delta =1.079\), g \(\delta =1.089\), h \(\delta =1.099\), i \(\delta =1.1099\), j \(\delta =1.1199\), k \(\delta =1.124\), l \(\delta =1.139\)

Full size image
Fig. 5
figure 5

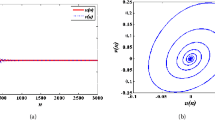
a Maximum Lyapunov exponents corresponding to Fig. 4. b Local amplification of Maximum Lyapunov exponents for \(1.05 \le \delta \le 1.0918\) corresponding to (a)

Full size image

For case (i), the bifurcation diagram of system (2.3) in \(({\alpha _1}, x)\) plane for \(9.75 \le {\alpha _1} \le 10.098\) is given in Fig. 1 with initial values \(({x_0},{y_0}) = (0.15,0.12)\). Equation (2.6) has two positive roots, which are \({\alpha _1}=9.8582\) and \({\alpha _1}=10\). According to Lemma 2.1, there is a unique positive fixed point when \( 0<{\alpha _1}<9.8582\). When \({\alpha _1}\) increases to 9.8582, system (2.3) has two positive fixed points (0.3281, 0.16405) and (0.6246, 0.3123). We have \({\lambda _1} = 1,\) \({\lambda _2} \approx 0.4672\) and \({\sigma _1} \approx 0.144 > 0\) at the fixed point (0.6246, 0.3123). From Fig. 1, we observe that a fold bifurcation occurs at (0.6246, 0.3123), so Theorem 3.1 is verified. Two fixed points bifurcate from (0.6246, 0.3123), and three fixed points exist for \( 9.8582<{\alpha _1}<10 \). They change into two fixed points (0.4, 0.2) and (0.8, 0.4) when \( {\alpha _1}=10 \). By calculation, we have \({\lambda _1} = 1,\) \({\lambda _2} \approx 0.483\) and \({\sigma _1} = -0.177 < 0\). From Theorem 3.1, the fold bifurcation occurs at the fixed point (0.4, 0.2). System (2.3) has a unique fixed point when \( {\alpha _1}>10 \). It should be noted that, although more than one fixed points may exist, which one the system converges to depends on the initial values.

Fig. 6
figure 6

a Asymptotically stable dynamics trajectories of system (2.2) with initial values \((x_0,y_0)=(2.5,1.7)\) and \(k_2=0.017\). b Phase portrait corresponding to (a). c Periodic oscillation of system (2.2) with \(k_2=0.01\). d Phase portrait corresponding to (c)

Full size image

For case (ii), the bifurcation diagram of system (2.3) in \((\delta ,x)\) plane for \(0.3 \le \delta \le 0.3895\) is presented in Fig. 2a with initial values \(({x_0},{y_0}) = (0.6,0.55)\). From Lemma 2.1, there is a unique positive fixed point (0.443, 2.213) which is stable when \(0.3 \le \delta < 0.327\). Flip bifurcation occurs at \(\delta = 0.327\), and we have \({\lambda _1} = -1,\) \({\lambda _2} \approx 0.351, {\rho _1} = - 6.112\) and \({\rho _2} = 0.167 > 0\), so Theorem 3.2 is verified. When \(\delta > 0.327\), the system becomes unstable and period-2 orbit appears. The maximum Lyapunov exponents corresponding to the bifurcation diagram are depicted in Fig. 2b, while the phase portraits are shown in Fig. 2c, d.

For case (iii), the bifurcation diagrams of system (2.3) for \(0.93 \le \delta \le 1.139\) are presented in Fig. 3 with initial values \(({x_0},{y_0}) = (1,0.5)\). There are three positive fixed points (0.2, 0.1), (0.4, 0.2) and (1.2, 0.6), and we analyze the local dynamics of the fixed point (1.2, 0.6). According to Lemma 2.2, it is stable when \(0.93 \le \delta < 0.94\). From Fig. 4, we observe that a Neimark–Sacker bifurcation occurs and an attracting invariant cycle bifurcates from the fixed point at \(\delta = 0.94\) with \({\lambda _1} \approx - 0.213 + 0.977i, {\lambda _2} \approx - 0.213 - 0.977i\) and \(\xi = -3.995 <0\). Along with the growth of \(\delta \), the cycle first becomes bigger and then disappears. Whereafter, system (2.3) exhibits period-7, -14, -5, -10 orbits and chaos until \(\delta = 1.139\). The maximum Lyapunov exponents are computed and depicted in Fig. 5 to show the existence of period orbits and strange attractors.

To compare the dynamics of discrete system (2.3) with that of continuous version (2.2), we show the dynamic characteristics of system (2.2) by the dynamics trajectories and phase portraits. We take \({k_1}=0.5, {\alpha _1}=2.1, {\alpha _2}=1, \beta =0.035\) and \({k_2}=0.017, 0.01\) in two cases, and the initial values are \((x_0,y_0)=(2.5,1.7)\). System (2.2) has an equilibrium (1.5406, 2.0965) at \({k_2}=0.01286\). When \({k_2}>0.01286\), the equilibrium is asymptotically stable. When \({k_2}=0.01286\), the system undergoes a Hopf bifurcation, and it is unstable when \({k_2}<0.01286\). From Fig. 6, we observe that system (2.2) is asymptotically stable when \({k_2}=0.017\), and it presents periodic oscillation when \({k_2}=0.01\). We know that the Hopf bifurcation in continuous systems can be seen as an analogue of the Neimark–Sacker bifurcation in discrete systems. Besides, system (2.2) can undergo a saddle-node bifurcation, which corresponds to a fold bifurcation that appears in discrete system (2.3). So Fig. 1 also shows how the number of the equilibria of system (2.2) changes. From all the above simulation results, we see that discrete system (2.3) presents diverse dynamic phenomena, which are not observed in continuous system (2.2). So the dynamic behaviors of system (2.3) are richer than those of system (2.2) to some extent.

5 Conclusion and discussion

In this paper, we have investigated diverse dynamic behaviors in a discrete-time genetic regulatory network. Taking the biological parameter \({\alpha _1}\) and discretization step size \(\delta \) as bifurcation parameters, we demonstrate the occurrence of fold bifurcation, flip bifurcation and Neimark–Sacker bifurcation. Apart from the bifurcations presented in theoretical results, the numerical simulations also demonstrate that the system can display an invariant cycle, period orbits and even strange attractors, which validates that the discrete-time genetic regulatory network can exhibit much richer dynamic phenomena than those observed in the continuous-time version. As to the future work, complex dynamics especially strange attractors in a large-scale genetic network should be concerned. Attention can also be paid to the dynamic behaviors influenced by the topological structure of a genetic network, which helps us to explore the dynamic mechanisms in complex networks.

As to the results obtained in this paper, we shall make a discussion about the meaning of them. Firstly, the research reveals the important role of step size in the genetic system. When the model is discretized for computer simulation in genetic engineering, the step size is included as an additional parameter. Knowing the threshold value of the step size for bifurcations helps us to better retain the properties of the original system. On the other hand, the occurrence of bifurcations and chaos indicates that it makes a difference to the dynamic behaviors of DGRNs. Secondly, for the genetic circuit proposed in [13], the overall results expand its capability to take on complex kinetics. Previous studies are mainly about the multistability and Hopf bifurcation. In this paper, diverse dynamics is analyzed in the discrete model that is established based on the circuit. It enriches the dynamic behaviors which could be exhibited by the simple genetic circuit. Finally, the results confirm a significant mechanism for the evolution of dynamical complexities of genetic networks. In previous studies, it has been verified that the combination of a Hopf bifurcation and a hysteresis dynamics can generate chaotic behaviors in a genetic system. We show that the Neimark–Sacker bifurcation provides another route to chaos for the genetic model. The relationships among bifurcations and other dynamics contribute to our understanding of the complexity and diversity of dynamics in genetic networks, especially DGRNs.