1 Introduction

As is well known, the dynamic research on neural network models has achieved fruitful results, and it has been applied in pattern recognition, automatic control, signal processing and artificial intelligence. However, most neural network models proposed and discussed in the literature are deterministic. It has the characteristics of being simple and easy to analyze. In fact, for any actual system, there is always a variety of random factors. However, in real nervous systems and in the implementation of artificial neural networks, noise is unavoidable [1, 2] and should be taken into consideration in modeling. Stochastic neural network is an artificial neural network and is used as a tool of artificial intelligence. Therefore, it is of practical importance to study the stochastic neural networks. The authors of [3] studied the stability of stochastic neural networks in 1996. Subsequently, some scholars carried out a lot of research work and made some progress [4–7]. Due to the finite switching speed of neurons and amplifiers, time delays inevitably exist in biological and artificial neural network models. In recent years, the study of the stability of delay stochastic neural networks has become a hot spot in many scholars [8–15]. It is well known that the external inputs can influence the dynamic behaviors of neural networks in practical applications. Therefore, it is significant to study the input-to-state stability problem in the field of stochastic neural networks [16–19].

Besides, the quaternion-valued neural network has been one of the most popular research hot spots, due to the storage capacity advantage compared to real-valued neural networks and complex-valued neural networks. It can be applied to the fields of robotics, attitude control of satellites, computer graphics, ensemble control, color night vision and image impression [20, 21]. The skew field of quaternion by

$$\begin{aligned} \mathbb{Q}:=\bigl\{ q=q^{R}+iq^{I}+jq^{J}+kq^{K} \bigr\} , \end{aligned}$$

where \(q^{R}\), \(q^{I}\), \(q^{J}\), \(q^{K}\) are real numbers, the three imaginary units i, j and k obey Hamilton’s multiplication rules:

$$ ij=-ji=k,\qquad jk=-kj=i,\qquad ki=-ik=j, \qquad i^{2}=j^{2}=k^{2}=ijk=-1. $$

Since quaternion-valued neural networks were proposed, the study of quaternion-valued neural networks has received much attention of many scholars, and some results have been obtained for the stability ([22–27]), dissipativity ([28, 29]), input-to-state stability [30] and anti-periodic solutions [31] for the quaternion-valued neural networks. Very recently, many scholars considered the problem of robust stability for stochastic complex-valued neural networks [32, 33]. Subsequently, some scholars considered the problem of stability for stochastic quaternion-valued neural networks [34, 35]. However, to the best of our knowledge, till now there is still no result about the mean-square exponential input-to-state stability analysis for the stochastic quaternion-valued neural networks by direct method. So it is a challenging and important problem in theories and applications.

With the inspiration from the previous research, in order to fill the gap in the research field of quaternion-valued stochastic neural networks, the work of this paper comes from two main motivations. (1) The stability criterion is the mean-square exponential input-to-state stability, which is more general than the traditional mean-square exponential stability. In the past decade, many authors studied the input-to-state stability analysis for a class of stochastic delayed neural networks [16–19]. (2) Recently, little literature [34, 35] had studied the square-mean stability of quaternion-valued stochastic neural networks, thus it is worth studying the mean-square exponential input-to-state stability of the quaternion-valued stochastic neural networks by direct method.

Motivated by the above statement, in this paper, we consider the following stochastic quaternion-valued neural network:

$$\begin{aligned} \mathrm{d}z_{l}(t) =& \Biggl[-a_{l}(t)z_{l}(t)+ \sum_{k=1}^{n}b_{lk}(t)f_{k} \bigl(z_{k}(t) \bigr) +\sum_{k=1}^{n}c_{lk}(t)g_{k} (z_{k}\bigl(t-\theta _{lk}(t) \bigr) \\ &{}+U_{l}(t) \Biggr]\,\mathrm{d}t +\sum_{k=1}^{n} \sigma _{lk} \bigl(z_{k}\bigl(t- \eta _{lk}(t) \bigr) \bigr)\,\mathrm{d}B_{k}(t), \end{aligned}$$
(1.1)

where \(l\in \{1,2,\ldots ,n\}=:\mathcal{N}\), n is the number of neurons in layers; \(z_{l}(t)\in \mathbb{Q}\) is the state of the pth neuron at time t; \(a_{l}(t)>0\) is the self-feedback connection weight; \(b_{lk}(t)\) and \(c_{lk}(t)\in \mathbb{Q}\) are, respectively, the connection weight and the delay connection weight from neuron k to neuron l; \(\theta _{lk}(t)\) and \(\eta _{lk}(t)\) are the transmission delays; \(f_{k}, g_{k}:\mathbb{Q}\rightarrow \mathbb{Q}\) are the activation functions; \(U(t)=(U_{1}(t),U_{2}(t),\ldots ,U_{n}(t))\) belongs to \(\ell _{\infty }\), where \(\ell _{\infty }\) denotes the class of essentially bounded functions U from \(\mathbb{R}^{+}\) to \(\mathbb{Q}^{n}\) with \(\|U\|_{\infty }=\operatorname{esssup}_{t\geq 0}\|U(t)\|_{\mathbb{Q}}< \infty \); \(B(t)= (B_{1}(t),B_{2}(t),\ldots ,B_{n}(t) )^{T}\) is an n-dimensional Brownian motion defined on a complete probability space space; \(\sigma _{lk}:\mathbb{Q}\rightarrow \mathbb{Q}\) is a Borel measurable function; \(\sigma =(\sigma _{lk})_{n\times n}\) is the diffusion coefficient matrix.

For every \(z\in \mathbb{Q}\), the conjugate transpose of z is defined as \(z^{\ast }=z^{R}-iz^{I}-jz^{J}-kz^{K}\), and the norm of z is defined as

$$ \Vert z \Vert _{\mathbb{Q}}=\sqrt{zz^{\ast }}=\sqrt{ \bigl(z^{R}\bigr)^{2}+\bigl(z^{I} \bigr)^{2}+\bigl(z^{J}\bigr)^{2}+ \bigl(z^{K}\bigr)^{2}}. $$

For every \(z=(z_{1},z_{2},\ldots ,z_{n})^{T}\in \mathbb{Q}^{n}\), we define \(\|z\|_{\mathbb{Q}^{n}}=\max_{l\in \mathcal{N}}\{\|z_{l}\|_{ \mathbb{Q}}\}\).

For convenience, we will adopt the following notation:

$$\begin{aligned}& a_{l}^{-}=\inf_{t\in \mathbb{R}}a_{l}(t),\qquad b_{lk}^{+}= \sup_{t\in \mathbb{R}} \bigl\Vert b_{lk}(t) \bigr\Vert _{\mathbb{Q}}, \qquad c_{lk}^{+}= \sup_{t\in \mathbb{R}} \bigl\Vert c_{lk}(t) \bigr\Vert _{\mathbb{Q}}, \\& \theta ^{+}=\max_{l,k\in \mathcal{N}} \Bigl\{ \sup _{t \in \mathbb{R}}\theta _{kl}(t) \Bigr\} ,\qquad \eta ^{+}= \max_{l,k \in \mathcal{N}} \Bigl\{ \sup_{t\in \mathbb{R}}\eta _{lk}(t) \Bigr\} , \qquad \tau =\max \bigl\{ \theta ^{+},\eta ^{+} \bigr\} . \end{aligned}$$

The initial conditions of the system (1.1) is of the form

$$\begin{aligned} z_{l}(s)=\phi _{l}(s),\quad s\in [-\tau ,0], \end{aligned}$$

where \(\phi _{l}\in BC_{\mathcal{F}_{0}}([-\tau ,0],\mathbb{Q})\), \(l\in \mathcal{N}\).

Comparing the previous results, we have the following advantages: Firstly, this is the first time to study this problem, and it fills the gap in the field of stochastic quaternion-valued neural networks. Secondly, quaternion-valued stochastic neural network (1.1) contains real-valued stochastic neural networks and complex-valued stochastic neural networks as its special cases, the main results of this paper are new and more general than those in the existing quaternion-valued neural network models in the literature. Thirdly, unlike some previous studies of quaternion-valued stochastic neural networks, we do not decompose the systems under consideration into real-valued systems, but rather directly study quaternion-valued stochastic systems. Finally, our method of this paper can be used to study the mean-square exponential input-to-state stability for other types of quaternion-valued stochastic neural networks.

This paper is organized as follows: In Sect. 2, we introduce some definitions and state some preliminary results which are needed in later sections. In Sect. 3, we establish some sufficient conditions for the mean-square exponential input-to-state stability of system (1.1). In Sect. 4, we give an example to demonstrate the feasibility of our results. Finally, we draw a conclusion in Sect. 5.

2 Preliminaries and basic knowledge

In this section, we introduce the quaternion version Itô formula and the definition of the mean-square exponential input-to-state stability.

Let \((\Omega ,\mathcal{F},\{\mathcal{F}_{t}\}_{t\geq 0},\mathrm{P})\) be a complete probability space with a natural filtration \(\{\mathcal{F}_{t}\}_{t\geq 0}\) satisfying the usual conditions (i.e., it is right continuous, and \(\mathcal{F}_{0}\) contains all P-null sets). Denote by \(BC_{\mathcal{F}_{0}}([-\tau ,0],\mathbb{Q}^{n})\) the family of all bounded, \(\mathcal{F}_{0}\)-measurable, \(C([-\tau ,0],\mathbb{Q}^{n})\)-valued random variables. Denote by \(\mathcal{L}_{\mathcal{F}_{0}}^{2}([-\tau ,0],\mathbb{Q}^{n})\) the family of all \(\mathcal{F}_{0}\)-measurable, \(C([-\tau ,0],\mathbb{Q}^{n})\)-valued random variables ϕ, satisfying \(\sup_{s\in [-\tau ,0]}\mathrm{E}\|\phi (s)\|_{\mathbb{Q}}^{2}< \infty \), where E denotes the expectation of the stochastic process.

Definition 2.1

Consider an n-dimensional quaternion-valued stochastic differential equation:

$$\begin{aligned} \mathrm{d}z(t)=f\bigl(t,z(t),z\bigl(t-\theta (t)\bigr)\bigr)\,\mathrm{d}t+g \bigl(t,z(t),z\bigl(t- \eta (t)\bigr)\bigr)\,\mathrm{d}B(t), \end{aligned}$$

where \(z(t)=(z_{1}(t),z_{2}(t),\ldots ,z_{n}(t))^{T}\in \mathbb{Q}^{n}\). For \(V(t,z):\mathbb{R}^{+}\times \mathbb{Q}^{n}\rightarrow \mathbb{R}^{+}\) (in fact, we can write \(V(t,z)=V(t,z^{R},z^{I},z^{J},z^{K})\)), define the \(\mathbb{R}\)-derivative of V as

$$\begin{aligned}& \frac{\partial V(t,z)}{\partial z^{R}}\bigg|_{z^{I},z^{J},z^{K}= \mathrm{const}} = \biggl(\frac{\partial V(t,z(t))}{\partial z_{1}^{R}}, \ldots , \frac{\partial V(t,z(t))}{\partial z_{n}^{R}} \biggr)\bigg|_{z^{I},z^{J},z^{K}= \mathrm{const}}, \\& \frac{\partial V(t,z)}{\partial z^{I}}\bigg|_{z^{R},z^{J},z^{K}= \mathrm{const}} = \biggl(\frac{\partial V(t,z(t))}{\partial z_{1}^{I}}, \ldots , \frac{\partial V(t,z(t))}{\partial z_{n}^{I}} \biggr)\bigg|_{z^{R},z^{J},z^{K}= \mathrm{const}}, \\& \frac{\partial V(t,z)}{\partial z^{J}}\bigg|_{z^{R},z^{I},z^{K}= \mathrm{const}} = \biggl(\frac{\partial V(t,z(t))}{\partial z_{1}^{J}}, \ldots , \frac{\partial V(t,z(t))}{\partial z_{n}^{J}} \biggr)\bigg|_{z^{R},z^{I},z^{K}= \mathrm{const}}, \\& \frac{\partial V(t,z)}{\partial z^{K}}\bigg|_{z^{R},z^{I},z^{J}= \mathrm{const}} = \biggl(\frac{\partial V(t,z(t))}{\partial z_{1}^{K}}, \ldots , \frac{\partial V(t,z(t))}{\partial z_{n}^{K}} \biggr)\bigg|_{z^{R},z^{I},z^{J}= \mathrm{const}}, \end{aligned}$$

where const represents constant. Let \(C^{1,2}(\mathbb{R}^{+}\times \mathbb{Q}^{n},\mathbb{R}^{+})\) denote the family of all nonnegative functions \(V(t,z)\) on \(\mathbb{R}^{+}\times \mathbb{Q}^{n}\), which are once continuously differentiable in t and twice differentiable in \(z^{R}\), \(z^{I}\), \(z^{J}\) and \(z^{K}\). Then, for \(V\in C^{1,2}(\mathbb{R}^{+}\times \mathbb{Q}^{n},\mathbb{R}^{+})\), the quaternion version of the Itô formula takes the following form:

$$\begin{aligned}& \mathrm{d}V(t,z) \\& \quad = \frac{\partial V(t,z)}{\partial t}\,\mathrm{d}t + \frac{\partial V(t,z)}{\partial z^{R}}\,\mathrm{d}z^{R} + \frac{\partial V(t,z)}{\partial z^{I}}\,\mathrm{d}z^{I}+ \frac{\partial V(t,z)}{\partial z^{J}}\,\mathrm{d}z^{J}+ \frac{\partial V(t,z)}{\partial z^{K}}\,\mathrm{d}z^{K} \\& \qquad {} +\frac{1}{2}\sum_{l,k=1}^{n} \frac{\partial ^{2} V(t,z)}{\partial z_{l}^{R}\partial z_{k}^{R}} \,\mathrm{d}z_{l}^{R}\,\mathrm{d}z_{k}^{R}+ \frac{1}{2}\sum_{l,k=1}^{n} \frac{\partial ^{2} V(t,z)}{\partial z_{l}^{I}\partial z_{k}^{I}} \,\mathrm{d}z_{l}^{I}\,\mathrm{d}z_{k}^{I} \\& \qquad {} +\frac{1}{2}\sum_{l,k=1}^{n} \frac{\partial ^{2} V(t,z)}{\partial z_{l}^{J}\partial z_{k}^{J}} \,\mathrm{d}z_{l}^{J}\,\mathrm{d}z_{k}^{J} +\frac{1}{2}\sum_{l,k=1}^{n} \frac{\partial ^{2} V(t,z)}{\partial z_{l}^{K}\partial z_{k}^{K}} \,\mathrm{d}z_{l}^{K}\,\mathrm{d}z_{k}^{K} \\& \qquad {} +\sum_{l,k=1}^{n} \frac{\partial ^{2} V(t,z)}{\partial z_{l}^{R}\partial z_{k}^{I}} \,\mathrm{d}z_{l}^{R}\,\mathrm{d}z_{k}^{I}+ \sum_{l,k=1}^{n} \frac{\partial ^{2} V(t,z)}{\partial z_{l}^{R}\partial z_{k}^{J}} \,\mathrm{d}z_{l}^{R}\,\mathrm{d}z_{k}^{J} \\& \qquad {} +\sum_{l,k=1}^{n} \frac{\partial ^{2} V(t,z)}{\partial z_{l}^{R}\partial z_{k}^{K}} \,\mathrm{d}z_{l}^{R}\,\mathrm{d}z_{k}^{K} + \sum_{l,k=1}^{n} \frac{\partial ^{2} V(t,z)}{\partial z_{l}^{I}\partial z_{k}^{J}} \,\mathrm{d}z_{l}^{I}\,\mathrm{d}z_{k}^{J} \\& \qquad {} +\sum_{l,k=1}^{n} \frac{\partial ^{2} V(t,z)}{\partial z_{l}^{I}\partial z_{k}^{K}} \,\mathrm{d}z_{l}^{I}\,\mathrm{d}z_{k}^{K} + \sum_{l,k=1}^{n} \frac{\partial ^{2} V(t,z)}{\partial z_{l}^{J}\partial z_{k}^{K}} \,\mathrm{d}z_{l}^{J}\,\mathrm{d}z_{k}^{K} \\& \quad = \mathcal{L}V(t,z)\,\mathrm{d}t+ \biggl[ \frac{\partial V(t,z)}{\partial z^{R}}g^{R}(t) + \frac{\partial V(t,z)}{\partial z^{I}}g^{I}(t)+ \frac{\partial V(t,z)}{\partial z^{J}}g^{J}(t) \\& \qquad {} +\frac{\partial V(t,z)}{\partial z^{K}}g^{K}(t) \biggr]\,\mathrm{d}B(t), \end{aligned}$$

where \(f(t)=f(t,z(t),z(t-\theta (t)))\), \(g(t)=g(t,z(t),z(t-\eta (t)))\), and operator \(\mathcal{L}V(t,z)\) is defined as

$$\begin{aligned}& \mathcal{L}V(t,z) \\& \quad = \frac{\partial V(t,z)}{\partial t} + \frac{\partial V(t,z)}{\partial z^{R}}f^{R}(t) + \frac{\partial V(t,z)}{\partial z^{I}}f^{I}(t)+ \frac{\partial V(t,z)}{\partial z^{J}}f^{J}(t) + \frac{\partial V(t,z)}{\partial z^{K}}f^{K}(t) \\& \qquad {}+\frac{1}{2}\bigl(g^{R}(t)\bigr)^{T} \frac{\partial ^{2} V(t,z)}{\partial (z^{R})^{2}}g^{R}(t) + \frac{1}{2}\bigl(g^{I}(t) \bigr)^{T} \frac{\partial ^{2} V(t,z)}{\partial (z^{I})^{2}}g^{I}(t) + \frac{1}{2} \bigl(g^{J}(t)\bigr)^{T} \frac{\partial ^{2} V(t,z)}{\partial (z^{J})^{2}}g^{J}(t) \\& \qquad {} +\frac{1}{2}\bigl(g^{K}(t)\bigr)^{T} \frac{\partial ^{2} V(t,z)}{\partial (z^{K})^{2}}g^{K}(t) +\bigl(g^{R}(t)\bigr)^{T} \frac{\partial ^{2} V(t,z)}{\partial z_{l}^{R}\partial z_{k}^{I}}g^{I}(t) +\bigl(g^{R}(t) \bigr)^{T} \frac{\partial ^{2} V(t,z)}{\partial z_{l}^{R}\partial z_{k}^{J}}g^{J}(t) \\& \qquad {} +\bigl(g^{R}(t)\bigr)^{T} \frac{\partial ^{2} V(t,z)}{\partial z_{l}^{R}\partial z_{k}^{K}}g^{K}(t) +\bigl(g^{I}(t)\bigr)^{T} \frac{\partial ^{2} V(t,z)}{\partial z_{l}^{I}\partial z_{k}^{J}}g^{J}(t) +\bigl(g^{I}(t)\bigr)^{T} \frac{\partial ^{2} V(t,z)}{\partial z_{l}^{I}\partial z_{k}^{K}}g^{K}(t) \\& \qquad {} +\bigl(g^{J}(t)\bigr)^{T} \frac{\partial ^{2} V(t,z)}{\partial z_{l}^{J}\partial z_{k}^{K}}g^{K}(t). \end{aligned}$$

Definition 2.2

The trivial solution of system (1.1) is mean-square exponentially input-to-state stable, if there exist constants \(\lambda >0\), \(\mathcal{M}_{1}>0\) and \(\mathcal{M}_{2}>0\) such that

$$\begin{aligned} \mathrm{E} \bigl\Vert z(t) \bigr\Vert _{\mathbb{Q}^{n}}^{2}\leq \mathcal{M}_{1}e^{- \lambda t}\mathrm{E} \Vert \phi \Vert _{1}^{2}+\mathcal{M}_{2} \Vert U \Vert _{\infty }^{2}, \end{aligned}$$

for \(\phi \in \mathcal{L}_{\mathcal{F}_{0}}^{2}([-\tau ,0],\mathbb{Q}^{n})\) and \(U\in \ell _{\infty }\), where

$$ \bigl\Vert z(t) \bigr\Vert _{\mathbb{Q}^{n}}= \Biggl[\sum _{l=1}^{n} \bigl\Vert z_{l}(t) \bigr\Vert _{ \mathbb{Q}}^{2} \Biggr]^{\frac{1}{2}},\qquad \Vert \phi \Vert _{1}= \Biggl[\sum_{l=1}^{n} \Bigl(\sup_{s\in [-\tau ,0]} \bigl\Vert \phi _{l}(s) \bigr\Vert _{ \mathbb{Q}}^{2} \Bigr) \Biggr]^{\frac{1}{2}}. $$

Lemma 2.1

([31])

For all \(a,b\in \mathbb{Q}\), \(a^{\ast }b+b^{\ast }a\leq a^{\ast }a+b^{\ast }b\).

Throughout the rest of the paper, we assume that:

\((H_{1})\):

There exist positive constants \(L_{k}^{f}\), \(L_{k}^{g}\), \(L_{lk}^{\sigma }\) such that for any \(x,y\in \mathbb{Q}\),

$$\begin{aligned}& \bigl\Vert f_{k}(x)-f_{k}(y) \bigr\Vert _{\mathbb{Q}} \leq L_{k}^{f} \Vert x-y \Vert _{\mathbb{Q}},\qquad \bigl\Vert g_{k}(x)-g_{k}(y) \bigr\Vert _{\mathbb{Q}} \leq L_{k}^{g} \Vert x-y \Vert _{\mathbb{Q}}, \\& \bigl\Vert \sigma _{lk}(x)-\sigma _{lk}(y) \bigr\Vert _{\mathbb{Q}} \leq L_{lk}^{ \sigma } \Vert x-y \Vert _{\mathbb{Q}},\qquad f_{k}(\mathbf{0})=g_{k}( \mathbf{0})= \sigma _{lk}(\mathbf{0})=\mathbf{0},\quad l,k\in \mathcal{N}. \end{aligned}$$
\((H_{2})\):

For \(l\in \mathcal{N}\), there exist positive constants λ and \(\xi _{k}\) such that

$$\begin{aligned} 2\xi _{l}a_{l}^{-} >& \lambda \xi _{l}+2\xi _{l} +\sum_{k=1}^{n} \xi _{k} \bigl(b_{kl}^{+} \bigr)^{2} \bigl(L_{k}^{f} \bigr)^{2} +\sum _{k=1}^{n}\xi _{k} \bigl(c_{kl}^{+} \bigr)^{2} \bigl(L_{k}^{g} \bigr)^{2} \frac{e^{\lambda \theta ^{+}}}{1-\gamma } \\ &{}+\sum_{k=1}^{n}\xi _{k} \bigl(L_{kl}^{\sigma } \bigr)^{2} \frac{e^{\lambda \eta ^{+}}}{1-\beta }, \end{aligned}$$

where \(\gamma =\sup_{t\in \mathbb{R}}\{\theta _{lk}'(t)\}\), \(\beta =\sup_{t\in \mathbb{R}}\{\eta _{lk}'(t)\}\).

3 Mean-square exponential input-to-state stability

In this section, we will consider the mean-square exponential input-to-state stability of system (1.1).

Theorem 3.1

Suppose that Assumptions \((H_{1})\)–\((H_{2})\) are satisfied, then, for any initial value of the dynamical system (1.1), there exists a trivial solution \(z(t)\), which is mean-square exponentially input-to-state stable.

Proof

Let \(\sigma (t)=(\sigma _{lk}(t))_{n\times n}\), where \(\sigma _{lk}(t)=\sigma _{lk}(z_{k}(t-\eta _{lk}(t)))\). We consider the Lyapunov function as follows:

$$\begin{aligned} V\bigl(t,z(t)\bigr)=e^{\lambda t}\sum_{l=1}^{n} \xi _{l}z_{l}^{\ast }(t)z_{l}(t)+ \sum _{l=1}^{n}\Theta _{l}\bigl(t,z(t) \bigr), \end{aligned}$$

where

$$\begin{aligned} \Theta _{l}\bigl(t,z(t)\bigr) =&\sum_{k=1}^{n} \bigl(c_{lk}^{+} \bigr)^{2} \bigl(L_{k}^{g} \bigr)^{2}\frac{e^{\lambda \theta ^{+}}}{1-\gamma } \int _{t-\theta _{kl}(t)}^{t}z_{k}^{ \ast }(s)z_{k}(s) e^{\lambda s}\,\mathrm{d}s \\ &{}+\sum_{k=1}^{n} \bigl(L_{lk}^{\sigma } \bigr)^{2} \frac{e^{\lambda \eta ^{+}}}{1-\beta } \int _{t-\eta _{lk}(t)}^{t}z_{k}^{ \ast }(s)z_{k}(s)e^{\lambda s} \,\mathrm{d}s. \end{aligned}$$

Then, by the Itô formula, we have the following stochastic differential:

$$\begin{aligned} \mathrm{d}V\bigl(t,z(t)\bigr)=\mathcal{L}V\bigl(t,z(t)\bigr) \,\mathrm{d}t+V_{z}\bigl(t,z(t)\bigr) \sigma (t)\,\mathrm{d}B(t), \end{aligned}$$

where \(V_{z}(t,z(t))= (\frac{\partial V(t,z(t))}{\partial z_{1}},\ldots , \frac{\partial V(t,z(t))}{\partial z_{n}} )\), and \(\mathcal{L}\) is the weak infinitesimal operator such that

$$\begin{aligned}& \mathcal{L}V\bigl(t,z(t)\bigr) \\& \quad = \sum_{l=1}^{n} \Biggl\{ \lambda e^{\lambda t}\xi _{l}z_{l}^{\ast }(t)z_{l}(t) +e^{\lambda t}\xi _{l}z_{l}(t) \Biggl[-a_{l}(t)z_{l}^{\ast }(t) +\sum_{k=1}^{n} \bigl(b_{lk}(t)f_{k} \bigl(z_{k}(t) \bigr) \bigr)^{\ast } \\& \qquad {} +\sum_{k=1}^{n} \bigl(c_{lk}(t)g_{k} \bigl(z_{k}\bigl(t-\theta _{kl}(t)\bigr) \bigr) \bigr)^{\ast }+U_{l}^{\ast }(t) \Biggr] +e^{\lambda t} \xi _{l}z_{l}^{ \ast }(t) \Biggl[-a_{l}(t)z_{l}(t) \\& \qquad {} +\sum_{k=1}^{n}b_{lk}(t)f_{k} \bigl(z_{k}(t) \bigr) +\sum_{k=1}^{n}c_{lk}(t)g_{k} \bigl(z_{k}\bigl(t-\theta _{kl}(t)\bigr) \bigr)+U_{l}(t) \Biggr] \\& \qquad {} +\xi _{l}\sum_{k=1}^{n} \bigl(c_{lk}^{+} \bigr)^{2} \bigl(L_{k}^{g} \bigr)^{2}\frac{e^{\lambda \theta ^{+}}}{1-\gamma } z_{k}^{\ast }(t)z_{k}(t)e^{ \lambda t} -\xi _{l}\sum_{k=1}^{n} \bigl(c_{lk}^{+} \bigr)^{2} \bigl(L_{k}^{g} \bigr)^{2}\frac{e^{\lambda \theta ^{+}}}{1-\gamma }\bigl(1-\theta _{kl}'(t) \bigr) \\& \qquad {} \times z_{k}^{\ast }\bigl(t-\theta _{kl}(t) \bigr)z_{k}\bigl(t-\theta _{kl}(t)\bigr)e^{ \lambda (t-\theta _{kl}(t))} \,\mathrm{d}s +\xi _{l}\sum_{k=1}^{n} \bigl(L_{lk}^{ \sigma } \bigr)^{2}\frac{e^{\lambda \eta ^{+}}}{1-\beta } z_{k}^{\ast }(t)z_{k}(t)e^{ \lambda t} \\& \qquad {} -\xi _{l}\sum_{k=1}^{n} \bigl(L_{lk}^{\sigma } \bigr)^{2} \frac{e^{\lambda \eta ^{+}}}{1-\beta } \bigl(1-\eta _{lk}'(t)\bigr) z_{k}^{\ast } \bigl(t- \eta _{lk}(t)\bigr)z_{k}\bigl(t-\eta _{lk}(t)\bigr)e^{\lambda (t-\eta _{lk}(t))} \\& \qquad {} +e^{\lambda t}\xi _{l} \times \sum_{k=1}^{n} \bigl[\sigma _{lk} \bigl(z_{k}\bigl(t- \eta _{lk}(t)\bigr) \bigr) \bigr]^{\ast } \bigl[\sigma _{lk} \bigl(z_{k}\bigl(t-\eta _{lk}(t)\bigr) \bigr) \bigr] \Biggr\} \\& \quad \leq \sum_{l=1}^{n} \Biggl\{ e^{\lambda t} \bigl(\lambda \xi _{l}-2 \xi _{l}a_{l}(t) \bigr)z_{l}^{\ast }(t)z_{l}(t) +e^{\lambda t} \xi _{l} \sum_{k=1}^{n} \bigl(b_{lk}(t)f_{k} \bigl(z_{k}(t) \bigr) \bigr)^{\ast } \\& \qquad {} \times \bigl(b_{lk}(t)f_{k} \bigl(z_{k}(t) \bigr) \bigr) +e^{\lambda t} \xi _{l}\sum _{k=1}^{n} \bigl(c_{lk}(t)g_{k} \bigl(z_{k}\bigl(t-\theta _{kl}(t)\bigr) \bigr) \bigr)^{\ast } \\& \qquad {} \times \bigl(c_{lk}(t)g_{k} \bigl(z_{k} \bigl(t-\theta _{kl}(t)\bigr) \bigr) \bigr)+e^{ \lambda t} \xi _{l}U_{l}^{\ast }(t)U_{l}(t)+2e^{\lambda t} \xi _{l}z_{l}^{ \ast }(t)z_{l}(t) \\& \qquad {} +e^{\lambda t}\sum_{p=1}^{n}\xi _{l}\sum_{k=1}^{n} \bigl(c_{lk}^{+} \bigr)^{2} \bigl(L_{k}^{g} \bigr)^{2} \frac{e^{\lambda \theta ^{+}}}{1-\gamma }z_{k}^{\ast }(t)z_{k}(t)-e^{ \lambda t} \xi _{l}\sum_{k=1}^{n} \bigl(c_{lk}^{+} \bigr)^{2} \bigl(L_{k}^{g} \bigr)^{2}\frac{e^{\lambda \theta ^{+}}}{1-\gamma } \\& \qquad {} \times (1-\gamma ) z_{k}^{\ast }\bigl(t-\theta _{kl}(t)\bigr)z_{k}\bigl(t-\theta _{kl}(t) \bigr)e^{- \lambda \theta ^{+}}\,\mathrm{d}s+e^{\lambda t}\xi _{l}\sum _{k=1}^{n} \bigl(L_{lk}^{\sigma } \bigr)^{2}\frac{e^{\lambda \eta ^{+}}}{1-\beta } z_{k}^{ \ast }(t)z_{k}(t) \\& \qquad {} -e^{\lambda t}\xi _{l}\sum_{k=1}^{n} \bigl(L_{lk}^{\sigma } \bigr)^{2} \frac{e^{\lambda \eta ^{+}}}{1-\beta }(1- \beta ) z_{k}^{\ast }\bigl(t-\eta _{lk}(t) \bigr)z_{k}\bigl(t- \eta _{lk}(t)\bigr)e^{-\lambda \eta ^{+}} \\& \qquad {} +e^{\lambda t}\xi _{l}\sum_{k=1}^{n} \bigl(L_{lk}^{\sigma } \bigr)^{2}z_{k}^{ \ast } \bigl(t-\eta _{lk}(t)\bigr)z_{k}\bigl(t-\eta _{lk}(t)\bigr) \Biggr\} \\& \quad \leq \sum_{l=1}^{n} \Biggl\{ e^{\lambda t} \bigl(\lambda \xi _{l}+2\xi _{l}-2 \xi _{l}a_{l}^{-} \bigr)z_{l}^{\ast }(t)z_{l}(t) +e^{\lambda t}\xi _{l} \sum_{k=1}^{n} \bigl(b_{lk}^{+} \bigr)^{2} \bigl(L_{k}^{f} \bigr)^{2}z_{k}^{ \ast }(t)z_{k}(t) \\& \qquad {} +e^{\lambda t}\xi _{l}\sum_{k=1}^{n} \bigl(c_{lk}^{+} \bigr)^{2} \bigl(L_{k}^{g} \bigr)^{2}\frac{e^{\lambda \theta ^{+}}}{1-\gamma } z_{k}^{\ast }(t)z_{k}(t)+e^{ \lambda t} \xi _{l}\sum_{k=1}^{n} \bigl(L_{lk}^{\sigma } \bigr)^{2} \frac{e^{\lambda \eta ^{+}}}{1-\beta }z_{k}^{\ast }(t)z_{k}(t) \\& \qquad {} +e^{\lambda t}\xi _{l}U_{l}^{\ast }(t)U_{l}(t) \Biggr\} \\& \quad = \sum_{l=1}^{n} \Biggl\{ e^{\lambda t} \Biggl\{ \Biggl(\lambda \xi _{l}+2 \xi _{l}-2\xi _{l}a_{l}^{-} +\sum _{k=1}^{n}\xi _{k} \bigl(b_{kl}^{+} \bigr)^{2} \bigl(L_{k}^{f} \bigr)^{2} \\& \qquad {}+ \sum_{k=1}^{n}\xi _{k} \bigl(c_{kl}^{+} \bigr)^{2} \bigl(L_{k}^{g} \bigr)^{2} \frac{e^{\lambda \theta ^{+}}}{1-\gamma } \\& \qquad {} +\sum_{k=1}^{n}\xi _{k} \bigl(L_{kl}^{\sigma } \bigr)^{2} \frac{e^{\lambda \eta ^{+}}}{1-\beta } \Biggr) z_{l}^{\ast }(t)z_{l}(t) \Biggr\} +e^{\lambda t}\xi _{l}U_{l}^{\ast }(t)U_{l}(t) \Biggr\} . \end{aligned}$$
(3.1)

From \((H_{2})\), we easily derive

$$\begin{aligned} \mathcal{L}V\bigl(t,z(t)\bigr)\leq e^{\lambda t}\sum _{l=1}^{n}\xi _{l}U_{l}^{ \ast }(t)U_{l}(t) \leq e^{\lambda t}\max_{l\in \mathcal{N}} \xi _{l} \Vert U \Vert _{\infty }^{2}. \end{aligned}$$
(3.2)

Now, similar to the previous literature, we define the stopping time (or Markov time) \(\varrho _{k}:=\inf \{s\geq 0: |z(s)|\geq k\}\), and by the Dynkin formula, we have

$$\begin{aligned} \mathrm{E} \bigl[V\bigl(t\wedge \varrho _{k},z(t\wedge \varrho _{k})\bigr) \bigr] = \mathrm{E} \bigl[V(0,z(0) \bigr]+\mathrm{E} \biggl[ \int _{0}^{t\wedge \varrho _{k}}\mathcal{L}V\bigl(s,z(s)\bigr) \,\mathrm{d}s \biggr]. \end{aligned}$$
(3.3)

Letting \(k\rightarrow \infty \) on both sides (3.3), from the monotone convergence theorem, we can get

$$\begin{aligned}& \mathrm{E} \bigl[V\bigl(t,z(t)\bigr) \bigr] \\& \quad \leq \mathrm{E} \bigl[V(0,z(0) \bigr] + \Vert U \Vert _{\infty }^{2} \max_{l \in \mathcal{N}}\xi _{l} \int _{0}^{t}e^{\lambda s}\,\mathrm{d}s \\& \quad = \sum_{l=1}^{n} \Biggl\{ \xi _{l}\mathrm{E}z_{l}^{\ast }(0)z_{l}(0) + \xi _{l}\sum_{k=1}^{n} \bigl(c_{lk}^{+} \bigr)^{2} \bigl(L_{k}^{g} \bigr)^{2} \frac{e^{\lambda \theta ^{+}}}{1-\gamma } \int _{-\theta _{kl}(0)}^{0} \mathrm{E}z_{k}^{\ast }(s)z_{k}(s)e^{\lambda s} \,\mathrm{d}s \\& \qquad {} +\xi _{l}\sum_{k=1}^{n} \bigl(L_{lk}^{\sigma } \bigr)^{2} \frac{e^{\lambda \eta ^{+}}}{1-\beta } \int _{-\eta _{lk}(0)}^{0} \mathrm{E}z_{k}^{\ast }(s)z_{k}(s)e^{\lambda s} \,\mathrm{d}s \Biggr\} \\& \qquad {}+\frac{1}{\lambda } \Vert U \Vert _{\infty }^{2}\max _{l\in \mathcal{N}}\xi _{l}\bigl(e^{\lambda t}-1\bigr) \\& \quad \leq \sum_{l=1}^{n} \Biggl\{ \Biggl(\xi _{l}+ \xi _{l}\sum_{k=1}^{n} \bigl(c_{kl}^{+} \bigr)^{2} \bigl(L_{k}^{g} \bigr)^{2}\theta ^{+} \frac{e^{\lambda \theta ^{+}}}{1-\gamma } +\xi _{l} \sum_{k=1}^{n} \bigl(L_{kl}^{\sigma } \bigr)^{2}\eta ^{+} \frac{e^{\lambda \eta ^{+}}}{1-\beta } \Biggr) \\& \qquad {} \times \mathrm{E}\sup_{s\in [-\tau ,0]} \bigl\Vert \phi _{l}(s) \bigr\Vert _{ \mathbb{Q}}^{2} \Biggr\} + \frac{1}{\lambda } \Vert U \Vert _{\infty }^{2}\max _{l\in \mathcal{N}}\xi _{l}\bigl(e^{\lambda t}-1\bigr). \end{aligned}$$
(3.4)

On the other hand, it follows from the definition of \(V(t,z(t))\) that

$$\begin{aligned} \mathrm{E} \bigl[V\bigl(t,z(t)\bigr) \bigr] \geq& \mathrm{E}e^{\lambda t}\sum_{l=1}^{n} \xi _{l}z_{l}^{\ast }(t)z_{l}(t) \\ \geq& e^{\lambda t}\min_{l \in \mathcal{N}}\xi _{l}\mathrm{E} \bigl\Vert z(t) \bigr\Vert _{\mathbb{Q}^{n}}^{2}. \end{aligned}$$
(3.5)

Combining (3.4) and (3.5), the following holds:

$$\begin{aligned}& \mathrm{E} \bigl\Vert z(t) \bigr\Vert _{\mathbb{Q}^{n}}^{2} \\& \quad \leq \frac{1}{\min_{l\in \mathcal{N}}\xi _{l}}\sum_{l=1}^{n} \Biggl\{ \Biggl(\xi _{l}+ \xi _{l}\sum _{k=1}^{n} \bigl(c_{kl}^{+} \bigr)^{2} \bigl(L_{k}^{g} \bigr)^{2} \theta ^{+} \frac{e^{\lambda \theta ^{+}}}{1-\gamma } +\xi _{l}\sum _{k=1}^{n} \bigl(L_{kl}^{\sigma } \bigr)^{2}\eta ^{+} \frac{e^{\lambda \eta ^{+}}}{1-\beta } \Biggr) \\& \qquad {} \times \mathrm{E}\sup_{s\in [-\tau ,0]} \bigl\Vert \phi _{l}(s) \bigr\Vert _{ \mathbb{Q}}^{2} \Biggr\} + \frac{1}{\lambda \min_{l\in \mathcal{N}}\xi _{l}}\max_{l\in \mathcal{N}}\xi _{l} \Vert U \Vert _{\infty }^{2} \\& \quad \leq \mathcal{M}_{1}e^{-\lambda t}\mathrm{E} \Vert \phi \Vert _{1}^{2}+ \mathcal{M}_{2} \Vert U \Vert _{\infty }^{2}, \end{aligned}$$

where

$$\begin{aligned} \mathcal{M}_{1} =&\frac{1}{\min_{l\in \mathcal{N}}\xi _{l}} \sum _{l=1}^{n}\xi _{l} \Biggl\{ 1+ \sum _{k=1}^{n} \bigl(c_{kl}^{+} \bigr)^{2} \bigl(L_{k}^{g} \bigr)^{2} \theta ^{+} \frac{e^{\lambda \theta ^{+}}}{1-\gamma }+\sum_{k=1}^{n} \bigl(L_{kl}^{ \sigma } \bigr)^{2}\eta ^{+} \frac{e^{\lambda \eta ^{+}}}{1-\beta } \Biggr\} , \\ \mathcal{M}_{2} =&\frac{1}{\lambda \min_{l\in \mathcal{N}}\xi _{l}} \max_{l\in \mathcal{N}}\xi _{l}, \end{aligned}$$

which together with Definition 2.2 verifies that trivial solution of system (1.1) is mean-square exponentially input-to-state stable. The proof is complete. □

Remark 3.1

In the calculation process of Theorem 3.1, by using stochastic analysis theory and the Itô formula, we obtain the mean-square exponential input-to-state stability of system (1.1).

Remark 3.2

Theorem 3.1 can be applied to stability criteria for the considered stochastic network models by employing a non-decomposing method.

4 Illustrative example

In this section, we give an example to illustrate the feasibility and effectiveness of our results obtained in Sect. 3.

Example 4.1

Let \(n=3\). Consider the following quaternion-valued stochastic neural network:

$$\begin{aligned} \mathrm{d}z_{l}(t) =& \Biggl[-a_{l}(t)z_{l}(t)+ \sum_{k=1}^{3}b_{lk}(t)f_{k} \bigl(z_{k}(t) \bigr) +\sum_{k=1}^{3}c_{lk}(t)g_{k} (z_{k}\bigl(t-\theta _{lk}(t) \bigr) \\ &{}+U_{l}(t) \Biggr]\,\mathrm{d}t +\sum_{k=1}^{3} \sigma _{lk} \bigl(z_{k}\bigl(t- \eta _{lk}(t) \bigr) \bigr)\,\mathrm{d}B_{k}(t), \end{aligned}$$
(4.1)

where \(l=1,2,3\), the coefficients are follows:

$$\begin{aligned}& f_{k}(z_{k}) = \frac{1}{14}\sin z_{k}^{R}+i \frac{1}{12} \bigl\vert z_{k}^{I} \bigr\vert +j \frac{1}{15}\sin \bigl(z_{k}^{I}+z_{k}^{J} \bigr)+k\frac{1}{10}\sin z_{k}^{K}, \\& g_{k}(z_{k}) = \frac{1}{12}\sin \bigl(z_{k}^{R}+z_{k}^{J}\bigr)+i \frac{1}{20} \sin \bigl(z_{k}^{R}+z_{k}^{I} \bigr)+j\frac{1}{15}\tanh z_{k}^{J}+k\frac{1}{10} \tanh z_{k}^{K}, \\& \sigma _{lk}(z_{k}) = \frac{1}{15}\sin z_{k}^{R}+i\frac{1}{10}\sin z_{k}^{I}+j \frac{1}{8}\sin \bigl(z_{k}^{R}+z_{k}^{J} \bigr)+k\frac{1}{12}\tanh z_{k}^{K}, \\& b_{lk}(t) = 0.4\sin (\sqrt{2}t)+i0.6\cos (\sqrt{3}t)+j0.7\sin t+k0.5 \cos (2t), \\& c_{lk}(t) = 1.2\sin t+i0.9\cos (2t)+j\sin (\sqrt{2}t)+k1.5\cos ( \sqrt{3}t), \\& U_{1}(t) = 0.2\sin (\sqrt{3}t)+i0.5\cos (2t)+j0.3\cos (\sqrt{2} t)+k0.3 \sin (\sqrt{3}t), \\& U_{2}(t) = 0.3\cos (\sqrt{2}t)+i0.4\sin (\sqrt{3}t)+j0.5\sin t+k0.2 \cos (\sqrt{3}t) ), \\& U_{3}(t) = 0.2\sin (2t)+i0.3\cos (\sqrt{2}t)+j0.4\cos t+k0.3\sin ( \sqrt{5}t) ), \\& a_{1}(t)=2+ \bigl\vert \sin (\sqrt{3}t) \bigr\vert ,\qquad a_{2}(t)=5-2\cos (\sqrt{2}t), \\& a_{3}(t)=7-3\cos (\sqrt{5}t), \\& \theta _{kl}(t)=\frac{1}{2} \bigl\vert \sin (\sqrt{2}t) \bigr\vert ,\qquad \eta _{lk}(t)= \frac{4}{5} \bigl\vert \cos (2t) \bigr\vert ,\quad l,k=1,2,3. \end{aligned}$$

Through simple calculations, we have

$$\begin{aligned}& a_{1}^{-}=2,\qquad a_{2}^{-}=3,\qquad a_{3}^{-}=4,\qquad L_{k}^{f}=L_{k}^{g}= \frac{1}{10},\qquad L_{lk}^{\sigma }=\frac{1}{8}, \\& \theta ^{+}=\frac{1}{2},\qquad \eta ^{+}= \frac{4}{5},\qquad \gamma = \frac{1}{2},\\& \beta =\frac{4}{5},\qquad b_{lk}^{+}\leq 1.1225,\qquad c_{lk}^{+}\leq 2.3452. \end{aligned}$$

Take \(\lambda =0.1\), \(\xi _{1}=0.3\), \(\xi _{2}=0.4\), \(\xi _{3}=0.5\), then we have

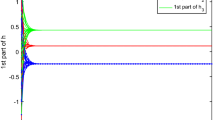
$$\begin{aligned}& 2\xi _{1}a_{1}^{-}=1.2 \\& \hphantom{2\xi _{1}a_{1}^{-}}> \lambda \xi _{1}+2\xi _{1} +\sum_{k=1}^{3} \xi _{k} \bigl(b_{k1}^{+} \bigr)^{2} \bigl(L_{k}^{f} \bigr)^{2} +\sum _{k=1}^{3} \xi _{k} \bigl(c_{k1}^{+} \bigr)^{2} \bigl(L_{k}^{g} \bigr)^{2} \frac{e^{\lambda \theta ^{+}}}{1-\gamma } \\& \hphantom{2\xi _{1}a_{1}^{-}=}{} +\sum_{k=1}^{3}\xi _{k} \bigl(L_{k1}^{\sigma } \bigr)^{2} \frac{e^{\lambda \eta ^{+}}}{1-\beta } \approx 0.8704, \\& 2\xi _{2}a_{2}^{-}=2.4 \\& \hphantom{2\xi _{2}a_{2}^{-}} > \lambda \xi _{2}+2\xi _{2} +\sum_{k=1}^{3} \xi _{k} \bigl(b_{k2}^{+} \bigr)^{2} \bigl(L_{k}^{f} \bigr)^{2} +\sum _{k=1}^{3} \xi _{k} \bigl(c_{k2}^{+} \bigr)^{2} \bigl(L_{k}^{g} \bigr)^{2} \frac{e^{\lambda \theta ^{+}}}{1-\gamma } \\& \hphantom{2\xi _{2}a_{2}^{-}=}{} +\sum_{k=1}^{3}\xi _{k} \bigl(L_{k2}^{\sigma } \bigr)^{2} \frac{e^{\lambda \eta ^{+}}}{1-\beta } \approx 1.0804, \\& 2\xi _{3}a_{3}^{-}=4 \\& \hphantom{2\xi _{3}a_{3}^{-}} > \lambda \xi _{3}+2\xi _{3} +\sum_{k=1}^{3} \xi _{k} \bigl(b_{k3}^{+} \bigr)^{2} \bigl(L_{k}^{f} \bigr)^{2} +\sum _{k=1}^{3} \xi _{k} \bigl(c_{k3}^{+} \bigr)^{2} \bigl(L_{k}^{g} \bigr)^{2} \frac{e^{\lambda \theta ^{+}}}{1-\gamma } \\& \hphantom{2\xi _{3}a_{3}^{-}=}{} +\sum_{k=1}^{3}\xi _{k} \bigl(L_{k3}^{\sigma } \bigr)^{2} \frac{e^{\lambda \eta ^{+}}}{1-\beta } \approx 1.2904. \end{aligned}$$

We can check that other conditions of Theorem 3.1 are satisfied. So, we know that a trivial solution of system (4.1) is mean-square exponentially input-to-state stable (see Figs. 1–4). The system (4.1) has the initial values \(z_{1}(0)=0.3-0.3i+0.5j-0.3k\), \(z_{2}(0)=-0.2+0.4i-0.4j-0.45k\) and \(z_{3}(0)=0.1-0.1i+0.2j+0.35k\). We use the Simulink toolbox of Matlab to get the numerical simulation diagram of this example.

Figure 1
figure 1

State trajectories of variables \(z_{l}^{R}(t)\) of system (4.1) with \(U_{l}^{R}(t)\neq 0\), \(l=1,2,3\)

Full size image
Figure 2
figure 2

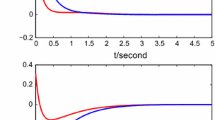
State trajectories of variables \(z_{l}^{R}(t)\) of system (4.1) with \(U_{l}^{R}(t)=0\), \(l=1,2,3\)

Full size image
Figure 3
figure 3

State trajectories of variables \(z_{l}^{I}(t)\) of system (4.1) with \(U_{l}^{I}(t)\neq 0\), \(l=1,2,3\)

Full size image
Figure 4
figure 4

State trajectories of variables \(z_{l}^{I}(t)\) of system (4.1) with \(U_{l}^{I}(t)=0\), \(l=1,2,3\)

Full size image
Figure 5
figure 5

State trajectories of variables \(z_{l}^{J}(t)\) of system (4.1) with \(U_{l}^{J}(t)\neq 0\), \(l=1,2,3\)

Full size image
Figure 6
figure 6

State trajectories of variables \(z_{l}^{J}(t)\) of system (4.1) with \(U_{l}^{J}(t)=0\), \(l=1,2,3\)

Full size image
Figure 7
figure 7

State trajectories of variables \(z_{l}^{K}(t)\) of system (4.1) with \(U_{l}^{K}(t)\neq 0\), \(l=1,2,3\)

Full size image

Remark 4.1

By using the Simulink toolbox in MATLAB, Figs. 1–8 show the time revolution of four parts of \(z_{1}\), \(z_{2}\), respectively. When \(U_{l}(t)=0\), our results will conclude the traditionally mean-square exponential stability for the considered stochastic neural networks.

Figure 8
figure 8

State trajectories of variables \(z_{l}^{K}(t)\) of system (4.1) with \(U_{l}^{K}(t)=0\), \(l=1,2,3\)

Full size image

Remark 4.2

Quaternion-valued stochastic system includes real-valued stochastic system as its special cases. In fact, in Example 4.1, if all the coefficients are functions from \(\mathbb{R}\) to \(\mathbb{R}\), and all the activation functions are functions from \(\mathbb{R}\) to \(\mathbb{R}\), then the state \(z_{l}(t) \equiv z_{l}^{R}(t)\in \mathbb{R}\), in this case, systems (4.1) is stochastic real-valued system. Then, similar to the proofs of 3.1 under the same corresponding conditions, one can show that a similar result to Theorem 3.1 is still valid (see [16–19]).

5 Conclusion

In this paper, we consider the problem of the mean-square exponential input-to-state stability for the quaternion-valued stochastic neural networks by direct method. Then, by constructing an appropriate Lyapunov functional, stochastic analysis theory and the Itô formula, a novel sufficient condition has been derived to ensure the mean-square exponential input-to-state stability for the considered stochastic neural networks. In order to demonstrate the usefulness of the presented results, a numerical example is given. This paper improves and extends the old results in the literature [34, 35], and proposes a good research framework to study the mean-square exponential input-to-state stability of quaternion-valued stochastic neural networks with time-varying delays. We expect to extend this work to the study of other types of stochastic neural networks.