Piezoelectric control of the Hopf bifurcation of Ziegler’s column with nonlinear damping

Abstract

Linear and nonlinear analyses of a piezoelectric-controlled Ziegler’s column, endowed with a Van der Pol-like nonlinear damping, are carried out in the present paper. The effects of three linear and passive piezoelectric controllers on the position and on the amplitude of the limit-cycle at the Hopf bifurcation, triggered by the follower force, are investigated. The controllers, previously introduced in the literature and here referred to as Non-Singular Resonant, Singular Non-Resonant, and Tuned Piezoelectric Damper, resemble well-known devices, adopted for controlling both linear and nonlinear oscillations, namely, a large-mass Tuned Mass Damper, a singular Energy Sink, and a classical small-mass Tuned Mass Damper. Numerical simulations on a linearly and uniformly damped column, under different nonlinear damping conditions, are carried out to show the effectiveness of the controllers in reducing the amplitude of the limit-cycle and their behavior with respect to the possible occurrence of the hard loss bifurcation.

1 Introduction

The Ziegler’s paradox or the ‘destabilizing effect of damping’ is a classical and widely studied topic in the dynamics of mechanical systems, see, e.g., [1–8] and the exhaustive review on the subject given in [9]. It takes place when a small and positive-definite damping is added to a linear circulatory system, consisting of an undamped system loaded by a non-conservative force of positional type, such as a follower force [10–12], producing a finite reduction in its critical load. With reference to finite-dimensional mechanical systems, a paradigmatic model exhibiting this paradoxical behavior is the Ziegler’s column [2–5], that is a double pendulum, with lumped masses and viscoelastic devices, loaded at the tip by a compression follower force.

The analysis on the effects of the paradox extended to the nonlinear behavior of the Ziegler’s column, i.e., when finite kinematics is assumed and nonlinear damping, in addition to the linear one, is introduced, is carried out in relatively few papers in the literature, e.g., in [13–17], with different aims. In [13, 14], the nonlinear analysis is performed to investigate the stability of the trivial equilibrium via the Normal Form Theory and the second method of Lyapunov, respectively, and for different damping forms, namely: linear in [13], linear and nonlinear of Van der Pol-type, also called ‘hysteretic,’ in [14]. In [15] a Multiple Time Scale analysis [18–20] is developed to analyze the nonlinear dynamics of the linearly and uniformly damped Ziegler’s column; the supercritical nature of the limit-cycle, occurring when the critical load is exceeded, is shown. In [16, 17] the Multiple Scale approach is followed, along the lines illustrated in [21–26] for bifurcation analysis, with the aim to detect the nonlinear behavior of the Ziegler’s column endowed with nonlinear damping, ruled by a Van der Pol-like law; it is seen that large-amplitude limit-cycles manifest themselves, in the absence of nonlinear damping, and that, if this kind of damping is added to the system, the amplitude of the limit-cycle can be reduced. However, it is also shown that nonlinear damping can have a detrimental effect on the nonlinear dynamics, due to the possible occurrence of the ‘hard loss of stability bifurcation’ (see, e.g., [27–29]), according to which a regain of stability is experienced after a subcritical branch of the periodic solution manifests itself.

The advantages in using piezoelectric controllers for reducing mechanical vibrations, with respect, e.g., to the classical devices based on added masses (see, e.g., [30–38]), can be summarized in: lower mass, higher performances and adaptability, the possibility to control a (wide) range of frequencies, and the capability of the piezoelectric devices to act as sensors and actuators, i.e., to realize both active [39, 40] and passive [41–52] control schemes, sometimes producing an unexpected detrimental effect on the structural stability when non-conservative actions are taken into account [53].

In a previous study [54] of the same author of the present paper, three linear and passive piezoelectric-based control strategies, giving rise to a (here referred) Non-Singular Resonant controller (NSR), Singular Non-Resonant controller (SNR), and Tuned Piezoelectric Damper (TPD), respectively, were defined with the aim to increase the critical load of a linear discrete structure in the presence of a follower action. The effectiveness of the proposed strategies on the Ziegler’s column, equipped with different piezoelectric arrangements, was also discussed. Remarkably, the working mechanism of each controller resembles that of well-known passive devices, namely: the controllers NSR and TPD are analogous to the Tuned Mass Damper [30, 32–34, 38], having large or small mass, respectively, and small stiffness; the controller SNR works by following the same principle of the Nonlinear Energy Sink (NES) [35–37], even if, differently from it, the controller is linear and the electromechanical coupling is of gyroscopic type.

In others recently appeared papers [55, 56], the nonlinear dynamics of the linearly damped and controlled Ziegler’s column, in finite kinematics, and equipped with one piezoelectric device, is investigated; in [55] the adopted control strategy was the SNR, while in [56] the TPD was used. In both the cases, it is shown that the effectiveness of the linear control in reducing the amplitude of the limit-cycle is mainly due to the forward shifting of the bifurcation diagram of the uncontrolled system, and that this effect is magnified when the value of the electromechanical coupling is increased.

The present paper is framed in the scenario illustrated above and has a twofold aim: (i) to evaluate the effectiveness of the NSR controller on the nonlinear behavior of the linearly damped Ziegler’s column and, possibly, to make comparisons with the other controllers, i.e., to complete the analysis already started in [55, 56]; (ii) to analyze the effects of each of the three piezoelectric controllers on the nonlinear response of the Ziegler’s column endowed with the nonlinear damping of Van der Pol-type and, in particular, to detect whether they are able to reduce or eliminate the undesirable behavior due to the occurrence of the hard loss of stability.

The paper is organized as follows. In Sect. 2, the equations of motion of the nonlinear Ziegler’s column, controlled and nonlinearly damped, are discussed. In Sect. 3, the behavior of the three controllers, applied to the linear column, is recalled and the electrical damping is optimized via a linear stability analysis. In Sect. 4, the response of the nonlinear and uncontrolled column is evaluated and the controlled problem is addressed. Section 5 resumes the main conclusions. Finally, an Appendix furnishes details on the derivation of the equations of motion.

2 The model

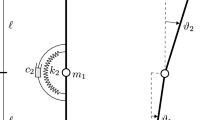
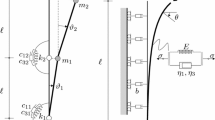
The system under study is a piezoelectric-controlled upward double pendulum, represented in Fig. 1. It is composed of: (i) two hinged rigid and weightless bars of equal length $\ell$; (ii) two lumped masses, $m_{1}=2m$ and $m_{2}=m$, in the correspondence of the common hinge (point B) and at the free-end C, respectively; (iii) viscoelastic constraints placed at the ground and at the common hinge (points A and B, respectively); (iv) a control system made of a piezoelectric device located at the ground hinge, which is connected to a one-node LR circuit, of inductance L and resistance R, and to the ground. Each of the two viscoelastic devices consists of a linear spring of stiffness $k_{j}=k$ ($j=1,2$) and a nonlinear dashpot, of linear viscosity coefficients $c_{1j}=c$ ($j=1,2$), and cubic viscosity coefficients $c_{3j}$ ($j=1,2$), these latter accounting for a nonlinear dissipation here assumed to be ruled by Van der Pol-type law (see, e.g., [14, 16, 17]); the piezoelectric stiffness is $k_{p}$ (assumed negligible throughout the paper), its capacitance $C_{p}$ and its coupling coefficient g. The column is loaded at the point C by a follower force of intensity F.

When the system is uncontrolled, nonlinear damping is absent, and infinitesimal rotations of the two bars are considered, the well-known Ziegler’s problem [2, 3] is obtained; in the same context, the equations of motion of the controlled system are derived (with different values of the lumped masses) in [54]. Moreover, when finite kinematics, in addition to the nonlinear damping, is considered for the uncontrolled system, the relevant equations of motion are those derived in [14, 16, 17]; finally, the relevant equations of the controlled and linearly damped column, in finite kinematics, are those discussed in [55, 56].

Fig. 1

Controlled nonlinear Ziegler’s column

The state of the system is described by taking as Lagrangian coordinates the rotations of the two bars, $\vartheta _{1}\left( t\right)$ and $\vartheta _{2}\left( t\right)$, and the flux linkage $\psi (t)$, namely the time integral of the voltage V, i.e., $\psi =\int Vdt$. The equations of motion of the piezoelectromechanical (PEM) system are obtained via the extended Hamilton principle (see the Appendix 1 and [54, 55] for a detailed derivation).

The non-dimensional equations of motion read:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} 3\ddot{\vartheta }_{1}+\ddot{\vartheta }_{2}\cos \left( \vartheta _{1}-\vartheta _{2}\right) +\dot{\vartheta }_{2}^{2}\sin \left( \vartheta _{1}-\vartheta _{2}\right) \\ &{} +\,2\vartheta _{1}-\vartheta _{2}+\xi _{m}\left( 2\dot{\vartheta }_{1}-\dot{\vartheta }_{2}\right) +\zeta {}_{1}\vartheta _{1}^{2}\dot{\vartheta }_{1}\\ &{} -\,\zeta _{2}\left( \vartheta _{2}-\vartheta _{1}\right) ^{2}\left( \dot{\vartheta }_{2}-\dot{\vartheta }_{1}\right) \\ &{} -\,\mu \sin \left( \vartheta _{1}-\vartheta _{2}\right) -\gamma \dot{\psi }=0\\ &{} \ddot{\vartheta }_{2}+\ddot{\vartheta }_{1}\cos \left( \vartheta _{1}-\vartheta _{2}\right) -\dot{\vartheta }_{1}^{2}\sin \left( \vartheta _{1}-\vartheta _{2}\right) \\ &{} +\,\vartheta _{2}-\vartheta _{1}+\xi _{m}\left( \dot{\vartheta }_{2}-\dot{\vartheta }_{1}\right) \\ &{} +\,\zeta _{2}\left( \vartheta _{2}-\vartheta _{1}\right) ^{2}\left( \dot{\vartheta }_{2}-\dot{\vartheta }_{1}\right) =0\\ &{} \nu _{e}\ddot{\psi }+\xi _{e}\dot{\psi }+\kappa _{e}\psi +\gamma \dot{\vartheta }_{1}=0 \end{array}\right. } \end{aligned}$$

(1)

where the dot denotes the time derivative and the following quantities are introduced for non-dimensionalization:

$$\begin{aligned}&\tilde{t} =\omega t, \quad \omega ^{2} =\frac{k}{m\ell ^{2}}, \quad \mu =\frac{F}{m\ell \omega ^{2}}\nonumber \\&\xi _{m} =\frac{c}{m\ell ^{2}\omega }, \quad \zeta _{1} =\frac{c_{31}}{m\ell ^{2}\omega }, \quad \zeta _{2} =\frac{c_{32}}{m\ell ^{2}\omega }\nonumber \\&\tilde{\psi } =\frac{\psi }{\psi _{0}}, \quad \nu _{e} =\frac{C_{p}}{C_{0}}, \quad \xi _{e} =\frac{1}{RC_{0}\omega }\nonumber \\&\kappa _{e} =\frac{1}{LC_{0}\omega ^{2}}, \quad \gamma =\frac{g}{\omega \ell \sqrt{mC_{0}}}, \quad \psi _{0} =\ell \sqrt{\frac{m}{C_{0}}} \end{aligned}$$

(2)

in which $C_{0}$ and $\psi _{0}$ are scaling capacitance and flux linkage, respectively. Moreover, $0<\mu \in {\mathbb {R}}$ is the load parameter (taken in the following as the bifurcation parameter); $0<\gamma \in {\mathbb {R}}$ is the electromechanical coupling coefficient; $\xi _{m}$ is the (mechanical) linear damping coefficient; $\zeta _{1}$ and $\zeta _{2}$ are the (mechanical) nonlinear damping coefficients. All the damping coefficients are assumed to be positive and reals. Finally, $\nu _{e}$, $\xi _{e}$, and $\kappa _{e}$ (all positive and real quantities) are electrical coefficients, here referred to as the ‘electrical mass’, ‘electrical damping’, and ‘electrical stiffness’, respectively.

3 Control of the linear systems

The control problem of the linear Ziegler’s column, as formulated in [54], is briefly recalled in this section. The equations of motion (1) are expanded for small rotations $\vartheta _{1}$ and $\vartheta _{2}$, and first-order terms are retained, while the nonlinear damping is ignored ($\zeta _{1}=\zeta _{2}=0$). The linear problem reads:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} 3\ddot{\vartheta }_{1}+\ddot{\vartheta }_{2}+\xi _{m}\left( 2\dot{\vartheta }_{1}-\dot{\vartheta }_{2}\right) +2\vartheta _{1}-\vartheta _{2}\\ &{} +\,\mu \left( \vartheta _{2}-\vartheta _{1}\right) -\gamma \dot{\psi }=0\\ &{} \ddot{\vartheta }_{1}+\ddot{\vartheta }_{2}+\xi _{m}\left( \dot{\vartheta }_{2}-\dot{\vartheta }_{1}\right) +\vartheta _{2}-\vartheta _{1}=0\\ &{} \nu _{e}\ddot{\psi }+\xi _{e}\dot{\psi }+\kappa _{e}\psi +\gamma \dot{\vartheta }_{1}=0 \end{array}\right. } \end{aligned}$$

(3)

3.1 Uncontrolled linearly damped systems

The linear stability domain of the uncontrolled column, that is when $\gamma =0$, is determined via the application of the Routh–Hurwitz criterion on the characteristic equation of the eigenvalue problem associated with Eq. (3-a,b) [4, 6]. A critical locus in the $\left( \xi _{m},\mu \right)$-plane is found, whose equation is:

$$\begin{aligned} \mu =\mu _{c}+\frac{\xi _{m}^{2}}{2}+\sqrt{2}-\frac{57}{28} \end{aligned}$$

(4)

where $\mu _{c}:=7/2-\sqrt{2}\simeq 2.086$ is the critical load of the circulatory (undamped) system. This latter is marginally stable when $\mu <\mu _{c}$, and becomes unstable through a circulatory (or reversible) Hopf bifurcation when $\mu =\mu _{c}$ [6–9]. The graph of Eq. (4) is a parabola in the $\left( \xi _{m},\mu \right)$-plane, and it is displayed in Fig. 2a. The points on the curve represent simple Hopf bifurcation states, occurring at $\mu =\mu _{d}$ (d having the meaning of damped), for the first mode of the column having frequency $\omega _{d}$, that is: for a given damping coefficient $\xi _{m}$, the first mode becomes incipiently unstable for a critical load furnished by Eq. (4); therefore, the locus divides the plane into a stable region (marked with S in Fig. 2a) and into an unstable one (marked with U in Fig. 2a). It is worth noting that, the effect of the Ziegler’s Paradox is detrimental, since, when $\xi _{m}\rightarrow 0$, the limit of Eq. (4) furnishes $\mu _{d}=41/28\simeq 1.464<\mu _{c}$, i.e., the critical load of the damped system does not recover that of the undamped one.

Fig. 2

Linear stability diagrams: a uncontrolled column in the $\left( \xi _{m},\mu \right)$-plane; b controlled column in the $\left( \Delta \mu ,\xi _{e}\right)$-plane

3.2 Controlled linearly damped systems

The underlying ideas of the control strategies, introduced in [54], are briefly recalled. The target of the analysis developed there was in finding the order of magnitude of the electrical parameters, with the aim to maximize the electrical dissipation during the energy exchange process between the mechanical and electrical sub-systems, for a small coupling parameter $\gamma$ and for given mechanical properties. Said in other words, passive control strategies were designed in such a way that the Hopf critical load of the controlled system could be greater than that of the uncontrolled one. By studying the sensitivity analysis of the eigenvalues, carried out via ad hoc perturbation methods [4, 57–59], the following three controllers, differing each other with respect the demand or not of the resonance condition, and for the order of magnitude of the electrical coefficients, were detected $(\varepsilon \,{\hbox {small parameter}})$:

• 1. Non-Singular Resonant (NSR) controller: $\kappa _{e} =\mathrm {\mathcal {O}}(1)$, $\nu _{e}=\mathcal {O}(1)$, $\kappa _{e} /\nu _{e}=\omega _{d}^{2}$, $\xi _{e}=\mathcal {O}(\varepsilon )$;

• 2. Singular Non-Resonant (SNR) controller: $\kappa _{e} =\mathcal {O}(\varepsilon )$, $\nu _{e}=\mathcal {O}(\varepsilon )$, $\kappa _{e} /\nu _{e}\ne \omega _{d}^{2}$, $\xi _{e}=\mathcal {O}\left( \varepsilon \right)$;

• 3. Tuned Piezoelectric Damper (TPD): $\kappa _{e} =\mathcal {O}(\varepsilon )$, $\nu _{e}=\mathcal {O}(\varepsilon )$, $\kappa _{e} /\nu _{e}=\omega _{d}^{2}$, $\xi _{e}=\mathcal {O}\left( \varepsilon ^{3/2}\right)$.

It is important to remark that each controller possesses a targeted energy transfer mechanism, which is related to the way in which the eigenvalues of the mechanical and electrical sub-systems interact, as highlighted in [54] through different perturbation algorithms. In particular:

• in the NSR-controlled system, the energy transfer is driven by the resonance conditions (Den Hartog principle [31]), the mechanical and electrical responses are of the same order of magnitude, and $i\omega _{d}$ is a semi-simple eigenvalue for the PEM system;

• in the SNR-controlled system, the energy transfer is driven by the evanescence of the electrical parameters in the absence of resonance, mechanical and electrical responses are of the same order of magnitude, the electrical sub-system is passive, and $i\omega _{d}$ is a simple eigenvalue for the PEM system;

• in the TPD-controlled system, the energy transfer is realized by both the resonance and the evanescent electrical characteristics, the electrical response is larger than the mechanical one, and $i\omega _{d}$ is a defective eigenvalue for the PEM system.

Table 1 Numerical values of the electrical coefficients

In the following numerical simulations, the mechanical linear damping coefficient is fixed at $\xi _{m}=0.1$, which corresponds to a Hopf critical load $\mu _{d}\simeq 1.469$ (point denoted with a bullet in Fig. 2a), and to a critical frequency $\omega _{d}\simeq 0.534$. The coupling coefficient is assumed as $\gamma =0.1$, and the electrical coefficients are chosen as it is shown in Table 1. In particular, concerning the electrical damping coefficient $\xi _{e}$, here an optimum value, for each of the controllers, has been determined by evaluating their exact stability domain, as explained ahead.

The linear stability diagram for the NSR-, SNR-, and TPD-controlled columns is displayed in Fig. 2b, in the $\left( \Delta \mu ,\xi _{e}\right)$-plane, being $\Delta \mu :=100\left( \mu -\mu _{d}\right) /\mu _{d}$ the percentage increment in the critical load. It is seen that a critical curve exists for each controller, which is the locus of the Hopf bifurcations of the controlled system; the stable region of the domain is on the left side of each curve. Therefore, the optimum electrical damping is determined by estimating the value of $\xi _{e}$ which maximizes $\Delta \mu$ (the points denoted with a bullet on each curve). When the optimum values of $\xi _{e}$, reported in Table 1, are selected, the following increments and critical load values are found: ${\hbox {(NSR)}}\, \Delta \mu \simeq 14\,\%, \mu _{d}\simeq 1.67; {\hbox {(SNR)}}\, \Delta \mu \simeq 23\,\%, \mu _{d}\simeq 1.80;\,{\hbox {(TPD)}}\, \Delta \mu \simeq 29\,\%, \mu _{d}\simeq 1.90$. As a consequence and consistently with the results of [54], it is found that the best controller is the TPD.

4 Nonlinear systems

The analysis of the behavior of the Ziegler’s column when geometrical nonlinearities, i.e., large rotations, and nonlinear damping of Van der Pol-type are introduced, is carried out in this section.

4.1 Uncontrolled systems

Relevant results concerning the nonlinear dynamical response of the uncontrolled Ziegler’s column, with or without nonlinear damping, are presented in [15–17] and are briefly recalled here. Mainly, they can be summarized in the following points: (i) if the column is linearly damped, supercritical limit-cycles manifest themselves, whose large amplitude increases as the destabilizing effect of the damping increases; (ii) if a proper nonlinear damping form, such as the Van der Pol-like damping, is introduced, the amplitude of the supercritical limit-cycles can be reduced; (iii) the same nonlinear damping can have a detrimental effect on the nonlinear dynamics of the column, by giving rise to subcritical limit-cycles and, in particular, to the hard loss of stability bifurcation, according to which a regain of stability is experienced by a subcritical branch of a periodic solution through a turning point.

It is important to remark that, as a consequence of the hard loss of stability, when the critical load is slightly increased from its critical value $\mu _{d}$, the amplitude of the limit-cycle jumps to a finite value, i.e., it is not zero at the critical load; this behavior may result in an unacceptable dynamical response from an engineering point of view and should be possibly eliminated or reduced by the control.

Table 2 Numerical values of the nonlinear damping coefficients

Fig. 3

Bifurcation diagrams in the $\left( \mu ,\max \left| u_{c}\right| \right)$-plane of the uncontrolled Ziegler’s column. LD linearly damped; NLD-A, NLD-B, NLD-C nonlinear damping case studies A, B, and C

The above-discussed qualitative response is reproduced in the following numerical simulations, by selecting the nonlinear damping coefficients as displayed in Table 2; in particular, three case studies, denoted with A, B and C, respectively, are defined. In the case study A, the nonlinear damping is uniform through the column, i.e., the ratio $\zeta _{1}/\zeta _{2}=1$, while, in the case studies B and C, it is $\zeta _{1}/\zeta _{2}\ne 1$ and the ratio of the case C is the inverse of that of case B.

In Fig. 3, the bifurcation diagrams, obtained via a numerical continuation of the periodic solutions, performed on Eq. (1a,b), when $\gamma =0$, are displayed; here, the values of $\mathrm {max}\left| u_{c}\right|$, being $u_{c}:=\sin \vartheta _{1}+\sin \vartheta _{2}$ the non-dimensional horizontal component of the column’s displacement at the tip (point C in Fig. 1), are plotted vs the load parameter $\mu$, for the linearly damped column (curve marked with LD in the figure), and for the three nonlinear damping case studies (marked with NLD-A, NLD-B, NLD-C, respectively). It is seen that, in both the case studies A and C, nonlinear damping is able to reduce the (large) amplitude of the supercritical limit-cycle of the LD column; moreover, the effectiveness of the nonlinear damping ratio in the case C is greater with respect to the case A. On the contrary, the diagram relevant to the case B shows the detrimental effect of the nonlinear damping which is revealed by the presence of a hard loss bifurcation, having a subcritical branch (dashed line in the figure) which regains its stability, and becomes supercritical, after a turning point occurring at $\left( \mu ,\mathrm {max}\left| u_{c}\right| \right) \simeq \left( 1.42,0.37\right)$; therefore, when $\mu =\mu _{d}$, the displacement $\mathrm {max}\left| u_{c}\right| \simeq 0.66$ and, in addition, when $\mu >\mu _{d}$, the curve NLD-B is above those of the cases A and C, even if the nonlinear damping still produces a beneficial effect, since the curve remains below that of the LD column.

4.2 Controlled systems

The bifurcation diagrams, obtained through a numerical continuation of the periodic solutions of Eq. (1), are shown for the column equipped with the controller: NSR in Fig. 4, SNR in Fig. 5, and TPD in Fig. 6. In particular, in the sub-figures (a), (b), and (c) of each figure, the values of $\mathrm {max}\left| u_{c}\right|$ vs $\mu$, relevant to the case studies A, B and C (black curves denoted with the prefix C and the label C-NLD), respectively, are reported; moreover, in the same sub-figures the bifurcation diagrams of the controlled and linearly damped systems (black curves labeled with C-LD), and of the uncontrolled (prefix U), linearly (label U-LD) and nonlinearly (U-NLD) damped systems (gray curves), respectively, are displayed for comparison. Finally, in the sub-figures (d) of Figs. 4, 5, and 6, the values of $\mathrm {max}\left| \psi \right|$ vs $\mu$ are shown for the controlled systems (prefix C omitted) in the cases LD, NLD-A, NLD-B, and NLD-C, respectively.

Fig. 4

Bifurcation diagrams of the NSR-controlled Ziegler’s column: a, b, c diagrams in the $(\mu , \text {max} |u_{c}|)$-plane for the case studies A, B, C, respectively; d diagrams in the $(\mu , \text {max} |\psi |)$-plane. U uncontrolled; C controlled; LD linearly damped; NLD nonlinearly damped; NLD-A, NLD-B, NLD-C nonlinear damping case studies A, B, and C

Fig. 5

Bifurcation diagrams of the SNR-controlled Ziegler’s column: a, b, c diagrams in the $(\mu , \text {max} |u_c|)$-plane for the case studies A, B, C, respectively; d diagrams in the $(\mu , \text {max} |\psi |)$-plane. U uncontrolled; C controlled; LD linearly damped; NLD nonlinearly damped; NLD-A, NLD-B, NLD-C nonlinear damping case studies A, B, and C

Fig. 6

Bifurcation diagrams of the TPD-controlled Ziegler’s column: a, b, c diagrams in the $(\mu , \text {max} |u_{c}|)$-plane for the case studies A, B, C, respectively; d diagrams in the $(\mu , \text {max} |\psi |)$-plane. U uncontrolled; C controlled; LD linearly damped; NLD nonlinearly damped; NLD-A, NLD-B, NLD-C nonlinear damping case studies A, B, and C

The effects of the NSR controller on the nonlinear dynamics of the column are displayed in Fig. 4. The C-LD system is addressed first. It is found that the main consequence of the NSR controller is the forward shifting of the bifurcation diagram of the uncontrolled system (U-LD); it is worth noting that the shifting effect was already discussed in [55, 56] for the SNR and TPD controllers, respectively, and that, with respect to this behavior, the best controller is found here to be the TPD (see also Figs. 5, 6). However, while the SNR and TPD controllers are also able to (slightly) flatten the curves on the $\mu$-axis, at least in a range of $\mu$-values close to $\mu _{d},$ the NSR is not. Indeed, the flattening effect can be detected by comparing the responses of the C-LD and U-LD systems, for each controller, in the neighborhood of the respective critical loads $\mu _d$ and at the same distance from them, i.e., for the same $\delta \mu :=\mu -\mu _{d}$; when, for example, $\delta \mu =0.2$, it is found that: $\mathrm {max}\left| u_{c}\right| \simeq 1.39$ (U-LD) and $\mathrm {max}\left| u_{c}\right| \simeq 1.4$ (C-LD with NSR, see Fig. 4), $\mathrm {max}\left| u_{c}\right| \simeq 1.16$ (C-LD with SNR, see Fig. 5), $\mathrm {max}\left| u_{c}\right| \simeq 1.21$ (C-LD with TPD, see Fig. 6).

When the NSR controller is applied to the NLD systems, its main result is still in shifting forward the U-NLD diagrams, as shown in the Fig. 4a–c. In the C-NLD-A case (Fig. 4a, suffix A omitted), differently from what happens in the C-LD system, the controller has a detrimental effect, since it gives rise to a hard loss bifurcation (not present in the U-NLD-A case), having a turning point $\left( \mu ,\mathrm {max}\left| u_{c}\right| \right) \simeq \left( 1.65,0.32\right)$; when stability is regained and $\mu >\mu _{d}$, the NSR controller weakly reduces the amplitude of the supercritical limit-cycle of the case U-NLD-A. In the C-NLD-B case (Fig. 4b, suffix B omitted), the detrimental effect of the sole nonlinear damping is magnified by the control via the hard loss bifurcation, which regains stability at $\left( \mu ,\mathrm {max}\left| u_{c}\right| \right) \simeq \left( 1.54, 0.53\right)$, and whose subcritical branch exploits a larger range of $\mu$-values with respect to the case U-NLD-B; again, when $\mu >\mu _{d}$, a weak reduction in the amplitude of the uncontrolled limit-cycle is found. In the C-NLD-C case (Fig. 4c, suffix C omitted), a beneficial effect of the NSR control is recognized, since the forward shifting of the uncontrolled curve is also accompanied by a supercritical limit-cycle, whose amplitude, for a fixed $\mu$, is less than that of the U-NLD-C case, at least close to $\mu _{d}$; however, for a fixed small increment $\delta \mu$, e.g., $\delta \mu =0.1$, the value of the amplitude $\mathrm {max}\left| u_{c}\right|$ in the C-NLD-C case, namely $\mathrm {max}\left| u_{c}\right| =0.45$, is greater than that of the U-NLD-C case, i.e., $\mathrm {max}\left| u_{c}\right| =0.16$, thus entailing an opposite behavior with respect to the flattening effect occurring in the above-discussed linearly damped column. Finally, in Fig. 4d the nonlinear dynamical response of the NSR controller is shown in terms of flux linkage: it is seen that a hard loss of stability manifests itself in the NLD-A and NLD-B case studies, while a supercritical limit-cycle occurs in the NLD-C case; in addition, when a sufficiently large $\mu >\mu _{d}$ is chosen, only the values of $\mathrm {max}\left| \psi \right|$ of the NLD-B case are greater than that of the LD column.

The effects of the SNR controller on the nonlinear response of the NLD columns are displayed in Fig. 5. They are qualitatively similar to those relevant to the NSR controller; however, a higher effectiveness of the SNR controller with respect to the NSR controller, in reducing the amplitude of the limit-cycle of the U-NLD cases, is found when $\mu >\mu _{d}$. In the C-NLD-A case (Fig. 5a, suffix A omitted), the effect of the controller is detrimental due to the occurrence of a hard loss bifurcation, having a turning point $\left( \mu ,\mathrm {max}\left| u_{c}\right| \right) \simeq \left( 1.71, 0.37\right)$. In the C-NLD-B case (Fig. 5b, suffix B omitted), the controlled column experiences a hard loss bifurcation, which regains stability at $\left( \mu ,\mathrm {max}\left| u_{c}\right| \right) \simeq \left( 1.55, 0.53\right)$, thus emphasizing the behavior of the U-NLD-B case; moreover, a larger extension of the subcritical branch with respect to the NSR controller is found. In the C-NLD-C case (Fig. 5c, suffix C omitted), the effect of the controller is beneficial, since the forward shifting of the uncontrolled curve goes with a reduction in the amplitude of the uncontrolled limit-cycle, for a fixed $\mu$; however, as it happens in the NSR controller, the flattening effect due to the control is not more recognized, i.e., the controlled amplitude grows steeper than the uncontrolled one. Finally, in Fig. 5d, it is seen that a hard loss occurs for the flux linkage bifurcation diagrams in the case studies NLD-A and NLD-B; differently from the NSR controller, when a sufficiently large $\mu >\mu _{d}$ is selected, the effect of nonlinear damping on the control yields to values of $\mathrm {max}\left| \psi \right|$ below that of the LD column for all the NLD case studies.

The nonlinear dynamics of the TPD-controlled column is shown in Fig. 6. It is seen that the TPD controller, which is the best controller in linear regime (remember Fig. 2b), possesses also the higher effectiveness in reducing the amplitude of the limit-cycles of the U-NLD-A and U-NLD-B case studies, when $\mu >\mu _{d}$. As a drawback, it is seen that it has also a detrimental effect; indeed, the hard loss bifurcation occurs in all the nonlinear damping case studies, differently from what happens for the other controllers. In particular, the regain of stability is detected at turning points having the following coordinates: (i) in the C-NLD-A case $\left( \mu ,\mathrm {max}\left| u_{c}\right| \right) \simeq \left( 1.78, 0.45\right)$; (ii) in the C-NLD-B case $\left( \mu ,\mathrm {max}\left| u_{c}\right| \right) \simeq \left( 1.69, 0.55\right)$; (iii) in the C-NLD-C case $\left( \mu ,\mathrm {max}\left| u_{c}\right| \right) \simeq \left( 1.86, 0.37\right)$. Finally, the bifurcation diagrams displayed in Fig. 6d show the presence of the hard loss bifurcation in the $\left( \mu ,\mathrm {max}\left| \psi \right| \right)$-plane; differently from what happens for the other controllers, only in the NLD-C case study, provided a sufficiently large load is considered, the values of $\mathrm {max}\left| \psi \right|$ are lower than that of the LD column.

5 Conclusions and perspectives

The effects of the piezoelectric control on both the linear stability and the nonlinear response of the Ziegler’s column, in regime of small or finite rotations, with or without Van der Pol-like nonlinear damping, have been addressed in this paper. The derivation of the exact equations of motion for the controlled column has been discussed. Three piezoelectric controllers, namely Non-Singular Resonant (NSR), Singular Non-Resonant (SNR), and Tuned Piezoelectric Damper (TPD), have been applied to a linearly and uniformly damped column, under different nonlinear damping conditions, and for a fixed electromechanical coupling parameter. Linear stability analysis has been carried out to show the influence of the controllers on the Hopf critical load. Numerical continuation of the periodic solutions of the exact equations of motion has been developed to investigate the effects of the controllers on the amplitude of the limit-cycle and on the hard loss of stability phenomenon.

The following main conclusions can be drawn.

• 1. All the proposed piezoelectric controllers, when applied to the linear system in regime of small rotations, have a beneficial effect, since they enlarges the stable region; if the electrical damping is optimized for maximizing the critical load increment, the best controller is the TPD.

• 2. The effectiveness of the three controllers, when applied to the linearly damped column in regime of finite rotations, is mainly revealed by the forward shifting of the bifurcation diagrams of the uncontrolled system. The best controller is again the TPD. In addition, while the beneficial effect of the controllers SNR and TPD is also in the flattening of the bifurcation diagram, in the NSR this effect is not recognized. Remarkably, both the shifting and the flattening produce a reduction in the amplitude of the supercritical limit-cycle.

• 3. The combined action of the control and of the nonlinear damping can produce different effects, depending on the controller and on the nonlinear damping ratio. The main consequence of the control on the nonlinearly damped column is again in shifting forward the uncontrolled bifurcation diagrams. It is found that, in some nonlinear damping case studies, control is detrimental, since it is able to magnify the undesirable effects of the hard loss bifurcation; in addition, none controller is recognized to be effective in eliminating the hard loss phenomenon. In other cases, the detrimental effect of the control is detected by the fact that it gives rise to the occurrence of the hard loss bifurcation, also when this latter is not present in the uncontrolled system. However, when the critical load is overcome, all the controllers have a beneficial effect on the nonlinearly damped systems, since, for a given load increment, the amplitude of the limit-cycle of the uncontrolled column is reduced; the best controller is, also in this case, the TPD.

In conclusion, it is believed that this work could represent a starting point in the analysis of the nonlinear response of non-conservative PEM systems, with the aim to improve the engineering design process. Such an analysis, however, calls for additional work to be done. Therefore, the main perspectives of this research are the followings: (i) development of parametric analyses for the optimization of the electrical characteristics of the controllers, under different nonlinear damping conditions, to be carried out, e.g., by using semi-analytical asymptotic methods, such as the Multiple Scale Method; (ii) improvement in the piezoelectric-based control, which can be performed through nonlinear electric elements as, e.g., a Van der Pol electrical circuit, but also, by modeling the nonlinear constitutive behavior of the piezoelectric material [60, 61], thus entailing a nonlinear electromechanical coupling; (iii) analysis of the nonlinear dynamics of the controlled systems for different topologies of the controllers as, e.g., the one realized via two piezoelectric transducers, placed at the pivots A and B, respectively, and connected with a two-node electrical circuit, whose effectiveness, in the linear stability of the SNR controller, has been already shown in [54]; (iv) experimental validation of the numerical results.

Finally, broader research themes, which deserve to be mentioned as possible perspectives of this work, are: (i) to explore the feasibility of considering such non-conservative discrete PEM systems as a part of more complex micro-structured materials, to form smart metamaterials, starting, e.g., from fabrics and pantographic lattices analyzed in [62, 63]; (ii) the possibility to perform energy harvesting with such non-conservative PEM systems, also when the non-conservativeness is due to velocity-dependent actions, as it occurs in aeroelastic phenomena, which, remarkably, are governed by Van der Pol-like oscillators [64, 65].

Appendix: Derivation of the equations of motion

The equations of motion of the controlled system are derived by following the approach discussed in [53–55]. However, differently from what is done in [53], where the ‘Principle of Similarity’ between the mechanical and electrical sub-systems was enforced, a not-similar system is here addressed. Moreover, in addition to what was done in [55], also the nonlinear damping terms are included in the formulation. The following steps are performed:

• 1. The non-conservative (follower) action and the dissipation due to the (linear and nonlinear) damping are initially neglected, thus rendering the system conservative. Therefore, the Lagrangian of the PEM system is written as the sum of three parts: (a) the mechanical Lagrangian $\mathcal {L}_{m}$, regarding the mechanical system without the control device, (b) the electrical Lagrangian $\mathcal {L}_{e}$, relevant to the electrical circuit, and (c) the piezoelectric Lagrangian $\mathcal {L}{}_{p}$, related to the piezoelectric device. Finally, the action functional $\mathcal {H}:=\int _{t_{1}}^{t_{2}}\left( \mathcal {L}_{m}+\mathcal {L}_{e} +\mathcal {L}_{p}\right) \text {d}t$ for the conservative system is built.

• 2. The internal dissipation and the non-conservative action are accounted for through the extended Hamilton principle.

1.1 The action functional for the conservative PEM system

The PEM system, in the absence of dissipation and follower action, is analogous to the one presented in [55, 56]. In order to render the present paper self-contained, the relevant steps, needed to build the action functional, are resumed.

The rotations of the two bars are taken as Lagrangian coordinates, namely $\vartheta _{1}\left( t\right)$ and $\vartheta _{2}\left( t\right)$, being t the time; the ‘lumped curvatures’ (i.e., the relative rotations) at the hinges, namely $\chi _{j}\left( t\right)$ ($j=1,2$), therefore, read:

$$\begin{aligned} \chi _{1}= & {} \vartheta _{1}\nonumber \\ \chi _{2}= & {} \vartheta _{2}-\vartheta _{1} \end{aligned}$$

(5)

A linear elastic constitutive behavior is assumed for the springs, linking the internal couples $M_{j}$ to the lumped curvatures $\chi _{j}\,(j=1,2)$; it reads:

$$\begin{aligned} M_{j}=k_{j}\chi _{j},\quad j=1,2 \end{aligned}$$

(6)

where $k_{j}$ ($j=1,2$) are the stiffness coefficients of the springs.

The mechanical Lagrangian is (see [55] for a detailed derivation):

$$\begin{aligned} \mathcal {L}_{m}= & {} \frac{1}{2}\ell ^{2}\left[ \left( m_{1}+m_{2}\right) \dot{\vartheta }_{1}^{2}+m_{2}\dot{\vartheta }_{2}^{2}\right. \nonumber \\&\left. +\,2m_{2} \dot{\vartheta }_{1}\dot{\vartheta }_{2}\cos \left( \vartheta _{1} -\vartheta _{2}\right) \right] \nonumber \\&-\,\frac{1}{2}\left[ k_{1}\vartheta _{1}^{2}+k_{2}\left( \vartheta _{2} -\vartheta _{1}\right) ^{2}\right] \end{aligned}$$

(7)

The electrical Lagrangian is identical to that written in [55], since the same electric circuit is here considered. However, it is important to recall that it is assumed that no capacitors are present in the circuit so that the electrical potential is only of inductive type. By taking the flux linkage $\psi \left( t\right)$ as the Lagrangian (electrical) coordinate, the electrical Lagrangian reads (see also [66]):

$$\begin{aligned} \mathcal {L}_{e}=-\frac{1}{2}\left( \frac{1}{L}\psi ^{2} \right) \end{aligned}$$

(8)

The piezoelectric Lagrangian is written by considering that the kinetic energy of the piezoelectric device is zero, due to its placement; to write the potential energy, it is assumed that the following linear piezoelectric constitutive equations [67] hold:

$$\begin{aligned} \left( \begin{array}{l} M_{p}\\ Q_{p} \end{array}\right) =\left[ \begin{array}{ll} k_{p} &{} -g\\ g &{} C_{p} \end{array}\right] \left( \begin{array}{l} \chi _{p}\\ \dot{\psi }_{p} \end{array}\right) \end{aligned}$$

(9)

Equation (9) link the piezoelectric internal couple $M_{p}$ and charge $Q_{p}$ to the piezoelectric lumped curvature $\chi _{p}$ and flux linkage $\psi _{p}$; moreover, g, $k_{p}$, and $C_{p}$ are the coupling, stiffness and capacitance coefficients, respectively. Therefore, the piezoelectric Lagrangian is:

$$\begin{aligned} \mathcal {L}_{p}= & {} -\frac{1}{2}\left( M_{p}\chi _{1}-Q_{p}\dot{\psi }_{p}\right) \nonumber \\= & {} \frac{1}{2}\left( C_{p}\dot{\psi }^{2}-k_{p}\chi _{1}^{2}+2g\dot{\psi } \chi _{1}\right) \nonumber \\= & {} \frac{1}{2}\left( C_{p}\dot{\psi }^{2}-k_{p}\vartheta _{1}^{2} +2g\dot{\psi }\vartheta _{1}\right) \nonumber \\\simeq & {} \frac{1}{2}\left( C_{p} \dot{\psi }^{2}+2g\dot{\psi }\vartheta _{1}\right) \end{aligned}$$

(10)

where, it is assumed that the piezoelectric device is perfectly glued to the structure, i.e., $\chi _{p}=\chi _{1}$, and that it is connected to the ground and, as capacitor, to the circuit node, thus implying $\psi _{p}=\psi$. Moreover, in deriving Eq. (10), use of Eq. (5) is made and, in addition, since $k_{p}\ll k_{j}\,(j=1\,{\hbox {or}}\,2)$, the contribution to the stiffness of the piezoelectric device is neglected.

Finally, the action functional H for the conservative PEM system is:

$$\begin{aligned} \mathcal {H}= & {} \frac{1}{2}\int _{t_{1}}^{t_{2}}\ell ^{2}\left[ \left( m_{1} +m_{2}\right) \dot{\vartheta }_{1}^{2}+m_{2}\dot{\vartheta }_{2}^{2}\right] \mathrm {d}t\nonumber \\ \quad&+\int _{t_{1}}^{t_{2}}\ell ^{2}m_{2}\dot{\vartheta }_{1} \dot{\vartheta }_{2}\cos \left( \vartheta _{1}-\vartheta _{2}\right) \mathrm {d}t \nonumber \\ \quad&-\,\frac{1}{2}\int _{t_{1}}^{t_{2}}\left[ k_{1}\vartheta _{1}^{2} +k_{2}\left( \vartheta _{2}-\vartheta _{1}\right) ^{2}\right] \mathrm {d}t \nonumber \\ \quad&-\frac{1}{2}\int _{t_{1}}^{t_{2}}\frac{1}{L}\psi ^{2}\mathrm {d}t +\,\frac{1}{2}\int _{t_{1}}^{t_{2}}\left( C_{p}\dot{\psi }^{2}+2g\dot{\psi } \vartheta _{1}\right) \mathrm {d}t\nonumber \\ \end{aligned}$$

(11)

1.2 Non-conservative actions and equations of motion

The extended Hamilton principle states that $\delta \tilde{\mathcal {H}}:=\delta \mathcal {H}+\delta \mathcal {W}=0$, for any kinematically (mechanical and electrical) admissible motion, being $\delta \mathcal {W}$ the work expended by the non-conservative actions in the $\left[ t_{1},t_{2}\right]$ interval. These latter are: (a) the linear configuration-dependent action of mechanical type (follower force); (b) the linear and nonlinear velocity-dependent mechanical actions (damping); (c) the linear velocity-dependent electrical action (circuit resistance).

The mechanical damping is assumed to be ruled by a Van der Pol-type law, so that the relevant constitutive equation reads:

$$\begin{aligned} M_{j}^{D}=c_{1j}\dot{\chi }_{j}+c_{3j}\chi _{j}^{2}\dot{\chi }_{j},\quad j=1,2 \end{aligned}$$

(12)

where $M_{j}^{D}$ is the internal action due to damping, $c_{1j}$ and $c_{3j}$ are the linear and cubic viscosity coefficients, respectively.

Therefore, the work $\delta \mathcal {W}$, which is the sum of a mechanical, $\delta \mathcal {W}_{m}$, and an electrical, $\delta \mathcal {W}_{e}$, contribution, i.e., $\delta \mathcal {W}=\delta \mathcal {W}_{m}+\delta \mathcal {W}_{e}$, reads:

$$\begin{aligned} \delta \mathcal {W}_{m}= & {} \int _{t_{1}}^{t_{2}}\left[ F\ell \sin \left( \vartheta _{1}-\vartheta _{2}\right) \delta \vartheta _{1}\right. \nonumber \\&\left. -\,\left( M_{1}^{D}\delta \chi _{1}+M_{2}^{D}\delta \chi _{2}\right) \right] \mathrm {d}t\nonumber \\= & {} \int _{t_{1}}^{t_{2}}\left[ F\ell \sin \left( \vartheta _{1}-\vartheta _{2}\right) \right. \nonumber \\&\left. -\,\left( c_{11}\dot{\vartheta }_{1}+c_{31}{\vartheta }_{1}^{2}\dot{\vartheta }_{1}\right) \right] \delta \vartheta _{1}\mathrm {d}t\nonumber \\&-\int _{t_{1}}^{t_{2}}c_{12}\left( \dot{\vartheta }_{2}-\dot{\vartheta }_{1}\right) \left( \delta \vartheta _{2}-\delta \vartheta _{1}\right) \mathrm {d}t\nonumber \\&-\int _{t_{1}}^{t_{2}}c_{32}\left( \vartheta _{2}-\vartheta _{1}\right) ^{2}\left( \dot{\vartheta }_{2}-\dot{\vartheta }_{1}\right) \left( \delta \vartheta _{2}-\delta \vartheta _{1}\right) \mathrm {d}t\nonumber \\ \delta \mathcal {W}_{e}= & {} -\int _{t_{1}}^{t_{2}}\frac{1}{R}\dot{\psi }\delta \psi \mathrm {d}t \end{aligned}$$

(13)

in which use of Eq. (5) is made. By requiring that $\delta \tilde{H}=0$ $\forall \;\delta \vartheta _{1},\delta \vartheta _{2},\delta \psi$, the following (dimensional) equations of motion are derived:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\left( m_{1}+m_{2}\right) \ell ^{2}\ddot{\vartheta }_{1}+m_{2}\ell ^{2}\ddot{\vartheta }_{2}\cos \left( \vartheta _{1}-\vartheta _{2}\right) \\ &{} +\,m_{2}\ell ^{2}\dot{\vartheta }_{2}^{2}\sin \left( \vartheta _{1}-\vartheta _{2}\right) +\left( k_{1}+k_{2}\right) \vartheta _{1}-k_{2}\vartheta _{2}\\ &{} +\,\left( c_{11}+c_{12}\right) \dot{\vartheta }_{1}-c_{12}\dot{\vartheta }_{2}+c{}_{31}\vartheta _{1}^{2}\dot{\vartheta }_{1}\\ &{} -\,c{}_{32}\left( \vartheta _{2}-\vartheta _{1}\right) ^{2}\left( \dot{\vartheta }_{2}-\dot{\vartheta }_{1}\right) \\ &{}-\,F\ell \sin \left( \vartheta _{1}-\vartheta _{2}\right) -g\dot{\psi }=0\\ &{} m_{2}\ell ^{2}\ddot{\vartheta }_{2}+m_{2}\ell ^{2}\ddot{\vartheta }_{1}\cos \left( \vartheta _{1}-\vartheta _{2}\right) \\ &{}-\,m_{2}\ell ^{2}\dot{\vartheta }_{1}^{2}\sin \left( \vartheta _{1}-\vartheta _{2}\right) \\ &{} +\,k_{2}\left( \vartheta _{2}-\vartheta _{1}\right) +c_{12}\left( \dot{\vartheta }_{2}-\dot{\vartheta }_{1}\right) \\ &{} +\,c_{32}\left( \vartheta _{2}-\vartheta _{1}\right) ^{2}\left( \dot{\vartheta }_{2}-\dot{\vartheta }_{1}\right) =0\\ &{} C_{p}\ddot{\psi }+\frac{1}{R}\dot{\psi }+\frac{1}{L}\psi +g\dot{\vartheta }_{1}=0 \end{array}\right. } \end{aligned}$$

(14)

Finally, by introducing the quantities defined in Eq. (2), accounting for $m_{1}=2m$, $m_{2}=m$, $k_{1}=k_{2}=k$, $c_{11}=c_{12}=c$, Eq. (1) is obtained (tilde removed).