Numerical Studies on the Nonlinear Dynamics of the Ziegler Column under Pulsating Follower Force

Abstract

The present contribution aims at numerically investigating the nonlinear dynamics of the Ziegler’s column under a harmonically varying follower force. The system’s dynamical response is ruled by the interaction of two types of instabilities, namely flutter and parametric instability. In this paper, we investigate the stability of periodic orbits and the nonlinear response of the Ziegler’s column as functions of the parameters that govern the parametric excitation. It is seen that structural viscous damping, besides diminishing the flutter critical load, is also seen to enlarge the unstable zones of the Strutt-like diagram that characterizes the parametric instability. On the other hand, an isolated region of stability of the trivial solution is also found, anticipating a rich and complex scenario.

1 Introduction

The response of the Ziegler column subjected to a follower force is a classical problem that has received studies in the last seven decades (see, for example, [1,2,3]). Despite its apparent simplicity, it reveals a number of intricate aspects, including dynamic instability (flutter) and possible mode localization [4]. Recently, [5] and [6] investigated the dynamic response of the Ziegler’s column considering the piezoelectric effects for both control of vibration and energy harvesting, respectively.

An interesting (sometimes referred to a “paradox”) regarding the response of the Ziegler’s column is the decrease in the critical value of the follower force when damping is included in the mathematical model. In [7], the author discusses the effects of nonlinearities associated with the torsional springs of the column and addresses non-periodic post-critical responses for the undamped column.

Reference [8] focuses on the effects of the nonlinear damping according to a van der Pol model on the post-critical response of the Ziegler’s column under follower force. Among other findings, the authors highlight that the Hopf bifurcation can be either supercritical or subcritical, which had already been anticipated in [9].

In [10], the authors readdress the influence of the linear damping on the dynamics of the Ziegler’s column under follower force. By using the multiple scale method and numerical integration of the mathematical model, they discuss, among other aspects, the post-critical responses.

If the follower force is further harmonically varying with time, parametric excitation also appears. Yet, it is remarkable that the interaction of the two instability mechanisms has not been previously addressed in the literature, as far as the authors are aware of. Therefore, they believe this is a novel aspect of the ongoing research herein reported. In this paper, focus is placed on the stability maps obtained in the plane of parameters that define the parametric excitation and on examples of post-critical time-histories.

The paper is organized as follows. Section 2 presents the mathematical models. The analysis methodology is detailed in Sect. 3. Section 4 brings the results and the corresponding discussions. The conclusions are addressed in Sect. 5.

2 Mathematical Model

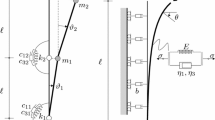
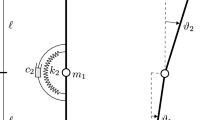
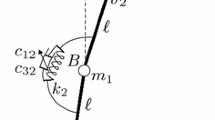
The model studied here is composed of two identical massless rigid bars of length L, connected by means of two torsional visco-elastic springs of stiffness k and damping constant c. Lumped masses 2 m and m are included at mid-span and tip, respectively. A pulsating compressive follower force $P(t)=\bar {P}+\varDelta P \sin \varOmega t$ is applied to the tip of the column. The angular coordinates q ₁ and q ₂ are measured with respect to the line that characterizes the straight column, and no gravitational effects are considered. Figure 1 illustrates the investigated problem.

Fig. 1

Ziegler’s column under pulsating follower force

The equations of motion are obtained using the Euler–Lagrange’s equation. For the sake of conciseness, the intermediate steps are not herein detailed and the final mathematical model is given, in its dimensional form, by Eqs. (1) and (2).

$$\displaystyle \begin{aligned} &mL^2(3\ddot{q}_1 +\cos{}(q_1-q_2)\ddot{q}_2+\sin{}(q_1-q_2)\dot{q}_2^2)+c(2\dot{q}_1-\dot{q}_2)+k(2q_1-q_2)=\\ &=(\bar{P}+\varDelta p \sin (\varOmega t))L\sin{}(q_1-q_2){} \end{aligned} $$

(1)

$$\displaystyle \begin{aligned} &mL^2(\cos{}(q_1-q_2)\ddot{q}_1 +\ddot{q}_2-\sin{}(q_1-q_2)\dot{q}_1^2)+c(-\dot{q}_1+\dot{q}_2)+k(-q_1+q_2)=0{} \end{aligned} $$

(2)

Aiming at generalizing the discussion, the mathematical model is rewritten in dimensionless form. For this, consider the reference frequency $\omega =\sqrt {\frac {k}{mL^2}}$ and the dimensionless quantities defined in Eq. (3).

$$\displaystyle \begin{aligned} \bar{p}=\frac{\bar{P}L}{k}, \varDelta p = \frac{\varDelta P L}{k}, n=\frac{\varOmega}{\omega}, \zeta=\frac{c}{2mL^2\omega}, \tau=t\omega {} \end{aligned} $$

(3)

Defining $(~)^\prime =\frac {d}{d\tau }(~)$, the governing dimensionless system of differential equations reads:

$$\displaystyle \begin{aligned} &3q_1^{\prime\prime}+\cos{}(q_1-q_2)q_2^{\prime \prime}+4\zeta q_1^\prime-2\zeta q_2^\prime+\sin{}(q_1-q_2)(q_2^\prime)^2+2q_1-q_2+\\ &=(\bar{p}+\varDelta p \sin (n\tau))\sin{}(q_1-q_2){} \end{aligned} $$

(4)

$$\displaystyle \begin{aligned} &\cos{}(q_1-q_2)q_1^{\prime \prime}+q_2^{\prime \prime}-2\zeta q_1^\prime+2\zeta q_2^\prime-\sin{}(q_1-q_2)(q_1^\prime)^2-q_1+q_2=0{} \end{aligned} $$

(5)

3 Analysis Methodology

The equations of motion are numerically integrated using DifferentialEquations.jl package programmed in Julia, version 1.5.1. This package is able to choose the proper numerical solver. A standard notebook (i7–10th gen processor, 8 Gb RAM) has been employed for the numerical integrations using a single core.

Analyses with both the linearized (around q ₁ = q ₂ = 0) and the nonlinear models are carried out. Firstly, the linearized and autonomous form of the mathematical model is used for the modal analyses. The linearized model is also useful for studying the stability of the straight configuration of the column under pulsating follower force. Similarly to what has been done in [11] for a chain of articulated rigid pipes ejecting fluid under support excitation, the stability analysis is presented in the form of colormaps showing the maximum absolute value of the Floquet’s multipliers (ρ ^∗) as function of the amplitude and frequency of the parametric excitation (Δp and n, respectively) for different values of averaged follower force $\bar {p}$ and structural damping ratio ζ. The reader interested in details regarding the Floquet’s theory is referred to [12].

The analyses with the nonlinear model are developed as follows. The mathematical model is integrated using initial conditions $q_1(0)=q^\prime _1(0)=q^\prime _2(0)=0$ and q ₂(0) = 0.05 during 1500 parametric excitation periods $\bar {\tau }=2\pi /n$. Then, time-histories q ₁(τ) and q ₂(τ) are presented with the corresponding amplitude spectra. In the amplitude spectra, ω ^∗ is the frequency normalized with respect to ω.

4 Results and Discussions

For the sake of organization, the results are discussed in two subsections. The natural modes and the stability maps are addressed in Sect. 4.1. Time-histories and maps of post-critical responses obtained with the nonlinear equations of motion are presented in Sect. 4.2.

4.1 Results from the Linearized Model

Modal analysis with the undamped Ziegler’s column (ζ = 0) with $\bar {p}=2$, which is slightly smaller than the critical load $\bar {p}_{cr}=2.09$ for the column with the non-pulsating follower force [9], results in λ ₁ = i0.707, $\lambda _2=\lambda _1^*$, λ ₃ = i and $\lambda _4=\lambda _3^*$ as eigenvalues, ( )^∗ representing the complex conjugate and i the imaginary unit. Hence, the natural frequencies are ω ₁ = 0.707 and ω ₂ = 1. The corresponding mode shapes are illustrated in Fig. 2. It is worth noting that the second mode is localized.

Fig. 2

Modal analysis—ζ = 0 and $\bar {p}=2$. (a) Mode 1—ω ₁ = 0.707. (b) Mode 2—ω ₂ = 1

Figure 3 brings the stability maps obtained at $\bar {p}=2$. These maps plot, in a color scale, the variation of ρ ^∗ (the maximum modulus of the Floquet’s multipliers) with the amplitude and frequency of parametric excitation (Δp and n, respectively). Each map is generated using a 2000 × 2000 grid in approximately half hour. The regions of stability are those characterized by ρ ^∗(n;Δp) ≤ 1. On the other hand, unbounded solutions appear if ρ ^∗(n;Δp) > 1.

Fig. 3

Stability maps $\bar {p}=2$. (a) ζ = 0.00. (b) ζ = 0.005. (c) ζ = 0.01. (d) ζ = 0.02. (e) ζ = 0.04. (f) ζ = 0.05

Figure 3a illustrates the stability map obtained for the undamped column. This map reveals two vertices of the instability region (i.e., the region shaded in red) arising at n ≈ 1.4 and n ≈ 2, corresponding to twice the undamped natural frequencies of the column and, consequently, to the principal parametric instabilities of the vibration modes. Besides the region associated with the principal parametric instability, Fig. 3a also shows the existence of another region of the plane of control parameters (n;Δp) associated with unbounded solutions. This secondary region of parametric instability is observed for low values of parametric excitation frequency n, with a vertex at n ≈ 0.29, possible “unfavorable” combination resonance (ω ₂ − ω ₁). Instability here would denote the system leaving the basin of attraction of the trivial equilibrium configuration, due to the closeness to the unstable subcritical Hopf bifurcation of the classical constant follower force problem. Notice that with the increasing of the damping, Fig. 3b–f, $\bar {p}=2$ becomes supercritical and the trivial equilibrium configuration becomes unstable, thus explaining the growing of the response amplitudes.

As seen in Fig. 3b, a slight increase in the structural damping to ζ = 0.005 decreases the size of the region of stability. The same figure reveals the appearance of a well defined region of stability at n ≈ 1.7 (possible “favorable” combination resonance (ω ₂ + ω ₁)) and 0.03 ≤ Δp ≤ 0.18 (see the region shaded in light blue). Notice that the increase of damping leads to $\bar {p}=2$ being supercritical with respect to the follower force problem, but the stable supercritical Hopf bifurcation indicates the possibility of a stable periodic attractor, which has been captured here. Further increase in the values of ζ enlarges the region of parametric instability, shifting the isolated region of bounded responses (see the region shaded in blue) to larger values of parametric excitation amplitude Δp; see Fig. 3d–f.

From the qualitative point of view, the enlargement of the region of the plane of control parameters (n;Δp) associated with unbounded responses (parametric instability) indicates that the presence of structural damping plays a destabilizing role on the parametric excitation of the Ziegler’s column under pulsating follower force. This result goes in line with the “counter-intuitive” and well-known fact that the presence of structural damping decreases the critical load for the stability of the trivial equilibrium configuration of the column (see, for example, [10]). At least to the best of the authors’ knowledge, the stability of the straight configuration of the Ziegler’s column under pulsating follower force has not been previously addressed in the literature and consists a novelty feature of the present study.

4.2 Results from the Nonlinear Model

Firstly, we discuss the time-histories q ₁(τ) and q ₂(τ) and the corresponding amplitude spectra obtained at n = 2, $\bar {p}=2$, three values of parametric excitation amplitude (Δp = 0, Δp = 0.10, and Δp = 0.30) and two values of dimensionless damping, namely ζ = 0 and ζ = 0.05. Notice that n = 2 is a favorable scenario for the parametric instability of the column with respect to the second mode, provided the natural frequency of the localized mode of the undamped column is ω ₂ = 1. For the sake of brevity, the results from the case with $n=2\omega _1=\sqrt {2}$ are not shown here.

Figure 4 presents the time-histories obtained for the undamped column. The illustrated responses reveal that the responses q ₂(τ) oscillate with much larger amplitude if compared to q ₁(τ). This indicates that the parametric resonance with the second undamped mode, in spite of the nonlinear modal coupling, still keeps essentially the character of a localized forced response.

Fig. 4

Time-histories and amplitude spectra for ζ = 0, n = 2, and $\bar {p}=2$. (a) q ₁(τ), Δp = 0. (b) q ₂(τ), Δp = 0. (c) q ₁(τ), Δp = 0.10. (d) q ₂(τ), Δp = 0.10. (e) q ₁(τ), Δp = 0.30. (f) q ₂(τ), Δp = 0.30

As seen in Fig. 4a,b, the response of the autonomous problem (i.e., the one with Δp = 0) is characterized by narrow-banded amplitude spectra, with well defined peaks at the undamped natural frequencies ω ₁ and ω ₂.

When the amplitude of the dynamic component of the follower force is Δp = 0.10, Fig. 4c,d indicate the presence of amplitude-modulated responses, basically because of lack of damping that is essential for reaching a possible steady state. Particularly, the amplitude spectrum presented in Fig. 4c reveals the presence of the frequency components around ω ₁, ω ₂, and 3ω ₂, the latter a subharmonic of the second natural frequency. Finally, Fig. 4e,f show irregular responses of the undamped column when Δp = 0.30. The amplitude spectra present larger bands than those for Δp = 0.10 (Fig. 4c,d).

Time-histories q ₁(τ) and q ₂(τ) and their amplitude spectra obtained with ζ = 0.05 are shown in Fig. 5. When compared to the undamped case, the presence of structural damping decreases the amplitude modulations and increases the maximum responses. Notice, also, that the characteristic oscillation amplitudes of q ₁(τ) and q ₂(τ) have the same order of magnitude, indicating that the presence of damping breaks down the localized vibrations.

Fig. 5

Time-histories and amplitude spectra for ζ = 0.05, n = 2, and $\bar {p}=2$. (a) q ₁(τ), Δp = 0. (b) q ₂(τ), Δp = 0. (c) q ₁(τ), Δp = 0.10. (d) q ₂(τ), Δp = 0.10. (e) q ₁(τ), Δp = 0.30. (f) q ₂(τ), Δp = 0.30

Despite the parametric excitation being a favorable scenario for oscillations in the second mode, all the amplitude spectra illustrated in Fig. 5 have a well defined dominant frequency around ω ^∗ = 0.707, corresponding to the first undamped vibration mode. Also counter-intuitive is the fact that the increase in the parametric excitation amplitude Δp leads to a decrease in the characteristic oscillation amplitudes of q ₁(τ) and q ₂(τ). On the other hand, as expected, the presence of damping leads to smaller amplitude modulations in the response the Ziegler’s column.

Aiming at improving the understanding of the response, Fig. 6 plots some of the trajectories already discussed in Figs. 4 and 5 in the form of colored 3D curves, the color being associated with the value of $\dot {q}_2$. The projections of the trajectories onto the phase-planes q ₁(τ) × q ₂(τ), $q_1(\tau )\times \dot {q}_1(\tau )$, and $q_2(\tau )\times \dot {q}_1(\tau )$ are also depicted.

Fig. 6

Projections of phase trajectories. (a) ζ = 0, Δp = 0. (b) ζ = 0.05, Δp = 0. (c) ζ = 0, Δp = 0.10. (d) ζ = 0.05, Δp = 0.10. (e) ζ = 0, Δp = 0.30. (f) ζ = 0.05, Δp = 0.30

While the trajectories obtained for the undamped case exhibit irregular behaviors, those from the simulations with ζ = 0.05 offer useful insights into the dynamics of the Ziegler’s column. For Δp = 0, Fig. 6b indicates a closed curve, corresponding to a periodic attractor (as foreseen by the stable supercritical Hopf bifurcation). When the parametric excitation amplitude is increased, this curve becomes “broader,” which might perhaps be interpreted as a quasi-periodic attactor (see Fig. 6d,f).

A multiple-scales analysis has been performed, but its detailing is avoided here for brevity. It revealed that, for the case n = 2, any added damping, however small, completely erases the second (localized) mode in spite that it is parametrically excited, fact that is confirmed by the numerical results of Fig. 5, while the fully undamped system does show an important second mode contribution, the lack of dissipation leading to a sort of “beating” pattern in both modes. This result is further illustrated by the Poincare’s section of Fig. 7, using the stroboscopic period τ _sb = 2π∕n and Δp = 0.30.

Fig. 7

Points in the Poincaré’s section. Δp = 0.30, n = 2, and ζ = 0

Hence, besides providing the well-known decrease in the critical follower force, damping also wipes out the localized mode. It is also to be noticed that other harmonic contributions arise, as shown in Figs. 5 and 6, due to the particular solutions associated with non-secular terms. Other scenarios, such as those of $n=2\omega _1=\sqrt {2}$ (principal parametric excitation of the first mode) or $n=\omega _1+\omega _2=\sqrt {2}/2+1$ (combination resonance of modes 1 and 2) could be further explored but were not included here due to lack of space.

5 Conclusions

In this paper, the authors addressed the Ziegler column problem, yet with a pulsating follower force, which constitutes a novelty, to the best of their knowledge. The interplay between two instability phenomena, namely, flutter and parametric resonance, plus the destabilizing effect of damping and the response localization are also discussed in this essentially numerical investigation.

The stability maps revealed that the presence of damping decreased the region of the plane of parameters that govern the parametric excitation associated with bounded solutions. Additionally, examples of post-critical time-histories exhibited amplitude modulations associated with the pulsating follower force. Other studies focusing on the nonlinear response of the parametrically excited Ziegler column will be addressed in the near future. Hence, it is reckoned that further analysis is still needed to fully explore the system complex dynamics.