1 Introduction

Real-time hybrid simulation (RTHS) is an extension of conventional hybrid simulations, also known as substructure testing, where a structural system is divided into physical substructures (PSs) that are experimentally tested and numerical substructures (NSs) that contain the rest of the structure, which are numerically simulated [1–3].

In RTHSs, hydraulic actuation systems (HASs) are typically employed for imposing a desired displacement to PSs [4]. In a HAS, inevitable amplitude and phase errors exist between the actuator command displacement and the effective one. Because of phase error (which can also be viewed as a time delay), the force measured on a PS and given as feedback to a NS does not correspond to the desired position (it is measured before the actuator has reached its target position). The effect of this error is to introduce additional energy into the system, which, unless properly compensated for, will cause the experiment to become unstable [5].

Various studies have been conducted to investigate compensation of the actuator dynamics. Horiuchi et al. [6] proposed a widely adopted compensation scheme for time delay that predicts the displacement through a polynomial extrapolation. Other approaches are based on: the derivative feedforward compensation [7], the phase-lead compensation [8], the inverse compensation [9] and the model-based compensation [10] that are based on the dynamic response of a mathematical model representing the overall experimental testing system (ETS), mainly composed by the HAS, the controller and the PS.

Most of the aforementioned compensation methods require a prior knowledge of the actuation system. Consequently, identification procedures must be conducted to obtain the system dynamics before performing a RTHS. In addition, a compensator designed with these methods is characterized by a set of fixed identified system parameters. However, actuator delay would vary during a hybrid test because of the nonlinearity of the test specimen [11]. Therefore, online procedures could be useful to detect the system parameters in order to improve the accuracy of the real-time hybrid testing.

Several papers have proposed online procedures to estimate and compensate actuator delay during RTHSs [12, 13]. The slopes of the desired and measured displacements are proposed in [14] to estimate the actuator delay. An adaptive compensation scheme is proposed in [15] to minimize the actuator delay by using the TI developed by Mercan and Ricles [16]. Alternatively, a dual compensation strategy is presented in [17] in which an adaptive phase-lead compensator has been developed on the basis of the control theory. In this approach, the weighted linear extrapolation and the inverse model principle are achieved in order to formulate the discrete transfer function of the phase-lead compensator.

In this paper, an adaptive ETS dynamics compensation method is proposed and experimentally verified. The method is based on the coupling of two successful approaches proposed in the literature and used in prior experiments, taking advantage of the best features of each technique. In particular, the adaptive compensator combines a nonlinear parameter estimator, based on the extended Kalman filter (EKF) [18], and a model-based compensator that depends on the estimated parameters. The compensation method is an adaptive version of the feedforward controller with modified inverse dynamics, proposed by Carrion and Spencer [19].

The EKF is a mathematical tool for an optimal state estimation of nonlinear systems widely used for the identification of system parameters [20–24]. The robustness of the EKF with respect to measurement noise makes this method particularly suitable for RTHSs. Moreover, the EKF has been already used in different experimental applications and, therefore, can be considered very effective for the purpose of parameter estimation.

Carrion and Spencer [19] identified an actuator linear model and generated a modified version of the inverse dynamics as a compensator to take into account both the magnitude and phase lag of the actuation systems, depending on the operative conditions and the specimen–actuator interaction. It should be noted that the compensation method proposed in [19] is based on a priori dynamic response of the ETS. This means that the tuning of the parameters of the compensation system should be done any time there is a change in the ETS components, for example in the case of a hydraulic actuator modification, or, a variation of the control algorithm, or again in the replacement of the PS.

Fig. 1
figure 1

A scheme of RTHS

Full size image

The compensator presented in this paper does not adopt fixed values of the parameters, but these are continuously updated with the EKF, making the technique more versatile than the one presented in [19].

The proposed EKF-based Adaptive ETS Dynamics Compensator (EADC) has been firstly evaluated in simulation and then with experiments. The EADC has been applied to a test rig for shear tests on seismic isolator. Moreover, the proposed method has been validated in the case of a RTHS for a base isolation problem.

The paper is organized as follows: in Sect. 2, the EADC mathematical derivation and simulation results are shown; the experimental results concerning the application of the EADC to a seismic isolator test rig are reported in Sect. 3; the results of RTHSs are shown in Sect. 4.

2 Numerical analysis of the proposed EADC

In a RTHS, the PS interacts with the NS by means of a feedback loop, exchanging information in real time with minimum error between them [1]. In Fig. 1, an example scheme for RTHS is shown, where \(\ddot{x}_\mathrm{g} \) is the ground acceleration, d is the command displacement obtained by numerical integration of the equations of motion, r is the compensated displacement, u is the control action, y is the measured displacement and F is the reaction force of the specimen that is used as the input of the numerical integration scheme.

In the scheme of Fig. 1, it is possible to see all the components of the RTHS and the input/output signals of each element. The input signals of the NS, represented by the equation of motion of the specific system, are the ground acceleration \(\ddot{x}_\mathrm{g} \) and the measured reaction force F of the PS, while the output signal is the desired displacement d that must be imposed to the PS. The aim of the ETS compensator is to make the actual displacement y of the PS as close as possible to the output signal of the NS. Therefore, the compensation algorithm provides the output signal r,  which will be the reference signal of the controller (see Fig. 1). The feedback signal of the controller is the signal y, and the output is the control action u to the HAS that, in turn, interacts with the PS through an actuation force.

The system considered in this paper is well approximated by a SISO first-order time-invariant plant that includes effects of the HAS, the controller and the PS. The approximation can be considered accurate when high-frequency dynamics can be neglected (e.g. dynamics associated with oil-column resonance and actuator–specimen interaction). A complete explanation of all the conditions necessary to model the ETS with a first-order model is presented in [19]. These conditions are satisfied for the specific ETS and for the frequency range considered in this study. The ETS transfer function (see Fig. 1) can be written as:

$$\begin{aligned} G_{yr} =\frac{k_{yr} }{\tau _{yr} s+1} \end{aligned}$$
(1)

where \(\tau _{yr}\) is a time constant and \(k_{yr}\) is an amplitude gain. The parameter values of Eq. (1) vary in function of the PS, the HAS and the actuator controller algorithm; moreover, the parameters change with respect to the amplitude of the reference signal because of inevitable nonlinearities.

The main and innovative idea of this paper is to use the EKF in order to identify the ETS model parameters in real time and to construct a model-based compensator, based on the actual parameters.

2.1 Parameter estimation based on the EKF

The EKF algorithm can be used to estimate unknown system parameters by taking the parameters as additional states and augmenting state equations [21, 22].

With reference to the case study, a suitable enlarged state vector has to be defined in order to estimate both the state variables and the desired parameters.

The differential equation associated with the transfer function (1) (see Fig. 1) is:

$$\begin{aligned} \tau _{yr} \dot{y}+y=k_{yr} r, \end{aligned}$$
(2)

that can be written in discrete time domain using the forward difference approximation:

$$\begin{aligned} y_k =\left( {1-\frac{\Delta t}{\tau _{yr} }} \right) y_{k-1} +\left( {\frac{k_{yr} \Delta t}{\tau }} \right) r_{k-1} , \end{aligned}$$
(3)

where \(\Delta t\) is a discretization time.

Considering the state vector

$$\begin{aligned} \mathbf{x}_k = \left[ {{\begin{array}{ccc} {y_k }&{}\quad {\tau _{yr,k} }&{}\quad {k_{yr,k} } \\ \end{array} }} \right] ^{\mathrm{T}}=\left[ {{ \begin{array}{ccc} {x_{1,k} }&{}\quad {x_{2,k} }&{}\quad {x_{3,k} } \\ \end{array} }} \right] ^{\mathrm{T}},\nonumber \\ \end{aligned}$$
(4)

Equation (3) can be formulated in the following state-space form:

$$\begin{aligned} \left\{ {\begin{array}{l} x_{1,k} \!=\!\left( {1-\frac{\Delta t}{x_{2,k-1} }} \right) x_{1,k-1} \!+\!\left( {\frac{x_{3,k-1} \Delta t}{x_{2,k-1} }} \right) r_{k-1} \!+\!w_{1,k-1} \\ x_{2,k} \!=\!x_{2,k-1} \!+\!w_{2,k-1} \\ x_{3,k} \!=\!x_{3,k-1} +w_{3,k-1} \\ \end{array}} \right. ,\nonumber \\ \end{aligned}$$
(5)

where \(w_{1}\) is a Gaussian noise associated with the actuator displacement dynamics, \(w_{2}\) and \(w_{3}\) are fictitious Gaussian noises related to the unknown parameters.

In addition to Eq. (5), the measurement equation has to be introduced:

$$\begin{aligned} z_k =x_{1,k} +v_k \end{aligned}$$
(6)

where \(v_{k}\) is the measurement noise.

Equations (5) and (6) can be written in a more general form:

$$\begin{aligned} \begin{aligned} \mathbf{x}_k&=\mathbf{f}(\mathbf{x}_{k-1} ,\mathbf{r}_{k-1} ,\mathbf{w}_{k-1}) \\ \mathbf{z}_k&=\mathbf{h}(\mathbf{x}_k ,\mathbf{v}_k), \end{aligned} \end{aligned}$$
(7)

being x the state vector, f the nonlinear function, r the input vector, \(\mathbf{w}_{k}\) the process noise vector with covariance \(\mathbf{Q}_k \), \(\mathbf{z}\) the measurement vector, h a measurement function, and v \(_{k}\) the Gaussian white measurement noise with covariance \(\mathbf{R}_k \).

The EKF methodology is conceptually based on two fundamental steps, namely a priori estimate (“−” superscript) and a posteriori estimate (“\(+\)” superscript). Denoting the estimates as \(\left( {\hat{{{\bullet }}}} \right) \), the following initializing conditions are applied to the state estimates (8) and to the error covariance (9):

$$\begin{aligned} \hat{\mathbf{x}}_0^+= & {} E(\mathbf{x}_0 )\end{aligned}$$
(8)
$$\begin{aligned} P_0^+= & {} E\left[ {\left( {\mathbf{x}_0 -\hat{{\mathbf{x}}}_0^+ } \right) \left( {\mathbf{x}_0 -\hat{{\mathbf{x}}}_0^+ } \right) ^\mathrm{T}} \right] \end{aligned}$$
(9)

being E the expected value.

The a priori state estimates and the a priori estimation of the error covariance are given by (10) and (11), respectively:

$$\begin{aligned} \hat{{\mathbf{x}}}_k^-= & {} \mathbf{f}\left( \hat{{\mathbf{x}}}^{+}_{k-1} ,\mathbf{r}_{k-1} \right) ,\end{aligned}$$
(10)
$$\begin{aligned} \mathbf{P}_k^-= & {} \mathbf{A}_{k-1} \mathbf{P}_{k-1}^+ \mathbf{A}_{k-1}^T +\mathbf{L}_{k-1} \mathbf{Q}_{k-1} \mathbf{L}_{k-1}^T , \end{aligned}$$
(11)

with

$$\begin{aligned} \mathbf{A}_{k-1}= & {} \left. {\frac{\partial \mathbf{f}}{\partial \hat{{\mathbf{x}}}}} \right| _{\hat{{\mathbf{x}}}^{+}_{k-1} } ,\end{aligned}$$
(12)
$$\begin{aligned} \mathbf{L}_{k-1}= & {} \left. {\frac{\partial \mathbf{f}}{\partial \mathbf{w}}} \right| _{\hat{{\mathbf{x}}}^{+}_{k-1} } . \end{aligned}$$
(13)

With the computation of the filter gain (14) and evaluating the measurement residual, the a posteriori state estimates (15) and the a posteriori estimation of the error covariance (16) can be determined:

$$\begin{aligned} \mathbf{K}_k= & {} \mathbf{P}_k^- \mathbf{H}_k^T (\mathbf{H}_k \mathbf{P}_k^- \mathbf{H}_k^T +\mathbf{M}_k \mathbf{R}_k \mathbf{M}_k^T )^{-1},\end{aligned}$$
(14)
$$\begin{aligned} \hat{{\mathbf{x}}}^{+}_k= & {} \hat{{\mathbf{x}}}^{-}_k +\mathbf{K}_k \left[ {\mathbf{z}_k -\mathbf{h}(\hat{{\mathbf{x}}}^{-}_k ,\mathbf{r}_k )} \right] ,\end{aligned}$$
(15)
$$\begin{aligned} \mathbf{P}_k^+= & {} (\mathbf{I}-\mathbf{K}_k \mathbf{H}_k )\mathbf{P}_k^- , \end{aligned}$$
(16)

where

$$\begin{aligned} \mathbf{H}_k= & {} \left. {\frac{\partial \mathbf{h}}{\partial \hat{{\mathbf{x}}}}} \right| _{\hat{{\mathbf{x}}}^{-}_k } ,\end{aligned}$$
(17)
$$\begin{aligned} \mathbf{M}_k= & {} \left. {\frac{\partial \mathbf{h}}{\partial \mathbf{v}}} \right| _{\hat{{\mathbf{x}}}^{-}_k } . \end{aligned}$$
(18)

As described in (4), the state vector contains information of not only the displacement of the actuator, but also of the time constant and the gain. This means that the parameter values are identified for each time step.

2.2 Online model-based compensation

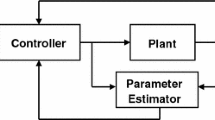
Figure 2 shows a schematic block diagram of the configuration for the compensation of the ETS dynamics. The compensation algorithm is based on the feedforward controller with modified inverse dynamics presented in [19], starting from the online estimation of the parameters of the transfer function \(G_{yr}(s)\) (see Eq. 1).

Fig. 2
figure 2

Scheme of the EADC

Full size image

The method is based on adding a linear transfer function \(G_{c}\) (see Fig. 2) that performs the compensation for the ETS dynamics represented by the transfer function \(G_{yr}\) (see Fig. 1). The transfer function \(G_{c}\) is not equal to the inverse transfer function of \(G_{yr}\), but it is modified in order to create a proper system (adding enough poles to the transfer function at least equal to the number of zeroes) [19]. The transfer function \(G_{c}\) of the feedforward controller with modified inverse dynamics can be expressed as

$$\begin{aligned} G_c =\frac{1}{\hat{{k}}_{yr} }\frac{\hat{{\tau }}_{yr} s+1}{\frac{\hat{{\tau }}_{yr} }{\alpha }s+1} \end{aligned}$$
(19)

where \(\alpha \) is assumed larger than one. Therefore, the poles are larger than the zeros, and the compensator provides a phase lead making the poles large enough in order to not influence the low-frequency dynamics of the original inverse controller [19]. The relation (19) is similar to the expression of a lead compensator [25].

Fig. 3
figure 3

EKF-based parameter estimation for Sim 1; a time constant diagram, b amplitude gain diagram

Full size image
Fig. 4
figure 4

EKF-based parameter estimation for Sim 2; a time constant diagram, b amplitude gain diagram

Full size image

The EKF provides the parameter estimations \(\hat{{k}}_{yr} \) and \(\hat{{\tau }}_{yr} \) in Eq. (19) starting from the knowledge of signals r and y (see Fig. 2).

2.3 Simulation analysis

Simulation studies have been conducted in order to evaluate the performances of the proposed method prior to the experimental validation. It is important to note that EKF does not assure the minimum variance estimate, and no convergence proof can be given. Nevertheless, the approach behaves well in many situations, as demonstrated by numerous applications [26]. For this reason, an extensive numerical simulation campaign is crucial to check the stability of the EKF for each specific case. Indeed, the EKF convergence is strictly related to the tuning of the Q and R matrices, and these can be determined with numerical tests that reproduce conditions similar to the actual ones.

Firstly, the parameter estimator has been verified for different sets of the actual plant parameters. Subsequently, the compensation capabilities of the EADC have also been verified. The ETS mathematical model adopted in simulation environment is represented by the transfer function (1). For the validation of the EKF, a 20 Hz band-limited white noise has been considered as input signal; a white noise has been added to the simulated actuator displacement in order to reproduce a more realistic scenario. Two different simulations have been performed to evaluate the capabilities of the EKF-based parameter estimation. In the first case (Sim 1), the referenced parameters \(k_{yr}=0.2\) and \(\tau _{yr}=0.02\hbox { s}\) have been defined. For the second case (Sim 2), the parameters \(k_{yr}=0.15\) and \(\tau _{yr}=0.04\hbox { s}\) have been chosen in order to reproduce a system dynamics very different with respect to Sim 1. For both the simulation cases, \(k_{yr}=0.1\) and \(\tau _{yr}=0.01\hbox { s}\) have been fixed as the initial values of the parameters to be identified.

Figures 3 and 4 show a comparison between the estimated parameters and the actual ones for Sim 1 and Sim 2, respectively.

The parameter estimation results confirm the effectiveness of the proposed method for both cases. The diagrams of Figs. 3 and 4 show how the EKF permits to track the actual parameters. The results also show that the time interval employed by the estimator to reach the actual parameters is satisfactory.

Fig. 5
figure 5

EKF-based actuator displacement estimation for Sim 1

Full size image
Fig. 6
figure 6

EKF-based actuator displacement estimation for Sim 2

Full size image

The effectiveness of the EKF is also demonstrated by results concerning the estimation of the actuator displacement reported in Figs. 5 and 6, respectively, for Sim 1 and Sim 2.

Fig. 7
figure 7

EADC results for Sim 3. a Uncompensated versus desired displacement b compensated versus desired displacement

Full size image

The EADC has been verified using a sinusoidal displacement with an amplitude of 0.05 m and a frequency of 2 Hz (Sim 3); the parameter values of the first-order model are \(k_{yr}=0.97\) and \(\tau _{yr}=0.025\hbox { s}\), and these values have been chosen in accordance with the experimental set-up used for a RTHS, presented in [27]. The performance of the compensation approach is analysed by comparing the desired, compensated and uncompensated actuator displacement. The plot of the desired versus the measured compensated displacements (Fig. 7b) is nearly a straight line with a slope of one, which demonstrates the accuracy of the compensation algorithm.

The results of the EKF-based estimator, reported in Fig. 8, also demonstrate the efficiency of the proposed method.

All the simulation results highlight the convergence of the EKF for this specific case study.

3 Experimental validation

To validate the performance of the novel adaptive compensation approach, experiments have been performed at the Department of Industrial Engineering, University of Naples Federico II (Italy). The experimental set-up has been designed to perform shear tests on seismic isolators [28–30]. The machine mainly consists of a sliding table (\(1.8\hbox { m} \times 1.59\hbox { m}\)) driven by a hydraulic cylinder that allows shear testing of isolators, while a vertical actuator imposes constant vertical loads on the devices being tested. The table motion is constrained to a single horizontal axis by means of recirculating ball-bearing linear guides. Figure 9 shows that the specimen is placed between a sliding table and a vertical slide that moves into suitable guides integrated in the reaction frame.

The test rig is instrumented to measure the following quantities used for the hybrid simulations:

  • table position is measured using a magnetostrictive position sensor (model EP2-0400M-A by “MTS Sensors”). The instrument is placed between the sliding table and the fixed base (see Fig. 9 for reference).

  • actuator force is measured using a strain gauge load cell (model AP7025-A1 by “S2Tech”) placed between the hydraulic actuator and the sliding table.

The isolator under test is commonly employed in seismic isolation, and it consists of alternate layers of steel and elastomer connected by curing (Fig. 10).

Fig. 8
figure 8

EKF-based parameter estimation for Sim 3; a time constant diagram, b amplitude gain diagram

Full size image

The actuator displacement control system has been implemented in a DS1103 controller board equipped with 16-bit analogical/digital and digital/analogical converters. The main objective of the control system is to make the measured displacement as close as possible to the desired one, minimizing phase lag and providing accurate tracking of the reference signal [31, 32]. The control consists of a feedforward action integrated with a feedback one. The feedforward control has been developed taking into account typical nonlinearities of HASs [33, 34]. The feedback control has been adopted to compensate for tracking errors due to model uncertainties and the unknown reaction force of the specimen under testing [35].

Fig. 9
figure 9

Test rig showing components

Full size image

As shown in Fig. 11, the feedforward control, starting from the reference r, generates the action \(u_\mathrm{ff}\) by means of model inversion (\(\hat{{G}}^{-1}\)). The differences between the model (\(\hat{{G}}\)) and the effective plant (G) determine table positioning errors (\(e=r-y\)) that are compensated by the feedback action \(u_\mathrm{fb}\) produced by the controller \(G_1 \).

Fig. 10
figure 10

Specimen adopted for the EADC experimental validation

Full size image
Fig. 11
figure 11

Controller scheme

Full size image

The dynamics of the controlled system depends on the actual plant (HAS, controller, specimen). Therefore, an adaptive approach for a model-based compensation is crucial to avoid laborious tuning procedures for different specimens and control algorithms.

As an example, the performances of the proposed EADC have been experimentally evaluated considering shear tests on the specimen shown in Fig. 10. Different gains of the feedback action, proportional to the table displacement error, \(u_\mathrm{fb}=K_\mathrm{p}\cdot e\), have been adopted, where \(K_\mathrm{p}\) is the feedback control proportional gain.

A sinusoidal law with an amplitude \(A=0.10\hbox { m}\) and a frequency \(f=0.5\hbox { Hz}\) has been adopted as target displacement. Two experimental demonstrations have been selected in order to highlight the effect of a controller modification on the overall system dynamics: a first one with \(K_\mathrm{p}=400\) (Test A), and a second one with \(K_\mathrm{p}=800\) (Test B). The behaviours of the estimated parameters for the Test A are shown in Fig. 12, while the results for the Test B are reported in Fig. 13.

Fig. 12
figure 12

EKF-based parameter estimation for Test A; a time constant diagram, b amplitude gain diagram

Full size image
Fig. 13
figure 13

EKF-based parameter estimation for Test B; a time constant diagram, b amplitude gain diagram

Full size image
Fig. 14
figure 14

EADC experimental results for Test A; a diagram (r–y), b diagram (d–y)

Full size image
Fig. 15
figure 15

EADC experimental results for Test B; a diagram (r–y), b diagram (d–y)

Full size image
Fig. 16
figure 16

EKF-based parameter estimation for Test C; a time constant diagram, b amplitude gain diagram

Full size image
Fig. 17
figure 17

EADC experimental results for Test C; a diagram (r–y), b diagram (d–y)

Full size image

For both the verifications, the diagrams (r–y) and (d–y) are shown in Figs. 14 and 15, respectively. The results of diagrams (r–y) are related to the controller performance. Indeed, with reference to Figs. 1 and 11, signals r and y are the input and output of the controlled ETS, respectively. The diagrams (d–y) show the relationship between the desired displacement d, provided by numerical integration of the equations of motion, and the actual displacement of the PS (see Fig. 1 for reference). Therefore, diagrams (d–y) provide information concerning the performance of the ETS compensation strategy.

An important result provided by the nonlinear parameter estimation concerns the variation of the time constant during both the experimental tests. This variation is due to system nonlinearities well managed by the proposed estimator that adaptively varies the system parameters. The ultimate demonstration of the good performance of the compensation strategy is provided by the diagram (d–y), which clearly shows that the two signals r and y are practically superimposable (see for reference Figs. 14b, 15b).

With reference to the estimated parameters for both experimental tests, it is interesting to note that for Test B, characterized by a higher value of the feedback controller gain, the medium value of the time constant is lower than the one for the Test A (see Figs. 12a, 13a). This result is in accordance with expected dynamics performance of the controller. The higher phase shift between the target displacement and the measured one for Test A is also evident considering the two diagrams reported in Figs. 14a and 15a. The two identified amplitude gains of the first-order model are almost equal for the two cases (see, for reference, Figs. 12b, 13b). This result means that for both tests there has not been a substantial attenuation of the input signal due to the control loop.

Another test (Test C) has been performed for a sinusoidal target displacement characterized by a higher value of the frequency \(f=1\hbox { Hz}\) and an amplitude \(A=0.05\hbox { m}\). The controller configuration has been chosen as equal as the one adopted for Test B.

The estimated parameters and the diagrams (r–y) and (d–y) are shown in Figs. 16 and 17, respectively.

Also for Test C, both parameter identification and compensation can be considered satisfactory. The diagrams of the estimated parameters, reported in Fig. 16a, b, show that the EKF converges to almost constant values for both parameters. The comparison between diagrams of Fig. 17a, b demonstrates that the phase shift between signals r and y is completely compensated, as clearly highlighted by the diagram (d–y).

For Test C, the hysteresis cycle of the seismic isolator is also reported in Fig. 18.

Fig. 18
figure 18

Specimen force–deformation diagram

Full size image
Fig. 19
figure 19

RTHS test set-up

Full size image

From the force–deformation diagram of Fig. 18, it is possible to identify an equivalent shear stiffness \(K_{h,\mathrm{eq}}=800\hbox { kN/m}\).

In the next paragraph, other experimental results are presented. In particular, the EADC has been used in a RTHS concerning a base isolation problem where the seismic isolator above described has been adopted as the PS.

4 Hybrid testing

The RTHS validation testing aimed to verify the applicability of the proposed EADC for the evaluation of seismic performance of base-isolated buildings with the isolator presented in Fig. 10. Two SDOF base-isolated structures have been used. Cases 1 and 2 correspond to a base-isolated undamped periods of 1 and 2 s, respectively. Both the structures for the two cases have a fixed-base natural period of 0.4 s and a damping ratio of 2 %. The base isolation frequency for each experiment has been modified by changing the structure mass and taking into account an equivalent horizontal stiffness of the seismic isolator \(K_{h,\mathrm{eq}}=800\hbox { kN/m}\). The system is divided into two parts: (1) the PS, consisting of the seismic isolator anchored between the sliding table and the reaction structure, and (2) the NS, consisting of an elastic SDOF structure. The overall test set-up is shown in Fig. 19. The NS sends the desired shear deformation of the seismic isolator (equal to the target sliding table displacement) to the PS, which, in turn, sends the measured reaction force of the specimen to the NS. Therefore, the controlled HAS and the EADC must ensure that the measured table displaced is as equal as possible to the commanded one.

Fig. 20
figure 20

Comparison between ground and base accelerations for Case 1

Full size image
Fig. 21
figure 21

EKF-based parameter estimation for Case 1; a time constant diagram, b amplitude gain diagram

Full size image
Fig. 22
figure 22

Time histories of the commanded and measured displacements for Case 1

Full size image
Fig. 23
figure 23

EADC results for Case 1; a diagram (r–y), b diagram (d–y)

Full size image

The Friuli Earthquake (1976, Italy) has been chosen as the input ground motion. The duration of the earthquake record used is 10 s. The central difference method has been used for the integration of the equation of motion, with a time step \(\Delta t = 0.1\,\hbox {ms}\). This time step has been adequate to accurately integrate the equation of motion for the natural frequencies considered in the experiments.

Figure 20 shows the comparison between the ground acceleration and the base one for the Case 1.

Fig. 24
figure 24

Comparison between ground and base accelerations for Case 2

Full size image

The acceleration diagrams of Fig. 20 show a substantial reduction in peak acceleration. This result demonstrates the effectiveness of the base isolation system and confirms the possibility of evaluating the performance of the seismic isolator in RTHS.

Figure 21 shows the estimated parameters for the Case 1. The identified values are in accordance with the ones obtained in the preview experimental tests.

Fig. 25
figure 25

EKF-based parameter estimation for Case 2; a time constant diagram, b amplitude gain diagram

Full size image
Fig. 26
figure 26

Time histories of the commanded and measured displacements for Case 2

Full size image

The comparison between the measured displacement and the commanded one is shown in Fig. 22. The diagrams are practically superimposed as demonstration of the goodness of the compensation method.

The performance of the proposed adaptive compensation scheme is also evident observing the two diagrams (r–y) and (d–y) reported in Fig. 23a, b, respectively.

An analogue experimental verification has been performed for the Case 2. The ground and the base accelerations are shown in Fig. 24.

For the Case 2, the base peak acceleration is lower than the one obtained in the Case 1. This results is in accordance with the base isolation theory. Indeed, the higher value of the base-isolated natural period for the Case 2 corresponds to a higher reduction in the acceleration transmitted to the structure.

Figure 25 shows the estimated parameters for the Case 2; both the time constant and the amplitude gain are comparable with the ones of Case 1 (see Fig. 21 for reference).

Fig. 27
figure 27

EADC results for Case 2; a diagram (r–y), b diagram (d–y)

Full size image

Comparison between the measured displacement and the commanded one is shown in Fig. 26. Also in this case the tracking performances of the controller, combined with the EADC, can be considered satisfactory. Moreover, the displacement diagrams of Figs. 22 and 26 show an increase in the isolator deformations for the Case 2, if compared with the Case 1. These results confirm the reliability of the RTHS because a higher value of the base-isolated natural period involves higher base displacements and lower transmitted acceleration (see for reference Figs. 20, 24).

The diagrams (r–y) and (d–y) for Case 2 are presented in Fig. 27a, b, respectively. The results concerning the EADC performance can be considered acceptable also for the Case 2. Indeed the displacement tracking errors due to the ETS dynamics (see Fig. 27a for reference) have been compensated as clearly shown in Fig. 27b.

The results of RTHSs have demonstrated the effectiveness of the EADC, and in addition, they have shown that the adaptive approach allows the testing of structures with different dynamic characteristics without user-defined settings.

5 Conclusion

An adaptive method for the dynamics compensation of an actuation system used in RTHS is proposed. It is a combination of a nonlinear parameter estimator, based on the EKF, and an adaptive compensator depending on the identified model parameters. For numerical studies, different actuator dynamics models have been evaluated, and simulation results have shown good performances of both the estimator and the compensator. The proposed adaptive compensator method has been applied to an experimental set-up for shear tests on seismic isolators. Experimental results have confirmed the adaptation capabilities of the strategy in the case of actuator dynamics variation due to modifications of the controller. In addition, a real-time hybrid testing set-up has been developed in order to evaluate the performances of a physical seismic isolator and, at the same time, to verify the adaptive compensator. The hybrid simulation results have shown that the proposed compensation strategy is particularly suitable for the case study, ensuring the test stability without influencing the signals between the numerical model and the experimental substructure.