1 Introduction

Real-time hybrid simulation (RTHS), or hybrid testing, combining numerical simulation with experimental testing, is an efficient and cost-effective methodology for evaluating the seismic performance of structural systems. In a hybrid test, a part of the structural system (e.g., the critical components) is experimentally tested, while the rest is computationally simulated. A numerical integration scheme is employed to obtain the displacement response of the computational structure, which is then imposed on the experimental substructure. The resulting restoring forces measured from the experimental components are then sent back to the integration algorithm to calculate the command displacement for the next time step. The key for RTHS is that the command displacements are imposed on the test specimen by hydraulic actuators in real-time. During the test, the computation, communication, and dynamics of the servo-hydraulic actuators cause time lag and delay between the displacement commands and measurements. These time lag and delay can introduce negative damping into the hybrid simulation, which would result in inaccuracies and potential instabilities. Thus, various studies have been conducted to investigate compensation of the actuator delay, including the polynomial extrapolation (Horiuchi et al. 1999; Nakashima and Masaoka 1999; Darby et al. 2002), the phase-lead compensation (Zhao et al. 2003), the derivative feedforward compensation (Jung et al. 2007), and the inverse compensation (Chen 2007; Chen and Tsai 2013). These studies have shown the challenges to achieve precise displacements in RTHS.

Most tracking control schemes have employed a simple model to portray the experimental system. Darby et al. (2002) demonstrated that the actuator delay depends on the current stiffness of the specimen. Two learning gains approach was proposed to control a tradeoff between the convergence rate and oscillation of the delay estimate. Ahmadizadeh et al. (2008) estimated the actuator delay by using the slopes of the desired and measured displacements. Chen and Ricles (2010) introduced an adaptive compensation scheme to minimize the actuator delay over a tracking indicator that was developed by Mercan and Ricles (2007). Chen and Tsai (2013) applied an adaptive control theory to obtain the delay constant online through a gradient adaptive law. These methods only adjust one parameter to realize an adaptive control scheme.

More effective compensators have been explored by the researchers using the linearized servo-hydraulic system model. Carrion and Spencer (2007) proposed a model-based compensation strategy by considering the dynamics of the servo-hydraulic system over a broad frequency range. The transfer function of the servo-hydraulic system was derived from system identification tests. The feedforward controller was realized by inverting the transfer function in series with a unity-gain low-pass filter to make the controller proper. Phillips and Spencer (2012) further improved the model-based tracking control framework by employing the displacement, velocity, acceleration, and higher order derivatives to implement this improper inverse model. The derivatives were taken directly from an integration algorithm. These two studies have demonstrated that the higher-order implementation compensates the servo-hydraulic system fairly well and extends the applicable frequency range as compared to other approaches.

Adaptive control combines a parameter estimator and a control law, providing an advanced approach to the model-based control scheme in RTHS. The parameter estimator generates parameter estimates online, while the control law stabilizes a time-variant system. The controller can be implemented on the system directly or indirectly. The estimate is used in the control law without intermediate calculations for direct adaptive control, whereas it needs additional calculations of control parameters for indirect adaptive control. The design philosophy of adaptive control can be divided into four steps: (1) initialize the parameters in the controller; (2) design the adaptive law to estimate the unknown parameters; (3) update the unknown controller parameters by the estimates; and (4) check the stability property of the controlled system. Adaptive controllers can effectively eliminate tracking errors of time-variant or nonlinear systems by self-tuning of parameters; however, their complexity induces more difficulty in implementation than that of traditional linear controllers with fixed parameters.

In this study, an adaptive control scheme that contains an adaptive control law and the feedfoward–feedback controllers is proposed for RTHS. The dynamics of the servo-hydraulic system would vary during a hybrid test due to the nonlinearity of the experimental specimen such as a magnetorheological (MR) damper (Yang et al. 2002; Carrion and Spencer 2007; Phillips and Spencer 2012). In previous work, a linearized model of the servo-hydraulic system was adopted to accommodate such nonlinearities. However, if the nonlinearities are significant, this linearized approach may not be robust and accurate enough for RTHS. In order to solve this problem and improve the tracking performance of actuators used in RTHS, an adaptive control scheme is proposed in this study. This control scheme applies the adaptive control theory to the feedforward controller. A 3rd-order feedforward controller using the central difference method (CDM) integration algorithm is adopted to compensate the servo-hydraulic system. The adaptive control strategy is used to online estimate the system parameters for the feedforward controller. In addition, the projection algorithm is employed to avoid the instability of the adaptive feedforward controller. Moreover, a feedback controller derived from the linear-quadratic-Gaussian (LQG) control algorithm is used to further eliminate the system and modeling uncertainties. A complete adaptive control scheme is composed of the adaptive feedforward controller with a LQG feedback controller. The tracking performance of the adaptive controller is evaluated in time domain using a predefined band-limited white noise (BLWN) displacement command history. The root-mean-square (RMS) error is used to explore the tracking performance between the desired and measured displacements. Finally, large-scale real-time hybrid tests for a nine-story steel frame benchmark shear building are conducted to verify the adaptive model-based actuator control strategy.

2 Adaptive law with projection

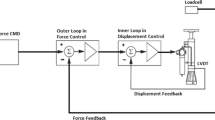
Adaptive control, a combination of a parameter estimator and a control law, can provide a solution to a complex control problem that needs good understanding of the system properties. The model-based feedforward controller (Phillips and Spencer 2011) is developed by a system identification process which provides prior and sufficient information about the servo-hydraulic system required by the adaptive control law. In this study, the servo-hydraulic system is modeled as a three-pole transfer function. The estimated parameters calculated by the adaptive law are used in the feedforward controller to improve the tracking performance of a nonlinear system. The implementation is considered as a direct adaptive control because no immediate calculation of the estimates is necessary. Figure 1 illustrates the block diagram of the direct adaptive control scheme in this study. Four conditions are taken into account in the adaptive control strategy (1) a numerical model of the feedforward controller containing uncertain parameters, (2) the boundary condition of the parameters for the system stability, (3) the adaptive control law, and (4) the projection algorithm for the adaptive control law. The remainder of this section addresses each of these points.

Fig. 1
figure 1

Illustration of direct adaptive control

Full size image

2.1 Feedforward controller

The feedforward controller, proposed by Phillips and Spencer (2011), is designed to cancel the modeled dynamics of the servo-hydraulic system. The servo-hydraulic system can be represented by a transfer function form as

$$\begin{aligned} G_{yu} (s)=\frac{n_m s^{m}+n_{m-1} s^{m-1}+\cdots +n_1 s+n_0 }{d_n s^{n}+d_{n-1} s^{n-1}+\cdots +d_1 s+d_0 } \end{aligned}$$
(1)

where \(d_{n},{\ldots }, d_{0}\) and \(n_{m},{\ldots }, n_{0}\) are the coefficients in the denominator and the numerator, respectively. The parameter \(s\) is a complex number in the Laplace transform. If \(n\geqq m\), the system is proper. Three-pole non-zero models (\(n=3\) and \(m=0\)) have been found sufficient enough from the previous research (Phillips and Spencer 2011). The feedforward controller is taken as the inverse of servo-hydraulic system, and the transfer function can be therefore written as

$$\begin{aligned} G_\mathrm{FF} (s)=\frac{d_3 s^{3}+d_2 s^{2}+d_1 s+d_0 }{n_0 }=a_3 s^{3}+a_2 s^{2}+a_1 s+a_0 \end{aligned}$$
(2)

where \(a_{3},{\ldots },a_{0}\) are the coefficients for the feedforward controller. Obviously, the feedforward controller is improper by three degrees. The magnitude of an improper controller approaches to infinity as the frequency approaches to infinity. In addition, the feedforward controller is formed by displacement, velocity, acceleration, derivative of the acceleration in time domain. Thus, implementing an improper controller is not feasible. Phillips and Spencer (2011) used the CDM with a linear acceleration extrapolation to calculate the necessary higher-order derivatives. Subsequently, the feedforward controller in discrete time can be expressed as

$$\begin{aligned} u_\mathrm{FF} [k]&= \left( {a_0 +\frac{2a_1 }{\Delta t}+\frac{2a_2 }{\Delta t^{2}}+\frac{a_3 }{\Delta t^{3}}} \right) x[k]+\left( {\frac{-7a_1}{2\Delta t}+\frac{-5a_2}{\Delta t^{2}}+\frac{-3a_3}{\Delta t^{3}}} \right) x[k-1]\nonumber \\&+\left( {\frac{2a_1 }{\Delta t}+\frac{4a_2 }{\Delta t^{2}}+\frac{3a_3 }{\Delta t^{3}}} \right) x[k-2]+\left( {\frac{-a_1 }{2\Delta t}+\frac{-a_2 }{\Delta t^{2}}+\frac{-a_3 }{\Delta t^{3}}} \right) x[k-3] \end{aligned}$$
(3)

where \(\Delta t\) is the sampling period of the discrete system; \(x[k], x[k-1], x[k-2]\) and \(x\)[\(k-\)3] are the command displacements at the k-th, (k-1)-th, (k-2)-th and (k-3)-th step, respectively.

2.2 Stability constraint

The stability of the feedforward controller is investigated by applying the Routh’s stability criteria. The feedforward controller is developed by inverting the transfer function of the servo-hydraulic system in which the poles can be assigned in the left half plane in s-domain to ensure the system stability. However, these parameters could vary significantly during the process of parameter estimation, and thus the derived controller may be unstable. To address this issue, the Routh’s stability criteria are used to limit these parameters and to ensure the stability of the adaptive feedforward controller. In this approach, the DC gain of the servo-hydraulic system is assumed to be equal to one. By arranging the coefficients of the characteristic equation of the transfer function, the Routh’s array can be formed as shown in Table 1. The number of sign changes in the first column in Table 1 indicates the number of unstable poles in the transfer function. To meet the stability condition, the parameters must satisfy the three inequalities as

$$\begin{aligned} a_2 >0;\quad a_3 >0;\quad a_1 a_2 -a_3 >0 \end{aligned}$$
(4)

The three inequalities become the pre-defined upper and/or lower bounds to constrain the online estimation within these boundaries. Consequently, the stability margin of the parameters for the feedforward controller is confirmed.

Table 1 Routh’s array of the servo-hydraulic system
Full size table

2.3 Gradient adaptive control law

The static parametric model (SPM) is formed in order to apply the adaptive control law. The first step in the online parameter estimation is to separate the unknown parameters from the known signals. For a three-pole model, the relation between the input \(u\) and the output \(y\) is described as

$$\begin{aligned} y=\frac{1}{a_3 s^{3}+a_2 s^{2}+a_1 s+a_0 }u \end{aligned}$$
(5)

The SPM can be obtained by separating the parameters from the input and output signals

$$\begin{aligned} u=\left[ {{\begin{array}{llll} {a_3 }&{} {a_2 }&{} {a_1 }&{} {a_0 } \\ \end{array} }} \right] \left[ {{\begin{array}{llll} {s^{3}y}&{} {s^{2}y}&{} {sy}&{} y \\ \end{array} }} \right] ^{T} \end{aligned}$$
(6)

It is found that improper terms are included in the right-hand side in Eq. 6. For this reason, a 3rd-order low-pass filter \(1/\Lambda (s)\) is applied on each term to make them proper where \(\Lambda (s)\) is a Hurwitz polynomials that all poles are located in the left-hand side of the s-plane. In this study, \(\Lambda (s)\) is selected as \((s+1)^{3}\). Consequently, the parametric model after filtering both sides by \(1/\Lambda (s)\) is given by

$$\begin{aligned} \frac{u}{\Lambda (s)}=\left[ {{\begin{array}{llll} {a_3 }&{} {a_2 }&{} {a_1 }&{} {a_0 } \\ \end{array} }} \right] \left[ {{\begin{array}{llll} {\frac{s^{3}}{\Lambda (s)}y}&{} {\frac{s^{2}}{\Lambda (s)}y}&{} {\frac{s}{\Lambda (s)}y}&{} {\frac{1}{\Lambda (s)}y} \\ \end{array} }} \right] ^{T} \end{aligned}$$
(7)

or equivalently,

$$\begin{aligned} z=\varvec{\uptheta }^{*T}\mathbf{w} \end{aligned}$$
(8)

where \(z\) and w are known signals; and \(\varvec{\uptheta }^{*}\) contains all the unknown parameters to be estimated. The estimate of \(z\) is generated from the estimation model by replacing the unknown parameter \(\varvec{\uptheta }^{*}\) with its estimated parameter, \(\varvec{\uptheta }(t)\), i.e.,

$$\begin{aligned} \hat{z}=\varvec{\uptheta }^{T}\mathbf{w} \end{aligned}$$
(9)

where \(\hat{z}\) is the estimate of \(z\). The difference between \(\hat{z}\) and \(z\) results from the difference between \(\varvec{\uptheta }(t)\) and \(\varvec{\uptheta }^{*}\). It appears that the estimate \(\hat{z}\) approaches to \(z\) as \(\varvec{\uptheta }(t)\) approaches \(\varvec{\uptheta }^{*}\). Nevertheless, the difference between \(\varvec{\uptheta }(t)\) and \(\varvec{\uptheta }^{*}\) is not available because \(\varvec{\uptheta }^{*}\) is unknown. Therefore, the estimation error \({\varepsilon }\), which can be obtained from the available measurements, is defined as

$$\begin{aligned} \varepsilon \equiv \frac{z-\hat{z}}{m_s^2}= \frac{z-\varvec{\uptheta }^{T}\mathbf{w}}{m_s^2 } \end{aligned}$$
(10)

where \(m_{s}^{2}\geqq 1\) is the normalizing signal designed to bound \(\mathbf{w}/m_{s}\) even when w is not bounded. Typically, \(m_{s}^{2 }= 1+ {\alpha }\mathbf{w}^\mathrm{T}\mathbf{w}\) is suggested where \({\alpha }\) is a real number larger than zero.

The gradient algorithm with instantaneous cost function is utilized in this study because its parameter convergence has been proved mathematically (Ioannou and Fidan 2006). The cost function can be written by

$$\begin{aligned} J(\theta )=\frac{\varepsilon ^{2}m_s^2 }{2}=\frac{\left( {z-\varvec{\uptheta }^{T}\mathbf{w}} \right) ^{2}}{2m_s^2 } \end{aligned}$$
(11)

The gradient algorithm is used to minimize the cost function with respect to the parameter vector \(\varvec{\uptheta }\) and given by

$$\begin{aligned} \varvec{\dot{\uptheta }}=-\varvec{\Gamma }\nabla J(\varvec{\uptheta })=\varvec{\Gamma }\varepsilon \mathbf{w} \end{aligned}$$
(12)

where \(\varvec{\Gamma }\) is the adaptive gain matrix. More details about the proof of parameter convergence can be found in Ioannou and Fidan (2006).

2.4 Parameter projection

In addition to the aforementioned stability constraint, the parameter estimates can be additionally bounded by a priori knowledge of the servo-hydraulic system. The gradient algorithm with projection is computed by minimizing the cost function with a convex subset of constraints \(S\) defined as

$$\begin{aligned} S=\left\{ {\varvec{\uptheta }\in \mathbf{R}^{n}|g\left( \varvec{\uptheta } \right) \le 0} \right\} \end{aligned}$$
(13)

where \(g\) is a smooth function mapping from \(\mathbf{R}^\mathrm{n}\) to R. Figure 2 illustrates the parameter projection in the subspace of \(S\) where \(\hbox {Pr}(^{.})\) represents the projection operator. When the estimated parameters approach to the boundary of \(S\), the derivatives of the estimated parameters are projected to the tangent direction of the boundary of \(S\). To ensure that the estimated parameters are always bounded within \(S\), the gradient adaptive algorithm in Eq. 12 can be modified as

(14)

The possible parameter drifts caused by modeling errors can be eliminated by applying parameter projection algorithm in order to constraint the estimated parameters inside a subset of the parameter space. Consequently, the resulting parameters are always bounded within the stable region at each time step. Figure 3 illustrates the control scheme in this study. By utilizing this adaptive law, the adaptive control scheme can be applied to the model-based feedforward controller.

Fig. 2
figure 2

Illustration of parameter projection

Full size image
Fig. 3
figure 3

Adaptive model-based feedforward and feedback control scheme

Full size image

3 Analytical studies

This section investigates the feasibility of the proposed adaptive control algorithms numerically. Four cases of actuator compensation schemes were used: (a) feedforward controller, (b) feedforward controller and feedback LQG controller (Phillips and Spencer 2012), (c) feedforward controller with adaptive control algorithm, and (d) feedforward controller with adaptive control algorithm and feedback LQG controller. In this analysis, the tracking performance among these four schemes was evaluated and discussed.

To minimize the errors between the command and measurement, the feedback LQG control was employed. This minimization process attempts to compensate the specimen condition changes, modeling errors, sensor noise, and disturbances. First, the model for designing the feedback controller was obtained from the identified system. The LQG controller was then developed by a two-step approach. The first step utilized the linear-quadratic-regulator (LQR) control theory to obtain a state feedback gain, while the second step facilitated the Kalman filter design to establish an observer. By combining the LQR state feedback gain with the Kalman observer, a model-based feedback controller can be created to perform better displacement tracking for the servo-hydraulic actuators. To further consider the controller robustness, an input shaping filter was incorporated in the identified model. The details have been well documented in Phillips and Spencer (2011). In RTHS, amplifying the high-frequency components appropriately can further extend the tracking capability; however, these high-frequency components may introduce instability to the system due to the modeling errors. Moreover, a LQG controller with a high control authority could significantly increase the high-frequency components to the system. These components would generate a lead phase in the high frequencies, resulting in an instability issue to the system. In this regard, the LQG feedback controller with a moderate control authority was used in this study. The LQG controller can fit well to the feedforward–feedback control scheme.

The transfer function of a servo-hydraulic system in Carrion and Spencer (2007) and a perturbed system were adopted to investigate the feasibility of the adaptive control law through the analytical studies. In the analyses, the feedforward controller was given by

$$\begin{aligned} G_\mathrm{p} (s)=\frac{6.12\times 10^{6}}{s^{3}+348s^{2}+73770s+6.12\times 10^{6}} \end{aligned}$$
(15)

The three poles of the identified plant are \(-\)162.24,and \(-110.88\pm 159.46i\), where \(i^{2}=-1\). It indicates that \(a_{3}=1.634\times 10^{-7}\), \(a_{2}=6.275\times 10^{-5}\), \(a_{1}=0.01204\), and \(a_{0}=1\). To consider a modeling error between the identified model and the nominal plant, the nominal plant was assumed as

$$\begin{aligned} \overline{G}_\mathrm{p} (s)=\frac{5.2\times 10^{6}}{s^{3}+360s^{2}+64500s+5.2\times 10^{6}} \end{aligned}$$
(16)

The three poles of the nominal plant are \(-\)160, and \(-110\pm 150i\), resulting in \(a_{3}=1.923\times 10^{-7}\), \(a_{2}=6.923\times 10^{-5}\), \(a_{1}=0.0124\), and \(a_{0}=1\). The upper and lower bounds for the parameters \(a_{3}\), \(a_{2}\), and \(a_{1}\) were determined by the priori knowledge of the identified transfer function. Subsequently, the parameters were assumed to be bounded within the pre-determined boundaries such as \(L_{a3}< a_{3} < U_{a3}\), \(L_{a2}< a_{2} < U_{a2}\), and \(L_{a1}< a_{1}< U_{a1}\). It is noted that only the diagonal terms in the adaptive gain matrix was considered for simplicity. The parameter projection algorithms were finally obtained by combining the constraints from Eq. 4 and 14 as

$$\begin{aligned} \dot{\hat{a}}_3&= \left\{ \begin{array}{l@{\quad }l} \gamma _3 \varepsilon w_3 &{} if(L_{a3} <\hat{a}_3{<U_{a3}})\cap \left( {\hat{a}_3 <\hat{a}_1 \hat{a}_2 } \right) \quad or\left( {\hat{a}_3 \le L_{a3} } \right) \cap \left( {0\le \gamma _3 \varepsilon w_3} \right) \\ &{} or\left( {U_{a3} \le \hat{a}_3 } \right) \cap \left( {\gamma _3 \varepsilon w_3 \le 0} \right) \quad or\left( {\hat{a}_1 \hat{a}_2 \le \hat{a}_3 } \right) \cap \left( {\gamma _3 \varepsilon w_3 \le 0} \right) \\ 0&{}{otherwise}\\ \end{array}\right. \nonumber \\ \dot{\hat{a}}_2&= \left\{ \begin{array}{l@{\quad }l} \gamma _2 \varepsilon w_2 &{} if (L_{a2} < \hat{a}_2 {<U_{a2}} )\cap \left( {\hat{a}_3<\hat{a}_1 \hat{a}_2 } \right) \quad or\left( {\hat{a}_2 \le L_{a2} } \right) \cap \left( {0\le \gamma _2 \varepsilon w_2 } \right) \\ &{} or\left( {U_{a2} \le \hat{a}_2 } \right) \cap \left( {\gamma _2 \varepsilon w_2 \le 0} \right) \quad or\left( {\hat{a}_1 \hat{a}_2 \le \hat{a}_3 } \right) \cap \left( {0\le \hat{a}_1 \gamma _2 \varepsilon w_2 } \right) \\ 0 &{} {otherwise}\\ \end{array}\right. \nonumber \\ \dot{\hat{a}}_1&= \left\{ \begin{array}{l@{\quad }l}\gamma _1 \varepsilon w_1 &{}if(L_{a1} <\hat{a}_1{<U_{a1}})\cap \left( {\hat{a}_3 <\hat{a}_1 \hat{a}_2 } \right) \quad or {\left( {\hat{a}_1 \le L_{a1} } \right) \cap \left( {0\le \gamma _1 \varepsilon w_1 } \right) } \\ &{} or\left( {U_{a1} \le \hat{a}_1 } \right) \cap \left( {\gamma _1 \varepsilon w_1 \le 0} \right) \quad or\left( {\hat{a}_1 \hat{a}_2 \le \hat{a}_3 } \right) \cap \left( {0\le \hat{a}_2 \gamma _1 \varepsilon w_1 } \right) \\ 0 &{}{otherwise}\\ \end{array}\right. \qquad \end{aligned}$$
(17)

where \(\hat{a}_1\), \(\hat{a}_2\), and \(\hat{a}_3\) are the estimated parameters of \(a_{1}\), \(a_{2}\), and \(a_{3}\), respectively. \({\gamma }_{1},{\gamma }_{2}\), and \(\gamma _{3}\) are the adaptive gains for \(\hat{a}_1\), \(\hat{a}_2\), and \(\hat{a}_3\). Note that the parameter \(a_{0}\) represents the DC gain of the transfer function (see Eq. 5). Therefore, \(a_{0}\) remained identical to the identified model. In the simulations, the boundaries \(5\times 10^{-8}< a_{3} < 3 \times 10^{-7}, 5\times 10^{-5}< a_{2} < 8\times 10^{-5}\), and \(0< a_{3}< 0.02\) were used. It is noted that in real application, the upper and lower bounds of each parameter can be determined from the system identification tests.

The configuration of the analytical studies is described in the following. The input excitation needed to be at least sufficient rich (SR) of order 4 because there were four unknown parameters. In this simulation, the chosen input was given by

$$\begin{aligned} r(t)=\sin (2\pi ft)+\frac{1}{2}\cos (\pi ft), \hbox {unit: mm} \end{aligned}$$
(18)

where \(f\) is the input frequency in the unit of Hz. Equation 18 implies that the persistently exciting (PE) condition of the signal \(\mathbf{w}/m_{s}\) was held as the input was SR of order 4. The PE condition required positive-definite integral over any interval of time (Ioannou and Fidan 2006). As a result, \(\varvec{\uptheta }\) was expected to approach to \(\varvec{\uptheta }^{*}\) as time goes to infinity, and the estimated parameters converged to the real system parameters exponentially because the PE condition was satisfied. All the numerical simulations were conducted with a 0.005  s. time step . The ode5 (Dormand-Prince) solver was adopted. The adaptive gains for each case were obtained by trial and error.

The tracking performance of the test system in the simulation was investigated by using the root-mean-square (RMS) error. The RMS error was defined as

$$\begin{aligned} RMS_\mathrm{error} (\% )=\sqrt{\frac{\sum \limits _{k=1}^N {\left( {x_\mathrm{c} [k]-x_\mathrm{m} [k]} \right) ^{2}} }{\sum \limits _{k=1}^N {x_\mathrm{c} [k]^{2}}}} {\times 100\,\%} \end{aligned}$$
(19)

where \(x_\mathrm{c}[k]\) and \(x_\mathrm{m}[k]\) are the command and measured displacements at the step \(k\), respectively. Table 2 shows the RMS error of the tracking performance in each case. Obviously, the feedforward controller with the adaptive laws performed better than the feedforward controller only. In addition, the feedback LQG controller further improved the tracking performance of both the feedforward controller with and without the adaptive laws. A set of progressive gains was also examined in the numerical simulation. As shown in Fig. 4, the estimated parameters converge within a small period. This figure shows the parameter estimates from the case (d) with the 30 Hz excitation. Each parameter oscillates in the very beginning and then converges to the exact given value. In practice, the adaptive gains must be carefully tuned to prevent the system from oscillating and damaging the specimen.

Table 2 Tracking performance in terms of RMS error in the simulations
Full size table

In summary, the adaptive control law is shown to improve the tracking performance of the model-based feedforward and feedback control scheme in the analytical studies.

Fig. 4
figure 4

Time history of parameter estimates from one of the cases in the simulation

Full size image

4 Experimental setup

All the experiments in this study were conducted by using the facility at the University of Illinois. In the test setup, a second generation, large-scale 200 kN MR damper was attached with a 556 kN (125 kips) hydraulic actuator as shown in Fig. 5. The MR damper was manufactured by the Lord Corporation and had a stroke of \(\pm 292\,\hbox {mm}\) \((\pm 13\,\hbox {in})\). The input currents to the MR damper were operated by a pulse-width modulator, which was comprised of an Advanced Motion Controls model PS2\(\times \)300W unregulated power supply providing 80 VDC to an Advanced Motion Controls model 20a8 analog servo-drive. In this study, the input currents were limited between 0 and 2.5 Amps. The overall setup allowed researchers to explore semi-actively controlled structures using a single MR damper. More details about this MR damper can be found in Yang et al. (2002) and Phillips and Spencer (2012).

Fig. 5
figure 5

RTHS experimental setup at the University of Illinois

Full size image

The actuator used in this setup was rated for dynamic testing. The double-rod, double-acting actuator, which was manufactured by the Shore Western Corporation, is comprised with a stroke of \(\pm 152.4 \,\hbox {mm}\) \((\pm 6\,\hbox {in})\) and an effective piston area of \(271\,\hbox {cm}^{2}\) \((42\,\hbox {in}^{2})\). A Schenck-Pegasus model 1,800 three-stage servo-valve rated at 300 lpm (80 gpm) was in charge of directing the hydraulic flow to both actuator chambers. A proportional-integral-derivative (PID) control loop was implemented to realize displacement feedback control in an 1104 digital servo controller which was also made from the Shore Western Corporation. In the PID loop, only the proportional gain was tuned and assured to be suitable for the RTHS testing.

The tracking performance and real-time hybrid testing in this study were carried out in a dSPACE model 1103 DSP board with a PPC 750GX processor. An I/O board CLP1103 was used to communicate with the servo-controller. This dSPACE system enabled the numerical model, additional actuator control loops, and data acquisition by programming block diagrams in Simulink and MATLAB. While testing, the dSPCAE’s ControlDesk software allowed adjusting parameters, collecting data, and displaying results in real-time. The entire dSPACE system was also capable of handling all I/O channels with a sampling rate of 2,000 Hz in this study.

5 Tracking performance testing

The tracking performance testing was conducted to investigate the stability and performance of the proposed adaptive control scheme prior to the RTHS. In this validation, system identification tests were first performed to determine the initial parameters for the feedforward controller, as well as the boundary conditions for the parameter estimates. Then, the tracking performance of each tracking control scheme was evaluated. Finally, the necessity of using the adaptive control scheme is addressed through the closed-loop frequency response functions.

5.1 System identification

System identification tests were conducted to identify the servo-hydraulic system used in this study. A transfer function from the commanded to the measured displacements was used to represent the servo-hydraulic system. This transfer function considered the dynamics of the actuator, servovalve, PID controller, physical specimen, and measuring instruments. The input command displacement was a BLWN, with a range from 0 to 50 Hz and a RMS power of 0.165 mm. The dSPACE system was used to generate the commanded signal and measure the responses at a sampling rate of 2,000 Hz. While processing data, the displacement histories were appropriately down-sampled to 100 Hz and then converted into a transfer function. The transfer function was calculated with a reasonable set of parameters. In this study, 512 FFT points, a Hanning window with 50 % overlap, and 60 averages were used in system identification. A higher number of FFT points (e.g., 1,024 points or more) can also be used to further check the quality of the identified model. Three cases of input current for the MR damper were adopted: (a) 0.0 Amp (passive-off), (b) 2.5 Amps (passive-on), and (c) a pulse between 0.0 and 2.5 Amps at 0.5 Hz. A system identification toolbox, MFDID (Kim et al. 2005), was utilized to fit the experimental transfer function data for a single-input single-output model with selected numbers of poles and zeros. In the study, the identified model employed three poles and no zero. The identified models of the three cases are given by

$$\begin{aligned} G_{0\mathrm{A}} (s)&= \frac{1.936\times 10^{7}}{\left( {s+196.6} \right) \left( {s^{2}+222.9s+1.003\times 10^{5}} \right) } \nonumber \\ G_{2.5\mathrm{A}} (s)&= \frac{1.984\times 10^{7}}{\left( {s+145.6} \right) \left( {s^{2}+355.3s+1.381\times 10^{5}} \right) } \nonumber \\ G_{\mathrm{pulse}} (s)&= \frac{1.998\times 10^{7}}{\left( {s+172.7} \right) \left( {s^{2}+354.9s+1.178\times 10^{5}} \right) } \end{aligned}$$
(20)

Figure 6 shows the transfer functions of the servo-hydraulic system and the corresponding identified models under the three scenarios of MR damper current inputs. As shown in this figure, both the magnitude and phase of the model fit the transfer function well as the frequency is lower than 35 Hz. The coefficients of the feedforward controller and the upper and lower bounds for the estimated parameters \(\hat{a}_1\), \(\hat{a}_2\), and \(\hat{a}_3\) can be then determined based on the identified model. Therefore, the boundaries \(5.004\times 10^{-8} < \hat{a}_3 < 5.166 \times 10^{-8}, 2.167\times 10^{-5}< \hat{a}_2 < 2.640 \times 10^{-5}\), and \(7.445\times 10^{-3}< \hat{a}_1 < 9.566\times 10^{-3}\) were adopted for Eq. 17. Similar to the numerical simuluation, the CDM and linear acceleration extrapolation was used to realize the feedforward controller. The initial and boundary conditions of the estimated parameters were then determined for each test case.

Fig. 6
figure 6

Transfer functions of the servo-hydraulic system and the identified models: a 0 Amp b 2.5 Amps, and c pulse

Full size image

5.2 Tracking performance

Prior to implementing the feedforward controller with a feedback LQG controller, the control performance of the feedforward–feedback controllers was first explored. As mentioned earlier, the LQG feedback control was designed with a moderate authority. Figure 7 demonstrates the LQG control design in the closed-loop compensation with the feedforward control included. The transfer function (labeled as “calculated” in Fig. 7) was derived from a combination of the experimental data and numerical calculation. For example, the uncompensated system (i.e., the plant) employed the experimental results obtained from the system identification tests, while the transfer functions of the feedforward and feedback controllers were numerically generated. In this transfer function, the magnitude remains unity over 0–50 Hz, and the phase almost stays at \(0^{\circ }\) in the same frequency range. It indicates that the LQG controller was appropriately designed. To validate the feedforward–feedback controllers, BLWN signals with 5 and 15 Hz cut-off frequencies were employed to excite the system. The magnitudes of the transfer functions are almost unity over both frequency ranges, while the phases are slightly off from \(0^{\circ }\) due to the fact that the pulse currents introduced variant dynamics into the MR damper. Therefore, the differential dynamics induced by the variable currents to the MR damper required additional control regulator such as the proposed adaptive method.

Fig. 7
figure 7

Design of the LQG feedback controller compared to the experimental results

Full size image

The tracking performance of each controller scheme was investigated with respect to the RMS error in time domain. A wide variety of tests were carried out as listed in Table 3. In each test, the height of power spectral density of the input BLWN was remained identical. The duration of excitations was 120 s. Four control strategies were evaluated with three scenarios of input currents to the MR damper. Table 3 indicates that the adaptive control law may not always improve the tracking performance for the two constant input current scenarios because linear models for the passive-off and passive-on cases are good enough within the test frequency range. On the contrary, the adaptive control law always improves the tracking performance for both feedforward controller only and feedforward–feedback controllers in the pulse input current cases. This table also demonstrates that the direct adaptive control scheme can effectively parameterize the feedforward controller with respect to the model-based inverse transfer function when the nonlinearity of the MR damper becomes significant. Figure 8 shows the time history of the estimated parameters for the case of adaptive feedforward controller and feedback LQG controller under the 15 Hz BLWN displacement input and pulse input current for the MR damper. The black dash lines are the upper and lower bounds obtained from the system identification tests. Apparently, the estimated parameters vary from time to time because the pulse input current yields the changes of the MR damper characteristics as a function of time.

Fig. 8
figure 8

Time histories of the estimated parameters

Full size image
Table 3 Tracking performance for predefined displacement time histories
Full size table

6 Real-Time hybrid testing

A nine-story steel frame benchmark shear building (Ohtori et al. 1994) was selected to further verify the performance of the adaptive model-based control strategy for RTHS. The first five natural frequencies of the structure were 0.443, 1.18, 2.05, 3.09, and 4.27 Hz, while all modes were assigned with 2 % damping ratios. For the ground excitation, the far-field 1940 El Centro and near-fault 1995 Kobe earthquake records were selected to evaluate seismic performance of the building, as shown in Fig. 9. The intensity of the records was adjusted by a factor of 0.2 and 0.5 in order to investigate the robustness of the proposed adaptive model-based control scheme.

Fig. 9
figure 9

Ground acceleration time histories: a 1940 EI-Centro, and b 1995 Kobe

Full size image

The real-time hybrid simulation validation testing aimed at evaluating the seismic performance of the benchmark building controlled by MR dampers. In this control application, the maximum damper force was determined as 10 % of the building weight, i.e., 4,410 kN. Thus, total 18 MR dampers with a force capacity of 200 kN were placed in parallel and installed at the 1st floor. Both passive-mode and semi-active control strategies were evaluated in the RTHS. The passive mode only considered the passive-on case with a constant input current of 2.5 Amps. The semi-active control utilized the clipped-optimal control algorithm (Dyke et al. 1996). Both the feedforward and feedback LQG controllers in the RTHS and the aforementioned tracking performance tests were identical. The numerical model, structural control algorithm, and adaptive model-based controller were implemented in dSPACE with a 2,000-Hz sampling rate.

6.1 Semi-active controller design

To demonstrate the proposed tracking control scheme, a semi-active control strategy was performed in this RTHS. The semi-active control strategy used in this study was a combination of the LQG and clipped-optimal control algorithm. The LQG design was focused on the minimization of the floor accelerations, while the feedback measurements in the LQG controller were all absolute floor accelerations. More details of the control development can be found in Dyke et al. (1996). To input the appropriate current to the MR damper, the control strategy adopted the clipped-optimal control algorithm which was proposed by Dyke et al. (1996) and given by

$$\begin{aligned} i_\mathrm{d} =i_{\max } H\left\{ {\left( {f_\mathrm{d} -f_\mathrm{m} } \right) f_\mathrm{m} } \right\} \end{aligned}$$
(21)

where \(i_\mathrm{d}\) is the desired input current, \(i_\mathrm{max}\) is the maximum input current (i.e., 2.5 Amps in this study); \(f_{d}\) is the desired control force that was calculated based on the LQG control algorithm; \(f_{m}\) is the measured force, and \(H\) is the Heaviside function.

6.2 Experimental results

The tracking performance in RTHS is first investigated. Table 4 demonstrates the RMS errors in the tests subjected to the El Centro earthquake. With the adaptive law, the RMS errors can be effectively reduced in RTHS. Relatively large RMS errors are also found in all tests under 0.2-intensity seismic excitation because of a larger noise-to-signal ratio in the load cell. Meanwhile, the RMS errors in the tests under 0.5-intensity excitation are within 1 %, indicating that accurate displacements were imposed on the MR damper in the RTHS. In the semi-active control cases, the adaptive control scheme performs even better than the passive-on cases in all tests. These tests successfully demonstrate the robustness of the proposed adaptive control scheme. Moreover, Table 5 shows the RMS error in the tests subjected to the Kobe earthquake. Due to the near-fault seismic effect, the Kobe earthquake record would result in significant displacements in the building. Even though the impulse-like displacements were observed in these tests, the adaptive control scheme still decreases the RMS errors as compared to the non-adaptive control schemes. Furthermore, the RMS errors are much lower in the tests under 0.5-intesity excitation particularly in the cases with the adaptive law. Figure 10 shows the partial time histories of MR damper accelerations under the 0.5-intesity El Centro earthquake excitation when the MR damper was controlled using the clipped-optimal control algorithm. In this figure, the errors are normalized by the maximum measured accelerations which are obtained from the derivative of measured displacements. Obviously, the proposed adaptive tracking control scheme demonstrates reduced errors as compared to other actuator control schemes. In short, the proposed adaptive control scheme further improves displacement tracking, as well as velocities and accelerations in the RTHS.

Fig. 10
figure 10

Time histories of the semi-active controlled MR damper accelerations subjected to 0.5-intensity El Centro earthquake

Full size image
Table 4 Tracking performance for the RTHS subjected to El Centro Earthquake
Full size table
Table 5 Tracking performance for the RTHS subjected to Kobe Earthquake
Full size table

As the proposed adaptive tracking control scheme has been demonstrated to be capable of imposing accurate displacements, the following results of the semi-active control implementation are derived based on this tracking control scheme in RTHS. Figure 11 shows the roof drift and 7F acceleration time histories of the uncontrolled building and the controlled building with the passive-on and semi-active strategies subjected to the El Centro earthquake record. As shown in this figure, the semi-active control strategy can surpass the passive-on case in structural response reductions. To further investigate the semi-active control effectiveness, Table 6 lists the maximum and root-mean-square (RMS) responses between the uncontrolled and semi-active control cases in both earthquake events. The developed semi-active control strategy demonstrates significant reductions in the structural responses against the earthquake loading. For example, the semi-active control strategy has a 35 % reduction in the maximum roof displacement in the El-Centro earthquake, and the maximum overturning moment is decreased to 65 % of the uncontrolled building. For the floor accelerations, the semi-active control strategy meets the design control objective that all RMS floor accelerations are effectively mitigated. In the Kobe earthquake event, the results exhibit similar performance as shown in Table 7. The maximum top floor drift has a 31 % reduction, while the maximum roof acceleration is also lowered to 72 % as compared to the uncontrolled building. The RMS floor accelerations have reductions ranging from 27 to 52 %. In summary, through the RTHS with the adaptive tracking control scheme, a semi-active control strategy was successfully implemented and experimentally verified with the control performance for the seismically excited building.

Fig. 11
figure 11

Structural response obtained from the uncontrolled building, passive-on control, and semi-active control under the El Centro earthquake

Full size image
Table 6 Semi-active control performance under the El Centro excitation
Full size table
Table 7 Semi-active control performance under the Kobe excitation
Full size table

7 Summary and conclusions

An adaptive model-based feedforward–feedback control scheme for real-time hybrid simulation (RTHS) was proposed in this study. The feedforward controller enabled the servo-hydraulic actuator to track displacements based on a time-invariant model. Due to the nonlinearity of the velocity-dependent components, this time-invariant model might yield significant displacement tracking errors in RTHS. In the study, the self-tuned control parameters following the projection algorithms were applied on the feedforward controller. The adaptive scheme not only considered the current system condition but also followed the Routh’s stability criteria to ensure the system stability. To further eliminate modeling error and system uncertainties, the feedback LQG control algorithm was employed to minimize the displacement tracking errors. By combining these two control strategies, the adaptive feedforward–feedback control scheme for RTHS was developed in order to further improve the tracking performance of the servo-hydraulic system.

The proposed adaptive control strategy was successfully validated for RTHS using a semi-actively controlled nine-story building. The accuracy and robustness of this control scheme were verified through both numerical and experimental approaches. As indicated in the numerical analysis, the adaptive tracking control enabled online updating of the parameters used in the feedforward controller and estimated the system dynamics in real time. In the tracking performance tests, this adaptive control scheme showed improved tracking performance of the displacements being imposed to the MR damper, in particular as the input currents to the MR damper were a function of time (i.e., the pulse current). Thus, the proposed adaptive control was beneficial to RTHS to implement semi-active control strategies in which the input currents to MR damper varied over the time. Finally, RTHS was carried out considering the ASCE benchmark control problem for buildings. In this hybrid test, a semi-active control device was experimentally evaluated, while a nine-story building was numerically examined. Due to the fact that the errors between the command and achieved displacements were effectively reduced by the adaptive tracking control, the semi-active control in RTHS subsequently showed more representative control performance. Consequently, the proposed adaptive model-based control scheme provides an effective means for conducting real-time hybrid simulation of complex structures .