1 Introduction

Two-wheeled inverted pendulum (TWIP, for short) robot has been a hot topic in recent years due to its wide applications as a robotics mobile platform and personal transporter. Comparing with the three-/four-wheeled mobile robots, it has some remarkable superiorities, such as good dexterity, true zero turning radius and small footprint. Segway human transporter and Segway robotic mobility platform are successful commercial products of TWIP robot. A TWIP is an essential nonlinear and under-actuated system [1], subjected to nonholonomic constraints [2]. It is a system of open-loop unstable; different control strategies are required for different control tasks under different environments.

When uncertainties are not considered, straightforward linearization can be used if the stabilization of the inverted pendulum is addressed only [3], or feedback linearization if the tilt angle of inverted pendulum cannot be small [4]. When uncertainties must be considered, \(H_\infty \) control [5], adaptive control [6] or adaptive back-stepping control [7], disturbance observer compensation [8] and adaptive sliding mode control [9] can be applied. Among these control methods, the sliding mode control seems having more advantages over the other methods: strong robustness, rapid response, no need for online identification and simple implementation. However, with perfect robustness on the one hand, the sliding mode control results in inevitable “chattering” phenomenon on the other hand. Chatter suppression must be considered in applications. The available techniques for suppressing “ chattering” include boundary layer control [10], dynamic sliding mode control [11], filter method [12], disturbance observer [13] and integral sliding mode control [14]. The integral sliding mode control, with the initial state defined on the sliding mode manifold to have smaller gains of the discontinuous control, has been shown useful in some applications [15]. The integral sliding mode manifold can be chosen according to the control task.

In addition, due to the intensive use of digital controllers and filters, the inevitable input delay, though very small in many applications, has an important influence to the system stability and control effect. As shown in [16], for example, a very small delay in the active control reduces the flutter velocity of an air wing dramatically. This implies that the safety of airplane may become a serious problem if the delay effect is neglected. A controller with an input delay for suppressing the chatter of air wing can also work better than that without a delay if the controller is properly designed [17]. This means that the delay effect can be intentionally used in control applications, such as using a time-delayed active control to improve the performance of a quasi-zero-stiffness vibration isolator [18], delayed feedback control to suppress the vibration of the dynamical system [19] and using delayed feedback controller to reduce the sway on container cranes [20]. The classical proportional-derivative (PD) feedback may lead to bad control effect to the human postural balance problem when input delay is considered, but the proportional- derivative acceleration (PDA) feedback provides better stability properties than the corresponding PD controller if there is noise in the system or the state is not completely observable [21, 22].

Fig. 1
figure 1

The back-and-forth motion of the TWIP, where the internal control torque generated by the motors acting on the TWIP works as the control

Full size image

A delayed dynamical system is infinite dimensional, no matter how small the delay is. This usually makes the controller design complicated, especially when the delay is an input delay from the controller, rather than a state delay from the control plant. In [23], the integral sliding mode control is extended to uncertain systems with a state delay only, where the controller uses the current state of an approximated system. No results have been reported for generalization of the integral sliding mode control to systems with an input delay. Actually, few works about the controller design of TWIP robots with an input delay have been reported in the literature [3, 24].

This paper aims at designing a robust controller to implement the back-and-forth motion of a TWIP system with both input delay and uncertainties, based on the combined application of optimal trajectory tracking control and integral sliding mode control. The model of the TWIP is described in Sect. 2, the robust control design for the back-and-forth motion is presented in Sect. 3, numerical simulation demonstrating the proposed approach is shown in Sect. 4, and finally, some concluding remarks are made in Sect. 5.

2 Modeling of the TWIP and statement of the control problem

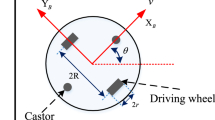
Back-and-forth motion is a basic motion function of a TWIP robot; it is required to move forward to pass some prefixed point and return back to the starting point, keeping the inverted pendulum stabilized during the whole process. The back-and-forth motion of the TWIP is a planar motion, without considering the turning motion in this paper. Figure 1 shows a 2-DOF (two degrees of freedom) model of the TWIP moving in the sagittal plane, which has two parts: two wheels and the intermediate body. The intermediate body is the center portion standing between the left and right wheels, and it consists of the rod of pendulum and the chassis. The definitions of the main parameters and variables are given in Table 1.

Table 1 The parameters and variables of the TWIP
Full size table

The kinetic energy of the wheels and the kinetic energy of the intermediate body are given by

$$\begin{aligned} T_\mathrm{w}=&\frac{1}{2}I_\mathrm{w}\left( \frac{\dot{x}}{r}\right) ^{2} +\frac{1}{2}M_\mathrm{w}\dot{x}^2\\ T_\mathrm{B}=&\frac{1}{2}M\left[ (\dot{x}+l\dot{\varphi }\mathrm{cos\varphi })^{2}+(l\dot{\varphi }\mathrm{sin\varphi })^{2}\right] +\frac{1}{2}I_\mathrm{B} \dot{\varphi }^2 \end{aligned}$$

respectively, and the gravitational potential energy of the system is

$$\begin{aligned} P=Mgl\mathrm{cos\varphi }. \end{aligned}$$

Let \(L=T_\mathrm{w}+T_\mathrm{B}-P\) be the Lagrangian function, and let \(\mathbf q =(\varphi ,x)^\mathrm{T}\) be the generalized coordinates of the TWIP, and then the Euler–Lagrange equation gives the dynamic equation of the TWIP as follows

$$\begin{aligned} \frac{{\hbox {d}}}{{\hbox {d}}t}\left( \frac{\partial L}{\partial \dot{\mathbf{q }}}\right) -\frac{\partial L}{\partial \mathbf q }=\mathbf E (\mathbf q )T \end{aligned}$$
(1)

without taking the input delay and system uncertainties into accounts, here \(\mathbf E (\mathbf q )=[-1,\frac{1}{r}]^\mathrm{T}\) is the matched matrix, and \(\mathbf E (\mathbf q )T\) can be considered as the control. More clearly, the dynamics equation of the TWIP reads:

$$\begin{aligned} \left\{ \begin{aligned}&(Ml^2+I_\mathrm{B})\ddot{\varphi }+Ml\mathrm{cos}\varphi \ddot{x}-Mgl{\sin }\varphi =-T \\&Ml\ddot{\varphi }{\cos }\varphi +\left( M_\mathrm{w}+M+\frac{I_\mathrm{w}}{r^2}\right) \ddot{x}-Ml\dot{\varphi }^2{\sin }\varphi =\frac{T}{r} \end{aligned} \right. \nonumber \\ \end{aligned}$$
(2)

With \(T(t)=u(t-\tau )\) where \(\tau \) is the input delay, the linearized equation of Eq. (2) reads

$$\begin{aligned} \left\{ \begin{aligned}&\ddot{\varphi }=\frac{-Mlg(Mr^2+I_\mathrm{w}+M_\mathrm{w} r^2)}{{\varDelta }}\varphi \\&~~~+\frac{Mr^2+I_\mathrm{w}+M_\mathrm{w} r^2+Mlr}{{\varDelta }}u(t-\tau ) ,\\&\ddot{x}=\frac{M^2 l^2 r^2 g}{{\varDelta }}\varphi -\frac{Mlr^2+Mrl^2+I_\mathrm{B} r}{{\varDelta }}u(t-\tau ), \end{aligned} \right. \end{aligned}$$
(3)

where

$$\begin{aligned} {\varDelta }=-Ml^2 I_\mathrm{w}-Ml^2 M_\mathrm{w} r^2-I_\mathrm{B} Mr^2 -I_\mathrm{B} I_\mathrm{w}-M_\mathrm{w} r^2 I_\mathrm{B}. \end{aligned}$$

Let \(\mathbf X =[x_1,x_2,x_3,x_4]^\mathrm{T}=[\varphi ,\dot{\varphi },x,\dot{x}]^\mathrm{T}\), and

$$\begin{aligned} \begin{aligned}&\mathbf A =\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0&{} 1&{} 0&{} 0 \\ \frac{-Mlg(Mr^2+I_\mathrm{w}+M_\mathrm{w} r^2)}{{\varDelta }}&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 1 \\ \frac{M^2 l^2 r^2 g}{{\varDelta }}&{} 0&{} 0&{} 0 \end{array} \right] , \\&\mathbf B =\left[ \begin{array}{c} 0 \\ \frac{Mr^2+I_\mathrm{w}+M_\mathrm{w} r^2+Mlr}{{\varDelta }} \\ 0 \\ -\frac{Mlr^2+Mrl^2+I_\mathrm{B} r}{{\varDelta }} \\ \end{array} \right] , \end{aligned} \end{aligned}$$

then, Eq. (3) can be rewritten as a standard state equation as follows

$$\begin{aligned} \dot{\mathbf{X }}(t)=\mathbf A {} \mathbf X (t)+\mathbf B u(t-\tau ). \end{aligned}$$
(4)

The delayed control in Eq. (4) takes place only when \(t\ge \tau \). Taking the linearization error and system uncertainties into account, it is required to introduce \(\varvec{\omega }(t)\) into the above system

$$\begin{aligned} \dot{\mathbf{X }}(t)=\mathbf A {} \mathbf X (t)+\mathbf B u(t-\tau )+\varvec{\omega }(t), \end{aligned}$$
(5)

where \(\varvec{\omega }(t)\) stands for the integrated effect of the linearization error and bounded system uncertainties. The linearization error depends nonlinearly on the state of the tilt angle of the pendulum.

The motion control can be converted to a trajectory tracking control problem. Let \(\bar{\mathbf{X }}:=[\bar{x}_1,\,\bar{x}_2,\) \(\bar{x}_3,\,\bar{x}_4]^\mathrm{T}=[\bar{\varphi }(t),\dot{\bar{\varphi }}(t),\bar{x}(t),\dot{\bar{x}}(t)]^\mathrm{T}\) be the trajectory tracking target vector according to the control task, and let \(\mathbf Y (t):=\mathbf X (t)-\bar{\mathbf{X }}(t)\), \(\varvec{\sigma }(t):=\mathbf A \bar{\mathbf{X }}-\dot{\bar{\mathbf{X }}}\), then Eq. (5) governing the tracking error takes the form

$$\begin{aligned} \dot{\mathbf{Y }}(t)=\mathbf A {} \mathbf Y (t)+\mathbf B u(t-\tau )+{\varvec{\omega }}(t)+{\varvec{\sigma }}(t). \end{aligned}$$
(6)

In order to reduce the linearization error, a quadratic performance criterion with large weight of tilt angle error is introduced as follows

$$\begin{aligned} \begin{aligned} J&=\frac{1}{2}{} \mathbf Y ^\mathrm{T}(t_f)\mathbf M {} \mathbf Y (t_f) \\&+\frac{1}{2}\int _0^{t_f}\left[ \mathbf Y ^\mathrm{T}(t)\mathbf Q {} \mathbf Y (t)+u^\mathrm{T}(t\!-\!\tau )\mathbf R u(t\!-\!\tau )\right] \mathrm{d}t, \end{aligned} \end{aligned}$$
(7)

where \(\mathbf M ,\mathbf Q \) are nonnegative definite symmetric matrices, \(\mathbf R \) is a positive definite matrix, and \(t_f\,(>2\tau )\) is the terminal time of the control. With a large weight of the tilt angle error in J, the tilt angle error can be “forced” to be small when an optimal control is applied. This is very important for designing a reliable controller from the linearized Eq. (6). In this case, the linearization error is small and can be considered as bounded. Hence, the integrated disturbance \(\varvec{\omega }(t)\) is also bounded, namely, there is a constant \(D>0\) such that

$$\begin{aligned} \Vert \varvec{\omega }(t)\Vert \le D. \end{aligned}$$
(8)

Due to the presence of \(\varvec{\omega }(t)\), the optimal control of system (6) does not exist in a strict conventional sense. However, by properly chosen weight matrices \(\mathbf Q ,\mathbf R \), the final optimal quadratic performance criterion value for both cases \(\varvec{\omega }(t)=0\) and \(\varvec{\omega }(t)\ne 0\) can be approximately the same. In this sense, the concept of “optimal control” in this paper is acceptable when a bounded disturbance is taken into account.

Although \(H_{\infty }\) control is very popular in robust control design, it does not work for the motion control of a TWIP, because the linearization error as bounded disturbance does not satisfy the strict conditions required by the \(H_{\infty }\) control theory.

3 Motion controller design

The key idea for the controller design is to design the robust controller in two parts, one is an optimal controller for the nominal error system [26] that minimizes the quadratic performance criterion, and the other is a switched control that is based on an integral sliding manifold for compensating the effect of the integrated disturbance significantly.

3.1 Simplification of the controlled system

The optimal control design is based on the error system, namely Eq. (6), which is equivalent to

$$\begin{aligned} {\mathbf{Y}}(t)= & {} {\mathrm{e}}^{\mathbf{A}t}{} \mathbf{Y}(0)\\&+\int _{0}^t{\mathrm{e}}^{\mathbf{A}(t-s)}[\mathbf{B}u(s-\tau )+\varvec{\omega }(s)+\varvec{\sigma (s)}]{\mathrm{d}}s. \end{aligned}$$

In order to simplify the control design, let us introduce a new integral state transformation of the following form

$$\begin{aligned} {\mathbf{Z}}(t)= & {} {\mathbf{Y}}(t)+\int _{t-\tau }^t{\mathrm{e}}^{-{\mathbf{A}}(s-t+\tau )}[{\mathbf{B}}u(s)+{\varvec{\omega }}(s+\tau ) \nonumber \\&+\,{\varvec{\sigma }}(s+\tau )]{\mathrm{d}}s \end{aligned}$$
(9)

to transform Eq. (6) into a delay-free one. This transformation is different from the conventional integral transformation [25] where \(\varvec{\omega }(s+\tau )+\varvec{\sigma }(s+\tau )\) is not appeared in the operand, and it changes Eq. (6) into

$$\begin{aligned} \dot{\mathbf{Z }}(t)=\mathbf A {} \mathbf Z (t)+\mathbf B _0u(t)+\mathrm{e}^{-\mathbf{A}\tau } \varvec{\omega }(t+\tau )+\mathrm{e}^{-\mathbf{A}\tau } \varvec{\sigma }(t+\tau ), \end{aligned}$$
(10)

where \(\mathbf B _0=\mathrm{e}^{-\mathbf A \tau }{} \mathbf B \). Then, the solution \(\mathbf Y (t)\) satisfies

(11)

This is a simple but key relationship between the original state variable \(\mathbf Y (t)\) and the new state variable \(\mathbf Z (t)\). Thus, the initial condition \(\mathbf Y (0)=\mathbf Y _{0}\) for system (6) is changed into \(\mathbf Z (0)=\mathrm{e}^{-\mathbf A \tau }{} \mathbf Y (\tau )\) for the new system (10).

By substituting Eq. (11) into Eq. (7), we obtain

$$\begin{aligned} J=J_1+J_2 \end{aligned}$$

where \(J_1=\frac{1}{2}\int _0^{\tau }{} \mathbf Y ^\mathrm{T}(t)\mathbf Q {} \mathbf Y (t)\mathrm{d}t\) is fixed because the control does not take effect when \(t\in [0,\tau )\), and

$$\begin{aligned} \begin{aligned} J_2=&\frac{1}{2}{} \mathbf Z ^\mathrm{T}(t_{f}-\tau )\tilde{\mathbf{M }}{} \mathbf Z (t_{f}-\tau ) \\&+\frac{1}{2}\int _0^{t_{f}-\tau }\left[ \mathbf Z ^\mathrm{T}(t)\tilde{\mathbf{Q }}{} \mathbf Z (t)+u^\mathrm{T}(t)\mathbf R u(t)\right] \mathrm{d}t, \end{aligned} \end{aligned}$$
(12)

where \(\tilde{\mathbf{Q }}=\left( \mathrm{e}^\mathbf{A \tau }\right) ^\mathrm{T}{} \mathbf Q \mathrm{e}^\mathbf{A \tau },\tilde{\mathbf{M }}=\left( \mathrm{e}^\mathbf{A \tau }\right) ^\mathrm{T}{} \mathbf M \mathrm{e}^\mathbf{A \tau }\). Hence,

$$\begin{aligned} J_d=J_1+J_2=\min \qquad \Leftrightarrow \quad J_2=\min . \end{aligned}$$

Therefore, the control design problem of system (6) with the quadratic performance criterion J given in Eq. (7) has been transformed into that of system (10) with the quadratic performance criterion \(J_2\) given in Eq. (12).

3.2 Optimal control of the nominal error system

The nominal error system is Eq. (10) with \(\varvec{\omega }(t+\tau )=0\), namely

$$\begin{aligned} \dot{\mathbf{Z }}(t)=\mathbf A {} \mathbf Z (t)+\mathbf B _{0}u(t)+\mathrm{e}^{-\mathbf A \tau } \varvec{\sigma }(t+\tau ), \end{aligned}$$
(13)

This is the form that can be used to design an optimal controller directly, see for example [26]. More precisely, by using Pontryagin’s maximum principle, the optimal control of the nominal system (13) that minimizes quadratic performance criterion \(J_2\) is given by

$$\begin{aligned} u(t)=u_{0}(t)=-\mathbf R ^{-1}{} \mathbf B _0^\mathrm{T}[\mathbf P _z(t)\mathbf Z (t)+\mathbf b _z(t)], \end{aligned}$$
(14)

where \(\mathbf P _z(t)\in \mathbb {R}^{n\times n}\) and \(\mathbf b _z(t)\in \mathbb {R}^{n}\) are the solutions of the following differential equations

$$\begin{aligned}&\left\{ \begin{aligned}&\dot{\mathbf{P _z}}=-\mathbf P _{z}{} \mathbf A -\mathbf A ^\mathrm{T}{} \mathbf P _z+\mathbf P _{z}{} \mathbf B _0\mathbf R ^{-1}{} \mathbf B _0^\mathrm{T}{} \mathbf P _z-\tilde{\mathbf{Q }}, \\&\mathbf P _z(t_f-\tau )=\tilde{\mathbf{M }}, \end{aligned} \right. \end{aligned}$$
(15)
$$\begin{aligned}&\left\{ \begin{aligned}&\dot{\mathbf{b }}_{z}=-[\mathbf A -\mathbf B _0\mathbf R ^{-1}{} \mathbf B _{0}^\mathrm{T}{} \mathbf P _{z}]^\mathrm{T}{} \mathbf b _{z}-\mathbf P _{z}\mathrm{e}^{-\mathbf A \tau }\varvec{\sigma }(t+\tau ), \\&\mathbf b _{z}(t_f-\tau )=0. \end{aligned} \right. \end{aligned}$$
(16)

Thus, to obtain the optimal trajectory tracking controller, it is required to solve a Riccati equation and a linear differential equation only. This is a standard and inevitable step required in optimal controller design.

The key role of \(\mathbf b _z(t)\) in Eq. (14) is to compensate the impact from \(\mathrm{e}^{-\mathbf A \tau } \varvec{\sigma }(t+\tau )\). Let \(\varvec{\varOmega }(t)=-[\mathbf A -\mathbf B _0\mathbf R ^{-1}{} \mathbf B _{0}^\mathrm{T}{} \mathbf P _z(t)]^\mathrm{T}\), and \(\varvec{\varPhi }_0(t,t_f-\tau )\) be the state transition matrix of system \(\dot{\varvec{\xi }}(t)=\varvec{\varOmega }(t)\varvec{\xi }(t)\), then solving Eq. (16) gives

$$\begin{aligned} \begin{aligned} {\mathbf{b}}_z(t) =&\,-{\varvec{\varPhi }}_{0}(t,t_f-\tau )\int _{t}^{t_f-\tau }{\varvec{\varPhi }}_{0}(t_f-\tau ,s)\\&\,\,\times {\mathbf{P}}_{0}(s)\mathrm{e}^{-{\mathbf{A}}\tau }{\varvec{\sigma }}(s+\tau ){\mathrm{d}}s \end{aligned} \end{aligned}$$

By substituting the expression of \(\mathbf b _z(t)\) into Eq. (14), the optimal control quantity \(u_0(t)\) is reduced when \(\mathrm{e}^{-\mathbf A \tau } \varvec{\sigma }(t+\tau )\) has the same direction of \(\mathbf Z (t)\); in this case, the disturbance is beneficial. On the contrary, the optimal control quantity \(u_0(t)\) is increased when \(\mathrm{e}^{-\mathbf A \tau } \varvec{\sigma }(t+\tau )\) is in the opposite direction of \(\mathbf Z (t)\). Therefore, if the disturbance is unknown, the optimal control does not exist. It is required to find an approximate optimal control.

3.3 Integral sliding mode control

The optimal controller is designed on the basis of linear control theory. To make the controller reliable for the back-and-forth motion of TWIP with strong nonlinearity, the effect of \(\varvec{\omega }(t+\tau )\ne 0\) must be taken into accounts. However, weak robustness against uncertainties is a major issue of optimal control. In order to design a robust optimal controller against the effect of \(\varvec{\omega }(t+\tau )\), a switched control based on integral sliding mode manifold is incorporated with the optimal control of the nominal system (13).

Let the sliding mode functional be

$$\begin{aligned} \begin{aligned} {\mathbf{s}}({\mathbf{Z}}(t))&={\mathbf{G}}[{\mathbf{Z}}(t)-{\mathbf{Z}}^{*}(0)] \\&-{\mathbf{G}}\int _0^{t}[({\mathbf{A}}-{\mathbf{B}}_0{\mathbf{R}}^{-1}{\mathbf{B}}_{0}^{\mathrm{T}}{\mathbf{P}}_{z}){\mathbf{Z}}(\eta ) \\&-{\mathbf{B}}_0{\mathbf{R}}^{-1}{\mathbf{B}}_{0}^{\mathrm{T}}{\mathbf{b}}_z(\eta )+{\mathrm{e}}^{-{\mathbf{A}}\tau }{\varvec{\sigma }}(\eta +\tau )]{\hbox {d}}\eta , \end{aligned} \end{aligned}$$
(17)

where \(\mathbf G \in \mathbb {R}^{m\times n}\) is a constant matrix, and \(\mathbf G {} \mathbf B _0\) is assumed nonsingular, \(\mathbf Z ^{*}(0)\) is the initial value of the nominal system (13) described by

$$\begin{aligned} \begin{aligned} {\mathbf{Z}}^{*}(0)&={\mathrm{e}}^{-{\mathbf{A}}\tau }\left( {\mathrm{e}}^{{\mathbf{A}}\tau }{\mathbf{Y}}(0)+{\mathrm{e}}^{{\mathbf{A}}\tau }\int _{0}^{\tau }{\mathrm{e}}^{-{\mathbf{A}}s}{\varvec{\sigma }}(s){\mathrm{d}}s\right) \\&={\mathbf{Y}}(0)+\int _{0}^{\tau }{\mathrm{e}}^{-{\mathbf{A}}s}{\varvec{\sigma }}(s){\mathrm{d}}s, \end{aligned} \end{aligned}$$

\(\mathbf s (\mathbf Z (t))=0\) is the sliding mode manifold, which is actually the optimal state of the nominal system (13).

The integral sliding mode control of system (10) is

$$\begin{aligned} u(t)=u_{0}(t)+u_1(t), ~t\in [\tau ,t_f], \end{aligned}$$
(18)

where \(u_{0}(t)\) given by Eq. (14) is the optimal control of the nominal system (13), and \(u_{1}(t)\) is a switched control which is used to compensate the integrated disturbance, defined by

$$\begin{aligned} u_{1}(t)=-(\mathbf G {} \mathbf B _{0})^{-1}(\mu +D\Vert \mathbf G \mathrm{e}^{-\mathbf A \tau }\Vert )\mathrm{sgn}(\mathbf s (\mathbf Z (t))).\nonumber \\ \end{aligned}$$
(19)

Let \(V(\mathbf{s})=\frac{1}{2}{} \mathbf s ^\mathrm{T}{} \mathbf s \), then

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}V(\mathbf{s})&=\mathbf s ^\mathrm{T}\dot{\mathbf{s }} \\&=\mathbf s ^\mathrm{T}[\mathbf G \dot{\mathbf{Z }}-\mathbf G (\mathbf A -\mathbf B _0\mathbf R ^{-1}{} \mathbf B _{0}^\mathrm{T}{} \mathbf P _z)\mathbf Z \\&~~~+\mathbf G {} \mathbf B _0\mathbf R ^{-1}{} \mathbf B _{0}^\mathrm{T}{} \mathbf b _{z}-\mathbf G \mathrm{e}^{-\mathbf A \tau }\varvec{\sigma }(t+\tau )] \\&=\mathbf s ^\mathrm{T}[\mathbf G {} \mathbf B _{0}u+\mathbf G \mathrm{e}^{-\mathbf A \tau }\omega (t+\tau )+\mathbf G {} \mathbf B _0\mathbf R ^{-1}{} \mathbf B _{0}^\mathrm{T}{} \mathbf P _z\mathbf Z \\&~~~+\mathbf G {} \mathbf B _0\mathbf R ^{-1}{} \mathbf B _{0}^\mathrm{T}{} \mathbf b _z] \\&=\mathbf s ^\mathrm{T}[-(\mu +D\Vert \mathbf G \mathrm{e}^{-\mathbf A \tau }\Vert )\mathrm{sgn}(\mathbf s )+\mathbf G \mathrm{e}^{-\mathbf A \tau } \varvec{\omega }(t+\tau )] \\&=-\mu \Vert \mathbf s \Vert _{1}-D\Vert \mathbf G \mathrm{e}^{-\mathbf A \tau }\Vert \cdot \Vert \mathbf s \Vert _{1}\!+\!\mathbf s ^\mathrm{T}{} \mathbf G \mathrm{e}^{-\mathbf A \tau } \varvec{\omega }(t+\tau ) \\&\le -\mu \Vert \mathbf s \Vert _{1}-D\Vert \mathbf G \mathrm{e}^{-\mathbf A \tau }\Vert \cdot \Vert \mathbf s \Vert _{1}\!+\!D\Vert \mathbf G \mathrm{e}^{-\mathbf A \tau }\Vert \cdot \Vert \mathbf s \Vert , \end{aligned}$$

where \(\Vert \bullet \Vert _{1}\) is the 1-norm. Since \(\Vert \mathbf s \Vert _{1}\ge \Vert \mathbf s \Vert \), it holds

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}V(\mathbf{s})=\mathbf s ^\mathrm{T}\dot{\mathbf{s }}\le -\mu \Vert \mathbf s \Vert _{1}. \end{aligned}$$

Thus, the sliding mode motion exists for all initial conditions, and the sliding mode manifold can be reached within finite time. Note that Eq. (11) implies the asymptotic stability of \(\mathbf Z (t)\) is equivalent to that of \(\mathbf Y (t)\), and the quadratic performance criterion (7) is completely equal to \(J_1+J_2\). Hence, the integral sliding mode control Eq. (18) is effective to stabilize the error system (6) and to minimize performance criterion (7).

3.4 The robust delayed optimal controller

By substituting Eq. (11) into Eq. (18), one has

$$\begin{aligned} u(t-\tau )=u_{0}(t-\tau )+u_{1}(t-\tau ),~t\in [\tau ,t_f], \end{aligned}$$

where

$$\begin{aligned}&u_0(t-\tau )=-\mathbf R ^{-1}{} \mathbf B _{0}^\mathrm{T}[\mathbf P _{z}(t-\tau )\mathrm{e}^{-\mathbf A \tau }{} \mathbf Y (t)+\mathbf b _{z}(t-\tau )], \\&\quad \begin{aligned} u_{1}(t-\tau )=&-(\mathbf G {} \mathbf B _{0})^{-1}(\mu +D\Vert \mathbf G \mathrm{e}^{-\mathbf A \tau }\Vert ) \\&\times \mathrm{sgn}(\mathbf s (\mathrm{e}^{-\mathbf A \tau }{} \mathbf Y (t))). \end{aligned} \end{aligned}$$

Due to the delay effect, it is the delayed feedback state \(\mathbf Y (t-\tau )\), not the current state information \(\mathbf Y (t)\), that is available timely. Thus, the current state should be replaced with a predictor state \(\bar{\mathbf{Y }}(t)\), which can be obtained numerically as done in [27]. Therefore, the final controller for implementing the back-and-forth motion can be designed as follows:

Theorem 1

Assume that the linear system (6) is completely measurable and controllable, then the delayed robust optimal controller is given by

$$\begin{aligned} u(t-\tau )=u_{0}(t-\tau )+u_{1}(t-\tau ),~t\in [\tau ,t_f], \end{aligned}$$
(20)

where

$$\begin{aligned} u_0(t-\tau )= & {} -\mathbf R ^{-1}{} \mathbf B _{0}^\mathrm{T}[\mathbf P _{z}(t-\tau )\mathrm{e}^{-\mathbf A \tau }\bar{\mathbf{Y }}(t)+\mathbf b _{z}(t-\tau )], \\ u_{1}(t-\tau )= & {} -(\mathbf G {} \mathbf B _{0})^{-1}(\mu +D\Vert \mathbf G \mathrm{e}^{-\mathbf A \tau }\Vert ) \\&\times \,\mathrm{sgn}(\mathbf s (\mathrm{e}^{-\mathbf A \tau }\bar{\mathbf{Y }}(t))), \end{aligned}$$

and \(\bar{\mathbf{Y }}(t)\) is the predictor state of \(\mathbf Y (t)\) defined by

$$\begin{aligned} \bar{\mathbf{Y }}(t):=\mathrm{e}^\mathbf{A \tau }{} \mathbf Y (t-\tau )+\int _{t-\tau }^{t}\mathrm{e}^\mathbf{A (t-s)}[\mathbf B u(s-\tau )+\varvec{\sigma }(s)]\mathrm{d}s. \end{aligned}$$

4 Simulation results

The trajectory tracking target for the back-and-forth motion can be chosen in different forms, for example, \([\bar{\varphi }(t),\bar{x}(t)]^\mathrm{T}=[0,(at-t^2)\mathrm{e}^{-\alpha t}]^\mathrm{T}\) for the simulation below, where \(\bar{\varphi }(t)=0\) means that the inverted pendulum should be kept stable, and the decaying factor \(\mathrm{e}^{-\alpha t}\) is introduced to make the TWIP back to the starting point softly. The numbers a and \(\alpha \) are to be determined by the distance s and the weight matrices in J. Hence, the trajectory tracking target vector is

$$\begin{aligned} \bar{\mathbf{X }}\!=\![0,0,(at-t^2)\mathrm{e}^{-\alpha t},(a-2t)\mathrm{e}^{-\alpha t}-\alpha (at-t^2)\mathrm{e}^{-\alpha t}]^\mathrm{T}. \end{aligned}$$

For simplicity, we consider the case of \(t_f=+\infty \), and the quadratic performance criterion is in this form

$$\begin{aligned} J=\frac{1}{2}\int _0^{+\infty }\left[ \mathbf Y ^\mathrm{T}(t)\mathbf Q {} \mathbf Y (t)\!+\!u^\mathrm{T}(t-\tau )\mathbf R u(t-\tau )\right] \mathrm{d}t. \end{aligned}$$

With fixed parameter values and initial values: M\(=\) 8 kg, \(M_\mathrm{w}=\) 4 kg, \(l=\) 1 m, \(r=\) 0.25 m, g\(=\) 10 m/s\(^2\), \(\tau \,=\) 0.01 s, \(s=\) 3.2 m, \(I_\mathrm{B}\,=\) 12 kg m\(^2\), \(I_\mathrm{w}\,=\,\frac{1}{8}\) kg m\(^2\), \(\mathbf R =1,~~ \mathbf M =\mathbf 0 ,~~\mathbf Q =\mathrm{diag}(10000,0,5,0), ~~ \varphi (0)=0\) rad, \(\dot{\varphi }(0)=0\) rad/s, \(x(0)=0\) m, \(\dot{x}(0)=0\) m/s. Then, the matrices \(\mathbf A \) and \(\mathbf B \) in Eq. (6) become

$$\begin{aligned} \begin{aligned}&\mathbf A =\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0&{} 1&{} ~0&{} ~0 \\ \frac{140}{27}&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 1 \\ -\frac{80}{27}&{} 0&{} 0&{} 0 \end{array} \right] , ~~\mathbf B =\left[ \begin{array}{c} 0 \\ -\frac{23}{108} \\ 0 \\ \frac{11}{27}\\ \end{array} \right] , \end{aligned} \end{aligned}$$

and \(\mathbf B _0=\mathrm{e}^{-\mathbf A \tau }{} \mathbf B =[0.0021,-0.2130,-0.0041,0.4074]^\mathrm{T}\). Under this parameter combination, the values of a and \(\alpha \) in \(\bar{\mathbf{X }}\) can be chosen carefully to be \(a=20,\alpha =0.5\), in order to meet the requirements of the control task. The MATLAB command lqr returns the solutions of (15) and (16) as follows

$$\begin{aligned} \begin{aligned}&\mathbf P _z=\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 4810.8~~&{} 1570.3~~&{} 125.33~~&{} 418.37 \\ 1570.3&{} 910.00&{} 90.053&{} 330.89 \\ 125.33&{} 90.053&{} 20.233&{} 41.141 \\ 418.37&{} 330.89&{} 41.141&{} 148.96 \end{array} \right] , \\&\mathbf b _z(t)=\left[ \begin{array}{c} (115.18t^2-3003.9t+7208.4)\mathrm{e}^{-0.5t} \\ (95.057t^2-2468.5t+5824.0)\mathrm{e}^{-0.5t} \\ (8.4867t^2-228.80t+618.51)\mathrm{e}^{-0.5t} \\ (42.604t^2-1106.8t+2615.4)\mathrm{e}^{-0.5t} \end{array} \right] . \end{aligned} \end{aligned}$$
Fig. 2
figure 2

The time histories of the tilt angle of the pendulum

Full size image
Fig. 3
figure 3

The time histories of the displacement of the TWIP

Full size image

To addresses the special feature of this paper that uses linear optimal control theory to design a robust controller for systems with strong nonlinearity and an input delay, \(\varvec{\omega }(t)\) is assumed for simplicity to be

$$\begin{aligned} \varvec{\omega }(t)=[0,\omega _2,0,\omega _4]^\mathrm{T} \end{aligned}$$

where \(\omega _2=c_1\varphi ^2+c_2\dot{\varphi }^2+c_3\varphi \dot{\varphi },~\omega _4=2.3c_1\varphi ^2+1.3c_2\dot{\varphi }^2+1.7c_3\varphi \dot{\varphi }\), and the coefficients \(c_1,~c_2\) and \(c_3\) are assumed in the form of \(c_i=f_i\sin ({\varOmega } t),~(i=1,\,2,\,3)\). Case studies on the effect of the uncertainty are made for \({\varOmega }=200\) Hz and \({\varOmega }=0.02\) Hz respectively. Moreover, let \(\mathbf G =[0,108/23,0,54/11]\), \(\mu =0.1,D=1\), used in the switched control, then all the quantities required in the delayed robust optimal controller (20) are available in hand. In all simulation results, the dimension of the tilt angle is rad.

Figures 2 and 3 show that the tilt angle of the pendulum is less than 0.13 rad in the whole motion process, and the back-and-forth motion can be well implemented. Moreover, the plots of the actual displacement variables are smooth enough without obvious chattering, while in Figs. 4 and 5, the plots of the actual velocity variables have obvious chattering. The reason for this phenomenon is that the chattering in velocity item is of high frequency and centralized on the integral sliding mode manifold, while the displacement variable is the integration of the velocity. Therefore, the actual displacement variable is nearly the same as the optimal displacement of the nominal error system due to the response characteristics of integral sliding mode control.

Fig. 4
figure 4

The time histories of the angular velocity of the tilt angle of the pendulum

Full size image
Fig. 5
figure 5

The time histories of the velocity of the TWIP

Full size image

In addition, the influence of \({\varOmega }\) on the control effect is very weak. A possible explanation of this finding is that the frequency of “chattering” is much larger than that of disturbance. The larger the gain of the switched control is, the stronger the robustness of the control is, and the larger the amplitude of the “chattering” is. The parameters used in the switch control must be chosen to have a good balance between robustness and chattering. Figure 6 shows that the value of input delay has a substantial influence on the “chattering.” The larger the input delay is, the stronger the amplitude of “chattering” becomes, which may lead to unstable. A possible explanation of this phenomena is that the error between the predictor state and the actual state may become large when the input delay is long enough.

Fig. 6
figure 6

a The time history of the angular velocity of the tilt angle of the pendulum when \(\tau =0.015\), b the time history of the velocity of the TWIP when \(\tau =0.015\)

Full size image

Figure 7 shows the optimal quadratic performance criterion value of nominal system and uncertainty system under the optimal integral sliding mode control with respect to time t, where the difference between the two curves is small. Moreover, the error approaches to zero when R tends to zero. Hence, the optimal integral sliding mode controller not only has strong robustness, but also keeps the value of the quadratic performance criterion J(t) slightly changed, where J(t) is defined by

(21)
Fig. 7
figure 7

Comparison of the quadratic performance criterion value

Full size image

In summary, when the dominated uncertainty is assumed to be a time-variant linear combination of quadratic terms of tilt angle position and tilt angle velocity, the optimal integral sliding mode control not only implements the control task of back-and-forth motion well, but also has strong robustness against the uncertainty. Among the amplitude of the disturbance, the frequency of the disturbance and the input delay, only the input delay has obvious impact on the “chattering.” The input delay has a substantial influence on the system stability and performance. A large input delay results in large amplitude of chattering, and it may lead to an unstable state of the TWIP system.

5 Conclusion

In this paper, a robust delayed controller has been designed for the back-and-forth motion of a TWIP system with an input delay and with disturbance. Analysis shows that the input delay has a substantial influence on the control performance, and thus, the delay effect cannot be neglected in the design phase.

Though a TWIP is essentially an unstable nonlinear system, the controller design can be carried out by using linear control theory, where the effect of the linearization error is considered as a disturbance of the nominal linearized error system. The robust controller is composed of two parts: One is the optimal controller that minimizes the quadratic performance criterion, and the other is the switched control that makes the controller robust against the disturbance. The quadratic performance criterion with large weight of the tilt angle error is used to “force” the tilt angle error to be small enough, so that the linearization error can be very small. As a result, the controller based on linear control theory works effectively for the motion control of the TWIP with strong nonlinearity.