1 Introduction

System identification (SI) plays an important role in dynamical analysis for increasingly complicated systems. As inverse problem of system modeling, the SI exploits the experimental input and output to identify the dominant characteristics of the system. In the absence of a complete physics-based description of a system, the SI can obtain the missed information of the system. Outcomes of the SI are to provide an alternative solution for the dynamical system modeling, to offer the proper parameters for system design and modification, to develop fault diagnosis tools [1, 2] and to estimate system states [3]. A significant amount of the SI researches has carried out for linear time-invariant (LTI) dynamical systems; however, mechanical vibration systems are not linear time invariant in real-life applications. Many engineering systems demonstrate both the time-varying and nonlinear behavior [4, 5]; e.g., the resonance frequencies of the most vibration parts of plane are functions of the flight speed and height; the stiffness of an elbow joint is time varying during a large voluntary movement [6]. The nonlinearities often arise from nonlinear properties in geometry, material and structure, as well as from the damaged structure. Compared to the LTI model, the nonlinear time-varying (NTV) model is more suitable to characterize real-life dynamical systems. However, the SI will face difficulty when the time-varying system involves nonlinearity, which causes both the nonlinear and nonstationary patterns in the system solution.

If a system has time-varying mass, stiffness or damping parameters, its natural frequency or solution amplitude will depend decisively on the variations, which also reflects in the system responses. The instantaneous feature of the system response strongly relates to the nonlinear and nonstationary characteristics of the system, which is underlying principle of the signal processing-based SI. There are two dominant problems in the signal processing-based SI methods: (1) establishing the relationship between the model parameters of system and the instantaneous features of response, e.g., frequency and amplitude; (2) detecting the frequency and amplitude variations in the response with the suitable signal processing techniques. An effective SI based on signal processing relies on the extracted time–frequency features, i.e., instantaneous amplitude (IA) and instantaneous frequency (IF), where the IA is also termed envelope.

To solve the first problem, Feldman [7, 8] adopted Hilbert transform (HT) to construct the relationships between the instantaneous amplitude and frequency and between instantaneous amplitude and damping coefficient. The HT is able to provide effective results for single degree of freedom (SDOF) yet it is sensitive to the noise. Based on Krylov–Bogoliubov method, called also the averaging method, Ta and Lardies [9] derived the relationship among the nonlinear modal frequency, the analytic amplitude and the derivatives of the response under the free vibration. This approach cannot be applied for all kinds of nonlinear dynamical systems, but for oscillators with weak nonlinearities on damping and stiffness. Considering the linear system with time-varying stiffness, Basu et al. [10] applied a modified Littlewood–Paley basis function to derive the explicit relationship between the transfer function and the wavelet transforms of the input and output. By assuming the narrow bandwidth system solution, the developed theory can identify online variation in nature frequency of a SDOF system and the natural frequency and mode shapes of a multi-degree-of-freedom (MDOF) system arising out of change in stiffness. Beyond these studies, there are many methods to construct the relationship between model parameters of the system and instantaneous features of the response, e.g., least square technique [11], harmonic balance [12–14], dissipation energy balancing [15] and experimental identification. However, these methods are restricted to the LTI systems. The relationship between the system and the response parameters depends on the system characteristics and the input–output condition, which determines the followed signal processing methods. No uniform rule exists through, to indicate which one should be adopted.

For the second problem, the responses of the NTV system may exhibit strongly nonlinear pattern, which makes it a good candidate for time–frequency analysis (TFA). The TFA projects time series into a function of time and frequency, so it is able to characterize the IF and IA in time–frequency domain intuitively. Existing TFAs that have been applied in the SI include short-time Fourier transform (STFT), wavelet transform (WT) and Wigner–Ville distribution (WVD).

The STFT and WT are linear transforms. The former adopts a fixed time–frequency resolution, and the latter applies a scalable time–frequency resolution. Yang and Nagarajaiah [16] combined the STFT and the principle component analysis to identify the model parameters of highly damped LTI systems. Staszewski [17, 18] used time-scale decomposition to identify the system damping and applied the WT to identify the nonlinear systems. Both of them extract the ridge and skeleton of the WT to reconstruct the characteristics of the system according to [7, 8]. Tjahjowidodo et al. [19] compared the performance of the HT and the WT for the nonlinear system identification, and they indicated that the WT outperformed the HT in terms of estimation accuracy. Le and Argoul [20] adopted the WT to identify the viscous damping and cubic stiffness of a supporting beam. Ta and Lardies [9] extracted the WT ridge of the response to estimate the nonlinear stiffness, the coulomb and the square damping. Considering the uncertainty of modal parameters, Yan et al. [21] combined the WT and bootstrap to estimate the modal parameters and the corresponding confidence zone. Shan and Burl [22] investigated time–frequency representation (TFR) of the response of a linear time-varying system using continuous WT. They formulated the SI as an optimization problem subjected to minimizing the difference between TFRs of the measurement and the predicted model output. Kijewski and Kareem [23] discussed the selection of wavelet central frequencies, the role of the WT in the modal separation and the end-effect errors. Limited by uncertainty principle, the STFT and the WT fail to generate the well-concentrated TFRs leading to the worse estimation for the IF and IA. To improve the concentration for the linear transforms, synchrosqueezed technique integrates the coefficients of a TFR in the vicinity of the ridge to sharpen the TFR, which increases the gradient around the ridge. Montejo et al. [24] evaluated synchrosqueezed WT, continuous WT and Hilbert–Huang transform (HHT) in extracting instant frequencies and damping values from the simulated noisy response. The results showed that the TFR obtained via the synchrosqueezed WT is sharper than the one obtained with the continuous WT and it allows the robust extraction of the individual modal responses than the one with the HHT. The sharpness of a TFR can be quantified by energy concentration, which relies on the fineness of the time–frequency resolution provided by the time–frequency transforms.

The bilinear TFAs, e.g., WVD, smoothed pseudo-WVD (SPWVD) and Cohen’s class were designed to provide the better energy concentration. Feldman et al. [25] proposed the WVD-based IF estimation to identify the characteristic parameters of the nonlinear system. Roshan-Ghias et al. [26] used the SPWVD to estimate the modal parameters based on the response under the free vibration. However, the WVD suffers from the interference of the cross-term leading to inaccuracy system identification. The SPWVD suppresses the cross-term using the sliding window at the expense of the concentration, and it cannot remove the inter-component cross-terms. Cohen’s class applies various kernels to suppress cross-terms, though most of them cannot delete the intra-component cross-terms of multi-component signals with strong nonlinearity. The key issues about the linear and nonlinear TFAs concerned in the SI are to improve the concentration and avoid cross-terms.

Beyond the time–frequency transforms, the Hilbert–Huang transform (HHT) provides a new method for analyzing nonstationary and nonlinear time series. It is consisted of empirical mode decomposition (EMD) and Hilbert spectral analysis (HAS), which decomposes the signal into a group of intrinsic mode functions (IMF) and then applies the HAS on the IMF to obtain the IF. Pai et al. [27] combined the sliding-window fitting and the HHT to identify the nonlinear system in both nonparametric and parametric ways. The nonlinear pattern and the order of the system are determined by using the perturbation method. Multi-faceted problem of the EMD includes: (1) Some undesired low-amplitude IMFs with pseudo-components will be generated in the low-frequency region; (2) the first IMF with a wide frequency range that is often not a mono-component IMF; (3) the closely spaced modes interfere each other and cannot be reliably separated; (4) it is highly sensitive to the noise. To avoid a few deficiencies of the HHT, Bao et al. [28] proposed an improved HHT to identify time-varying system by introducing autocorrelation function. Nevertheless, the HHT has not been widely applied for the NTV system mainly due to the complicity in the responses of nonlinear time-varying systems and the poor robustness to the noise.

The main usage of the TFA in the SI is to characterize the time variations of the amplitude and spectral characteristics, IF and IA. The major drawback of the existing TFAs in the SI is that they cannot provide well-concentrated and cross-term free TFR that matches the instantaneous patterns of the response, preventing the accurate identification of the system parameters. This paper aims to identify the system with linear or nonlinear time-varying characteristics using parametric time–frequency transform with spline kernel, which is known for offering the great energy concentration for the TFR and allows the accurate extraction of the nature frequency. The efficacy of the proposed method is demonstrated with the SDOF systems comprised of three types of nonlinear time-varying stiffness, including time-varying periodic modulation of stiffness, time-varying piecewise modulation of nonlinear stiffness and time-varying periodic modulation of nonlinear stiffness. Comparisons with the conventional time–frequency methods and the HT-based SI validated that the proposed method is more robust in characterizing the nonlinear time-varying stiffness of the system with the presence of the noise.

The remainder of the paper is organized as follows. For the sake of completeness, the parametric time–frequency transform with spline kernel (PTFT_S) is briefly introduced in Sect. 2. Section 3 gives the guideline of the proposed method based on the PTFT_S. Section 4 presents the simulation examples to verify the proposed method. Finally, Sect. 5 concludes the paper.

2 Background of parametric time–frequency transform and spline kernel

Parametric time–frequency transform (PTFT) is known to provide a signal-dependent analysis for nonlinear and nonstationary signals. The most attracted merits of PTFT are to highly improve energy concentration by using the signal-dependent kernel function and avoid cross-terms [29]. Implementations of PTFT include linear transform, bilinear transform and sparse decomposition. Among them, the sparse decomposition decomposes the signal into a series of atoms sparsely, which is not suitable for the SI.

In this paper, the formulation based on rotation and shift operators is applied for the PTFT [30], which was initially proposed as linear transform and later was further developed in the form of bilinear transform. Both of them embed the kernel function into these two operators.

For any signal s(t), whose HT is \(\tilde{s}\left( t \right) \), the linear PTFT is defined as [30]

$$\begin{aligned}&{\text {TF}}_s \left( {t_0 ,\omega ;\mathbf{P}} \right) \nonumber \\&\quad =\int _{-\infty }^{+\infty } {z\left( {t_0 ,\tau } \right) g_\sigma ^{*} \left( {\tau -t_0 } \right) \exp \left( {-j\omega \tau } \right) \mathrm{d}\tau } , \end{aligned}$$
(1)

with

$$\begin{aligned} \left\{ {\begin{array}{l} z\left( {t_0 ,\tau } \right) =\tilde{s}\left( \tau \right) \Phi _\mathbf{P}^{R} \left( \tau \right) \Phi _{t_0 ,\mathbf{P}}^S (\tau )\\ \Phi _\mathbf{P}^R \left( \tau \right) =\exp \left[ {-j\int {\kappa _\mathbf{P} \left( \tau \right) \mathrm{d}\tau } } \right] \\ \Phi _{t_0 ,\mathbf{P}}^S \left( \tau \right) =\exp \left[ {j\tau \cdot \kappa _\mathbf{P} \left( {t_0 } \right) } \right] \\ \end{array}} \right. , \end{aligned}$$
(2)

where \(\omega \) stands for angular frequency, * denotes conjugate. \(g_{\sigma }{(t)}\) denotes the window function with parameter of \(\sigma \). \(\Phi _\mathbf{P}^R \left( \tau \right) \) and \(\Phi _{t_0 ,\mathbf{P}}^{S} \left( \tau \right) \) are the frequency rotation and shifting operators, respectively. \(\kappa _\mathbf{P} \left( t \right) \in \hbox {L}^{2}\left( \hbox {R} \right) \) is an integrable kernel function, where P is the associated kernel parameters. Noticed that the modulus of the PTFT is ignored in Eq. (1). Since the IA is critical for the SI, it is necessary to investigate the modulus of the linear PTFT. According to Ref. [31], where provided explicit STFT for an exponential tone, the STFT of any arbitrary signal, e.g., \(s\left( t \right) =A\left( t \right) \exp \left[ {j\omega \left( t \right) } \right] \), is

$$\begin{aligned}&S_s \left( {t_0 ,\omega } \right) \nonumber \\&\quad =\left( {\pi \sigma _h^2 } \right) ^{-1/4}\sqrt{2\sigma _h^2 \pi }\cdot \left[ {A\left( {t_0 } \right) +o\left( {\hbox {A}^{\prime }\left( {t_0 } \right) } \right) } \right] \nonumber \\&\qquad \times \exp \left[ {-\frac{\sigma _h^2 \left( {\omega -\omega _0 -o\left( {\omega ^{\prime }\left( {t_0 } \right) } \right) } \right) ^{2}}{2}} \right] \nonumber \\&\qquad \times \exp \left[ -j\left( \omega -\omega _0 -o\left( {\omega ^{\prime }\left( {t_0 } \right) } \right) \right) t \right] , \end{aligned}$$
(3)

where \(\sigma _h\) stands for the parameter of Gaussian window function. The time-varying amplitude and the frequency are expanded in Taylor’s series around the center of the complex window, \(t_{0}\). \(o\left( {\hbox {A}^{\prime }\left( {t_0 } \right) } \right) \) and \(o\left( {\omega ^{\prime }\left( {t_0 } \right) } \right) \) are high-order term of the time-varying amplitude and frequency after Taylor’s expansion, respectively. The Gaussian window function is defined as,

$$\begin{aligned} g_{\sigma _h } =\left( {\pi \sigma _h^2 } \right) ^{-1/4}\exp \left[ {-\left( {\frac{t^{2}}{2\sigma _h^2 }} \right) } \right] . \end{aligned}$$
(4)

When \(\omega -\omega _0 -o\left( {\omega ^{\prime }\left( {t_0 } \right) } \right) =0\), the modulus of the STFT will become

$$\begin{aligned} \left| {S_s \left( {t_0 ,\omega } \right) } \right|= & {} \left( {\pi \sigma _h^2 } \right) ^{-1/4}\sqrt{2\sigma _h^2 \pi }\nonumber \\&\times \left[ {A\left( {t_0 } \right) +o\left( {\hbox {A}^{\prime }\left( {t_0 } \right) } \right) } \right] . \end{aligned}$$
(5)

Assuming that the signal is asymptotic within the applied window, the high-order term in Eq. (5) is neglected to yield

$$\begin{aligned} \left| {S_s \left( {t_0 ,\omega } \right) } \right| =\left( {\pi \sigma _h^2 } \right) ^{-1/4}\sqrt{2\sigma _h^2 \pi }\cdot A\left( {t_0 } \right) . \end{aligned}$$
(6)

When \(\kappa _\mathbf{P} \left( t \right) \equiv 0\), the linear PTFT will degrade to the STFT according to Eq. (23). When the window of Eq. (4) is adopted, the modulus of the PTFT will be

$$\begin{aligned} \left| {{\text {TF}}_s \left( {t,\omega ;\mathbf{P}} \right) } \right| =\left( {\pi \sigma _h^2 } \right) ^{-1/4}\sqrt{2\sigma _h^2 \pi }\cdot A\left( t \right) . \end{aligned}$$
(7)

According to Eq. (7), the modulus of the PTFT is independent to the kernel parameter and only related to the window width and the IA. In the linear PTFT, frequency rotation and shift operators have two functionalities: (1) The rotation operator rotates signal with a degree of \(\arctan \kappa _\mathbf{P} \left( \tau \right) \) in time–frequency domain; (2) the shift operator shifts the rotated signal with an amount of \(\kappa _\mathbf{P} \left( {t_0 } \right) \) at each time instance. The problem of the linear PTFT is that it cannot provide the satisfied energy concentration as the bilinear transform does.

Second, the bilinear PTFT is defined as [32],

$$\begin{aligned} {\text {TF}}_s \left( {t_0 ,\omega ;\mathbf{P}} \right)= & {} \int _{-\infty }^{+\infty } y\left( {t_0 -\tau } \right) y^{*}\left( t_0 -\tau \right) \nonumber \\&\times \,\Phi _{t_0 ,\mathbf{P}}^S \left( \tau \right) \exp \left( {-j\omega \tau } \right) \mathrm{d}\tau , \end{aligned}$$
(8)

with

$$\begin{aligned} y\left( {t_0 -\tau } \right) =\tilde{s}\left( {t_0 -\tau } \right) \Phi _\mathbf{P}^R \left( {t_0 -\tau } \right) . \end{aligned}$$
(9)

When \(\kappa _\mathbf{P} \left( t \right) \equiv 0\), Eq. (9) will degrade to WVD. Although it is able to achieve the best concentration for nonlinear auto-term, it still cannot avoid the cross-terms between the components. Moreover, the bilinear PTFT is difficult to estimate the IA accurately since it is formulated as the global Fourier transform of the instantaneous autocorrelation function, which makes it inappropriate for the SI.

In addition, whether the kernel function of the PTFT matches instantaneous pattern of the signal or not determines the final performance of the SI. An optimal kernel is required to characterize signal IF accurately. For the signals with continuous IF, the existing kernels include linear function, polynomial [33, 34], spline [35], trigonometric function, exponential function, logarithmic function and Fourier series [36]. In this paper, the spline kernel is selected considering the highly nonlinear response of nonlinear time-varying systems, which is given as,

$$\begin{aligned}&\Phi _\mathbf{C}^{R} \left( \tau \right) =\exp \left[ {-j\sum _{i=1}^n {\frac{C_{l,i} }{i}\left( {\tau -t_l } \right) ^{i}+o_l } } \right] ,\end{aligned}$$
(10)
$$\begin{aligned}&\Phi _{t_0 ,\mathbf{C}}^S \left( \tau \right) =\exp \left[ {j\tau \cdot \sum _{i=1}^n {C_{l,i} } \left( {t_0 -t_l } \right) ^{i-1}} \right] , \end{aligned}$$
(11)

where \(\mathbf{C}=\left\{ {C_{l,i} } \right\} \), \(i=1,\ldots ,n\), \(l=1,\ldots ,N-1\), is parameters of spline function. \(O_{l}\) is integration constant,

$$\begin{aligned} o_{l} -o_{l+1} =\sum _{i=1}^{n} {\frac{c_{l+1,i} }{i}\left( {x_l -x_{l+1} } \right) ^{i}} , \end{aligned}$$
(12)

where \(o_{1} =0\), \(t_{l}\) is the lth knot of spline, and \(-\infty =t_0 <t_{1} <\cdots <t_{N} <t_{N+1} =\infty \).

Fig. 1
figure 1

Comparison of HT and PTFT_S in IA and IF extraction

Full size image
Fig. 2
figure 2

Different time–frequency representation. a STFT; b synchrosqueezed STFT; c WVD; d CWT; e synchrosqueezed CWT; f PTFT_S

Full size image

To illustrate the PTFT with spline kernel (PTFT_S), a signal is considered as,

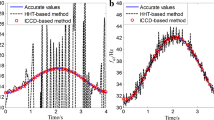
$$\begin{aligned} s\left( t \right) =\sin \left[ {20\pi t+10\pi \arctan \left( {t-5} \right) ^{2}} \right] , \end{aligned}$$
(13)

whose IF is \(10 + 10 \times (t-5)/(1+(t-5)^{\wedge }\)4). The signal is contaminated by white Gaussian noise with signal-to-noise rate (SNR) of 20 dB. Figure 1 shows the IA and IF extracted by the HT and the PTFT, respectively. The kernel parameters of the PTFT_S are obtained by approximating the signal IF with the spline function. The IA extracted by the HT is further low-pass filtered so it can approximate the real IA properly. The top plot shows the real IA and the estimated IAs obtained by the HT and the PTFT_S (also named spline chirplet transform (SCT) in the literatures) are overlapped, indicating that both the two methods can estimate the IA with small errors. On the other hand, the bottom plot shows that the IF extracted by the HT is far away from the real IF during 3–6 s and oscillates at right end. Comparatively, the PTFT_S is capable of extracting the IA and IF accurately even with the presence of noise.

To compare performances of different TFAs, Fig. 2 shows TFRs obtained by the STFT, synchrosqueezed STFT, WVD, CWT, synchrosqueezed CWT and the PTFT_S. According to Fig. 2a, b, d, e, the STFT, CWT and their synchrosqueezed versions are unable to characterize the accurate IA as the signal IF varies fast with the time. Due to the nonlinearity of the signal, the WVD suffers from the cross-terms significantly as shown in Fig. 2c. Figure 2f shows PTFT_S which characterizes the IA and the IF for the considered signal accurately.

3 Guideline SI by using PTFT_S

3.1 Nonlinear and time-varying system identification

In this section, we start from a simple case of SDOF nonlinear system under free vibration,

$$\begin{aligned} m\ddot{x}+C\left( {\dot{x}} \right) +K\left( x \right) =0, \end{aligned}$$
(14)

where \(C\left( {\dot{x}} \right) \) and K(x) are real odd functions of \(\dot{x}\) and x, denoting nonlinear damping and restoring force. The second-order differential equation in Eq. (14) can be rewritten as the damping system of unit mass as,

$$\begin{aligned} \ddot{x}+2h\left( {\dot{x}} \right) \dot{x}+\omega _0^2 x=0, \end{aligned}$$
(15)

where \(h\left( {\dot{x}} \right) \dot{x}={C\left( {\dot{x}} \right) }/{2m}\) stands for the damping of unit mass and \(\omega _0^2 \) is the square of damping-free nature frequency. Since the nonlinear restoring force varies with time, it can be converted to the multiplication form as

$$\begin{aligned} \omega _0^2 \left( x \right) x=\omega _0^2 \left( t \right) x\left( t \right) , \end{aligned}$$
(16)

where \(\omega _{0}^{2} \left( t \right) \) is fast time-varying nature frequency. x(t) is the system solution with overlapped spectrum. Similarly, nonlinear damping force can also be expressed as multiplication of the fast instantaneous damping coefficient and the velocity as

$$\begin{aligned} h_{0} \left( {\dot{x}} \right) \dot{x}=h_{0} \left( t \right) \dot{x}\left( t \right) , \end{aligned}$$
(17)

where \(h_{0}(t)\) denotes instantaneous damping coefficient. Spectrums of \(h_{0}(t)\) and \(\dot{x}\left( t \right) \) are assumed to be overlapped. Correspondingly, the instantaneous nature frequency and the damping coefficient are high-pass overlapped, so Eq. (15) can be rewritten as,

$$\begin{aligned} \ddot{x}+2h_0 \left( t \right) \dot{x}+\omega _{0}^{2} \left( t \right) x=0. \end{aligned}$$
(18)

Equation (18) indicates that a SDOF nonlinear system can be characterized by a time-varying system with the fast time-varying instantaneous nature frequency and the damping coefficient.

Second, we consider the time-varying system in civil and mechanical engineering characterized by the motion equation as,

$$\begin{aligned} m\left( t \right) \ddot{x}+C\left( t \right) \dot{x}+K\left( t \right) x=0, \end{aligned}$$
(19)

where m(t), \(C\left( t \right) \dot{x}\) and K(t)x are time-varying mass, frictional force as a function of velocity \(\dot{x}\) and restoring force as a function of the displacement x. The second-order differential equation in Eq. (19) can be rewritten as the damped system of unit mass as,

$$\begin{aligned} \ddot{x}+2h\left( t \right) \dot{x}+\omega _0^2 \left( t \right) x=0, \end{aligned}$$
(20)

where \(h\left( t \right) \dot{x}={C\left( t \right) }/{2m\left( t \right) }\) stands for damping force for unit mass as a function of the velocity and h(t) is the instantaneous damping coefficient. \(\omega _{0}^{2} \left( t \right) ={K\left( t \right) }/{m\left( t \right) }\) is the square of damping-free time-varying nature frequency.

Comparing Eqs. (18) and (20), both the nonlinear and the time-varying system confirm to the similar motion equation, whose parameters are the time-varying instantaneous damping coefficient and the nature frequency. Such similarity provides basis that these two systems parameters are not only able to represent nonlinearity, but also able to reveal time-varying pattern of the system. For example, the instantaneous damping coefficient and the nature frequency of a nonlinear time-invariant system are modulated by time-varying pattern in NTV case. In another word, for a NTV system, its damped system of unit mass holds the same formulations as in Eqs. (18) and (20), which are unified as

$$\begin{aligned} \ddot{x}+2h_{ntv} \left( t \right) \dot{x}+\omega _{ntv}^{2} \left( t \right) x=0, \end{aligned}$$
(21)

The difference is that the instantaneous damping coefficient \(h_{ntv} \left( t \right) \) is consisted of the nonlinear function of velocity and the time-varying function, and instantaneous nature frequency square \(\omega _{ntv}^2 \left( t \right) \) includes the nonlinear function of displacement and the time-varying function. By involving the analytical impulse response function, as well as its first and second derivatives, the instantaneous damping coefficient \(h_{ntv}(t)\) and the instantaneous nature frequency \(\omega _{ntv}^2 \left( t \right) \) can be derived analogous to the nonlinear SI using the HT [7],

$$\begin{aligned}&h_{ntv} \left( t \right) ={-\dot{A}}/A-{\dot{\omega }}/{2\omega }, \end{aligned}$$
(22)
$$\begin{aligned}&\omega _{ntv}^2 \left( t \right) =\omega ^{2}-{\ddot{A}}/A+{2\dot{A}}/{A^{2}}+{A\dot{\omega }}/{A\omega }. \end{aligned}$$
(23)

where A and \(\omega \) denote the IA and the IF of solution, respectively. Equations (22) and (23) reveal that \(h_{ntv}(t)\) and \(\omega _{ntv}^{2} \left( t \right) \) relate to the IA and the IF of the solution, as well as their derivatives.

3.2 Instantaneous feature extraction using PTFT_S

3.2.1 IF estimation and kernel parameter

Given the spline kernel, the PTFT_S will be able to provide the better characterization of IF and IA for the signal when the kernel parameters are properly estimated in terms of the analyzed signal. Estimation of the kernel parameters is analogous to the IF estimation in most cases. The latter can be realized in many ways, i.e., phase difference, zero-crossing, Teager energy operator, HT, maximum likelihood estimation, optimization-based estimator, skeleton of time–frequency representation (TFR), etc. In this paper, the TFR-based IF estimator is applied since it is more robust for nonstationary signals with the presence of noise. Specifically, the ridge of the TFR is detected to locate corresponding skeleton, and then, kernel parameters can be obtained by approximating the skeleton.

In order to improve the estimation accuracy, an iterative procedure is introduced to obtain the kernel parameters. In the each iteration, the ridge of the TFR is detected, and then, the skeleton is located and approximated. The underlying principle of the iterative estimation for the PTFT_S is that the more accurate kernel parameters, the better TFR. The extracted skeleton \(\bar{{\omega }}_i \left( t \right) \) is obtained as

$$\begin{aligned}&\frac{\sigma \left[ {\hbox {TF}_s \left( {t,\omega ;{\bar{\mathbf{P}}}_{i-1} } \right) } \right] }{\sigma \omega }=0,\nonumber \\&\quad \omega :\left| {\arg \mathop {\max }\limits _\omega \hbox {TF}_s \left( {t,\omega ;{\bar{\mathbf{P}}}_{i-1} } \right) } \right| \le {\Delta \omega }/2, \end{aligned}$$
(24)

where i denotes the ith iteration. \(\bar{{\omega }}\) and \({\bar{\mathbf{P}}}\) are estimated IF and kernel parameters. \({\bar{\mathbf{P}}}\) can be obtained as,

$$\begin{aligned} {\bar{\mathbf{P}}}_i =\mathop {\min }\limits _{\mathbf{P}_i } \sum {\left[ {\tilde{\kappa }_\mathbf{P} \left( t \right) -\omega _{i-1} \left( t \right) } \right] ^{2}} . \end{aligned}$$
(25)

The loop stops until

$$\begin{aligned} \left| {\bar{{\omega }}_{i+1} \left( t \right) -\bar{{\omega }}_i \left( t \right) } \right| \le \delta , \end{aligned}$$
(26)

where \(\delta \) is predefined threshold. Finally, the obtained IF is s spline approximation of detected skeleton after the last iteration. A reliable recursive TFR-based kernel parameter estimator for the SI has to cope with several problems, i.e., TFR initialization, determination of the time–frequency resolution, feature extraction for the attenuated noisy signal. Ultimately, these factors will influence the accuracy of the SI.

  1. (1)

    TFR initialization

In the iterative procedure of kernel parameter estimation, the initial estimation is of great importance. The better initialization, the better estimation accuracy. The error caused by worse initialization could be aggravated in the following cycles. Nonparametric TFAs are often used to initialize PTFT_S. For the sake of consistency, the linear nonparametric TFA is applied for the initialization in this paper. However, the standard linear nonparametric TFAs, i.e., STFT, WT and S transform (which combines STFT and WT), cannot fulfill the task due to their unsatisfied time–frequency resolution; post-processing methods can be adopted to improve the TFR quality, e.g., re-assignment, synchrosqueezing, image processing, etc. Re-assignment is to sharp a TFR by move the amplitude to the time–frequency coordinate that is gravity of its neighbors. Synchrosqueezing is to sum the amplitude within predefined frequency neighborhood at every time instant. Their problem lies in the distortion of the IF trajectory; comparatively, the Synchrosqueezing performs better to characterize the IF trajectory. Hereinafter, the STFT, CWT and their synchrosqueezed versions are considered to initialize the PTFT_S. How well the initialization affects the IF estimation depends to on the inherent structure of the signal to be analyzed.

  1. (2)

    Time–frequency resolution

The advantage of the PTFT_S is to provide a signal-dependent analysis. The TFR tiling is illustrated in Fig. 3, where the bold line is the real IF and the stars denote the coefficients calculated within one logon, i.e., time–frequency cell as shown in Fig. 3. At the each time instant, the logon is rotated according to the spline kernel function so the calculated coefficient concentrates at the center of the logon. The maximum coefficients will align with the signal IF when the spline kernel approximates the IF accurately. Such layout is able to match the shape of the real signal. The time–frequency resolution trade-off is well known as,

$$\begin{aligned} \Delta _{t} \Delta _{f} =K \end{aligned}$$
(27)

where \(\Delta _{t}\) is width of time window, \(\Delta _{f}\) is the measure of frequency resolution and K is a constant that depends on the window shape. Equation (27) suggests that the time and frequency resolution cannot be the best simultaneously. Higher time resolution leads to lower frequency resolution and vice versa. As the PTFT_S concentrates the signal energy along the trajectory formed by the kernel function, it is recommended to use the longer window while the IF varies fast with the time. In this case, one can obtain the better IF estimation and the more accurate kernel parameters.

  1. (3)

    Noise and spline approximation

Fig. 3
figure 3

TFR tiling of PTFT_S

Full size image
Fig. 4
figure 4

Extracted IA in terms of different window length: a 1024; b 512; c 256; d 128

Full size image

The spline kernel uses the piecewise low-order polynomial to avoid the oscillation in high-order polynomial approximation, which is called “Runge” phenomenon. To fit a complicated curve accurately, the spline kernel requires more knots, which leads to the overfitting with the presence of noise. In another word, the spline with less knots is more robust to the noise. On the other hand, it is necessary to reduce the noise to improve the estimation performance. Various signal de-noising methods have be developed, among which the average method and the band-pass filtering are two simple candidates in our study. Without special note, 30 noisy responses are averaged to obtain the de-noised response in this paper. It is worth mentioning that like the most TFAs, the PTFT_S assumes the interested signal component dominants the measured response.

3.2.2 IA estimation

Another time–frequency feature to be extracted is the IA. Conventionally, the envelope can be obtained using the HT, but it is very sensitive to the noise and results in the strong oscillation even without the presence of noise [7]. The TFA projects a signal into the time–frequency domain; the IA corresponds to the TFR ridge or modulus. In this paper, the IA is extracted from the concentrated TFR. Two aspects related to the TFR-based IA extraction are: (1) energy leakage due to the window operation; (2) the IA oscillation with the large window length.

At first, as suggested in Eq. (7), the modulus of the PTFT_S is proportional to the real IA and is related to the parameters of Gaussian window. Since window spectrum contains sidebands in digital signal processing, the convolution of window and signal will inevitably cause the energy leakage in the time–frequency domain. The signal IA can be recovered based on the TFR as,

$$\begin{aligned} \tilde{A}\left( t \right) =\lambda \cdot \frac{\left| {\hbox {TF}_s \left( {t,\omega ;\mathbf{P}} \right) } \right| }{\left( {\pi \sigma _h^2 } \right) ^{-1/4}\sqrt{2\sigma _h^2 \pi }}, \end{aligned}$$
(31)

where \(\lambda \) stands for calibration parameter. The calibration parameter can be estimated as follows,

$$\begin{aligned} \lambda =1 \Bigg /{\frac{{\mathop {\max }\limits _{\omega }} \left| {\hbox {TF}_{\hat{{s}}} \left( {t,\omega ;\mathbf{P}} \right) } \right| }{\left( {\pi \sigma _h^2 } \right) ^{-1/4}\sqrt{2\sigma _h^2 \pi }}}, \end{aligned}$$
(32)

where the signal considered for the calibration is \(\hat{{s}}\left( t \right) =\exp \left( {j\omega _0 t} \right) \).

Second, the larger window, the more sidebands. The more sidebands cause the more energy leakage, leading to the strongly oscillation in the extracted IA. Figure 4 shows the extracted IA of the signal with deteriorate amplitude, which shows the IA highly oscillates as the window length increases. To remove the IA oscillation, two steps are involved: (1) selecting optimal window length to balance the trade-off between the IA oscillation and the IF characterization; (2) low-pass filtering the extracted IA.

Table 1 lists relative errors in the IA and IF estimations using different TFAs for the signal in Eq. (31). The relative error is calculated as,

$$\begin{aligned} r_\mathrm{error}=\frac{1}{N}\sum _{i=1}^N {\frac{\left| {\tilde{y}\left( {t_i } \right) -y\left( {t_i } \right) } \right| }{\left| {y\left( {t_i } \right) } \right| }} , \end{aligned}$$
(33)

where y(t) denotes any function of time. It validates that the PTFT_S outperforms others in both the IA and IF estimations. The STFT and CWT are able to achieve the accurate IF estimation, yet they fails to characterize the IA accurately due to the smeared TFR. Their synchrosqueezed versions perform worse than they do since the former reallocates the energy and distorts the ridge. The WVD is the worst in this case, which is highly interfered by the cross-terms. For such complicated signal, the PTFT_S is proved to be the better choice. Meanwhile, it is fair to use the former four TFAs to initialize PTFT_S.

Table 1 IA and IF estimation errors
Full size table

3.3 Reconstruction of backbone and static forces

To illustrate the inherent characteristics of the nonlinear and time-varying system intuitively, backbone, damping curve and static force curve are common tools. The backbone and damping curve display how the nature frequency and the damping coefficient vary with the displacement and the velocity, respectively. The static forces include restoring force and friction force, both of which vary with the displacement and the velocity too. For symmetric system, the restoring force, K(x), can be computed as,

$$\begin{aligned} k\left( x \right) =\left\{ {{\begin{array}{l@{\quad }l} \omega _c^2 A_c , &{} x>0 \\ -\omega _c^2 A_c , &{} x<0 \\ \end{array} }} \right. , \end{aligned}$$
(34)

where \(\omega _{c}(t)\) and \(A_{c}\) are congruent nature frequency and amplitude, respectively, which are formulated as,

$$\begin{aligned}&\omega _c \left( t \right) =\sum _{l=1}^N {\omega _{0l} \left( t \right) \cos \phi _l \left( t \right) } , \end{aligned}$$
(35)
$$\begin{aligned}&A_c \left( t \right) =\sum _{l=1}^N {A_l \left( t \right) \cos \phi _l \left( t \right) } , \end{aligned}$$
(36)

where \(\omega _{0l}(t)\) and \(A_{l}(t)\) denote the IF and the IA of the lth harmonic. \(\phi _{l}\) is phase difference between the primary component and the lth harmonic. In real practice, the IA and IF of the primary component will be considered to be the congruent frequency and amplitude when the high-order harmonics are small enough to be neglected. The characteristic parameters of the nonlinearity can be identified based on the static force curves.

Specially, when the restoring force is expressed as power series,

$$\begin{aligned}&K\left( x \right) =\left( {\alpha _1 +\alpha _3 x^{2}+\alpha _5 x^{4}+\cdots } \right) \nonumber \\&x=\left( {\mathop {\sum }\nolimits _{n=1}^N {\alpha _{2n-1} x^{2n-2}} } \right) x, \end{aligned}$$
(37)

where \((\alpha _{1}\), \(\alpha _{3}, {\ldots }\), \(\alpha _{2\mathrm{n}-1})\) are coefficients of the power series. The average of the instantaneous nature frequency, \(\left\langle {\omega ^{2}\left( A \right) } \right\rangle \), is obtained as,

$$\begin{aligned} \left\langle {\omega ^{2}\left( A \right) } \right\rangle= & {} T^{-1}{\mathop {\int }\limits _{0}^{T}} {\omega ^{2}\left( t \right) \mathrm{d}t}\nonumber \\= & {} \alpha _1 +\frac{3}{4}\alpha _3 A^{2}+\frac{5}{8}\alpha _5 A^{4}+ \cdots , \end{aligned}$$
(38)

which is exactly the backbone curve. The damping curve can be derived in the same way.

To sum up, the SI for NVT system mainly includes five steps:

  1. (1)

    Performing the TFA on the system response;

  2. (2)

    Extracting the IF and IA of the response;

  3. (3)

    Using the derivatives of IF and IA to estimate the instantaneous modal parameters;

  4. (4)

    Reconstructing the backbone, damping curve and static force model;

  5. (5)

    Identifying the nonlinear and time-varying pattern and estimating the characteristic parameters.

In the nonlinear time-varying system, the stronger component dominated the system can be identified at first and others can be obtained by removing the components one by one. The guideline is shown in Fig. 5.

Fig. 5
figure 5

Guideline of output-based SI using PTFT_S

Full size image

4 Linear and nonlinear time-varying system identification

In this section, the SDOF systems comprised of three types of nonlinear time-varying stiffness are considered, including time-varying periodic modulation of stiffness, time-varying piecewise modulation of nonlinear stiffness and time-varying periodic modulation of nonlinear stiffness. For all examples, the sampling frequency is 13 Hz and the window length is 256. It is noticed that the SI under free vibration is considered only to emphasize the applicability of the proposed method, while the application in various systems under different external forces will be investigated in future works.

Example 1

For a system with time-varying periodic modulation of stiffness as,

$$\begin{aligned}&\ddot{x}+0.05\dot{x}+\left[ {25+20\cos (0.1t)} \right] x=0,x_0 =1,\nonumber \\&\quad \dot{x}_0 =0. \end{aligned}$$
(39)

Figure 6 shows the solution of the system for nonzero initial condition. Eighteen knots were used in the PTFT_S. In Fig. 6a, the IF and IA variations of solution reflect the periodic time-varying stiffness. In Fig. 6b, the twisted backbone curve shows how the displacement varies with the nature frequency, which is in agreement with the linear and periodic time-varying behavior of the system. The centerline of backbone is vertical to the frequency axis, meaning that the system does not contain the nonlinear stiffness. This is also verified by left plot of Fig. 6c. The periodical time-varying pattern of the elastic static force is oscillated along a centerline whose slope is 25, corresponding to the initial nonlinear force. In right plot of Fig. 6c, the approximated slope of the friction force is 0.5, yet it is modulated slightly because the IA of the velocity follows the same time-varying pattern.

Fig. 6
figure 6

Identification for example 1: a signal and its IA (top) and IF (bottom), b backbone curve, c static force [left elastic static force (red line time-invariant stiffness, green line time-varying stiffness) right friction force]. (Color figure online)

Full size image

Example 2

For a system with piecewise time-varying quasiperiodic modulation of nonlinear stiffness as,

$$\begin{aligned}&\ddot{x}+0.04\dot{x}+\left[ {15+30x^{2}+10{\text {sign}}\left( {\cos (0.1t)} \right) } \right] \nonumber \\&\quad x=0,x_0 =1,\dot{x}_0 =0. \end{aligned}$$
(40)

Figure 7 shows the solution of the system for nonzero initial condition. A total of 45 knots were used in the PTFT_S. In Fig. 7a, the estimated IF and IA carry the piecewise time-varying patterns. In Fig. 7b, the twisted backbone curve shows the stepwise nature frequency varies with the displacement, which is consistent with the cubic nonlinear and the stepwise time-varying behavior of the system. The centerline of the backbone curve is slant to the right, meaning that the system has hard spring characteristics. The left plot of Fig. 7c shows the piecewise time-varying pattern twists above the initial nonlinear force characteristic (red dot line), which is 30*3/4*\(A^{2}\). In top plot of Fig. 7d, the congruent stiffness is obtained by fitting the square IF. As the NTV pattern is the sum of the time-varying and nonlinear part, the time-varying part can be obtained by removing the fitted curve from the congruent stiffness. The identified stiffness variation reveals the true time-varying pattern of the system stiffness as shown in bottom plot of Fig. 7d, though it also shows the errors increase at falling and rising edges and the oscillation at stationary region. This is because the PTFT_S uses the spline kernel with less knots to approximate the response IF. Such oscillation also affects the friction force with respect to velocity as shown in left plot of Fig. 7c.

Example 3

For a system with periodic modulation of nonlinear stiffness as,

$$\begin{aligned}&\ddot{x}+0.04\dot{x}+\left[ {1+0.6\cos (0.15t)} \right] \cdot \left( {1+13x^{2}} \right) \nonumber \\&\quad x=0,x_0 =1,\dot{x}_0 =0. \end{aligned}$$
(41)

Figure 8 shows the solution of the system for nonzero initial condition. Twenty-five knots were used in the PTFT_S. In Fig. 8a, the estimated IF and IA carry periodic time-varying patterns. In Fig. 8b, the twisted backbone curve shows the periodic nature frequency varies with the displacement, which agrees with cubic nonlinear and periodic time-varying behavior of the system. The centerline of backbone curve is slant to the right, also meaning that the system has hard spring characteristics. According to Eq. (23), the identified instantaneous nature frequency squared function (the instantaneous modal stiffness) agrees with the initial square wave stiffness (see bottom figure Fig. 8d). The identified instantaneous modal stiffness allows the identification of the time-invariant static force characteristic \(k(A)= 13*3/4*\hbox {A}^{2}\) (red dot line in left plot of Fig. 8c), which the congruent stiffness is divided by the fitted stiffness to obtain the time-varying pattern of stiffness (see top plot of Fig. 8d).

Fig. 7
figure 7

Identification for example 2: a signal and its IA (top) and IF (bottom), b backbone curve, c left elastic static force (red line time-invariant stiffness, green line time-varying stiffness), right friction force (red line true friction force, green line identified friction force); d stiffness (top) and its variation estimation (bottom). (Color figure online)

Full size image
Fig. 8
figure 8

Identification for example 3: a signal and its IA (top) and IF (bottom); b backbone curve; c left elastic static force (red line time-invariant stiffness, green line time-varying stiffness); right friction force (red line true friction force, green line identified friction force); d stiffness (top) and its variation estimation (bottom). (Color figure online)

Full size image
Table 2 Estimation log error of time-varying stiffness
Full size table

In addition, the SI performance for the above three examples with the presence of noise is compared using the STFT, continuous wavelet transform (CWT), synchrosqueezed STFT, synchrosqueezed CWT, HT and PTFT_S-based methods. Table 2 lists relative log errors of time-varying stiffness estimation. Comparison results validated that the proposed method is more suitable in characterizing the nonlinear time-varying stiffness with the presence of noise. Except for example 2, the PTFT_S is still able to analyze system with stepwise time-varying stiffness, but it introduces many errors in the IF and the IA estimation. The PTFT_S-based SI depends on the compatibility of the kernel function. It is expected to obtain the better SI performance with the more matched kernels.

5 Conclusion

The applications of the PTFT on the free response of the system showed the significant potential for the TFA-based SI. The PTFT_S can estimate the IF and the IA accurately from well-concentrated TFR. The efficacy of the proposed method was validated with the SDOF systems comprised of three types of nonlinear time-varying stiffness. The results showed time-varying pattern modulated nonlinear nature frequencies can be well characterized, and the nonlinear and time-varying patterns were properly estimated. Comparisons with other time–frequency methods and HT-based SI validated that the proposed method is more suitable in characterizing the nonlinear time-varying stiffness with the presence of noise. In addition, the performance of the proposed method is highly related to the fitness of the kernel function to the response IF. The better-matched kernel is expected to achieve the better SI performance. Moreover, the accurate IA and IF estimations based on the PTFT_S will be the dominant concern in the SI for NTV system. Future works include applying the PTFT in the SI for a wide variety of nonlinear time-varying systems and MDOF systems under different vibration conditions, on which we are currently working to complete the research.