1 Introduction

Electronic throttle (ET) valve systems have been receiving considerable attention of automotive engineers and researchers in the area of vehicle dynamics and control since last two decades [1, 2]. Compared with the conventional throttle valve plate in an automotive engine, the ET systems aim at reducing gas emission, providing a better fuel economy and further improving the vehicle drivability. The ET systems are superior to its mechanical counterpart when the control loop fulfils the pre-determined requirements: a fast transient response without overshoot, a high static position precision, easy implementation and strong robustness against the parameter variations and disturbances. However, in practical applications, there exist various types of parameter uncertainties and nonlinearities, i.e., transmission friction, return-spring limp-home (LH), gear backlash and the external disturbance caused by the effect of air flow force. All these uncertain parameter variations and nonlinearities not only significantly enhance the difficulty of the control design, but affect the system performance.

Since the core issue on the performance of ET control systems is the tracking precision and robustness against parameter variations and nonlinearities, a number of researchers have used advanced control methods in the ET control systems for the purpose of ensuring the throttle plate angle to accurately track the reference command. In [3–5], the conventional linear proportional-integral-derivative (PID) control methods were adopted together with feedforward/feedback compensation for the parameter variations and nonlinearities. However, when the ET system frequently experiences a wide range of parameter variations and nonlinearities, the acceptable tracking performance cannot be ensured. In [6, 7], time-optimal control technique was used for the purpose of achieving fast and high-accuracy of reference tracking of throttle plate angle. Nevertheless, since these control methods significantly depend on the modelling accuracy, once large parameter uncertainties and nonlinearities occur leading to the inaccurate system model, the tracking performance and robustness of the ET control system would be deteriorated. Further, several intelligent control methodologies have been used in order to improve the ET control performance particularly under the friction and LH, i.e., neural-network-based ET control and fuzzy control [8–11]. Please note the practical issues are that the adopted back-propagation training algorithm [8, 9] may cause slow training and local minima, while the simple fuzzy rules in [10, 11] may not fully indicate the working conditions of nonlinear hysteretic ET systems. In [12–15], adaptive control has been applied to ET systems such that the requirement of the system knowledge was successfully relaxed. However, because the system identification of the main component was first used, followed by the adaptively update for the process parameters, the system performance may be affected if large parameter uncertainties and nonlinearities exist resulting in the inaccurate system identification. From the robustness point of view, sliding mode control [16–27] and observer techniques were employed in the ET systems, such that the effects of the parametric variations and nonsmooth nonlinearities can be alleviated [28, 29]. However, how the uncertainty bound can be appropriately obtained without causing control saturation is still challenging.

Motivated by the advantages of both adaptive control and sliding mode control methods, in this paper, we develop a PID-type sliding mode-based adaptive control scheme for adaptively estimating both the lumped uncertainty bound and the control gains in Lyapunov sense. Thus, not only the influences of the lumped uncertainty can be alleviated, but also the PID-type sliding mode control gains are adaptively adjusted for both transient and steady-state tracking purpose based on the closed-loop tracking error. It will be shown from the simulation results that the proposed control scheme exhibits an excellent tracking performance in terms of the step and sinusoidal reference commands. Also, the strong robustness against the parameter variations, nonlinearities and external disturbance is guaranteed.

Fig. 1
figure 1

ET system model

Full size image

The rest of this paper is organized as follows: In Sect. 2, the dynamic model of ET systems is presented and the expression of the bounded lumped uncertainty is provided. In Sect. 3, a robust adaptive sliding mode (RASM) controller is developed where the lumped uncertainty bound and sliding mode control gains are both adaptively estimated based on the designed update laws, and the asymptotic error convergence as well as the closed-loop error convergence analysis is discussed. Finally, Sects. 4 and 5 present the simulation and experimental results for verifying the remarkable reference tracking characteristic of the proposed RASM control. Section 6 gives the conclusion and some further work.

2 Problem formulation

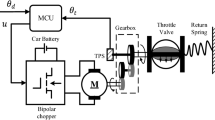
The architecture of an ET control system is shown in Fig. 1 [15, 19]. It is clearly seen that the ET system involves the following parts: an accelerator pedal, a microcontrol unit (MCU), a DC motor, a throttle valve plate, a reduction gear set including a motor pinion gear, an intermediate gear, and a sector gear, respectively, two nonlinear return springs, and two position sensors for measuring the pedal movement and the actual throttle position, respectively.

When the accelerator pedal is pressed down by the driver, the reference command for the throttle valve to track is first measured by the pedal position sensor and then sent to the MCU in Engine Management System for the purpose of determining the appropriate air-fuel mixture to be fed into the engine. Also, the actual throttle opening is measured by the throttle position sensor. The control voltage provided by the MCU with the help of PWM control module, is to power the DC motor and generate the rotational torque. As a result, the actual throttle opening is obtained or maintained, through the reduction gear set, to follow the desired opening angle.

Considering the fact that the armature current dynamics can be neglected resulting from the small value of armature inductance, the system dynamics of the ET valve and the DC motor are given by [9, 15]:

$$\begin{aligned}&J_\mathrm{m} {\dot{\omega }}_\mathrm{m}=\tau _{a}-B_\mathrm{m}{\omega _\mathrm{m}-\tau _\mathrm{m}} \end{aligned}$$
(1)
$$\begin{aligned}&\tau _{a} =k_\mathrm{t} \frac{u-k_\mathrm{e} \omega _\mathrm{m} }{R} \end{aligned}$$
(2)
$$\begin{aligned}&J_{t} {\dot{\omega }}_{t}=\tau _\mathrm{l}-B_\mathrm{t}{\omega _\mathrm{t}-\tau _\mathrm{f}-\tau _\mathrm{sp}-\tau _\mathrm{L}} \end{aligned}$$
(3)

where \(J_\mathrm{m}\) and \(J_\mathrm{t}\) are the moments of inertia of the motor and throttle valve, respectively, \(B_\mathrm{m} \) and \(B_\mathrm{t} \) are the viscous damping coefficients of the motor and throttle valve, respectively, \(\omega _\mathrm{m} \) and \(\omega _\mathrm{t} \) are angular velocities of the motor and throttle plate, satisfying \(\omega _\mathrm{m} =N\omega _\mathrm{t} \) with N defined as the gear ratio, \(k_\mathrm{t} \) and \(k_\mathrm{e} \) are the constants of motor torque and electromotive force, respectively, \(\tau _{a} \) is the motor torque, \(\tau _\mathrm{m} \) and \(\tau _{l} \) are the gear input and output torque, \(\tau _\mathrm{f} \) is the friction torque, \(\tau _{\mathrm{sp}} \) is the return-spring torque, \(\tau _\mathrm{L} \) is the load disturbance torque resulting from the effect of the air flow force applying on the throttle plate, R is the total resistance of the armature circuit, u is the control input voltage.

Although many types of friction exist in the motion of throttle plate including Coulomb, viscous and rising static friction, the following Coulomb friction model is only considered in this paper for the simplicity:

$$\begin{aligned} \tau _\mathrm{f} =F_{s} \hbox {sign}\left( {\omega _\mathrm{t} } \right) \end{aligned}$$
(4)

with \(F_{s}\) the Coulomb friction constant and \(\hbox {sign}\left( {\omega _\mathrm{t} } \right) \) the sign function expressed as:

$$\begin{aligned} \hbox {sign}\left( {\omega _\mathrm{t} } \right) =\left\{ {{\begin{array}{l@{\quad }l} 1&{} {\hbox { for }\omega _\mathrm{t} >0} \\ 0&{} {\hbox { for }\omega _\mathrm{t} =0} \\ -1&{} {\hbox { for }\omega _\mathrm{t} <0} \\ \end{array} }} \right. \end{aligned}$$
(5)

The throttle return-spring torque is given by the following nonlinear function

$$\begin{aligned} \tau _{\mathrm{sp}}= & {} \left\{ {{\begin{array}{l@{\quad }l} {\tau _{\mathrm{LH}} +k_{\mathrm{sp}} \left( {\theta _\mathrm{t} -\theta _{0} } \right) ,\qquad \theta _{0} <\theta _\mathrm{t} <\theta _\mathrm{max} } \nonumber \\ {-\tau _{\mathrm{LH}} -k_{\mathrm{sp}} \left( {\theta _{0} -\theta _\mathrm{t} } \right) ,\quad \theta _\mathrm{min} <\theta _\mathrm{t} <\theta _{0} } \nonumber \\ \end{array} }} \right. \nonumber \\= & {} \tau _{\mathrm{LH}} \hbox {sgn}\left( {\theta _\mathrm{t} -\theta _{0} }\right) \nonumber \\&+\,k_\mathrm{sp} \left( {\theta _\mathrm{t} -\theta _{0} } \right) ,\theta _\mathrm{min} <\theta _\mathrm{t} <\theta _\mathrm{max} \end{aligned}$$
(6)

where \(k_\mathrm{sp} \) is the spring elastic coefficient, \(\tau _\mathrm{LH} \) is the spring offset, \(\theta _\mathrm{t} \) is the opening angle of the ET plate and thus \({\dot{\theta }=\omega _\mathrm{t}}\), \(\theta _0 \) is the default opening angle of the throttle plate, which is also called the LH position, \(\theta _\mathrm{min} \) and \(\theta _\mathrm{max} \) are the minimum and maximum opening angles of the throttle plate, respectively.

Due to the fact that three gears exist in the ET valve in order to transfer the torque from the motor to the valve plate, the backlash nonlinearity between gears is generally expressed as

$$\begin{aligned} \tau _{l}(t)=\left\{ \begin{array}{ll} N\left( {\tau _\mathrm{m} -\delta } \right) ,&{} \quad {\dot{\tau }_\mathrm{m}}>0 \hbox { and }\; \tau _{l}=N(\tau _\mathrm{m}(t)-\delta ) \\ N\left( {\tau _\mathrm{m} +\delta } \right) ,&{} \quad {\dot{\tau }_\mathrm{m}}<0 \hbox { and }\; \tau _{l}=N(\tau _\mathrm{m}(t)+\delta )\\ \tau (t\_),&{}\quad \hbox {otherwise}\\ \end{array}\right. \nonumber \\ \end{aligned}$$
(7)

where \(\delta \) is the backlash distance, \(\tau _{l} \left( {t\_} \right) \) indicates that there is no change in \(\tau _{l} \left( t \right) \).

For the controller design, it is worth noting that the backlash model in (7) can be further described by [15]

$$\begin{aligned} \tau _{l} \left( t \right) =N\tau _\mathrm{m} \left( t \right) +d\left( {\tau _\mathrm{m} \left( t \right) } \right) \end{aligned}$$
(8)

where \(d(\cdot )\) is a bounded nonlinear function regarding \(\tau _\mathrm{m}(t)\) and \({\dot{\tau }_\mathrm{m}(t)}\) such that, \(| {d( {\tau _\mathrm{m}(t)})}|\le {\bar{d}} \), where \({\bar{d}}\) is the corresponding upper bound.

As a result, using (1) and (2) in (3) by eliminating \(\omega _\mathrm{m} \), the aforementioned dynamic equations of the ET control system can be simplified as

$$\begin{aligned} J_\mathrm{eq} {\dot{\omega }_\mathrm{t}}\left( B_\mathrm{eq}+\frac{k_\mathrm{t}k_\mathrm{e}}{R} N^{2}\right) \omega _\mathrm{t} +\tau _\mathrm{f}+\tau _\mathrm{sp}-\tau _{D}=\frac{Nk_{t}}{R}u\nonumber \\ \end{aligned}$$
(9)

where \(J_\mathrm{eq} \) and \(B_\mathrm{eq} \) are the equivalent inertia and damping coefficient of the ET system model, respectively, which are defined as

$$\begin{aligned}&J_\mathrm{eq} =N^{2}J_\mathrm{m} +J_\mathrm{t} \end{aligned}$$
(10)
$$\begin{aligned}&B_\mathrm{eq} =B_\mathrm{t} +N^{2}B_\mathrm{m} \end{aligned}$$
(11)

and \(\tau _{D} \) is the generalized bounded disturbance toque, which is given by

$$\begin{aligned} \tau _{D} =d\left( {\tau _\mathrm{m} } \right) -\tau _\mathrm{L} \end{aligned}$$
(12)

where \(\tau _{D}\) is bounded by

$$\begin{aligned} \left| {\tau _{D} } \right| \le \rho \end{aligned}$$
(13)

where \(\rho \) is a positive constant. Let

$$\begin{aligned}&a=\frac{J_\mathrm{eq} R}{Nk_{t} } \end{aligned}$$
(14)
$$\begin{aligned}&b=\frac{\left( {B_\mathrm{eq} +\frac{k_\mathrm{t} k_\mathrm{e} }{R}N^{2}} \right) R}{Nk_{t} } \end{aligned}$$
(15)
$$\begin{aligned}&\tau _\mathrm{fa} =\frac{F_{s} \hbox {sign}\left( {\omega _\mathrm{t} } \right) R}{Nk_{t} } \end{aligned}$$
(16)
$$\begin{aligned}&\tau _\mathrm{spa} =\frac{\left[ {\tau _\mathrm{LH} \hbox {sgn}\left( {\theta _\mathrm{t} -\theta _0 } \right) +k_\mathrm{sp} \left( {\theta _\mathrm{t} -\theta _0 } \right) } \right] R}{Nk_{t} } \end{aligned}$$
(17)
$$\begin{aligned}&\tau _\mathrm{Da} =\frac{\tau _{D} R}{Nk_{t} } \end{aligned}$$
(18)

We can rewrite (9) in the form of throttle position \(\theta _\mathrm{t} \) as

$$\begin{aligned} a{\ddot{\theta }}_{t}+b{\dot{\theta }}_{t}+\tau _\mathrm{fa}+\tau _\mathrm{spa}-\tau _\mathrm{Da}=u \end{aligned}$$
(19)

Taking into account the uncertainties, we express (14)–(17) as:

$$\begin{aligned}&a=a_0 +{\Delta a} \end{aligned}$$
(20)
$$\begin{aligned}&b=b_0 +{\Delta b} \end{aligned}$$
(21)
$$\begin{aligned}&\tau _\mathrm{fa} =\tau _\mathrm{fa0} +\Delta \tau _\mathrm{fa} \end{aligned}$$
(22)
$$\begin{aligned}&\tau _\mathrm{spa} =\tau _\mathrm{spa0} +\Delta \tau _\mathrm{spa} \end{aligned}$$
(23)

where \(a_0 =\frac{J_\mathrm{eq0} R_0 }{N_0 k_{t0} }\), \(b_0 =\frac{\left( {B_\mathrm{eq0} +\frac{k_{t0} k_{e0} }{R_0 }N_0^2 } \right) R_0 }{N_0 k_{t0} }\), \(J_\mathrm{eq0} \), \(B_\mathrm{eq0} \), \(N_0 \), \(k_{t0} \), \(k_{e0} \), and \(R_0 \) are the nominal values of the system parameters, \(\tau _\mathrm{fa0} =\frac{F_{s0} \hbox {sign}\left( {\omega _{t} } \right) R_0 }{N_0 k_{t0} }\), \(\tau _\mathrm{spa0} =\frac{\left[ {\tau _\mathrm{LH0} \hbox {sgn}\left( {\theta _{t} -\theta _0 } \right) +k_\mathrm{sp0} \left( {\theta _{t} -\theta _0 } \right) } \right] R_0 }{N_0 k_{t0} }\) are the nominal values of friction and return-spring torque disturbances, \(\Delta a\), \(\Delta b\), \(\Delta \tau _\mathrm{fa} =\Delta _1 \hbox {sign}\left( {\omega _{t} } \right) \), \(\Delta \tau _\mathrm{spa} =\left[ {\Delta _2 \hbox {sgn}\left( {\theta _{t} -\theta _0 } \right) +\Delta _3 \theta _{t} -\Delta _4 } \right] \), \(\Delta _{i} \left( {\hbox {i}=1,2,3,4} \right) \) denote the unknown bounded uncertainties of the system coefficients.

Now, (19) can be written as:

$$\begin{aligned} a_0 {\ddot{\theta }}_{t}+b_{0}{\dot{\theta }}_\mathrm{t}+\tau _\mathrm{fa0}+\tau _\mathrm{spa0}=u+\tau _\mathrm{lum} \end{aligned}$$
(24)

where \(\tau _{lum} \) represents the total lumped uncertainty of ET as follows:

$$\begin{aligned} \tau _\mathrm{lum} =-\Delta a{\ddot{\theta }}_\mathrm{t}-\Delta b{\dot{\theta }}_\mathrm{t}-\Delta \tau _\mathrm{fa}-\Delta \tau _\mathrm{spa}+\tau _\mathrm{Da} \end{aligned}$$
(25)

and \(\tau _\mathrm{lum} \) is bounded by a positive constant \(\eta \) such that

$$\begin{aligned} \left| {\tau _\mathrm{lum} } \right| \le \eta \end{aligned}$$
(26)

Thus, we have the following nominal system model:

$$\begin{aligned} a_0 {\ddot{\theta }}_\mathrm{t}+b_{0}{\dot{\theta }}_\mathrm{t}+\tau _\mathrm{fa0}+\tau _\mathrm{spa0}=u_\mathrm{nom} \end{aligned}$$
(27)

where \(u_\mathrm{nom} \) is the nominal control signal.

Remark 1

It is easily seen from (25) that, the lumped uncertainty of the ET system in (24) consists of the parameter uncertainties in the DC motor and the valve plate, and the estimation errors of the Coulomb friction torque and the throttle return-spring torque, and the uncertain disturbances including load torque and the gear backlash nonlinearity. In reality, it is difficult to obtain the bound information of the lumped uncertainty due to the high complexity of the uncertainty structure and thus it is essential that the uncertainty bound can be online estimated for the purpose of eliminating the effects of the lumped uncertainty.

3 Design of RASM control scheme

In this section, an RASM control scheme is designed for eliminating the effects of the system lumped uncertainty such that the ET plate angle can track the desired reference signal \(\theta _\mathrm{des} \) with a satisfactory performance, i.e., transient performance (settling time and overshoot), steady-state error, and robustness with respect to parameter variations and external disturbances.

First, the tracking error between the actual ET opening angle \(\theta _\mathrm{t} \) and the reference angle \(\theta _\mathrm{des} \) is defined as:

$$\begin{aligned} \varepsilon _{\theta } =\theta _\mathrm{t} -\theta _\mathrm{des} \end{aligned}$$
(28)

Given the system model in (24), we have the error dynamics of the closed-loop ET system as follows:

$$\begin{aligned} \ddot{\varepsilon }_{\theta }=-\frac{b_{0}}{a_{0}}{\dot{\theta }_\mathrm{t}}+\frac{u-\tau _\mathrm{fa0}-\tau _\mathrm{spa0}}{a_{0}} +\frac{\tau _\mathrm{lum}}{a_{0}}-\ddot{\theta }_\mathrm{des} \end{aligned}$$
(29)

In order to use the sliding mode technique in the control design for achieving the aforementioned performance indexes, we adopt the following PID-type sliding variable:

$$\begin{aligned} s={\dot{\varepsilon }}_{\theta }+{\hat{\varLambda }_{1}}\varepsilon _{\theta }+{\hat{\varLambda }_{2}}\int ^{t}_{0}{\varepsilon }_{\theta }(\tau )\hbox {d} \tau \end{aligned}$$
(30)

where \({\hat{\varLambda }_{1}}\) and \({\hat{\varLambda }_{2}}\) are two control gains to be online estimated by the corresponding adaptive laws.

Then, the RASM control design and the convergence analysis of the closed-loop error dynamics of the ET system are given in the following theorem.

Theorem 1

Considering the ET system in (24) with the error dynamics in (29), the output position tracking error \(\varepsilon _{\theta } \) will asymptotically converge to zero if the control law is designed such that

$$\begin{aligned} u= & {} \tau _\mathrm{fa0} +\tau _\mathrm{spa0} +\left( b_0 -a_0 {\hat{\varLambda }_{1}}\right) {\dot{\theta }}_{t}\nonumber \\&+\,a_{0}\left( \ddot{\theta }_\mathrm{des}+{\hat{\varLambda }_{1}}\dot{\theta }_\mathrm{des} +{\hat{\varLambda }_{2}}\theta _\mathrm{des}\right) \nonumber \\&-\,a_0 {\hat{\varLambda }_{2}} \theta _{t} -{\hat{\eta }} \hbox {sign}\left( s \right) -ks \end{aligned}$$
(31)

where k is a designed control parameter for the reaching phase of the sliding mode, \({\hat{\eta }}\) is the online estimated bound of the lumped uncertainty bound \(\eta \), \({\hat{\varLambda }_{1}}\) and \({\hat{\varLambda }_{2}}\) are two estimated control gains, according to the following update laws:

$$\begin{aligned}&{\dot{\hat{\eta }}}=\xi _1 \left| s \right| \end{aligned}$$
(32)
$$\begin{aligned}&{\dot{\hat{\varLambda }}_{1}}=-\xi _2 s\varepsilon _{\theta } \end{aligned}$$
(33)
$$\begin{aligned}&{\dot{\hat{\varLambda }}_{2}}=-\xi _3 s{\mathop {\int }\nolimits _0^{t}} \varepsilon _\theta \left( \tau \right) \hbox {d}\tau \end{aligned}$$
(34)

Proof

Consider a Lyapunov function \(V=\frac{a_0 }{2}s^{2}+\frac{\xi _1^{-1} }{2}\left( {\hat{\eta }-\eta } \right) ^{2}\) and taking the time derivative of V, we obtain

$$\begin{aligned} {\dot{V}}= & {} a_{0}s{\dot{s}}+\xi _{1}^{-1}(\hat{\eta }-\eta ){\hat{\eta }}\nonumber \\= & {} a_0 s\left( {\ddot{\varepsilon }}+{\hat{\varLambda }}_{1}{\dot{\varepsilon }}_{\theta }+\,{\hat{\varLambda }}_{2}{\varepsilon }_{\theta }+{\dot{\hat{\varLambda }}}_{1}{\varepsilon }_{\theta }\right. \nonumber \\&\left. +{\dot{\hat{\varLambda }}}_{2}\int \nolimits _{0}^{t}\varepsilon _{\theta }(\tau )\hbox {d} \tau \right) +\,\xi _1^{-1} \left( {\hat{\eta }} -\eta \right) {\dot{\hat{\eta }}}\nonumber \\= & {} a_0 s\left( -\frac{b_0 }{a_0}{\dot{\theta }}_{t}+\frac{u-\tau _\mathrm{fao}-\tau _\mathrm{spa0}}{a_{0}}+\frac{\tau _\mathrm{lum}}{a_{0}}\right. \nonumber \\&\left. -\,\ddot{\theta }_\mathrm{des}+{\hat{\varLambda }}_{1}{\dot{\varepsilon }}_{\theta } \right. \left. +\,{\hat{\varLambda }}_{2}{\varepsilon }_{\theta }\right) +a_0 s{\dot{\hat{\varLambda }}_{1}}\varepsilon _{\theta }\nonumber \\&+\,a_0 s{\dot{\hat{\varLambda }}_{2}} \int \nolimits _0^{t} \varepsilon _{\theta }(\tau )d {\tau } +\xi _1^{-1} ({\hat{\eta }-\eta })\mathop {\dot{\hat{\eta }}}\nonumber \\ \end{aligned}$$
$$\begin{aligned}= & {} s\Big [ -b_0 {\dot{\theta }}_{t}+{u-\tau _\mathrm{fao}-\tau _\mathrm{spa0}}+{\tau _\mathrm{lum}}-{a_{0}}\ddot{\theta }_\mathrm{des} \nonumber \\&+\,a_0{\hat{\varLambda }}_{1}\left( {\dot{\theta }}_{t}-{\dot{\theta }}_\mathrm{des}\right) \nonumber \\&+\,a_0{\hat{\varLambda }}_{2}\left( {\theta }_{t}-{\theta }_\mathrm{des}\right) \Big ] \xi _{1}^{-1}({\hat{\eta }}-\eta ){\dot{\hat{\eta }}}\nonumber \\&+\,a_0 s{\dot{\hat{\varLambda }}_{1}}\varepsilon _{\theta } +a_0 s{\dot{\hat{\varLambda }}_{2}} \int \nolimits _0^{t} \varepsilon _{\theta }(\tau )d {\tau }\nonumber \\= & {} s\left[ \left( {-b_0 +a_0{\hat{\varLambda }}_{1}}\right) {\dot{\theta }}_{t} -a_0\left( {\ddot{\theta }}_\mathrm{des}+{\hat{\varLambda }}_{1} {\dot{\theta }}_\mathrm{des}\right. \right. \nonumber \\&\left. \left. +\,{\hat{\varLambda }}_{2}{\theta }_\mathrm{des}\right) \right. \left. +\,a_0 {\hat{\Lambda }}_{2} \theta _t +u-\tau _\mathrm{fa0} -\tau _\mathrm{spa0}\right. \nonumber \\&\left. +\,\tau _\mathrm{lum} \right] +\xi _1^{-1} \left( {\hat{\eta }-\eta } \right) {\dot{\hat{\eta }}}\nonumber \\&+\,a_0 s{\dot{\hat{\Lambda }}_{1}} \varepsilon _\theta +a_0 s{\dot{\hat{\Lambda }}_{2}} \int \nolimits _{0}^{t} \varepsilon _\theta \left( \tau \right) \hbox {d}\tau \nonumber \\= & {} -{\hat{\eta }} \left| s \right| +\tau _\mathrm{lum} s-ks^{2}+\xi _1^{-1} \left( {\hat{\eta }-\eta } \right) \dot{\hat{\eta }}\nonumber \\&+\,a_{0} s{\dot{\hat{\Lambda }}_{1}} \varepsilon _\theta +\,a_0 s{\dot{\hat{\Lambda }}_{2}} \int \nolimits _{0}^{t} \varepsilon _\theta \left( \tau \right) \hbox {d}\tau \nonumber \\= & {} -{\hat{\eta }} \left| s \right| +\tau _\mathrm{lum} s-ks^{2}+\xi _1^{-1} \left( {{\hat{\eta }} -\eta } \right) \xi _1 \left| s \right| \nonumber \\ \end{aligned}$$
$$\begin{aligned}&-\,a_0 \xi _2 s^{2}\varepsilon _\theta ^2 -a_0 \xi _3 s^{2}\left( {\mathop \int \nolimits _0^t \varepsilon _\theta \left( \tau \right) \hbox {d}\tau } \right) ^{2}\nonumber \\= & {} \tau _\mathrm{lum} s-\eta \left| s \right| -ks^{2}-a_0 \xi _2 s^{2}\varepsilon _\theta ^{2} \nonumber \\&-\,a_0 \xi _3 s^{2}\left( {\int \nolimits _{0}^{t} \varepsilon _\theta \left( \tau \right) \hbox {d}\tau } \right) ^{2}\nonumber \\&\le -\left| s \right| \left( {\eta -\left| {\tau _\mathrm{lum} } \right| } \right) -ks^{2}-a_0 \xi _2 s^{2}\varepsilon _\theta ^{2}\nonumber \\&\quad -\,a_0 \xi _3 s^{2}\left( {\int \nolimits _{0}^{t} \varepsilon _\theta \left( \tau \right) \hbox {d}\tau } \right) ^{2}\nonumber \\&\le -\sigma \left| s \right| <0\qquad \hbox { for }\left| s \right| \ne 0 \end{aligned}$$
(35)

where \(\sigma \) is a positive constant that can always be found satisfying \(\eta -\max \left\{ {\left| {\tau _\mathrm{lum} } \right| } \right\} \ge \sigma \). Expression (35) ensures that the sliding variable s reaches the sliding mode surface \(s=0\) in a finite time [19]. Thus, the error dynamics of the closed-loop ET system exponentially converges to zero on the sliding mode surface.

Remark 2

It has been seen from the control law in (31) that the control parameters k and \(\xi _{i} \left( {i=1,2,3} \right) \) play an important role in ensuring a remarkable control performance. Thus, the control parameters should be properly chosen and the selection criteria are given as follows: (i) The parameter k is designed for controlling the convergence of the sliding variable in the reaching phase, however, it cannot be too large in order to avoid the control saturation. (ii) It is observed from the above stability proof that the adaption rates \(\xi _{i} \left( {i=1,2,3} \right) \) determine the closed-loop convergence performance and thus should be carefully selected.

Remark 3

It should be noted that the pre-determined two constant gains \({\hat{\varLambda } _{1}} \) and \({\hat{\varLambda }_{2}} \) in [3] may not be optimal for the both cases of step and sinusoidal reference inputs, which may increase the oscillations and introduce high-frequency unmodeled dynamics in the ET control system. In addition, the well-tuned gains can ensure an acceptable tracking performance in normal operating conditions. However, once large parameter variations and nonlinearities of ET systems occur, the control gains are no longer optimal such that both the robustness and the tracking performance will be deteriorated. As a result, we adopt the adaptive laws for updating the variable gains in order to avoid the above issues.

Fig. 2
figure 2

Control diagram of ET system

Full size image

Remark 4

Due to the signum function \(\hbox {sign}\left( s \right) \) included in the RASM control in (31), the chattering phenomenon occurs in the control signal. This chattering issue can be tackled by using the following boundary-layer RASM (BRASM) control method:

$$\begin{aligned} u= & {} \tau _\mathrm{fa0} +\tau _\mathrm{spa0} +\left( {b_0 -a_0 {\hat{\varLambda _{1} }}}\right) {\dot{\theta }}_{t}+a_0\left( {\ddot{\theta }}_\mathrm{des}+{\hat{\varLambda _{1}}}{\dot{\theta }}_\mathrm{des}\right. \nonumber \\&\left. +\,{\hat{\varLambda _{2}}\theta _\mathrm{des}}\right) -a_0 {\hat{\varLambda _{2}}}\theta _{t} -{\hat{\eta }} \hbox { sat }\left( s \right) -ks \end{aligned}$$
(36)

where \(\hbox {sat}\left( s \right) \) is the saturation function defined as:

$$\begin{aligned} \hbox {sat}\left( s \right) =\left\{ \begin{array}{l@{\quad }l} \frac{s}{\xi _4 }&{} \hbox {for}\left| s \right| <\xi _{4} \\ \hbox {sign}\left( s \right) &{} \hbox {for}\left| s \right| \ge \xi _{4} \\ \end{array} \right. \end{aligned}$$
(37)

where \(\xi _{4} >0\) denotes the boundary-layer thickness ensuring that s is bounded by \(\xi _{4} \). Please note that, although the closed-loop error dynamics of the ET system with the BRASM control in (36) cannot have a zero-error convergence, through the appropriate selection of the positive constant \(\xi _{4} \), the tracking error remains ultimately bounded within a neighborhood of the sliding mode surface, which satisfies the tracking precision requirement in practice.

The complete control diagram of the ET system is summarized in Fig. 2 and the tracking performance of the proposed RASM control will be validated by simulation studies in the following section.

4 Simulation results and discussion

In order to verify the efficacy and advantages of the proposed RASM control for the ET system, a few computer simulations are carried out in comparison with the traditional PID control and the \(H_{\infty }\) control, respectively.

Table 1 Nominal parameters of ET system [15]
Full size table
Fig. 3
figure 3

Control performance of RASM control in Case 1. a Tracking performance. b Tracking error. c Control voltage. d Lumped uncertainty and its estimated upper bound. e Estimated gains \({\hat{\Lambda }_{1}}\) and \({\hat{\Lambda }_{2}}\). f Sliding variable s and its first derivative. g First derivative of sliding variable at time 2 s (zoom in). h Changing rate of Lyapunov function V

Full size image

4.1 Simulation environment and parameter setting

In practical applications, since the ET system often experiences sudden changes from large to small opening angles or vice versa, parametric variations and external disturbances. Thus, we adopt the following two cases in simulation (20 s) for demonstrating the validity and excellent performance of the proposed RASM control.

Case 1 Note that the reference command \(\theta _{des} \) is a combination of step signals with different amplitudes through the LH position \(\theta _0 \) such that the fast transient performance can be evaluated. In addition, the external load disturbance \(\tau _L =0.1\sin \left( {2\pi t} \right) \) N m and the 10 % parametric variations in (14)–(17) are both considered.

Case 2 The reference command is a periodical sinusoidal signal \(\theta _\mathrm{des} =35+5\hbox {sin}\left( {\pi t} \right) \,(^{\circ })\). The external load disturbance \(\tau _\mathrm{L} =0.1\sin \left( {2\pi t} \right) \) N m and the 10 % parametric variations in (14)–(17) are also considered when simulation starts in order to test the control robustness.

For the comparison purpose, the PID control with feed-forward compensation [3] and the \(H_{\infty } \) control laws [30] are given as follows:

$$\begin{aligned}&u_\mathrm{PID} =-5e-1.2{\mathop {\int } \nolimits _0^{t}} e\hbox {d}\tau -0.1{\dot{e}}+\tau _\mathrm{fa0}+\tau _\mathrm{spa0} \end{aligned}$$
(38)
$$\begin{aligned}&u_{H_\infty } =0.15{\ddot{\theta }}_\mathrm{des}+0.5{\dot{\theta }}_{t}-14e-0.6{\dot{e}} \end{aligned}$$
(39)

Note that the \(H_{\infty } \) controller is designed optimally for minimizing the effects of parameter uncertainties and disturbances and achieving a bounded tracking error. The values of the nominal parameters of the ET system in (24) are listed in Table 1 [15]. The parameters of the proposed RASM control scheme for the ET system are chosen as: \(k=0.3,\xi _{1} =0.0063,\xi _{2} =\xi _{3} =0.001,\xi _{4} =0.3\). The initial values of the estimated parameters are set as \({\hat{\varLambda _{1}}} \left( 0 \right) =10\), \({\hat{\varLambda _{2}}} \left( 0 \right) =0.2, {\hat{\eta }} \left( 0 \right) =0.001.\) The sampling period is chosen as \(\Delta T=0.005\hbox {s}\). Then, the RASM control law in (31) is given by:

$$\begin{aligned} u_\mathrm{RASM}= & {} \tau _\mathrm{fa0} +\tau _\mathrm{spa0} +\left( {0.616-0.063{\hat{\varLambda }_{1}}}\right) {\dot{\theta }_{t}}\nonumber \\&+\,0.063\left( {\ddot{\theta }}_\mathrm{des}+{\hat{\varLambda }_{1}}{\dot{\theta }}_\mathrm{des}+{\hat{\varLambda }_{2}}{\theta }_\mathrm{des}\right) \nonumber \\&-\,0.063{\hat{\varLambda }_{2}}{\theta }_{t}-{\hat{\eta }}\hbox {sign}\left( {s}\right) -0.15\,\hbox {s} \end{aligned}$$
(40)

where \({\hat{\varLambda }_{1}},{\hat{\varLambda }_{2}}, \hbox {and} \,{\hat{\eta }} \) are given in (32)–(34).

Fig. 4
figure 4

Control performance of PID control in Case 1. a Tracking performance. b Tracking error. c Control voltage

Full size image
Fig. 5
figure 5

Control performance of \(H_{\infty } \) control in Case 1. a Tracking performance. b Tracking error. c Control voltage

Full size image

4.2 Simulation results

Figure 3 shows the throttle tracking performance of the proposed RASM control under set-point regulation in Case 1. It can be seen from Fig. 3a, b that, the actual throttle opening angle is able to closely track the reference command, with the settling time around 0.4 s and almost zero steady-state error during the whole period, which perfectly meets the requirement of both the transient and steady-state tracking. Moreover, the online estimated bound of the lumped uncertainty \({\hat{\eta }} \), and the control gains \({\hat{\Lambda }_{1}} \) and \({\hat{\Lambda }_{2}} \) are shown in Fig. 3d, e, respectively. It should be noted that all of the three parameters are adaptively adjusted in Lyapunov sense for ensuring the closed-loop stability and it is unnecessary for them to converge to their real values. It is seen from Fig. 3f, g that, at each throttle change period, the sliding variable s and its changing rate are driven by the proposed control to converge to zero at a very fast convergence rate such that the closed-loop stability can be guaranteed. In particular, it is noted from Fig. 3g that the changing rate of the sliding variable \({\dot{s}}\) at time 2 s is negative, which keeps consistency with the deceasing trend of the sliding variable shown in Fig. 3f. The cases of \({\dot{s}}\) at time 10 and 15 s are similar to the one at time 2 s and thus here is omitted. In addition, Fig. 3h shows that the changing rate of the Lyapunov function V is always non-positive, indicating the stability of the closed-loop error dynamics under the changes of the reference commands, parameter variations and external disturbances.

Fig. 6
figure 6

Control performance of RASM control in Case 2. a Tracking performance. b Tracking error. c Control voltage. d Lumped uncertainty and its estimated upper bound. e Estimated gains \({\hat{\Lambda }_{1}}\) and \({\hat{\varLambda }_{2}}\). f Sliding variable s and its first derivative. g Changing rate of Lyapunov function V

Full size image

For the comparison purpose, Figs. 4 and 5 show the time responses of the throttle opening angles and tracking errors under the PID and \(H_{\infty } \) controllers in Case 1. We can see that although the PID control achieves the similar steady-state error to the proposed control except the starting period (2 s), the settling time of 1 s is more than double the time by the proposed control. For the \(H_{\infty } \) control, although its setting time is smaller than the one of the proposed control and PID control, it has about \(2^{\circ }\) steady-state error when the throttle operates from \(40^{\circ }\) to \(70^{\circ }\).

Fig. 7
figure 7

Control performance of PID control in Case 2. a Tracking performance. b Tracking error. c Control voltage

Full size image
Fig. 8
figure 8

Control performance of \(H_\infty \) control in Case 2. a Tracking performance. b Tracking error. c Control voltage

Full size image

In order to test the robustness of the three controllers under sinusoidal tracking purpose, Figs. 6, 7 and 8 demonstrate the tracking performance of the closed-loop ET system for sinusoidal reference angle under parameter variations and external disturbances in Case 2. It is observed that the tracking precision with the proposed RASM control in Fig. 6 is much better than the ones with the PID and \(H_{\infty } \) controllers in Figs. 7 and 8. We can see that the proposed control achieves the smallest steady-state tracking error bound (TEB) of 0.4 deg, while the values of TEB of the PID and \(H_{\infty } \) control are around \(1.0^{\circ }\) and \(1.1^{\circ }\), respectively. In addition, the estimated lumped uncertainty bound \({\hat{\eta }} \), and the control gains \({\hat{\Lambda }_{1}} \) and \({\hat{\Lambda }_{2}}\) are all adaptively adjusted as the sliding mode parameters in the sense that the sliding variable can converge to zero and after that, they become certain constants to guarantee the closed-loop stability condition. Due to the fact that proposed RASM control with the adaptive laws for the lumped certainty bound and the two control gains can eliminate the effects of the parametric variations and external disturbances on the throttle tracking performance, the proposed control is thus capable of achieving a stronger robustness against uncertainties than the ones of the conventional PID and \(H_{\infty } \) control methods.

5 Experimental results

In this section, in order to verify the effectiveness of the proposed control, we carry out a series of DC motor-based hardware-in-loop experiments. It is seen from Fig. 9 that, a brushless DC motor is connected with a gearhead and an encoder installed inside the motor is used to provide with the angular velocity and position information of the motor shaft.

Although there are no mechanical loads of the throttle valve plate and gears included due to the hardware limitation, the robust control performance of the proposed control can still be validated by imposing an equivalent electronic voltage signal to the system once the experiments start, as \(V_{\tau _{L} } =0.45\sin \left( {0.2t} \right) \).

Fig. 9
figure 9

Image of hardware-in-loop experimental system

Full size image
Table 2 Control parameters of the proposed and PID control in experiments
Full size table
Fig. 10
figure 10

Control performance of RASM control at Case 1 in experiments. a Tracking performance. b Tracking error. c Control voltage. d Estimated upper bound of lumped uncertainty. e Estimated gains \({\hat{\varLambda }_{1}}\) and \({\hat{\Lambda }_{2}}\)

Full size image
Fig. 11
figure 11

Control performance of PID control at Case 1 in experiments. a Tracking performance. b Tracking error. c Control voltage

Full size image
Fig. 12
figure 12

Control performance of RASM control at Case 2 in experiments. a Tracking performance. b Tracking error. c Control voltage. d Estimated upper bound of lumped uncertainty. e Estimated gains \({\hat{\Lambda }_{1}}\) and \({\hat{\Lambda }_{2}}\)

Full size image
Fig. 13
figure 13

Control performance of PID control at Case 2 in experiments. a Tracking performance. b Tracking error. c Control voltage

Full size image

Please note that the control algorithms are implemented on a Freescale microcontroller (MCU) board (MC9S12XEP100) using the “C” languages using CodeWarrior Development Studio V5.1 from Metrowerks incorporated in a laptop and downloaded to the MCU. The control voltage is given in the form of pulse width modulation (PWM) with the frequency of 3.2 kHz. The sampling period is chosen as 10 ms.

In this section, we carry out the experiments under the proposed control and the PID control only for comparison and the corresponding parameters are listed in Table 2.

The experimental results of the two controllers for Cases 1 and 2 are shown in Figs. 10, 11, 12 and 13. It is observed that although the PID control presents a smaller overshoot than the proposed control at Case 1, the smaller steady-state error of the proposed control is achieved compared with the PID counterpart particularly from 12 to 15 s. Moreover, the proposed control exhibits an apparently smaller tracking error compared with the PID control under the disturbances at Case 2. It thus indicates that the proposed RASM control performs very well and behaves with a strong robustness against the changes of the reference commands and the external disturbances.

It should be noted from Fig. 12 that, the chattering occurring in the first 0.5 s is caused by the adaption process of the proposed RASM control in order to alleviate the effects of the external disturbance. After that, it is clearly seen that the control smoothness can be guaranteed until the experiments stop.

6 Conclusion

In this paper, the RASM control scheme for automotive ET systems has been proposed. It has been demonstrated that the proposed control can achieve a fast and robust tracking performance. Both the lumped uncertainty bound and the control gains are adaptively adjusted using update laws such that the requirements of the information of the uncertainty and control gains can be released. Both the simulation and experimental results have verified the validity and the excellent tracking performance of the proposed control, in comparison with PID and \(H_{\infty } \) controllers. The future research work to design a super-twisting sliding mode control scheme with an uncertainty observer for ET systems is under the authors’ investigation.