1 Introduction

Most of the spatiotemporal systems such as ecological, biological, physical-chemical systems can present regular spatial patterns due to internal competition and collaboration, or under appropriate external forcing as well [1–12]. In ecological systems, species enjoy their lives by improving its adaption to circumstance. However, the ecosphere could be destructed badly when disasters such as infectious disease, earthquake, bushfire and human destruction invade the system abruptly. In a harmonious society, the social behaviors are regulated by laws and social norms, but rumor spreading in more large area could cause panic in society and unpredictable accidents could occur. Therefore, it is important to find warning information from slight changes before the emergence of collapse. As a result, some premonitions from natural world often give us some important clues before the emergence of disasters such as earthquake, flood, typhoon, forest fire, even rumor spreading and disease in neuronal system. The normal rhythm of heart is dominated by electric signals emitted from the atrionector and also associated with the continuous shrinkage and relaxation of the heart. The spatial distribution of membrane potentials of cells in cardiac tissue can support spiral waves, which is associated with heart disease as arrhythmia [13–15]; furthermore, the breakup of spiral wave in heart tissue counts for the potential mechanism of ventricular fibrillation [16–18] that causes sudden death of heart. Indeed, spiral waves are also observed in the cortex, and these ordered waves seem to play a role in regulating the collective behaviors of neurons as a pacemaker in local area [19–21]. As it is well known, spiral wave is self-sustained, and it keeps certain robustness to external forcing and even noise, and breakup also occurs when the wave profile is badly damaged under strong noise or suppressed by continuous target waves [22–25].

The realistic neuronal system is composed of a large number of neurons, and neurons show much diversity in function and geometry. Neurons can select different types of coupling, realized by chemical synapse or electric synapse [26–28], so that signals can be propagated effectively. Some neurons have developed certain specific synapses connected to their somas, and this type of synapses is called as autapse [29]; autapse can excite and also suppress the electric activity of isolated neuron by switching the feedback modes (negative or positive). Particularly, the collective behaviors could be regulated by developing target wave or spiral wave induced by autapse distribution [30, 31] in the network; thus, some regularity and ordered states are formed. This topic is an investigation about the transition from normal state to collapse in neuronal system induced by intrinsic collapse in parameter. For a well-known example, in case of temulence, or nerve agent poisoning, more and more ion channels are poisoned and blocked; thus, the normal electric activities of neurons are interrupted greatly. In this paper, the transition of regularity of neuronal network dominated by stable rotating spiral wave is investigated by introducing continuous diffusive damage [32, 33] in local area of the network, and the local kinetics of node is described by Hindmarsh–Rose neuron [34]. In our studies, four nodes placed symmetrically in the network are monitored, and statistical correlations from sampled time series for membrane potentials are calculated to discern the occurrence of collapse of the network. One controllable parameter in a local area is changed in a jump shift to produce the collapse in parameter, and the area size in collapse is diffused in random way.

2 Model and scheme

The dynamical equations for the network of Hindmarsh–Rose neurons in two-dimensional space with nearest-neighbor connection [35, 36] could be described as follows

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{dx_{ij} }{dt}=y_{ij} -ax_{ij} ^{3}+bx_{ij} ^{2}-z_{ij} +I_{ext} \\ \quad +\,D(x_{i+1j} +x_{i-1j} +x_{ij+1} +x_{ij-1} -4x_{ij} ) \\ \frac{dy_{ij} }{dt}=c-dx_{ij} ^{2}-y_{ij} \\ \frac{dz_{ij} }{dt}=r[s(x_{ij} -\lambda _0 )-z_{ij} ] \\ \end{array}} \right. \end{aligned}$$
(1)

The local kinetics of the network is described by the three-variable Hindmarsh–Rose model for each node, and the subscript i, j denotes the node position in the network. The variables x, y, z represent the membrane potential, recovery variable associated with slow current and the adaption current, respectively. The term \(I_\mathrm{ext}\) defines the external forcing current, and D measures the coupling intensity between adjacent neurons. For an isolate neuron model, this model can show different electric modes such as quiescent, spiking and bursting even chaotic by just increasing the external forcing current carefully when parameters are fixed at \(a=1.0, b=3.0, c=1.0, d=5.0, s=4.0, r=0.006,\lambda _{0}=-1.6\). Furthermore, the collective behaviors of network could also be changed by the external forcing due to the change in excitability. For simplicity, the external forcing current is fixed at \(I_\mathrm{ext}=1.315\) for each node and the distribution for initial values is set as wedge-shaped type. As a result, a stable rotating spiral wave could be generated to occupy the network completely. The network shows distinct periodicity and regularity when a stable rotating spiral wave occupies the network completely. The process of diffusive collapse is processed as follows

  1. (1)

    Parameter a (or c) for certain node is suddenly changed to another value;

  2. (2)

    Then the adjacent nodes changed their parameters in the similar way; then more and more nodes are included into the tainted area with irregular boundary;

  3. (3)

    When the number of destructed or tainted nodes reaches a fixed threshold about 10,000, the diffusive area is terminated in the network that contains 40,000 nodes;

  4. (4)

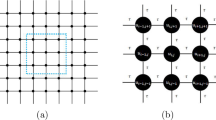
    Four nodes with symmetric distribution in the network are monitored to find the time series for membrane potentials, and the diagram is shown in Fig. 1. The node position for the four nodes is marked as node 1:(50, 100), node 2:(100,50), node 3:(150,100), node 4:(100, 150), and their membrane potentials are denoted as x1, x2, x3, x4, respectively.

  5. (5)

    To discern the source of collapse node, statistical correlation functions for the four nodes are defined in Eq. (2) by using sampled time series. Where \(k_{0}\) is the gain value to enlarge the exponential error between any two nodes, for simplicity, \(k_{0}= \) exp(5) is used.

$$\begin{aligned} \left\{ {\begin{array}{l} m_{41} =k_0 \exp (x_4 -x_1 ) \\ m_{42} =k_0 \exp (x_4 -x_2 ) \\ m_{43} =k_0 \exp (x_4 -x_3 ) \\ m_{32} =k_0 \exp (x_3 -x_2 ) \\ m_{31} =k_0 \exp (x_3 -x_1 ) \\ m_{21} =k_0 \exp (x_2 -x_1 ) \\ \end{array}} \right. \end{aligned}$$
(2)

It finds that the statistical function could be sensitive to slight changes in membrane potentials when abnormality or damage occurs on the area close to the monitoring nodes.

Fig. 1
figure 1

Diagram for the two-dimensional network of coupled oscillators; four nodes (red points) are marked as monitoring points; time series for membrane potentials are recorded as x1 for node (50, 100), x2 for node (100, 50), x3 for node (150, 100), x4 for node (100, 150). (Color figure online)

Full size image

3 Numerical results and discussion

In the numerical section, \(200\times 200\) neurons are placed on nodes in the square array uniformly, and nodes are coupled with nearest-neighbor connection type. The Euler forward algorithm is used for numerical calculation with no-flux boundary condition being used for the network under appropriate time step. For higher exactness, the fourth-order Runge–Kutta algorithm should be used for stable convergence, but it could cost longer period for calculation in network problems. To our experience, Euler forward algorithm is good enough for convergence calculation by carefully selecting the time step but should be verified by using algorithm of Runge–Kutta with fourth order. The coupling intensity is fixed at \(D=2\), external forcing current is selected as \(I_\mathrm{ext}=1.315\), time step is \(h=0.01\), and the calculating period is about 3000 time units. For simplicity, the time series of sampled membrane potentials will be represented by symbol V instead of x. In study of pattern selection and control, the spatial distribution of any observable variables could be used to plot snapshots; thus, the pattern could be discerned and observed. In this paper, the variable x (membrane potential) will be used to present the spatial distribution (snapshots) in the network.

3.1 Generation of stable rotating spiral wave

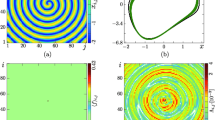
It is important to generate a stable rotating spiral wave by selecting specific initial values, and the developed spiral wave can dominate the network to keep periodicity and regularity in the network. Similar to the case for reaction–diffusion system for selecting wedge-shaped initial values, specific initial values are selected as \((2.0,-1.0, 0)\) for nodes \((i=94{:}96, j=1{:}100)\) and \((-1.0, 2.0, 2.0)\) for nodes \((i=97{:}99, j=1{:}100)\); the other nodes can be endowed with random value or fixed value as well, and the developed pattern can be illustrated in Fig. 2.

Fig. 2
figure 2

Development of spiral waves by using wedge-shaped initial values. The other nodes are endowed with values for equilibrium point \((-1.31742,-7.67799, 1.13032)\) for (a), (b), and random values for (c), (d); \(t=10{,}000\) time units (a), (c), \(t=20{,}000\) time units for (b), (d). The variable x is used in these snapshots to present the distribution of membrane potential of neurons on different nodes, and the color difference discerns the difference between membrane potentials

Full size image

It finds that spiral waves can be developed in the network when wedge-shaped initial values are used, and the network could be occupied by perfect spiral wave when other nodes are selected with homogeneous values. Furthermore, the growth of the spiral wave is plotted in Fig. 3.

Fig. 3
figure 3

Development of spiral wave driven by wedge-shaped initial values, and other nodes are selected by \((-1.31742,-7.67799, 1.13032)\). For \(t=500\) (a), 800 (b), 2000 time units (c)

Full size image

It confirms that the spiral in the center begins to grow up and occupy more area of the network with increasing calculating time. Furthermore, artificial damage or abnormality with certain diffusive velocity will be considered, and the transition of spiral wave is detected. It is thought that the breakup of spiral wave and complete collapse of the network could be detected beforehand.

3.2 Diffusion of the emergence of damage

In a realistic system, natural disaster often emerges suddenly, and then, it begins to diffuse the damage with certain velocity. As a result, it is reasonable to reproduce this process by changing certain parameter sharply in the theoretical model. For simplicity, we investigate the case for jump in parameter a, c in Eq. (1). It supposes that the size of the damaged area is increased with a period about 0.3, or the adjacent neurons close to the damaged area will be included in the damaged area within 0.3 time units. For the first case, parameter a in certain area is switched from a=1 to \(a=0.4\) (Fig. 4a), \(a=0.6\) (Fig. 4b), \(a=0.8\) (Fig. 4c) at \(t=900\) time units, and the results are plotted in Figs. 4.

Fig. 4
figure 4

The developed spatial pattern at \(t=3000\) time units when the parameter a is switched at \(t=900\) time units from \(a=1\) to \(a=0.4\) for (a), \(a=0.6\) for (b), \(a=0.8\) for (c)

Full size image
Fig. 5
figure 5

Diffusion of damage area (kermesinus) at \(t=1080\) time units when the parameter a is switched at \(t=900\) time units from \(a=1\) to \(a=0.4\) for (a), \(a=0.6\) for (b), \(a=0.8\) for (c). The blue area denotes the area out of collapse. (Color figure online)

Full size image

It is found that the profile of the diffusive damage area is much dependent on the diversity in parameter a even if the damage area is expanded with the same velocity or rating. When the ordered spiral wave is invaded by the diffusive damage area, the wave front is blocked and thus breakup of spiral wave occurs in local area. The ordered state is destructed more seriously, and more areas step into disorder state by further increasing the calculating time and damage area. It is also confirmed that the perfect spiral wave keeps robustness to the damage invasion when the parameter a is slightly switched from the normal value \(a=1\). The competition between spiral wave and diffusive damage is shown in Fig. 6, and the diffusion of damaged area is shown in Fig. 7.

Fig. 6
figure 6

Competition and evolution of spiral wave versus damage diffusion, for \(t=800\) (a), 1080 (b), 1680 (c), 1980 (d), 2580 (e), 2880 time units (f); the parameter a is set as 0.8 in the damage area

Full size image
Fig. 7
figure 7

Diffusion of damage area for parameter a, for \(t=960\) (a), 1020 (b), 1080 (c), 1200 time units (d); the parameter a is set as 0.8 in the damage area. The blue area denotes the area out of collapse. (Color figure online)

Full size image

According to the results in Figs. 6, and 7, the developed spiral wave keeps alive and shows great robustness to the diffusive invasion of damage with increasing the damage size. Furthermore, it also investigated the case that the damage degree is increased by setting parameter a with large diversity from normal value \(a=1\), and the results are shown in Figs. 8, and 9.

Fig. 8
figure 8

Competition and evolution of spiral wave versus damage diffusion, for \(t=800\) (a), 1080 (b), 1680 (c), 1980 (d), 2580 (e), 2880 time units (f); the parameter a is set as 0.4 in the damage area

Full size image
Fig. 9
figure 9

Diffusion of damage area for parameter a, for \(t=960\) (a), 1020 (b), 1080 (c), 1200 time units (d); the parameter a is set as 0.4 in the damage area. The blue area denotes the area out of collapse. (Color figure online)

Full size image

It is confirmed that damage area expands its size outwardly and seldom invades the untouched area by preferring none of the orientation when damage degree is high (large diversity from normal parameter \(a=1\)), and the wave propagation and regularity are destructed greatly. As a result, a breakup of spiral wave occurs. However, in the case of small diversity from normal parameter \(a=1\) (weak damage or invasion), the damage area was used to prefer certain orientation along narrow area; thus, the spiral wave keeps robustness well to the invasion. In our studies, it supposes that the damage area begins in the area close to the node 2, and the sampled time series for membrane potentials are calculated in Fig. 10, and the statistical correlation function is calculated in Fig. 11.

Fig. 10
figure 10

Time series for sampled membrane potentials at \(a=0.8\) (damage areas), for node 1 (a), node 2 (b), node 3 (c) and node 4 (d)

Full size image

It is found that the sampled time series for the nodes close to the damage area can respond to the damage due to the coupling connection by discerning the time series of membrane potentials for the four monitoring nodes. The sampled time series show distinct transition in the electrical modes when the monitored nodes are invaded. It is also interesting to detect the transition in the statistical correlation functions, and the results are shown in Fig. 11.

Fig. 11
figure 11

Time series for statistical correlation function between two nodes at \(a=0.8\), for \(\mathrm{m}_{41 }\) (a), \(\mathrm{m}_{42 }\) (b), \(\mathrm{m}_{43 }\) (c), \(\mathrm{m}_{32 }\) (d), \(\mathrm{m}_{31 }\) (e), \(\mathrm{m}_{21 }\) (f)

Full size image

It is confirmed that the statistical correlation function \((\mathrm{m}_{42}, \mathrm{m}_{32, }\mathrm{m}_{21})\) associated with node 2 shows sensitivity to the damage invasion when the damage effect is considered at \(t=900\) time units, while the time series for the other three nodes show weak response and slight transition after long time delay period. Indeed, most of the correlation functions could detect transition induced by collapse when the collapse is diffused with long enough time. In practical way, it is better to find distinct transition in correlation functions at the time as early as possible. The prediction also depends on the coupling intensity because signal can be propagated with higher speed when stronger coupling intensity is used. It indicates that the damage area could be detected quickly by analyzing the statistical correlation functions. Furthermore, slight damage invasion, which parameter a associated with damage area selected other values with slight shift diversity from the normal parameter \(a=1\), could also be detected by further increasing the gain in statistical correlation functions in Eq. (2).

It is also interesting to investigate the case that the damage or abnormality is described by diversity in parameter c, and the results are shown in Fig. 12.

Fig. 12
figure 12

The developed spatial pattern invaded by damage at \(t=3000\) time units when the parameter c is switched at \(t=900\) time units from \(c=1\) to \(c=0.4\) for (a), \(c=0.6\) for (b), \(c=0.8\) for (c)

Full size image
Fig. 13
figure 13

Diffusion of damage area (kermesinus) at \(t=1080\) time units when the parameter c is switched at \(t=900\) time units from \(c=1\) to \(c=0.4\) for (a), \(c=0.6\) for (b), \(c=0.8\) for (c). The blue area denotes the area out of collapse. (Color figure online)

Full size image

The results in Fig. 13 show that the damaged area increases its size by expanding the boundary in random way, and the regularity and periodicity of the network are continuously invaded. Distinctly, the dominated and perfect spiral wave is destroyed when the damage effect is described by diversity in parameter c between the untouched and damaged area. Furthermore, the transition of spiral wave induced by continuous invasion is plotted in Fig. 14, and the size growth of damaged area is shown in Fig. 15.

Fig. 14
figure 14

Competition and evolution of spiral wave versus damage diffusion, for \(t=800\) (a), 1080 (b), 1680 (c), 1980 (d), 2580 (e), 2880 time units (f); the parameter c is set as 0.8 in the damage area from \(t=900\) time units

Full size image
Fig. 15
figure 15

Diffusion of damaged area for parameter a, for \(t=960\) (a), 1020 (b), 1080 (c), 1200 (d); the parameter c is set as 0.8 in the damage area. The blue area denotes the area out of collapse. (Color figure online)

Full size image

Indeed, the ordered state previously dominated by single perfect spiral wave began to form more spirals when the center of network is invaded by the damaged area. As a result, spirals also occupy the network; thus, periodicity could be detected as well. The results for sampled time series are plotted in Fig. 16, and the statistical correlation functions are calculated in Fig. 17.

Fig. 16
figure 16

Time series for sampled membrane potentials at \(c=0.8\) (damaged areas), for node 1 (a), node 2 (b), node 3 (c) and node 4 (d)

Full size image
Fig. 17
figure 17

Time series for the statistical correlation function between two nodes at \(c=0.8\), for \(\mathrm{m}_{41 }\) (a), \(\mathrm{m}_{42 }\) (b), \(\mathrm{m}_{43 }\) (c), \(\mathrm{m}_{32 }\) (d), \(\mathrm{m}_{31 }\) (e), \(\mathrm{m}_{21 }\) (f)

Full size image

As mentioned in the previous cases, the sampled time series for membrane potentials of nodes close to the damaged area show sensitive response to the shift in parameter and damage invasion. However, the statistical correlation function in Fig. 17 just shows slight response and transition at the beginning though the amplitudes show some transitions. The potential mechanism could be that the collective behaviors of network could not be sensitive to the switch in parameter c but sensitive to the shift in parameter a. By comparing the results from Figs. 3, 4, 5, 6, 7, 8, 9, 10, and 11 and the results from Figs. 12, 13, 14, 15, 16, and  17, it confirms that collapse (or jump shift) in parameter a, c makes the ordered state give different responses because the distribution and regularity of the network depend on the parameters in different degrees. In fact, parameter a does affect the dynamics of membrane potential immediately, while the parameter c changes the slow recovery variable so that the membrane potentials could be adjusted insensitively. To discern the dependence of the two parameters, the bifurcation analysis is carried out by calculating the interspike interval (ISI) for isolated neuron, and the results are shown in Fig. 18.

Fig. 18
figure 18

Bifurcation diagram for ISI versus parameter c (left) and a (right). In the bifurcation diagram for parameter c, no ISI could be detected under quiescent state \((c <0.9)\) at appropriate forcing used in this paper

Full size image

It is found that the sampled ISI and dynamics of membrane potentials are much dependent on the parameter a, while the parameter c plays finite role in regulating the dynamics of electric activity of neuron.

Above all, it supposes that the nervous system described by neuronal network could be regulated by a pacemaker-like wave source, spiral wave, and thus, the network shows distinct periodicity and order in spatial distribution. The collapse of the network is described by introducing parameter shift in a local area with certain diffusive velocity. It is interesting to find the spatial ordering of the network could be destructed by continuous diffusive invasion associated with certain controllable parameters. It indicates the importance of detecting the emergence of diffusive invasion as soon as possible. Switch in different parameters has been verified to model the attack or collapse in the network, and correlation function for monitored nodes could be sensitive to slight switch for some parameters while keeps bovine to switch in another parameter. Indeed, in realistic ecological networks, most of the critical parameters are dependent on each other, and collapse in one parameter may cause breakdown in another parameter. For example, for social network and people in big cities, breakdown in power supply will cause the breakdown in water supply and then breakdown in traffic as well.

For ecological systems, infectious disease kills one species (preys) and so make the predators starve, when it goes one, more predators but also preys could be killed, as a result, the ecological system is in breakdown even death completely. Therefore, a slight collapse or destruction cannot destroy the network, but collapse in sensitive critical parameter of network can be detected in time.

4 Conclusions

The ecological and biological systems can encounter some attacks or infectious diseases, and these invasions could be diffusive in space and cause serious destruction in large space. Indeed, realistic biological systems show certain regularity and spatial distribution, and the regularity could be broken under external attack or internal collapse. Spiral wave can regulate the network as a pacemaker; thus, distinct spatial distribution could be formed in the spatial systems. Our aim is to study the breakdown of regularity of network dominated by spiral wave by introducing collapse in parameter in the network. Based on the theory of pattern selection and control, a two-dimensional network of Hindmarsh–Rose neurons is designed to detect the transition from ordered state to turbulence induced by damage invasion in a diffusive way. Its background could be that the natural system, ecological system or normal nervous keeps normal states; that certain regularity could be destroyed when disaster or disease invades the system. It is critical to detect and predicate the outburst of collapse by analyzing some time series for observable variables. In this way, the neuronal network dominated by spiral wave is regarded as normal order state due to self-organization. Certain parameter in local area is switched to another value to reproduce the parameter collapse process, and the collapse area is increased in size to model the diffusive invasion process. Interestingly, with increasing the size of damaged area, the ordered states of the network are changed and the statistical correlation function between several monitored nodes could be effective to predicate the occurrence of the damage invasion. This scheme could be also useful to predicate the collapse of realistic networks such ecological, electric power and communication network.