1 Introduction

Nature provides many examples of coherent nonlinear structures and waves which have been observed in various fields ranging form fluids, plasmas, solid state physics, chemistry and biology. Among these beautiful nonlinear phenomena, localized large-amplitude waves called solitons, which propagate without spreading and have particle-like properties, and which are a continuous source of fascination for mathematicians and physicists, represent one of the most striking aspects of nonlinear phenomena. However, all kinds of wave patterns, from linear systems to nonlinear ones, contribute to understanding complex wave phenomena. All these systems are only approximately described by the equations of the mathematical theory of solitons. Examples are the sine-Gordon (sG) equation, the nonlinear Schrödinger (NLS) equation and the Korteweg–de Vries (KdV) equation , just to name a few. These completly integrable equations, with their remarkable soliton solutions, have proved to be very efficient to predict their typical dynamical properties.

In fact, in the real world none of these integrable field equations is ever realized exactly; instead, they are obtained by a small parameter expansion: They correspond to the lowest nonlinear approximation. Today, the experiments are becoming more and more sensitive and accurate, allowing the observation of effects which could not be detected before. Meanwhile, the models can be improved: The higher-order terms first ignored in the expansion can be taken into account, leading generally to near integrable or partially integrable equations with quasi-soliton solutions.

In the context of nonlinear optics, the standard model for describing propagation of pulses in the well-known NLS family of equations with cubic nonlinear terms is derived from the slowly varying envelope approximation of the Maxwell’s equations [1]. However, as one increases the intensity of the light power to produce light pulses with shorter and shorter duration, non-Kerr nonlinearity effects become important. Such ultra-short pulses named in the literature as few-cycles, video pulses, need other approaches to describe their dynamics. In general, the dynamics of pulses should be described by the NLS family of equations with higher-order nonlinear terms [2–5].

In a recent experiment, it has been established that the optical susceptibility of \(\hbox {Cd}S_x S_{e1 - x}\)-doped glass possesses a considerable level of fifth-order susceptibility \(\chi ^{(5)} \). In semiconductor double-doped optical fibers [6, 7], the doping of silica fibers with two appropriate semiconductor particles may lead to an increased value of third-order susceptibility \(\chi ^{(3)} \) and a decreased value of \(\chi ^{(5)} \). Thus, in order to investigate pulse propagation in such materials, it is necessary to consider higher-order nonlinearities in place of the usual Kerr nonlinearity. However, when the saturation is very strong, a self-focusing \(\chi ^{(7)} \) is also needed. Quite recently, an experiment has been reported in material such as chalcogenide glass which exhibits not only third- and fifth-order nonlinearities but even seventh-order nonlinearity [8, 9]. In other word, chalcogenide glass can be classified as a cubic-quintic-septic nonlinear material.

In magnetic chains, the importance of theoretically tractable models, describing experimentally accessible systems including the nonlinear excitations and their interactions, is clearly central to developing the understanding of nonlinear phenomena. Starting from model Hamiltonians, in the continuum limit, the spin dynamics of \(\hbox {C}_s\hbox {N}_i\hbox {F}_3\) and TMMC can be described by complicated nonlinear partial differential equations. However, as in nonlinear optics, to lowest nonlinear order of approximation, the nonlinear excitations are frequently taken to be solutions of an integrable prototype equation which in this case is the sG equation. The approximate validity of this model is limited to low or high external magnetic field. In the low-amplitude limit, the spin dynamics can be modeled by NLS-like equations. Dynamical theory of solitary wave excitations in spin chains has been studied by Nguenang and Kofané [10] by a revised Hamiltonian in which the dipole–dipole and biquadratic exchange interactions are taken into account in addition to the Zeemann energy, uniaxial anisotropy and the exchange energy. They have shown that at sufficiently low temperature and with only a few spin waves of sufficiently large magnitude which are excited, the nonlinear terms in the Holstein–Primakoff representation cannot be neglected. The NLS equation previously obtained in other works [11] which describes the evolution of modulations of dispersive waves with weak nonlinearity suffered from highly inconsistent comparison of terms within the framework of the Holstein–Primakoff representation. To avoid this inconsistency, Shi et al. [12] and Nguenang and Kofané have used the Ursell theory of shallow water waves [13, 14].

The modulation of a one-dimensional weakly nonlinear purely dispersive quasi-monochromatic wave is usually governed by the NLS equation. The critical wave number for which the carrier is marginally modulationally unstable is determined by the condition that the product of the coefficients of the nonlinear and dispersive terms in the NLS equation is zero. However, near this marginal state the assumptions that lead to the NLS equation are invalid and a modified form of the NLS equation that involves higher-order nonlinearities is appropriate [15].

The problem of incorporating higher-order terms into the theory of long waves on a water surface has recently attracted much attention [16–21]. For examples, in the field of fluid dynamics, the standard NLS equation gives a good description of nonlinear deep water waves in the case of small steepness, while it fails when considering large steepness. In the latter case, a significant improvement can be achieved by taking into account higher-order terms in perturbation analysis, that is, considering a higher-order nonlinear Schrödinger equation [22]. More recently, by means of this equation, Yemélé et al. [23] have studied the long-time dynamics of modulational instability of deep water waves and have obtained the following results: (i) The standard NLS equation yields satisfactory description of long-time envelope solitons dynamics for considered time scales. (ii) On the contrary, for modulated periodic Stoke waves, serious nonlinear instabilities and chaos may develop in the medium such that the standard NLS equation fails to describe, but which can be explained by means of the nonlinear Schrödinger equation.

The Euler equation for a nonviscous and incompressible fluid, the boundary conditions at the bottom and at the surface, and the assumption of an irrotational flow lead to the KdV equation, which is valid in the weakly nonlinear case. The KdV equation shows up in many areas of physics, when waves can propagate in a weakly nonlinear long waves when nonlinearity and dispersion are in balance at leading order. If higher-order nonlinear and dispersive effects are of interest, then the asymptotic expansion can be extended to the higher orders in the wave amplitude which leads to the KdV equation with higher-order corrections [16–21, 24, 25]. The main purpose of this article is to go beyond the new seventh-order KdV equation derived by Burde [19], for the right-moving wave assumed to have a smaller amplitude \(0(\varepsilon ^{3})\). We show that the dynamics of the wave amplitude for the unidirectional propagation of long waves over shallow water assumed to have a smaller amplitude \(0(\varepsilon {4})\), is governed by a new KdV equation with nonlinear and nonlocal terms

$$\begin{aligned}&u_t + u_x + \varepsilon (\alpha _1 uu_x + \alpha _2 u_{3x} ) + \varepsilon ^2 (\beta _1 u_{5x} \nonumber \\&\quad +\, \beta _2 uu_{3x} + \beta _3 u_x u_{2x} + \beta _4 u^2 u_x ) \nonumber \\&\quad +\, \varepsilon ^3 (\gamma _1 u_{7x} + \gamma _2 uu_{5x} + \gamma _3 u_x u_{4x} + \gamma _4 u^2 u_{3x} \nonumber \\&\quad +\, \gamma _5 u_{2x} u_{3x}+ \gamma _6 uu_x u_{2x} + \gamma _7 u^3 u_x + \gamma _8 u_x^3 )\nonumber \\&\quad +\, \varepsilon ^4\left( \delta _1 u_{9x} + \delta _2 uu_{7x} + \delta _3 u_x u_{6x} + \delta _4 u^2 u_{5x}\right. \nonumber \\&\quad +\, \delta _5 u_{2x} u_{5x} + \delta _6 uu_x u_{4x} + \delta _7 u_{3x} u_{4x} + \delta _8 u^3 u_{3x}\nonumber \\&\quad +\, \delta _9 uu_{2x} u_{3x} + \delta _{10} u_x^2 u_{3x} + \delta _{11} u^2 u_x u_{2x}\nonumber \\&\quad +\, \delta _{12} uu_{2x}^2 + \delta _{13} u^4 u_x + \delta _{14} uu_x^3 + \delta _{15} \int u_{2x}^3 \hbox {d}x \nonumber \\&\quad +\, \delta _{16} u_x \int {u_x^3\hbox {d}x} + \delta _{17}\int u_x^3\hbox {d}x \nonumber \\&\quad \left. +\, \delta _{18} \int u_x^2\hbox {d}x \right) = 0, \end{aligned}$$
(1)

Here x and t are the space and time variables, and subscripts of the form “nx”denote derivatives of the order n with respect to x. Coefficients in Eq. (1) will be defined in the next section.

Then, we obtain the exact-one and two-solitary wave solutions for this equation.

The paper is organized, as follows. In Sect. 2, we present the shallow water problem and in nondimensional variables. We describe briefly the Boussinesq equations, from which the KdV equation with higher-order corrections will be derived. Then, a new equation for KdV equation with higher-order corrections with nonlocal terms is proposed for the right-moving wave at \(0(\varepsilon {4} )\) smaller amplitude. In Sect. 3, the one- and two-solitary wave solutions are found using the Hirota’s direct method. Section 4 concludes the paper.

2 Mathematical formulation of the problem

Let us consider a layer of an inviscid and incompressible fluid, which has the mean depth h, lying above a horizontal plane situated at altitude \(z=0\). We assume that the motion of the fluid is two dimensional, i.e., all the properties of the system are independent of the coordinate y and the component of the velocity along y is zero.

We denote by u(x, z, t), 0 and w(x, z, t) the components of the velocity field inside the fluid, and by \(z=h+\eta (x,t)\) the equation of its surface, where \(\eta (x,t)\) is the surface elevation.

Above the fluid, there is a gaz at pressure \(p_A\), which is variable and uniform in space. The fluid experiences the force \(\overrightarrow{f} = \rho \overrightarrow{g} \) per unit volume due to gravity, where \(\rho \) is the density of the fluid, \(\overrightarrow{g} \) the gravity field. Equations defining the problem include [26, 27]:

(i) The Euler equation inside the volume of the fluid. If we divide it by \(\rho \) and express its z-momentum, it gives

$$\begin{aligned}&w_t + uw_x + ww_z = - {1 \over \rho }p_z - g \quad \hbox {with} \nonumber \\&\quad p = \sigma {{\eta _{xx} } \over {(1 + \eta _x^2 )^{{3 \over 2}} }}, \end{aligned}$$
(2)

where p is the pressure in the fluid and \(\sigma \) is the surface tension. These equations must be completed by the mass conservation requirement

$$\begin{aligned} u_x+w_z=0. \end{aligned}$$
(3)

(ii) The boundary condition at the bottom, which says that the velocity of the fluid when \(z=0\), does not have any vertical component,

$$\begin{aligned} w=0 \quad \hbox {for}\quad z=0. \end{aligned}$$
(4)

(iii) The kinematic boundary condition at the surface,

$$\begin{aligned} w = \eta _t+u\eta _x \quad \hbox {for}\quad z=h+\eta (x,t). \end{aligned}$$
(5)

(iv) The physical condition at the surface,

$$\begin{aligned} p_A-p=0 \quad \hbox {for}\quad z=h+\eta (x,t). \end{aligned}$$
(6)

Introducing the potential velocity \(v(x,z,t) = \nabla \phi (x,z,t)\), where \(\nabla \) is the Nabla operator, we have \(u = \phi _x \) and \(w = \phi _z\) for the horizontal and vertical velocity components. The velocity potential \(\phi (x,z,t)\) must satisfy Laplace’s equation in the interior. Equation (5) becomes

$$\begin{aligned} \eta _t + \alpha \phi _x \eta _x - {1 \over \beta }\phi _z = 0\quad \hbox {for}\quad {z} = 1 + \alpha \eta \end{aligned}$$
(7)

Equation (2) can now be integrated to yield the dynamic boundary condition

$$\begin{aligned}&\varphi _t + {1 \over 2}\alpha \left( \phi _x^2 + {1 \over \rho }\phi _z^2 \right) + \eta - {{\tau \beta \eta _{xx} } \over {1 + \alpha ^2 \beta \eta _x^2 }} \nonumber \\&\quad \hbox {for}\quad {z} = 1 + \alpha \eta \end{aligned}$$
(8)

In the following, we use the characteristic length L along the direction x and the characteristic speed \(c_0 = \sqrt{gh} \) of the long-wavelength waves to define a characteristic time \(t_0=L/c_0\), which will be used to measure time. The equations for a fluid are written in a nondimensionalized form by introducing

$$\begin{aligned}&t' = {t \over {t_0 }}, \quad {x}' = {{x} \over {L}}, \quad {z}' = {{{z}} \over h}, \nonumber \\&\eta ' = {\eta \over {{A}}}, \quad \phi ' = {\phi \over {L(A/h)\sqrt{gh}}}, \end{aligned}$$
(9)

where A is a typical amplitude of a surface wave \(\eta \). The Euler equations and the boundary conditions at the free surface and at the bottom take the form

$$\begin{aligned}&\beta \phi _{2x} + \phi _{2z} = 0\quad \hbox {for} \quad 0 \le z \le 1 + \alpha \eta (x,t),\end{aligned}$$
(10)
$$\begin{aligned}&\phi _z = 0\quad \hbox {for} \quad z = 0,\end{aligned}$$
(11)
$$\begin{aligned}&\eta _t + \alpha \phi _x \eta _x - {1 \over \beta }\phi _z = 0\quad \hbox {for}\quad z = 1 + \alpha \eta ,\end{aligned}$$
(12)
$$\begin{aligned}&\varphi _t + {1 \over 2}\alpha \left( \phi _x^2 + {1 \over \rho } \phi _z^2 \right) + \eta - {{\tau \beta \eta _{xx} } \over {1 + \alpha ^2 \beta \eta _x^2 }} = 0,\nonumber \\&{z} = 1 + \alpha \eta . \end{aligned}$$
(13)

where \(\alpha \) and \(\beta \) are small parameters given by \(\alpha = {A \over h}\), \(\beta = ({h \over L})^2 \) and the Bond number \(\tau = {T \over {\rho gh^2 }}\), where T is the surface tension coefficient.

3 Shallow water waves

3.1 Modelization of Boussinesq equations

More appropriate methods for approximating irregular wave kinematics are those which do not compromise the requirements of satisfying both the field equation and bottom and free surface boundary conditions. The basis of such methods is the representation of the velocity potential function \(\phi \) within each local window in the form of power series of z [28–30]. The power series expansion used for the approximation of the velocity potential \(\phi \) is

$$\begin{aligned} \phi = \sum \limits _{i = 0}^\infty {( - 1)^i } \beta ^i {{z^{2i} } \over {(2i)!}}{{\partial ^{2i} g} \over {\partial x^{2i} }} \end{aligned}$$
(14)

where the function g(x, t) is the value of the velocity potential at the bottom \(z=0\). Within each moving window, the velocity potential satisfies the Laplace’s equation and the boundary condition at the bottom exactly. On substitution of Eq. (14) in kinematic boundary condition and dynamic boundary condition, we obtain a system of equations for \(\eta (x,t)\) and g(x, t) in the form of infinite series with respect to \(\beta \).

In the following, \(\alpha \) and \(\beta \) are assumed to be of the order of \(0(\varepsilon )\) [19]. Then, make expansion at order \(0(\varepsilon ^4 )\), we obtain the Boussinesq equations

$$\begin{aligned}&\eta _t {+} w_x {+} \varepsilon \left( \eta w_x + \eta _x w - {1 \over 6}w_{3x} \right) + \varepsilon ^2 \left( - {1 \over 2}\eta _x w_{2x} \right. \nonumber \\&\left. \quad -\, {1 \over 2}\eta w_{3x} {+} {1 \over {120}}w_{5x} \right) {+} \varepsilon ^3 \left( - {1 \over 2}\eta ^2 w_{3x} + {1 \over {24}}\eta _x w_{4x} \right. \nonumber \\&\left. \quad -\, \eta \eta _x w_{2x} {+} {1 \over {24}}\eta w_{5x} {-} {1 \over {5040}}w_{7x} \right) {+} \varepsilon ^4 \left( {-} {1 \over 6}\eta ^3 w_{3x} \right. \nonumber \\&\quad + \,{1 \over {12}}\eta ^2 w_{5x} - {1 \over {720}}\eta w_{7x} - {1 \over 2}\eta _x \eta ^2 w_{2x} + {1 \over 6}\eta \eta _x w_{4x} \nonumber \\&\quad \left. - \,{1 \over {720}}\eta _x w_{6x} + {1 \over {362880}}w_{9x} \right) = 0,\end{aligned}$$
(15)
$$\begin{aligned}&\eta _x + w_t + \varepsilon \left( ww_x - {1 \over 2}w_{2xt} - \tau \eta _{3x} \right) + \varepsilon ^2 \left( - \eta _x w_{xt} \right. \nonumber \\&\left. \quad \ +\, {1 \over 2}w_x w_{2x} - \eta w_{2xt} - {1 \over 2}ww_{3x} + {1 \over {24}}w_{4xt} \right) \nonumber \\&\quad \ + \,\varepsilon ^3 \left( \eta _x w_x^2 - \eta \eta _x w_{xt} - w\eta _x w_{2x} + {1 \over 6}\eta _x w_{3xt}\right. \nonumber \\&\quad \ -\, {1 \over 2}\eta ^2 w_{2xt} + {1 \over {12}}w_{2x} w_{3x} - {1 \over 8}w_x w_{4x} + \eta w_x w_{2x} \nonumber \\&\left. \quad \,- \,\eta ww_{3x} + {1 \over 6}\eta w_{4xt} + {1 \over {24}}ww_{5x} - {1 \over {720}}w_{6xt} \right) + \varepsilon ^4 \nonumber \\&\quad \left( {1 \over 2}\eta ^2 w_x w_{2x} - {1 \over 2}\eta w_x w_{4x} - \eta \eta _x ww_{2x} \right. \nonumber \\&\quad +\, {1 \over {144}}w_x w_{6x} - {1 \over {120}}\eta _x w_{5xt} - {1 \over 2}\eta ^2 ww_{3x} \nonumber \\&\quad +\, {1 \over 6}w\eta _x w_{4x} + {1 \over 6}\eta ww_{5x} - {1 \over {720}}ww_{7x} \nonumber \\&\quad +\, {1 \over 3}\eta w_{2x} w_{3x} + {1 \over {144}}w_{3x} w_{4x} \nonumber \\&\quad + \,{1 \over 2}\eta _x w_{2x}^2 - {1 \over {80}}w_{2x} w_{5x} + {1 \over 2}\eta \eta _x w_{3xt} \nonumber \\&\quad + \,{1 \over 4}\eta ^2 w_{4xt} + \eta \eta _x w_x^2 \nonumber \\&\quad \left. -\, {2 \over 3}\eta _x w_x w_{3x} - {1 \over {120}}\eta w_{6xt} + {1 \over {40320}}w_{8xt} \right) = 0 . \nonumber \\ \end{aligned}$$
(16)

that depend on the functions w(x, t) and \(\eta (x,t)\), where \(w(x,t) = {{\partial g(x,t)} \over {\partial x}}\) is the scaled horizontal velocity at the bottom of the channel.

3.2 Unidirectional waves

As in the derivation of the KdV equation in Whitham [26], we now restrict to unidirectional waves by assuming a relationship \(w = \eta + \varepsilon f(\eta )\) between w, the horizontal velocity at the mean height, and elevation \(\eta \), where the function f shall be determined so that the Eqs. (15) and (16) both reduce to the same single equation for the height field \(\eta \).

To lowest (zero) order in both \(\alpha \) and \(\beta \), the system of equations for w and \(\eta \) reads \(\eta _t+w_x=0\), \(w_t+\eta _x=0\), so both w and \(\eta \) satisfy the linear wave equation \(\zeta _{tt} - \zeta _{xx} = 0\), which describes waves traveling in two directions \(\eta (x,t) = \eta _R (x - t) + \eta _L (x + t)\). A wave moving to the right corresponds in this order of approximation to \(w=\eta \) and \(\eta _t + \eta _x = 0\). In the next iterations, we assume that w can be represented by an expansion having the form

$$\begin{aligned} w = \eta + \varepsilon A(\eta ) + \varepsilon ^2 B(\eta ) + \varepsilon ^3 C(\eta ) + \varepsilon ^4 D(\eta ) \end{aligned}$$
(17)

where \(A(\eta ), B(\eta ), C(\eta )\) and \(D(\eta )\) are unknown functions of \(\eta \) at this point and their derivatives.

Upon ordering in powers of the small parameters, the coefficients in the transformation (17) are determined by requiring that Boussinesq system equations in (15) and (16) are satisfied simultaneously at each order. To first order, we substitute Eq. (17) into Eqs. (15) and (16) with terms of order higher than \(0(\varepsilon )\) neglected, and we obtain

$$\begin{aligned}&\eta _t + \eta _x + \varepsilon (2\eta \eta _x - {1 \over 6}\eta _{3x} + A_x^{(1)} ) = 0, \nonumber \\&\eta _t + \eta _x + \varepsilon (\eta \eta _x - {1 \over 2}\eta _{2xt} - \tau \eta _{3x} + A_t^{(1)} ) = 0 . \end{aligned}$$
(18)

The function A is such that the two equations in (18) agree (up to the first order in \(\varepsilon \)) upon expressing all the t-derivatives of \(\eta \) in terms of the x-derivatives using the lower-order equation \(\eta _t+\eta _x=0\). The equation defining A is

$$\begin{aligned} 2\eta \eta _x - {1 \over 6}\eta _{3x} + A_x^{(1)}=\eta \eta _x - {1 \over 2}\eta _{2xt} - \tau \eta _{3x} + A_t^{(1)}\nonumber \\ \end{aligned}$$
(19)

Because the correction functions appear already in the second order, it is enough to use the lowest order relation between their time and space derivatives (\(\eta _t=-\eta _x\) and \(A_t=-A_x\)) in Eq. (18). We obtain after integration

$$\begin{aligned} A= - {1 \over 4}\eta ^2 + \left( {1 \over 3} - {1 \over 2}\tau \right) \eta _{2x}. \end{aligned}$$
(20)

Then, Eqs. (17) and (18) become

$$\begin{aligned}&{{w}} = \eta +\varepsilon \left( - {1 \over 4} \eta ^2 + {1 \over 6}(2 - 3\tau )\eta _{3x} \right) + \varepsilon ^2 B(\eta ) \nonumber \\&\quad +\, \varepsilon ^3 C(\eta )+ \varepsilon ^4 D(\eta )\end{aligned}$$
(21)
$$\begin{aligned}&\eta _t + \eta _x + \varepsilon \left( {3 \over 2}\eta \eta _x + {1 \over 6} (1 - 3\tau )\eta _{3x} \right) = 0. \end{aligned}$$
(22)

Equation (22) is now reduced to the KdV equation in a standard form

$$\begin{aligned} \eta _{{\tilde{t}}} + 6\eta \eta _{{\tilde{x}}} + \eta _{3{\tilde{x}}} = 0, \end{aligned}$$
(23)

provided that

$$\begin{aligned} {\tilde{x}} = \sqrt{{3 \over 2}} (x - t),\quad \quad {\tilde{{t}}} = {1 \over 4}\sqrt{{3 \over 2}} \varepsilon t \end{aligned}$$
(24)

hold.

At the next step, Eq. (21) is substituted into Eqs. (15) and (16), and then all the t-derivatives of \(\eta \) are replaced by their expressions through the x derivatives using the lowest order equation, namely Eq. (21). A condition for the two equations obtained in such a way leads to an equation for A, a solution of which is expressed in terms of \(\eta \) and its x-derivatives. As a result, we have

$$\begin{aligned} {w}= & {} \eta +\varepsilon ( - {1 \over 4} \eta ^2 + {1 \over 6}(2 - 3\tau )\eta _{3x} ) + \varepsilon ^2 {1 \over 8}\eta ^3 \nonumber \\&+\, {1 \over {16}}(3 + 7\tau )\eta _x^2 + {1 \over 4}(2 + \tau )\eta \eta _{2x} \nonumber \\&+\, {1 \over {120}} (12 - 20\tau - 15\tau ^2 )\eta _{4x} + \varepsilon ^3 C(\eta )\nonumber \\&+\, \varepsilon ^4 D(\eta ), \end{aligned}$$
(25)

where the perturbation of second order is given by

$$\begin{aligned} B(\eta )= & {} {1 \over 8}\eta ^3 + {1 \over {16}}(3 + 7\tau )\eta _x^2 + {1 \over 4}(2 + \tau )\eta \eta _x \nonumber \\&+\, {1 \over {120}}(12 - 20\tau - 15\tau ^2 )\eta _{4x} . \end{aligned}$$
(26)

Inserting Eq. (25) into Eq. (15), yields in second order, the equation

$$\begin{aligned}&\eta _t + \eta _x + \varepsilon \left( {3 \over 2}\eta \eta _x + {1 \over 6}(1 - 3\tau )\eta _{3x} \right) + \varepsilon ^2 \nonumber \\&\quad \times \left( - {3 \over 8}\eta ^2 \eta _x + {1 \over {24}}(23 + 15\tau )\eta _x \eta _{2x} + {1 \over {12}}\right. \nonumber \\&\left. \quad \times (5 - 3\tau )\eta \eta _{3x} + {1 \over {360}} (19 - 30\tau - 45\tau ^2 )\eta _{5x} \right) = 0.\nonumber \\ \end{aligned}$$
(27)

Comparing Eq. (1) with Eq. (27), we obtain the coefficients \(\beta _1\), \(\beta _2\), \(\beta _3\) and \( \beta _4\) which depend on \(\tau \). Taking account of Eq. (25), from Eqs. (15) and (16), we get in the third order the following equations

$$\begin{aligned} {w}= & {} \eta +\varepsilon \left( - {1 \over 4}\eta ^2 + {1 \over 6}(2 - 3\tau )\eta _{2x} \right) + \varepsilon ^2 {1 \over 8}\eta ^3 \nonumber \\&+\, {1 \over {16}}(3 + 7\tau )\eta _x^2 + {1 \over 4}(2 + \tau )\eta \eta _{2x} + {1 \over {120}}\nonumber \\&\times (12 - 20\tau - 15\tau ^2 )\eta _{4x} + \varepsilon ^3 \left( - {5 \over {64}}\eta ^4 \right. \nonumber \\&+ \left( {1 \over 8} - {3 \over {16}}\tau \right) \eta ^2 \eta _{2x} +\left( {3 \over {32}} - {{21} \over {32}}\tau \right) \eta \eta _x^2 \nonumber \\&+\left( {{1091} \over {1440}} + {1 \over 3}\tau + {{21} \over {32}}\tau ^2 \right) \eta _x \eta _{3x} \nonumber \\&+ \left( {7 \over {20}} - {1 \over 4}\tau + {1 \over {16}}\tau ^2 \right) \eta \eta _{4x} + \left( {{61} \over {1890}} - {1 \over {20}}\tau \right. \nonumber \\&\left. - {1 \over {24}}\tau ^2 - {1 \over {16}}\tau ^3 \right) \eta _{6x} + \left( {3 \over {16}} - {3 \over {16}}\tau \right) \nonumber \\&\left. \int {\eta ^3 \hbox {d}x} \right) + \varepsilon ^4 D(\eta ),\end{aligned}$$
(28)
$$\begin{aligned}&\eta _t + \eta _x + \varepsilon \left( {3 \over 2}\eta \eta _x + {1 \over 6}(1 - 3\tau )\eta _{3x} \right) \nonumber \\&+\, \varepsilon ^2 \left( - {3 \over 8}\eta ^2 \eta _x \right. + {1 \over {24}}(23 + 15\tau )\eta _x \eta _{2x} \nonumber \\&+ \,{1 \over {12}}(5 - 3\tau )\eta \eta _{3x} + {1 \over {360}}\nonumber \\&\left. \times (19 - 30\tau - 45\tau ^2 )\eta _{5x} \right) + \varepsilon ^3 \left( {1 \over {15120}}\right. \nonumber \\&\times (275 - 399\tau - 315\tau ^2 - 945\tau ^4 ) u_{7x} + {1 \over {240}}\nonumber \\&\times (57 - 50\tau - 15\tau ^2 )uu_{5x} + {1 \over {1440}}\nonumber \\&\times (1079 - 150\tau + 855\tau ^2 )u_x u_{4x} \nonumber \\&+ {1 \over {16}}(5 + \tau )u^2 u_{3x} + \left( {{317} \over {288}} + {15 \over {16}}\tau \right. \nonumber \\&\left. + {{49} \over {32}}\tau ^2 \right) u_{2x} u_{3x} + {1 \over {16}}(23 - 5\tau )\nonumber \\&uu_x u_{2x} + {3 \over {16}}u^3 u_x + {1 \over {32}}\nonumber \\&\left. \times (19 - 13\tau )u_x^3 \right) = 0, \end{aligned}$$
(29)

where the correction at third order is given by

$$\begin{aligned} C(\eta )= & {} - {5 \over {64}}\eta ^4 + \left( {1 \over 8} - {3 \over {16}}\tau \right) \eta ^2 \eta _{2x} \nonumber \\&+ \left( {3 \over {32}} - {{21} \over {32}}\tau \right) \eta \eta _x^2 + \left( {{1091} \over {1440}}\right. \nonumber \\&\left. - {1 \over 6}\tau + {{25} \over {32}}\tau ^2 \right) \eta _x \eta _{3x} \nonumber \\&+ \left( {7 \over {20}} - {1 \over 4}\tau + {1 \over {16}}\tau ^2 \right) \eta \eta _{4x} \nonumber \\&+ \left( {{61} \over {1890}} - {1 \over {20}}\tau - {1 \over {24}}\tau ^2 - {1 \over {16}}\tau ^3 \right) \eta _{6x} \nonumber \\&+ \left( {3 \over {16}} - {3 \over {16}}\tau \right) \int {\eta ^3 \hbox {d}x}. \end{aligned}$$
(30)

At the next step, the derivation to fourth order corrections is quite similar as discussed above, where again, comparing Eq. (1) with Eq. (31) leads to the coefficients \(\alpha _i \) (\({i}=1,2\)), \(\beta _i \) (\({i}=1\ldots 4\)), \(\gamma _i \) (\({i}=1\ldots 8\)) and \(\delta _i \) (\({i}=1\ldots 19\)). Without details concerning the derivation, the main results are given by

$$\begin{aligned}&\eta _t + \eta _x + \varepsilon \left( {3 \over 2}\eta \eta _x + {1 \over 6}(1 - 3\tau )\eta _{3x} \right) \nonumber \\&\quad +\, \varepsilon ^2 \left( - {3 \over 8}\eta ^2 \eta _x + {1 \over {24}}(23 + 15\tau )\eta _x \eta _{2x}\right. \nonumber \\&\quad \left. + {1 \over {12}}(5 - 3\tau )\eta \eta _{3x} + {1 \over {360}} \left( 19 - 30\tau - 45\tau ^2 \right) \eta _{5x} \right) \nonumber \\&\quad +\, \varepsilon ^3 \left( {1 \over {15120}}(275 - 399\tau - 315\tau ^2 - 945\tau ^4 )u_{7x} \right. \nonumber \\&\quad +\, {1 \over {240}} (57 - 50\tau - 15\tau ^2 )uu_{5x} + {1 \over {1440}}\nonumber \\&\quad \times (1079 - 150\tau + 855\tau ^2 )u_x u_{4x} + {1 \over {16}}\nonumber \\&\quad \times (5 + \tau )u^2 u_{3x} + \left( {{317} \over {288}} + {7 \over {16}}\tau + {{53} \over {32}}\tau ^2 \right) u_{2x} u_{3x} \nonumber \\ \end{aligned}$$
$$\begin{aligned}&\quad +\, {1 \over {16}}(23 - 5\tau )uu_x u_{2x} + {3 \over {16}}u^3 u_x + {1 \over {32}}\nonumber \\&\quad \quad \left. (19 - 13\tau )u_x^3 \right) + \varepsilon ^4 \left( \left( {{11813} \over {1814400}} - {{55} \over {6048}}\tau \right. \right. \nonumber \\&\quad \quad \left. - {{19} \over {2880}}\tau ^2- {1 \over {96}}\tau ^3 - {5 \over {128}}\tau ^4 \right) u_{9x} \nonumber \\&\qquad + \left( {{715} \over {6048}} - {{19} \over {160}}\tau - {5 \over 96}\tau ^2- {1 \over {32}}\tau ^3\right) uu_{7x}\nonumber \\&\qquad + \left( {{26893} \over {60480}} - {{57} \over {320}}\tau + {{5} \over {192}}\tau ^2 + {37 \over {64}}\tau ^3\right) u_x u_{6x} \nonumber \\ \end{aligned}$$
$$\begin{aligned}&\quad \quad + \left( {{133} \over {320}} - {5 \over {32}}\tau + {1\over {64}}\tau ^2 \right) u^2 u_{5x} \nonumber \\&\quad \quad +\left( {{8657} \over {8640}} + {{1003} \over {2880}}\tau + {{163} \over {192}}\tau ^2 + {129 \over {64}}\tau ^3 \right) u_{2x} u_{5x} \nonumber \\&\qquad + \left( {{7553} \over {2880}} - {{5} \over {32}}\tau - {{19} \over {64}}\tau ^2\right) uu_x u_{4x} \nonumber \\&\quad \quad +\left( {{4973} \over {3456}} + {{1217} \over {1152}}\tau + {{707} \over {384}}\tau ^2 + {{443} \over {128}}\tau ^3 \right) u_{3x} u_{4x}\nonumber \\ \end{aligned}$$
$$\begin{aligned}&\qquad + \left( {5 \over {96}} - {1 \over {32}}\tau \right) u^3 u_{3x} \nonumber \\&\quad \quad + \left( {{{2219}} \over {{576}}} + {{45} \over {32}}\tau - {{49} \over {64}}\tau ^2 \right) uu_{2x} u_{3x} \nonumber \\&\quad \quad +\left( {{3941} \over {2880}} + {{47} \over {96}}\tau - {{105} \over {32}}\tau ^2 \right) u_x^2 u_{3x} \nonumber \\&\quad \quad + \left( {23 \over {64}} + {{15} \over {64}}\tau \right) u^2 u_x u_{2x} \nonumber \\&\qquad + \left( -{6149 \over {11520}} + {7 \over {32}}\tau -{{851} \over {256}}\tau ^2 \right) u_x u_{2x}^2\nonumber \\&\qquad + \left( {{19} \over {128}} + {{39} \over {64}}\tau \right) uu_x^3 \nonumber \\ \end{aligned}$$
$$\begin{aligned}&\quad \quad +\left( -{3 \over 64} + {{12} \over {64}}\tau -{{9} \over {64}}\tau ^2 \right) \int u_{2x}^3\text{ d }x \nonumber \\&\quad \quad + \left( {3 \over {16}} + {3 \over {16}}\tau \right) u_x \int u_x^3 \text{ d }x + \left( {{9} \over {64}} - {{9} \over {64}}\tau \right) \int u_x^3 \text{ d }x\nonumber \\&\quad \quad + \left( - {27 \over {64}} + {27 \over {64}}\tau \right) \int u_x^2 \text{ d }x=0, \end{aligned}$$
(31)

and

$$\begin{aligned} D(\eta )= & {} -\left( {{3} \over {128}} + {{105} \over {128}}\tau \right) \eta ^2 \eta _x^2 \nonumber \\&+ \left( {{163} \over {144}} + {{129} \over {96}}\tau - {{21} \over {32}}\tau ^2 \right) \eta \eta _{2x}^2\nonumber \\&+ \left( {{7} \over {16}} - {{1} \over {16}}\tau - {{3} \over {64}}\tau ^2 \right) \eta ^2 \eta _{4x} \nonumber \\&+ \left( - {{31} \over {128}} + {{15} \over {32}}\tau \right) \int {\eta \eta _x^3 \text{ d }x} \nonumber \\ \end{aligned}$$
$$\begin{aligned}&+ \left( - {{8177} \over {2304}} - {{67} \over {96}}\tau + {{645} \over {256}}\tau ^2 \right) \int {\eta _x \eta _{2x}^2 \text{ d }x}\nonumber \\&+ \left( -{{3} \over {64}} + {{3} \over {16}}\tau - {{9} \over {64}}\tau ^2 \right) \int {\eta _{3x} \eta _x^2 \text{ d }x} \nonumber \\&+ \left( {{673} \over 576} - {{107} \over 192}\tau - {{45} \over {16}}\tau ^2 \right) \eta _x^2 \eta _{2x}\nonumber \\ \end{aligned}$$
$$\begin{aligned}&+ \left( {{35303} \over {60480}} - {{37} \over {360}}\tau + {5 \over 24}\tau ^2 + {39 \over {64}}\tau ^3 \right) \eta _x \eta _{5x}\nonumber \\&+ \left( {{16019} \over {15120}} + {{457} \over {720}}\tau + {{55} \over {48}}\tau ^2 +{{45} \over {32}}\tau ^3 \right) \eta _{2x} \eta _{4x}\nonumber \\&+ \left( {{158323} \over {241920}} +{{6349} \over {11520}}\tau + {{607} \over {768}}\tau ^2 + {{263} \over {256}}\tau ^3 \right) \eta _{3x}^2 \nonumber \\&+ \left( {1091 \over {576}} + {1\over {6}}\tau -{{63} \over {64}}\tau ^2\right) \eta \eta _x\eta _{3x} \nonumber \\ \end{aligned}$$
$$\begin{aligned}&+ \left( {1261 \over {113400}} - {61 \over {3780}}\tau - {1 \over {80}}\tau ^2-{1 \over {48}}\tau ^3\right. \nonumber \\&\left. -{5 \over {128}}\tau ^4 \right) \eta _{8x} \nonumber \\&+ \left( {671 \over {3780}} - {7 \over {40}}\tau -{1 \over {16}}\tau ^2 + {1 \over {32}}\tau ^3 \right) \eta \eta _{6x} \nonumber \\&+ {7 \over {128}}\eta ^5 + \left( -{{1} \over {48}} + {{5} \over {32}}\tau \right) \eta ^3\eta _{2x}\nonumber \\ \end{aligned}$$
$$\begin{aligned}&+ \left( -{{3} \over {64}} + {{3} \over {16}}\tau - {{9} \over {64}}\tau ^2\right) \int \int \eta _{2x}^3 \text{ d }x\text{ d }x \nonumber \\&+ \left( {{9} \over {64}} - {{9} \over {64}}\tau \right) \int \int \eta _x^3 \hbox {d}x\text{ d }x \nonumber \\&+ \left( -{{27} \over {64}} + {{27} \over {64}}\tau \right) \int \int \eta _x^3 \text{ d }x\text{ d }x \end{aligned}$$
(32)

It should be noted that Eq. (31) is the same as Eq. (1), where all the coefficient expressions are dependent strongly on the surface tension coefficient. We will seek thereafter one- and two-soliton solutions of this new KdV equation with nonlinear and nonlocal terms equation by using Hirota’s bilinear method.

4 Soliton solutions and Hirota’s bilinear method

Many powerful methods for searching for exact solutions to nonlinear evolution equations have been proposed. Among these are inverse scattering method, Bäcklund transformation, Darboux transformation, Hirota method [31–35]. In recently years, some other ansätz method have been developed, such as, tanh method [36–38], extended tanh function method [39, 40], modified extended tanh function method [41], generalized hyperbolic function method [42–44], variable separation method, the sine–cosine method [45–48], the tanh–sech method [49–51], the tanh–coth method [52].

Among the different available methods [26, 31–52] for solving soliton equations, the Hirota bilinear method and its multilinear refinements has been one of the most successful direct technique for constructing exact solutions, in particular, the N-soliton solutions. The method also allows testing if a certain equation satisfies the necessary requirements to admit solitary wave solutions and soliton solutions. The drawback of Hirota’s method is that the bilinear form of the partial derivative equations (PDE) must be known. Once the bilinear form is obtained the method becomes algorithmic. The calculations, however, become very lengthy and involved, in particular for PDEs of high order or with highly nonlinear terms. The complexity of the calculations also drastically increases with the type of soliton solution one desires to obtain. Single soliton solutions are easy to calculate; two- and three-soliton solutions are barely manageable by hand. Once the form of the two- and three-soliton solutions is known, its structure reveals the form of higher soliton solutions.

4.1 One-soliton solution

Now, let us look for solutions of the traveling wave type of our higher-order KdV equation (1). The general form of solution is given by

$$\begin{aligned} \eta (x,t) = R{{\partial ^2 } \over {\partial x^2 }}\ln (f(x,t)), \end{aligned}$$
(33)

where R is constant and the function f is given by the perturbation expansion,

$$\begin{aligned} f(x,t) = 1 + \sum \limits _{n = 0}^\infty {\nu ^n f_n (x,t)}, \end{aligned}$$
(34)

where \(\nu \) is a bookkeeping nonsmall parameter [31], and \(f_n(x,t)\), \(n=1,2,\ldots \), which are independent of \(\nu \), are unknown functions that will be determined by substituting the Eq. (34) into the bilinear form and solving the resulting equations by equating different powers of \(\nu \) to zero.

The simplest solution of the higher-order KdV equation is the one-soliton solution (\(N= 1 \)) generated from

$$\begin{aligned} f_1(x,t) = \exp \theta \end{aligned}$$
(35)

where the phase \(\theta \) is given by

$$\begin{aligned} \theta = k x - \omega t + \delta \end{aligned}$$
(36)

where k is the wave number, \(\omega \) is the angular frequency and \(\delta \) is the phase shift. Substituting Eq. (27) into the linear terms of Eq. (1) and solving the resulting equation, we obtain the dispersion law, in absence of the surface tension

$$\begin{aligned} \omega = k {+} {1 \over 6}\varepsilon k^3 - {3 \over 8}\varepsilon ^2 k^5 {+} {{55} \over {3024}}\varepsilon ^3 k^7 + {{11813} \over {181440}}\varepsilon ^4 k^9\nonumber \\ \end{aligned}$$
(37)

To determine R, we substitute Eq. (33) into Eq. (31) where, f(x, t) is replaced by

$$\begin{aligned} f(x,t) = 1 +\nu f_1(x,t), \end{aligned}$$
(38)

with (\(N=1\)) and after resolution, we find that \(R=2\). Without loss of generality, let \(\nu =1\). By using Eqs. (33), (34), (35), (36) and (37), we obtain one-soliton solution of Eq. (31) as follows

$$\begin{aligned} u(x,t) = {{2k_1^2 \exp ( - \omega t + k_1 x)} \over {(1 + \exp ( - \omega t + k_1 x))^2 }} \end{aligned}$$
(39)

After some transformations [28], we get

$$\begin{aligned} u(x,t)= & {} {{k_1^2 } \over 2}\sec h^2 \left( 0.5\left( - \left( k_1 + {1 \over 6}\beta k_1^3 - {3 \over 8}\beta ^2 k_1^5 \right. \right. \right. \nonumber \\&\left. \left. \left. + {{55} \over {3024}}\beta ^3 k_1^7 + {{11813} \over {181440}}\beta ^4 k_1^9 \right) t + k_1 x\right) \right) .\nonumber \\ \end{aligned}$$
(40)

If one takes into account the surface tension, the solution becomes

$$\begin{aligned} u(x,t)= & {} {{k_1^2 } \over 2}\sec h^2 \left( 0.5\left( - \left( k_1 + {1 \over 6}(1 - 3\tau )\beta k_1^3\right. \right. \right. \nonumber \\&-\, {3 \over 8}\beta ^2 k_1^5 + {1 \over {15120}}(275 - 399\tau - 315\tau ^2 \nonumber \\&- \, 945\tau ^3 )\beta ^3 k_1^7 + \left( {{11813} \over {181440}} - {{55} \over {6048}}\tau \right. \nonumber \\&\left. -\, {{19} \over {2880}}\tau ^2 - {1 \over {96}}\tau ^3- {5 \over {128}}\tau ^4 \right) \nonumber \\&\left. \left. \left. \beta ^4 k_1^9 \right) t + k_1 x\right) \right) , \end{aligned}$$
(41)

where the dispersion law is given by

$$\begin{aligned} \omega= & {} \left( k + {1 \over 6}(1 - 3\tau )\beta k^3 - {3 \over 8}\beta ^2 k^5\right. \nonumber \\&+\, {1 \over {15120}}(275 - 399\tau - 315\tau ^2 - 945\tau ^3 )\nonumber \\&\times \beta ^3 k^7 + \left( {{11813} \over {181440}} - {{55} \over {6048}}\tau \right. \nonumber \\&\left. \left. -\, {{55} \over {2880}}\tau ^2 - {1 \over {96}}\tau ^3 - {5 \over {128}}\tau ^4 \right) \beta ^4 k^9 \right) . \end{aligned}$$
(42)

4.2 Two-soliton solutions

In addition to the one-soliton solution as given in Eq. (40), there exists also two-, three-soliton solutions, etc. In particular, the two-soliton solution \((N=2)\) is typically of the form

$$\begin{aligned} f(x,t)=1+\nu f_1(x,t)+\nu ^2 f_2(x,t), \end{aligned}$$
(43)

where \(\textit{f}_\textit{1}(x,t)\) is defined by

$$\begin{aligned} f_1 (x,t)=\exp \theta _1+\exp \theta _2 \end{aligned}$$
(44)

and \(\textit{f}_\textit{2}(x,t)\) by

$$\begin{aligned} f_2 (x,t)=a_{12} \exp (\theta _1 + \theta _2 ), \end{aligned}$$
(45)

respectively, where the phases \(\theta _1\) and \(\theta _2\) are given by \(\theta _1 = k_1 x - \omega _1 t + \delta _1 \) and \(\theta _2 = k_2 x - \omega _2 t + \delta _2 \). Again Eq. (35) determines the dispersion laws with and without surface tension

$$\begin{aligned} \omega _i= & {} k_i + {1 \over 6}(1 - 3\tau )\beta k_i^3 - {3 \over 8}\beta ^2 k_i^5 + {1 \over {15120}}\nonumber \\&\times (275 - 399\tau - 315\tau ^2 - 945\tau ^3 )\beta ^3 k_i^7\nonumber \\&+ \left( {{11813} \over {181440}} - {{55} \over {6048}}\tau - {{55} \over {2880}}\tau ^2- {1 \over {96}}\tau ^3 \right. \nonumber \\&\left. - {5 \over {128}}\tau ^4 \right) \beta ^4 k_i^9, \quad i=1, 2. \end{aligned}$$
(46)

Inserting Eq. (33) into Eq. (31), at \(0(\nu ^2)\), we obtain

$$\begin{aligned} a_{12} = - {A \over B}, \end{aligned}$$
(47)
Fig. 1
figure 1

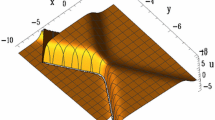
One-soliton solution of the higher-order equations (39) and (40) (\({k}=0.5, \tau =0.0\)) for different values of \(\varepsilon \): a \(\varepsilon =0.0\), b \(\varepsilon =0.1\), c \(\varepsilon =0.3\), d \(\varepsilon =1.0\); (\({k}=0.5\), \(\tau =0.6\)) for different values of \(\varepsilon \): i \(\varepsilon =0.0\), j \(\varepsilon =0.1\), k \(\varepsilon =0.3\), l \(\varepsilon =1.0\); (\({k}=1\), \(\tau =0\)) for different values of \(\varepsilon \): e \(\varepsilon =0.0\), f \(\varepsilon =0.1\), g \(\varepsilon =0.3\), h \(\varepsilon =1.0\); (\({k}=1\), \(\tau =0.6\)) for different values of \(\varepsilon \): m \(\varepsilon =0.0\), n \(\varepsilon =0.1\), o \(\varepsilon =0.3\), p \(\varepsilon =1.0\)

Full size image
Fig. 2
figure 2

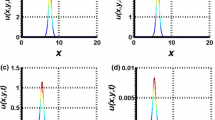
Two-soliton solutions of the higher-order equation (48) (\(k_1=1\), \(k_2=2\), \(\tau =0\)) for different values of \(\varepsilon \): a \(\varepsilon =0.7\), b \(\varepsilon =0.8\), c \(\varepsilon =0.9\), d \(\varepsilon =1.0\); (\(k_1=1\), \(k_2=2\), \(\tau =12\)) for different values of \(\varepsilon \): e \(\varepsilon =0.05\), f \(\varepsilon =0.08\), g \(\varepsilon =0.09\), h \(\varepsilon =0.1\); (\(k_1=0.5\), \(k_2=1\), \(\tau =0.0\)) for \(\varepsilon \): i \(\varepsilon =1\); (\(k_1=1\), \(k_2=2\, \tau =0.0\)) for value of \(\varepsilon \): j \(\varepsilon =1.0\); (\(k_1=2\), \(k_2=3\), \(\tau =0.0\)) for value of \(\varepsilon \): (k) \(\varepsilon =1.0\); (\(k_1=3\), \(k_2=4\), \(\tau =0.0\)) for value of \(\varepsilon \): l \(\varepsilon =1.0\); (\(k_1=0.5\), \(k_2=1\), \(\tau =12\)) for value of \(\varepsilon \): m \(\varepsilon =0.0001\); (\(k_1=1\), \(k_2=2\), \(\tau =12\)) for value of \(\varepsilon \) n \(\varepsilon =0.0001\); (\(k_1=2\), \(k_2=3\), \(\tau =12\)) for value of \(\varepsilon \) o \(\varepsilon =0.0001\); (\(k_1=3\), \(k_2=4\), \(\tau =12\)) for value of \(\varepsilon \) p \(\varepsilon =0.0001\)

Full size image

where A is given by

$$\begin{aligned} {A}= & {} \varepsilon ^{3} (118130{k}_{1}^{{10}} - 153569{k}_{1}{9} {{k}}_{2} + 208764{k}_{1}{8} {{k}}_{2}{2} \nonumber \\&-\, 96909{k}_{1}{7} {{k}}_{2}^{3} + 186739{k}_{1}{6} {{k}}_{2}{4} \nonumber \\&-\, 108087{k}_{1}{5} {{k}}_{2}{5} - 186739{k}_{1}{4} {{k}}_{2}{6} - 96909{k}_{1}^{3} {{k}}_{2}{7} \nonumber \\&+ \, 208764{k}_{1}{2} {{k}}_{2}{8} - 153569{k}_{1} {{k}}_{2}{9} + 118130{k}_{2}^{{10}}) \nonumber \\&+\,\varepsilon {2} (27500{k}_{1}{7} {{k}}_{2} + 15860{k}_{1}{6} {{k}}_{2}{2} - 7040{k}_{1}{5} {{k}}_{2}^{3}\nonumber \\&+\, 34340{k}_{1}{4} {{k}}_{2}{4} - 7040{k}_{1}^{3} {{k}}_{2}{5} + 15860{k}_{1}{2} {{k}}_{2}{6} \nonumber \\&+\, 27500{k}_{1} {{k}}_{2}{7}) +\varepsilon (-715680{k}_{1}{6} \nonumber \\&+ \,945840{k}_{1}{5}{{k}}_{2} - 885360{k}_{1}{4} {{k}}_{2}{2} + 927360{k}_{1}^{3} {{k}}_{2}^{3} \nonumber \\&-\, 885360{k}_{1}{2} {{k}}_{2}{4} + 945840{k}_{1} {{k}}_{2}{5} - 715680{k}_{2}{6} )\nonumber \\&+\,302400{k}_{1}^{3} {{k}}_{2} - 1209600{k}_{1}{2} {{k}}_{2}{2} + 302400{k}_{1} {{k}}_{2}^{3} ,\nonumber \\ \end{aligned}$$
(48)

and B by

$$\begin{aligned} {B}= & {} ({k}_{1} + {k}_{2} ){2} (\varepsilon ^{3} (35439{k}_{1}{8} - 70878{k}_{1}{7} {{k}}_{2}\nonumber \\&-\, 70878{k}_{1}{6} {{k}}_{2}{2} - 259886{k}_{1}{5} {{k}}_{2}^{3} \nonumber \\&- \,236260{k}_{1}{4} {{k}}_{2}{4} - 259886{k}_{1}^{3} {{k}}_{2}{5} \nonumber \\&-\, 70878{k}_{1}{2} {{k}}_{2}{6} - 70878{k}_{1} {{k}}_{2}{7} \nonumber \\&+\, 35439{k}_{2}{8}) +\varepsilon {2} (5500{k}_{1}{6} - 44000{k}_{1}{5} {{k}}_{2}\nonumber \\&-\, 71500{k}_{1}{4} {{k}}_{2}{2} - 121000{k}_{1}^{3} {{k}}_{2}^{3} \nonumber \\&-\, 71500{k}_{1}{2} {{k}}_{2}{4} - 44000{k}_{1} {{k}}_{2}{5} + 5500{k}_{2}{6} ) \nonumber \\&+\, \varepsilon (-194880{k}_{1}{4} + 354480{k}_{2} {{k}}_{1}^{3} - 35280{k}_{1}{2} {{k}}_{2}{2} \nonumber \\&+ \,354480{k}_{1} {{k}}_{2}^{3} - 194880{k}_{2}{4} ) - 302400{k}_{1} {{k}}_{2}).\nonumber \\ \end{aligned}$$
(49)

For comparison, following Burde [19], we take \(k_1=1\) and \(k_2=2\), that leads to

$$\begin{aligned} a_{12} = {-} {1 \over 9}{{1814400 {+} 24648960\varepsilon - 4921320\varepsilon ^2 - 94728136\varepsilon ^3 } \over {604800 - 90720\varepsilon + 3536500\varepsilon ^2 + 19101621\varepsilon ^3 }}.\nonumber \\ \end{aligned}$$
(50)

If one takes into account the surface tension, it becomes

$$\begin{aligned} a_{12} = - {{(8 + \alpha _1 \varepsilon + \alpha _{2} \varepsilon ^2 + \alpha _{3} \varepsilon ^3 + \alpha _{4} \varepsilon ^4 )} \over {\gamma _{1} \varepsilon + \gamma _{2} \varepsilon ^2 + \gamma _{3} \varepsilon ^3 + \gamma _{4} \varepsilon ^4 }}, \end{aligned}$$
(51)

with

$$\begin{aligned} \alpha _1= & {} \left( {{82} \over 3} + 134\tau \right) \nonumber \\ \alpha _{2}= & {} \left( {{2273} \over {15}} - 238\tau - 321\tau ^2 \right) , \nonumber \\ \alpha _{3}= & {} \left( - {{229399} \over {7560}} {+} {{150071} \over {360}}\tau {+} {{13901} \over {24}}\tau ^2 {+} {{8429} \over 8}\tau ^3 \right) \nonumber \\ \alpha _4= & {} \left( - {{14378461} \over {56700}} - {{1450667} \over {945}}\tau - {{217118} \over {45}}\tau ^2\right. \nonumber \\&\left. + \, {{399} \over 2}\tau ^3 + {{9887} \over 4}\tau ^4 \right) \nonumber \\ \gamma _{1}= & {} (54 - 243\tau ), \nonumber \\ \gamma _{2}= & {} \left( - {{81} \over {10}} + {{729} \over 2}\tau + {{2187} \over 4}\tau ^2 \right) \nonumber \\ \gamma _{3}= & {} \left( {{35365} \over {112}} - {{41553} \over {80}}\tau - {{6561} \over {16}}\tau ^2 - {{19683} \over {16}}\tau ^3 \right) , \nonumber \\ \gamma _{4}= & {} \left( {{2728803} \over {1600}} - {{150903} \over {560}}\tau + {{1043199} \over {160}}\tau ^2 \right. \nonumber \\&\left. -\, {{177147} \over {64}}\tau ^4 \right) . \end{aligned}$$
(52)
Fig. 3
figure 3

Dependence of the angular frequency versus the wave number without surface tension(\(\tau =0\)) for different values of \(\varepsilon \): a \(\varepsilon =0.0\), b \(\varepsilon =0.1\), c \(\varepsilon =0.3\), d \(\varepsilon =1.0\); with surface tension (\(\tau =0.6\)) for different values of \(\varepsilon \): e \(\varepsilon =0.0\), f \(\varepsilon =0.1\), g \(\varepsilon =0.3\), h \(\varepsilon =1.0\)

Full size image

Finally, let \(\nu =1\), one found the two-soliton solutions of Eq. (31) as

$$\begin{aligned}&\eta (x,t)\nonumber \\&\quad = {{2(k_1^2 \exp (\theta _1 ) + k_2^2 \exp (\theta _2 ) + a_{12} (k_1 + k_2 )^2 \exp (\theta _1 + \theta _1 )} \over {1 + \exp (\theta _1 ) + \exp (\theta _2 ) + a_{12} \exp (\theta _1 + \theta _2 )}} \nonumber \\&\qquad - {{2(k_1 \exp (\theta _1 ) {+} k_2 \exp (\theta _2 ) + a_{12} (k_1 + k_2 )\exp (\theta _1 {+} \theta _2 ))^2 } \over {(1 {+} \exp (\theta _1 ) + \exp (\theta _2 ) + a_{12} \exp (\theta _1 + \theta _2 ))^2 }} ,\nonumber \\ \end{aligned}$$
(53)

Rearranging Eq. (51) [53] can produce

$$\begin{aligned} \eta (x,t)= & {} \left( {{k_2^2 - k_1^2 } \over 2}\right) \nonumber \\&\times \left( {{k_2^2 \cos ech^2 \left( {{{\tilde{\theta }}_2 } \over 2}\right) + k_1^2 \sec h^2 \left( {{{\tilde{\theta }}_1 } \over 2}\right) } \over {\left( k_2 \coth \left( {{{\tilde{\theta }}_2 } \over 2}\right) - k_1 \tanh \left( {{{\tilde{\theta }}_1 } \over 2}\right) \right) ^2 }}\right) .\nonumber \\ \end{aligned}$$
(54)

where \({\tilde{\theta }}_1 = k_1 x - \omega _1 t + \Delta _1 ,\quad {\tilde{\theta }}_2 = k_2 x - \omega _2 t + \Delta _2 \), where the phases shift \(\Delta _1\) and \(\Delta _2\) are constants.

Figures 1 and 2 show one- and two-soliton solutions of Eqs. (40), (41) and (48) which have been constructed by Hirota’s bilinear method. As seen, solutions of Eq. (48) are strongly dependent on the amplitude parameter \(\varepsilon \) and surface tension coefficient \(\tau \) (see Fig. 2). We remark also that the wave amplitude increases when the wave number increases as indicated in Fig. 2. In Fig. 3, we note that the dispersion law is a increasing function of the surface tension coefficient.

5 Conclusion

We have studied the dynamics of nonlinear excitations in the two-dimensional shallow water wave problems from the equations of hydrodynamics, with and without surface tension. The Boussinesq perturbation expansion of the Euler equations has given a system of coupled equations for the scaled horizontal velocity w and the surface elevation \(\eta \). The above system has been decoupled, restricting to unidirectional waves, by assuming a relationships between the horizontal velocity at the mean height, and elevation. Equation of motion which governs the dynamics of the elevation has been found, which is a new KdV evolution equation with nonlinear and nonlocal terms for the water wave problem. The Hirota’s bilinear method was used to derive the single and two-soliton solutions. Periodic solutions can be derived by using the tanh–coth method [28, 30, 46, 47]. The model can be extended to other physically interesting situations, such as bidirectional water wave problems [19]. These problems are under consideration and will be published in future works.