Effects produced by oscillations applied to nonlinear dynamic systems: a general approach and examples

Abstract

A general approach to study effects produced by oscillations applied to nonlinear dynamic systems is developed. It implies a transition from initial governing equations of motion to much more simple equations describing only the main slow component of motions (the vibro-transformed dynamics equations). The approach is named as the oscillatory strobodynamics, since motions are perceived as under a stroboscopic light. The vibro-transformed dynamics equations comprise terms that capture the averaged effect of oscillations. The method of direct separation of motions appears to be an efficient and simple tool to derive these equations. A modification of the method applicable to study problems that do not imply restrictions on the spectrum of excitation frequencies is proposed. It allows also to abandon other restrictions usually introduced when employing the classical asymptotic methods, e.g., the requirement for the involved nonlinearities to be weak. The approach is illustrated by several relevant examples from various fields of science, e.g., mechanics, physics, chemistry and biophysics.

1 Introduction

Oscillations applied to nonlinear dynamic systems give rise to several unusual, seemingly paradoxical phenomena [1, 2]. Stabilization of pendulum upper position, vibrational maintaining or braking of rotations, changing in materials rheological properties, excitation or suppression of chaotic motions and many other effects can be mentioned here (see, e.g., [1–4]). These phenomena in some cases can be employed to improve existing technological processes and machines and in others, in contrary, lead to accidents and even catastrophes. Such phenomena arising in the field of mechanics are relatively well studied, in particular by means of the general approach, named vibrational mechanics (VM) [1], and the corresponding analytical method, the method of direct separation of motions (MDSM). Analysis of effects produced by oscillations applied to physical, chemical, biological systems and production processes is, however, just getting started. Only several studies conducted by different, mostly numerical, methods are published (see, e.g., [5, 6]). On the other hand, it is hard to indicate a phenomenon or a process for which such effects are of no practical or scientific interest.

The first aim of the present work is to extend the VM approach and the MDSM for studying dynamic systems from various fields of science, e.g., physics, chemistry, biology and others. The basic idea of such extension has been discussed in the papers [7, 8]. The section of nonlinear dynamics studying effects produced by oscillations applied to dynamic systems was proposed to be named as the oscillatory strobodynamics (OS). The name is motivated by the fact that the corresponding solution approach implies system behavior to be perceived as under a stroboscopic light, so that only the main, slow component of motions is captured.

Most of the problems considered by the MDSM can be solved also by the other methods of nonlinear dynamics, e.g., the multiple scales method [9] or the method of averaging [10, 11]. However, the MDSM features several significant advantages over these methods, e.g., the simplicity in application, and the transparency of the physical interpretation. A detailed comparison of the MDSM with the other methods is given in the monographs [1, 2].

The conventional MDSM implies frequency of oscillating excitation to be high, i.e., much larger than the system characteristic (natural) frequency. The classical asymptotic methods, e.g., the multiple scales method [9] and the method of averaging [10, 11], also imply restrictions on the excitation frequency spectrum: Only near-resonant, low-frequency or high-frequency excitations can be captured. The second aim of the present work is to develop a modification of the MDSM for solving a broader range of problems, namely problems that do not imply restrictions on the spectrum of excitation frequencies. Such a modification is especially relevant for continuous systems having multitude of natural frequencies. This version of the MDSM allows also to abandon other restrictions usually introduced when employing the classical asymptotic methods, e.g., the requirement for the involved nonlinearities to be weak. So that problems without an explicit small parameter can be considered by means of the method. The idea of such modification of the MDSM has been discussed in the papers [12, 13]. It is closely related to the main aim of the paper discussed above, since such modification of the method is particularly relevant for problems arising in electrical engineering, physics, chemistry, biology, etc.

In the present paper, the proposed extension of the VM approach and the modification of the MDSM are illustrated by several relevant examples. The paper is structured as follows. In Sect. 2, the basics of the OS approach for treating nonlinear systems under high-frequency excitations are explained. Section 3 is devoted to describing the corresponding method, the MDSM and its application for the OS problems. In Sect. 4, the validity of the method is briefly discussed. Section 5 describes the modification of the MDSM for solving problems without restrictions on the spectrum of excitation frequencies. In Sect. 6, several relevant examples are studied: Sects. 6.1–6.5 consider dynamics of systems from various fields of science under high-frequency excitation, and Sects. 6.6–6.8 are concerned with the problems that do not imply the excitation frequency to be high. In Sect. 7, the main conclusions of the paper are outlined.

2 Slow and fast motions of nonlinear systems under high-frequency excitation: the main idea of the OS approach

First, we consider high-frequency excitations. Motion ${\varvec{x}}(t)$ of a dynamic system arising due to such excitation can be usually separated into two components: slow ${\varvec{X}}(t)$ and fast ${\varvec{\psi }}(t)$ (notions “high-frequency,” “fast” and “slow” can be formalized [1]). Figure 1 illustrates this for the simple one-dimensional case. Note that exactly the same figure illustrates the well-known definition of oscillations as a process described by the coordinate x(t) which from time to time intersects a certain constant or slowly varying level [14]. Thus the above statement is rather general: It merely means that the system under oscillating excitation exhibits oscillations.

Fig. 1

Fast and slow motions of an oscillating dynamic system; definition of oscillations

The main idea of the proposed approach lies in the transition from initial governing equations of motions to equations describing only the slow component ${\varvec{X}}(t)$. This component is usually of primary interest; and equations describing it can be much simpler than the initial equations for vector ${\varvec{x}}(t)$.

Let dynamics of a process be described by the relation:

$$\begin{aligned} {\varvec{Z}}\left( {{\varvec{x}},\,{\varvec{a}},t} \right) =0, \end{aligned}$$

(1)

where ${\varvec{x}}$ is state vector of the considered system, a vector of parameters and t time. Operator Z can represent finite, differential, integral and other equations with the corresponding initial and boundary conditions.

In the presence of high-frequency excitation, this relation takes the form:

$$\begin{aligned} {{\varvec{Z}}}[{{\varvec{x}}}+{\varvec{\psi } }_{{\varvec{x}}} (\omega t),{{\varvec{a}}}+{\varvec{\psi } }_{{\varvec{a}}} (\omega t),t]={{\varvec{F}}}(\omega t) \end{aligned}$$

(2)

where ${\varvec{\psi } }_{{\varvec{x}}}$, ${\varvec{\psi } }_{\varvec{a}}$ and ${{\varvec{F}}}$ are functions periodic in the “fast time” $\tau =\omega t$, and $\omega \gg 1$. It is assumed therefore that the high-frequency excitation can be applied directly through the state vector ${{\varvec{x}}}$, or the vector of parameters ${{\varvec{a}}}$; external excitation ${{\varvec{F}}}$ is also possible.

Practically in all cases the change in the vector x due to high-frequency excitations can be represented as

$$\begin{aligned} {{\varvec{x}}}(t)={{\varvec{X}}}(t)+{\varvec{\psi } }(t,\omega t) \end{aligned}$$

(3)

where ${{\varvec{X}}}$ is slow, and ${\varvec{\psi } }$ is fast $2\pi$-periodic in time $\tau =\omega t$ variable, with average zero:

$$\begin{aligned} \left\langle {\varvec{\psi } } \right\rangle =\frac{1}{2\pi }\int \limits _0^{2\pi } {{\varvec{\psi } }(t,\tau )\hbox {d}\tau } =0 \end{aligned}$$

(4)

angular brackets designate averaging in the period $2\pi$ on time $\tau$. Variable ${{\varvec{X}}}(t)$, as it was noted above, is of primary interest; and relations (3)–(4) represent the assumption that periodic oscillations arise in the system due to high-frequency excitations.

By means of one mathematical method or another, and with the averaging procedure being employed, under certain assumptions regarding the operator ${{\varvec{Z}}}$, it is possible to obtain equation that involves only the slow component ${{\varvec{X}}}$:

$$\begin{aligned} {{\varvec{Z}}}^{*}({{\varvec{X}}},{{\varvec{a}}}^{*},t)=0 \end{aligned}$$

(5)

Note that operator ${{\varvec{Z}}}^{*}$ is much simpler than ${{\varvec{Z}}}$, e.g., it can be of a lower dimension. The same applies to the vectors of parameters ${{\varvec{a}}}$ and ${{\varvec{a}}}^{*}$.

So, slow motions ${{\varvec{X}}}$ of the system obey dynamic laws that differ from those for motions ${{\varvec{x}}}$. In [8], this dynamics was proposed to be named as the oscillatory strobodynamics (OS). The OS is the dynamics perceived by an observer with special glasses through which fast motions cannot be seen. Note that the OS may be considered also as a particular case of the dynamics of systems with partially ignored motions [1, 2].

Equation (5) is proposed to be named as the equation of oscillatory strobodynamics (EOS) [8] or the vibro-transformed dynamics equation (VDE), in contrast to Eq. (1) that describes “normal” dynamics.

3 The method of direct separation of motions for problems of high-frequency oscillating excitations on dynamical systems

The method of direct separation of motions [1] appears to be a convenient and simple tool for obtaining Eq. (5). Its application for solving mechanical problems is discussed in [1, 2]. Here, the basics of this method for treating a broader range of problems, namely the OS problems, are described.

Inserting expression (3) into (2), we get

$$\begin{aligned}&{{\varvec{Z}}}[{{\varvec{X}}}(t)+{\varvec{\psi } }(t,\omega t)+{\varvec{\psi } }_{\varvec{x}} (\omega t),{{\varvec{a}}}+{\varvec{\psi } }_{\varvec{a}} (\omega t),t]\nonumber \\&\quad ={{\varvec{F}}}(\omega t) \end{aligned}$$

(6)

Due to the fact that we have introduced two unknown variables ${{\varvec{X}}}$ and ${\varvec{\psi } }$ instead of the initial one ${{\varvec{x}}}$, we are allowed to impose additional constraint on these variables. As this constraint, we require variables ${{\varvec{X}}}$ and ${\varvec{\psi } }$ to satisfy the averaged Eq. (6), so that the following relation holds true:

$$\begin{aligned}&\left\langle {{{\varvec{Z}}}[{{\varvec{X}}}(t)+{\varvec{\psi } }(t,\omega t)+{\varvec{\psi } }_{\varvec{x}} (\omega t),{{\varvec{a}}}+{\varvec{\psi } }_{\varvec{a}} (\omega t),t]} \right\rangle \nonumber \\&\quad =\left\langle {{{\varvec{F}}}(\omega t)} \right\rangle \end{aligned}$$

(7)

Consequently, for the initial Eq. (6) to be satisfied we also get:

$$\begin{aligned}&{{\varvec{Z}}}[{{\varvec{X}}}(t)+{\varvec{\psi } }(t,\omega t)+{\varvec{\psi } }_{\varvec{x}} (\omega t),{{\varvec{a}}}+{\varvec{\psi } }_{\varvec{a}} (\omega t),t] \nonumber \\&\qquad -\,\left\langle {{{\varvec{Z}}}[{{\varvec{X}}}(t)+{\varvec{\psi } }(t,\omega t)+{\varvec{\psi } }_{\varvec{x}} (\omega t),{{\varvec{a}}}+{\varvec{\psi } }_{\varvec{a}} (\omega t),t]} \right\rangle \nonumber \\&\quad ={{\varvec{F}}}(\omega t)-\left\langle {{{\varvec{F}}}(\omega t)} \right\rangle \end{aligned}$$

(8)

In a more compact form, Eqs. (7) and (8) can be written as:

$$\begin{aligned}&\left\langle {{\varvec{Z}}} \right\rangle =\left\langle {{\varvec{F}}} \right\rangle \end{aligned}$$

(9)

$$\begin{aligned}&{{\varvec{Z}}}-\left\langle {{\varvec{Z}}} \right\rangle ={{\varvec{F}}}-\left\langle {{\varvec{F}}} \right\rangle \end{aligned}$$

(10)

Combining Eqs. (7) and (8) or (9) and (10), and taking (3) into account, allows to obtain initial Eq. (2). Note that Eqs. (7)–(8) are not simpler than the initial equation; in particular, if operator ${{\varvec{Z}}}$ represents a system of differential equations, then (7)–(8) represent a system of integro-differential equations. However, (7)–(8) are much more convenient for the approximate solving. Equations (7) and (8) are proposed to be named as the equations of slow and fast motions, respectively.

The following statements form the basis of the MDSM:

• (1) Slow motion ${{\varvec{X}}}$ is of primary interest.

• (2) It is sufficient to determine variable ${\varvec{\psi } }$ approximately, since it is present in Eqs. (7) and (9) only under the averaging operator, and thus this approximation will not lead to any considerable errors in the resulting equation for the variable ${{\varvec{X}}}$.

• (3) As one of the approximations, slow variables ${{\varvec{X}}}$ and t are considered as constants (“frozen”) when solving fast motions Eqs. (8) and (10).

Having determined the component ${\varvec{\psi } }={\varvec{\psi } }({{\varvec{X}}},t,\omega t)$ from (8) or (10) and performing the averaging operation, Eq. (7) or (9) takes the form:

$$\begin{aligned}&{{\varvec{Z}}}^{*}({{\varvec{X}}},{{\varvec{a}}}^{*},t)\equiv \left\langle {{\varvec{Z}}}[{{\varvec{X}}}(t)+{\varvec{\psi } }(t,\omega t)+{\varvec{\psi } }_{\varvec{x}} (\omega t),{{\varvec{a}}}\right. \nonumber \\&\quad \left. +\,{\varvec{\psi } }_{\varvec{a}} (\omega t),t] \right\rangle =0 \end{aligned}$$

(11)

As it was noted, operator ${{\varvec{Z}}}^{*}$ can be considerably simpler than ${{\varvec{Z}}}$.

The approximate approach described above implies that the velocity of component ${\varvec{\psi } }$ variations is much larger than the velocity of ${{\varvec{X}}}$ variations, i.e., component ${{\varvec{X}}}$ is indeed slow, and component ${\varvec{\psi } }$ fast. This requirement is the main assumption of the OS. Its rigorous mathematical description for mechanical problems is given in [1]; this description can be extended also for problems considered within the OS. The most important conditions under which the main assumption of the OS holds true are the following:

• (1) Frequency $\omega$ should be much larger than the characteristic frequency of the slow component ${{\varvec{X}}}$ variations (for applied problems three–five times larger).

• (2) Periodic solutions ${\varvec{\psi } }$ of the fast motions equations should be asymptotically stable with respect to all fast components of the vector ${{\varvec{x}}}$ in the whole considered range of parameters.

The last condition may be explained as follows. If some components of the state vector ${{\varvec{x}}}$ are fast, i.e., for them ${{\varvec{X}}}=0$, ${{\varvec{x}}}={\varvec{\psi } }$, then these components will not be present in Eq. (11). Consequently, dimension of the system will be reduced by the number of the fast components, so that the requirement for the solution to be asymptotically stable with respect to all fast components becomes necessary [1].

The approximate method described above is based on the paper [3] by P.L. Kapitsa in which motions of a pendulum with vibrating suspension axis were considered. This method was generalized by the author and employed by him and other scientists for solving various problems of action of vibration on mechanical systems [1, 2, 4, 15].

4 On the validity of the MDSM

Application of the MDSM for most of the considered problems, described by differential equations, is justified by the theorems of V.M. Volosov and B.I. Morgunov [16, 17]. Generalization for cases beyond these theorems is discussed in Sect. 5.

However, as is known (see, e.g., [18]), even a theoretically justified approximate solution requires a posteriori validation. Comparison with numerical solution can be also useful. It becomes especially important for cases when strict mathematical justification is not presented or omitted. In such cases, from mathematicians’ point of view, the method employed may be considered as a heuristic approach for determining solutions. If the obtained solution has been validated a posteriori, then it is considered as correct [18].

Similarly to the other approximate methods, e.g., the method of harmonic balance [14, 19] and Hill’s method of infinite determinants [19], the MDSM provides an explicit condition under which the obtained results are valid for every particular problem considered. Also an explicit expression which estimates the error in the obtained solution is provided.

5 Modification of the MDSM: problems without an explicit small parameter

For many practically important problems, external excitation of the system cannot be considered as high frequency, but, instead, is low frequency, or near resonant, or non-resonant, etc. Often, response of the system to excitation from the widest possible frequency range is of interest. The modification of the MDSM discussed in the present section of the paper is for studying such cases (see also [12, 13]).

The modified MDSM implies considering dimensionless equations; in particular, the shift from the original dimensional time t to the non-dimensional one $\tau =\omega t$ is implemented. Solution is proposed to be sought in the form, similar to (3):

$$\begin{aligned} {{\varvec{x}}}={{\varvec{X}}}(T_1 )+{\varvec{\psi } }(T_1 ,T_0 ), \end{aligned}$$

(12)

where the new timescales $T_0 =\tau$ and $T_1 =\varepsilon T_0$ are introduced, and $\varepsilon \ll 1$ is a formal small parameter, and variables X and ${\varvec{\psi }}$ have the same meaning as above. Variable ${\varvec{\psi }}$ is $2\pi$-periodic in time $T_0$, with average zero:

$$\begin{aligned} \left\langle {{\varvec{\psi } }(T_1,T_0 )} \right\rangle =\frac{1}{2\pi }\int \limits _0^{2\pi } {{\varvec{\psi } }(T_1,T_0 )\hbox {d}T_0 } =0 \end{aligned}$$

Similarly to the multiple scales method [9], the modified MDSM implies timescales $T_1$ and $T_0$ to be considered independent, so that $\frac{\hbox {d}^{2}}{\hbox {d}t_0^2 }=\frac{\partial ^{2}}{\partial T_0^2 }+2\varepsilon \frac{\partial ^{2}}{\partial T_1 \partial T_0 }+\varepsilon ^{2}\frac{\partial ^{2}}{\partial T_1^2 }$.

As appears the requirement for the excitation frequency $\omega$ to be much larger than the characteristic frequency of the system’s oscillations, implied in the conventional MDSM, is abandoned, . Instead of this, the restriction on the sought solutions is imposed: Only solutions that are close to periodic and describe oscillations with slowly varying amplitudes can be determined. These solutions feature two distinct timescales and are similar to those obtained by the classical asymptotic methods, e.g., the multiple scales method [9]. Such solutions are usually of interest for applications.

Note, however, that the introduced small parameter $\varepsilon$ is not a feature of the considered problem or the corresponding governing equations. It is the feature of the sought solution. This constitutes the main difference of the modified MDSM from the conventional asymptotic methods.

Introducing the small parameter $\varepsilon$ in the way described above enables to employ the modified MDSM for problems in which it is impossible to assign a small parameter in the governing equations. In particular, strongly nonlinear problems can be studied (see Sects. 6.7 and 6.8). The introduced small parameter $\varepsilon$ defines proximity of the solution to pure periodic one, i.e., how slow the amplitudes are varying. This small parameter differs from the one implied in the classical bifurcation theory [20], since it is not present explicitly in the considered governing equations.

It should be noted, however, that the modified MDSM implies the conventional simplifications of the method to be abandoned. In particular, when solving fast motions equations (for variable ${\varvec{\psi }}$), slow variables X and $T_1$ cannot be considered as constants.

The discussed modification of the MDSM may be considered as a development of the ideas proposed in [1] for solving equations without an explicit small parameter: A certain restriction on the sought solutions is imposed to resolve the problem. However, the problems considered in [1] implied the sought motion ${{\varvec{x}}}$ to be close to motion ${{\varvec{x}}}_0$ of a prescribed type, e.g., describing harmonic oscillations or uniform rotation. Consequently, the formal small parameter was introduced in front of the residual ${{\varvec{Z}}}({{\varvec{x}}})-{{\varvec{Z}}}({{\varvec{x}}}_0 )$.

For every particular problem considered, the modified MDSM provides an explicit condition under which the obtained results are valid and estimates the error in the solution (see Sects. 6.6–6.8).

6 Examples

In this section, the approach described above will be illustrated by several relevant examples from various fields of science: Sects. 6.1–6.5 consider dynamics of systems under high-frequency excitations, and Sects. 6.6–6.8 are concerned with the problems that do not imply restrictions on the spectrum of excitation frequencies.

Problems in Sects. 6.1–6.4 were briefly discussed in the monograph [2] (in Russian); also some results are given in the paper [8]. Examples considered in Sects. 6.5 and 6.8 are novel, while those in Sects. 6.6 and 6.7 were partially studied in the papers [12, 13].

6.1 String with pulsating tension: “transformation” into a beam

As a mechanical example, we consider a string with the harmonically varying tension (Fig. 2a). The governing equation of motions of the string is the following:

$$\begin{aligned} \frac{\partial ^{2}u}{\partial t^{2}}-\frac{P_0 +P_1 \cos \omega t}{m}\frac{\partial ^{2}u}{\partial x^{2}}=0, \end{aligned}$$

(13)

and the boundary conditions are:

$$\begin{aligned} u \big |_{x=0} =0,\quad u \big |_{x=l} =0, \end{aligned}$$

(14)

where u is the transverse deflection of the string, m its mass per unit length, $P_0$ constant and $P_1 \cos \omega t$ varying components of tension, $\omega$ pulsations frequency and l length of the string.

Fig. 2

String with pulsating tension transforming into a simply supported beam

Employing the MDSM, we search a solution to (13) in the form:

$$\begin{aligned} u=U(x,t)+\psi (x,t,\omega t), \end{aligned}$$

(15)

where U is slow and $\psi$ fast component of the string deflection, so that

$$\begin{aligned} \left\langle {\psi (x,t,\omega t)} \right\rangle =0. \end{aligned}$$

(16)

Composing (7) and (8), one obtains the following equations of slow and fast motions, respectively:

$$\begin{aligned}&\frac{\partial ^{2}U}{\partial t^{2}}-\frac{P_0 }{m}\frac{\partial ^{2}U}{\partial x^{2}}-\frac{P_1 }{m}\left\langle {\frac{\partial ^{2}\psi }{\partial x^{2}}\cos \omega t} \right\rangle =0, \end{aligned}$$

(17)

$$\begin{aligned}&\frac{\partial ^{2}\psi }{\partial t^{2}}-\frac{P_0 }{m}\frac{\partial ^{2}\psi }{\partial x^{2}}-\frac{P_1 }{m}\left[ \frac{\partial ^{2}U}{\partial x^{2}}\cos \omega t+\frac{\partial ^{2}\psi }{\partial x^{2}}\cos \omega t\right. \nonumber \\&\quad \left. -\,\left\langle {\frac{\partial ^{2}\psi }{\partial x^{2}}\cos \omega t} \right\rangle \right] =0, \end{aligned}$$

(18)

and the boundary conditions take the form:

$$\begin{aligned} U \big |_{x=0}= & {} 0,\quad U \big |_{x=l} =0, \end{aligned}$$

(19)

$$\begin{aligned} \psi \big |_{x=0}= & {} 0,\quad \psi \big |_{x=l} =0. \end{aligned}$$

(20)

The fast motions Eq. (18) is then solved approximately, assuming that $\frac{\partial ^{2}U}{\partial x^{2}}\gg \frac{\partial ^{2}\psi }{\partial x^{2}}$ and terms U, $\frac{\partial ^{2}U}{\partial x^{2}}$ are “frozen.” Consequently, the following equation for $\psi$ is obtained:

$$\begin{aligned} \frac{\partial ^{2}\psi }{\partial t^{2}}=\frac{P_1 }{m}\frac{\partial ^{2}U}{\partial x^{2}}\cos \omega t, \end{aligned}$$

(21)

which allows for periodic solution of the form:

$$\begin{aligned} \psi =-\frac{P_1 }{m\omega ^{2}}\frac{\partial ^{2}U}{\partial x^{2}}\cos \omega t. \end{aligned}$$

(22)

Inserting this expression into (17), and performing the averaging operation, we get the following equation of slow motions, the VDE:

$$\begin{aligned} \frac{P_1^2 }{2m^{2}\omega ^{2}}\frac{\partial ^{4}U}{\partial x^{4}}+\frac{\partial ^{2}U}{\partial t^{2}}-\frac{P_0 }{m}\frac{\partial ^{2}U}{\partial x^{2}}=0 \end{aligned}$$

(23)

As is seen, this equation describes transverse oscillations of a beam with the effective stiffness

$$\begin{aligned} (EI)_\upsilon =\frac{P_1^2 }{2m\omega ^{2}}, \end{aligned}$$

(24)

which is subjected to action of the longitudinal force $P_0$. So, with respect to slow motions, the string “transforms” into the beam (Fig. 2b).

Requiring the following boundary conditions to be fulfilled

$$\begin{aligned} U \big |_{x=0}= & {} 0,\quad U \big |_{x=l} =0,\quad {\frac{\partial ^{2}U}{\partial x^{2}}} \big |_{x=0} \nonumber \\= & {} {\frac{\partial ^{2}U}{\partial x^{2}}} \big |_{x=l} =0, \end{aligned}$$

(25)

according to (22) we satisfy the boundary conditions (20) and (14).

According to the main assumption of the OS, the obtained result is correct for frequencies $\omega \gg \lambda _n$, where $\lambda _n$ is one of the beam natural frequencies; in practice, it is sufficient to require $\omega >(3\div 5)\lambda _n$. Note that this condition is checked a posteriori, basing on the obtained Eq. (23) of slow motions. If bending stiffness of the string is taken into account, then the corresponding initial governing equation is of the fourth order. In this case, term ${P_1^2 }/({2m\omega ^{2}})$ represents additional bending stiffness $(EI)_\upsilon$. This corresponds to the well-known problem of the so-called Indian magic rope considered by means of the MDSM in [21] (cf. also monograph [15]). The phenomenon of increased bending stiffness of a rope due to high-frequency actions was observed experimentally by V.B. Vasilkov [22]. Papers by V.N. Chelomey [23] and S.V. Chelomey [24], where similar effects were studied by means of various analytical and other methods, should be also mentioned here. An overview of the subsequent papers concerned with the problem of Indian magic rope is given in the monograph [15] and also in the paper [21].

Note that the phenomenon of increased bending stiffness occurs also in the case of a pipe conveying pulsating fluid [25, 26]. In paper [26], this result was obtained by the MDSM, whereas in the pioneering work [25] a much more elaborate solution procedure has been employed.

6.2 Lorenz oscillator: suppression and excitation of chaotic motions by an oscillating action

The following system of equations is considered:

$$\begin{aligned}&\ddot{\xi }+(\eta -1)\xi +\xi ^{3}=-\mu \dot{\xi }, \end{aligned}$$

(26)

$$\begin{aligned}&\dot{\eta }=-\frac{\mu }{\sigma +1}\left[ {b\eta -(2\sigma -b)\xi ^{2}} \right] +A\cos \omega t, \end{aligned}$$

(27)

where $\mu$, $\sigma$ and b are positive constants and $\mu$ can be considered as small, $\mu \ll 1$. These equations for $A=0$ represent the well-known Lorenz system [6]. It approximately describes the thermo-convection process and is thoroughly studied; the “deterministic chaos” arises in the system at certain values of the parameters.

For $\mu =0$, i.e., in the zeroth approximation, Eq. (27) has periodic solution $\eta _0 =\frac{A}{\omega }\sin \omega t$. Inserting it into (26), we get:

$$\begin{aligned} \ddot{\xi }_0 +\left( {\frac{A}{\omega }\sin \omega t-1} \right) \xi _0 +\xi _0^3 =0. \end{aligned}$$

(28)

Assuming, as before,

$$\begin{aligned} \xi _0 =B(t)+\psi (t, \omega t), \end{aligned}$$

(29)

where B is slow and $\psi$ is fast $2\pi$-periodic in time $\tau =\omega t$ variable with average zero, we get the following equations of slow and fast motions, respectively:

$$\begin{aligned}&\ddot{B}-B+\frac{A}{\omega }\left\langle {\psi \sin \omega t} \right\rangle +B^{3}+3B\left\langle {\psi ^{2}} \right\rangle \nonumber \\&\quad +\,\left\langle {\psi ^{3}} \right\rangle =0 \end{aligned}$$

(30)

$$\begin{aligned}&\ddot{\psi }+\frac{AB}{\omega }\sin \omega t-\psi +\frac{A}{\omega }\left( {\psi \sin \omega t-\left\langle {\psi \sin \omega t} \right\rangle } \right) \nonumber \\&\quad +\,\left( {\psi ^{3}-\left\langle {\psi ^{3}} \right\rangle } \right) +3B^{2}\psi +3B\left( {\psi ^{2}-\left\langle {\psi ^{2}} \right\rangle } \right) =0 \end{aligned}$$

(31)

Assuming $\omega \gg 1$, and the first two terms in (31) to be much larger than others, one obtains approximate periodic solution of (31) as:

$$\begin{aligned} \psi =\frac{AB}{\omega ^{3}}\sin \omega t, \end{aligned}$$

(32)

Consequently, Eq. (30), the VDE, takes the form of the Duffing equation:

$$\begin{aligned} \ddot{B}+\left( {\frac{1}{2}\frac{A^{2}}{\omega ^{4}}-1} \right) B+\left( {1+\frac{3}{2}\frac{A^{2}}{\omega ^{6}}} \right) B^{3}=0. \end{aligned}$$

(33)

And if

$$\begin{aligned} A>\sqrt{2}\omega ^{2}, \end{aligned}$$

(34)

the trivial solution of this equation is stable, otherwise its solutions oscillate near the points

$$\begin{aligned} B=\pm \sqrt{1-\frac{1}{2}\frac{A^{2}}{\omega ^{4}}}\Bigg /\sqrt{1+\frac{3}{2}\frac{A^{2}}{\omega ^{6}}} \end{aligned}$$

(35)

As is seen, under the made assumptions chaotic motions will not arise in the considered system. Note that the other ways of chaos suppression in the system are also possible, with high-frequency action being introduced in various manners, e.g., by parametric excitation.

Considering Eq. (28), one can also conclude that the system will exhibit rather complex motions in certain ranges of the parameters. For example, for $A/\omega \gg 1$ and relatively small $\omega$, the coefficient of $\xi _0$ in this equation varies slowly from negative to positive values and vice versa. This leads to a repeated change in the system behavior. If variable $\eta$ is changing in a similar way, described by Eq. (27), then complex (chaotic) motions arise in the system. In this case, the phase diagram $\xi _0$, $\dot{\xi }_0$ of the system shows the well-known “Lorenz butterfly.” These results may be useful for understanding the mechanism of complex motions arising in the Lorenz system.

Note also that the problem of chaos controlling by means of periodic excitations has been considered by several authors, mostly with the numerical methods being employed (see, e.g., [6, 27]).

6.3 Periodic excitations of Lotka–Volterra oscillator: predator–prey system and chemical reactions

Next we consider the following system of equations:

$$\begin{aligned} \begin{array}{l} \dot{n}_1 =n_1 \left( {\varepsilon _1 -\gamma _1 n_2 } \right) +A\sin \omega t, \\ \dot{n}_2 =-n_2 \left( {\varepsilon _2 -\gamma _2 n_1 } \right) +B\sin \left( {\omega t+\delta } \right) , \\ \end{array} \end{aligned}$$

(36)

where $\varepsilon _1$, $\varepsilon _2$, $\gamma _1$ and $\gamma _2$ are positive constants and A, B, $\omega$ and $\delta$ amplitudes, frequency and phase of periodic excitations, respectively.

For $A=B=0$, these equations represent Lotka–Volterra oscillator that describes oscillations in the predator–prey system and also several oscillating chemical reactions [6, 28]. The behavior of this system under external periodic excitations has been studied in several papers, discussed in the monograph [6]; in particular, it was revealed that regular or chaotic oscillations can arise in the system due to such excitation.

Here, the system (36) is studied with the aim to reveal the effect of periodic excitations on its regular (oscillating) motions. Such excitations may be due to periodically changing properties of the environment or media in which the corresponding process is taking place. Also, for generality, we allow oscillating actions on different populations or chemical elements to have different amplitudes and phases.

In the absence of external excitation, system (36) performs free oscillations near points $n_{10} =\varepsilon _2 /\gamma _2$ and $n_{20} =\varepsilon _1 /\gamma _1$, with the linearized natural frequency defined by the expression:

$$\begin{aligned} \lambda =\sqrt{\varepsilon _1 \varepsilon _2 }. \end{aligned}$$

(37)

Assuming frequency $\omega$ to be much larger than $\lambda$, we search solution in the form:

$$\begin{aligned} n_1 =N_1 (t)+\psi _1 (t,\omega t),\quad n_2 =N_2 (t)+\psi _2 (t,\omega t), \end{aligned}$$

(38)

where $N_1$ and $N_2$ are slow and $\psi _1$ and $\psi _2$ fast $2\pi$-periodic in time $\omega t$ variables with average zero.

Equations of slow and fast motions take the form:

$$\begin{aligned}&\dot{N}_1 =N_1 \left( {\varepsilon _1 -\gamma _1 N_2 } \right) -\gamma _1 \left\langle {\psi _1 \psi _2 } \right\rangle \nonumber \\&\dot{N}_2 =-N_2 \left( {\varepsilon _2 -\gamma _2 N_1 } \right) +\gamma _2 \left\langle {\psi _1 \psi _2 } \right\rangle \end{aligned}$$

(39)

$$\begin{aligned}&\dot{\psi }_1 =\psi _1 \varepsilon _1 -\gamma _1 N_1 \psi _2 -\gamma _1 N_2 \psi _1 \nonumber \\&\quad -\,\gamma _1 \left( {\psi _1 \psi _2 -\left\langle {\psi _1 \psi _2 } \right\rangle } \right) +A\sin \omega t \nonumber \\&\dot{\psi }_2 =-\psi _2 \varepsilon _2 +\gamma _2 N_1 \psi _2 +\gamma _2 N_2 \psi _1 \nonumber \\&\quad +\,\gamma _2 \left( {\psi _1 \psi _2 -\left\langle {\psi _1 \psi _2 } \right\rangle } \right) +B\sin \left( {\omega t+\delta } \right) \end{aligned}$$

(40)

Assuming external periodic excitation to be strong, we get approximate solution of (40) in the form:

$$\begin{aligned} \psi _1 =-\frac{A}{\omega }\cos \omega t,\quad \psi _2 =-\frac{B}{\omega }\cos (\omega t+\delta ). \end{aligned}$$

(41)

Note that a more accurate solution of Eq. (40) is possible, as well as the analysis of the other ways of periodic excitations of Lotka–Volterra system [6].

Equations of slow motions (39), the VDE, can be written as:

$$\begin{aligned} \begin{array}{l} \dot{N}_1 =N_1 \left( {\varepsilon _1 -\gamma { }_1N_2 } \right) -\gamma _1 a,\quad \\ \dot{N}_2 =-N_2 \left( {\varepsilon _2 -\gamma _2 N_1 } \right) +\gamma _2 a, \\ \end{array} \end{aligned}$$

(42)

here $a=\frac{AB\cos \delta }{2\omega ^{2}}$.

Without the periodic excitation, $a=0$, the equilibrium positions of the system are $N_{10}^{(1)} =\varepsilon _2 /\gamma _2$, $N_{20}^{(1)} =\varepsilon _1 /\gamma _1$ and $N_{10}^{(2)} =N_{20}^{(2)} =0$. For $a\ne 0$, such positions appear to be defined by the relations:

$$\begin{aligned}&N_{10}^2 -\frac{\varepsilon _2 }{\gamma _2 }N_{10} +\frac{a}{q}=0,\quad N_{20} =qN_{10}, \hbox { there }\nonumber \\&q=\frac{\varepsilon _1 \gamma _2 }{\varepsilon _2 \gamma _1 }. \end{aligned}$$

(43)

So that:

$$\begin{aligned} N_{10} =\frac{1}{2}\frac{\varepsilon _2 }{\gamma _2 }\pm \sqrt{\frac{\varepsilon _2^2 }{4\gamma _2^2 }-\frac{a}{q}} \end{aligned}$$

(44)

As follows from (44), at the presence of the periodic excitation, equilibrium positions will exist only if condition

$$\begin{aligned} a\frac{\gamma _1 \gamma _2 }{\varepsilon _1 \varepsilon _2 }=\frac{AB\cos \delta }{2\omega ^{2}}\frac{\gamma _1 \gamma _2 }{\varepsilon _1 \varepsilon _2 }<\frac{1}{4} \end{aligned}$$

(45)

is satisfied. Introducing new variables $M_1 =N_1 -N_{10}$, $M_2 =N_2 -N_{20}$, Eq. (42) can be reformulated as

$$\begin{aligned} \begin{array}{l} \dot{M}_1 =M_1 \left( {\varepsilon _1 -\gamma _1 qN_{10} } \right) -\gamma _1 M_2 N_{10} -\gamma _1 M_1 M_2 \\ \dot{M}_2 =-M_2 \left( {\varepsilon _2 -\gamma _2 N_{10} } \right) +\gamma _2 M_1 qN_{10} +\gamma _2 M_1 M_2 \\ \end{array}, \end{aligned}$$

(46)

Stability of the equilibrium positions is determined by the roots of the equation:

$$\begin{aligned} \left| {\begin{array}{l} b_1 -\lambda ,\,\,\,-\gamma _1 N_{10} \\ \gamma _2 qN_{10},\,\,-b_2 -\lambda \\ \end{array}} \right| =0, \end{aligned}$$

where $b_1 =\varepsilon _1 -\gamma _1 qN_{10}$, and $b_2 =\varepsilon _2 -\gamma _2 N_{10}$. Then we rewrite this equation in the form:

$$\begin{aligned}&\lambda ^{2}+\left( {1-\frac{\gamma _2 N_{10} }{\varepsilon _2 }} \right) \left( {\varepsilon _2 -\varepsilon _1 } \right) \lambda \nonumber \\&\quad +\,\varepsilon _1 (2\gamma _2 N_{10} -\varepsilon _2 )=0, \end{aligned}$$

(47)

which, with expression (44) for $N_{10}$ being taken into account, gives:

$$\begin{aligned}&\lambda ^{2}+\left( {\frac{1}{2}\mp \sqrt{\frac{1}{4}-a\frac{\gamma _1 \gamma _2 }{\varepsilon _1 \varepsilon _2 }}} \right) \left( {\varepsilon _2 -\varepsilon _1 } \right) \lambda \nonumber \\&\quad \pm \, 2\varepsilon _{2}\varepsilon _{1} \sqrt{\frac{1}{4}-a\frac{\gamma _1 \gamma _2 }{\varepsilon _1 \varepsilon _2}}=0. \end{aligned}$$

(48)

As is seen, the equilibrium position corresponding to the negative sign in (44) is always unstable. The second equilibrium position is stable if the following condition fulfills:

$$\begin{aligned} \left( {\frac{1}{2}-\sqrt{\frac{1}{4}-a\frac{\gamma _1 \gamma _2 }{\varepsilon _1 \varepsilon _2 }}} \right) \left( {\varepsilon _2 -\varepsilon _1 } \right) >0, \end{aligned}$$

(49)

which, with the expression for a taken into account, can be reduced to:

$$\begin{aligned} (\varepsilon _2 -\varepsilon _1 )\cos \delta >0. \end{aligned}$$

(50)

Expressions (48) and (50) show that the considered periodic excitation considerably affects motion of the system, making it non-conservative. As is known, Lotka–Volterra system is a “rigid,” structurally unstable model. At the presence of the excitation, periodic motions for $\varepsilon _{2}\ne \varepsilon _{1}$ vanish, and the system trajectories either approach or move away from the equilibrium positions, so that these positions become stable or unstable, respectively. Trajectories ending on axis $N_{2}$ emerge that corresponds to extinction of the population. The averaged “populations sizes” either decrease or increase. This is illustrated by the dependences presented in Fig. 3, obtained by numerical integration of (42).

Fig. 3

Phase trajectories of the system (42) for a $a=0$, $\varepsilon _{1}=\varepsilon _{2}=\gamma _{1}=\gamma _{2}=1$ (conservative Lotka–Volterra system); b $a=0.15,\,\varepsilon _{1}=\varepsilon _{2}=\gamma _{1}=\gamma _{2}=1$; c $a=0.15,\,\varepsilon _{1}=\gamma _{1}=\gamma _{2}=1$, $\varepsilon _{2}=0.5$; d $a=0.15,\,\varepsilon _{1}=\gamma _{1}=\gamma _{2}=1$, $\varepsilon _{2}=1.5$

Note that the case of periodically pulsating coefficient $\varepsilon _{1}$ in Lotka–Volterra equations has been studied numerically in the monograph [29]. Some of the results obtained are outlined briefly in [8].

6.4 Brusselator under high-frequency actions

The discovery of the oscillating chemical reaction by B. Belousov and A. Zhabotinsky gave rise to many papers devoted to the analysis of such reactions. One of the simplest models of an oscillating chemical reaction is described by the following equations [28]:

$$\begin{aligned} \dot{x}=a-(b+1)x+x^{2}y,\quad \dot{y}=bx-x^{2}y. \end{aligned}$$

(51)

Here x and y are non-dimensional concentrations of reactants; a and b positive constants; and dots denote derivatives with respect to the non-dimensional time t. Equation (51) describes the so-called Brusselator considered by I. Prigogine and R. Lefever [28, 30]. If

$$\begin{aligned} b>a^2+1, \end{aligned}$$

(52)

then the equilibrium state, $x_0 =a$, $y_0 =b/a$, becomes unstable, and the system performs self-excited oscillations [28].

We consider a system

$$\begin{aligned} \dot{x}= & {} a-(b+1)x+x^{2}y+A\sin \omega t,\nonumber \\ \dot{y}= & {} bx-x^{2}y+B\sin (\omega t+\delta ), \end{aligned}$$

(53)

in which variations of concentrations of reactants x and y are subjected to periodic actions with amplitudes A and B, phase shift $\delta$ and frequency $\omega$, which is assumed to be much larger than the frequency $\lambda \approx a$ of the self-excited oscillations.

Employing the MDSM, a solution to (53) is sought in the form

$$\begin{aligned} x=X+\psi _x,\quad y=Y+\psi _y, \end{aligned}$$

(54)

where X and Y are slow and $\psi _x$ and $\psi _y$ fast $2\pi$-periodic in time $\tau =\omega t$ variables with average zero. Equations of slow and fast motions are, respectively:

$$\begin{aligned} \dot{X}= & {} a-(b+1)X+X^{2}Y+2X\left\langle {\psi _x \psi _y } \right\rangle +Y\left\langle {\psi _x^2 } \right\rangle \nonumber \\&+\left\langle {\psi _x^2 \psi _y } \right\rangle \nonumber \\ \dot{Y}= & {} bX-X^{2}Y-2X\left\langle {\psi _x \psi _y } \right\rangle -Y\left\langle {\psi _x^2 } \right\rangle \nonumber \\&-\left\langle {\psi _x^2 \psi _y } \right\rangle \end{aligned}$$

(55)

$$\begin{aligned} \dot{\psi }_x= & {} A\sin \omega t+\cdots ,\quad \dot{\psi }_y =B\sin (\omega t+\delta )+\cdots \end{aligned}$$

(56)

Terms that are not presented in the fast motions Eq. (56) are assumed to be relatively small.

Substituting the obtained periodic solutions of Eq. (56) into (55), we compose the following system of the slow motions equations, the VDE:

$$\begin{aligned} \dot{X}= & {} a-(b+1)X+X^{2}Y+cX+dY \nonumber \\ \dot{Y}= & {} bX-X^{2}Y-cX-dY, \end{aligned}$$

(57)

where

$$\begin{aligned} c=AB\cos \delta /\omega ^{2},\quad d=\frac{1}{2}A^{2}/\omega ^{2}. \end{aligned}$$

(58)

Equation (57) differ from (51) by the presence of two additional linear terms in the right-hand sides. This leads to the shift of the equilibrium position to the point $X_0 =a$, $Y_0 =a(b-c)/(d+a^{2})$, so that self-excited oscillations occur when the following condition fulfills:

$$\begin{aligned} b(a^{2}-d)>(a^{2}-d)c+(a^{2}+d)(a^{2}+d+1). \end{aligned}$$

(59)

As appears this condition differs considerably from (52), though reducing to (52) at $c=d=0$.

6.5 Processes of flame and nerve impulse propagation under high-frequency actions, Zel’dovich–Frank–Kamenetskii model

The following partial differential equation is considered:

$$\begin{aligned} \frac{\partial ^{2}u}{\partial x^{2}}-\frac{\partial u}{\partial t}=f(u)+A\sin \omega t, \end{aligned}$$

(60)

where

$$\begin{aligned} f(u)=u(u-a)(u-1),\quad a<1,\quad \omega \gg 1. \end{aligned}$$

(61)

Equation of nonlinear diffusion (60) without the term $A\sin \omega t$ in the right-hand side was proposed by Y.B. Zel’dovich and D.A. Frank-Kamenetskii to describe the process of flame propagation, cf. [30, 31]. The same equation models propagation of a nerve impulse in nerve fibers [30, 32].

Searching a solution to (60) in the form:

$$\begin{aligned} u=U(x,t)+\psi (x,t,\omega t), \end{aligned}$$

(62)

we obtain equations of slow and fast motions:

$$\begin{aligned} \frac{\partial ^{2}U}{\partial x^{2}}-\frac{\partial U}{\partial t}= & {} \left\langle {f(U+\psi )} \right\rangle \end{aligned}$$

(63)

$$\begin{aligned} \quad -\frac{\partial \psi }{\partial t}= & {} -\frac{\partial ^{2}\psi }{\partial x^{2}}+f(U+\psi )\nonumber \\&-\left\langle {f(U+\psi )} \right\rangle +A\sin \omega t \end{aligned}$$

(64)

Assuming the amplitude of the high-frequency excitation to be large, so that all other terms in the right-hand side of (64) can be neglected, we get the following simple equation for the variable $\psi$:

$$\begin{aligned} -\frac{\partial \psi }{\partial t}=A\sin \omega t. \end{aligned}$$

(65)

The periodic solution of (65) is:

$$\begin{aligned} \psi =\frac{A}{\omega }\cos \omega t \end{aligned}$$

(66)

Employing this expression, we obtain:

$$\begin{aligned} F(U)= & {} \left\langle {f(U+\psi )} \right\rangle \nonumber \\= & {} \left\langle {(U+\psi )(U+\psi -a)(U+\psi -1)} \right\rangle \nonumber \\= & {} f(U)+\frac{3}{2}\frac{A^{2}}{\omega ^{2}}U-\frac{1}{2}(a+1)\frac{A^{2}}{\omega ^{2}} \end{aligned}$$

(67)

Consequently, the equation of slow motions, the VDE, takes the form:

$$\begin{aligned} \frac{\partial ^{2}U}{\partial x^{2}}-\frac{\partial U}{\partial t}=F(U) \end{aligned}$$

(68)

This equation differs from Zel’dovich–Frank–Kamenetskii equation by the presence of two additional terms in F(U); these considerably affect solutions of the equation, since polynomials f(u) and F(U) have different roots. Polynomial f(u) has three roots, $u=0$, $u=1$ and $u=a$, while F(U) can have no roots in the interval (0,1). This illustrates the capability to control processes of flame and nerve impulse propagation by means of the oscillating actions.

6.6 Mathieu equation without an explicit small parameter: mechanical and electrical oscillators

As the first example of application of the modified MDSM, we consider the classical Mathieu equation that describes oscillations arising in various mechanical, electrical and other systems, cf. [33]:

$$\begin{aligned} \frac{\hbox {d}^{2}\varphi }{\hbox {d}t_0^2 }-\delta (1+\chi \cos t_0 )\varphi =0. \end{aligned}$$

(69)

The case of negative stiffness is studied, $\delta >0$, so that the problem of motion stabilization by means of the oscillating action is considered. Note that the equation does not involve a small parameter, $\delta \sim 1$, $\chi \sim 1$, and the classical asymptotic methods [9–11] cannot be used.

Employing the modified MDSM, we search a solution to (69) in the form:

$$\begin{aligned} \varphi =\alpha (T_1 )+\psi (T_1,T_0 ), \end{aligned}$$

(70)

describing oscillations with slowly varying amplitudes. Here the new timescales $T_1$ and $T_0$ are defined as $T_0 =t_0$, $T_1 =\varepsilon T_0$; $\varepsilon \ll 1$ is a formal small parameter, $\alpha$ “slow,” and $\psi$ “fast,” $2\pi$-periodic in dimensionless time $T_0$ variable, with average zero:

$$\begin{aligned} \left\langle {\psi (T_1,T_0 )} \right\rangle =0 \end{aligned}$$

Thus the small parameter $\varepsilon$, which is a feature of the sought solution, not of the considered governing Eq. (69), is introduced. In what follows, this parameter will be employed to resolve the problem considered.

Equations of slow and fast motions take the form:

$$\begin{aligned}&\varepsilon ^{2}\frac{\hbox {d}^{2}\alpha }{\hbox {d}T_1^2 }-\delta (\alpha +\chi \left\langle {\psi \cos T_0 } \right\rangle )=0, \end{aligned}$$

(71)

$$\begin{aligned}&\frac{{{\partial ^2}\psi }}{{\partial T_0^2}} + 2\varepsilon \frac{{{\partial ^2}\psi }}{{\partial {T_1}\partial {T_0}}} + {\varepsilon ^2}\frac{{{\partial ^2}\psi }}{{\partial T_1^2}} - \delta \psi \nonumber \\&\quad = \delta \chi \left( {\left( {\alpha + \psi } \right) \cos {T_0} - \left\langle {\psi \cos {T_0}} \right\rangle } \right) \end{aligned}$$

(72)

As appears in the present case, the conventional simplifications of the MDSM should be abandoned. In particular, it is not valid to consider slow variables involved in (72) as constants. Indeed, term $\varepsilon ^{2}\frac{\hbox {d}^{2}\alpha }{\hbox {d}T_1^2 }$ is retained in Eq. (71) of slow motions, and relations $\delta \sim 1$, $\chi \sim 1$ hold true, so solution of the fast motions’ equation should be determined with the accuracy of order of $\varepsilon ^{2}$. Thus terms of this and lower order, particularly $2\varepsilon \frac{\partial ^{2}\psi }{\partial T_1 \partial T_0 }$ and $\varepsilon ^{2}\frac{\partial ^{2}\psi }{\partial T_1^2 }$, should be retained in Eq. (72).

Taking into account that $\psi (T_1,T_0 )$ is a time $T_0$ periodic function, solution of the fast motions Eq. (72) is sought in the form of a series

$$\begin{aligned} \psi= & {} B_{11} (T_1 )\cos T_0 +B_{12} (T_1 )\sin T_0 \nonumber \\&+\,B_{21} (T_1 )\cos 2T_0 +B_{22} (T_1 )\sin 2T_0 \nonumber \\&+\,\cdots +B_{n1} (T_1 )\cos nT_0 +B_{n2} (T_1 )\sin nT_0 \end{aligned}$$

(73)

Inserting (73) into (72), and gathering the coefficients of the involved harmonics $\cos T_0, \sin T_0,\cos 2T_0$,..., we compose equations for the amplitudes $B_{11} (T_1 )$, ..., $B_{n2} (T_1 )$. Solving these equations by means of the classical procedure of expansion in the small parameter $\varepsilon$ [9] gives:

$$\begin{aligned} B_{11} (T_1)= & {} -F_0 \alpha (T_1)+\varepsilon ^{2}F_2 \frac{\hbox {d}^{2}\alpha }{\hbox {d}T_1^2 }+O(\varepsilon ^{3}),\nonumber \\ B_{12} (T_1)= & {} \varepsilon F_1 \frac{d\alpha }{\hbox {d}T_1 }+O(\varepsilon ^{3}). \end{aligned}$$

(74)

Expressions for the amplitudes $B_{21} (T_1),\,{\ldots },\,B_{n2}(T_1 )$ are not given here for brevity. Here, $F_j =F_j (\delta ,\chi )$, $j=0,1,2$; and asymptotic expansions (74) are uniform and valid, since $F_0 (\delta ,\chi )\sim F_2 (\delta ,\chi )$, and $\alpha (T_1 )$ is a slowly varying function, so that $\alpha (T_1 )\sim {\hbox {d}^{2}\alpha }/{\hbox {d}T_1^2 }$.

Functions $F_j$, $j=0,1,2$, depend on the number of retained harmonics in the series (73). Discarding the $n\hbox {th}$ harmonic leads to the error of order of

$$\begin{aligned} \mu =\frac{1}{4}\frac{\delta \chi }{\delta +n^{2}}\frac{\delta \chi }{\delta +(n-1)^{2}}. \end{aligned}$$

(75)

Thus the modified MDSM estimates the error in the obtained solution of the fast motion equation. For example, for $\delta <0.5$, $\chi \sim 1$, and $n=4$ we get $\mu \sim 10^{-3}$. In this case, i.e., with only three harmonics taken into account in (73), expressions for the functions $F_0 (\delta ,\chi )$ and $F_2 (\delta ,\chi )$ take the form

$$\begin{aligned}&F_0 (\delta ,\chi )\nonumber \\&\quad =\frac{\delta \chi (144+52\delta -\delta ^{2}(-4+\chi ^{2}))}{2(72+98\delta +\delta ^{3}(2-\chi ^{2})+\delta ^{2}(28-5\chi ^{2}))};\nonumber \\&F_2 (\delta ,\chi )=\frac{\delta \chi }{2}\frac{F_{21} (\delta ,\chi )}{F_{22} (\delta ,\chi )}, \end{aligned}$$

(76)

where $F_{22} (\delta ,\chi )=(72+98\delta +\delta ^{3}(2-\chi ^{2})+\delta ^{2}(28-5\chi ^{2}))^{3}$,

$$\begin{aligned}&F_{21} (\delta ,\chi )\nonumber \\&\quad =2239488+1679616\delta +1296\delta ^{2}(196+171\chi ^{2})\\&\qquad +\,60\delta ^{3}(-1900+2889\chi ^{2}) \\&\qquad +\,8\delta ^{5}(-996+763\chi ^{2}+85\chi ^{4})\\&\qquad +\,\delta ^{4}(-50560+46512\chi ^{2}+594\chi ^{4}) \\&\qquad +\,\delta ^{6}(-576+416\chi ^{2}+50\chi ^{4}-11\chi ^{6})\\&\qquad +\,\delta ^{7}(-16+12\chi ^{2}-4\chi ^{4}+\chi ^{6}). \end{aligned}$$

Employing the obtained solution of the fast motions equation, the equation of slow motions (71) is written in the form:

$$\begin{aligned}&\varepsilon ^{2}\left( 1-\delta \frac{\chi }{2}F_2 (\delta ,\chi )\right) \frac{\hbox {d}^{2}\alpha }{\hbox {d}T_1^2 }\nonumber \\&\quad -\,\delta \left( 1-\frac{\chi }{2}F_0 (\delta ,\chi )\right) \alpha =0. \end{aligned}$$

(77)

Returning to the “initial” time variable $t_0$, this equation can be rewritten as:

$$\begin{aligned}&\left( 1-\delta \frac{\chi }{2}F_2 (\delta ,\chi )\right) \frac{\hbox {d}^{2}\alpha }{\hbox {d}t_0^2 }\nonumber \\&\quad -\,\delta \left( 1-\frac{\chi }{2}F_0 (\delta ,\chi )\right) \alpha =0. \end{aligned}$$

(78)

From (78), it follows that motions of the oscillator will become stable due to the oscillating excitation if the following condition holds true:

$$\begin{aligned} {\lambda ^2} = \delta \frac{{\frac{\chi }{2}{F_0}\left( {\delta ,\,\chi } \right) - 1}}{{1 - \delta \frac{\chi }{2}{F_2}\left( {\delta ,\,\chi } \right) }} > 0, \end{aligned}$$

(79)

Here, $\lambda$ is natural frequency of the oscillator slow motions near the equilibrium position.

The modified MDSM implies that the solutions obtained are close to periodic and describe oscillations with slowly varying amplitudes. That gives the requirement for the frequency $\lambda$ of the system slow oscillations to be much smaller than the frequency of its fast oscillations, i.e., unity:

$$\begin{aligned} \lambda \sim \varepsilon \ll 1. \end{aligned}$$

(80)

This condition defines the applicability range of the modified MDSM for the problem considered, with the small parameter $\varepsilon$ (or $\lambda$) being the feature of the obtained solution.

As follows from (75), functions $F_0 (\delta ,\chi )$ and $F_2 (\delta ,\chi )$, which are present in the resulting slow motion Eq. (78), are determined with the error of order of $\mu$. Consequently, the effective natural frequency $\lambda$ is determined with the error of the same order. Thus, for the approximation of the method to be valid the following condition should hold true:

$$\begin{aligned} \mu \ll \lambda . \end{aligned}$$

(81)

So, in fact we have two small parameters $\mu$ and $\lambda$: One is associated with the specific type of the solutions sought and another with the truncation of the harmonic series employed. However, both of them are not present explicitly in the considered governing Eq. (69), which constitutes the main difference of the modified MDSM from the conventional asymptotic methods.

Figure 4 shows analytical and numerical solutions of Eq. (69) for various values of the parameters. The numerical solution was obtained by direct integration of (69) by means of the Wolfram Mathematica 7. Solid lines represent the numerical solution, dotted lines represent the solution $\alpha (t_0 )$ of the obtained equation of slow motions (78), and dashed lines represent the analytical solution, i.e., the sum of $\alpha$ and $\psi$.

Fig. 4

Dependencies of $\varphi$ on time $t_0$ for initial conditions $\varphi (0)=0.01$, $\dot{\varphi }(0)=0$ and a $\delta =0.4$, $\chi =2.59$; b $\delta =1$, $\chi =1.906$; c $\delta =1.4$, $\chi =1.7395$

As appears from Fig. 4, dashed and solid lines almost coincide with each other, so the obtained analytical solution is in good agreement with the results of numerical experiments.

The analytical solution has been validated also by the classical theory of Mathieu functions and Floquet theory [34]. Particularly, the obtained stabilization condition (79) was compared with the classical Ince–Strutt diagram [19, 33, 34]. Parameters of this diagram a and q can be expressed via $\delta$ and $\chi$ as $a=4\delta$, $q=2\delta \chi$. A part of the diagram is shown in Fig. 5 by solid lines; curves which correspond to the stabilization condition (79) (dotted line) and to the condition of the MDSM applicability (80) (dashed lines) are also presented. In the domain of parameters between two dashed lines, the solution obtained by means of the modified MDSM is valid; this domain is shaded in Fig. 5 and implies close to periodic solutions. As is seen, the curve which corresponds to the stabilization condition (79) coincides with the one of the Ince–Strutt diagram. Thus there is a good agreement between the obtained analytical solution and the classical theory.

Fig. 5

Ince–Strutt diagram (solid lines) and curves corresponding to the stabilization condition (79) (dotted line) and the condition of the MDSM applicability (80) (dashed lines); shaded region: the domain of parameters in which the obtained analytical solution is valid

6.7 Nonlinear parametric amplifier: micro- and nanoscale electromechanical systems

Many small-scale parametric amplifiers based on resonant micro- and nanosystems exhibit a distinctly nonlinear behavior when amplitude of their response is sufficiently large [35]. So, it becomes necessary to consider such systems dynamics in a nonlinear context, and the Duffing-type nonlinearity can serve as the simplest model. In paper [36], the near-resonant response of such system was studied for small values of the parametric excitation amplitude and the nonlinearity coefficient. Here, these restrictions on the system parameters are abandoned. The governing equation is:

$$\begin{aligned} {z^{\prime \prime }} + \gamma {z^{\prime }} + \delta z + \chi z\cos 2{t_0} + k{z^3} = A\cos \left( {{t_0} + \phi } \right) , \end{aligned}$$

(82)

Here, z represents the amplifier response, $\gamma$ is the coefficient of dissipation, which is assumed to be linear, A and $\chi$ are the amplitudes of the external and parametric excitations, respectively, $\phi$ is the relative phase term, $\delta$ is the squared natural frequency of the linearized system, and $t_0$ is the dimensionless time.

Noting that $\delta \sim 1$ and $\chi \sim 1$, so that the classical asymptotic methods cannot be used, we employ the modified MDSM and search a solution to (82) in the form:

$$\begin{aligned} z = \alpha \left( {{T_1}} \right) + \psi \left( {{T_1},{T_0}} \right) , \end{aligned}$$

(83)

describing oscillations with slowly varying amplitudes. Consequently, we obtain the following equations of slow and fast motions, respectively:

$$\begin{aligned}&{\varepsilon ^2}\frac{{{\hbox {d}^2}\alpha }}{{\hbox {d}T_1^2}} + \varepsilon \gamma \frac{{d\alpha }}{{d{T_1}}} + \delta \alpha + \chi \left\langle {\psi \cos 2{T_0}} \right\rangle \nonumber \\&\quad +\,k\left( {{\alpha ^3} + 3\alpha \left\langle {{\psi ^2}} \right\rangle + \left\langle {{\psi ^3}} \right\rangle } \right) = 0, \end{aligned}$$

(84)

$$\begin{aligned}&\frac{\partial ^{2}\psi }{\partial T_0^2 }+2\varepsilon \frac{\partial ^{2}\psi }{\partial T_1 \partial T_0 }+\varepsilon ^{2}\frac{\partial ^{2}\psi }{\partial T_1^2 }+\gamma \left( {\frac{\partial \psi }{\partial T_0 }+\varepsilon \frac{\partial \psi }{\partial T_1 }} \right) \nonumber \\&\quad +\,k\left( {\psi ^{3}+3\alpha \psi ^{2}+3\alpha ^{2}\psi }-3\alpha \left\langle {\psi ^{2}} \right\rangle \right. \nonumber \\&\quad \left. -\,\left\langle {\psi ^{3}} \right\rangle \right) +\delta \psi =-\chi \left( (\alpha +\psi )\cos 2T_0\right. \nonumber \\&\quad \left. -\left\langle {\psi \cos 2T_0 } \right\rangle \right) +A\cos (T_0 +\phi ) \end{aligned}$$

(85)

Taking into account that $\psi (T_1,T_0 )$ is a time $T_0$ periodic function, solution of the fast motions Eq. (85) is sought in the form of a series

$$\begin{aligned} \psi= & {} {B_1}\left( {{T_1}} \right) \cos \left( {{T_0} + \theta _{1} \left( {{T_1}} \right) } \right) + {B_2}\left( {{T_1}} \right) \cos \left( 2{T_0} \right. \nonumber \\&\left. +\,{\theta _2}\left( {{T_1}} \right) \right) + \cdots \end{aligned}$$

(86)

Influence of the second, the third and all higher harmonics on the system response for $\delta \sim 1$ and $\chi \sim 1$ turns out to be negligibly weak when either the nonlinearity coefficient k or the external excitation amplitude A is small, $k\ll 1$ or $A\ll 1$. In particular, no super- or sub-harmonic resonances can occur. So, in this range of parameters it is valid to take into account only the first harmonic to predict the system response. The accounting of the other harmonics is not difficult, but leads only to a minor quantitative change in the results. So, similarly to the problem considered in Sect. 6.6, the modified MDSM provides the explicit condition under which the results obtained by means of the method are valid.

For amplitude $B_{1}$ and phase $\theta _{1}$, the following equations are obtained:

$$\begin{aligned}&\varepsilon ^{2}\frac{\hbox {d}^{2}B_1 }{\hbox {d}T_1^2 }+\varepsilon \gamma \frac{dB_1 }{\hbox {d}T_1}-B_1 \left( 1+\varepsilon \frac{\hbox {d}\theta _1 }{\hbox {d}T_1}\right) ^{2}+\delta B_1 \nonumber \\&\qquad +\,\frac{3}{4}kB_1^3 +3k\alpha ^{2}B_1 \nonumber \\&\quad =-\frac{1}{2}\chi B_1 \cos 2\theta _1 +A\cos (\theta _1 -\phi ) \end{aligned}$$

(87)

$$\begin{aligned}&\varepsilon ^{2}B_1 \frac{\hbox {d}^{2}\theta _1 }{\hbox {d}T_1^2 }+\left( {\gamma B_1 +2\varepsilon \frac{dB_1 }{\hbox {d}T_1 }} \right) \left( {1+\varepsilon \frac{\hbox {d}\theta _1 }{\hbox {d}T_1 }} \right) \nonumber \\&\quad =\frac{1}{2}\chi B_1 \sin 2\theta _1 -A\sin (\theta _1 -\phi ), \end{aligned}$$

(88)

The steady-state response of the amplifier is of primary interest. The following system of equations is composed to describe it:

$$\begin{aligned}&\delta \alpha + k\left( {{\alpha ^3} + 3\alpha \frac{{B_1^2}}{2}} \right) = 0, \end{aligned}$$

(89)

$$\begin{aligned}&- {B_1} + \delta {B_1} + \frac{3}{4}kB_1^3 + 3k{\alpha ^2}{B_1}\nonumber \\&\quad = - \frac{1}{2}\chi {B_1}\cos 2{\theta _1} + A\cos \left( {{\theta _1} - \phi } \right) \end{aligned}$$

(90)

$$\begin{aligned}&\gamma {B_1} = \frac{1}{2}\chi {B_1}\sin 2{\theta _1} - A\sin \left( {{\theta _1} - \phi } \right) , \end{aligned}$$

(91)

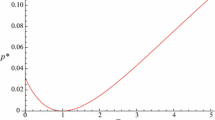
Assuming relations $\delta >0$, $k>0$ to be fulfilled, one obtains that Eq. (89) allows for a single real solution, $\alpha =0$. From the equation of slow motions (84), it follows that this solution is always stable. Solving Eqs. (90)–(91), we obtain five expressions for the amplitude $B_1$ of the amplifier steady-state response. As an illustration, Fig. 6 shows the dependency of the amplitude $B_1$ on the parameter $\delta$; here solid lines correspond to stable branches and dashed lines to unstable branches.

Fig. 6

Dependencies of the steady-state amplitude of the nonlinear parametric amplifier response on the parameter $\delta$ for $\gamma =0.02$, $\phi =-\pi /4$, $\chi =1.2$, $k=0.5$, and $A=0.01$

As shown in Fig. 6, the response features five distinct branches, three of which are stable. Similar structure of the nonlinear amplifier response was noticed, apparently for the first time, in the paper [36] which is devoted to the analysis of the near-resonant behavior of the system (82). The present study significantly broadens these results, since the amplifier response is studied for the wider range of parameters, particularly when $\delta$ is not close to unity.

As is seen, the modified MDSM is able to predict stability of the obtained steady-state solutions, which is an important advantage over the classical harmonic balance method.

6.8 Van der Pol equation without an explicit small parameter: oscillations in electrical circuits

Finally, to illustrate that the applicability range of the modified MDSM is not restricted to problems with non-autonomous excitation, self-excited oscillations in autonomous systems are considered for Van der Pol equation with strong nonlinearity:

$$\begin{aligned} \ddot{v}+v-\mu (1-v^{2})\dot{v}=0, \end{aligned}$$

(92)

where parameter $\mu$ is not required to be small, . Employing the modified MDSM, we search a solution to (92) in the form of oscillations with slowly varying amplitudes:

$$\begin{aligned} v= & {} {B_{11}}\left( {{T_1}} \right) \cos \left( {\lambda {T_0}} \right) + {B_{12}}\left( {{T_1}} \right) \sin \left( {\lambda {T_0}} \right) \nonumber \\&+\,{B_{21}}\left( {{T_1}} \right) \cos \left( {3\lambda {T_0}} \right) + {B_{22}}\left( {{T_1}} \right) \sin \left( {3\lambda {T_0}} \right) \nonumber \\&+\, \cdots \end{aligned}$$

(93)

Here, $T_0$ and $T_1$ are new timescales implied in the MDSM, $T_0 =t_0$, $T_1 =\varepsilon \lambda T_0$, and $\varepsilon \ll 1$ is a formal small parameter; $\lambda$ is unknown frequency of self-excited oscillations to be determined. As appears the form of the solution (93) differs from those employed in Sects. 6.6–6.7: It involves the unknown frequency $\lambda$ and does not imply the explicit slow component $X(T_1 )$ (or $\alpha (T_1 )$). This is due to the fact that here the self-excited oscillations are considered, and frequency of these oscillations is to be determined. The main principle of the modified MDSM, however, is preserved: The solution is sought in the form of oscillations with slowly varying amplitudes.

Substituting (93) into (92) and equating the coefficients of $\cos (\lambda T_0 )$, $\sin (\lambda T_0 )$, $\cos (3\lambda T_0 )$ and $\sin (3\lambda T_0 )$ to zero, one obtains equations for the amplitudes $B_{11} (T_1 )$, $B_{12} (T_1 )$, $B_{21} (T_1 ),\,B_{22} (T_1 )$. Note that only the written terms are taken into account in the series (93). The neglecting of higher harmonics is justified for $\mu \sim 1$ (that comprises also the case $\mu \ll 1$). So, similarly to Sects. 6.6–6.7, the modified MDSM provides the explicit condition under which the results obtained by means of the method are valid.

The steady-state response with constant amplitudes $B_{11st}$, $B_{12st}$, $B_{21st}$ and $B_{22st}$ describing stationary oscillations is of primary interest. The following equations for these amplitudes are obtained:

$$\begin{aligned}&\lambda \mu \left( B_{11st}^2 B_{22st} +B_{12st} (B_{12st}^2 +B_{11st}^2 -B_{12st} B_{22st} \right. \nonumber \\&\qquad \left. -\,2B_{11st} B_{21st} +2B_{21st}^2 +2B_{22st}^2 -4) \right) \nonumber \\&\quad =4(\lambda ^{2}-1)B_{11st}, \end{aligned}$$

(94)

$$\begin{aligned}&\lambda \mu \left( -B_{12st}^2 B_{21st} +B_{11st} (B_{11st}^2 +B_{12st}^2 +B_{11st} B_{21st} \right. \nonumber \\&\qquad \left. +\,2B_{12st} B_{22st} +2B_{21st}^2 +2B_{22st}^2 -4) \right) \nonumber \\&\quad =4(1-\lambda ^{2})B_{12st}, \end{aligned}$$

(95)

$$\begin{aligned}&\lambda \mu \left( 3B_{11st}^2 B_{12st} -B_{12st}^3 +3B_{22st} (B_{22st}^2 +2B_{12st}^2 \right. \nonumber \\&\quad \left. +\,2B_{11st}^2 +B_{21st}^2 -4) \right) =4(9\lambda ^{2}-1)B_{21st}, \end{aligned}$$

(96)

$$\begin{aligned}&\lambda \mu \left( B_{11st}^3 -3B_{11st} B_{12st}^2 +3B_{21st} (2B_{11st}^2 \right. \nonumber \\&\qquad \left. +\,2B_{12st}^2 +B_{21st}^2 +B_{22st}^2 -4) \right) \nonumber \\&\quad =4(1-9\lambda ^{2})B_{22st}, \end{aligned}$$

(97)

Equations (94)–(97) are then solved to determine the frequency $\lambda$ of the system self-excited oscillations. Consequently, we get two real values: $\lambda _{1}$ and $\lambda _{2}$, and $\lambda _{1}=-\lambda _{2}$. The expressions for $\lambda _1,\lambda _2$ are rather cumbersome and thus not given here. As an illustration in Fig. 7, the dependency of $\lambda _{1}$ on $\mu$ is shown.

Thus, the steady-state response of the considered system has been determined. A series of numerical experiments was conducted to validate the obtained results in all cases showing good agreement (see below).

To study the system non-stationary behavior, we employ the virtue of the small parameter, $\varepsilon \ll 1$, and neglect the third harmonic in the solution series, since its influence is relatively weak for $\mu \sim 1$. Consequently, we obtain the following equations that approximately describe the system non-stationary behavior:

$$\begin{aligned}&\lambda \mu \left( -4B_{12} -4\varepsilon {B}_{11}^{\prime } +B_{12} (B_{12}^2 +B_{11}^2 +\varepsilon B_{12} {B}_{11}^{\prime } \right. \nonumber \\&\qquad \left. +\,2\varepsilon B_{11} {B}_{12}^{\prime } )+3\varepsilon B_{11}^2 {B}_{11}^{\prime } \right) \nonumber \\&\quad =4B_{11} (\lambda ^{2}-1)-8\lambda ^{2}\varepsilon {B}_{12}^{\prime }, \end{aligned}$$

(98)

$$\begin{aligned}&\lambda \mu \left( -4B_{11} +4\varepsilon {B}_{12}^{\prime } +B_{11} (B_{11}^2 +B_{12}^2 -2\varepsilon B_{12} {B}_{11}^{\prime } \right. \nonumber \\&\qquad \left. -\,\varepsilon B_{11} {B}_{12}^{\prime } )-3\varepsilon B_{12}^2 {B}_{12}^{\prime } \right) \nonumber \\&\quad =4B_{12} (1-\lambda ^{2})-8\lambda ^{2}\varepsilon {B}_{11}^{\prime }, \end{aligned}$$

(99)

Then, employing the shift of variables from $B_{11}(T_{1})$, $B_{12}(T_{1})$ to $B_{1}(T_{1})$, $\varphi (T_{1})$:

$$\begin{aligned} {B_{11}} = {B_1}\cos \varphi ,\,{B_{12}} = {B_1}\sin \varphi , \end{aligned}$$

(100)

we get:

$$\begin{aligned}&8\lambda \varepsilon {B}_1^{\prime } +\mu B_1 (1-\varepsilon {\varphi }^{\prime })(B_1^2 -4)=0, \end{aligned}$$

(101)

$$\begin{aligned}&(3B_1^2 -4)\lambda \varepsilon \mu {B}_1^{\prime } +(4-4\lambda ^{2}+8\lambda ^{2}\varepsilon {\phi }^{\prime })B_1 =0. \end{aligned}$$

(102)

Consequently obtain:

$$\begin{aligned}&\varepsilon {B}_1^{\prime } =-\frac{4\mu B_1 \left( B_1^2 -4\right) (1+\lambda ^{2})}{\lambda \left( 64\lambda ^{2}+(16-16B_1^2 +3B_1^4 )\mu ^{2}\right) }, \end{aligned}$$

(103)

$$\begin{aligned}&\varepsilon {\varphi }^{\prime }=\frac{32(\lambda ^{2}-1)+\mu ^{2}\left( 16-16B_1^2 +3B_1^4 \right) }{64\lambda ^{2}+\left( 16-16B_1^2 +3B_1^4 \right) \mu ^{2}}. \end{aligned}$$

(104)

So that the problem is reduced to solving Eq. (103). The solution can be obtained by the classical separation of variables technique. As an illustration, the dependency of the amplitude $B_{1}$ on time $t_0$ is shown in Fig. 8 by the solid line for $\mu =1$; the dashed line represents the numerical solution obtained by direct integration of the initial Eq. (92) using Wolfram Mathematica 7.

Fig. 7

Dependency of the frequency of the system self-excited oscillations on the parameter $\mu$

Fig. 8

Dependency of the response amplitude $B_{1}$ on time $t_0$ (solid line) and the numerical solution v of the initial Eq. (92) (dashed line) for $\mu =1$; $\lambda =0.943$

Note that in the conventional case $\mu \ll 1$, when $\lambda =1$, one can rewrite Eqs. (103)–(104) as:

$$\begin{aligned}&\varepsilon {B}_1^{\prime } =\frac{1}{2}\mu B_1 \left( 1-\frac{1}{4}B_1^2 \right) , \end{aligned}$$

(105)

$$\begin{aligned}&\varepsilon {\varphi }^{\prime }=0, \end{aligned}$$

(106)

which coincide with the known results (see, e.g., [9]).

The considered example clearly illustrates that the modified MDSM can be employed to study self-excited oscillations in strongly nonlinear autonomous systems.

7 Conclusion

The present paper considers effects produced by oscillations applied to nonlinear dynamic systems from various fields of science. It is noted that such effects can be of significant applied and theoretical importance, particularly, due to the fact that generic properties of dynamic systems can be considerably affected by oscillating excitations.

The general approach for treating problems of the considered type is proposed. This approach implies the transition from the initial governing equations of motions to equations describing only the slow component of motions which is usually of primary interest. The approach is named as the oscillatory strobodynamics.

The modification of the approach applicable for problems that do not imply restrictions on the spectrum of excitation frequencies is proposed. In particular, it can be employed when frequency of oscillating excitation is not high, i.e., not much larger than the system characteristic (natural) frequency. The modified approach in certain cases allows also to abandon other restrictions usually introduced when employing the classical asymptotic methods, e.g., the requirement for the involved nonlinearities to be weak. So, problems without an explicit small parameter can be considered by means of the method.

The efficiency of the OS approach is illustrated in several relevant examples.