The chaotic dynamics of drilling

Abstract

In the study of drilling dynamics, many investigations are limited to laboratory systems and simple mathematical models. Using field measurement data and a new dynamical model in a rotary steerable drilling system, we demonstrate the existence of low-dimensional chaos in drilling. The behaviors of the mathematical model and actual measurement are shown to be consistent. The revealing of chaos provides a new way to detect early fatigue cracks as weak signals in a noisy environment to reduce engineering cost and the possibility of disaster.

1 Introduction

Oil spill disaster as in the Gulf of Mexico has caused great impact on lost assets, health, safety, and environment. The cement work has agreed to be the main reason relating to the investigation of the disaster. But what are the factors that affect the quality of cementing? Drilling dynamics [1] is a crucial problem that must be attached great importance to. Many dangerous phenomena related to drilling are normally caused by the dynamics of the drillstring and its interactions with the surroundings. Such as deterioration of the borehole quality caused by the drilling dynamics will directly affect the cementing quality. At a minimum, we should kill a well [2] if the oil spill has begun. The directional drilling technology can help us to reach its target, and drilling dynamics play an important role in the directional drilling control. Most of all, the drilling dynamics will accelerate fatigue damage to the downhole tools and drillstring, which is the most common phenomenon in the drilling process. Drillstring failure may occur frequently. Not only does it cost billions of dollars per year, but it also puts the drilling engineering at risk.

Around 73 % of inspected drillstrings are defective because of fatigue cracks. In order to improve the drilling efficiency and tools reliability, an effective detection [3] of downhole drillstring dynamics should be done in order to detect the early fatigue cracks. Nowadays, the three-dimensional downhole measurements could provide us the vibration signals supporting the study. However, it is a great challenge like financial crisis forecasting because the potential signals are so weak. Fortunately, the detection of the “drilling chaos” in this paper may provide a new way to amplify the detection of these weak signals.

Since Lorenz revealed that small uncertainties in an initial state can indeed lead to large errors [4], many ordered and disordered system behaviors have been interpreted using chaos theory [5–8]. The butterfly effect [4] is discovered with regard to the aerodynamics, and chaotic dynamics are found in many hydrodynamical phenomena [7, 8] and even in granular materials [9]. A solid can move like liquids as well when the world’s slowest-moving drop caught on camera at last [10]. Drilling through the formation can also be regarded as a solid flow, which is different from above. In oil and gas drilling engineering, drillstring torsional vibration is a very common phenomenon that has attracted great interest of researchers. Because of its great dangers and inevitability in the drilling process, it caused widespread concern after it has been discovered [11–14]. The possibility of deterministic chaos in the drillstring vibration also became a topic of interest. Yigit and Christoforou [15] employed an Euler–Bernoulli beam coupling of axial and lateral vibrations resulted in chaotic response. Van Der Heijden [16] used a model of differential equations proposed to describe lateral drillstring vibrations, and analysis the bifurcation and chaos in the simulation signals. Divenyi [17] paid a special attention to stick-slip and bit-bounce behaviors that are normally treated as the non-smooth dynamics. However, direct evidence that deterministic chaos of drillstring torsional vibration in practice is missing. Additionally, previous studies are based on some simple models that cannot be verified in a real drilling system. Therefore, further investigation of the new bifurcations numerically found in the present paper should be of much interest from drilling dynamical systems point of view.

We develop a push-the-bit rotary steerable drilling system [18] (RSS), which is the fastest method for turning a borehole in a preferred direction, to investigate drilling dynamics. A rotary steerable system is a new form of drilling technology used in directional drilling. It employs the use of specialized downhole equipment to replace conventional directional tools such as mud motors. Specifically, the behavior of the drillstring while operating under torsional vibrations [19], the main cause of damages to the drillstring, is of great importance. In this article, we report the observation of low-dimensional chaos in the drillstring torsional vibration using measurement data from the field test using the RSS. The results are in good match with mathematical models. To our knowledge, this is the first report of the finding of order–chaos transitions in a real drillstring system. In addition, we observe that the change of the largest Lyapunov exponent can predict the fatigue damage of the drillstring. And we provide an index Fr, which can quantify the drillstring integrity failure risk, is shown to be more reliable than current measure used in drilling engineering.

2 Data acquisition and processing

RSS is a new technology used in directional drilling, and the whole drillstring is rotated from the surface by a hydraulically driven top drive, as show in Fig. 1a.

Fig. 1

Data acquisition system. a Rotary steerable drilling system, E1–E9, indicates the field experiments using the RSS in China, and the map is created by the Microsoft PowerPoint; b construction of the downhole measurement system, three-axis magnetometers and three-axis accelerometers arranged in three mutually orthogonal directions

We develop a strap-down measurement-while-drilling (MWD) surveying system that incorporates three-axis magnetometers and three-axis accelerometers arranged in three mutually orthogonal directions [20]. The sensors are installed inside non-magnetic drill collar that can avoid the external magnetic interferences [21]. Performance characteristics of the accelerometers and magnetometers are summarized in Table 1.

Figure 1b shows the installing structure of downhole measurement system. E1–E9 in Fig. 1a indicates the field experiments in China between the years of 2011–2013. $a_{x}, a_{y}, a_{z}$ are defined as survey signals of triaxial accelerometers on the xyz axis, respectively. $m_{x}, m_{y}, m_{z}$ are defined as survey signals of triaxial magnetometers on the xyz axis, respectively, the sampling frequency $f_\mathrm{s}$ is 100 Hz. Assume that the Earth’s magnetic field strength as M. Obviously, $M=\sqrt{m_{x}^{2}+m_{y}^{2}+m_{z}^{2}}$. Under certain sample frequency, measuring signal is time series and can be expressed as time function. We can use $a_{h} =\pm \sqrt{a_{x}^{2}+a_{y}^{2}}$ define the lateral vibration of the BHA and use $a_{z}$ express the longitudinal vibration.

Table 1 Characteristics of sensors

Triaxial magnetometers are installed $90^{\circ }$ phase difference between $m_{x}$ and $m_{y}$, assume $m_h$ is the horizontal projection of the Earth’s magnetic field, after $\Delta t$, the drillstring rotates an angle of $\alpha _{n}$.

$$\begin{aligned} tg(\alpha _{n})=\frac{m_h \cdot \sin (\alpha _{n} )}{m_h \cdot \cos (\alpha _{n})}=\frac{m_{x}}{m_{y}} \end{aligned}$$

(1)

Thus, $\alpha _{n} =arctg(\frac{m_{x}}{m_{y}})$, as show in Fig. 2a, b, drillstring rotary from $\alpha _{n}$ to $\alpha _{n+1}$ though time $\Delta t$, it defines the rotary angle as a time series $\alpha (\alpha _1, \alpha _2, \ldots , \alpha _{n-1}, \alpha _{n} )$, drillstring rotational speed (RPM) is then defined as follows:

$$\begin{aligned} \hbox {RPM}=\frac{60}{2\pi }\omega =\frac{60}{2\pi }\cdot \frac{(| {\alpha _{n}}|-|\alpha _{n+1}|)}{\Delta t}\;(\hbox {r/min}) \end{aligned}$$

(2)

Fig. 2

The rotation speed calculation schematics of magnetometers, a the model of rotation speed calculation; b survey signals of magnetometers and calculational speed. When the drillstring rotates from $\alpha _{n}$ to $\alpha _{n+1}$ though time $\Delta t$, drillstring rotational speed (RPM) will be obtained using the survey signals of triaxial magnetometers on the xy axis

There is a more practical approach to quantitative analysis the bottom drilling tool motion characteristics, through the measurement of the bottom drilling bit rotation speed, as well as some other downhole measurement parameters. Field observations based on downhole and surface vibration measurements have indicated that drillstrings exhibit severe vibrations. These vibrations are observed to become more severe at the bottom-hole assembly (BHA). As shown in the Fig. 3b, the value of the angular speed fluctuates between 0 and 120 r/min, which indicates that the system is in the state of stick-slip. The survey signals of triaxial accelerometers on the xyz axes as show in the Fig. 3a. These measured signals are used to analyze the drilling dynamics.

Moreover, as shown in Fig. 3a, when the drillstring rotates, we define the displacement of point A at the x axis as a time series $S(s_{1}, s_{2}, \ldots , s_{n-1}, s_{n})$, with the circle radius of R. Obviously, $s_i =R\sin (\omega t)$. Then the velocity time series $V(v_1, v_2, \ldots , v_{n-1}, v_{n})$, the acceleration time series $A(a_1, a_2, \ldots , a_{n-1}, a_{n})$ can be obtained.

Fig. 3

The time series of measurement. a Survey signals of triaxial accelerometers on the xyz axes; b the time series of the drillstring rotary speed calculated by Eq. (2), the unstable angular speed indicates that the system is in the stick-slip state

3 Torsional dynamics model of rotary steerable system

We developed a rotary steerable drilling system (RSS) that mainly included two parts: strap-down measurement-while-drilling (MWD) surveying system (Fig. 1b) and oriented actuator (Fig. 4b). Next, we try to develop a new model of the RSS to analyse the drilling dynamics. In the outside of bottom-hole assembly (BHA) of the RSS, we use three pads (Fig. 4b, c) which press against the well bore thereby causing the bit to press on the opposite side causing a direction change. The pads of the implementing agency constantly push against the borehole wall, making bottom hole a cycle of nonlinear damping force. The oriented actuator is used to push the pads to steer the drilling trajectory. Power section consists of turbo generator, which is basically driven by drilling fluid. The servo section stabilizes the disk valve at a certain tool face angle, and then drilling fluid moves the pads out by flowing through valves (Fig. 4b). Drilling fluid pushes one of the pads to the borehole and produces the steering force (Fig. 4c) that can orient the drilling.

Fig. 4

Torsional dynamics model. a Drillstring torsional vibration model, there are many drillstrings not indicated in the figure; b structure of the strap-down rotary steerable drilling system; c the cross-sectional view of the pads coming from (b), if has three pads, and the outside is borehole wall

3.1 Drillstring model of RSS

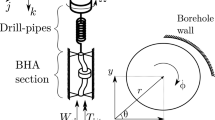
The RSS is assumed as a rigid body, and the drillstring is homogenous along its entire length and simply considered as a single linear torsional spring [22] of torsional stiffness $K_{t}$ and torsional damping $C_{t}$. The number of drillstrings can be modified depending on system analysis requirements. The jth drillstring is connected to the BHA by means of $K_{b}$ and $C_{b}$. The simplified drillstring torsional vibration model is shown in Fig. 2a. The top drive torque is supposed to be constant and positive. The drillstrings are considered to have the same inertia, and the drilling fluid is simplified by a viscous-type friction element at the hit. The drillstring torsional model [22] takes the following form:

$$\begin{aligned}&J_{s}\dot{\Omega }+C_{t}\left( \dot{\phi }_{r}-{\dot{\phi }}_{j}\right) +K_{t} (\phi _{r}-\phi _{j})=T_\mathrm{drive} \end{aligned}$$

(3)

$$\begin{aligned}&J\ddot{\phi }_{j}+C_{t} \left( 2{\dot{\phi }}_{j} -{\dot{\phi }}_{j+1}-{\dot{\phi }}_{j-1}\right) \nonumber \\&\quad +K_{t}\left( 2\phi _{j} -\phi _{j+1} -\phi _{j-1} \right) =0 \end{aligned}$$

(4)

$$\begin{aligned}&J_{b} \dot{\omega }+C_{b} \left( {\dot{\phi }}_{b} -{\dot{\phi }}_{j}\right) \nonumber \\&\quad +K_{b} \left( \phi _{b}-\phi _{j} \right) =T_{Y}+T_\mathrm{bit} \end{aligned}$$

(5)

where $\phi _{b}$ is the angular displacement of BHA; $\omega$ is the angular speed of BHA; $\phi _{r}$ is the angular displacement of the top drive; $\Omega$ is the angular speed of the top drive; $\phi _{j}$ is the angular displacement of jth drillstring; $J_{b}$ is the moment of the inertia of BHA; $J_{s}$ is the moment of the inertia of the rotary table; J is the moment of the inertia of drillstring; $T_\mathrm{drive}$ is top drive input torque and $T_\mathrm{bit}$ is the torque on the bit.

From the Eq. (4), angular acceleration of the jth drillstring $\ddot{\phi }_{j}$ can be expressed as:

$$\begin{aligned} \ddot{\phi }_{j}= & {} -\frac{C_{t} }{J}\left( 2{\dot{\phi }}_{j} -{\dot{\phi }}_{j+1} -{\dot{\phi }}_{j-1}\right) \nonumber \\&-\frac{K_{t} }{J}\left( 2\phi _{j} -\phi _{j+1} -\phi _{j-1}\right) \end{aligned}$$

(6)

Assume that the drillstring number is p, except both sides, $j=2,3,\ldots , p-1$. Obviously, ${\dot{\phi }}_{r} =\Omega , {\dot{\phi }}_{b} =\omega$, we will obtain the following equations:

$$\begin{aligned} \ddot{\phi }_{r}= & {} -\frac{C_{t}}{J_{s}}\left( {\dot{\phi }}_{r} -{\dot{\phi }}_1\right) -\frac{K_{t}}{J_{s}}(\phi _{r} -\phi _{1})+\frac{T_\mathrm{drive}}{J_{s}} \end{aligned}$$

(7)

$$\begin{aligned} \ddot{\phi }_1= & {} -\frac{C_{t} }{J}\left( 2{\dot{\phi }}_1 -{\dot{\phi }}_{r} -{\dot{\phi }}_2 \right) -\frac{K_{t} }{J}(2\phi _1 -\phi _{r} -\phi _2 ) \nonumber \\\end{aligned}$$

(8)

$$\begin{aligned} \ddot{\phi }_{p}= & {} -\frac{C_{t} }{J}\left( {\dot{\phi }}_p -{\dot{\phi }}_{p-1} \right) -\frac{K_{t} }{J}(\phi _p -\phi _{p-1})\nonumber \\&\quad -\frac{C_{b} }{J}\left( {\dot{\phi }}_p-{\dot{\phi }}_{b} \right) -\frac{K_{b} }{J}(\phi _p -\phi _{b} ) \end{aligned}$$

(9)

$$\begin{aligned} \ddot{\phi }_{b}= & {} -\frac{C_{b}}{J_{b}}\left( {\dot{\phi }}_{b} -{\dot{\phi }}_p \right) -\frac{K_{b}}{J_{b}}(\phi _{b} -\phi _p )+\frac{T_Y +T_\mathrm{bit}}{J_{b}}\nonumber \\ \end{aligned}$$

(10)

From the Eqs. (5)–(9), define a vector $X=(\phi _{r}, {\dot{\phi }}_{r}, \ldots$, $\phi _{j}, {\dot{\phi }}_{j}, \ldots , \phi _{b}, {\dot{\phi }}_{b} )^\mathrm{T}$, then:

$$\begin{aligned} \dot{X}(t)=AX(t) \end{aligned}$$

(11)

Assume $p=4$ in our simulation, the matrix of coefficients can be expressed as:

$$\begin{aligned} A=\left[ {{\begin{array}{cccc} 0&{}\quad 1&{}\quad 0&{}\quad 0 \\ -\frac{K_{t}}{J_{s}}&{}\quad -2\frac{C_{t}}{J_{s}}&{}\quad \frac{K_{t}}{J_{s}}&{}\quad \frac{C_{t} }{J_{s}} \\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \\ \frac{K_{t}}{J_{b}}&{}\quad \frac{C_{t}}{J_{b}}&{}\quad -\frac{K_{t} }{J_{b}}&{}\quad -\frac{C_{t} +C_{b}}{J_{b}}\\ \end{array} }} \right] \end{aligned}$$

(12)

The parameters in the simulation are show in the Table 2.

Table 2 System parameter values used to generate numerical results for comparison with experimental results

Fig. 5

Schematic and model of hydraulic actuator adopted in this paper illustrating the drilling fluid dynamics

Fig. 6

Ground tests to obtain the relationship between $F_\mathrm{steering}$ and the drilling fluid pressure. a The flowchart of the steering force test; b least-squares fitting of the experimental data

3.2 Steering force

$T_Y$ is the main difference between an ordinarily drilling system and a RSS. As shown in Fig. 4c, $T_{Y}$ is the cycle torque force generated by the pads pushing the borehole during the process of oriented drilling. The push-the-bit RSS works at automatic control mode that three pads push in turn when the drillstring rotates. The friction torque generated by pads can be expressed as:

$$\begin{aligned} T_{Y}=F_\mathrm{steering} \cdot \sin \left( \frac{1}{2\pi f_F}t\right) \cdot \mu (\omega )\cdot R \end{aligned}$$

(13)

where R is the borehole radius, 0.0841 m. The function $\mu (\omega )$ represents the dry friction, and it uses the sign of the angular velocity. We use the harmonic vibration model (Fig. 5) to define the drilling fluid dynamics [23, 24] of hydraulic drive, and the hydraulic actuator is modeled as a combination of an ideal velocity source and a spring for modeling the compressibility affects of the fluid medium. A schematic of this model is shown in Fig. 5 (up), and the flow rate to/from the actuator is related to the ideal velocity as,

$$\begin{aligned} \dot{X}_{i} =\frac{Q_1}{A_1}=-\frac{Q_2}{A_2} \end{aligned}$$

(14)

where $\dot{X}_{i}$ is the ideal velocity, and $Q_{i}$ and $A_{i}$ correspond to the flow rate and piston area in chamber $i\in (1,2)$, respectively. The modeling paradigm of the actuator is as shown in Fig. 5 (down), and the dynamics of a hydraulic actuator is more aptly captured by a nonlinear spring. The dynamics of master and slave inertias is given by,

$$\begin{aligned}&M_{a}\ddot{X}_a=F_a -F_v \end{aligned}$$

(15)

$$\begin{aligned}&M_p \ddot{X}_p =F_a +F_{s} \end{aligned}$$

(16)

and the vibration frequency of the $M_{p}$ is expressed as,

$$\begin{aligned} f_F =\frac{1}{2\pi }\frac{M_{a}+M_{p}}{M_{a} M_{p}}K_{s} \end{aligned}$$

(17)

wherein $K_{s}$ is the equivalent stiffness.

$F_\mathrm{steering}$ is defined as the maximum of the steering force (Fig. 4c) that associates with the drilling fluid pressure. We conduct the ground tests to obtain the relationship between $F_\mathrm{steering}$ and the drilling fluid pressure ($\varDelta p$, MPa), as show in Fig. 6a. Least-squares fitting of the experimental data points can be obtained:

$$\begin{aligned} F_\mathrm{steering} =5.4275\Delta p+0.1057 \end{aligned}$$

(18)

Wherein $\Delta p$ is the drilling fluid pressure, which can be obtained from experimental data, as show in the Fig. 6b.

We use the equation proposed by Spanos et al. [25], assuming that the friction is considered to be evenly distributed on the front face of the bit.

$$\begin{aligned} T_\mathrm{bit} =F_{w} \left[ \frac{2}{3}r_h u(\omega )+\zeta \sqrt{r_h \delta _{c}}\right] \end{aligned}$$

(19)

where $F_{w}$ is the weight on bit, $r_{h}$ is the drill bit radius, $\delta _{c}$ is the average cutting depth, and $\zeta$ is a dimensionless parameter that characterizes the force necessary to cut the rock. The average cutting depth, $\delta _{c}$, is obtained from the following relation:

$$\begin{aligned} \delta _{c} =\frac{2\pi r_{p}}{\Omega } \end{aligned}$$

(20)

where $r_{p}$ is the average rate of penetration, calculated as a function of the applied weight on bit, $F_{w}$, and the rotary table rotation, $\Omega$, using the following empirical relation:

$$\begin{aligned} r_{p} =e_{1} F_{w} \sqrt{\Omega }+e_{2} \end{aligned}$$

(21)

where $e_{1}$ and $e_{2}$ are constants.

Fig. 7

The curve generated from a dry friction of model

Fig. 8

Time series of the top drive input torque $T_\mathrm{drive}$, drilling fluid pressure $\Delta p$, and weight on bit $F_w$ are measurement data of the field test, with sample frequency of 0.1 Hz

3.3 Friction model

We define the dry friction as a continuous function to describe both the static and dynamic friction. Using the coulomb friction model [26], as shown in Fig. 7, the constants $\mu _{s}$ and $\mu _{d}$ are the static and dynamic friction coefficients, respectively. Assuming that v is the slip velocity at the friction point, $v_{s}$ is stiction transition velocity; $v_{d}$ is the friction transition velocity.

Fig. 9

The 3D phase-space trajectory of real and simulated data; Part a, c are produced by experimental data (E3), Part b, d are produced by simulation data, and the simulation results and real data results match well; the limit cycle has lost its stability. The colored shades of Part c, d correspond to projections of the set on the different coordinate planes of Part a, b, respectively. (Color figure online)

Set $\mu (-v_{s} )=\mu _{s}$, $\mu (v_{s} )=-\mu _{s}$, $\mu (0)=0$, $\mu (-v_{d} )=\mu _{d}$, $\mu (v_{d} )=-\mu _{d}$. Then the function u(v) can be defined as follows:

$$\begin{aligned} \mu (v)= & {} -\hbox {sign}(v)\cdot \mu _{d} \quad | v |>v_{d} \end{aligned}$$

(22)

$$\begin{aligned} \mu (v)= & {} -s(| v|,v_{d}, \mu _{d}, v_{s}, \mu _{s} )\cdot \hbox {sign}(v) \quad v_{s} \le | v |\le v_{d} \nonumber \\\end{aligned}$$

(23)

$$\begin{aligned} \mu (v)= & {} s(v-v_{s}, \mu _{s}, v_{s} -\mu _{s} ) \quad |v|<v_{s} \end{aligned}$$

(24)

The $s(x,x_0, h_0, x_1, h_1 )$ function can be defined as follows, assume that x is the independent variable, $x_0$ is a real variable that specifies the x value at which the s function begins, $x_1$ is a real variable that specifies the x value at which the s function ends, $h_0$ is the initial value of the step, $h_1$ is the final value of the step, and assume $a=h_1 -h_0$, $\varDelta =(x-x_0 )/(x_1 -x_0 )$, then:

$$\begin{aligned}&s(x,x_0, h_0, x_1, h_1 )\nonumber \\&\quad =\left\{ {\begin{array}{ll} h_{0} &{}\quad x\le x_0 \\ h_{0}+a\cdot \varDelta ^{2}(3-2\varDelta ) &{}\quad x_0 <x<x_1 \\ h_{1} &{}\quad x\ge x_1 \\ \end{array}} \right. \end{aligned}$$

(25)

We do not allow $v_{s} =0$, the friction transition velocity $v_{d}$ is greater than the stiction transition velocity $v_{s}$ by definition.

4 Chaos identification

In the simulation, the top drive input torque $T_\mathrm{drive}$, drilling fluid pressure $\Delta p$, and weight on bit $F_w$ can be used the experimental data, as show in the Fig. 8.

Fig. 10

Phase-space of experimental data and simulation data. The first row a.1–a.3 is produced by the system only has the torque on the bit, the red dot of the a.1 is the experimental data come from the ordinarily drilling system, we can see the phase-space of our system has a limit cycle. The second row b.1–b.3 is produced when the RSS is worked, and pads pushed to the bit generated the torque $T_{Y}$ lead to the system to chaotic. The third row c.1–c.3 is produced by the $T_\mathrm{bit}=0$, just the simulation results which will not present to the real drilling process. In addition, the first column is the phase-space of torsional velocity and acceleration, the second column is the phase-space of torsional velocity and steering force, and the third column is the phase-space of torsional velocity and the one of pads shift. Along with the $T_{Y}$ increased, we first found the sequence of order to chaos transitions in the drillstring system. (Color figure online)

4.1 Phase-space reconstruction

To perform dynamical analyses, we use the phase-space reconstruction method [27] (apply the mutual information [28] to estimate embedding delay, and Cao’s method [29] to determine the embedding dimension) to reconstruct the attractor and estimate the correlation dimension [30] and largest Lyapunov exponents (LLE) [31].

We obtained the first minimum of the mutual information calculated at $\tau =10$ and the embedding dimension is 6. We then represent the system by a phase-space trajectory $\bar{X}(t)=(A(t),V(t),S(t))$, as shown in Fig. 9. We compare the phase-space trajectory $\bar{X}(t)$ using the experimental data of E3 and simulated data. The phase-space of our system is at least three-dimensional, and the oscillatory tends to give rise to a strange attractor in both real and simulated data.

The main difference between the push-the-bit RSS and ordinary drilling system is the friction torque $(T_{Y})$ that generated in the process of pads pushed against the borehole wall. The simulation results show that the drilling bit torsional vibration phenomena perceptible increased when the friction torque exist.

As show in the Fig. 10, we found that the $T_{Y}$ will change the kinetic properties of the system. Figure 10a1–a3 is the simulation results when we set as $F(f_{F})=0$, like the ordinarily drilling system, shows the dynamics of the system only have the torque on the bit $(T_\mathrm{bit})$, the stable limit cycle indicates that the system incline to a period. When the $F(f_{F})$ increases, the limit cycle loses its stability gradually, and we can see from the Fig. 10b1–b3, which produced by $T_\mathrm{bit}+T_{Y}$, the phase-space trajectory shows fractal. Figure 10c1–c3 shows the dynamics of the system having only the torque $T_{Y}$, which is more obvious that the chaos exists in the system. We can found the vibration sequences are transition from order to chaos along with the $T_{Y}$ increased. Generally, the drilling system will worked on the pattern of A and B, the red dot in the Fig. 10a.1, b.1 is generated from measurement data, which are good matched to the simulation results. However, we have not measured the steering force and the pads shift that is why we cannot obtain the phase-space in the column 2 and 3 of Fig. 10.

4.2 Largest Lyapunov exponent and correlation dimension

The LLE estimation is derived on the algorithm in [32]. The positive value indicates exponential divergence of trajectories and hence an evidence of chaos. Furthermore, we use the Grassberger–Procaccia (GP) [30] algorithm to estimate the correlation dimension $D_{2}$. We use 100,000 data points as one data set, and the whole drilling experimental data are calculated. Data from all nine fields in China are used in our studies. The results are shown in Table 3. Both measures indicate the existence of low-dimensional chaos in drillstring torsional vibration. The results are carried out with Tisean package [33], version 3.01.

Table 3 Chaos identification of test data

As show in the Fig. 11a, b, the largest Lyapunov exponent is estimated through least-squares line fit for the time series and is found to be 0.011 of the experimental data of E3 field test and 0.013 of simulation data. This positive value indicates exponential divergence of trajectories and hence an evidence of chaos. Furthermore, as show in Fig. 11c, d, the slope of $\log (C_D (r))$ gives us an estimation of the correlation dimension $D_{2}$. We present the estimated slope as a function of logr for embedding dimensions $m =1$ up to 10. In all cases we obtain a convergence toward a correlation dimension of $D_{2}\approx 1.6$ with the experimental data and a correlation dimension of $D_{2}\approx 1.8$ with the simulation data.

Fig. 11

Chaos identification, Part a, b estimating the maximal Lyapunov exponent of torsional vibration time series. The part a shows the result for the experimental data, the straight line indicates $\lambda = 0.011$. For comparison, part b shows the result for the simulation data, the straight line indicates $\lambda = 0.013$. Part c, d give us an estimation of the correlation dimension $D_{2}$. In all two cases the GP algorithm converges, creating a plateau on the slope of the correlation integral. The red-dashed curves give estimates of the correlation dimension in all two cases: experimental time series $D_{2}=1.6$ and simulation time series $D_{2}=1.8$. The all results in these figures were carried out with Tisean package [33], version 3.01. (Color figure online)

4.3 Stationarity and determinism tests

Since linear statistics, such as the mean or standard data deviation, usually do not possess enough discrimination power when analyzing irregular signals, nonlinear statistics have to be applied. We apply the stationarity test [34] program stationarity.exe provided by Perc [35, 36]. They split the time series into several short non-overlapping segments and then use a particular data segment to make predictions in another data segment. By calculating the cross-prediction error $(\delta _{gh})$ when considering points in segment g to make predictions in segment h, the cross-prediction error as a function of g and h then reveals which segments differ in their dynamics. They obtained a very sensitive statistic capable of detecting changes in dynamics and thus a very powerful probe for stationarity.

The average cross-prediction errors for all possible combinations of g and h are presented in Fig. 12. The whole time series was partitioned into 56 non-overlapping segments each occupying 1000 data points. The average value of all $\delta _{gh}$ is 0.17, while the minimum and maximum values are 0.03 and 0.3, respectively. Since the maximal cross-prediction error is not one time larger than the average, we can determine that the studied time series is stationarity. We just consider only 1000 s of the torsional vibration time series. Otherwise, longer data sets of the vibration time series almost yield non-stationary.

Fig. 12

Stationarity test. The color map displays average cross-prediction errors $\delta _{\mathrm{gh}}$ in dependence on different segment combinations. (Color figure online)

Additionally, the results of the surrogate data analysis could be further confirmed by applying the determinism test [37], which enables us to verify whether the time series we have obtained originated from a deterministic process. In this paper, we use the method developed by Kaplan and Glass [38] in order to examine the possible deterministic nature of the underlying process, if the system is deterministic, the average length of all directional vectors k will be 1, while for a completely random system $k\approx 0$.

As shown in Fig. 13, the value of the determinism factor k is in the range 0.5–0.9, indicating the possible stochastic nature of the underlying process.

Fig. 13

Deterministic test for measurement time series. The values of determinism factor k are given for embedding dimensions in the range $m=2{-}10$. It is evident that $k\leqslant 0.95$, indicating the possible random (stochastic) behavior

5 Quantification of drillstring integrity failure risk

The drillstrings are mechanical systems which undergo complex dynamical phenomena, often involving non-desired oscillations. Three main types of oscillations are distinguished: torsional, axial and lateral vibration [12, 39–41]. These oscillations are a source of failures that reduce penetration rates and increase drilling operation costs. Stick-slip phenomenon appearing at the bottom-hole assembly (BHA) is particularly harmful for the drillstring, and it is a major cause of drill pipes and bit failures, in addition to well bore instability problems [41].

The risk of a vibration-related integrity failure of drillstring can be predicted by using vibration measurement to calculate some severity index [42], defined as $I_c =a_\mathrm{rms}^{1.5} t_{d}^{0.5}$ . It relates to the average root-mean-square (RMS) acceleration $(a_\mathrm{rms})$ and duration of the run time $(t_{d})$, where the RMS acceleration is defined as,

$$\begin{aligned} a_\mathrm{rms} =\sqrt{\frac{1}{t_{d}}\int _{0}^{t_{d}}{a(t)^{2}\hbox {d}t}} \end{aligned}$$

(26)

RMS increases with the presence of increasing vibration level. The number of vibration samples used to calculate each feature sample is set to be $N=50{,}000$, which means that the time interval between two successive feature samples is $\Delta t=N/f_{s} =500$ s. The authors and field engineers have found that this time frame is acceptable for the requirement of time accuracy. Additionally, Field data indicates that higher rotary speeds generally lead to increased levels of lateral vibration, as shown in the Fig. 14.

Fig. 14

Statistical analyses indicated there is direct relationship between RPM and lateral vibration levels (RMS lateral acceleration)

This failure detection is a very important issue in drilling. It is difficult to extract the weak signals in such a drilling system. The measured data from such a system contain detailed dynamic characteristics of the measured structure, but the amount of data is often huge. How to efficiently and accurately extract concise, clear, and unique system dynamic characteristics and health information from such a large set of data is very difficult. Moreover, dynamics-based system identification is a very challenging reverse engineering task. It is even more important to have a signal processing and data mining method that can extract from each set of experimental data as many system parameters as possible. A damaged structure shows nonlinearities and intermittent transient response in its time traces of measured points. The acquisition and analysis of this data provided new insights into the dynamic behavior of drillstring.

Nonlinear dynamical systems sometimes exhibit chaotic behavior, and the Lyapunov exponent is a useful tool to distinguish and measure the extent of chaos. Previous studies on chaos and on the Lyapunov exponents have found applications to several fields such as turbulence, communication, and heartbeats. However, little research has been done on the relationship between the behavior of Lyapunov exponents and fault detection. In the history of the field of fault detection, many methods have been proposed to extract and analyze experimental data in order to detect faults and assist in diagnosis [43–45]. Difficult to detect faults early on due to certain weakly developing faults is usually covered by background noise and other chaotic elements. If the signal to noise ratio (SNR) is low, weak fault signals may not be extracted from background noise using only the above-mentioned methods. In recent years, as chaos theory has developed, some new technologies (especially phase-space reconstruction) have begun to be applied to extract information hidden beneath experimental data [46, 47]. The largest Lyapunov exponent is usually used to distinguish and to measure chaos of dynamical systems. The exponent or its change can have some relationships with system faults. Usually, the equations of the dynamical systems are difficult to obtain directly; only time series data sets are observable. There are varieties of faults which are hard to detect directly from the data itself. The LLE is the indicator of divergence or convergence of two trajectories with nearby initial conditions, and it could be sensitive to small changes of the systems. However, the relationship between the LLE and the system damage level is not clear and rarely studied up to now. Based on the LLE calculation method and considering the conditions of a real system and the measured data, the changes of the LLE are applied to fault detection of the RSS in this paper.

The severity index of vibration measurement is lack of sensitivity. Assume that $L_{n}$ is the LLE of nth data set; we define the drillstring integrity failure risk parameter $F_{r}$ as,

$$\begin{aligned} F_{r}= & {} \sum _{n\rightarrow N} {\left( \frac{L_{n} -L_{n+1} }{L_{n} }+1\right) } \cdot a_\mathrm{rms}^{1.5}\cdot t_{d}^{0.5} \end{aligned}$$

(27)

We got the results of the risk parameter $F_{r}$ and compare it with the $I_{c}$ as shown in Fig. 15.

Fig. 15

Vibration index charts. We use 1e6 data points as one data set to calculate the vibration index. In the six field tests as shown in Fig. 1a, E3, E5 and E7 are failure cases. Both indices $I_{c}$ and $F_{r}$ are less than one at the beginning of the drilling process, and the indices increase at the end of the drilling process. This is different from the normal cases E1, E6 and E9, in which the drillstrings are in good condition for the entire drilling process. It is noted that $I_{c}$ cannot identify the failure in sample 2, while the ruptured dynamical approach can detect the weak failure signal

We chose six field test data sets as shown in Fig. 1a. Three of them are from drillstring failure, and three of them are in good condition. We calculate both indices at the beginning and the end of the drilling process. By comparing the variation of coefficients, we observe that the proposed measure provides a more reliable solution to support risk management processes with regard to drillstring failures. The chaos detected is related to the inner dynamic characteristics of drillstring.

6 Discussion

Torsional dynamics can be extremely damaging to downhole drilling tools and can significantly affect drilling efficiency. The effort to prevent this phenomenon has led to the development of various downhole mitigation tools, improved bit technologies and bottom-hole assembly (BHA) designs, and better management of drilling parameters. This article proposes a theoretical model of push-the-bit RSS that lesser-known types of torsional dynamics observed while drilling. In addition, a real drilling system is developed to validate the theoretical dynamical behavior. It is observed here that drilling can lead to drilling chaos and the observation can be used to detect weak failure signal in a complicated and noisy drilling environment for early warning detection. Since most researches in universities are limited to laboratory or theoretical studies due to the high cost of drilling, our findings reduce this gap by calculating physical nonlinear dynamical model with real drilling experiments. The existence of chaos in drilling may open a new concept of drilling chaos in the solid flow mechanics that will benefit to both the physicists and the drilling engineers.

7 Methods

7.1 Phase-space reconstruction

The dynamics of the time series $x_0, x_1, \ldots , x_{n-1}$ are fully captured or embedded in the m-dimensional phase space, $m\ge d$ where d is the dimension of the original attractor. A vector $\vec {x}_{i}$ in the reconstructed phase space [27] is constructed from the time series as follows:

$$\begin{aligned} \vec {x}_{i}=\left[ x_{i}, x_{i-\tau }, \ldots , x_{i-(m-1)\tau }\right] \end{aligned}$$

(28)

where $\tau$ is the delay time.

Cao’s method [29] computes $E_{1}$ and $E_{2}$ for the data set of dimension 1 up to a dimension of D, which is the largest embedding dimension, used for calculation. $E_{1}$ and $E_{2}$ are defined as follows:

$$\begin{aligned} E_{1} (d)= & {} \frac{1}{N-d\tau }\Bigg |\sum _{i=1}^{N-d\tau } {\big | {x_{i+d\tau }-x_{n(\mathrm{i,d})+\mathrm{d}\tau }}\big |}\Bigg | \end{aligned}$$

(29)

$$\begin{aligned} E_{2}(d)= & {} E_1 (d+1)/E_1 (d) \end{aligned}$$

(30)

wherein d is the embedding dimension, N is the number of data points, $\tau$ is the embedding delay, $x_{i+d\tau }$ and $x_{n(i,d)+d\tau }$ is the i-th vector in the data sets and its nearest neighbors of d-dimensional phase space.

7.2 Largest Lyapunov exponent (LLE)

The basic characteristics of chaotic motion are that the movement is extremely sensitive to initial conditions, two very close initial values resulting in orbit over time by separating exponentially, Lyapunov exponent [31, 32] that describes the amount of this phenomenon.

We use the algorithm of Rosenstein et al. [32] to calculate the LLE. The results were carried out with Tisean package [33], version 3.01. Consider the representation of the time series data as a trajectory in the embedding space and assume that observe a very close return $s_{{n}'}$ to a previously visited point $s_{n}$. Then consider the distance $\Delta _0 =s_{n} -s_{{n}'}$ as a small perturbation, $\Delta l=s_{n+l}-s_{{n}'+l}$. If one finds that $\big |{\Delta _l }\big |\approx \Delta _{0}e^{\lambda l}$, then $\lambda$ is the largest Lyapunov exponent.

Assuming $S(\varepsilon , m,t)$ exhibits a linear increase with identical slope for all m larger than some $m_{0}$ and for a reasonable range of $\varepsilon$, and then this slope can be taken as an estimate of the largest exponent.

$$\begin{aligned} S(\varepsilon , m,t)=\left\{ \ln \left( \frac{1}{u_{n}}\sum _{s_{{n}'} \in u_{n}}{\big |s_{n+t}-s_{{n}'+t}\big |}\right) \right\} _{n} \end{aligned}$$

(31)

7.3 Correlation dimension

The correlation dimension method is used for detecting the presence possibility of chaos. An algorithm proposed by Grassberger and Procaccia [30] is the most commonly applied method. According to this method, the correlation sum, C(r), is expressed as:

$$\begin{aligned} C(r)=\frac{2}{N(N-1)}\sum _{i=1}^N {\sum _{j=i+1}^N {H\left( r-\Vert {x_i -x_{j}}\Vert \right) } }\nonumber \\ \end{aligned}$$

(32)

where H is Heaviside step function defined as:

$$\begin{aligned} H(x)=\left\{ {\begin{array}{lll} 0&{}\quad \hbox {when}&{}\quad x\le 0 \\ 1&{}\quad \hbox {when}&{}\quad x\ge 0 \\ \end{array}}\right. \end{aligned}$$

(33)

N is the number of points in time series; r is the radius of a sphere with its center at either of current points. Then the correlation dimension is:

$$\begin{aligned} \hbox {D}_{2}= {\mathop {\lim }\limits _{\begin{array}{c} D\rightarrow \infty \\ r\rightarrow 0 \end{array}}}\frac{d\ln (\hbox {C(r))}}{d\ln \hbox {r}} \end{aligned}$$

(34)

When the system is chaotic, the slope of $\log C(r)$ versus $\log r$ converges to $D_{2}$ over an appropriate interval as m increases. The results were carried out with Tisean package [33], version 3.01.