1 Introduction

Since the pioneering work of Ott, Grebogi and Yorke on chaos control in 1990, the problem of chaos control has received considerable attention from the scientific community. Multiple methods for chaos control have been introduced and successfully applied. These methods can be based on either external and/or parametric excitation, such as the passive, the adaptive and the robust adaptive feedback control techniques, just to name a few [1–4, 9].

In many practical applications of control theory, parameters of the system to be controlled may be unknown or known with uncertainties; it can also happen that information about the model structure is incomplete (for instance dimensionality of the system and the form of the nonlinear characteristics of the equations). To deal with these challenges, during the past few decades, a tremendous attention has been devoted on developing efficient adaptive control techniques. For instance, many adaptive control techniques based on artificial intelligent, such as Neural Networks controllers, Gaussian radial basis adaptive backstepping controllers, T-S Fuzzy, affine T-S controllers and neuro-fuzzy systems controllers, have been developed and successfully implemented in many applications [5, 10–13, 16]. One important application of these techniques is the control of chaotic systems, used, for instance, in telecommunication systems (receiver and transmitter synchronization, chaotic signal generation, secure communication), chemical reaction, power energy systems and biology [6, 17].

Chaotic systems are known to be very sensitive to external disturbances and to be highly uncertain nonlinear systems whose underlying dynamics are poorly known such that least prior system information should be required for controller’s implementation [18]. This explains why adaptive controllers are very interesting for these systems. It is worth to be mentioned that with the techniques for adaptive control, the controller is usually designed using the reference model or the methods of feedback linearization. Therefore, the system to be controlled must be linearizable or strict-feedback [19, 22, 27].

There exists one important family of linearizable or strict-feedback chaotic systems for which multiple adaptive or intelligent control strategies have been developed, enabling them to be controlled as single-input and single-output (SISO) systems. The Chua’s circuit, the Lur’e-like system, the Genesio system and the Duffing forced system are typical examples of these types of chaotic systems [8, 19–21]. In some cases, these chaotic systems can be controlled by some of the adaptive controllers developed for classical SISO nonlinear systems but with a different control objective, which can be either chaos suppression, or system’s equilibrium point stabilization, or chaos generation, or chaos synchronization [2, 22]. For instance, in [23] is introduced a hybrid fuzzy system, made of a combined direct and indirect adaptive control schemes for adjusting an adaptive fuzzy controller, for a general class of nth-order nonlinear system in canonical form. This controller is applied to a Duffing forced system, and its effectiveness in controlling chaotic systems is clearly demonstrated. In [24], a cluster-based Self-Organizing Neuro-Fuzzy System (SO-NFS) is proposed for the control of unknown plants. This control method requires the availability of some input–output training data that is used by the neuro-fuzzy system (NFS) to learn its knowledge base, making this control technique unusable for chaotic systems which are known for their unpredictable output. In [25], an Adaptive Neuro-Fuzzy Controller (ANFC) in combination with a Sliding Mode Control-based learning algorithm is used to guarantee the asymptotic stability of an uncertain spherical rolling robot in a compact space. In [10] is proposed a sliding mode synchronization controller in which a radial basis function neural network (RBFNN) is used to construct a compound disturbance observer. It is shown that the proposed controller can get the synchronization error convergent to zero and overcome the disruption of the uncertainty and external disturbance on the chaotic system under control. In [26], a decoupled Neural Fuzzy Sliding Mode Control design method is proposed for a class of fourth-order nonlinear systems. The method consists of separating the system into two second-order subsystems and designing a controller for each subsystem, each of which has its own sliding surface.

To the best of our knowledge, the singularity problem that may arise in the control law is not satisfactorily addressed by the state of the art. This problem is an important issue to be addressed when an approximation of the control gain function appears at the denominator of the control law. Thus, there is a risk of system’s instability, and even destruction that may be caused by a very large or infinite control action caused by the fact that the denominator is not guaranteed to be nonzero or not close to zero. To tackle the underlined problem, some new neural network-based adaptive control schemes for strict-feedback nonlinear systems have been recently introduced. In [13], a switching adaptive control scheme using a Hopfield-based dynamic neural network for nonlinear systems with external disturbances is introduced. The scheme uses a combination of direct and indirect adaptive controllers to avoid the singularity issues. In [14] is proposed a simplified adaptive backstepping neural network control strategy. This approach is based on the fact that in the backstepping design, all unknown functions at intermediate steps are passed down. Therefore, it is suggested that only a single neural network should be used to approximate a lumped uncertainty at the last step. In [15], an adaptive neural dynamic surface control scheme is introduced for disturbed systems. The authors used radial basis function neural networks with the composite laws constructed by prediction error and compensated tracking error between system state and serial–parallel estimation model for the neural networks weights updating.

Nevertheless, all these schemes are proven to be applicable to linearizable or strict-feedback nonlinear systems under the assumption that their control gain function remains definite positive with known upper and lower bounds. Therefore, controllers designed with these approaches fail to control some strict-feedback systems for which the control gain function is with unknown bounds or cannot be guaranteed to remain positive definite. Another issue, which is not satisfactorily addressed, is the possibility of controlling chaotic systems with some realistic control actions.

The main contributions of this paper lie in the following:

  1. (a)

    An extended Neuro-Fuzzy Robust Adaptive SMC-based controller design approach is introduced, for which the bounds and the positive definitiveness of the control gain function are not required.

  2. (b)

    Applied for controlling chaotic systems, most of the control strategies available in the literature require large control actions (because of the instability of the chaotic trajectories) and unrealistic control task (e.g. with discontinuous control signal, and very high switching frequency, which may excite some unmodelled dynamics) [18, 22]. Compared to previous works, the controller design approach presented here ensures that the control action remains as low as possible while being bounded to a realistic level, especially during the transient phase.

  3. (c)

    Furthermore, this approach ensures that asymptotical stability of the closed-loop system is guaranteed despite errors introduced by the Neuro-Fuzzy approximation of the unknown nonlinear functions, the design parameter for singularity avoidance, and the limit imposed to the input signal for the sake of protection.

  4. (d)

    A new three-dimensional linearizable chaotic system with two cubic terms is introduced and studied numerically. After feedback linearization, the control gain of this system is obtained as a semi-definite negative function, which makes it uncontrollable by most of the neural networks-based controllers available in the literature, which are mainly based on the assumption that this function is always positive definite or not close to zero or nonzero (see, for instance, in [14, 15, 36]). Therefore, this system is a good candidate for illustrating the efficiency of the approach introduced in this paper. Even though this chaotic system belongs to the general class of linearizable or strict-feedback nonlinear systems as the one considered for the design strategies introduced in [13–15], controllers designed based on these strategies fail to control it. In contrast, the controller designed with the strategy introduced here is successful to the control of such system.

To demonstrate the applicability of the proposed approach to non-chaotic systems, a MATLAB simulation is performed on a disturbed uncertain nonlinear system controlled first by a NFS-based adaptive controller designed with the introduced approach, and then by the adaptive controllers presented in [14, 15].

The rest of this paper is organized as follows. In Sect. 2, we define the control objective and review the concept of feedback linearization Sliding Mode Control. In Sect. 3, the neuro-fuzzy system, which is used for nonlinear functions approximation throughout this paper, is presented. In Sect. 4, the neuro-fuzzy system-based robust adaptive sliding mode control (NFSRASM) strategy is introduced. In Sect. 5, the new three-dimensional chaotic system is presented with its properties. In Sect. 6, we present some numerical simulation results of the new chaotic system. We also present another nonlinear dynamical system controlled by the NFSRASM and by two recent adaptive neural networks-based controllers available in the literature(see [14, 15]). In order to prove the effectiveness of the proposed scheme, its performances during transient and steady states are compared with those obtained with the other schemes. Sect. 7 concludes the paper.

2 Problem statement and preliminaries

Let us consider the general SISO affine nonlinear system in non-canonical form:

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{\mathbf {x}}(t)= \mathbf {f(x}(t),u(t))+\varvec{\sigma }(t) \\ y(t)=h(\mathbf {x}(t)) \\ \end{array} \right. \end{aligned}$$
(1)

where \(\mathbf {x}(t)\in R^n\) is the vector of the state variables, \(u(t)\in R\) is the control input, \(\mathbf {f(x}(t),u(t))\in R^n\) is the vector of nonlinear functions usually assumed to be continuous, \(\sigma (t)\) is the external disturbance and y(t) is the measured system output.

The control objective is to apply a suitable control signal u(t) that forces the system output y(t) to track a given desired trajectory \(y_d (t)\) while keeping the whole state bounded. System (1) is characterized by the fact that the output y(t) is related to the input u(t) only indirectly through the state variables \(\mathbf {x}(t)\). Therefore, it is not obvious to see how the control law u(t) can be designed for the tracking behaviour of y(t). In order to overcome this difficulty, ignoring the perturbations terms in (1), we apply feedback linearization to (1) as follows [19, 22, 27]:

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{y}= L^1_f h (\mathbf {x}) +L_g(h (\mathbf {x}))u=L^1_f h (\mathbf {x}) &{} \quad \text{ if } {\quad }L_g(h (\mathbf {x})) =0 \\ \ddot{y}= L^2_f h (\mathbf {x})+L_g \left( L_f^1(h (\mathbf {x}))\right) u=L^2_f h (\mathbf {x}) &{} {\quad }\text{ if }{\quad }L_g \left( L_f^1(h (\mathbf {x}))\right) =0 \\ \cdots \\ y^{(r)}=L_f^r h (\mathbf {x}) + L_g\left( L_f^{r-1}(h (\mathbf {x}))\right) u &{}{\quad } \text{ if }{\quad }L_g(L_f^{r-1} h (\mathbf {x})) \ne 0 \\ \end{array} \right. \end{aligned}$$
(2)

with \(L_f h (\mathbf {x})= \nabla h (\mathbf {x}) \cdot f=\left[ \frac{\partial h (\mathbf {x})}{\partial x_1} \cdots \frac{\partial h (\mathbf {x})}{\partial x_n}\right] [f_1 (\mathbf {x}) \cdots f_n (\mathbf {x})]^T\) being the lie derivative of \(h(\mathbf {x}(t))\) with respect to \(\mathbf {f(x)}\).

The last equation of (2) shows the direct and simple relationship between y(t) and u(t). In this equation, r denotes the relative degree of y(t) for \(L_g(L_f^{r-1} h (\mathbf {x})) \ne 0\). In other words, this is the smallest integer for which the coefficient of u(t) or the control gain is nonzero over the space we want to control the system [22].

Assumption 1

For system (1), the relative degree is assumed to be equal to the system’s dimension, i.e. \(r=n\) so that there are no problems related to internal dynamics.

By setting \( \alpha (\mathbf {x})=L_f^r h (\mathbf {x})\) and \(\beta (\mathbf {x})=L_g (L_f^{r-1} h (\mathbf {x}))\), and considering the disturbance terms, we have:

$$\begin{aligned} y(t)^{(r)}= \alpha (\mathbf {x})+ \beta (\mathbf {x})u+\psi (t) \end{aligned}$$
(3)

where \( \beta (\mathbf {x}) \ne 0\) and the disturbance term is bounded by \(\varPsi =\max |\psi (t)|\).

Assumption 2

All the states of system (1) are available through measurements for all time t and are bounded on a compact set \( \varOmega \in R^n \).

Let us denote the tracking error as:

$$\begin{aligned} e(t)=y(t)-y_d(t) \end{aligned}$$
(4)

and define the sliding function giving the error dynamics as:

$$\begin{aligned} s(t)={e(t)}^{(r-1)}+\lambda _{r-1} {e(t)}^{(r-2)} + \cdots + \lambda _1 e(t) \end{aligned}$$
(5)

where \( \lambda _i (i=1,2,\ldots , r-1)\) are positive constants chosen carefully such that:

$$\begin{aligned} p^{r-1}+ \lambda _{r-1} p^{r-2}+ \cdots + \lambda _1=0 \end{aligned}$$
(6)

is a Hurwitz polynomial corresponding to \(\lim _{t \rightarrow \infty } e(t)=0\).

Differentiating s(t) with respect to the time t, we get:

$$\begin{aligned} \dot{s} (t)={e(t)}^{(r)}+\lambda _{r-1} {e(t)}^{(r-1)} + \cdots + \lambda _1 \dot{e}(t) \end{aligned}$$
(7)

Assumption 3

\( y_d (t)\) and its time derivatives up to a sufficiently high order are known and bounded.

Knowing that \( {e(t)}^{(r)}=y^{(r)}-{y_d}^{(r)}\) and using it in (7), we obtain:

$$\begin{aligned} \dot{s}(t)= & {} \alpha (\mathbf {x}) +\beta (\mathbf {x}) u (t) +\psi (t)-{y_d (t)}^{(r)} \nonumber \\&+\lambda _{r-1} {e(t)}^{(r-1)} + \cdots + \lambda _1 \dot{e}(t) \end{aligned}$$
(8)

Let us define a synthetic or intermediate controller as:

$$\begin{aligned} \nu (t)=-{y_d (t)}^{(r)}+\lambda _{r-1} {e (t)}^{(r-1)} + \cdots + \lambda _1 \dot{e} (t) \end{aligned}$$
(9)

This implies that:

$$\begin{aligned} \dot{s}(t)=\alpha (\mathbf {x}) +\beta (\mathbf {x}) u (t) +\psi (t)+\nu (t) \end{aligned}$$
(10)

If \(\alpha (\mathbf {x})\) and \(\beta (\mathbf {x})\) are exactly known and \(\beta (\mathbf {x})\) is guaranteed to be nonzero or not close to zero at all moment, the Sliding Mode Control approach based on a constant rate reaching law can be used for the controller design [27]. The constant rate reaching law is given by:

$$\begin{aligned} \dot{s}(t)=-\eta \mathsf {sign} (s(t)) \end{aligned}$$
(11)

where \(\eta \) represents the constant rate chosen such that \( \eta > \varPsi =\max |\psi (t)|\) in order to unsure the closed-loop system’s robustness against external disturbances. By equalizing (10) (neglecting the disturbance term \(\psi (t))\) and (11), one can derive the control law as:

$$\begin{aligned} u(t)=\frac{1}{\beta ({\mathbf {x}})} [-\alpha (\mathbf {x})-\nu (t)-\eta \mathsf {sign} (s(t)) ] \end{aligned}$$
(12)

By applying (12) in (10), we obtain:

$$\begin{aligned} \dot{s}(t)=-\eta \mathsf {sign} (s(t))+\psi (t) \end{aligned}$$
(13)

In order to analyse the global stability of (1) when (12) is applied, we select a positive definite Lyapunov function as follows:

$$\begin{aligned} V(t)=\frac{1}{2} {s(t)}^2 \end{aligned}$$
(14)

and check whether \(\dot{V}(t)\le 0\) for all time t.

Using (13) in the time derivative of (14), knowing that \(|s(t)|=s(t)\mathsf {sign}(s(t))\), we obtain:

$$\begin{aligned} \dot{V}(t)= & {} s(t) \dot{s}(t)=-\eta |s(t)|+s(t) \psi (t) \nonumber \\\le & {} -\eta |s(t)|+s(t) \varPsi \end{aligned}$$
(15)

\(\eta > \varPsi \) leads to \(\dot{V}(t)\le 0\). This implies achievement of global stability. Hence e(t) converges to zero exponentially in finite time and the control objective is met.

If \(\alpha (\mathbf {x})\) and \(\beta (\mathbf {x})\) are unknown, (12) cannot be used. We should approximate these nonlinear functions by some algorithms and use their estimations \(\hat{\alpha } (\mathbf {x})\)and \(\hat{\beta } (\mathbf {x})\) in the control law (12). This justifies the use of a NFS, which is simply recalled in the next section.

3 Configuration of the neuro-fuzzy system

Considering assumption 2 is valid so that the state variables remain bounded in the compact set \(\varOmega \in R^n\) at all instants t, we can use the universal approximation theorem to get the approximate values of the unknown functions. The universal approximation theorem by a fuzzy logic system can be summarized as follows [13, 27]:

  • For the n system’s inputs \(x_j\) (with \(j=1,2,\ldots ,n\)), define the fuzzy sets \(A_j^i\) (with \(i=1,2,\ldots ,m \) where m is the number of rules)

  • Adopt m fuzzy rules to construct the fuzzy systems \(\hat{\alpha }(\mathbf {x}|\theta _\alpha )\) and \(\hat{\beta }(\mathbf {x}|\theta _\beta )\). The fuzzy rules are in the form:

    $$\begin{aligned}&R^{(i)}:\hbox { If }x_1\hbox { is }A_1^i\hbox { and }\cdots \hbox { and }x_n\hbox { is }A_n^i\\&\quad \hbox {Then }\hat{\alpha }\hbox { is }E_{\hat{\alpha }}^i\hbox { and }\hat{\beta }\hbox { is }E_{\hat{\beta }}^i \end{aligned}$$

    where \(A_1^i, A_2^i,\ldots , A_n^i, E_{\hat{\alpha }}^i\) and \(E_{\hat{\beta }}^i\) are fuzzy sets corresponding to the membership functions \(\mu _{A_1^i}, \mu _{A_2^i}, \ldots , \mu _{A_n^i}\) and \(\mu _{E_{\hat{\alpha }}^i}\) and \(\mu _{E_{\hat{\beta }}^i}\), respectively. \(\mu _{E_{\hat{\alpha }}^i}\) and \(\mu _{E_{\hat{\beta }}^i}\) are fuzzy singletons, while \(\mu _{A_1^i}, \mu _{A_2^i}, \ldots , \mu _{A_n^i}\) are calculated for each input \(x_j\) from the Gaussian function:

    $$\begin{aligned} \mu _{A_j^i} (x_j )=\exp \left[ -\frac{(x_j-p_j^i )^2}{2q^2} \right] \end{aligned}$$
    (16)

    where \(p_j^i\) and q are the parameters of the Gaussian function. These parameters and the number of fuzzy rules (m) are very relevant for the accuracy of the system’s output. In fact, these parameters must be chosen so that the membership functions covers the space containing all possible values of the normalized inputs. On the other hand, the more fuzzy rules we use, the more accurate becomes the approximation. However, a high number of fuzzy rules yields increased computation load and system’s cost [13].

  • Using the average defuzzification techniques, the outputs of the fuzzy system are calculated from:

    $$\begin{aligned} \hat{\alpha }(\mathbf {x}|\hat{\theta }_\alpha )\!= & {} \!\frac{\sum \nolimits _{i=1}^m \hat{\theta }_{\alpha i} (t) \left( \prod \limits _{j=1}^n \mu _{A_j^i} (x_j)\!\right) }{{\sum \nolimits _{i=1}^m \left( \prod \limits _{j=1}^n \mu _{A_j^i} (x_j)\!\right) }}=\hat{\theta }_\alpha ^T (t) \varphi (\mathbf {x})\nonumber \\ \end{aligned}$$
    (17)
    $$\begin{aligned} \hat{\beta }(\mathbf {x}|\hat{\theta }_\beta )= & {} \frac{\sum \nolimits _{i=1}^m \hat{\theta }_{\beta i} (t) \left( \prod \limits _{j=1}^n \mu _{A_j^i} (x_j)\!\right) }{{\sum \nolimits _{i=1}^m \left( \prod \limits _{j=1}^n \mu _{A_j^i} (x_j)\!\right) }}=\hat{\theta }_\beta ^T (t) \varphi (\mathbf {x})\nonumber \\ \end{aligned}$$
    (18)

    where \(\hat{\theta }_\alpha ^T (t) =[\hat{\theta }_{\alpha 1} (t),\hat{\theta }_{\alpha 2} (t),\ldots ,\hat{\theta }_{\alpha m} (t) ] \) and \(\hat{\theta }_\beta ^T (t) =[\hat{\theta }\theta _{\beta 1} (t),\hat{\theta }_{\beta 2} (t),\ldots ,\hat{\theta }_{\beta m} (t) ] \) are the weighting vectors, for which we will select (in the next section) update rules that ensure the achievement of the control objective. The fuzzy singletons \(\mu _{E_{\hat{\alpha }}^i}\) and \(\mu _{E_{\hat{\beta }}^i}\) reach their maximum with the weights \(\hat{\theta }_{\alpha i}\) and \(\hat{\theta }_{\beta i}\), i.e. \(\mu _{E_{\hat{\alpha }}^i} (\hat{\theta }_{\alpha i})=\mu _{E_{\hat{\beta }}^i} (\hat{\theta }_{\beta i})=1\) [13, 23]. The components of the vector of fuzzy basis functions \(\varphi (\mathbf {x})^T=[\varphi _1 (\mathbf {x}),\varphi _2 (\mathbf {x}),\ldots ,\varphi _m (\mathbf {x})]\) are calculated as follows:

    $$\begin{aligned} \varphi _i (\mathbf {x})=\frac{\prod \limits _{j=1}^n \mu _{A_j^i} (x_j)}{\sum \nolimits _{i=1}^m \left( \prod \limits _{j=1}^n \mu _{A_j^i} (x_j)\right) } \end{aligned}$$
    (19)

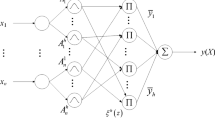
In order to exploit the learning ability of neural networks in addition to the structural advantage of fuzzy logic systems, we use the NFS depicted in Fig. 1. The fuzzy neural network is made of four layers: the input layer, the membership layer, the basis function layer and the output layer.

Fig. 1
figure 1

Synthetic representation of the neuro-fuzzy system where \(x_i (i=1, 2,\ldots , n)\) are the inputs and \(\hat{\alpha }(\mathbf {x}|\hat{\theta }_\alpha )\) and \(\hat{\beta }(\mathbf {x}|\hat{\theta } _\beta )\) are the outputs

Full size image

The common selection of the fuzzy system or neuro-fuzzy inputs in many applications is either the error e(t) and its derivative (or its rate of change) or the n state variables of the system to be controlled [13, 28]. The values applied to the input nodes are directly transmitted to the membership layer, which has \(n\times m\) nodes. Each node in this layer uses (16) to calculate the membership values to be used in the basis function layer. This late layer has m nodes; each node stands for an element of the vector \(\varphi (\mathbf {x})\) calculated from (19) using the membership values provided directly by the preceding layer. The links between the nodes of the basis function layer and the nodes of the output layer are weighted by the elements of the vectors \(\hat{\theta }_\alpha (t)\) and \(\hat{\theta } _\beta (t)\), which are tuned online to provide \(\hat{\alpha }(\mathbf {x}|\hat{\theta }_\alpha )\) and \(\hat{\beta }(\mathbf {x}|\hat{\theta } _\beta )\) at the two output nodes.

Suppose the optimal values of the weights are \(\theta _\alpha ^* \in R^m\) and \(\theta _\beta ^* \in R^m\) defined by:

$$\begin{aligned} \theta _\alpha ^*= & {} \arg \min _{\hat{\theta }_\alpha \in \varTheta _\alpha } \left[ \max _{\mathbf {x} \in \varOmega } |\hat{\alpha }(\mathbf {x}|\hat{\theta }_\alpha )-\alpha (\mathbf {x})|\right] \end{aligned}$$
(20)
$$\begin{aligned} \theta _\beta ^*= & {} \arg \min _{\hat{\theta }_\beta \in \varTheta _\beta } \left[ \max _{\mathbf {x} \in \varOmega } |\hat{\beta }(\mathbf {x}|\hat{\theta }_\beta )-\beta (\mathbf {x})|\right] \end{aligned}$$
(21)

where \(\varTheta _\alpha \in R^m\) and \(\varTheta _\beta \in R^m\) are the sets of acceptable values for the weighting vectors approximations \(\hat{\theta } _\alpha \) and \(\hat{\theta } _\beta \), respectively. The exact nonlinear functions \(\alpha (\mathbf {x})\) and \(\beta (\mathbf {x})\) can therefore be expressed as:

$$\begin{aligned} \alpha (\mathbf {x})= & {} \theta _\alpha ^* \varphi (\mathbf {x})+\varepsilon _\alpha (\mathbf {x}) \end{aligned}$$
(22)
$$\begin{aligned} \beta (\mathbf {x})= & {} \theta _\beta ^* \varphi (\mathbf {x})+\varepsilon _\beta (\mathbf {x}) \end{aligned}$$
(23)

where \(\varepsilon _\alpha (\mathbf {x})\) and \(\varepsilon _\beta (\mathbf {x})\) are the approximation errors.

Assumption 4

The approximation errors \(\varepsilon _\alpha (\mathbf {x})\) and \(\varepsilon _\beta (\mathbf {x})\) are bounded by some constants \(\varepsilon _{\alpha M} > 0\) and \(\varepsilon _{\beta M} > 0\), respectively, over the compact set \(\varOmega \in R^n\), i.e. \(\max _{\mathbf {x} \in \varOmega } |\varepsilon _\alpha (\mathbf {x})| \le \varepsilon _{\alpha M}\) and \(\max _{\mathbf {x} \in \varOmega } |\varepsilon _\beta (\mathbf {x})| \le \varepsilon _{\beta M}\).

The differences between the NFS outputs and the exact nonlinear functions are given by:

$$\begin{aligned} \hat{\alpha } (\mathbf {x} |\hat{\theta }_\alpha )-\alpha (\mathbf {x})= & {} \tilde{\theta }_\alpha ^T \varphi (\mathbf {x})-\varepsilon _\alpha (\mathbf {x})\end{aligned}$$
(24)
$$\begin{aligned} \hat{\beta } (\mathbf {x} |\hat{\theta }_\beta )-\beta (\mathbf {x})= & {} \tilde{\theta }_\beta ^T \varphi (\mathbf {x})-\varepsilon _\beta (\mathbf {x}) \end{aligned}$$
(25)

where \(\tilde{\theta }_\alpha (t)=\hat{\theta }_\alpha (t) -\theta _\alpha ^* \) and \(\tilde{\theta }_\beta (t)=\hat{\theta } _\beta (t) -\theta _\beta ^* \) are the errors on approximated weights.

4 Design of the NFS robust adaptive sliding mode controller (NFSRASMC)

Applying the neuro-fuzzy system outputs (17) and (18) in the control law given by (12), we obtain:

$$\begin{aligned} u(t)=\frac{1}{\hat{\beta } (\mathbf {x} |\hat{\theta }_\beta )} [-\hat{\alpha } (\mathbf {x} |\hat{\theta }_\alpha )-\nu (t)-\eta \mathsf {sign} (s(t))] \end{aligned}$$
(26)

Using the control law given by (26), if the value of \(\hat{\beta } (\mathbf {x} |\hat{\theta }_\beta )\) gets too close to zero or is equal to zero, the control signal becomes very large such that the system’s controllability is not guaranteed and there is a risk of breaking the whole system. Therefore, this control law cannot be used and consequently must be improved.

Assumption 5

Whatever are the values of the system’s (1) parameters, the sign of \(\beta (\mathbf {x})\) is known for all \(\mathbf {x} \in \varOmega \) and there is no guarantee that the approximate value \(\hat{\beta } (\mathbf {x} |\hat{\theta }_\beta )\) will remain different or not close to zero for all \(\mathbf {x} \in \varOmega \) at all moment.

In order to cope with the singularity problem and ensure at all moment that the system controllability is not lost, the control law is designed as follows:

$$\begin{aligned} u(t)=\pm \frac{|\hat{\beta } (\mathbf {x} |\hat{\theta }_\beta )|}{\hat{\beta } (\mathbf {x} |\hat{\theta }_\beta )^2+\delta } [-\hat{\alpha } (\mathbf {x} |\hat{\theta }_\alpha )-\nu (t)-\eta \mathsf {sign} (s(t))] \end{aligned}$$
(27)

Remark 1

The negative sign is chosen if \(\beta (\mathbf {x})\) is known to be negative definite for all \(\mathbf {x} \in \varOmega \) whatever are the system parameters values, which are known to be always positive; otherwise, the positive sign is chosen; \(\delta \) is a small positive constant chosen arbitrary to ensure that singularity is avoided in (27).

Let us select the switching gain as:

$$\begin{aligned} \eta =\rho (\epsilon _{\alpha M}+\epsilon _{\beta M} \cdot u_\mathrm{max}+u_\mathrm{max}+\varPsi ) \end{aligned}$$
(28)

where \(\rho >1\) is a positive design parameter, \(\epsilon _{\alpha M}\) and \(\epsilon _{\beta M}\) are the assumed maximum values of the NFS approximation errors, \(u_\mathrm{max}\) is the maximum value of the amplitude of the control signal and \(\varPsi \) is the upper bound of the external disturbance term.\(\square \)

Theorem 1

By selecting the value of the switching gain as in (28), the effects of the design parameter \(\delta \) and the approximation errors \(\epsilon _\alpha \) and \(\epsilon _\beta \) on the system’s stability are cancelled. (See the proof further in the global stability analysis.)

By adding and subtracting the term \(\hat{\beta } (\mathbf {x} |\hat{\theta }_\beta ) u(t)\) to (10), we obtain (omitting (t) for simplicity):

$$\begin{aligned} \dot{s}= & {} \alpha (\mathbf {x}) +\beta (\mathbf {x}) u (t)+\psi (t)+\nu (t)-\hat{\beta } (\mathbf {x} |\hat{\theta }_\beta )u (t)\nonumber \\&+\hat{\beta } (\mathbf {x} |\hat{\theta }_\beta ) u (t)\nonumber \\= & {} \alpha (\mathbf {x}) +(\beta (\mathbf {x})-\hat{\beta } (\mathbf {x} |\hat{\theta }_\beta )) u (t)+\psi (t) +\nu (t)\nonumber \\&+\hat{\beta } (\mathbf {x} |\hat{\theta }_\beta ) u (t) \end{aligned}$$
(29)

Let us design a second intermediate controller as:

$$\begin{aligned} u_1(t)=-\hat{\alpha } (\mathbf {x} |\hat{\theta }_\alpha )-\nu (t)-\eta \mathsf {sign} (s(t)) \end{aligned}$$
(30)

and rewrite (27) as follows:

$$\begin{aligned} u(t)=\pm \frac{|\hat{\beta } (\mathbf {x} |\hat{\theta }_\beta )|}{\hat{\beta } (\mathbf {x} |\hat{\theta }_\beta )^2+\delta } u_1(t) \end{aligned}$$
(31)

By using (31) only in the last term of (29), we obtain:

$$\begin{aligned} \dot{s}= & {} \alpha (\mathbf {x}) +(\beta (\mathbf {x})-\hat{\beta } (\mathbf {x} |\hat{\theta }_\beta )) u (t) +\psi (t) +\nu (t)\nonumber \\&\pm \hat{\beta } (\mathbf {x} |\hat{\theta }_\beta ) \frac{|\hat{\beta } (\mathbf {x} |\hat{\theta }_\beta )|}{\hat{\beta } (\mathbf {x} |\hat{\theta }_\beta )^2+\delta } u_1 (t) \end{aligned}$$
(32)

Let us set another auxiliary controller as:

$$\begin{aligned} u_1^*(t)=\left[ \pm \hat{\beta } (\mathbf {x} |\hat{\theta }_\beta ) \frac{|\hat{\beta } (\mathbf {x} |\hat{\theta }_\beta )|}{\hat{\beta } (\mathbf {x} |\hat{\theta }_\beta )^2+\delta }-1 \right] u_1 (t) \end{aligned}$$
(33)

By adding and subtracting the term \(u_1\) to (32) and using (30) and (33), we obtain:

$$\begin{aligned} \dot{s}(t)= & {} \alpha (\mathbf {x}) +(\beta (\mathbf {x})-\hat{\beta } (\mathbf {x} |\hat{\theta }_\beta ) u (t) +\psi (t) +\nu (t)\nonumber \\&+u_1^* (t) -\hat{\alpha } (\mathbf {x} |\hat{\theta }_\beta )-\nu (t)-\eta (t) \mathsf {sign} (s (t))\nonumber \\= & {} (\alpha (\mathbf {x})-\hat{\alpha } (\mathbf {x} |\hat{\theta }_\beta )+(\beta (\mathbf {x})-\hat{\beta } (\mathbf {x} |\hat{\theta }_\beta )) u (t)\nonumber \\&+ \psi (t)+u_1^* (t)-\eta (t) \mathsf {sign} (s(t)) \end{aligned}$$
(34)

Applying the identities given by (24) and (25), (34) becomes:

$$\begin{aligned} \dot{s}(t)= & {} -(\tilde{\theta }_\alpha ^T \varphi (\mathbf {x})-\epsilon _\alpha (\mathbf {x}))+\psi +u_1^* (t)\nonumber \\&-(\tilde{\theta }_\beta ^T \varphi (\mathbf {x})-\epsilon _\beta (\mathbf {x})) u (t) -\eta \mathsf {sign} (s (t)) \end{aligned}$$
(35)

Theorem 2

Considering system (1) controlled by the controller given in (31), if all the aforementioned assumptions hold, and if the weights of the NFS are updated by the laws derived with the Lyapunov method, the global stability of the control system is ensured such that the tracking error e(t) converges to a small neighbourhood of zero in finite time.

Proof of theorems 1 and 2

For global stability analysis, we select a positive definite function as a candidate Lyapunov function given by (the independent variable t is ignored for simplicity in notations):

$$\begin{aligned} V=\frac{1}{2} s^2+\frac{1}{2} \gamma \tilde{\theta }_\alpha ^T \tilde{\theta }_\alpha +\frac{1}{2} \gamma \tilde{\theta }_\beta ^T \tilde{\theta }_\beta \end{aligned}$$
(36)

where \(\gamma \) denotes the learning rate of the NFS. \(\square \)

The derivative of V(t) with respect to time corresponds to:

$$\begin{aligned} \dot{V}= s \dot{s}+\gamma \tilde{\theta }_\alpha ^T \dot{\tilde{\theta }}_\alpha +\gamma \tilde{\theta }_\beta ^T \dot{\tilde{\theta }}_\beta \end{aligned}$$
(37)

As \(\dot{\tilde{\theta }}_\alpha =\dot{\hat{\theta }}_\alpha \) and \(\dot{\tilde{\theta }}_\beta =\dot{\hat{\theta }}_\beta \), (35) and (37) can be combined to obtain:

$$\begin{aligned} \dot{V}= & {} -s (\tilde{\theta }_\alpha ^T \varphi (\mathbf {x})-\epsilon _\alpha (\mathbf {x}))+s \psi - s (\tilde{\theta }_\beta ^T \varphi (\mathbf {x})-\epsilon _\beta (\mathbf {x}))u\nonumber \\&+\,\gamma \tilde{\theta }_\alpha ^T \dot{\hat{\theta }}_\alpha +\gamma \tilde{\theta }_\beta ^T \dot{\hat{\theta }}_\beta +s u_1^*-\eta s \cdot \mathsf {sign} (s)\nonumber \\= & {} \tilde{\theta }_\alpha ^T(-s \varphi (\mathbf {x}) + \gamma \dot{\hat{\theta }}_\alpha )+s \epsilon _\alpha (\mathbf {x})\nonumber \\&+\,\tilde{\theta }_\beta ^T(-s \cdot u \cdot \varphi (\mathbf {x}) + \gamma \dot{\hat{\theta }}_\beta ) +s \epsilon _\beta (\mathbf {x}) \cdot u+s \cdot \psi \nonumber \\&+\, s \cdot u_1^* - \eta |s| \end{aligned}$$
(38)

In order to ensure that the parameter \(\gamma \), the NFS membership function \(\varphi (\mathbf {x})\), and approximate parameters \(\hat{\theta }_\alpha \) and \(\hat{\theta }_\beta \) do not affect the system’s stability, we (38) set to zero the terms in which they appear as follows:

$$\begin{aligned}&\tilde{\theta }_\alpha ^T(-s \varphi (\mathbf {x}) + \gamma \dot{\hat{\theta }}_\alpha )=0\end{aligned}$$
(39)
$$\begin{aligned}&\tilde{\theta }_\beta ^T(-s \cdot u \cdot \varphi (\mathbf {x}) + \gamma \dot{\hat{\theta }}_\beta )=0 \end{aligned}$$
(40)

From (39) and (40), we obtain:

$$\begin{aligned} \dot{\hat{\theta }}_\alpha= & {} \frac{1}{\gamma } s \cdot \varphi (\mathbf {x})\end{aligned}$$
(41)
$$\begin{aligned} \dot{\hat{\theta }}_\beta= & {} \frac{1}{\gamma } s \cdot u \cdot \varphi (\mathbf {x}) \end{aligned}$$
(42)

which are the update laws for parameters \(\hat{\theta }_\alpha \) and \(\hat{\theta }_\beta \), respectively. Applying these update laws in (38) we obtain:

$$\begin{aligned} \dot{V}= & {} s \cdot \epsilon _\alpha (\mathbf {x})+s \cdot \epsilon _\beta (\mathbf {x}) \cdot u+s \cdot \psi + s \cdot u_1^* - \eta |s|\nonumber \\\le & {} |s| (\epsilon _{\alpha M} +\epsilon _{\beta M} \cdot u_\mathrm{max} + \varPsi + |u_1^*|) - \eta |s|\nonumber \\\le & {} |s| (\epsilon _{\alpha M} +\epsilon _{\beta M} \cdot u_\mathrm{max} + \varPsi + u_\mathrm{max}) - \eta |s| \end{aligned}$$
(43)

According to (38), it appears that the approximation errors \(\epsilon _\alpha (\mathbf {x}) \) and \(\epsilon _\beta (\mathbf {x})\), the design parameter \(\delta \) (which is used in \(u_1^*\) ) and the external disturbance \(\psi (t)\) may affect the system’s stability. In order to tackle this problem, \(\eta \) in (43) must be selected as follows:

$$\begin{aligned} \eta > \epsilon _{\alpha M} +\epsilon _{\beta M} \cdot u_\mathrm{max} + \varPsi + u_\mathrm{max} \end{aligned}$$
(44)

Therefore, selecting the switching gain as in (44) ensures that the system remains stable, i.e. \(\dot{V} \le 0\), then \(\lim _{t\rightarrow \infty } e(t) =0\). Theorems 1 and 2 are thus proven.

In order to meet the prescribed control objective, especially if the system’s trajectory is chaotic, and during the transient phase in general, the control law given in (31) can lead to excessively large control actions, which cannot be available in practice or if applied to the system can cause its destruction. To avoid this situation, the following hard-limiting function is used [18]:

$$\begin{aligned} u(t)= \left\{ \begin{array}{ll} u_\mathrm{max} &{} \text{ if } u^* \ge u_\mathrm{max} \\ u_\mathrm{min} &{} \text{ if } u^* \le u_\mathrm{min} \\ u^* &{} \text{ otherwise } \end{array} \right. \end{aligned}$$
(45)

where we set \(u^*(t)=\pm \frac{|\hat{\beta } (\mathbf {x}|}{\hat{\beta } (\mathbf {x})^2+\delta } u_1(t)\) and \(u_\mathrm{max}\) is the chosen upper bound of the control signal.

In order to avoid chattering effects (the very high switching frequency which may excite some unmodelled dynamics), the signum function in (30) is replaced by the following continuous function:

$$\begin{aligned} T(s(t))=\frac{1-\exp (-q \cdot s(t))}{1+\exp (-q \cdot s(t))} \end{aligned}$$
(46)

where q is a positive design constant.

Finally, the block diagram of the NFSRASMC is shown in Fig. 2 along with the description of all components.

Fig. 2
figure 2

The block diagram of the Neuro-Fuzzy robust adaptive sliding mode control system (NFSRASMC)

Full size image

For any given uncertain linearizable system, the functioning principle can be summarized as follows:

  • Set the values of the design parameters \(\lambda _1, \ldots , \lambda _{r-1}, q, \gamma , \epsilon _{\alpha M}, \epsilon _{\beta M}, \eta , u_\mathrm{max}\), and the initial values for the system’s state, the NFS weights approximation and the control signal u(t); then for each time t

  • Measure the desired trajectory or reference for the system’s output and its rth derivative

  • Measure the system output

  • Compute the output tracking error e(t) and its first, second, \(\cdots , r-1\)th derivatives

  • Compute the sliding variable s(t) and the intermediate controller \(\nu (t)\)

  • Use the NFS inputs (error e(t) and its derivatives or the system’s state variables) to compute the membership functions and then the basis function vector \(\varphi (x)\)

  • Use the basis function vector, the available measured control signal u(t) and the sliding variable s(t) to tune online the NFS weights

  • Use the NFS outputs to compute the new control signal u(t)

  • Apply the control signal to the hard-limiting function, for which the output is applied to the system to be controlled.

5 The new chaotic system and its properties

The new chaotic system proposed in this paper is a highly nonlinear system with two cubic terms modelled mathematically as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x_1}(t)= a(x_2-x_1) \\ \dot{x_2}(t)= -cx_3^3 \\ \dot{x_3}(t)= -d+bx_2^3 \end{array} \right. \end{aligned}$$
(47)

where a, b, c and d are the positive system’s parameters.

A MATLAB simulation is performed with the initial conditions selected as (0.1, 0.8, 1.2). The system exhibits transient chaotic behaviour when its parameters are selected as \(a=1.8, b=5, c=1.5, d=10\) (see Fig. 3) and finally settles to torus at long term. This torus state of the system is illustrated by the phase portraits in Fig. 4.

Fig. 3
figure 3

Phase portrait revealing the transient chaos (\(\lambda _\mathrm{max}=0.0623\)) exhibited by the system (47) with the parameters \(a=1.8, b=5, c=1.5, d=10\) and initial conditions (0.1, 0.8, 1.2): a represents the 3D view of the state variables; b represents the \(x_1-x_2\) phase portrait; c represents the \(x_2-x_3\) phase portrait; and d represents the \(x_1-x_3\) phase portrait

Full size image
Fig. 4
figure 4

Phase portrait of the torus dynamics (\(\lambda _\mathrm{max}= 0\)) exhibited by the system (47) with the parameters \(a=1.8, b=5, c=1.5, d=10\) and initial conditions (0.1, 0.8, 1.2): a represents the 3D view of the state variables; b represents the \(x_1-x_2\) phase portrait; c represents the \(x_2-x_3\) phase portrait; and d represents the \(x_1-x_3\) phase portrait

Full size image

5.1 System’s equilibrium point

The equilibrium point of system (47) is obtained by solving the following system of nonlinear algebraic equations:

$$\begin{aligned} \left\{ \begin{array}{ll} 0= a(x_2-x_1) \\ 0= -cx_3^3 \\ 0= -d+bx_2^3 \end{array} \right. \end{aligned}$$
(48)

Three solutions are found, which depend on values of parameters b and d. They correspond to:

  • one coordinate in the real plane: \(\left( (\frac{d}{b})^\frac{1}{3}, (\frac{d}{b})^\frac{1}{3}, 0\right) \)

  • and two coordinates in the complex plane: \(\left( -\frac{1}{2}(\frac{d}{b})^\frac{1}{3}\right. \left. \pm j \frac{\sqrt{3}}{2} (\frac{d}{b})^\frac{1}{3}, -\frac{1}{2}(\frac{d}{b})^\frac{1}{3} \pm j \frac{\sqrt{3}}{2} (\frac{d}{b})^\frac{1}{3}, 0\right) \).

As the equilibrium points must be localized in the real plane, only the first solution is considered. Therefore, by applying the aforementioned parameter values in this solution, the system’s equilibrium point is found as: (1.2599, 1.2599, 0).

By setting \(f (\mathbf {x}) = \left[ \begin{array}{rr} f_1 (\mathbf {x}) \\ f_2 (\mathbf {x}) \\ f_3 (\mathbf {x}) \end{array}\right] =\left[ \begin{array}{rr} a(x_2-x_1) \\ -cx_3^3 \\ -d+bx_2^3 \end{array}\right] \), the Jacobian matrix of \(f (\mathbf {x})\) is obtained as: \(J (\mathbf {x})= \left[ \begin{array}{rrr} -a &{} a &{} 0\\ 0 &{} 0 &{} -3cx_3^2 \\ 0 &{} 3bx_2^2 &{} 0\end{array}\right] \)

In order to find the Eigenvalues, let us solve the following characteristic equation (obtained from \(\det [\lambda I-J(\mathbf {x})]=0\), where I is a \(3 \times 3\) identity matrix):

$$\begin{aligned} \lambda ^3+a \lambda ^2 + 9 bc x_2^2 x_3^2 \lambda + 9 abc x_2^2 x_3^2 =0 \end{aligned}$$
(49)

In order to obtain the Eigenvalues at the equilibrium point (1.2599, 1.2599, 0), we solve the following equation obtained from (49):

$$\begin{aligned} \lambda ^3+a \lambda ^2 =0 \end{aligned}$$
(50)

We obtain \(\lambda _1=0, \lambda _2=0\) and \(\lambda _3=-a=-1.8\). Thus, the equilibrium point is non-hyperbolic and the corresponding bifurcation is a Bogdanov–Takens bifurcation [38, 39]. Two types of attractors can be generated: an homoclinic orbit or a limit cycle of type Andronov–Hopft.

5.2 Dissipativity

In order to measure how fast volumes change, under the flow \(\varPhi _t\) of the vector field \(f (\mathbf {x})\), the divergence of \(f (\mathbf {x})\) is used. The divergence of the vector field \(f (\mathbf {x})\) on \(R^3\) is given by:

$$\begin{aligned} \nabla \mathbf {f}=\frac{\partial f_1}{\partial x_1}+\frac{\partial f_2}{\partial x_2}+\frac{\partial f_3}{\partial x_3}=-a<0 \end{aligned}$$
(51)

Suppose \(\varOmega \) is a region in \(R^3\) with smooth boundary, and let \(\varOmega (t) = \varPhi _t (\varOmega )\) the image of \(\varOmega \) under the time t map of the flow [29]. Let V(t) be the volume of \(\varOmega (t)\). Then using the Liouville’s theorem, we get:

$$\begin{aligned} \dot{V} (t)=\int _{\varOmega (t)} (\nabla \mathbf {f}) dx_1 dx_2 dx_3 = -a V(t) \end{aligned}$$
(52)

Solving the differential equation (52), we obtain:

$$\begin{aligned} V (t)=\exp (-at) V(0) \end{aligned}$$
(53)

Since \(a>0\), this means that any volume V(t) must shrink exponentially fast to zero as t tends to infinite. Therefore, the new chaotic system (47) is dissipative. Hence, all orbits of system (47) are eventually confined to a specific subset \(\varOmega \) that has zero volume [29, 37]. This late conclusion is very important as it proves that assumption 2 holds for the new chaotic system (47). Therefore, it satisfies the criteria for applicability of the universal approximation theorem for unknown nonlinear functions so that the approach developed in this paper can be successfully applied to it.

5.3 Bifurcation analysis and largest Lyapunov exponent

The Lyapunov exponents measure the rates of divergence or convergence of two neighbouring trajectories in the phase space [30]. It is also a quantitative measure of sensitive dependence of the system on the initial conditions [31]. If one speaks about the Lyapunov exponent, the largest one is meant. The mean growth rate of the distance \(\parallel \delta x(t) \parallel /\parallel \delta x_0 \parallel \) between neighbouring trajectories is given by the largest Lyapunov exponent (LLE), which is estimated at long term as [32]:

$$\begin{aligned} \lambda _\mathrm{max} \cong \lim _{t\rightarrow \infty } \left[ \frac{1}{t} \ln \frac{\parallel \delta x(t) \parallel }{\parallel \delta x_0 \parallel } \right] \end{aligned}$$
(54)

The value \(\lambda _\mathrm{max}>0\) corresponds to chaos and \(\lambda _\mathrm{max} \le 0\) stands for non-chaotic states (\(\lambda _\mathrm{max}=0\) shows a torus) [7, 8].

Figure 5 presents the bifurcation diagram and the corresponding largest Lyapunov exponent when the control parameter c is monitored in the range [0, 10]. According to Fig. 5, the largest Lyapunov exponent is \(\lambda _\mathrm{max}\) is always nearly zero in the full range of the control parameter. This justifies the presence of torus within the system.

Fig. 5
figure 5

a Bifurcation diagram and b corresponding largest Lyapunov Exponent. This figure confirms the presence of Torus when monitoring the control parameter c in the window [0 10]. The system parameters used are a = 1.8, b = 5 and d = 10. The initial condition is (1, 8, \(-1.2\))

Full size image

6 Illustrative examples

6.1 Example 1: Control of a disturbed strict-feedback nonlinear system

Let us consider the example used in [14, 33] given as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x_1}= 0.5 x_1 +(1+0.1 x_1^2) x_2 \\ \dot{x_2}= x_1 x_2 + (2+\cos x_1)u(t)+d(t) \\ y=x_1 \end{array} \right. \end{aligned}$$
(55)

where \(x_1\) and \(x_2\) are the state variables, y is the system’s output, \(d(t)=5 \sin (t)\) is the external disturbance and u(t) is the control action. The initial state vector for this system is selected as [1.2, 1.0].

The reference signal for the system’s output \(y_d\) is generated by the van der Pol oscillator given as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x}_{d1}= x_{d2} \\ \dot{x}_{d2}= -x_{d1} + \beta (1-x_{d1}^2) x_{d2} \\ y_d=x_{d1} \end{array} \right. \end{aligned}$$
(56)

with a nonlinear damping parameter selected as \(\beta =3\) such that the reference signal \(y_d\) is non-sinusoidal (unlike in [14] and [33]) and therefore more challenging to track. This is better for a good assessment of performances (during transient phase and steady state) obtained for cases when the design approaches introduced either in this paper or in [14] or in [15] are used to design u(t). The initial state vector for the system (56) is selected as [1.5, 0.8].

Case 1: \(\mathbf {u(t)}\) designed with the approach presented in this paper (NFSRASMC)

In this case, the approach introduced in this paper is applied to design the control law u(t). The inputs to the NFS are selected as the system’s states \(x_1\) and \( x_2\). We select nine membership functions obtained from:

$$\begin{aligned} \mu _{A_j^i}=\exp \left[ - \frac{\left( x_j +2 - \frac{i-1}{2}\right) ^2}{2\times 0.2^2} \right] \end{aligned}$$
(57)

for \(i=1,2,\ldots ,9\) and \(j=1,2\). The membership functions curves are shown in Fig. 6.

Fig. 6
figure 6

Membership functions for example 1

Full size image

The sliding function is obtained from (5) as follows:

$$\begin{aligned} s(t)=\dot{e} (t) + \lambda e (t) \end{aligned}$$
(58)

where we choose \(\lambda =6\) (optimal value obtained from a trial and error process).

The controller is designed as follows:

$$\begin{aligned} u(t)= \frac{|\hat{\beta } (\mathbf {x} |\hat{\theta }_\beta )|}{\hat{\beta } (\mathbf {x} |\hat{\theta }_\beta )^2+\delta }u_1(t) \end{aligned}$$
(59)

where \(u_1(t)=-\hat{\alpha } (\mathbf {x})-\nu (t) - \eta \cdot T(s(t))\) with \(T(s(t))=[1-\exp (-4s(t))]/[1+\exp (-4s(t))]\)

The intermediate controller \(\nu (t)\) is given by:

$$\begin{aligned} \nu (t) = -\ddot{y}_{d}+\lambda \dot{e} (t) \end{aligned}$$
(60)

The controller’s parameter \(\delta \) is selected as: \(\delta =0.05\). The parameter for the hard-limiter or the maximal input signal is selected as \(u_\mathrm{max}=12\). We select \(\eta =(\epsilon _{\alpha M}+\epsilon _{\beta M} \cdot u_\mathrm{max}+\varPsi +u_\mathrm{max})*2\) where \(\varPsi \) is the upper bound of d(t), which is 5, and \(\epsilon _{\alpha M}=\epsilon _{\beta M}=0.05\).

Table 1 Steady state and transient phase performances specifications for the three controllers applied on system (55)
Full size table

Remark 2

As the exact nonlinear control gain function of (55) can take only positive values whatever may be the values that the variable \(x_1\) can take, the control law (31) is used with the positive sign chosen.

The update rules given in (41) and (42) are used with the learning rate selected as \(\gamma =0.005\), and the initial values for the elements of the approximate vector weights are selected as \(\hat{\theta }_{\alpha k}=0.1\) and \(\hat{\theta }_{\beta k}=0.2\) with \(k=1,2,\ldots ,81\).

Figure 7 shows results of numerical simulation of system (55) controlled by the NFSRASMC. On the top of this image is the plot showing comparison between the system output y(t) and the desired trajectory \(y_d(t)\). This plot shows that the NFSRASMC forces y(t) to track \(y_d(t)\) with accuracy and without any overshoot. This is achieved in a finite time, approximately \(t_s=0.5\). On the bottom is the plot of the control signal u(t), which remains limited bellow \(u_\mathrm{max}=12\) even during the transient phase. In order to provide a broad insight of the controller’s performances, we use the following performance specifications:

  • The mean square error (MSE) (during steady state), which is calculated as follows:

    $$\begin{aligned} \text{ MSE }=\frac{1}{N} \sum _{i=1}^N e(i)^2 \end{aligned}$$
    (61)

    where N is the length of the vector e.

  • The peak overshoot \(M_p\) in \(\%\) of the reference signal maximum amplitude

  • The settling time \(t_s\)

  • Steady state error upper bound: \(\max _{t\rightarrow \infty } |e(t)|\) (which shows the size of the neighbourhood of zero to which the tracking error is confined)

  • The control signal energy (obtained using the two-norm method) (to assess the control signal performance). This energy is desired as low as possible for better power management

  • The total variation (TV) to assess the smoothness of the control signal [34]. It is desired to have a small value because a large value of TV means more complicated or too much solicited or unrealistic controller [35]. For a discretized signal, i.e. \(u_1, u_2, \ldots , u_n\) the TV can be defined as:

    $$\begin{aligned} \text{ TV }=\sum _{i=1}^{n-1} |u_{i+1}-u_i|. \end{aligned}$$
    (62)

For this simulation case, the values of these performance indexes are found in Table 1.

Fig. 7
figure 7

Results for case 1 with the NFSRASMC; On the top: comparison of system output y(t) (dashed line) and the desired trajectory \(y_d (t)\) (continuous line); On the bottom: the control signal u(t)

Full size image

Case 2: \(\mathbf {u(t)}\) designed with the approach presented in [14]

In this case, the approach introduced in [14] is applied to design the control law u(t). The controller is given by equation (27) in [14]. It uses the NFS output and update law given by (26) and (30), respectively, in [14]. This approach is also based on a NFS, so we use a NFS with the same membership functions as in the previous case but with five inputs as suggested in [14]. These inputs are \(\mathbf {X_e}=\left[ x_1, x_2, y_d, \dot{y}_d, \ddot{y}_d\right] \). The other controller’s parameters are chosen as \(k_1=200, k_2=10, \gamma =5000, \sigma =0.001\). The initial weight vector is selected as \(\hat{W}=[0, 0, \ldots , 0]^T \in R^{9^5}\). For more information about this design approach, the reader is referred to [14].

Numerical simulation results obtained when this controller is applied to the system (55) are depicted in Fig. 8.

Fig. 8
figure 8

Results for case 2 with the controller from [14]; On the top: comparison of system output y(t) (dashed line) and the desired trajectory \(y_d (t)\) (continuous line); On the bottom: the control signal u(t)

Full size image

On the top of this image is the plot showing comparison between the system output y(t) and the desired trajectory \(y_d(t)\). This plot shows that the controller forces y(t) to track \(y_d(t)\) with accuracy but with some pick overshoot (14 %). The tracking is achieved in a finite time, approximately \(t=1\). On the bottom is the plot of the control signal u(t), which appears to undergo some oscillations during the transient phase. In order to provide a broad insight of the controller’s performances, we use the performance specifications defined in the previous case. The values of these performance metrics for this case are found in Table 1.

Case 3: \(\mathbf {u(t)}\) designed with the approach presented in [15]

For this case, we use the adaptive controller given by the equation (32) of [15]. This controller uses a radial basis function neural network for which the update rule is given by (29) in [15]. The controller parameters selected as \(k_1=200, k_2=20, \gamma _1=\gamma _2=10, \delta _1=\delta _2=1, \beta _1=\beta _2=5, \gamma _{z1}=\gamma _{z2}=1\). For the neural network design, the inputs are selected as \(x_1\) with the centre evenly spaced in \([-1, 1]\) and \([x_1, x_2]\) with the centre evenly spaced in \([-3, 3]\). For more information about this design approach, the reader is invited to read [14].

Numerical simulation results obtained when this controller is applied to the system (55) are depicted in Fig. 9. On the top of this image is the plot showing comparison between the system output y(t) and the desired trajectory \(y_d(t)\). This plot shows that the controller forces y(t) to track \(y_d(t)\) with accuracy but with an important pick overshoot (166.67 %). The tracking is achieved in a finite time, approximately \(t=1.678\). On the bottom is the plot of the control signal u(t), which appears to undergo important oscillations during the transient phase, leading to some very large amplitude of the control signal. In order to provide a broad insight of the controller’s performances, we use the same performance specifications defined in case 1. The values of these performance metrics for this case are found in Table 1.

Fig. 9
figure 9

Results for case 3 with the controller from [15]; On the top: comparison of system output y(t) (dashed line) and the desired trajectory \(y_d (t)\) (continuous line); On the bottom: the control signal u(t)

Full size image

Remark 3

From the data provided in Table 1, one can immediately see that with the methodology introduced in this paper, good results are obtained in terms of transient phase response, steady state response and control energy characteristics. Compared to the controller from [14], the NFSRASMC provides better transient phase performances (a smaller settling time, no overshoot, a shorter settling time), better steady state performances (a lower MSE, a lower upper bound of the steady state error or a smaller neighbourhood of zero to which the errors dynamics is confined) and better controller performances (lower TV and control energy). However, compared to the controller from [15], if one relies on the numbers showing the steady state performances (MSE and error bounds), a conclusion can be drawn that our controller is slightly outperformed during this phase. But one should notice that a very large control action is needed (\(5.5 \times 10^4\)) so that the controller from [15] could provide such performances, which is not interesting in practice. In addition, an important pick overshoot is observed, which may cause the system destruction in practical application. The controller designed with our approach provides nearly the same performances in steady state, but with better performances in transient phase and better control signal features.

6.2 Example 2: Control of the new chaotic system

Let us consider system (47) transformed into a non-homogeneous uncertain and disturbed system as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x_1}(t)= a(x_2-x_1) \\ \dot{x_2}(t)= -cx_3^3 \\ \dot{x_3}(t)= -d+b x_2^3+u(t)+\psi (t) \end{array} \right. \end{aligned}$$
(63)

for which the nominal values of the parameters are \(a=1.8, b=5, c=1.5, d=10\). The actual values of these parameters are not known.

Selecting the output as \(y(t)=x_1\) and applying (2) for feedback linearization, we obtain:

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{y}= a(x_2-x_1) \\ \ddot{y}= -acx_3^3-a^2 (x_2-x_1) \\ y^{(3)}= 3acd x_3^2-3abcx_2^3x_3^2+a^2cx_3^2 \\ \qquad +\,a^3(x_2-x_1)-3acx_3^2 u \end{array} \right. \end{aligned}$$
(64)

Therefore, the relative degree of y(t) is \(r=n=3\), which is in accordance with assumption 1.

Putting the last equation of (64) into the form of (3) and adding the external disturbance term \(\psi (t)\), we obtain:

$$\begin{aligned} y^{(3)}=\alpha (\mathbf {x})+\beta (\mathbf {x})+\psi (t) \end{aligned}$$
(65)

where:

  • \(\alpha (\mathbf {x})=3acd x_3^2-3abcx_2^3x_3^2+a^2cx_3^2+a^3(x_2-x_1)\),

  • \(\beta (\mathbf {x})=-3acx_3^2\) and

  • \(\psi (t)=5 \sin (t)\) (therefore \(\varPsi =5\)).

Since the system parameters a, b, c and d are not known, assumption 2 is valid in the case of system (63), as proven in the previous section. Let us use the NFS presented in Sect. 3 to approximate the unknown nonlinear functions \(\alpha (\mathbf {x})\) and \(\beta (\mathbf {x})\).

Remark 4

It is easily noticed that for all nonzero values of \(x_3\), the control gain function \(\beta (\mathbf {x})\) is semi-definite negative (i.e. \(\beta (\mathbf {x}) \le 0\)) whatever the values of the system’s parameters are. Hence, assumption 5 is validated in this case. Therefore, the negative sign is selected in the controller given in (31). System (63) will be controlled by the NFSRASMC given as follows:

$$\begin{aligned} u(t)=- \frac{|\hat{\beta } (\mathbf {x} |\hat{\theta }_\beta )|}{\hat{\beta } (\mathbf {x} |\hat{\theta }_\beta )^2+\delta } u_1(t) \end{aligned}$$
(66)

where:

  • \(u_1(t) = -\hat{\alpha } (\mathbf {x} |\hat{\theta }_\alpha )-\nu (t)-\eta \mathsf {sign} (s(t))\)

  • \(T(s(t))=[1-\exp (-4s(t))]/[1+\exp (-4s(t))]\) and

  • \(\nu (t) = -y_d^{(3)}+\lambda _2 \ddot{e} (t)+\lambda _1 \dot{e} (t)\)

The switching gain is selected as \(\eta =20*(\epsilon _{\alpha M}+\epsilon _{\beta M} \cdot u_\mathrm{max}+u_\mathrm{max}+\varPsi )\). The assumed upper bounds on the approximation error are selected as \(\epsilon _{\alpha M}=\epsilon _{\beta M}=0.05\). The controller parameters are selected as: \(\delta =0.05, \lambda _1=\lambda _2=3\). The parameter for the hard-limiter or the maximal input signal is selected as \(u_\mathrm{max}=12\). For this example, the three state variables of the system \(x_1, x_2\) and \(x_3 (n=3)\) are the input of the NFS. Considering that the inputs are normalized in the range \([-2,2]\), let us use seventeen fuzzy rules (\(m=17\)), for which the corresponding membership functions represented in Fig. 10 are obtained from:

$$\begin{aligned} \mu _{A_j^i}=\exp \left[ -\frac{\left( x_j+2-\frac{i-1}{4}\right) ^2}{2 \times 0.2^2} \right] \end{aligned}$$
(67)

for \(i=1, 2,\ldots , 17\) and \(j=1, 2, 3\)

Fig. 10
figure 10

Membership functions for example 2

Full size image

The weights vectors of the NFS are updated online using the update rules given in (41) and (42) with the learning rate chosen as \(\gamma =0.001\).

Table 2 Steady state and transient phase performance specifications for the NFSRASMC applied on the new system
Full size table

The control objective is the complete synchronization of system (63) with the homogeneous system (47). The initial conditions are selected as (1.6, 0.8, 1.2) and \((1,-1,-1.2)\) for system (47) and system (63), respectively. Numerical simulation is performed with the fourth-order Runge–Kutta algorithm implemented in MATLAB with the integration step size \(\Delta t= 10^{-4}\). Figure 11 shows the simulation results proving that the controller successfully synchronizes the two different systems.

Fig. 11
figure 11

Numerical simulation results of the new chaotic system before and after activation of the NFSRASMC at \(t=10\): a state \(x_1\) and its reference \(x_{1d}\); b synchronization error on the state \(x_1\); c state \(x_2\) and its reference \(x_{2d}\); d synchronization error on the state \(x_2\); e state \(x_3\) and its reference \(x_{3d}\); f synchronization error on the state \(x_3\)

Full size image

During simulation, the controller is not used until the simulation time 10. We can see in Fig. 11 that between the times 0 and 10, starting from different initial conditions, the states of the two systems evolve on two completely different trajectories, which is in accordance with the inherent nature of chaotic systems. When the controller is introduced at the simulation time 10, the states of the system (63) are rapidly forced to track the trajectories of system (47) states for all subsequent simulation time. The plots (b), (d) and (f) of Fig. 11 show how the tracking errors on the three state variables decay abruptly towards zero despite the risks of instability introduced by the NFS approximation errors, the additional design parameter for singularity avoidance and the external disturbance. For plotting these error dynamics, we used a large simulation time to show how the system remains stable, while the tracking errors remain oscillatory within a small neighbourhood of zero (e.g. for the first state variable \(x_1, |e_1 (t)| \le 0.0032)\). Figure 12 represents the control signal that is continuous and becomes relatively small as soon as the steady state is achieved. In order to assess the performances of the controllers for this example, we used the same performance specifications as in the previous example. These are found in Table 2 for the state variable \(x_1\) for illustration.

Fig. 12
figure 12

The control signal introduced at simulation time 10

Full size image

For benchmarking, we made an attempt to control the same system with the controllers from [14, 15] used in the previous example, but this late controllers failed whatever are the chosen controllers’ parameters. As it can be observed in Fig. 13, the system’s stability is lost from the moment these controllers are activated (at \(t=10\)). This proves that the design approach introduced in this paper is more general that those neural networks-based approaches proposed in the literature based on the assumption that \(\beta (\mathbf {x}) \ge 0\) or \(\beta (\mathbf {x}) \ne 0 \forall t\).

Fig. 13
figure 13

System’s response when the controllers from [14, 15] are used

Full size image

7 Conclusion

In this paper, we have presented a new approach for Robust Adaptive Sliding Mode Controller design for a class of uncertain and disturbed nonlinear systems. As the adaptive building block of the control system, which approximates the unknown nonlinear functions, we used the NFS in order to exploit the learning ability of the neural network in addition to the structural advantage of fuzzy systems. The new design approach is characterized by its particular robustness. In fact, problems as singularity in the control law, the effects of the introduced design parameter for singularity cancellation, the external disturbances and NFS approximation errors on the system stability are avoided. We also introduce a new chaotic system characterized by its high nonlinearity and that can have multiple uses in several applications where chaotic systems are needed. Using this new chaotic system as an example, we prove that controllers designed with our approach are able to successfully synchronize challenging nonlinear systems, while the approaches available in the literature cannot guarantee the same. Therefore, this approach is more general than the others. In order to prove that our approach suits for classical nonlinear systems as well, a controller for a given strict-feedback or linearizable nonlinear dynamical system is designed. Using two of the most recent neural network-based design approaches for adaptive controllers reported in the literature, we designed controllers for the same system. By simulation, we proved that, with the new design approach, the controller does not only show effectiveness in controlling classical nonlinear systems, but it also outperforms the controller from the literature in terms of accuracy or meeting the control objective during the steady state and with best transient performances. Another important characteristic of the introduced design approach is that it ensures that the control signal remains realistic and relatively small for practical applications, especially when the controlled plant is characterized by highly unstable trajectory as for chaotic systems.