Stability and Hopf bifurcation of a predator–prey model with stage structure and time delay for the prey

Abstract

A predator–prey system with stage structure and time delay for the prey is investigated. By analyzing the corresponding characteristic equations, the local stability of a positive equilibrium and two boundary equilibria of the system is discussed, respectively. By using persistence theory on infinite dimensional systems and comparison argument, respectively, sufficient conditions are obtained for the global stability of the positive equilibrium and one of the boundary equilibria of the proposed system. Further, the existence of a Hopf bifurcation at the positive equilibrium is studied. Numerical simulations are carried out to illustrate the main results.

1 Introduction

The predator–prey system is an important population model, which has received extensive attention [1–3]. But all of these works ignore the stage structure of species. However, in natural world, there are many species whose individuals have a history that can be divided into two stages, immature and mature. As is common, the dynamics—eating habits, susceptibility to predators, etc.—are often quite different in these two subpopulations. Hence, it is of ecological importance to investigate the effects of such a subdivision on the interaction of species.

Aiello and Freedman [4] proposed and studied the stage-structured single-species population model with time delay

$$\begin{aligned} \begin{array}{l} \dot{x}_i (t)=\alpha x_m (t)-\gamma x_i (t)-\alpha \mathrm{e}^{-\gamma \tau }x_m (t-\tau ), \\ \dot{x}_m (t)=\alpha \mathrm{e}^{-\gamma \tau }x_m (t-\tau )-\beta x_m^2 (t), \\ \end{array} \end{aligned}$$

where $x_i (t)$ and $x_m (t)$ represent the densities of the immature and the mature populations at time t, respectively; $\alpha$ is the birth rate of the immature population at time t; $\gamma$ and $\beta$ are the death rates of the immature and the mature at time t, respectively; $\tau$ is the maturity; $\alpha \mathrm{e}^{-\gamma \tau }x_m (t-\tau )$ represents the quantity which the immature born at time $t-\tau$ can survive at time t. Based on the ideas above, many authors studied different kinds of ecology models with stage structure [5–13].

In this paper, we study the following predator- prey system with stage structure and time delay for the prey

$$\begin{aligned} {\begin{array}{l} {\dot{x}_1 (t)=rx_2 (t)-r\mathrm{e}^{-d_1 \tau }x_2 (t-\tau )-d_1 x_1 (t),} \\ {\dot{x}_2 (t)=r\mathrm{e}^{-d_1 \tau }x_2 (t-\tau )-d_2 x_2^2 (t)-\frac{k_1 x_2 (t)y(t)}{1+\alpha x_2 (t)},} \\ {\dot{y}(t)=\frac{k_2 x_2 (t)y(t)}{1+\alpha x_2 (t)}-d_3 y(t).} \\ \end{array} } \end{aligned}$$

(1)

In (1), $x_1 (t)$ and $x_2 (t)$ represent the densities of the immature and the mature prey at time t, respectively; y(t) represents the density of the predator at time t. The model is derived under the following assumptions.

• (A) The prey population: The birth rate is proportional to the existing mature population with a proportionality $r>0$; the death rate of the immature population is proportional to the existing immature population with a proportionality $d_1 >0$; the death rate of the mature population is proportional to the square of the existing mature population with a proportionality $d_2 >0$; $\tau >0$ is the maturity.

• (B) The predator population: The predators feed only on the mature prey (this seems reasonable for a number of mammals, where the immature prey concealed in the mountain cave and is raised by their parents; they do not necessarily go out for seeking food; the rate they are attacked by the predators can be ignored). The growth of the species obeys a Holling type II functional response. $k_1 >0$ is the capturing rate of the predator; $\frac{k_2 }{k_1 }>0$ is the conversion rate of nutrients into the reproduction of the predator; $\alpha >0$ is the half saturation rate of the predator; $d_3 >0$ is the death rate of the predator.

The initial conditions for system (1) take the form

$$\begin{aligned}&x_1 (\theta )=\phi _1 (\theta )\ge 0,\quad x_2 (\theta )=\phi _2 (\theta )\ge 0,\nonumber \\&y(\theta )=\phi _3 (\theta )\ge 0, \quad \theta \in [-\tau ,0),\nonumber \\&\phi _i (0)>0, \quad i=1,2,3, \end{aligned}$$

(2)

where

$$\begin{aligned}&(\phi _1 (\theta ),\phi _2 (\theta ),\phi _3 (\theta ))\in C([-\tau ,0],R_{+0}^3 ),\\&R_{+0}^3 =\{(x_1 ,x_2 ,x_3 )|x_i \ge 0,i=1,2,3\}. \end{aligned}$$

In order to ensure the initial continuous, we suppose further that

$$\begin{aligned} x_1 (0)=\int _{-\tau }^0 {r\phi _2 } (s)\mathrm{e}^{d_1 s}\hbox {d}s. \end{aligned}$$

By the fundamental theory of functional differential equations [14], it is well known that system (1) has a unique solution $(x_1 (t),x_2 (t),y(t))$ satisfying initial conditions (2). Further, it is easy to show that all solutions of system (1) with initial conditions (2) are defined on $[0,+\infty )$ and remain positive for all $t\ge 0$.

Lemma 1

[5] Consider the following equation

$$\begin{aligned} \dot{x}(t)=ax(t-\tau )-bx(t)-cx^{2}(t), \end{aligned}$$

where $a,c>0$, $b\ge 0$; $x(t)>0$ for $-\tau \le t\le 0$, we have

(i):

If $a>b$, then $\lim \nolimits _{t\rightarrow +\infty } x(t)=\frac{a-b}{c}\mathrm{;}$

(ii):

If $a<b$, then $\lim \nolimits _{t\rightarrow +\infty } x(t)=0$.

Theorem 1

All positive solutions of system (1) satisfying initial conditions (2) are ultimately bounded.

Proof

We know that all solutions of system (1) are positive. Hence, we study only in the domain

$$\begin{aligned} R_+^3 =\{(x_1 ,x_2 ,x_3 )|x_i >0,i=1,2,3\}. \end{aligned}$$

We derive from the second equation of system (1) that

$$\begin{aligned} \dot{x}_2 (t)\le r\mathrm{e}^{-d_1 \tau }x_2 (t-\tau )-d_2 x_2^2 (t). \end{aligned}$$

By comparison and Lemma 1, for $\varepsilon >0$ small enough, there exists a $T_1 >0$ such that

$$\begin{aligned} x_2 (t)\le \frac{r\mathrm{e}^{-d_1 \tau }}{d_2 }+\varepsilon =\;:M_1 \end{aligned}$$

for all $t>T_1$.

Let $V(t)=k_2 x_1 (t)+k_2 x_2 (t)+k_1 y(t)$, then the derivative of V(t) along solution of system (1) is

$$\begin{aligned} \dot{V}(t)\le & {} rk_2 x_2 (t)-d_1 k_2 x_1 (t)-d_3 k_1 y(t)\\\le & {} -\mu V(t)+(r+d_1 )k_2 x_2 (t), \end{aligned}$$

where $\mu =\min \{d_1 ,d_3 \}$. Therefore, we derive that for $t>T_1$

$$\begin{aligned} V\left( t\right)\le & {} \mathrm{e}^{-\mu \left( t-T_1 \right) }\nonumber \\&\times \left[ V\left( T_1 \right) +\int _{T_1 }^{t} {\left( r+d_1 \right) k_2 x_2 \left( s\right) \mathrm{e}^{\mu \left( s-T_1 \right) }\hbox {d}s} \right] \\\le & {} \mathrm{e}^{-\mu \left( t-T_1 \right) }V\left( T_1 \right) +\frac{\left( r+d_1 \right) k_2 M_1 }{\mu }\\&\times \left( 1-\mathrm{e}^{-\mu \left( t-T_1 \right) }\right) \\\rightarrow & {} \frac{\left( r+d_1 \right) k_2 M_1 }{\mu }\;\;\left( t\rightarrow +\infty \right) . \end{aligned}$$

So there exists a constant $M>0$ and a $T_2 >T_1$ such that $x_1 (t)\le M,x_2 (t)\le M,y(t)\le M$ for $t>T_2$.

The proof of Theorem 1 is completed. $\square$

The organization of this paper is as follows. In the next section, by analyzing the corresponding characteristic equations, the local stability of a positive equilibrium and two boundary equilibria of system (1) is discussed, respectively; by using persistence theory on infinite dimensional systems and comparison argument, respectively, the global stability of the positive equilibrium and one of the boundary equilibria of system (1) is discussed. In Sect. 3, the existence of a Hopf bifurcation is studied. Numerical simulations are carried out to illustrate the main results. A brief discussion is given in Sect. 4 to conclude this work.

2 Existence and stability of equilibria

In this section, we discuss the existence and stability of each of equilibria of system (1).

It is easy to show that system (1) always has a trivial equilibrium $E_0 (0,0,0)$ and a predator-extinction equilibrium $E_1 (\hat{{x}}_1 ,\hat{{x}}_2 ,0)$, where

$$\begin{aligned} \hat{{x}}_1 =\frac{r^{2}\mathrm{e}^{-d_1 \tau }(1-\mathrm{e}^{-d_1 \tau })}{d_1 d_2 },\quad \hat{{x}}_2 =\frac{r\mathrm{e}^{-d_1 \tau }}{d_2 }. \end{aligned}$$

Further, if $r\mathrm{e}^{-d_1 \tau }(k_2 -\alpha d_3 )-d_2 d_3 >0$ holds, then system (1) has a unique positive equilibrium $E_2 (x_1^{*} ,x_2^{*} ,y^{{*}})$, where

$$\begin{aligned} x_1^{*}= & {} \frac{rd_3 (1-\mathrm{e}^{-d_1 \tau })}{d_1 (k_2 -\alpha d_3 )},\;\;\;x_2^{*} =\frac{d_3 }{k_2 -\alpha d_3 },\\ y^{{*}}= & {} \frac{k_2 [r\mathrm{e}^{-d_1 \tau }(k_2 -\alpha d_3 )-d_2 d_3 ]}{k_1 (k_2 -\alpha d_3 )^{2}}. \end{aligned}$$

Theorem 2

The trivial equilibrium $E_0$ is always unstable.

Proof

The characteristic equation of (1) at $E_0 (0,0,0)$ has the form

$$\begin{aligned} (\lambda +d_1 )\big (\lambda -r\mathrm{e}^{-(\lambda +d_1 )\tau }\big )(\lambda +d_3 )=0. \end{aligned}$$

(3)

Clearly, $\lambda _1 =-d_1$ and $\lambda _3 =-d_3$ are two negative real roots of Eq. (3). Another root of (3) is given by the root of equation

$$\begin{aligned} \lambda -r\mathrm{e}^{-(\lambda +d_1 )\tau }=0. \end{aligned}$$

Let $f_1 (\lambda )=\lambda -r\mathrm{e}^{-(\lambda +d_1 )\tau }$. Since

$$\begin{aligned} f_1 (0)= & {} -r\mathrm{e}^{-d_1 \tau }<0, \lim \limits _{\lambda \rightarrow +\infty } f_1 (\lambda )=+\infty ,\\ {f}'_1 (\lambda )= & {} 1+r\tau \mathrm{e}^{-(\lambda +d_1 )\tau }>0. \end{aligned}$$

Then, $f_1 (\lambda )=0$ has a positive real root. Therefore, the equilibrium $E_0$ is unstable. This proves Theorem 2. $\square$

Theorem 3

If $r\mathrm{e}^{-d_1 \tau }(k_2 -\alpha d_3 )-d_2 d_3 >0$, then the equilibrium $E_1 (\hat{{x}}_1 ,\hat{{x}}_2 ,0)$ is unstable, while the positive equilibrium $E_2 (x_1^{*} ,x_2^{*} ,y^{{*}})$ exists; if $r\mathrm{e}^{-d_1 \tau }(k_2 -\alpha d_3 )-d_2 d_3 <0$, then $E_1$ is globally asymptotically stable.

Proof

The characteristic equation of (1) at $E_1 (\hat{{x}}_1,\hat{{x}}_2 ,0)$ has the form

$$\begin{aligned} (\lambda +d_1 )\big (\lambda +2d_2 \hat{{x}}_2 -r\mathrm{e}^{-(\lambda +d_1 )\tau }\big )\left( {\lambda +d_3 -\frac{k_2 \hat{{x}}_2 }{1+\alpha \hat{{x}}_2 }} \right) =0\nonumber \\ \end{aligned}$$

(4)

Clearly, $\lambda _1 =-d_1 <0$ and

$$\begin{aligned} \lambda _3 =\frac{k_2 \hat{{x}}_2 }{1+\alpha \hat{{x}}_2 }-d_3 =\frac{r\mathrm{e}^{-d_1 \tau }(k_2 -\alpha d_3 )-d_2 d_3 }{d_2 +\alpha r\mathrm{e}^{-d_1 \tau }} \end{aligned}$$

are two real roots of Eq. (4). Another root of (4) is given by the root of equation

$$\begin{aligned} \lambda +2d_2 \hat{{x}}_2 -r\mathrm{e}^{-(\lambda +d_1 )\tau }=0. \end{aligned}$$

Let

$$\begin{aligned} f_2 (\lambda )= & {} \lambda +2d_2 \hat{{x}}_2 -r\mathrm{e}^{-(\lambda +d_1 )\tau }\\= & {} \lambda +r\mathrm{e}^{-d_1 \tau }\big (2-\mathrm{e}^{-\lambda \tau }\big ). \end{aligned}$$

Since

$$\begin{aligned} f_2 (0)=r\mathrm{e}^{-d_1 \tau }>0, {f}'_2 (\lambda )=1+r\tau \mathrm{e}^{-(\lambda +d_1 )\tau }>0, \end{aligned}$$

and the real part of root of equation $\lambda =r\mathrm{e}^{-d_1 \tau }(\mathrm{e}^{-\lambda \tau }-2)$ is of the form

$$\begin{aligned} {\text {Re}}\lambda =r\mathrm{e}^{-d_1 \tau }[\mathrm{e}^{-\tau {\text {Re}}\lambda }\cos (\tau \mathrm{Im}\lambda )-2]<0, \end{aligned}$$

then the equilibrium $E_1$ is unstable if

$$\begin{aligned} r\mathrm{e}^{-d_1 \tau }(k_2 -\alpha d_3 )-d_2 d_3 >0 \end{aligned}$$

and is locally asymptotically stable if

$$\begin{aligned} r\mathrm{e}^{-d_1 \tau }(k_2 -\alpha d_3 )-d_2 d_3 <0. \end{aligned}$$

Next, we prove that $E_1$ is globally asymptotically stable with the above condition.

Let $(x_1 (t),x_2 (t),y(t))$ be any positive solution of system (1) with initial conditions (2). Since $r\mathrm{e}^{-d_1 \tau }(k_2 -\alpha d_3 )-d_2 d_3 <0$, we can choose $\varepsilon >0$ small enough such that

$$\begin{aligned}&(r\mathrm{e}^{-d_1 \tau }+\varepsilon d_2 )(k_2 -\alpha d_3 )-d_2 d_3 <0,\\&r\mathrm{e}^{-d_1 \tau }>k_1 \varepsilon . \end{aligned}$$

We derive from the first and the second equations of system (1) that

$$\begin{aligned} {\begin{array}{l} {\dot{x}_1 (t)=rx_2 (t)-r\mathrm{e}^{-d_1 \tau }x_2 (t-\tau )-d_1 x_1 (t),} \\ {\dot{x}_2 (t)\le r\mathrm{e}^{-d_1 \tau }x_2 (t-\tau )-d_2 x_2^2 (t).} \\ \end{array} } \end{aligned}$$

Consider the following auxiliary equations

$$\begin{aligned} {\begin{array}{l} {\dot{u}_1 (t)=ru_2 (t)-r\mathrm{e}^{-d_1 \tau }u_2 (t-\tau )-d_1 u_1 (t),} \\ {\dot{u}_2 (t)=r\mathrm{e}^{-d_1 \tau }u_2 (t-\tau )-d_2 u_2^2 (t).} \\ \end{array} } \end{aligned}$$

(5)

It is easy to see that system (5) has two equilibria $F_0 (0,0)$ and $F_1 (\hat{{u}}_1 ,\hat{{u}}_2 )$, where

$$\begin{aligned} \hat{{u}}_1 =\frac{r^{2}\mathrm{e}^{-d_1 \tau }(1-\mathrm{e}^{-d_1 \tau })}{d_1 d_2 }, \hat{{u}}_2 =\frac{r\mathrm{e}^{-d_1 \tau }}{d_2 }, \end{aligned}$$

and easily show that $F_0$ is unstable and $F_1$ is locally asymptotically stable.

By the second equation of system (5) and Lemma 1, we derive that

$$\begin{aligned} \lim \limits _{t\rightarrow +\infty } u_2 (t)=\frac{r\mathrm{e}^{-d_1 \tau }}{d_2 }=\hat{{u}}_2 =\hat{{x}}_2 . \end{aligned}$$

Therefore, the limit equation of the first equation of system (5) takes the form

$$\begin{aligned} \dot{u}_1 (t)=\frac{r^{2}\mathrm{e}^{-d_1 \tau }(1-\mathrm{e}^{-d_1 \tau })}{d_2 }-d_1 u_1 (t), \end{aligned}$$

which implies that

$$\begin{aligned} \lim \limits _{t\rightarrow +\infty } u_1 (t)=\frac{r^{2}\mathrm{e}^{-d_1 \tau }(1-\mathrm{e}^{-d_1 \tau })}{d_1 d_2 }=\hat{{u}}_1 =\hat{{x}}_1 , \end{aligned}$$

that is, the equilibrium $F_1$ is globally asymptotically stable. By comparison, there exists a $T_1 >0$ such that

$x_1 (t)\le \hat{{x}}_1 +\varepsilon , x_2 (t)\le \hat{{x}}_2 +\varepsilon$ for all $t>T_1$.

It follows from the third equation of system (1) that for $t>T_1 +\tau$

$$\begin{aligned} \dot{y}(t)\le \left[ {\frac{k_2 (\hat{{x}}_2 +\varepsilon )}{1+\alpha (\hat{{x}}_2 +\varepsilon )}-d_3 } \right] y(t). \end{aligned}$$

By comparison, it is easy to know that $\lim \nolimits _{t\rightarrow +\infty } y(t)=0$. Therefore, there exists a $T_2 >T_1$ such that $y(t)<\varepsilon$ for $t>T_2$.

We derive from the first and the second equations of system (1) that

$$\begin{aligned} {\begin{array}{l} {\dot{x}_1 (t)=rx_2 (t)-r\mathrm{e}^{-d_1 \tau }x_2 (t-\tau )-d_1 x_1 (t),} \\ {\dot{x}_2 (t)\ge r\mathrm{e}^{-d_1 \tau }x_2 (t-\tau )-d_2 x_2^2 (t)-k_1 \varepsilon x_2 (t).} \\ \end{array} } \end{aligned}$$

Consider the following auxiliary equations (for $t>T_2 +\tau$)

$$\begin{aligned} {\begin{array}{l} {\dot{u}_1 (t)=ru_2 (t)-r\mathrm{e}^{-d_1 \tau }u_2 (t-\tau )-d_1 u_1 (t),} \\ {\dot{u}_2 (t)=r\mathrm{e}^{-d_1 \tau }u_2 (t-\tau )-d_2 u_2^2 (t)-k_1 \varepsilon u_2 (t).} \\ \end{array} } \end{aligned}$$

(6)

Similar with system (5), we know that system (6) has a globally asymptotically stable equilibrium $F_2 (\bar{{u}}_1 ,\bar{{u}}_2 )$, where

$$\begin{aligned} \bar{{u}}_1 {=}\frac{r(1-\mathrm{e}^{-d_1 \tau })(r\mathrm{e}^{-d_1 \tau }-k_1 \varepsilon )}{d_1 d_2 }, \bar{{u}}_2 {=}\frac{r\mathrm{e}^{-d_1 \tau }-k_1 \varepsilon }{d_2 }. \end{aligned}$$

By comparison, there exists a $T_3 >T_2$ such that $x_1 (t)\ge \bar{{u}}_1 -\varepsilon$, $x_2 (t)\ge \bar{{u}}_2 -\varepsilon$ for $t>T_3$. Since this is true for arbitrary and sufficiently small $\varepsilon >0$, we conclude that $\lim \nolimits _{t\rightarrow +\infty } x_1 (t)=\hat{{x}}_1$, $\lim \nolimits _{t\rightarrow +\infty } x_2 (t)=\hat{{x}}_2$, that is, the equilibrium $E_1$ is globally asymptotically stable. The proof is completed. $\square$

Definition 1

System (1) is said to be permanent (uniformly persistent) if there are positive constants m and M such that each positive solution of system (1) satisfies

$$\begin{aligned}&m\le \lim \limits _{t\rightarrow +\infty } \inf x_i (t)\le \lim \limits _{t\rightarrow +\infty } \sup x_i (t)\le M, i=1,2,\\&m\le \lim \limits _{t\rightarrow +\infty } \inf y(t)\le \lim \limits _{t\rightarrow +\infty } \sup y(t)\le M. \end{aligned}$$

In order to prove the stability of the equilibrium $E_2$, we present the persistence theory on infinite dimensional systems from [15].

Let X be a complete metric space with metric d. The distance d(x, Y) of a point $x\in X$ from a subset Y of X is defined by

$$\begin{aligned} d(x,Y)=\mathop {\inf }\limits _{y\in Y} d(x,y). \end{aligned}$$

Assume that $X_0 \subset X,\;X^{0}\subset X$, and $X_0 \cap X^{0}=$ $\phi$. Also, assume that T(t) is a $C_0$ semigroup on X satisfying

$$\begin{aligned} T(t):X_0 \rightarrow X_0 , T(t):X^{0}\rightarrow X^{0}. \end{aligned}$$

(7)

Denote $T_b (t)=T(t)|_{X_0 }$ and $A_b$ be the global attractor for $T_b (t)$.

Lemma 2

Suppose that T(t) satisfies (7) and the following conditions:

• (i) There is a $t_0 \ge 0$ such that T(t) is compact for $t>t_0$;

• (ii) T(t) is point dissipative in X;

• (iii) $\tilde{A}_b =\mathop \cup \limits _{x\in A_b } \omega (x)$ is isolated and has an acyclic covering $\bar{{M}}$, where

  $$\begin{aligned} \bar{{M}}=\{M_1 ,M_2 ,\ldots ,M_n \}; \end{aligned}$$

• (iv) $W^{s}(M_i )\cap X^{0}=\phi$ for $i=1,2,\ldots ,n$.

Then, $X_0$ is a uniform repeller with respect to $X^{0}$, that is, there is an $\varepsilon >0$ such that for any $x\in X^{0}$, $\lim \nolimits _{t\rightarrow +\infty } \inf d(T(t)x,X_0 )\ge \varepsilon$.

Theorem 4

If

$$\begin{aligned} 0<r\mathrm{e}^{-d_1 \tau }(k_2 -\alpha d_3 )-d_2 d_3 <\frac{d_2 k_2 }{\alpha } \end{aligned}$$

holds, then system (1) has a unique positive equilibrium $E_2 (x_1^{*} ,x_2^{*} ,y^{{*}})$ and is permanent; furthermore, the equilibrium $E_2$ is globally asymptotically stable.

Proof

The characteristic equation of (1) at $E_2 (x_1^{*} ,x_2^{*} ,y^{{*}})$ has the form

$$\begin{aligned}&(\lambda +d_1 )\left[ \lambda ^{2}+\left( {2d_2 x_2^{*} +\frac{k_1 y^{{*}}}{(1+\alpha x_2^{*} )^{2}}} \right) \right. \nonumber \\&\quad \left. \times \,\lambda -r\lambda \mathrm{e}^{-(\lambda +d_1 )\tau } {+\frac{k_1 k_2 x_2^{*} y^{{*}}}{(1+\alpha x_2^{*} )^{3}}} \right] =0 \end{aligned}$$

(8)

Clearly, $\lambda _1 =-d_1$ is a negative real root of Eq. (8). Another two roots of (8) are given by the roots of equation

$$\begin{aligned}&\lambda ^{2}+\left[ {2d_2 x_2^{*} +\frac{k_1 y^{{*}}}{(1+\alpha x_2^{*} )^{2}}} \right] \lambda -r\lambda \mathrm{e}^{-(\lambda +d_1 )\tau } \\&\quad +\frac{k_1 k_2 x_2^{*} y^{{*}}}{(1+\alpha x_2^{*} )^{3}}=0. \end{aligned}$$

Denote

$$\begin{aligned} m= & {} 2d_2 x_2^{*} +\frac{k_1 y^{{*}}}{(1+\alpha x_2^{*} )^{2}},\quad p=\frac{k_1 k_2 x_2^{*} y^{{*}}}{(1+\alpha x_2^{*} )^{3}},\\ n= & {} -r\mathrm{e}^{-d_1 \tau }; \end{aligned}$$

then, the above equation is written in the form

$$\begin{aligned} \lambda ^{2}+m\lambda +n\lambda \mathrm{e}^{-\lambda \tau }+p=0. \end{aligned}$$

(9)

If $\lambda =\omega i\;(\omega >0)$ is a purely imaginary root of Eq. (9), separating real and imaginary parts, we have

$$\begin{aligned}&p-\omega ^{2}+n\omega \sin (\omega \tau )=0,\\&m\omega +n\omega \cos (\omega \tau )=0. \end{aligned}$$

Eliminating $\sin (\omega \tau )$ and $\cos (\omega \tau )$, we obtain the equation with respect to $\omega$

$$\begin{aligned} \omega ^{4}+(m^{2}-n^{2}-2p)\omega ^{2}+p^{2}=0. \end{aligned}$$

(10)

Its discriminant is of the form

$$\begin{aligned} \Delta= & {} (m^{2}-n^{2}-2p)^{2}-4p^{2}\\= & {} (n-m)(n+m)(n^{2}+4p-m^{2}). \end{aligned}$$

By calculation, we derive that

$$\begin{aligned}&n+m=2d_2 x_2^{*} +\frac{k_1 y^{{*}}}{(1+\alpha x_2^{*} )^{2}}-r\mathrm{e}^{-d_1 \tau }\\&\quad =\frac{d_2 d_3 k_2 -\alpha d_3 [r\mathrm{e}^{-d_1 \tau }(k_2 -\alpha d_3 )-d_2 d_3 ]}{k_2 (k_2 -\alpha d_3 )}>0, \end{aligned}$$

and $n^{2}-m^{2}<0$. Hence, if $n^{2}+4p-m^{2}>0$, then $\Delta <0$, that is, Eq. (10) has no positive real roots; if $n^{2}+4p-m^{2}\le 0$, then $\Delta \ge 0$ and $n^{2}+2p-m^{2}<0$, and then

$$\begin{aligned} \omega _{1,2}^2 =\frac{(n^{2}+2p-m^{2})\pm \sqrt{\Delta }}{2}<0, \end{aligned}$$

that is, Eq. (10) has no positive real roots. When $\tau =0$, Eq. (9) becomes

$$\begin{aligned} \lambda ^{2}+(m+n)\lambda +p=0. \end{aligned}$$

Noting that $p>0$ and $m+n>0$, the positive equilibrium $E_2$ is locally asymptotically stable when $\tau =0$. By Theorem 3.4.1 in [16], we see that if $0<r\mathrm{e}^{-d_1 \tau }(k_2 -\alpha d_3 )-d_2 d_3 <\frac{d_2 k_2 }{\alpha }$ holds, then the positive equilibrium of system (1) $E_2$ is locally asymptotically stable for all $\tau \ge 0$.

Now we state and prove the permanence of system (1) with the condition

$$\begin{aligned} 0<r\mathrm{e}^{-d_1 \tau }(k_2 -\alpha d_3 )-d_2 d_3 <\frac{d_2 k_2 }{\alpha }. \end{aligned}$$

Choose $\varepsilon >0$ small enough such that

$$\begin{aligned} r\mathrm{e}^{-d_1 \tau }(k_2 -\alpha d_3 )-d_2 d_3 -\varepsilon d_2 (k_2 -\alpha d_3 )>0. \end{aligned}$$

Firstly, we prove that the $x_1 ox_2$ plane and the $x_1 oy$ plane repel positive solutions of system (1) uniformly.

Set

$$\begin{aligned} X_1= & {} \{(x_1 ,x_2 ,y)\in R^{3}|x_1 \ge 0,x_2 \ge 0,y=0\},\\ X_2= & {} \{(x_1 ,x_2 ,y)\in R^{3}|x_1 \ge 0,x_2 =0,y\ge 0\},\\ X_0= & {} X_1 \cup X_2 ,\\ X^{0}= & {} \{(x_1 ,x_2 ,y)\in R^{3}|x_1 >0,x_2 >0,y>0\}. \end{aligned}$$

In the following, we verify that the conditions in Lemma 2 are satisfied. By the definition of $X^{0}$ and $X_0$, and by Theorem 1, it is easy to see that the conditions (i) and (ii) in Lemma 2 are clearly satisfied (see, for instance, [16], Theorem 2.2.8). Thus, we need only to show that the conditions (iii) and (iv) hold.

There are two constant solutions in $X_0$ corresponding to $E_0 (0,0,0)$ and $E_1 (\hat{{x}}_1 ,\hat{{x}}_2 ,0)$, respectively. In $x_1 ox_2$ plane, system (1) can be written in the form

$$\begin{aligned} {\begin{array}{l} {\dot{x}_1 (t)=rx_2 (t)-r\mathrm{e}^{-d_1 \tau }x_2 (t-\tau )-d_1 x_1 (t),} \\ {\dot{x}_2 (t)=r\mathrm{e}^{-d_1 \tau }x_2 (t-\tau )-d_2 x_2^2 (t).} \\ \end{array} } \end{aligned}$$

By Theorem 2 in [4], we know that the equilibrium $\bar{{E}}_1 (\hat{{x}}_1 ,\hat{{x}}_2 )$ is globally asymptotically stable, that is, if $(x_1 (t),x_2 (t),y(t))$ is a solution of system (1) initiating from $X_1$, then

$(x_1 (t),x_2 (t),y(t))\rightarrow E_1 (\hat{{x}}_1 ,\hat{{x}}_2 ,0)$ as $t\rightarrow +\infty$.

In $x_1 oy$ plane, system (1) can be written in the form

$$\begin{aligned} {\begin{array}{l} {\dot{x}_1 (t)=-d_1 x_1 (t),} \\ {\dot{y}(t)=-d_3 y(t).} \\ \end{array} } \end{aligned}$$

Clearly, $x_1 (t)\rightarrow 0$ and $y(t)\rightarrow 0$ as $t\rightarrow +\infty$, that is, if $(x_1 (t),x_2 (t),y(t))$ is a solution of system (1) initiating from $X_2$, then

$(x_1 (t),x_2 (t),y(t))\rightarrow E_0 (0,0,0)$ as $t\rightarrow +\infty$.

Noting that the equilibrium $E_0$ is isolated in $X_2$ and the equilibrium $E_1$ is isolated in $X_1$, it follows that if $E_0$ and $E_1$ are the isolated invariant sets of system (1) then $\{E_0 ,E_1 \}$ is isolated and is an acyclic covering. It is easy to see that $E_0$ is isolated invariant. By verifying the condition $(\mathrm{iv})$, we can derive that $E_1$ is isolated invariant.

For the condition (iv), we only prove that $W^{s}(E_1 )\cap X^{0}=\phi$ holds since the proof of $W^{s}(E_0 )\cap X^{0}=\phi$ is similar. Assume that $W^{s}(E_1 )\cap X^{0}\ne \phi$. Then, there is a positive solution of system (1) $(x_1^0 (t),x_2^0 (t),y^{0}(t))$ initiating from $X^{0}$ with

$$\begin{aligned} \lim \limits _{t\rightarrow +\infty } (x_1^0 (t),x_2^0 (t),y^{0}(t))=E_1 (\hat{{x}}_1 ,\hat{{x}}_2 ,0). \end{aligned}$$

Therefore, we have $\lim \nolimits _{t\rightarrow +\infty } x_2^0 (t)=\hat{{x}}_2 =\frac{r\mathrm{e}^{-d_1 \tau }}{d_2 }$, that is, for $\varepsilon >0$ small enough, there exists a $t_0 >0$ such that

$$\begin{aligned} \frac{r\mathrm{e}^{-d_1 \tau }}{d_2 }-\varepsilon <x_2^0 (t)<\frac{r\mathrm{e}^{-d_1 \tau }}{d_2 }+\varepsilon \end{aligned}$$

for all $t>t_0 +\tau$.

It follows from the third equation of system (1) that for $t>t_0 +\tau$

$$\begin{aligned} \dot{y}^{0}(t)\ge \left[ {\frac{k_2 \left( {\frac{r\mathrm{e}^{-d_1 \tau }}{d_2 }-\varepsilon } \right) }{1+\alpha \left( {\frac{r\mathrm{e}^{-d_1 \tau }}{d_2 }-\varepsilon } \right) }-d_3 } \right] y^{0}(t), \end{aligned}$$

and then,

$$\begin{aligned} y^{0}(t)\ge & {} y^{0}(t_0 )\\&\times \exp \left\{ {\left[ {\frac{k_2 \left( {\frac{r\mathrm{e}^{-d_1 \tau }}{d_2 }-\varepsilon } \right) }{1+\alpha \left( {\frac{r\mathrm{e}^{-d_1 \tau }}{d_2 }-\varepsilon } \right) }-d_3 } \right] (t-t_0 )} \right\} \\\rightarrow & {} +\infty \;\;\;(t\rightarrow +\infty ), \end{aligned}$$

which contradicts Theorem 1. Hence, we have $W^{s}(E_1 )\cap X^{0}=\phi$. By Lemma 2, we are now able to conclude that $x_1{\circ }x_2$ plane and $x_1{\circ }y$ plane uniformly repel positive solutions of system (1) initiating from $X^{0}$, that is, there exists an $\varepsilon _0 >0$, such that

$$\begin{aligned} \lim \limits _{t\rightarrow +\infty } \inf y(t)\ge \varepsilon _0 \quad {\text {and}} \quad \lim \limits _{t\rightarrow +\infty } \inf x_2 (t)\ge \varepsilon _0 . \end{aligned}$$

Next, we prove that there is an $\varepsilon _1 >0$ such that $\lim \nolimits _{t\rightarrow +\infty } \inf x_1 (t)\ge \varepsilon _1$. With the condition

$$\begin{aligned} \varepsilon _0 \le \lim \limits _{t\rightarrow +\infty } \inf x_2 (t)\le \lim \limits _{t\rightarrow +\infty } \sup x_2 (t)\le M \end{aligned}$$

and the first equation of system (1), we derive that

$$\begin{aligned} \dot{x}_1 (t)=-d_1 x_1 (t)+rx_2 (t)-r\mathrm{e}^{-d_1 \tau }x_2 (t-\tau ). \end{aligned}$$

There exists a $T>0$ such that for $t>T+\tau$

$$\begin{aligned}&x_1 \left( t\right) =\mathrm{e}^{-d_1 \left( t-T\right) }\Bigg [x_1 \left( T\right) \\&\qquad +\int _{T}^{t} {\left( rx_2 \left( s\right) -r\mathrm{e}^{-d_1 \tau }x_2 \left( s-\tau \right) \right) \mathrm{e}^{d_1 \left( s-T\right) }\hbox {d}s} \Bigg ]\\&\quad >\mathrm{e}^{-d_1 \left( t-T\right) }\int _{T}^{t} {rx_2 \left( s\right) \mathrm{e}^{d_1 \left( s-T\right) }\hbox {d}s}\\&\qquad -\mathrm{e}^{-d_1 \left( t-T\right) }\int _{T}^{t} {r\mathrm{e}^{-d_1 \tau }x_2 \left( s-\tau \right) \mathrm{e}^{d_1 \left( s-T\right) }\hbox {d}s}\\&\quad =r\mathrm{e}^{-d_1 t}\int _{T}^{t}{x_2 \left( s\right) \mathrm{e}^{d_1 s}\hbox {d}s-r\mathrm{e}^{-d_1 t}\int _{T-\tau }^{t-\tau }{x_2 \left( s\right) \mathrm{e}^{d_1 s}\hbox {d}s} }\\&\quad =r\mathrm{e}^{-d_1 t}\int _{t-\tau }^{t}{x_2 \left( s\right) \mathrm{e}^{d_1 s}\hbox {d}s} -r\mathrm{e}^{-d_1 t}\int _{T-\tau }^{T}{x_2 \left( s\right) \mathrm{e}^{d_1 s}\hbox {d}s}\\&\quad \ge \frac{r\varepsilon _0 }{d_1 }\left( 1-\mathrm{e}^{-d_1 \tau }\right) -\frac{rMe^{-d_1 t}}{d_1 }\left( \mathrm{e}^{d_1 T}-\mathrm{e}^{d_1 \left( T-\tau \right) }\right) \\&\quad \rightarrow \frac{r\varepsilon _0 \left( 1-\mathrm{e}^{-d_1 \tau }\right) }{d_1 }\;\;\;\left( t\rightarrow +\infty \right) . \end{aligned}$$

Set $\varepsilon _1 =\frac{r\varepsilon _0 (1-\mathrm{e}^{-d_1 \tau })}{d_1 }$, then $\lim \nolimits _{t\rightarrow +\infty } \inf x_1 (t)\ge \varepsilon _1$. Hence, system (1) is permanent.

By the locally asymptotical stability of $E_2$ and Theorem 8.2.3 in [16], we derive that the positive equilibrium $E_2$ of system (1) is globally asymptotically stable with the condition

$$\begin{aligned} 0<r\mathrm{e}^{-d_1 \tau }(k_2 -\alpha d_3 )-d_2 d_3 <\frac{d_2 k_2 }{\alpha }. \end{aligned}$$

The proof is completed. $\square$

3 Hopf bifurcation and numerical simulations

In this section, we study the existence of a Hopf bifurcation at the positive equilibrium. Numerical simulations are carried out to illustrate the main results.

If $r\mathrm{e}^{-d_1 \tau }(k_2 -\alpha d_3 )-d_2 d_3 >\frac{d_2 k_2 }{\alpha }$ holds, from the proof of  Theorem 4, we see that $m+n<0$, $n^{2}-m^{2}>0$ and $\Delta >0$; therefore, Eq. (10) has two positive real roots, denoted by

$$\begin{aligned} \omega _+= & {} \sqrt{\frac{1}{2}(n^{2}+2p-m^{2})+\frac{1}{2}\sqrt{\Delta }},\\ \omega _-= & {} \sqrt{\frac{1}{2}(n^{2}+2p-m^{2})-\frac{1}{2}\sqrt{\Delta }}, \end{aligned}$$

respectively.

Denote

$$\begin{aligned} \tau _+^{(k)}= & {} \frac{2k\pi +\arccos \left( {-\frac{m}{n}} \right) }{\omega _+ },\\ \tau _-^{(k)}= & {} \frac{2k\pi +\arccos \left( {-\frac{m}{n}} \right) }{\omega _- }, k=0,1,2\ldots ; \end{aligned}$$

then, $\pm i\omega _\pm$ is a pair of purely imaginary roots of (9) with $\tau =\tau _\pm ^{(k)}$, $k=0,1,2\ldots$.

Define $\tau _0 =\tau _-^{(0)}$. In the following, we verify transversality condition of Eq. (9). Differentiating (9) with respect to $\tau$, it follows that

$$\begin{aligned} (2\lambda +m+ne^{-\lambda \tau }-n\tau \lambda \mathrm{e}^{-\lambda \tau })\frac{d\lambda }{d\tau }-n\lambda ^{2}\mathrm{e}^{-\lambda \tau }=0. \end{aligned}$$

By direct calculation, we derive that

$$\begin{aligned}&\begin{aligned} \left( {\frac{\hbox {d}\lambda }{\hbox {d}\tau }} \right) ^{-1}&=\frac{2\lambda +m+ne^{-\lambda \tau }-n\tau \lambda \mathrm{e}^{-\lambda \tau }}{n\lambda ^{2}\mathrm{e}^{-\lambda \tau }}\\&=-\frac{2\lambda +m}{\lambda (\lambda ^{2}+m\lambda +p)}+\frac{1}{\lambda ^{2}}-\frac{\tau }{\lambda }, \end{aligned}\\&\begin{aligned} \left. {{\text {Re}}\left( {\frac{\hbox {d}\lambda }{\hbox {d}\tau }} \right) ^{-1}} \right| _{\lambda =\omega i}&={\text {Re}}\left[ {-\frac{2\omega i+m}{\omega i(-\omega ^{2}+p+\omega mi)}-\frac{1}{\omega ^{2}}} \right] \\&=\frac{\omega ^{2}m^{2}+2\omega ^{2}(\omega ^{2}-p)}{\omega ^{4}m^{2}+\omega ^{2}(\omega ^{2}-p)^{2}}-\frac{1}{\omega ^{2}}\\&=\frac{(\omega ^{2}-p)(\omega ^{2}+p)}{\omega ^{2}[\omega ^{2}m^{2}+(\omega ^{2}-p)^{2}]},\\ \end{aligned} \end{aligned}$$

$$\begin{aligned}&\left. {{\text {sign}}\left\{ {\frac{\hbox {d}{\text {Re}}\lambda }{\hbox {d}\tau }} \right\} } \right| _{\lambda =\omega i}\\&\quad =\left. {{\text {sign}}\left\{ {{\text {Re}}\left( {\frac{\hbox {d}\lambda }{\hbox {d}\tau }} \right) ^{-1}} \right\} } \right| _{\lambda =\omega i}\\&\quad ={\text {sign}}\{\omega ^{2}-p\}. \end{aligned}$$

Therefore,

$$\begin{aligned} \left. {{\text {sign}}\left\{ {\frac{\hbox {d}{\text {Re}}\lambda }{\hbox {d}\tau }} \right\} } \right| _{\lambda =\omega _+ i}= & {} {\text {sign}}\{\omega _+^2 -p\}\\= & {} {\text {sign}}\left\{ {\frac{1}{2}(n^{2}-m^{2})+\frac{1}{2}\sqrt{\Delta }} \right\} \\&>0,\\ \left. {{\text {sign}}\left\{ {\frac{\hbox {d}{\text {Re}}\lambda }{\hbox {d}\tau }} \right\} } \right| _{\lambda =\omega _- i}= & {} {\text {sign}}\{\omega _-^2 -p\}\\= & {} {\text {sign}}\left\{ {\frac{1}{2}(n^{2}-m^{2})-\frac{1}{2}\sqrt{\Delta }} \right\} \\&<0. \end{aligned}$$

In such cases, we see that at $\tau =\tau _+^{(0)}$ a stability switch from stable to unstable may occur. Since at $\tau =0$ the equilibrium $E_2$ is unstable, then it remains unstable for all $\tau \in [0,\tau _+^{(0)} )$. We also see that at $\tau =\tau _-^{(0)} >\tau _+^{(0)}$ a stability switch from unstable to stable may occur. By Theorem 4.1 in [17] and above results, we obtain the following conclusion.

Theorem 5

Suppose that

$$\begin{aligned} r\mathrm{e}^{-d_1 \tau }(k_2 -\alpha d_3 )-d_2 d_3 \ge \frac{d_2 k_2 }{\alpha } \end{aligned}$$

holds, then system (1) exists Hopf bifurcation at $E_2$ when $\tau =\tau _0$.

Now we give some numerical simulations to illustrate the main results.

Example 1

In (1), we let $r=0.2$, $d_1 =0.2$, $d_2 =0.1, \quad k_1 =0.2, \quad k_2 =0.1, \quad \alpha =0.7, \quad d_3 =0.4$, and $\tau =1$. It is easy to know that

$$\begin{aligned} r\mathrm{e}^{-d_1 \tau }(k_2 -\alpha d_3 )-d_2 d_3 <0 \end{aligned}$$

holds. By Theorem 3, we see that the equilibrium $E_1 \approx (0.2968,\;1.6375,\;0)$ of system (1) is globally asymptotically stable. Numerical simulation illustrates our result (see Fig. 1). The above fact implies that the prey species will persist and predator will become extinct.

Fig. 1

Graph of stability of the equilibrium $E_1$ with parameters and condition in Example 1

Example 2

In (1), we let $r=0.8$, $d_1 =0.1$, $d_2 =0.8, \quad k_1 =0.2, \quad k_2 =0.3, \quad \alpha =0.2, \quad d_3 =0.1$, and $\tau =2.6$. System (1) with above coefficients has a unique positive equilibrium $E_2 \approx (0.6543,\;0.357,\;1.7736).$ It is easy to know that

$$\begin{aligned} 0<r\mathrm{e}^{-d_1 \tau }(k_2 -\alpha d_3 )-d_2 d_3 <\frac{d_2 k_2 }{\alpha } \end{aligned}$$

holds. By Theorem 4, we see that the positive equilibrium $E_2$ is globally asymptotically stable. Numerical simulation illustrates our result (see Fig. 2). The above fact implies that both the prey and predator species will coexist.

Fig. 2

Graph of stability of the equilibrium $E_2$ with parameters and condition in Example 2

Example 3

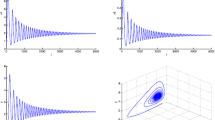
In (1), we let $r=0.9$, $d_1 =0.1$, $d_2 =0.01, \quad k_1 =0.2, \quad k_2 =0.3, \quad \alpha =0.1, d_3 =0.1,$ and then, there exists a $\tau _0 \approx 1.218$ such that the positive equilibrium $E_2$ of system (1) is unstable if $\tau <\tau _0$ (see Fig. 3a) and is locally stable if $\tau >\tau _0$ (see Fig. 3b), where $\tau$ satisfies the condition

$$\begin{aligned} r\mathrm{e}^{-d_1 \tau }(k_2 -\alpha d_3 )-d_2 d_3 \ge \frac{d_2 k_2 }{\alpha }. \end{aligned}$$

Moreover, when $\tau$ passes through the critical value $\tau _0$, a Hopf bifurcation occurs (see Fig. 3c). Numerical simulations illustrate these results. The above facts imply that the positive equilibrium changes its stability and a periodic solution through Hopf bifurcation occurs when $\tau$ passes through $\tau _0$, that is, a periodic evolution of the prey and predator populations occurs.

Fig. 3

A series of solutions of system (1) with parameters and condition in Example 3. a $\tau =0.5$. b $\tau =3$. c $\tau =1.218$

4 Discussion

Population dynamics are an important subject in mathematical biology. Understanding the dynamics of predator–prey models will be very helpful for investigating multiple species interactions. It is well known that the introduction of time delay into the predator–prey system may cause the periodic oscillations of populations and can make the behavior of the model more complex.

In this paper, we have investigated a predator–prey model with stage structure and time delay for the prey. By using comparison argument and persistence theory on infinite dimensional system, respectively, we have obtained the sufficient conditions for the global stability of the positive equilibrium and the boundary equilibrium. Further, we have discussed the existence of Hopf bifurcation of system (1). From Theorem 3, we obtain the conclusion: The boundary equilibrium $E_1$ of system (1) is globally asymptotically stable under the condition $r\mathrm{e}^{-d_1 \tau }(k_2 -\alpha d_3 )-d_2 d_3 <0$, which leads that the prey species persists and predator becomes extinct. According to Theorem 4, we obtain the conclusion: The positive equilibrium $E_2$ of system (1) is globally asymptotically stable under the condition $0<r\mathrm{e}^{-d_1 \tau }(k_2 -\alpha d_3 )-d_2 d_3 <\frac{d_2 k_2 }{\alpha }$, which leads both the prey and predator species to coexist. Moreover, these results suggest that the capturing rate of the predator $k_1$ does not affect the permanence and the extinction of predator species. By the discussion of Theorem 5, we can see that under some conditions the positive equilibrium changes its stability and a periodic solution through Hopf bifurcation occurs when the delay $\tau$ passes through a critical value $\tau _0$. This implies that the time delay is able to cause a periodic evolution of the prey and predator populations and alter the dynamics of system (1) significantly.