1 Introduction

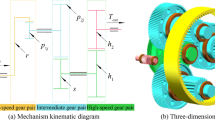
Compound planetary gear sets have been widely used in a variety of industrial machinery areas including automotive transmissions, aircraft engines, energy development, etc. Compared with simple planetary gear sets, they can sustain larger loads and transmission ratio. One of the classic compound planetary gear sets, as shown in Fig. 1, is commonly named as a “Ravigneaux” compound planetary gear sets, has been widely applied in transmission system of Lexus LS 460, 2008 GS 460, and 2009 IS-F etc. for shifting since it can bear heavy loads, provide larger transmission ratio, yield more shift, and consume less space [1]. It consists of one ring gear, two sun gears, one planet carrier ,and two kinds of planet gears. Ten different combinations (ten shifts) exist in the compound planetary gear sets since only three parts are needed to construct a power transmission path. By changing the assignments to input, output, and stationary members, 24 different kinds of speed and torque ratios make it very desirable for smooth gear shifting in passenger vehicle automatic transmissions system.

Fig. 1
figure 1

The “Ravigneaux” compound planetary gear sets

Full size image

Although the dynamic characteristics of gear system have been extensively studied in the past years, the past studies outlined below were mainly about the simple planetary gear sets or the numerical method to study the dynamic characteristics of the system. Meanwhile, it is complex and difficult to solve by the numerical method for the planetary gear sets which is a strong nonlinear system. In Refs. [2, 3], it was stated and shown experimentally that a spur gear pair exhibits a nonlinear, time-varying behavior due to the backlash nonlinearity (piecewise-linear) and the periodically time-varying gear mesh stiffness. Saada [4] established the dynamic model of a gear system considering the bending, torsion, and the axial displacement to predict the critical frequency in the 1990s. Parker [5] examined the effect of planet phasing to suppress planetary gear vibration in certain harmonics of the mesh frequency. Meanwhile, he investigated the dynamic response of spur gear pair by using a finite element/contact mechanics model [6]. Kahraman [7] developed a family of torsional dynamic models of compound gear sets to predict the free vibration characteristics under different kinematic configurations that result in different speed ratios. The analysis indicated that the contact loss of the meshing teeth is the nonlinearity source, which was significant for the future research. Abousleiman and Velex [8] analyzed the three-dimensional dynamic behavior of planetary/epicyclic spur and helical gears by using a hybrid finite element/lumped parameter model. Dhouib et al. [9] studied the vibration mode of the Ravigneaux compound planetary gear sets by establishing a translational–torsional-coupled dynamic model. Qian et al. [10], developed a pure torsional dynamic model of compound planetary gear sets under each work situation and analyzed the free vibration through the computer programs written by differential equations. Kim [11] analyzed the dynamic response of a planetary gear sets when component gears had time-varying pressure angles and contact ratios caused by bearing deformations. The incremental harmonic balance method (IHBM) was used to study a variety of problems in nonlinear dynamics by Lau [12, 13]. Then Pierre [14] presented a multi-harmonic frequency-domain analysis of dry friction damped system by using an IHBM. Raghothama [15] investigated the periodic motions of a nonlinear geared rotor-bearing system by IHBM in which the results compared well with those obtained by numerical integration. Zhang et al. [16] researched the dynamic characteristics of the geared rotor-bearing system including the time-varying mesh stiffness and the frictional force based the harmonic balance method (HBM). IHBM for computation of periodic solutions of nonlinear dynamical system with piecewise-linear viscous damping of a general form is extended by Xu [17]. And the results compare very well with direct numerical integration. Sun and Hu [18] studied the nonlinear dynamics of a planetary gear system with multiple clearances, such as backlash. A nonlinear time-varying dynamic model of a typical multi-mesh gear train is proposed by Al-Shyyab [19], which including three rigid shafts coupled by two gear pairs in the physical system, with the dimensionless equations of motion solved by a multi-term HBM in conjunction with discrete Fourier Transforms and a parametric continuation scheme for the steady-state period-1 response. Shen et al. [20] researched the nonlinear dynamics of gear system with the backlash, time-varying stiffness and static transmission error based on IHBM. Al-shyyab [21] established a nonlinear dynamic model of a multistage planetary gear sets and solved semi-analytically using a hybrid HBM. Cui [22] analyzed the influence of the gear backlash on the frequency curves for the gear–rotor–oil journal bearing system based on the HBM. Guo and Parker [23] analyzed the structural vibration mode for a type of compound planetary gear sets. Yang [24] studied the sub-harmonic motions by adopting a nonlinear time-varying dynamic model of right-angle gear pair system. It can be seen after a review of the literature that the HBM is a very well-known method for solving nonlinear problems and has been used by many authors. The key factor of HBM is the computation of steady-state solution without the transient part. Meanwhile, it is well designed for system under periodic excitation, which is very fit for the gear system. Although there is a vast body of literature concerned with the planetary gear sets, the studies on nonlinear dynamic characteristics of the Ravigneaux compound planetary gear sets based on HBM are still very limited. So it is important to research the nonlinear frequency response characteristics influenced by the system parameters based on the HBM.

In this paper, a purely rotational nonlinear dynamic model of a typical Ravigneaux compound planetary gear sets is established, which includes time-varying mesh stiffness, transmission errors and gear backlash simultaneously. The model is solved by applying HBM to acquire the nonlinear frequency response characteristics of the system. The impact of typical nonlinear factor on system dynamic characteristics is researched in the paper. The results show the effects of the time-varying mesh stiffness, transmission errors, and the gear backlash individually and coupled on the frequency response of the system. Furthermore, the main factor is analyzed that causes the vibration and noise of the system. Meanwhile, the method to reduce the vibration and noise of the system is presented in this paper. And the results provide some basis on researching the dynamic characteristics and reducing vibration and noise of compound planetary gear sets by using nonlinear theories.

2 Dynamic model of the system

To establish the mathematical model of the system, some assumptions are made as follows:

  1. 1.

    The wheel body and planet carrier are rigid body; support and wheel teeth are considered as springs.

  2. 2.

    The rotational inertias of the planet gears in the same type are equal and are distributed equably on the planet carrier.

  3. 3.

    The stiffness of transmission shafts and steady bearings are sufficiently large. Compared with torsional vibration, the translational vibration can be neglected.

The purely rotational nonlinear dynamic model of the Ravigneaux compound planetary gear sets on the basis of above assumptions is shown as Fig. 2. Two coordinates (OXY, Oxy) are created in order to establish and solve the dynamic equations of the system easily. The former is a fixed coordinate system with center located at the center of the sun gear. The latter is a moving coordinate system which is fixed with planet carrier and rotates with it by theoretical angular velocity \(\omega _c\). The \(x\) axis of Oxy passes through the theoretical center of the planet gear of \(a_1\).

Fig. 2
figure 2

The dynamic model of “Ravigneaux” compound planetary gear sets

Full size image

2.1 System differential equation of motion

Define \(u_i (i=s_1 ,s_2 ,c,r,a_n ,b_n ,n=1,2,\ldots ,N)\) as the equivalent gear-meshing displacements, which are measured in the moving coordinate system. The general coordinate \(q\) is introduced in order to establish the motion differential equations of the gear system.

$$\begin{aligned} q=[u_{s_1 } ,u_{s_2 } ,u_c ,u_r ,u_{a_1 c} ,u_{a_2 c} ,u_{a_3 c} ,u_{b_1 c} ,u_{b_2 c} ,u_{b_3 c} ]^\mathrm{T}\nonumber \\ \end{aligned}$$
(1)

According to the principle of the gear meshing, the relative gear mesh displacement \(\delta _k\) is defined as \((k=s_1 a_n ,s_2 b_n ,rb_n ,a_n b_n )\)

$$\begin{aligned} \left\{ {\begin{array}{l} \delta _{s_1 a_n } =u_{s_1 } -\frac{r_{s_1 } }{r_c }u_c +u_{a_n c} -e_{s_1 a_n } \\ \delta _{s_2 b_n } =u_{s_2 } +u_{b_n c} -\frac{r_{s_2 } }{r_c }u_c -e_{s_2 b_n } \\ \delta _{rb_n } =u_{b_n c} +\frac{r_r }{r_c }u_c -u_r -e_{rb_n } \\ \delta _{a_n b_n } =u_{a_n c} +u_{b_n c} -e_{a_n b_n } \\ \end{array}} \right. \end{aligned}$$
(2)

Here, \(e_k\) is the transmission error.

Then the differential equations of motion of the purely rotational nonlinear dynamic model for the Ravigneaux compound planetary gear sets are given as

$$\begin{aligned} \left\{ \begin{array}{l} M_{ce} \ddot{u}_c +\frac{r_a }{r_c }\sum \limits _{n=1}^N {M_a \ddot{u}_{a_n c} } +\frac{r_b }{r_c }\sum \limits _{n=1}^N {M_b r_b \ddot{u}_{b_n c} } \\ \quad -\,\frac{r_{s_1 }}{r_c }\sum \limits _{n=1}^N {k_{s_1 a_n } (t)f\left( \delta _{s_1 a_n } \right) } -\frac{r_{s_1 } }{r_c }\sum \limits _{n=1}^N {c_{s_1 a_n } \dot{\delta }_{s_1 a_n } } \\ \quad -\,\frac{r_{s_2 } }{r_c }\sum \limits _{n=1}^N {k_{s_2 b_n } (t)f\left( \delta _{s_2 b_n } \right) } -\frac{r_{s_2 } }{r_c }\sum \limits _{n=1}^N {c_{s_2 b_n } \dot{\delta }_{s_2 b_n } } \\ \quad +\,\frac{r_r }{r_c }\sum \limits _{n=1}^N {k_{rb_n } (t)f\left( \delta _{rb_n } \right) }{\,+\,}\frac{r_r }{r_c }\sum \limits _{n=1}^N {c_{rb_n } \dot{\delta }_{rb_n } }\\ \quad +\,k_c u_c =F_c \\ M_r \ddot{u}_r -\sum \limits _{n=1}^N {k_{rb_n } (t)f\left( \delta _{rb_n } \right) } -\sum \limits _{n=1}^N {c_{rb_n } \dot{\delta }_{rb_n } }\\ \quad +\,k_r u_r =F_r \\ M_{s_1 } \ddot{u}_{s_1 } +\sum \limits _{n=1}^N {k_{s_1 a_n } (t)f\left( \delta _{s_1 a_n } \right) }\\ \quad +\,\sum \limits _{n=1}^N {c_{s_1 a_n } \dot{\delta }_{s_1 a_n } } +k_{s_1 } u_{s_1 } =F_{s_1 } \\ M_{s_2 } \ddot{u}_{s_2 } +\sum \limits _{n=1}^N {k_{s_2 b_n } (t)f\left( \delta _{s_2 b_n } \right) }\\ \quad +\,\sum \limits _{n=1}^N {c_{s_2 b_n } \dot{\delta }_{s_2 b_n } } +k_{s_2 } u_{s_2 } =F_{s_2 } \\ M_a \ddot{u}_{a_n c} +\frac{r_a }{r_c }M_a \ddot{u}_c +k_{s_1 a_n } (t)f\left( \delta _{s_1 a_n } \right) +c_{s_1 a_n } \dot{\delta }_{s_1 a_n } \\ \quad -\,k_{a_n b_n } (t)f\left( \delta _{a_n b_n } \right) -c_{a_n b_n } \dot{\delta }_{a_n b_n } =0 \\ M_b \ddot{u}_{b_n c} +\frac{r_b }{r_{ca} }M_b \ddot{u}_c +k_{s_2 b_n } (t)f\left( \delta _{s_2 b_n } \right) +c_{s_2 b_n } \dot{\delta }_{s_2 b_n } \\ \quad +\,k_{rb_n } (t)f\left( \delta _{rb_n } \right) +c_{rb_n } \dot{\delta }_{rb_n } -k_{a_n b_n } (t)f\left( \delta _{a_n b_n } \right) \\ \quad -\,c_{a_n b_n } \dot{\delta }_{a_n b_n} =0 \\ \end{array}\right. \end{aligned}$$
(3a)

Here

$$\begin{aligned} \left\{ \begin{array}{ll} k_i =k_{it} /r_i^2,\quad F_i =T_i /r_i,\\ M_{ce} =I_{ce} /r_c^2,\quad M_i =I_i /r_i^2 \\ c_k =2\xi \sqrt{k_k^m /(1/M_i +1/M_j )}\end{array} \right. \end{aligned}$$
(3b)

where \(M_i\) is the equivalent mass, \(I_{ce} =I_c +NI_a +NI_b \), \(I_{i}\) represents the moment of inertia; \(k_{it}\) represents the torsional stiffness of the center components, where \(k_k (t)\) is defined as time-varying mesh stiffness between two mesh gears, \(\xi \) is damping coefficient of the mesh, and \(T_i\) represents the torque transferred by the center components.

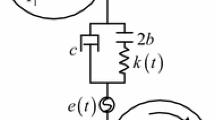
The gear backlash exists in the meshing gear teeth due to the need of lubrication, the errors caused by manufacturing and installing and the wear during operation. The mathematical model is shown in Fig. 3. And the piecewise-linear backlash functions are defined as

$$\begin{aligned} f(\delta _k )=\left\{ \begin{array}{ll} \delta _k -\frac{b_k}{2} &{}\quad {\delta _k >\frac{b_k }{2}} \\ 0&{}\quad {\left| {\delta _k } \right| <\frac{b_k }{2}} \\ \delta _k +\frac{b_k}{2} &{}\quad {\delta _k <-\frac{b_k}{2}} \\ \end{array} \right. \end{aligned}$$
(4)

Here, \(b_k\) represents the gear backlash.

Fig. 3
figure 3

The mathematical model of the gear backlash

Full size image

Equations (3a) are the semi-definite nonlinear second-order differential equations with ten degrees of freedom, which are difficult to solve directly. Thus a new general coordinates \(q^{\prime }\) is introduced to solve the problem.

$$\begin{aligned} q^{\prime }= & {} \left[ \delta _{s_1 a_1 } ,\delta _{s_1 a_2 } ,\delta _{s_1 a_3 } ,\delta _{rb_1 } ,\delta _{rb_2 } ,\delta _{rb_3 } ,\delta _{s_2 b_1 } ,\right. \nonumber \\&\left. \delta _{s_2 b_2 } ,\delta _{s_2 b_3 } ,\delta _{a_1 b_1 } ,\delta _{a_2 b_2 } ,\delta _{a_3 b_3 }\right] ^{T} \end{aligned}$$
(5)

The differential equations of motion of the gear system based on the new general coordinates \(q^{\prime }\) can be expressed as follows

$$\begin{aligned}&\ddot{\delta }_{s_1 a_n } +\,\left( \frac{r_{s_1 }^2 }{I_{s_1 } }+\frac{r_{ca}^2 }{I_c }\right) \sum _{n=1}^N {\left( k_{s_1 a_n } f\left( \delta _{s_1 a_n } \right) +c_{s_1 a_n } \dot{\delta }_{s_1 a_n } \right) }\\&\quad -\,\frac{r_{ca} r_{cb} }{I_c }\sum _{n=1}^N {\left( k_{rb_n } f\left( \delta _{rb_n } \right) +c_{rb_n } \dot{\delta }_{rb_n } \right) } \\&\quad +\,\frac{r_{ca} r_{cb} }{I_c }\times \sum _{n=1}^N {\left( k_{s_2 b_n } f\left( \delta _{s_2 b_n } \right) +c_{s_2 b_n } \dot{\delta }_{s_2 b_n } \right) }\\&\quad -\,\frac{r_{ca} \left( r_a +r_b \right) }{I_c }\sum _{n=1}^N {\left( k_{a_n b_n } f\left( \delta _{a_n b_n } \right) +c_{a_n b_n } \dot{\delta }_{a_n b_n } \right) } \\&\quad +\,\frac{r_a^2 }{I_a }\left( k_{s_1 a_n } f\left( \delta _{s_1 a_n } \right) +c_{s_1 a_n } \dot{\delta }_{s_1 a_n } \right) \\&\quad -\,\frac{r_a^2 }{I_a }\left( k_{a_n b_n } f\left( \delta _{a_n b_n } \right) +c_{a_n b_n } \dot{\delta }_{a_n b_n } \right) =\frac{r_{s_1 } }{I_{s_1 } }T_{s_1 }\\&\quad -\,\frac{r_{ca} }{I_c }T_c +\ddot{e}_{s_1 a_n } \\&\ddot{\delta }_{rb_n } +\frac{r_{cb} \left( r_a +r_b \right) }{I_c}\sum _{n=1}^N {\left( k_{a_n b_n } f\left( \delta _{a_n b_n } \right) +c_{a_n b_n } \dot{\delta }_{a_n b_n } \right) } \\&\quad -\,\frac{r_{cb} r_{ca} }{I_c }\sum _{n=1}^N {\left( k_{s_1 a_n } f\left( \delta _{s_1 a_n } \right) +c_{s_1 a_n } \dot{\delta }_{s_1 a_n } \right) } +\frac{r_{cb}^2 }{I_c } \\&\quad \times \sum _{n=1}^N {\left( k_{rb_n } f\left( \delta _{rb_n } \right) +c_{rb_n } \dot{\delta }_{rb_n } \right) }\\&\quad -\, \frac{r_{cb}^2 }{I_c }\sum _{n=1}^N {\left( k_{s_2 b_n } f\left( \delta _{s_2 b_n } \right) +c_{s_2 b_n } \dot{\delta }_{s_2 b_n } \right) }\\&\quad +\frac{r_b^2 }{I_b }\left( k_{rb_n } f\left( \delta _{rb_n } \right) +c_{rb_n } \dot{\delta }_{rb_n } \right) + \\&\frac{r_b^2 }{I_b }\left( k_{s_2 b_n } f\left( \delta _{s_2 b_n } \right) +c_{s_2 b_n } \dot{\delta }_{s_2 b_n } \right) \\&\quad -\,\frac{r_b^2 }{I_b }\left( k_{a_n b_n } f\left( \delta _{a_n b_n } \right) +c_{a_n b_n } \dot{\delta }_{a_n b_n } \right) =\frac{r_{cb} }{I_c }T_c +\ddot{e}_{rb_n } \\&\ddot{\delta }_{s_2 b_n } +\left( \frac{r_{s_2 }^2 }{I_{s_2 } }+\frac{r_{cb}^2 }{I_c }\right) \times \sum _{n=1}^N {\left( k_{s_2 b_n } f\left( \delta _{s_2 b_n } \right) +c_{s_2 b_n } \dot{\delta }_{s_2 b_n } \right) }\\&\quad +\,\frac{r_{ca} r_{cb} }{I_c }\sum _{n=1}^N {\left( k_{s_1 a_n } f\left( \delta _{s_1 a_n } \right) +c_{s_1 a_n } \dot{\delta }_{s_1 a_n } \right) } -\frac{r_{cb}^2 }{I_c }\\ \end{aligned}$$
$$\begin{aligned}&\quad \times \sum _{n=1}^N {\left( k_{rb_n } f\left( \delta _{rb_n } \right) +c_{rb_n } \dot{\delta }_{rb_n } \right) } \nonumber \\&\quad -\,\frac{r_{cb} \left( r_a +r_b \right) }{I_c }\sum _{n=1}^N {\left( k_{a_n b_n } f\left( \delta _{a_n b_n } \right) +c_{a_n b_n } \dot{\delta }_{a_n b_n } \right) }\nonumber \\&\quad +\frac{r_b^2 }{I_b }\left( k_{rb_n } f\left( \delta _{rb_n } \right) +c_{rb_n } \dot{\delta }_{rb_n } \right) \nonumber \\&\quad +\,\frac{r_b^2 }{I_b }\left( k_{s_2 b_n } f\left( \delta _{s_2 b_n } \right) +c_{s_2 b_n } \dot{\delta }_{s_2 b_n } \right) \nonumber \\&\quad -\,\frac{r_b^2 }{I_b }\left( k_{a_n b_n } f\left( \delta _{a_n b_n } \right) +c_{a_n b_n } \dot{\delta }_{a_n b_n } \right) \nonumber \\&\quad =\frac{r_{s_2 } }{I_{s_2 } }T_{s_2 } +\frac{r_{cb} }{I_c }T_c +\ddot{e}_{s_2 b_n } \nonumber \\&\ddot{\delta }_{a_n b_n } -\frac{r_{ca} \left( r_a +r_b \right) }{I_c }\sum _{n=1}^N {\left( k_{s_1 a_n } f\left( \delta _{s_1 a_n } \right) +c_{s_1 a_n } \dot{\delta }_{s_1 a_n } \right) }\nonumber \\&\quad -\frac{r_{cb} \left( r_a +r_b \right) }{I_c }\sum _{n=1}^N {\left( k_{s_2 b_n } f\left( \delta _{s_2 b_n } \right) +c_{s_2 b_n } \dot{\delta }_{s_2 b_n } \right) } \nonumber \\&\quad +\,\frac{r_{cb} \left( r_a +r_b \right) }{I_c }\sum _{n=1}^N {\left( k_{rb_n } f\left( \delta _{rb_n } \right) +c_{rb_n } \dot{\delta }_{rb_n } \right) }\nonumber \\&\quad +\,\frac{\left( r_a +r_b \right) ^{2}}{I_c }\sum _{n=1}^N {\left( k_{a_n b_n } f\left( \delta _{a_n b_n } \right) +c_{a_n b_n } \dot{\delta }_{a_n b_n } \right) } -\frac{r_a^2 }{I_a }\nonumber \\&\left( k_{s_1 a_n } f\left( \delta _{s_1 a_n } \right) +c_{s_1 a_n } \dot{\delta }_{s_1 a_n } \right) \nonumber \\&\quad -\,\frac{r_b^2 }{I_b }\left( k_{rb_n } f\left( \delta _{rb_n } \right) +c_{rb_n } \dot{\delta }_{rb_n } \right) \nonumber \\&\quad -\,\frac{r_b^2 }{I_b }\left( k_{s_2 b_n } f\left( \delta _{s_2 b_n } \right) +c_{s_2 b_n } \dot{\delta }_{s_2 b_n } \right) +\left( \frac{r_a^2 }{I_a }+\frac{r_b^2 }{I_b }\right) \nonumber \\&\quad \times \left( k_{a_n b_n } f\left( \delta _{a_n b_n } \right) +c_{a_n b_n } \dot{\delta }_{a_n b_n } \right) =\ddot{e}_{a_n b_n} \end{aligned}$$
(6)

2.2 Solution procedure of harmonic balance method

In engineering practice, the fundamental frequency steady-state response of the system, which is of great interest, plays a dominant role in almost all cases. Equation (6) can be dimensionless by using a characteristic length \(b_d\) and a characteristic frequency \(\omega _d\). Here, \(\omega _d =\sqrt{k_{s_1 a}^m (r_a^2 /I_a +r_{s_1 }^2 /I_{s_1 } )},\, k_{s_1 a}^m\) is the average mesh stiffness between the gear \(s_1\) and the planet gear \(a\). And the other variables can be expressed as

$$\begin{aligned}&\bar{{\delta }}_k =\frac{\delta _k }{b_d },\bar{{b}}_k =\frac{b_k }{b_d },\bar{{r}}_{bi} =\frac{r_{bi} }{b_d }\end{aligned}$$
(7a)
$$\begin{aligned}&\bar{{k}}_k =\frac{k_k }{\omega _d^2 },\bar{{c}}_k =\frac{c_k }{\omega _d },\bar{{T}}_i =\frac{T_i }{b_d \cdot \omega _d^2 }\end{aligned}$$
(7b)
$$\begin{aligned}&f\left( \bar{{\delta }}_k \right) =\left\{ \begin{array}{ll} \bar{{\delta }}_k -\frac{\bar{{b}}_k }{2} &{}\quad {\bar{{\delta }}_k >\frac{\bar{{b}}_k }{2}} \\ 0 &{}\quad {-\frac{\bar{{b}}_k }{2}\le \bar{{\delta }}_k \le \frac{\bar{{b}}_k }{2}} \\ \bar{{\delta }}_k +\frac{\bar{{b}}_k }{2} &{}\quad {\bar{{\delta }}_k <-\frac{\bar{{b}}_k }{2}} \\ \end{array} \right. \end{aligned}$$
(7c)

Thus the dimensionless equations of motion of the system can be expressed as

$$\begin{aligned}&\ddot{\bar{{\delta }}}_{s_1 a_n } +\left( \frac{\bar{{r}}_{s_1 }^2 }{I_{s_1 } }+\frac{\bar{{r}}_{ca}^2 }{I_c }\right) \sum _{n=1}^N {\left( \bar{{k}}_{s_1 a_n } f\left( \bar{{\delta }}_{s_1 a_n } \right) +\bar{{c}}_{s_1 a_n } \dot{\bar{{\delta }}}_{s_1 a_n } \right) }\\&\quad -\,\frac{\bar{{r}}_{ca} \bar{{r}}_{cb} }{I_c }\sum _{n=1}^N {\left( \bar{{k}}_{rb_n } f\left( \bar{{\delta }}_{rb_n } \right) +\bar{{c}}_{rb_n } \dot{\bar{{\delta }}}_{rb_n } \right) +\frac{\bar{{r}}_{ca} \bar{{r}}_{cb} }{I_c } } \\&\quad \times \sum _{n=1}^N {\left( \bar{{k}}_{s_2 b_n } f\left( \bar{{\delta }}_{s_2 b_n } \right) +\bar{{c}}_{s_2 b_n } \dot{\bar{{\delta }}}_{s_2 b_n } \right) }\\&\quad -\,\frac{\bar{{r}}_{ca} \left( \bar{{r}}_a +\bar{{r}}_b \right) }{I_c }\sum _{n=1}^N {\left( \bar{{k}}_{a_n b_n } f\left( \bar{{\delta }}_{a_n b_n } \right) +\bar{{c}}_{a_n b_n } \dot{\bar{{\delta }}}_{a_n b_n } \right) }\\&\quad +\,\frac{\bar{{r}}_a^2 }{I_a }\left( \bar{{k}}_{s_1 a_n } f\left( \bar{{\delta }}_{s_1 a_n } \right) +\bar{{c}}_{s_1 a_n } \dot{\bar{{\delta }}}_{s_1 a_n } \right) \\&\quad -\,\frac{\bar{{r}}_a^2 }{I_a }\left( \bar{{k}}_{a_n b_n } f\left( \bar{{\delta }}_{a_n b_n } \right) +\bar{{c}}_{a_n b_n } \dot{\bar{{\delta }}}_{a_n b_n } \right) \\&\quad =\frac{\bar{{r}}_{s_1 } }{I_{s_1 } }\bar{{T}}_{s_1 } -\frac{\bar{{r}}_{ca} }{I_c }\bar{{T}}_c +\ddot{\bar{{e}}}_{s_1 a_n } \\&\ddot{\bar{{\delta }}}_{rb_n } +\frac{\bar{{r}}_{cb} \left( \bar{{r}}_a +\bar{{r}}_b \right) }{I_c }\sum _{n=1}^N {\left( \bar{{k}}_{a_n b_n } f\left( \bar{{\delta }}_{a_n b_n } \right) +\bar{{c}}_{a_n b_n } \dot{\bar{{\delta }}}_{a_n b_n } \right) }\\&\quad -\,\frac{\bar{{r}}_{cb} \bar{{r}}_{ca} }{I_c }\sum _{n=1}^N {\left( \bar{{k}}_{s_1 a_n } f\left( \bar{{\delta }}_{s_1 a_n } \right) +\bar{{c}}_{s_1 a_n } \dot{\bar{{\delta }}}_{s_1 a_n } \right) } +\frac{\bar{{r}}_{cb}^2 }{I_c } \\&\quad \times \sum _{n=1}^N {\left( \bar{{k}}_{rb_n } f\left( \bar{{\delta }}_{rb_n } \right) +\bar{{c}}_{rb_n } \dot{\bar{{\delta }}}_{rb_n } \right) }\\&\quad -\,\frac{\bar{{r}}_{cb}^2 }{I_c }\sum _{n=1}^N {\left( \bar{{k}}_{s_2 b_n } f\left( \bar{{\delta }}_{s_2 b_n } \right) +\bar{{c}}_{s_2 b_n } \dot{\bar{{\delta }}}_{s_2 b_n } \right) }\\&\quad +\,\frac{\bar{{r}}_b^2 }{I_b }\left( \bar{{k}}_{rb_n } f\left( \bar{{\delta }}_{rb_n } \right) +\bar{{c}}_{rb_n } \dot{\bar{{\delta }}}_{rb_n } \right) \\&\quad +\frac{\bar{{r}}_b^2 }{I_b }\left( \bar{{k}}_{s_2 b_n } f\left( \bar{{\delta }}_{s_2 b_n } \right) +\bar{{c}}_{s_2 b_n } \dot{\bar{{\delta }}}_{s_2 b_n } \right) \\&\quad -\,\frac{\bar{{r}}_b^2 }{I_b }\left( \bar{{k}}_{a_n b_n } f\left( \bar{{\delta }}_{a_n b_n } \right) +\bar{{c}}_{a_n b_n } \dot{\bar{{\delta }}}_{a_n b_n } \right) =\frac{\bar{{r}}_{cb} }{I_c }\bar{{T}}_c +\ddot{\bar{{e}}}_{rb_n} \\&\ddot{\bar{{\delta }}}_{s_2 b_n } +\left( \frac{\bar{{r}}_{s_2 }^2 }{I_{s_2 } }+\frac{\bar{{r}}_{cb}^2 }{I_c }\right) \\&\quad \times \sum _{n=1}^N {\left( \bar{{k}}_{s_2 b_n } f\left( \bar{{\delta }}_{s_2 b_n } \right) +\bar{{c}}_{s_2 b_n } \dot{\bar{{\delta }}}_{s_2 b_n } \right) }\\&\quad +\,\frac{\bar{{r}}_{ca} \bar{{r}}_{cb} }{I_c }\sum _{n=1}^N {\left( \bar{{k}}_{s_1 a_n } f\left( \bar{{\delta }}_{s_1 a_n } \right) +\bar{{c}}_{s_1 a_n } \dot{\bar{{\delta }}}_{s_1 a_n } \right) } -\frac{\bar{{r}}_{cb}^2 }{I_c } \\ \end{aligned}$$
$$\begin{aligned}&\quad \times \sum _{n=1}^N {\left( \bar{{k}}_{rb_n } f\left( \bar{{\delta }}_{rb_n } \right) +\bar{{c}}_{rb_n } \dot{\bar{{\delta }}}_{rb_n } \right) }\nonumber \\&\quad -\,\frac{\bar{{r}}_{cb} \left( \bar{{r}}_a +\bar{{r}}_b \right) }{I_c }\sum _{n=1}^N {\left( \bar{{k}}_{a_n b_n } f\left( \bar{{\delta }}_{a_n b_n } \right) +\bar{{c}}_{a_n b_n } \dot{\bar{{\delta }}}_{a_n b_n } \right) } \nonumber \\&\quad +\,\frac{\bar{{r}}_b^2 }{I_b }\left( \bar{{k}}_{rb_n } f\left( \bar{{\delta }}_{rb_n } \right) +\bar{{c}}_{rb_n } \dot{\bar{{\delta }}}_{rb_n } \right) \nonumber \\&\quad +\,\frac{\bar{{r}}_b^2 }{I_b }\left( \bar{{k}}_{s_2 b_n } f\left( \bar{{\delta }}_{s_2 b_n } \right) +\bar{{c}}_{s_2 b_n } \dot{\bar{{\delta }}}_{s_2 b_n } \right) \nonumber \\&\quad -\,\frac{\bar{{r}}_b^2 }{I_b }\left( \bar{{k}}_{a_n b_n } f\left( \bar{{\delta }}_{a_n b_n } \right) +\,\bar{{c}}_{a_n b_n } \dot{\bar{{\delta }}}_{a_n b_n } \right) \nonumber \\&\quad =\frac{\bar{{r}}_{s_2 } }{I_{s_2 } }\bar{{T}}_{s_2 } +\frac{\bar{{r}}_{cb} }{I_c }\bar{{T}}_c +\ddot{\bar{{e}}}_{s_2 b_n } \nonumber \\&\ddot{\bar{{\delta }}}_{a_n b_n } -\frac{\bar{{r}}_{ca} \left( \bar{{r}}_a +\bar{{r}}_b \right) }{I_c }\sum _{n=1}^N {\left( \bar{{k}}_{s_1 a_n } f\left( \bar{{\delta }}_{s_1 a_n } \right) +\bar{{c}}_{s_1 a_n } \dot{\bar{{\delta }}}_{s_1 a_n } \right) }\nonumber \\&\quad -\,\frac{\bar{{r}}_{cb} \left( \bar{{r}}_a +\bar{{r}}_b \right) }{I_c }\sum _{n=1}^N {\left( \bar{{k}}_{s_2 b_n } f\left( \bar{{\delta }}_{s_2 b_n } \right) +\bar{{c}}_{s_2 b_n } \dot{\bar{{\delta }}}_{s_2 b_n } \right) } \nonumber \\&\quad +\,\frac{\bar{{r}}_{cb} \left( \bar{{r}}_a +\bar{{r}}_b \right) }{I_c }\sum _{n=1}^N {\left( \bar{{k}}_{rb_n } f\left( \bar{{\delta }}_{rb_n } \right) +\bar{{c}}_{rb_n } \dot{\bar{{\delta }}}_{rb_n } \right) }\nonumber \\&\quad +\,\frac{\left( \bar{{r}}_a +\bar{{r}}_b \right) ^{2}}{I_c }\sum _{n=1}^N {\left( \bar{{k}}_{a_n b_n } f\left( \bar{{\delta }}_{a_n b_n } \right) +\bar{{c}}_{a_n b_n } \dot{\bar{{\delta }}}_{a_n b_n } \right) }\nonumber \\&\quad -\frac{\bar{{r}}_a^2 }{I_a } \left( \bar{{k}}_{s_1 a_n } f\left( \bar{{\delta }}_{s_1 a_n } \right) +\bar{{c}}_{s_1 a_n } \dot{\bar{{\delta }}}_{s_1 a_n } \right) \nonumber \\&\quad -\,\frac{\bar{{r}}_b^2 }{I_b }\left( \bar{{k}}_{rb_n } f\left( \bar{{\delta }}_{rb_n } \right) +\bar{{c}}_{rb_n } \dot{\bar{{\delta }}}_{rb_n } \right) \nonumber \\&\quad -\,\frac{\bar{{r}}_b^2 }{I_b }\left( \bar{{k}}_{s_2 b_n } f\left( \bar{{\delta }}_{s_2 b_n } \right) +\bar{{c}}_{s_2 b_n } \dot{\bar{{\delta }}}_{s_2 b_n } \right) + \left( \frac{\bar{{r}}_a^2 }{I_a }+\frac{\bar{{r}}_b^2 }{I_b }\right) \nonumber \\&\quad \times \left( \bar{{k}}_{a_n b_n } f\left( \bar{{\delta }}_{a_n b_n } \right) +\bar{{c}}_{a_n b_n } \dot{\bar{{\delta }}}_{a_n b_n } \right) =\ddot{\bar{{e}}}_{a_n b_n } \end{aligned}$$
(8)

For the purpose of calculating efficiently, time-varying mesh stiffness and transmission errors are defined as simple harmonic functions containing average components and fundamental frequency components. Just considering internal excitation, the relative displacement can be written as

$$\begin{aligned} \bar{{\delta }}_k =\bar{{\delta }}_k^m +\bar{{\delta }}_k^c \cos (\omega t)+\bar{{\delta }}_k^s \sin (\omega t) \end{aligned}$$
(9a)

where the \(\bar{{\delta }}_k^m\) is the average of the steady-state response; \(bar{{\delta }}_k^c\) and \(\bar{{\delta }}_k^s\) are cosine and sine components. The time-varying mesh stiffness and transmission errors can be written as

$$\begin{aligned} \bar{{k}}_k (t)= & {} \bar{{k}}_k^m +\bar{{k}}_k^c \cos (\omega t)+\bar{{k}}_k^s \sin (\omega t)\end{aligned}$$
(9b)
$$\begin{aligned} \bar{{e}}_k (t)= & {} \bar{{e}}_k^m +\bar{{e}}_k^c \cos (\omega t)+\bar{{e}}_k^s \sin (\omega t) \end{aligned}$$
(9c)

where the fluctuation amplitudes of mesh stiffness and dimensionless transmission error are defined as

$$\begin{aligned} \bar{{k}}_k^a =\sqrt{(\bar{{k}}_k^c )^{2}+(\bar{{k}}_k^s )^{2}}, \quad \bar{{e}}_k^a =\sqrt{(\bar{{e}}_k^c )^{2}+(\bar{{e}}_k^s )^{2}} \end{aligned}$$
(9d)

The force transmitted through the gear pair can be expressed as

$$\begin{aligned} \bar{{F}}_i =\bar{{F}}_i^m +\bar{{F}}_i^c \cos (\omega t)+\bar{{F}}_i^s \sin (\omega t) \end{aligned}$$
(9e)

The piecewise-linear backlash functions can be taken as

$$\begin{aligned} f(\bar{{\delta }}_k )=\bar{{N}}_k^m \bar{{\delta }}_k^m +\bar{{N}}_k^a \bar{{\delta }}_k^c \cos (\omega t)+\bar{{N}}_k^a \bar{{\delta }}_k^s \sin (\omega t)\nonumber \\ \end{aligned}$$
(10a)

The describing functions \(\bar{{N}}_k^m\) and \(\bar{{N}}_k^p \) are defined as

$$\begin{aligned}&\bar{{N}}_k^m =1+\frac{\bar{{\delta }}_k^a }{2\bar{{\delta }}_k^m }\left[ {G\left( {\frac{\bar{{b}}_k -\bar{{\delta }}_k^m }{\bar{{\delta }}_k^a }} \right) -G\left( {\frac{-\bar{{b}}_k -\bar{{\delta }}_k^m }{\bar{{\delta }}_k^a }} \right) } \right] \nonumber \\&\bar{{N}}_k^a =1-\frac{1}{2}\left[ {H\left( {\frac{\bar{{b}}_k -\bar{{\delta }}_k^m }{\bar{{\delta }}_k^a }} \right) -H\left( {\frac{-\bar{{b}}_k -\bar{{\delta }}_k^m }{\bar{{\delta }}_k^a }} \right) } \right] \nonumber \\ \end{aligned}$$
(10b)

where

$$\begin{aligned}&\bar{{\delta }}_k^a =\sqrt{(\bar{{\delta }}_k^c )^{2}+(\bar{{\delta }}_k^s )^{2}}\end{aligned}$$
(10c)
$$\begin{aligned}&G\left( \mu \right) =\left\{ \begin{array}{ll} \left( {\frac{2}{\pi }} \right) \left[ {\mu \cdot \arcsin \left( \mu \right) +\sqrt{1-\mu ^{2}}} \right] , &{} \left| \mu \right| \le 1 \\ \left| \mu \right| &{} {\left| \mu \right| >1} \\ \end{array}\right. \nonumber \\ \end{aligned}$$
(10d)
$$\begin{aligned}&H\left( \mu \right) =\left\{ \begin{array}{ll} -1&{}{\mu <-1} \\ \left( {\frac{2}{\pi }} \right) \left[ {\arcsin \left( \mu \right) +\mu \times \sqrt{1-\mu ^{2}}} \right] , &{} {\left| \mu \right| \le 1} \\ +1&{} {\mu >1} \end{array} \right. \nonumber \\ \end{aligned}$$
(10e)
$$\begin{aligned}&\mu =\frac{\pm \bar{{b}}_k -\bar{{\delta }}_k^m }{\sqrt{(\bar{{\delta }}_k^c )^{2}+(\bar{{\delta }}_k^s )^{2}}} \end{aligned}$$
(10f)

By introducing \(\tau =\varOmega t\) and \(\varOmega =\omega /\omega _d \) and substituting Eqs. (9–10) into Eq. (8), a set of nonlinear algebraic equations are obtained as Eq. (11), which can be solved iteratively by using single- rank inverse Broyden quasi-Newton method.

$$\begin{aligned}&{\mathbf {M}}=\left\{ {\frac{I_i }{\bar{{r}}_{bi}^2 }} \right\} _{n\times 1}\!,{\mathbf {C}}=\left\{ {\bar{{c}}_k } \right\} _{n\times 1}\end{aligned}$$
(11a)
$$\begin{aligned}&{\mathbf {K}}^{{\mathbf {m}}}=\left[ {\bar{{k}}_k^m } \right] _{n\times n}\!,\quad {{\mathbf {K}}^{{\mathbf {c}}}=\left[ {\bar{{k}}_k^c } \right] _{n\times n}}\!,\quad {{\mathbf {K}}^{{\mathbf {c}}}=\left[ {\bar{{k}}_k^s } \right] _{n\times n}}\nonumber \\ \end{aligned}$$
(11b)
$$\begin{aligned}&{\mathbf {F}}^{{\mathbf {m}}}=\left\{ {\bar{{F}}_i^m } \right\} _{n\times 1}\!,\quad {\mathbf {F}}^{{\mathbf {c}}}=\left\{ {\bar{{F}}_i^c } \right\} _{n\times 1}\!, \quad {{\mathbf {F}}^{{\mathbf {s}}}=\left\{ {\bar{{F}}_i^s } \right\} _{n\times 1} }\nonumber \\ \end{aligned}$$
(11c)
$$\begin{aligned}&{\varvec{\delta }}^{{\mathbf {m}}}=\left\{ {\bar{{\delta }}_k^m } \right\} _{n\times 1}\!,\quad {\varvec{\delta }} ^{{\mathbf {c}}}=\left\{ {\bar{{\delta }}_k^c } \right\} _{n\times 1}\!,\quad {{\varvec{\delta }} ^{{\mathbf {s}}}=\left\{ {\bar{{\delta }}_k^s } \right\} _{n\times 1} } \end{aligned}$$
(11d)
$$\begin{aligned}&{\mathbf {g}}^{{\mathbf {m}}}=\left\{ {\bar{{N}}_k^m \bar{{\delta }}_k^m } \right\} _{n\times 1}\!,\quad {\mathbf {g}}^{{\mathbf {c}}}=\left\{ {\bar{{N}}_k^a \bar{{\delta }}_k^c } \right\} _{n\times 1}\!, \nonumber \\&{\mathbf {g}}^{{\mathbf {s}}}=\left\{ {\bar{{N}}_k^a \bar{{\delta }}_k^s } \right\} _{n\times 1}\nonumber \\ \end{aligned}$$
(11e)
$$\begin{aligned}&\left\{ \begin{array}{l} {\mathbf {K}}^{{\mathbf {m}}}{\mathbf {g}}^{{\mathbf {m}}}-{\mathbf {F}}^{{\mathbf {m}}}=\mathbf{0} \\ -\varOmega ^{2}{\mathbf {M}}{\varvec{\delta }}^{{\mathbf {c}}}+\varOmega {\mathbf {C}}{\varvec{\delta }}^{{\mathbf {s}}}+{\mathbf {K}}^{{\mathbf {m}}}{\mathbf {g}}^{{\mathbf {c}}}+{\mathbf {K}}^{{\mathbf {c}}}{\mathbf {g}}^{{\mathbf {m}}}-{\mathbf {F}}^{{\mathbf {c}}}=\mathbf{0} \\ -\varOmega ^{2}{\mathbf {M}}{\varvec{\delta }}^{{\mathbf {s}}}-{\varvec{\varOmega }}{\mathbf {C}}{\varvec{\delta }}^{{\mathbf {c}}}+{\mathbf {K}}^{{\mathbf {m}}}{\mathbf {g}}^{{\mathbf {s}}}+{\mathbf {K}}^{{\mathbf {s}}}{\mathbf {g}}^{{\mathbf {m}}}-{\mathbf {F}}^{{\mathbf {s}}}=\mathbf{0} \\ \end{array} \right. \nonumber \\ \end{aligned}$$
(11f)

3 Nonlinear frequency-domain dynamic characteristics

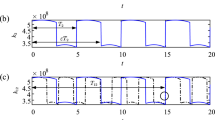
The parameters of the Ravigneaux compound planetary gear sets are listed in Table 1. The torque inputs from the sun gear are \(s_{1}\), and outputs from the sun gear are \(s_{2}\) with the ring gear fixed, where \(T_{s_1} =150{\text {N}}\,{\text {m}},T_{s_2} =392{\text {N}}\,{\text {m}}\). The average mesh stiffness and the dimensionless transmission error are \(k_{s_1 a_n }^m =5.028\times 10^{8}{\text {N}}\,{\text {m}}^{-1},\, k_{s_2 b_n }^m =4.809\times 10^{8}{\text {N}}\,{\text {m}}^{-1},\, k_{a_n b_n }^m =4.015\times 10^{8}{\text {N}}\,{\text {m}}^{-1},\, k_{rb_n }^m =2.529\times 10^{8}{\text {N}}\,{\text {m}}^{-1},\, \bar{{e}}_k^m =0.4\) and \(b_d =50um\). The frequency response curves are illustrated in Fig. 4.

Fig. 4
figure 4

Frequency response of the system

Full size image
Table 1 Basic parameters of the Ravigneaux compound planetary gear sets
Full size table

Here, we compare the fundamental frequency steady-state solutions of nonlinear system with linear system by HBM. It can be seen from the results that:

  1. 1.

    The dash line represents the frequency response curve of the linear system without the gear backlash. As can be seen from the Fig. 4, in linear system, the obvious resonances of the system occur at two different frequencies, \(\varOmega =0.389\) and \(\varOmega =1.287\), when \(0\le \varOmega \le 2\). Furthermore, the relative vibration of meshing pair \(rb_1,\,a_1 b_1\) and \(s_2 b_1\) are intensive when \(\varOmega =0.389\); while the relative vibration of meshing pair \(s_1 a_1 \)is intensive when \(\varOmega =1.287\).

  2. 2.

    Due to the introduction of strong nonlinear factors, the frequency response curve shows typical nonlinear characteristics of amplitude jump discontinuities and multi-value in which non-impact, single-sided and double-sided impact vibration simultaneously exist (close to resonant frequencies). From this point of view, we can see that the internal impact is often the responsible for the large amplitude vibration of the gear system. Meanwhile, this state of motion does not exist in all the excitation frequency, but close to the resonant frequency. However, the resonant frequency does not necessarily coincide with the natural frequency in the nonlinear system. The two resonant frequencies are close to each other with the first larger than the first natural frequency and the second smaller than the second natural frequency as can be seen from Fig. 4.

4 Investigation of parameter influence on dynamic characteristic

4.1 Gear backlash

Figure 5 shows the influence of the gear backlash on the amplitude–frequency response. Letting \(C_k =k_k^a /k_k^m =0.25\), \(\bar{{e}}_k^a =2\) and assigning 1, 2, and 4 to dimensionless gear backlash \(\bar{{b}}_k \), the results of the amplitude–frequency response are shown in Fig. 5.

Fig. 5
figure 5

The influence of gear backlash

Full size image

The system exhibits strong nonlinear characteristics with the effect of the gear backlash. By comparing the results, as can be seen, the amplitude jump discontinuities and the multi-valve exist near the resonant frequencies in the frequency response curves. The amplitude of the response in the different gear backlash almost overlaps under the range of \(0<\varOmega <0.52\) and \(1.1\le \varOmega \le 2.0\), which represents there is no contact loss phenomenon in the meshing pair under the lower frequency and the higher frequency of the nonlinear system. While the double-valued solutions occur near the resonant frequency, which indicates that the teeth of the meshing pair experiences contact loss. The range of the double-valued solutions is \(0.56\le \varOmega \le 0.68\) when \(\bar{{b}}_k =1\), and the range of the double-valued solutions is \(0.52\le \varOmega \le 0.535\) and \(0.92\le \varOmega \le 0.985\) when \(\bar{{b}}_k =2\), while the range of the double-valued solutions is \(0.88\le \varOmega \le 0.95\) when \(\bar{{b}}_k =4\).

Furthermore, the phenomenon of the frequency response curve sloping to the right,termed as hardening effect, exhibits near the resonant frequencies when \(\bar{{b}}_k =1\). This phenomenon indicates that the double-sided impact vibration exists during the meshing process of the gears. As can be seen from Fig. 5, when the dimensionless gear backlash increases to \(\bar{{b}}_k =2\), the impact phenomenon is more complicated. The phenomenon of the frequency response curve sloping to the left, termed as softening effect, and the hardening effect all exist within the range of \(0.52\le \varOmega \le 0.535\), which means the single-sided and double-sided impact vibration all exist during the meshing process of the gears. However, as the dimensionless gear backlash keeps increasing to 4, there exists only softening effect near the resonant frequencies, which indicates that there is just the single-sided impact vibration exists. It can be observed that the double-sided impact vibration (hardening effect) is prone to happen when the dimensionless gear backlash is small. Conversely, the single-sided impact vibration is predominant when the dimensionless gear backlash increases to a certain extent.

4.2 Time-varying Mesh Stiffness

To describe the extent of stiffness variation, a stiffness ratio is introduced as \(C_k =k_k^a /k_k^m \). Figure 6 shows the results of frequency response of the compound planetary gear sets as given \(\bar{{b}}_k =2,\,\bar{{e}}_k^a =2\), and assigning 0, 0.25, and 0.5 to the stiffness ratio \(C_k\).

Fig. 6
figure 6

The influence of time-varying mesh stiffness

Full size image

As can be seen from the frequency response, the frequency response curve shows typical nonlinear characteristics of amplitude jump discontinuities close to resonant frequencies of the nonlinear system. When gear backlash exists, amplitude jump discontinuities always exist in the frequency response curve. It means that time-varying mesh stiffness makes no impression on impact characteristic of the compound planetary gear sets. The range of the double-valued solutions is \(0.55\le \varOmega \le 0.57\) and \(0.96\le \varOmega \le 0.99\) when \(C_k =0\); and the range of the double-valued solutions is \(0.53\le \varOmega \le 0.535\) and \(0.92\le \varOmega \le 0.985\) when \(C_k =0.25\); while the range of the double-valued solutions is \(0.86\le \varOmega \le 0.9\) when \(C_k =0.5\). It can be revealed that with the increasing of \(C_k \), the principal frequencies shift left and the converting frequencies corresponding to amplitude jump discontinuities decrease gradually. Meanwhile, the maximum vibration amplitude increases with the increment of \(C_k \) in a certain degree, while there is no linear corresponding relationship between \(C_k\) and the maximum vibration amplitude.

4.3 Transmission Error

Neglecting loads variation, the average excitations contain loads and average transmission errors and alternating components of transmission errors are corresponding to alternating excitation. When load torque is fixed, the frequency response curves under three different \(\bar{{e}}_k^a\) of 0.2, 1 and 2 with \(\bar{{b}}_k =2,\,C_k =0.25\) are shown in Fig. 7.

Fig. 7
figure 7

The influence of transmission error

Full size image

Because transmission error is contained in the expression of relative displacement and the backlash is a piecewise-linear function of relative displacement, the amplitude of transmission error variation is directly related to elastic restoring force, which impacts the nonlinearities of the compound planetary gear sets as well as the response amplitudes. When \(\bar{{e}}_k^a \) varies in a certain value, the nonlinearities of the system enhances with the increase in the amplitude of transmission error. However, when it comes to a certain value, the nonlinearity will get lower. It can be seen from the Fig. 7, the relative displacement between \(s_{2}\) and \(b_{1}\) is not excited near the resonance frequency \(\omega _{1}\) when \(\bar{{e}}_k^a=0.2\). Because of the couple of spare parts, the vibration can be reduced as well as enhanced. The nonlinear characteristic of the amplitude jump discontinuities and the single-impact state exist near the resonance frequencies in the system when \(\bar{{e}}_k^a =1\). The increasing of the transmission errors will strengthen the nonlinearity of the system when \(\bar{{e}}_k^a =2\). By comparing the different influences of transmission errors shown in Fig. 7, it can be observed that the response amplitudes of the system increase with the transmission errors increasing.

4.4 Numerical method

Here, we compare the results obtained by HBM with the results by numerical method. From above analyzing, we know the backlash makes large contribution to the nonlinear vibration of the system. Figure 8 shows the relative gear mesh displacement of \(\bar{{\delta }}_{s_2 b_1}\) at several typical dimensionless meshing frequencies under different gear backlash to verify the results shown in Fig. 5.

Fig. 8
figure 8

Time histories of \(\delta _{s_2 b_1}\) under different parameters. a \({\bar{b}_k} = 1, \varOmega = 0.65\), b \({\bar{b}_k} = 1, \varOmega = 0.95\), c \({\bar{b}_k} = 1, \varOmega = 1.5\), d \({\bar{b}_k} = 2, \varOmega = 0.52\), e \({\bar{b}_k} = 2, \varOmega = 0.95\), f \({\bar{b}_k} = 2, \varOmega = 1.5\), g \({\bar{b}_k} = 4, \varOmega = 0.55\), h \({\bar{b}_k} = 4, \varOmega = 0.88\), i \({\bar{b}_k} = 4, \varOmega = 1.5\),

Full size image

As can be seen from Fig. 5, when the dimensionless gear backlash are given as different values, the frequency response curve shows typical nonlinear characteristics of amplitude jump discontinuities and multi-valve. The relative displacement curves are shown in Fig. 8a–c with the backlash being given as 1, when dimensionless meshing frequencies are given as 0.65, 0.95 and 1.5. The minimum value of \(\bar{{\delta }}_{s_2 b_1 } \)is close to \(-\)2.5 \((\bar{{\delta }}_{s_2 b_1 } (\min )<-\bar{{b}}_k )\), which indicates that the double-sided impact exists when \(\varOmega =0.65\); while the minimum value of \(\bar{{\delta }}_{s_2 b_1}\) is larger than -1 \((-\bar{{b}}_k <\bar{{\delta }}_{s_2 b_1 } (\min )<0)\), which indicates that the single-sided impact exists when \(\varOmega =0.95\); and the minimum value of \(\delta _{s_2 b_1 }\) is larger than 0, which indicates that the non-impact exists when \(\varOmega =1.5\). The results obtained here are coincident with the Fig. 5. Figure 8d–f show the relative displacement curves as given \(\bar{{b}}_k =2,\,\varOmega =0.52,0.95,1.5\). Similarly, the double-sided impact, single-sided impact and non-impact exist respectively under the three different dimensionless meshing frequencies. Figure 8g–i show the relative displacement curves as given \(\bar{{b}}_k =4,\,\varOmega =0.55,0.88,1.5\). However, the minimum value of \(\bar{{\delta }}_{s_2 b_1}\) is larger than \(-\bar{{b}}_k \), which indicates that there is no double-sided impact. The results obtained by numerical method are very coincident with the results shown in Fig. 5, which explain the main reason of the nonlinear vibration of the system, and also verify the accuracy and the precision of the method used in this paper. The conclusions related to the phenomenon of contact loss when \(\bar{{\delta }}_{s_2 b_1 } (\min )<0\), which is the source of the nonlinearity of the system and explained in Ref. [6], are coincident with the Refs. [6, 22].

Only single-frequency harmonic component contained in the response of the system is the key to success of HBM in the research of this paper. However, higher frequency harmonic component must be contained in the response if more accurate solving results are acquired, and the magnitude order of harmonic coefficient ignored should be checked. But the unknown variables of equations will increase tremendously and introduce more difficulties of iterative solving of the nonlinear algebraic equations converted. Although HBM cannot obtain the solution of unsteady-state response, fundamental frequency steady-state response can meet the requirement of practical engineering. Thus, using HBM to solve this problem has a relative advantage.

5 Conclusion

In this paper, the HBM is extended to research the nonlinear dynamic response of the compound planetary gear sets with the time-varying mesh stiffness, gear backlash, and transmission error. The following conclusions based on the analysis are,

  1. 1.

    A theoretical nonlinear time-varying dynamic model for the Ravigneaux compound planetary gear sets has been presented, which incorporates the time-varying mesh stiffness, transmission error, and gear backlash. Then, the nonlinear dynamic characteristics of compound planetary gear sets are investigated. Based on HBM, the dimensionless equations of motion are converted to algebraic equations and solved by using single-rank inverse Broyden quasi- Newton method.

  2. 2.

    The frequency response curves are obtained. Comparison and analysis are made by changing the fluctuant stiffness coefficient, the value of the gear backlash and the amplitude of transmission error. Meanwhile, the influences of the system parameters on nonlinear dynamic characteristic are investigated.

  3. 3.

    The typical nonlinear vibration of the system is mainly induced by the existence of gear backlash. The existence of mesh stiffness variation and the transmission error will make the nonlinear degree of the clearance-contained system further enhanced. The time-varying mesh stiffness, gear backlash, and transmission error have different extend of impacts on the dynamic response of compound planetary gear sets and the coupled effects make nonlinear characteristics more complicated of the system.

  4. 4.

    The dynamic response of a purely rotational nonlinear dynamic model of compound planetary gear sets is researched in terms of frequency response. The HBM, which provides some basis on researching the dynamic characteristics and reducing vibration and noise of compound planetary gear sets, can be further extended to “translational–rotational” model.