Dynamics of dipole breathers in nonlinear media with a spatial exponential-decay nonlocality

Abstract

By applying the variational approach, the analytical expression of dipole breathers is obtained in nonlinear media with an exponential-decay nonlocal response. The parameters of the width, the amplitude, the phase-front curvature, and the phase of the complex amplitude of the dipole breathers are all given in analytical expressions. It is found that the input power plays a key role in the evolution of dipole breathers, whose magnitude decides the change of the beam width (compressed or broadened) during propagation. The physical reason for the evolution of dipole breathers is analyzed in detail. Numerical simulations are also carried out, and the analytical solutions are in good agreement with numerical simulations.

1 Introduction

Nonlinear equations are very interesting because they can describe some real situations in science and engineering [1–10]. As a class of solutions of nonlinear equations, soliton solutions have unique characters and have been investigated widely. In optics, spatial solitons are self-trapped optical beams without shape change which exist in nonlinear media by virtue of the balance between diffraction and nonlinearity. Some of them have been realized in experiments and been applied to optical communications, light-controlled switch, and so on. The propagation dynamics of optical solitons are described by the well-known nonlinear Schrödinger equation (NLSE) [1]. Although NLSE has been studied extensively in the past several decades, these researches almost focus on the local nonlinearity. In 1997, Snyder and Mitchell proposed the nonlocal nonlinear model and gave the soliton and the breather solutions of the nonlocal nonlinear Schrödinger equation, i.e., accessible solitons [3]. The nonlocality allows the refractive index of a material at a particular point to be related to the beam intensity over a finite volume surrounding that point, which is distinctly different from the conventional local nonlinearity. Subsequently various soliton solutions of the nonlocal nonlinear Schrödinger equation are obtained in theory, such as Gaussian and higher-order Gaussian solitons [3–7], vortex solitons [11–14], dark solitons [15, 16], dipole solitons [17, 18], surface solitons [19, 20], and so on. Their propagation dynamics is studied deeply, even some have been observed in experiments [11, 16, 19].

On the other hand, although some analytical solutions can be obtained by solving nonlinear equations directly, it is indeed a difficult task. Variational approach is a valid method to solve some nonlinear equations, and it is introduced into optics firstly by Anderson [21]. For the nonlocal nonlinear Schrödinger equation, some soliton solutions are obtained by applying this method [15, 18, 20, 22, 23]. Recently, Aleksić et al. [24] studied the fundamental solitons in ($1+2$)-dimensional highly nonlocal nematic liquid crystals using the variational approach. The ($1+1$)-dimensional nematic liquid crystals can be reduced to the nonlinear media with an exponential-decay nonlocal response phenomenologically [25]. Although many solitons and breathers have been found in theory and even been observed in experiments, to the best of our knowledge, almost all previous investigations on solitons and breathers in nonlinear media with a nondifferentiable nonlocal response are based on numerical simulations, and no one clearly gives the analytical expression of dipole breathers in such media and investigate them thoroughly. The analytical results can provide more information and can be applied to investigating the beam dynamics conveniently. In this paper, the analytical expression of dipole breathers is obtained in nonlinear media with an exponential-decay nonlocal response by applying the variational approach. We mainly focus on the evolution of the width of dipole breathers. Some simulations are carried out to prove the validity of our analytical results.

2 Nonlocal nonlinear Schrödinger equation and its variational equations

The propagation dynamics of optical beams in nonlocal nonlinear media is governed phenomenologically by the nonlocal nonlinear Schrödinger equation [1, 4, 25, 26]

$$\begin{aligned}&2ik\frac{\partial \varPhi }{\partial Z}+\frac{\partial ^2\varPhi }{\partial X^2}+\,2k^2\eta \varPhi \nonumber \\&\times \int ^{+\infty }_{-\infty } R_i(X-X')|\varPhi (X',Z)|^2\hbox {d}X'=0,\nonumber \\ \end{aligned}$$

(1)

where $\varPhi (X,Z)$ is the complex amplitude of paraxial beams, $k$ is the wave number in the media without nonlinearity, $\eta$ is a material constant ($\eta >0$ or $\eta <0$ corresponds to a focusing or defocusing material), $Z$ is the longitudinal coordinate (i.e., the propagation direction), $X$ and $X'$ are the transverse coordinates, and $R_i$ is the symmetrical real spatial nonlocal response function of the media. The last term on the left in Eq. (1) represents the nonlinearity. If $R_i=0$, i.e., the last term on the left in Eq. (1) is ignored, and Eq. (1) reduces to the paraxial wave equation in free space, which has been thoroughly investigated in the past decades. If $R_i$ is a delta function, the above equation degenerates to the well-known nonlinear Schrödinger equation in the local nonlinear media.

For the convenience of discussion in the following, we simplify Eq. (1) using the normalized parameters

$$\begin{aligned} z&=\frac{Z}{z_R},\end{aligned}$$

(2a)

$$\begin{aligned} x&=\frac{X}{w_0},\end{aligned}$$

(2b)

$$\begin{aligned} \phi&=kw_0\sqrt{\eta }\varPhi , \end{aligned}$$

(2c)

where $w_0$ is the beam waist width of a Gaussian beam, $z_R=kw_0^2$ is the Rayleigh distance of a Gaussian beam. As a result, Eq. (1) reduces to

$$\begin{aligned} i\frac{\partial \phi }{\partial z}+\frac{1}{2}\frac{\partial ^2\phi }{\partial z^2}\!+\!\phi \int ^{+\infty }_{-\infty } R(x-x')|\phi (x',z)|^2\hbox {d}x'\!=\!0,\nonumber \\ \end{aligned}$$

(3)

where $R(x)=w_0R_i(X)$, and $\int ^{+\infty }_{-\infty } R(x-x')|\hbox {d}x'=1$. Here, we take the response function as a spatial exponential-decay nonlocal response, i.e.,

$$\begin{aligned} R(x)=\frac{1}{2w_m}\exp \left( -\frac{|x|}{w_m}\right) , \end{aligned}$$

(4)

where $w_m$ represents the characteristic length of the nonlocality. If $w_m\rightarrow 0$, $R$ becomes a delta function, i.e., the local case. If $w_m\rightarrow \infty$, it represents the case of strongly nonlocality. If $w_m\sim w_0$, it is the general nonlocal case. This exponential-decay nonlocal response can be encountered in nematic liquid crystals or in diffusion models [25, 26].

Equation (3) can be regarded as an Euler–Lagrange equation which corresponds to the variational problem

$$\begin{aligned} \delta \int _{0}^{+\infty }\int _{-\infty }^{+\infty } \mathcal {L}\left( \phi ,\phi ^*,\frac{\partial \phi }{\partial x},\frac{\partial \phi ^*}{\partial x},\frac{\partial \phi }{\partial z},\frac{\partial \phi ^*}{\partial z}\right) \hbox {d}x\hbox {d}z=0\nonumber \\ \end{aligned}$$

(5)

with the Lagrangian density given by

$$\begin{aligned} \mathcal {L}&= \frac{i}{2}\left( \phi ^*\frac{\partial \phi }{\partial z}-\phi \frac{\partial \phi ^*}{\partial z}\right) -\frac{1}{2}\left| \frac{\partial \phi }{\partial x}\right| ^2 \nonumber \\&\quad +\,\frac{1}{2}\left| \phi \right| ^2\int ^{+\infty }_{-\infty }R(x-x') \left| \phi (x')\right| ^2\hbox {d}x'. \end{aligned}$$

(6)

Substituting Eq. (6) into Eq. (5), the reduced variational problem is obtained as follows

$$\begin{aligned} \delta \int _{0}^{+\infty }[\mathcal {L}]\hbox {d}z=0, \end{aligned}$$

(7)

where

$$\begin{aligned}{}[\mathcal {L}]=\int _{-\infty }^{+\infty } \mathcal {L}\left( \phi ,\phi ^*,\frac{\partial \phi }{\partial x},\frac{\partial \phi ^*}{\partial x},\frac{\partial \phi }{\partial z},\frac{\partial \phi ^*}{\partial z}\right) \hbox {d}x. \end{aligned}$$

(8)

We employ the following ansatz as the trial solution of dipole breathers

$$\begin{aligned} \phi (x,z)\!=\!a(z)x\exp \left[ -\frac{x^2}{2w(z)^2}\!+\!ic(z)x^2+i\theta (z)\right] ,\nonumber \\ \end{aligned}$$

(9)

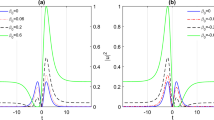
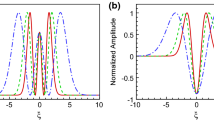
where $a(z)$, $w(z)$, $c(z)$, and $\theta (z)$ denote the amplitude, the width, and the phase-front curvature, the phase of the complex amplitude of the dipole breathers, respectively. They are all allowed to vary with propagation distance. If the soliton case is considered, $a(z)$ and $w(z)$ are constants independent of $z$, $c(z)\equiv 0$, and $\theta (z)$ can be expressed as $\theta (z)=\beta z$ with $\beta$ being the propagation constant. Figure 1 shows the electronic field distributions of $\phi (x)$ with different beam waists at the initial position.

Fig. 1

Normalized electronic field distributions of $\phi (x)$ with different beam waists at the initial position. The red solid curve, the green dashed curve, and the blue dash-dotted curve represent, respectively, $w(0)=1.0, 1.5$, and $2.0$. (Color figure online)

Generally speaking, substituting Eqs. (6) and (9) into Eq. (8), one can obtain $[\mathcal {L}]$, and then follow the common process of variational approach to get the parameters $a(z)$, $w(z)$, $c(z)$ and $\theta (z)$. Thus, the analytical solution of dipole breathers can be obtained finally. However, the analytical expression of $[\mathcal {L}]$ cannot be obtained because of the complication in mathematics, especially the integration induced by $R$. For the strongly nonlocal case, we can expand the response function into power series at the origin. If it is expanded into the second order, the response function is expressed as

$$\begin{aligned} R(x)\simeq \frac{1}{2w_m}\left( 1-\frac{|x|}{w_m}+\frac{x^2}{2w^2_m}\right) . \end{aligned}$$

(10)

Substituting Eqs. (6), (9) and (10) into Eq. (8), one can obtain the analytical expression of $[\mathcal {L}]$,

$$\begin{aligned}{}[\mathcal {L}]&= -\frac{1}{4}\sqrt{\pi }a^2w^3\left( 3w^2\frac{\hbox {d}c}{\hbox {d}z} +2\frac{\hbox {d}\theta }{\hbox {d}z}\right) \nonumber \\&\quad -\,\frac{3}{8}\sqrt{\pi }a^2w(1+4c^2w^4)\nonumber \\&\quad +\,\frac{a^4w^6}{64w_m^3}(4\pi w_m^2-7\sqrt{2\pi }w_mw+6\pi w^2). \end{aligned}$$

(11)

The corresponding Euler–Lagrangian equations are expressed as

$$\begin{aligned}&\frac{\partial [\mathcal {L}]}{\partial \theta }+\frac{\partial }{\partial z}\left( \frac{\partial [\mathcal {L}]}{\partial \theta _z}\right) =0, \end{aligned}$$

(12)

$$\begin{aligned}&\frac{\partial [\mathcal {L}]}{\partial c}+\frac{\partial }{\partial z}\left( \frac{\partial [\mathcal {L}]}{\partial c_z}\right) =0,\end{aligned}$$

(13)

$$\begin{aligned}&\frac{\partial [\mathcal {L}]}{\partial a}+\frac{\partial }{\partial z}\left( \frac{\partial [\mathcal {L}]}{\partial a_z}\right) =0,\end{aligned}$$

(14)

$$\begin{aligned}&\frac{\partial [\mathcal {L}]}{\partial w}+\frac{\partial }{\partial z}\left( \frac{\partial [\mathcal {L}]}{\partial w_z}\right) =0. \end{aligned}$$

(15)

Substituting Eq. (11) into Eqs. (12)–(15), we get

$$\begin{aligned}&2w\frac{\hbox {d}a}{\hbox {d}z}+3a\frac{\hbox {d}w}{\hbox {d}z}=0,\end{aligned}$$

(16)

$$\begin{aligned}&2w\frac{\hbox {d}a}{\hbox {d}z}+a\left( 5\frac{\hbox {d}w}{\hbox {d}z}-4cw\right) =0,\end{aligned}$$

(17)

$$\begin{aligned}&\frac{a^2w^5}{w_m^3}(4\pi w_m^2-7\sqrt{2\pi }w_mw+6\pi w^2)\nonumber \\&\quad -12\sqrt{\pi }(1+4c^2w^4)\nonumber \\&\quad -\,8\sqrt{\pi }w^2\left( 3w^2\frac{\hbox {d}c}{\hbox {d}z}+ 2\frac{\hbox {d}\theta }{\hbox {d}z}\right) =0,\end{aligned}$$

(18)

$$\begin{aligned}&-\,24\sqrt{\pi }a^2w_m^2w^5+49\sqrt{2} a^2w_mw^6-48\sqrt{\pi }a^2w^2\nonumber \\&\quad +\,24w_m^3\left( 1+20c^2w^4+10w^4\frac{\hbox {d}c}{\hbox {d}z} +4w^2\frac{d\theta }{dz}\right) =0.\nonumber \\ \end{aligned}$$

(19)

Based on Eqs. (16), (17), (18) and (19), we obtain

$$\begin{aligned}&\frac{\hbox {d}}{\hbox {d}z}\left( \frac{\sqrt{\pi }}{2} a^2w^3\right) =0,\end{aligned}$$

(20)

$$\begin{aligned}&\frac{\hbox {d}w}{\hbox {d}z}=2cw, \end{aligned}$$

(21)

$$\begin{aligned}&\frac{\hbox {d}\theta }{\hbox {d}z}=\frac{3}{4w^3(6\sqrt{2\pi }w-7w+m)}\nonumber \\&\qquad \quad \times \,\left[ 5-3w^3\frac{\hbox {d}^2w}{\hbox {d}z^2}+6\sqrt{2\pi }w^2\left( w^3 \frac{\hbox {d}^2w}{\hbox {d}z^2}-3\right) \right. \nonumber \\&\qquad \quad \left. +\,8\sqrt{2\pi }w_m^2\left( w^3\frac{\hbox {d}^2w}{\hbox {d}z^2}-1\right) \right] ,\end{aligned}$$

(22)

$$\begin{aligned}&\frac{\hbox {d}^2w}{\hbox {d}z^2}=\frac{1}{w^3}-\frac{7a^2w^3}{24\sqrt{2}w_m^2}+ \frac{\sqrt{\pi }a^2w^4}{4w_m^3}. \end{aligned}$$

(23)

Equation (20) reveals the energy conservation when the dipole breathers propagate in the media, which can be explained as follows. The input power of dipole breathers is $P_0=\int _{-\infty }^{+\infty }|\phi (x,z)|^2\hbox {d}x=\sqrt{\pi }a^2w^3/2$, and one can get $\sqrt{\pi }a^2w^3/2=\text {constant}$ based on Eq. (20), which indicates the power of dipole breathers keep invariant during propagation, i.e., the energy conservation.

In theory, solving Eqs. (20)–(23), one can get the expressions of $a(z)$, $w(z)$, $c(z)$, and $\theta (z)$, and then the analytical expression of dipole breathers is obtained. In the following section, Eqs. (20)–(23) are solved and the evolution of dipole breathers is investigated in detail.

3 Solution of dipole breathers and their propagation dynamics

We first consider the special case of $\hbox {d}w/\hbox {d}z=\hbox {d}^2w/\hbox {d}z^2=0$, i.e., the width of dipole breathers keeps invariant during propagation, which is the soliton case. Combining Eqs. (20) and (23), the soliton power is obtained as follows [18]

$$\begin{aligned} P_s=\frac{24\sqrt{\pi }w_m^3}{w_0^3(7\sqrt{2}w_m-12\sqrt{\pi }w_0)}, \end{aligned}$$

(24)

where $w_0=w(0)$ is the beam waist width at the initial position. The soliton power is much different from the soliton power of Snyder–Mitchell model or Gaussian nonlocal response [3–7]. Figure 2 shows the variation of the soliton power with the beam waist and the characteristic length of the nonlocality. It is found that the soliton power becomes larger and larger with $w_m$ increasing or $w_0$ decreasing.

Fig. 2

Variations of the soliton power with the nonlocal characteristic length and the beam waist. a Variations in $P_s$ with $w_m$; b variations in $P_s$ with $w_0$

We now focus on the general case, i.e., the breather case, which is the emphasis of this paper. For this case, the beam width $w(z)$ varies during propagation, which is described by Eq. (23). If we assume that $w$ and $z$ are, respectively, equivalent to the spatial and temporal coordinates of a particle in classical mechanics, Eq. (23) is equivalent to Newton’s second law for the motion of an one-dimensional particle with the equivalent mass 1 acted by the equivalent force $F$, and

$$\begin{aligned} F=\frac{1}{w^3}-\frac{7P_0}{12\sqrt{2\pi }w_m^2}+ \frac{P_0w}{2w_m^3}. \end{aligned}$$

(25)

Because $F$ is a conservative force, the equivalent potential $V(w)=-\int F\hbox {d}w$ is obtained as follows

$$\begin{aligned} V=\frac{1}{2w^2}+\frac{7P_0w}{12\sqrt{2\pi }w_m^2} -\frac{P_0w^2}{4w_m^3}+C_0, \end{aligned}$$

(26)

where $C_0$ is an integral constant, and $P_0=\int _{-\infty }^{+\infty }|\phi (x,z)|^2\hbox {d}x$ is the input power. If we define the initial condition $V(w_0)=0$, then

$$\begin{aligned} C_0=-\frac{1}{2w_0^2}-\frac{7P_0w_0}{12\sqrt{2\pi }w_m^2} +\frac{P_0w_0^2}{4w_m^3}. \end{aligned}$$

(27)

Therefore, the equivalent potential takes the form

$$\begin{aligned} V=\frac{w_0^2-w^2}{2w_0^2w^2}+\frac{7P_0(w-w_0)}{12\sqrt{2\pi }w_m^2} -\frac{P_0(w^2-w_0^2)}{4w_m^3}.\nonumber \\ \end{aligned}$$

(28)

Figure 3 illustrates the equivalent potential $V$ and the equivalent force $F$ for three typical input powers. When the input power is equal to the soliton power, the particle locates at the balance position of $V=0$ and $F=0$, and the system is situated at a stationary state corresponding to the soliton state (see Fig. 3c, d). When the input power is not equal to the soliton power, the balance between the nonlinearity and the beam diffraction is destroyed, and the dipole breathers come into being. If $P_0<P_s$, the nonlinearity is weaker than the diffraction, as a result, the beam width becomes wide firstly under the competition of the two effects. When the beam width increases to $w_b$ at the bottom of the potential well, the direction of the equivalent force reverses, but the beam width increases continually due to inertia, up to its maximum. Subsequently, the beam width decreases gradually and varies periodically (see Fig. 3a, b). If $P_0>P_s$, the process is similar except the beam width is compressed firstly, as the nonlinearity is stronger than the diffraction (see Fig. 3e, f).

Fig. 3

Equivalent potential $V$ (left column) and equivalent force $F$ (right column) for three typical input powers with $w_m=10, w_0=1$. The input power is $P_0=0.8P_s$ for (a) and (b); $P_0=P_s$ for (c) and (d); $P_0=1.2P_s$ for (e) and (f)

In order to further understand the evolution of the beam width, we calculate the analytical expression of the beam width. We expand the equivalent potential $V(w)$ into the second order with respect to the balance position $w_b$ at the bottom of the potential well,

$$\begin{aligned} V(w)&\simeq V(w_b)+V'(w_b)(w-w_b)\nonumber \\&+\frac{1}{2}V''(w_b)(w-w_b)^2\nonumber \\&= -\left( \frac{1}{2w_0^2}-\frac{1}{2w_b^2}-\frac{P_0w_0^2}{4w_m^3} +\frac{P_0w_b^2}{4w_m^3}\right. \nonumber \\&\left. \quad +\,\frac{7P_0w_0}{12\sqrt{2\pi }w_m^2}-\frac{7P_0w_b}{12\sqrt{2\pi }w_m^2}\right) \nonumber \\&\quad -\,\left( \frac{1}{w_b^3}+\frac{P_0w_b}{2w_m^3}- \frac{7P_0}{12\sqrt{2\pi }w_m^2}\right) (w-wb)\nonumber \\&\quad +\,\left( \frac{3}{2w_b^4}-\frac{P_0}{4w_m^3}\right) (w-w_b)^2, \end{aligned}$$

(29)

where $V'=\hbox {d}V/\hbox {d}w$ and $V''=\hbox {d}^2V/\hbox {d}w^2$. Because the point of $w_b$ is a steady and balance point, one can get $V'=0$ and $V''>0$. According to $V'=0$, we obtain

$$\begin{aligned} w_b^4-\frac{7w_m}{6\sqrt{2\pi }}w_b^3+\frac{2w_m^3}{P_0}=0. \end{aligned}$$

(30)

Equation (30) can be rewritten as a standard quartic equation

$$\begin{aligned} w_b^4+aw_b^3+bw_b^2+cw_b+d=0, \end{aligned}$$

(31)

where

$$\begin{aligned} a&= -\frac{7w_m}{6\sqrt{2\pi }},\\ b&= 0,\\ c&= 0,\\ d&= \frac{2w_m^3}{P_0}. \end{aligned}$$

Following the traditional process of solving a quartic equation, one can get the solution of $w_b$,

$$\begin{aligned} w_b=-\frac{1}{2}\left( \frac{a}{2}-\sqrt{\frac{a^2}{4}+t}\right) -\sqrt{\varDelta }, \end{aligned}$$

(32)

where

$$\begin{aligned} \varDelta&= \left( \frac{a}{2}-\sqrt{\frac{a^2}{4}-b+t}\right) ^2 -4\left( \frac{t}{2}+\sqrt{\frac{t^2}{4}-d}\right) ,\\ t&= \left( \frac{q}{2}+\sqrt{\frac{q^2}{4} +\frac{p^3}{27}}\right) ^{\frac{1}{3}}+\left( \frac{q}{2} -\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}\right) ^{\frac{1}{3}},\\ p&= ac-4d,\\ q&= a^2d-4bd+c^2. \end{aligned}$$

As we know, a quartic equation has several solutions; however, it requires that the solution must be a real root and $V''>0$ due to the physical reason. Equation (32) is the only exact solution satisfying all conditions.

Because the dipole breather is regarded as a particle with the mass being 1, the total energy of the equivalent particle is $E=T+V$, where $T=(\hbox {d}w/\hbox {d}z)^2/2$ is the kinetic energy. Under the on-waist incident condition, we have the initial conditions $\hbox {d}w/\hbox {d}z|_{z=0}=0$ and $V(w_0)=0$. According to $E=T+V=0$ at the initial position and Eq. (28), we obtain the following differential equation for $w(z)$,

$$\begin{aligned} \left( \frac{\hbox {d}w}{\hbox {d}z}\right) ^2+V''(w_b)[(w-w_b)^2-(w_0-w_b)^2]=0,\nonumber \\ \end{aligned}$$

(33)

where

$$\begin{aligned} V''(w_b)=\frac{3}{w_b^4}-\frac{P_0}{2w_m^3}. \end{aligned}$$

Solving Eq. (33), we get the analytical expression of the beam width of dipole breathers,

$$\begin{aligned} w(z)=w_b+(w_0-w_b)\cos \left( \sqrt{\frac{3}{w_b^4}- \frac{P_0}{2w_m^3}}z\right) .\nonumber \\ \end{aligned}$$

(34)

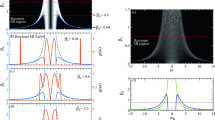
Comparing with the breather solutions for Gaussian response or Snyder–Mitchell model [3–7], the width variation in dipole breathers in this paper is different, although they are all periodical. For Gaussian response or Snyder–Mitchell model, the period of the width variation is proportional to $\sqrt{P_0}$, while the period becomes more complicated for the exponential-decay response, and it is proportional to $(3/w_b^4-P_0/2w_m^3)^{1/2}$. Figure 4 shows the evolutions of the width of dipole breathers with different input powers during propagation. The solid curves are plotted using our analytical solution, and the dashed curves are the results of numerical simulations directly based on Eq. (3). It can be found that the solitons appear when $P_0=P_s$, namely the width keeps invariant during propagation (see Fig. 4a). When $P_0>P_s$, the width of dipole breathers decreases firstly because the high input power leads to a strong self-focusing. The narrower the width, the stronger the diffraction. With the width decreasing gradually, the diffractions become stronger and stronger comparing with the self-focusing induced by the nonlinearity. As a result, after the width arrives at its minimum, it increases and varies periodically. The periodical variation in the width is the homeostasis between the nonlinearity and the diffraction (see Fig. 4b, c). When $P_0<P_s$, the evolution of the width is similar to the case of $P_0>P_s$, except that the width increases firstly since the nonlinearity is weaker than the diffraction at the beginning (see Fig. 4d, e). These results agree with the results obtained by using the theory of the equivalent potential and the equivalent force.

Fig. 4

Evolutions of the width of dipole breathers with different input powers during propagation. The input powers in (a), (b), (c), and (d) are, respectively, $1.0P_0, 1.15P_0, 1.5P_0, 0.85P_0$, and $0.5P_0$. The red solid curve and the green dashed curve represent the analytical results and the numerical results, respectively. The other parameters are $w_m=10$ and $w_0=1$. (Color figure online)

In addition, we find that the analytical results are in good agreement with the numerical calculations when the beam width is much smaller than the characteristic length of the nonlocality, i.e., under the condition of the strong nonlocality (see Fig. 4b, c). When the beam width becomes wider and $w_m$ is fixed, the degree of nonlocality decreases and the analytical results become somewhat inaccurate (see Fig. 4e).

Combining Eqs. (20)–(23) and (34), after somewhat complicated calculations, we get the solutions of $a(z)$, $c(z)$, and $\theta (z)$,

$$\begin{aligned}&a(z)=\frac{2\root 4 \of {8}\sqrt{3w_m}w_m}{[\cos (\beta z)(w_0-w_b)+w_b]^3}\nonumber \\&\qquad \qquad \times \,\sqrt{\frac{\beta ^2(w_0\!-\!w_b)[\cos (\beta z)(w_0-w_b)\!+\!w_b]^3-1}{6\sqrt{2\pi }[\cos (\beta z)(w_0\!-\!w_b)\!+\!w_b]-7w_m}}, \end{aligned}$$

(35)

$$\begin{aligned}&c(z)=\frac{\beta \sin (\beta z)(w_b-w_0)}{2[\cos (\beta z) (w_0-w_b)+w_b]},\end{aligned}$$

(36)

$$\begin{aligned}&\theta (z)=\frac{3\text {arctanh}\left[ \sqrt{\frac{w_0-2w_b}{w_0}}\tan \left( \beta z/2\right) \right] w_b}{\beta [w_0(w_0-2w_b)]^{\frac{3}{2}}}\nonumber \\&\qquad \qquad +\,\frac{3\sin (\beta z)(w_b-w_0)}{2\beta w_0(w_0-2w_b)[\cos (\beta z)w_0\!-\!w_b(\cos (\beta z)\!-\!1)]}\nonumber \\&\qquad \qquad +\,\frac{3P_0\sin (2\beta z)(w_0-w_b)^2}{32\beta w_m^3}\nonumber \\&\qquad \qquad +\,\frac{3P_0\sin (\beta z)(w_0-w_b)\left( 8w_b-7\sqrt{2/\pi w_m}\right) }{32\beta w_m^3}\nonumber \\&\qquad \qquad +\,\frac{P_0z}{32w_m^3}\left( 6w_0^2-12w_0w_b+18w_b^2\right. \nonumber \\&\left. \qquad \qquad -\,21\sqrt{2/\pi }w_bw_m+16w_m^2\right) , \end{aligned}$$

(37)

where $\beta =\sqrt{\frac{3}{2w_b^4}-\frac{P_0}{4w_m^3}}$ and $\text {arctanh}(\cdot )$ denotes the inverse hyperbolic tangent function. Thus, we obtain the analytical expression of dipole breathers.

Figure 5 gives the evolutions of the phase-front curvature of dipole breathers with different input powers during propagation. It can be found that when $P_0=P_s$, the curvature equals zero, which means the cophasal surface is a plane and the breathers become the solitons. When $P_0>P_s$ ($P_0<P_s$), the curvature radius is negative (positive) at the initial point, which represents that the cophasal surface is concave (convex) and induces the self-focusing (self-defocusing) of dipole breathers. So the width decreases (increases) firstly. When the breather arrives at its minimum (maximum) width, the sign of the curvature radius reverses; hence, the variation of the width also reverses.

Fig. 5

Evolutions of the phase-front curvature of dipole breathers with different input powers during propagation. The parameters are the same as those in Fig. 4

In the above, the response function is only expanded into second order. However, when the characteristic length of the nonlocality keep invariant and the width of dipole breathers increases (i.e., the degree of nonlocality becomes weaker), the analytical solutions are invalid gradually (see Figs. 4e and 5e). If we expand the response function into higher order, the more exact solutions can be obtained. Of course, more complicated calculations will be encountered. As an example, we expand the response function into sixth and tenth order, i.e.,

$$\begin{aligned} R^{(6)}(x)&\simeq \frac{1}{2w_m}\left( 1-\frac{|x|}{w_m} +\frac{x^2}{2w^2_m}-\frac{1}{3!}\frac{|x|^3}{w_m^3}\right. \nonumber \\&\left. \quad +\,\frac{1}{4!}\frac{|x|^4}{w_m^4}-\frac{1}{5!}\frac{|x|^5}{w_m^5} +\frac{1}{6!}\frac{|x|^6}{w_m^6}\right) ,\end{aligned}$$

(38)

$$\begin{aligned} R^{(10)}(x)&\simeq \frac{1}{2w_m}\left( 1-\frac{|x|}{w_m} +\frac{x^2}{2w^2_m}-\frac{1}{3!}\frac{|x|^3}{w_m^3}\right. \nonumber \\&\quad +\,\frac{1}{4!}\frac{|x|^4}{w_m^4}-\frac{1}{5!}\frac{|x|^5}{w_m^5} +\frac{1}{6!}\frac{|x|^6}{w_m^6}-\frac{1}{7!}\frac{|x|^7}{w_m^7}\nonumber \\&\left. \quad +\,\frac{1}{8!}\frac{|x|^8}{w_m^8}-\frac{1}{9!}\frac{|x|^9}{w_m^9} +\frac{1}{10!}\frac{|x|^{10}}{w_m^{10}}\right) . \end{aligned}$$

(39)

After tedious calculations, we obtain the soliton power

$$\begin{aligned} P_s^{(6)}&= \frac{48\sqrt{2\pi }w_m^7}{w_0^3}(28w_m^5-24\sqrt{2\pi } w_0w_m^4\nonumber \\&+76w_0^2w_m^3\nonumber \\&\quad -\,28\sqrt{2\pi }w_0^3w_m^2+52w_0^4w_m-13\sqrt{2\pi }w_0^5), \end{aligned}$$

(40)

$$\begin{aligned} P_s^{(10)}&= \frac{80640\sqrt{2\pi }w_m^{11}}{w_0^3}(47040w_m^9\nonumber \\&\quad -\,40320\sqrt{2\pi }w_0w_m^8+127680w_0^2w_m^7\nonumber \\&\quad -\,47040\sqrt{2\pi }w_0^3w_m^6+87360w_0^4w_m^5\nonumber \\&\quad -\,21840\sqrt{2\pi }w_0^5w_m^4+30016w_0^6w_m^3\nonumber \\&\quad -\,5880\sqrt{2\pi }w_0^7w_m^2+6592w_0^8w_m\nonumber \\&\quad -\,1085\sqrt{2\pi }w_0^9). \end{aligned}$$

(41)

$P_s^{(6)}$ is more exact than $P_s^{(2)}=P_s$, and $P_s^{(10)}$ is more exact than $P_s^{(6)}$.

In order to illustrate the improvement of the analytical soliton powers by expanding the response function into higher orders, we present the comparison between the analytical results and the numerical ones in Fig. 6. One can find that if $w_m=10$, $P_s^{(2)}$ is valid approximately when $w_0<3$, which is the case of strong nonlocality. However, $P_s^{(6)}$ is valid when $w_0<8$, and $P_s^{(10)}$ is still valid when $w_0=10$, which is already the case of general nonlocality.

Fig. 6

Variations in the soliton power with the beam waist by expanding the response function into different orders. The triangles denote the numerical results. The parameter $w_m=10$

4 Conclusions

In conclusion, we have investigated the dipole breathers in nonlinear media with a spatial exponential-decay nonlocality. The analytical expression of dipole breathers is given by using the variational approach. It is found that the evolution of the width is periodical and the input power affects the dynamics of dipole breathers greatly. The magnitude of the input power decides the change of the beam width (compressed or broadened). The physical reason for the evolution of dipole breathers is analyzed in detail. Numerical simulations are also performed, and the results confirm our analytical solutions.