1 Introduction

Derivatives and integrals of fractional order have found many applications in recent studies in mechanics and physics. It includes chaotic dynamics [1], mechanics of fractal media [2], quantum mechanics [3], physical kinetics [4], plasma physics [5, 6], astrophysics [7], mechanics of non-Hamiltonian systems [8], theory of long range interaction [9], anomalous diffusion and transport theory [10] and many other physical topics [11, 12].

The most methods of classical mechanics deal with conservative systems, while almost all processes observed in the physical real world are non-conservative. It was shown that non-integer derivatives in the Lagrangian describe non-conservative forces. Riewe [13, 14] derived a method using a fractional Lagrangian that leads to a fractional Euler–Lagrange equation that is, in some sense, equivalent to the desired equation of motion. Hamilton’s equations are derived from the Lagrangian and are equivalent to the Euler–Lagrange equation. Further study of the fractional Euler–Lagrange can be found in the works of Agrawal [15, 16]. He presented generalized Euler–Lagrange equations for unconstrained and constrained fractional variational problems. Baleanu et al. [17–20] used the fractional Euler–Lagrange equation to model fractional Lagrangian and Hamiltonian formulations. Many other authors exploited the fractional variational principles to study different problems in sciences and technology [19–31] and references therein.

The fractional integration and differentiation operators had different kinds of definitions. The most famous one is the Riemann–Liouville definition (e.g., [32, 33]), which has been used in various fields of science and engineering successfully, but this definition leads to the result that constant function differentiation is not zero. Caputo’s definition gives zero value for fractional differentiation of constant function, but this definition requires that the function should be smooth and differentiable (e.g., [32, 33]). These two definitions are examples of the nonlocal fractional derivatives [34–38]. Definitions of local fractional derivatives have been proposed as Kolwankar and Gangal fractional derivative [39], Cresson’s derivative [40], Chen’s fractional derivative [41] and the modified Riemann–Liouville (mRL) derivative derived by Jumarie (e.g., [42, 43]). Recently, the mRL definition for the fractional integral and derivative is used to solve some science and technology problems (e.g., [44, 45]).

The Boussinesq equations arise in hydrodynamics to describe propagation of waves in nonlinear and dissipative media [46, 47]. This equation was formulated as part of an analysis of long waves in shallow water. It was subsequently applied to problems in the percolation of water in porous subsurface strata. Boussinesq equations are widely used in coastal and ocean engineering [48, 49]. Also, Boussinesq equations are the basis of several models used to describe unconfined groundwater flow and subsurface drainage problems. Recently, fractional differential equations have attracted considerable interest because of their ability to model particle transport in heterogeneous media and complex phenomena. The fractional Boussinesq equation is suitable for studying the water propagation through heterogeneous porous media. A fractional Boussinesq equation is obtained assuming power law changes of flux in a control volume and using a fractional Taylor series [50].

The fractional differential equations have been solved using several methods such as Laplace transformation method, Fourier transformation method, iteration method and operational method (e.g., [32, 33, 51]). However, most of these methods are suitable for special types of fractional differential equations, namely the linear with constant coefficients. However, there are some papers dealing with the existence and multiplicity of solution of nonlinear fractional differential equation using techniques of nonlinear analysis such as Adomian decomposition method [52], homotopy perturbation method [53], fractional variational iteration method [54], Exp-function method [55] and fractional sub-equation method [56, 57]. The space- and time-fractional Boussinesq equations in Caputo sense derivatives are solved using homotopy perturbation method [58]. The space–time fractional Boussinesq (STFBq) equation was solved by applying a fractional Riccati expansion method, which gave closed analytical solutions [59].

In this paper, the classical Lagrangian of the regular Boussinesq equation is calculated using the semi-inverse method [60]. The fractional Lagrangian is derived from the classical one by the direct way. The STFBq equation is derived by applying the fractional variational principle [14, 15] in terms of the mRL derivative operator [42, 43]. The fractional sub-equation technique [56, 57] is devoted to solve STFBq equation. The solutions of the resultant equation are given in terms of the Mittag–Liffler function. The STFBq equation has five solutions: Two of them are represented by fractional hyper-geometric functions and two others in terms of fractional triangle functions, while the fifth solution is appeared in a rational form. The effect of the fractional order on some of these solutions is studied and represented graphically.

The rest of this paper is outlined as follows: Sect. 2 is devoted to the derivation of the STFBq equation by applying the semi-inverse method and the fractional variational principle. Considering a traveling wave transformation, the STFBq equation is solved by the fractional sub-equation method in Sect. 3. In Sect. 4, the effects of the fractional order on the results represented by the figures are discussed. Section 5 is devoted to the conclusions on the work.

2 Derivation of space–time fractional Boussinesq equation

The semi-inverse method [60] and the fractional variational principle [15, 16] are applied to derive STFBq equation that is considered to describe physical phenomena.

The regular Boussinesq equation of (\(1+1\))-dimensional has the form

$$\begin{aligned}&\frac{\partial ^{2}}{\partial t^{2}}u(x, t)+A\frac{\partial ^{2}}{\partial x^{2}}u^{2}(x, t)+B\frac{\partial ^{2}}{\partial x^{2}}u(x, t)\nonumber \\&\quad +\,C\frac{\partial ^{4}}{\partial x^{4}}u(x, t)=0, \end{aligned}$$
(1)

where \(u(x, t)\) is a field function and \(A\) is the constant nonlinear coefficient; \(B\) is the dissipation coefficient and \(C\) is the higher order dissipation coefficient.

The space–time fractional Boussinesq equation can be formulated as follows:

Assuming a potential function \(U(x, t)\) as \(u(x, t)=U_x (x, t)\) gives the potential equation of the regular Boussinesq equation (1) in the form

(2)

where the subscripts denote the partial differentiation of the function with the parameter.

The functional of this equation can be represented by

(3)

where \(c_1, c_2, c_3 \) and \(c_4 \) are Lagrangian multipliers.

Integrating this equation by parts where \(U_x \;|_R =U_t \;|_T =U_{xx} \;|_R =U_{xxx} \;|_R =0\) and \(([u(x, t)]^{2})_{xx} \) is considered as a fixed function, applying the variation of this functional with respect to \(U(x, t)\), integrating by parts, optimizing of this variation, \(\delta J(U)=0\) and comparing the resultant equation with (2) give the constant multipliers as: \(c_1 =\frac{1}{2}, c_2 =1, c_3 =\frac{1}{2}\) and \(c_4 =\frac{1}{2}\).

The functional relation yields directly the Lagrangian of the Boussinesq equation as

$$\begin{aligned}&L(U_{xt} , U_x , U_{xx} , U_{xxx} )\nonumber \\&\quad =-\frac{1}{2}[U_{xt} (x, t)]^{2}+A\{[u(x, t)]^{2}\}_{xx} U_x (x, t)\nonumber \\&\qquad -\,\frac{1}{2}B[U_{xx} (x, t)]^{2}+\frac{1}{2}C[U_{xxx} (x, t)]^{2}. \end{aligned}$$
(4)

Similarly, the Lagrangian of the space–time fractional version of the Boussinesq equation could be written in the form

$$\begin{aligned}&F\left( D_t^\alpha D_x^\beta U, D_x^\beta U, D_x^{\beta \beta } U,D_x^{\beta \beta \beta } U\right) \nonumber \\&\quad = -\frac{1}{2}\left[ D_t^\alpha D_x^\beta U(x, t)\right] ^{2}+A\left\{ D_x^{\beta \beta } [u(x, t)]^{2}\right\} \nonumber \\&\qquad \times D_x^\beta U(x, t)-\frac{1}{2}B\left[ D_x^{\beta \beta } U(x, t)\right] ^{2}\nonumber \\&\qquad +\frac{1}{2}C\left[ D_x^{\beta \beta \beta } U(x, t)\right] ^{2}, \end{aligned}$$
(5)

where \(D_z^{\gamma \gamma } f=D_z^\gamma [D_z^\gamma f]\) and \(D_z^\gamma f(z)\) is the mRL fractional derivative defined by [42, 43]

$$\begin{aligned} D_z^\gamma f(z)&= \frac{1}{\Gamma (1-\gamma )}\frac{\mathrm{d}}{\mathrm{d}z}\left\{ \mathop \int \nolimits _a^z \mathrm{d}\zeta \frac{[f(\zeta )-f(a)]}{(z-\zeta )^{\gamma }}\right\} ,\nonumber \\&\quad 0\le \gamma <1 \end{aligned}$$
(6)

The functional of the space–time fractional Boussinesq equation takes the form

$$\begin{aligned} J_F (U)&= \mathop \int \nolimits _R (\mathrm{d}x)^{\beta } \mathop \int \nolimits _T (\mathrm{d}t)^{\alpha } \nonumber \\&\quad F\left( D_t^\alpha D_x^\beta U, D_x^\beta U,D_x^{\beta \beta } U,D_x^{\beta \beta \beta } U\right) , \end{aligned}$$
(7a)

where [42, 43]

$$\begin{aligned} \int _a^t {(\mathrm{d}\tau )^{\gamma }f(\tau )} =\gamma \int _a^t {\mathrm{d}\tau } (t-\tau )^{\gamma }f(\tau ). \end{aligned}$$
(7b)

Integrating by parts using the relation [42, 43]

$$\begin{aligned}&\mathop \int \nolimits _a^b (\mathrm{d}\tau )^{\gamma } f(z)D_z^\gamma g(z)=\Gamma (1+\gamma )[g(z)f(z)|_a^b \nonumber \\&{\quad }-\,\mathop \int \nolimits _a^b (\mathrm{d}z)^{\gamma } g(z)D_z^\gamma f(z), f(z), g(z)\in [a, b]. \end{aligned}$$
(8)

and optimizing the variation of this functional, \(\delta J_F (U)=0\), the Euler–Lagrange equation of space–time fractional Boussinesq equation has the form

$$\begin{aligned}&- D_t^\alpha \left( \frac{\partial F}{\partial D_t^\alpha D_x^\beta U}\right) +\left( \frac{\partial F}{\partial D_x^\beta U}\right) -D_x^\beta \left( \frac{\partial F}{\partial D_x^{\beta \beta } U}\right) \nonumber \\&\qquad +\,D_x^{\beta \beta } \left( \frac{\partial F}{\partial D_x^{\beta \beta \beta } U}\right) =0. \end{aligned}$$
(9)

Substituting the Lagrange of the STFBq given by (5) into this Euler–Lagrange formula and using the definition of the fractional potential function as \(D_x^\beta U(x, t)=u(x, t)\) lead to

$$\begin{aligned}&D_t^{\alpha \alpha } u(x, t)+AD_x^{\beta \beta } [u(x, t)]^{2}+BD_x^{\beta \beta } u(x, t)\nonumber \\&\quad +\,C D_x^{\beta \beta \beta \beta } u(x, t)=0, \end{aligned}$$
(10)

which is the space–time fractional Boussinesq equation.

3 Solution of space–time fractional Boussinesq equation

In this section, the STFBq equation will be solved using a fractional sub-equation method [56, 57]. Considering the traveling wave transformations \(u(x,t)=\Phi (\xi ), \xi =x+vt\), (10) can be reduced to the following nonlinear fractional ordinary differential equation using the relations

$$\begin{aligned}&D_x^\alpha [u(x) v(x)] =D_x^\alpha [u(x) ]v(x)+u(x) D_x^\alpha [v(x)],\nonumber \\\end{aligned}$$
(11a)
$$\begin{aligned}&D_x^\alpha f(u(x))=D_x^\alpha u(x) ({\mathrm{d}f}/{\mathrm{d}u})=D_u^\alpha f(u) ({\mathrm{d}u}/{\mathrm{d}x})^{\alpha },\nonumber \\ \end{aligned}$$
(11b)

for the case of \(\beta =\alpha \):

$$\begin{aligned}&v^{2\alpha }D_\xi ^{\alpha \alpha } \Phi (\xi )+AD_\xi ^{\alpha \alpha } [\Phi (\xi )]^{2}+BD_\xi ^{\alpha \alpha } \Phi (\xi )\nonumber \\&\quad +\,C D_\xi ^{\alpha \alpha \alpha \alpha } \Phi (\xi )=0. \end{aligned}$$
(12)

The fractional sub-equation method [56, 57] assumes solution of this equation as

$$\begin{aligned} \Phi (\xi )=\sum _{k=0}^n {a_k \varphi ^{k}(\xi )}, \end{aligned}$$
(13)

where \(\varphi (\xi )\) satisfies the following fractional Riccati equation:

$$\begin{aligned} D_\xi ^\alpha \varphi (\xi )=\sum _{j=0}^m {b_j } \varphi ^{j}(\xi ), \end{aligned}$$
(14)

where \(a_k,\,k=0,\ldots , n\) are constant coefficients to be determined later and \(b_j ,\,j=0,\ldots , m\) are arbitrary coefficients.

By balancing the highest order derivative term and nonlinear term in (12), the value of \(n\) can be determined, which has, in this problem, the value \(n=2\).

We suppose that (12) has the following formal solution:

$$\begin{aligned} \Phi (\xi )=a_0 +a_1 \varphi (\xi )+a_2 [\varphi (\xi )]^{2}, \end{aligned}$$
(15)

where \(a_0,\,a_1\) and \(a_2 \) are constant coefficients to be determined and \(\varphi (\xi )\) satisfies the following fractional Riccati equation:

$$\begin{aligned} D_\xi ^\alpha \varphi (\xi )=b_0 +b_1 \varphi ^{2}(\xi ), \end{aligned}$$
(16)

where \(b_0 \) and \(b_1 \) are arbitrary coefficients.

Using the generalized Exp-function method via Mittag–Leffler functions, Zhang et al. [61] first obtained the following solution of fractional Riccati equation (16)

$$\begin{aligned} \varphi _1 (\xi )&= -\sqrt{-b_0 }\tanh _\alpha (\sqrt{-b_0 }\xi ),\quad b_0 <0, b_1 =1,\nonumber \\\end{aligned}$$
(17a)
$$\begin{aligned} \varphi _2 (\xi )&= -\sqrt{-b_0 }\coth _\alpha (\sqrt{-b_0 }\xi ), \quad b_0 <0, b_1 =1,\nonumber \\\end{aligned}$$
(17b)
$$\begin{aligned} \varphi _3 (\xi )&= \sqrt{b_0 }\tan _\alpha (\sqrt{b_0 }\xi ), \quad b_0 >0, b_1 =1,\nonumber \\\end{aligned}$$
(17c)
$$\begin{aligned} \varphi _4 (\xi )&= -\sqrt{b_0 }\cot _\alpha (\sqrt{b_0 }\xi ), \quad b_0 >0, b_1 =1,\nonumber \\\end{aligned}$$
(17d)
$$\begin{aligned} \varphi _5 (\xi )&= -\Gamma (1+\alpha )/(\xi ^{\alpha }+\omega ), \nonumber \\&\quad b_0 =0, b_1 =1, \omega =\hbox {constant}, \end{aligned}$$
(17e)

with the generalized hyperbolic and trigonometric functions

$$\begin{aligned}&\tanh _\alpha (x)=\sinh _\alpha (x)/\cosh _\alpha (x), \nonumber \\&\coth _\alpha (x)=\cosh _\alpha (x)/\sinh _\alpha (x),\end{aligned}$$
(18a)
$$\begin{aligned}&\sinh _\alpha (x)=[E_\alpha (x)-E_\alpha (-x)]/2,\nonumber \\&\cosh _\alpha (x) =[E_\alpha (x)+E_\alpha (-x)]/2,\end{aligned}$$
(18b)
$$\begin{aligned}&\tan _\alpha (x)=\sin _\alpha (x)/\cos _\alpha (x), \nonumber \\&\cot _\alpha (x) =\cos _\alpha (x)/\sin _\alpha (x),\end{aligned}$$
(18c)
$$\begin{aligned}&\sin _\alpha (x)=[E_\alpha (ix)-E_\alpha (-ix)]/(2i), \nonumber \\&\cos _\alpha (x) =[E_\alpha (ix)+E_\alpha (-ix)]/2, \end{aligned}$$
(18d)

where \(i=\sqrt{-1}\) and \(E_\alpha (x)\) is the Mittag–Leffler function defined by

$$\begin{aligned} E_\alpha (x)=\sum _{k=0}^\infty {{x^{k}}/{\Gamma (1+k\alpha )}} . \end{aligned}$$
(18e)

Substituting (15) along with (16) and setting the coefficient of \(\varphi ^{k}(\xi )\) equal to zero lead to a set of algebraic equations in terms of the coefficients \(a_0,\,a_1 , a_2 \) and \(b_0 \). Solving the algebraic set of equations by Maple gives the following case:

$$\begin{aligned} a_0&= -(v^{2\alpha }+B+8Cb_0 )/(2A),\quad a_1 =0,\nonumber \\ a_2&= -6C/A,\quad b_0 =b_0 , b_1 =1, \end{aligned}$$
(19)

where the nonlinear coefficient \(A\ne 0\).

This set of coefficients gives the following set of solutions for the space–time fractional Boussinesq equation:

$$\begin{aligned} \Phi _1 (\xi )&= -(v^{2\alpha }+B+8Cb_0 )/(2A)\nonumber \\&\quad +\,(6C/A)b_0 [\tanh _\alpha (\sqrt{-b_0 }\xi )]^{2},\quad b_0 <0,\nonumber \\\end{aligned}$$
(20a)
$$\begin{aligned} \Phi _2 (\xi )&= -(v^{2\alpha }+B+8Cb_0 )/(2A)\nonumber \\&\quad +\,(6C/A)b_0 [\coth _\alpha (\sqrt{-b_0 }\xi )]^{2},\quad b_0 <0,\nonumber \\\end{aligned}$$
(20b)
$$\begin{aligned} \Phi _3 (\xi )&= -(v^{2\alpha }+B+8Cb_0 )/(2A)\nonumber \\&\quad -\,(6C/A)b_0 [\tan _\alpha (\sqrt{b_0 }\xi )]^{2},\quad b_0 >0,\nonumber \\\end{aligned}$$
(20c)
$$\begin{aligned} \Phi _4 (\xi )&= -(v^{2\alpha }+B+8Cb_0 )/(2A)\nonumber \\&\quad -\,(6C/A)b_0 [\cot _\alpha (\sqrt{b_0 }\xi )]^{2},\quad b_0 >0,\nonumber \\\end{aligned}$$
(20d)
$$\begin{aligned} \Phi _5 (\xi )&= -(v^{2\alpha }+B)/(2A)\nonumber \\&\quad -\,(6C/A)[\Gamma (1+\alpha )]^{2}/(\xi ^{\alpha }+\omega )^{2},\nonumber \\&\quad \omega =\hbox {constant}. \end{aligned}$$
(20e)

The solutions given by (20a) and (20c) are the same solutions appeared by (34) in [59], but other three solutions here may not be represented before.

4 Results and discussion

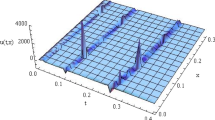
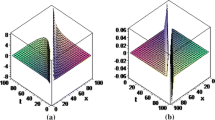
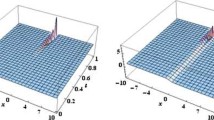
Our main motive in this paper is to study the effect of the fractional order \((\alpha )\) of the Boussinesq equation on its solution forms. The fractional sub-equation method [56, 57] is applied to solve the derived STFBq equation. The solutions of STFBq equation are given by equations (20) where two of these solutions are in terms of fractional hyper-geometric functions and two solutions in terms of fractional triangle functions, while the fifth one is represented as a rational solution. Refereeing to the solution of the regular Boussinesq equation [62], the free parameter \((b_0 )\) of solutions (20) is chosen to be \(b_0 =\mp \left| {(2v^{2\alpha }-B-3)/(8C)} \right| \). The effects of the space–time fractional derivative order (\(\alpha )\) on the shape of the solutions have been studied in Figs. 1, 2, 3, 4 and 5.

Fig. 1
figure 1

Solution (20a) of STFBq equation with parameters \(A=-3, B=-1,\,C=0.5,\,v=1.5\)

Full size image
Fig. 2
figure 2

Solution (20b) of STFBq equation with parameters \(A=-3, B=-1,\,C=0.5,\,v=1.5\)

Full size image
Fig. 3
figure 3

Solution (20c) of STFBq equation with parameters \(A=-3, B=-1,\,C=0.5,\,v=1.5\)

Full size image
Fig. 4
figure 4

Solution (20d) of STFBq equation with parameters \(A=-3, B=-1,\,C=0.5,\,v=1.5\)

Full size image
Fig. 5
figure 5

Solution (20e) of STFBq equation with parameters \(A=-3,\,B=-1, C=0.5,\,v=1.5,\,w=1\)

Full size image

Figure 1 shows the solution (20a), which represents a soliton solution. The increasing of \(\alpha \) increases the height while deceases the width of the soliton wave solution. Therefore, the fractional order can be used to modulate the soliton shape. The solution (20b) describes an explosive soliton and is represented in Fig. 2 where the increasing of \(\alpha \) increases the wave width. This type of solutions shows that the Boussinesq equation can represent explosive wave form. The third type of fractional Boussinesq equation, given by (20c), represents a periodic explosive wave. Figure 3 illustrates that the increasing of the fractional order (\(\alpha \)) decreases the wavelength and increases the number of explosive waves. The solution indicated by (20d) describes another explosive soliton. This solution is elucidated in Fig. 4, which shows that the increasing of \(\alpha \) increases the width of the explosive wave. The rational solution represented by (20e) shows decreasing wave as in Fig. 5.

5 Conclusion

In this work, the space–time fractional nonlinear Boussinesq equation that has many different applications in science and engineering is derived. The semi-inverse method [60] is used to find the Lagrangian of the Boussinesq equation. The classical derivatives in the Lagrangian are directly replaced by the fractional derivatives. Then, the fractional variational principles [14, 15] are devoted to lead to the fractional Euler–Lagrange equation, which gives the fractional Boussinesq equation. The modified Riemann–Liouville fractional derivative [42, 43] is employed to obtain the derived space–time fractional Boussinesq equation.

The fractional sub-equation method [56, 57] is applied to solve the derived STFBq equation. The solutions of STFBq equation are given by equations (20) where two of these solutions are in terms of fractional hyper-geometric functions and two solutions in terms of fractional triangle functions, while the fifth one is represented as a rational solution.

The calculations of these solutions show that the fractional order of the STFBq equation changes both the height and the width of the waves. This means that the fractional order can be used to modulate the shape of the waves described by the Boussinesq equation. We remark that more pronounced effects and deeper insight into the formation and properties of the resulting waves are added by considering the fractional order derivatives beside the nonlinearity.

Some advantages of this study are as follows: The derivation of the space–time fractional Boussinesq equation from the classical one employs a variational technique. The solutions of the fractional Boussinesq equation are appeared in closed analytical forms in terms of the Mittag–Leffler function. The used technique leads to new solutions describe periodic, soliton and explosive waves that can explain different physical, biological and engineering problems.