A new approach for dynamic modeling of n-viscoelastic-link robotic manipulators mounted on a mobile base

Abstract

In this article, the mathematical modeling of a robotic system composed of n flexible links and a mobile platform has been considered. Most of the mechanical systems including the nonholonomic constraints are analyzed by Lagrangian formulation and its associated “Lagrange multipliers.” Eliminating these variables from the obtained equations is a time-consuming and cumbersome task. So, the Gibbs–Appell formulation and the assumed mode method are used to make the derivation of motion equations easier. Also, to model the system thoroughly and accurately, the dynamic interactions between the manipulator and the mobile platform and the coupling effects arising simultaneously from large motions and small deflections are taken into consideration. The links (assumed as 3D Timoshenko beams) undergo tension-compression, torsion and spatial bending (in two directions), while the effects of internal and external damping (as dissipative forces) are also considered in the mathematical modeling. A systematic approach is developed based on the derived formulation to establish the dynamic equations of motion. In order to alleviate the computational complexity of the suggested method, all the mathematical operations are carried out through $3\times 3$ and $3\times 1$ matrices only. Finally, this method is applied to a mobile manipulator with two flexible links to demonstrate the ability of the proposed method in deriving the equations of motion of such complex systems.

1 Introduction

Spatial mobile manipulators consisting of flexible robotic arms mounted on a mobile platform are complex systems. Owing to the mobility feature of the mobile base and the dexterity of the manipulator, these robots are increasingly used in space applications such as planetary explorations, launch of satellites, spacecraft recovery (for inspection, maintenance and repair) and cargo displacement. All these missions require high precision. However, in order to reduce the total mass at launch, usually, very light and flexible manipulator arms are used; these manipulators experience substantial structural vibrations as they move, especially after they complete a maneuver. So, to properly design these types of mobile robotic manipulators which can accomplish their intended maneuvers, it is essential to appropriately model them, from the platform, to the elastic characteristics of the links.

Since the flexible manipulator and the mobile base have an integrated mechanical structure, the motion of any part affects the entire system configuration. This makes the dynamic equations of such robotic systems highly nonlinear and fully coupled. However, it is necessary to develop a complete and precise dynamic model for these kinds of robots. The dynamic interactions between the manipulator and the mobile platform have been studied by Staicu [1], Wiens [2] and Meghdari et al. [3]. Yamamoto and Yun [4] improved the mathematical modeling of mobile robots and included all nonholonomic constraints of such systems. In their works, the equations of motion are derived based on the Lagrangian formulation and its associated Lagrange multipliers. However, it is cumbersome to calculate the Lagrange multipliers. So, to do away with Lagrange multipliers, Thanjavur and Rajagopala [5] and Tanner and Kyriakopouos [6] modeled the mobile manipulators on the basis of Kane’s equations.

With the addition of more arms to the mobile platform, the complete modeling of the wheeled mobile manipulator system becomes more complicated. In such cases, systematic approaches have to be employed to make the derivation of the governing equations easier. Examples of automatic formulation of elastic robotic manipulators with fixed base can be found in the works of Book [7], Changizi and Shabana [8], Kim and Haug [9], Amirouche and Xie [10], Nikravesh and Ambrosio [11], Znamenacek and Valasek [12], Lugris et al. [13] and Bae and Haug [14]. However, there are just a few works on systematic modeling on mobile manipulators. For example, Yu and Chen [15] applied forward recursive formulation to obtain the governing equations of nonholonomic mobile manipulators based on the principle of virtual work. Also, a recursive Newton–Euler formulation is used in Ref [16] to present the inverse and forward dynamics of robot manipulators with a moving base.

The derivation of the dynamic equations of motion by Gibbs–Appell (G–A) formulation begins with a definition of Gibbs’ function (acceleration energy). Next, a set of independent quasi-velocities (linear combination of generalized velocities) should be selected. The above-mentioned equations are then obtained by taking the derivatives of Gibbs’ function with respect to quasi-accelerations (time derivatives of quasi-velocities) and setting them equal to the generalized forces. Despite the great ability of this method in deriving the equations of motion, it has been used the least for deriving the dynamic equations of manipulator robots. In the field of robotics, more recent investigations can be found in [17] where G–A formulation has been used by Vosoughi et al. for motion equations of snake-like robots; in [18], where forward dynamics equations of motion of n-rigid links have been presented in recursive form by Mata et al.; and in [19, 20], where motion equations of viscoelastic link manipulators and nonholonomic wheeled mobile robotic manipulators have been presented by Korayem et al.

As mentioned above, in this article, by applying the G–A formulation and the assumed mode method (AMM), the mathematical model of an n-viscoelastic-link robotic manipulator on a mobile base has been presented. The paper’s focus is on obtaining precise and complete equations of motion that include the most relevant structural properties of lightweight elastic manipulators and the nonholonomic constraints of the mobile base. In this study, two important damping mechanisms including structural viscoelasticity (Kelvin–Voigt) effect (as internal damping) and the viscous air effect (as external damping) have been considered. To include the effects of shear and rotational inertia, the assumption of Timoshenko beam theory (TBT) has been applied. Gravity, torsion and longitudinal elongation effects have also been considered in the formulations. A recursive approach has been applied in the modeling to systematically derive the equations of motion and to improve the computational efficiency. Finally, a computer simulation has been performed for a manipulator with two viscoelastic links on a mobile base to validate the proposed method.

2 Kinematics of the system

2.1 Kinematics of the manipulator

In this section, the kinematics of a chain of n-viscoelastic links, interconnected by revolute joints and mounted on a mobile platform, is considered. The coordinate system of every link $(x_i y_i z_i, \hat{{x}}_i \hat{{y}}_i \hat{{z}}_i)$ is attached according to the rules developed in Ref [19]. Figure 1 shows an arbitrary differential element $Q$ of the $i$th link. The position vector of this element with respect to the origin of $x_i y_i z_i$ coordinate system is composed of two components. The first component shows the position of this differential element when the $i$th link is not deformed, and the second component displays the small displacements of this element, which are measured from the undeformed link’s centerline. So,

$$\begin{aligned} { }^i\vec {r}_{Q/O_i } =\eta _i { }^i\vec {x}_i +\left\{ {{\begin{array}{lll} {u_i }&{} {v_i }&{} {w_i } \\ \end{array} }} \right\} ^{T} \end{aligned}$$

(1)

where ${ }^i\vec {x}_i =\left\{ {{\begin{array}{lll} 1&{} 0&{} 0 \\ \end{array} }} \right\} ^{T}$, $\eta _i$ is the distance between point $O_i$ and differential element $Q$ (when link $i$ is not deformed) and $u_i$, $v_i$ and $w_i$ are the small displacements in the $O_i x_i$, $O_i y_i$ and $O_i z_i$ directions, respectively. By using the AMM, these small displacements can be presented as

$$\begin{aligned} \left\{ {{\begin{array}{lll} {u_i }&{} {v_i }&{} {w_i } \\ \end{array} }} \right\} ^{T}=\sum _{j=1}^{m_i } {\delta _{ij} \left( t \right) \vec {r}_{ij} \left( \eta \right) } \end{aligned}$$

(2)

where $\vec {r}_{ij} =\left\{ {{\begin{array}{lll} {x_{ij} }&{} {y_{ij} }&{} {z_{ij} } \\ \end{array} }} \right\} ^{T}$ is the eigenfunction vector whose components ($x_{ij}, y_{ij}$ and $z_{ij}$) are the $j$th longitudinal and transverse mode shapes of link $i$; $\delta _{ij}$ is the $j$th time-dependent modal generalized coordinate of link $i$; and $m_i$ is the number of modes used to model the deflection of link $i$.

Fig. 1

Manipulator with mobile platform and flexible links

The total slopes of the deflected link centerline about the $O_i y_i$ and $O_i z_i$ directions, based on TBT, are given by:

$$\begin{aligned}&-\frac{\partial w_i }{\partial \eta } = \theta _{yi} +\phi _{yi}\end{aligned}$$

(3)

$$\begin{aligned}&\frac{\partial v_i }{\partial \eta } = \theta _{zi} +\phi _{zi} \end{aligned}$$

(4)

where $\theta _{yi}$ and $\theta _{zi}$ are the slopes of the deflected centerline due to bending; and $\phi _{yi}$ and $\phi _{zi}$ are the slopes of the deflected centerline due to shear. Shear has no effect on the rotation of differential element $Q$, and this differential element undergoes rotation only because of bending and torsion. So, the rotations of this element in the $O_i x_i$, $O_i y_i$ and $O_i z_i$ directions can be considered as $\theta _{xi}$, $\theta _{yi}$ and $\theta _{zi}$, respectively. These small angles by using the AMM can be represented as

$$\begin{aligned} { }^i\vec {\theta }_i =\left\{ {{\begin{array}{lll} {\theta _{xi} }&{} {\theta _{yi} }&{} {\theta _{zi} } \\ \end{array} }} \right\} ^{T}=\sum _{j=1}^{m_i } {\delta _{ij} \left( t \right) } \vec {\theta }_{ij} \left( \eta \right) \end{aligned}$$

(5)

where $\vec {\theta }_{ij} =\left\{ {{\begin{array}{lll} {\theta _{xij} }&{} {\theta _{yij} }&{} {\theta _{zij} } \\ \end{array} }} \right\} ^{T}$ is the eigenfunction vector, whose components ($\theta _{xij}$, $\theta _{yij}$ and $\theta _{zij}$) are the $j$th rotational mode shapes of link $i$ in the $O_i x_i$, $O_i y_i$ and $O_i z_i$ directions, respectively.

The absolute acceleration of differential element $Q$ expressed in the $i$th body’s local reference system can be presented as

$$\begin{aligned} { }^i\ddot{\vec {r}}_Q&= { }^i\ddot{\vec {r}}_{O_i } +{ }^i\ddot{\vec {r}}_{Q/O_i } +2{ }^i\vec {\omega }_i \times { }^i\dot{\vec {r}}_{Q/O_i } \nonumber \\&\quad +\,{ }^i\dot{\vec {\omega }}_i \times { }^i\vec {r}_{Q/O_i } +{ }^i\vec {\omega }_i \times \left( {{ }^i\vec {\omega }_i \times { }^i\vec {r}_{Q/O_i } } \right) \qquad \end{aligned}$$

(6)

where ${ }^i\ddot{\vec {r}}_{O_i}$ is the absolute acceleration of the origin of the $i$th body’s local reference system and ${ }^i\vec {\omega }_i$ and ${ }^i\dot{\vec {\omega }}_i$ are the angular velocity and acceleration of the $i$th link, respectively. Also ${ }^i\dot{\vec {r}}_{Q/O_i}$ and ${ }^i\ddot{\vec {r}}_{Q/O_i }$ are the velocity and acceleration of differential element $Q$ with respect to the origin of the $i$th body’s local reference system. In Section 4, Eq. (6) will be used to construct the acceleration energy due to links’ motion.

2.2 Kinematics of the mobile platform and driving wheels

The wheeled mobile platform moves on the ground is subjected to two nonholonomic constraints. The no-skidding condition states that the platform has no sideway motion. So, the absolute velocity of point $A$ in the $x_0 y_0 z_0$ coordinate system can be expressed as

$$\begin{aligned} { }^0\vec {v}_A =v_A { }^0\vec {x}_0 \end{aligned}$$

(7)

Also, the angular velocity of the platform is ${ }^0\dot{\vec {\varphi }}=\dot{\varphi }{ }^0\vec {y}_0$, where ${ }^i\vec {y}_i =\left\{ {{\begin{array}{lll} 0&{} 1&{} 0 \\ \end{array} }} \right\} ^{T}$. Now, by using Eq. (7), the absolute acceleration of the platform and wheels’ center of mass (i.e., $G$), can be presented as

$$\begin{aligned} { }^0\dot{\vec {v}}_G =\left( {\dot{v}_A -d\dot{\varphi }^{2}} \right) { }^0\vec {x}_0 -\left( {v_A \dot{\varphi }+d\ddot{\varphi }} \right) { }^0\vec {z}_0 \end{aligned}$$

(8)

where ${ }^i\vec {z}_i =\left\{ {{\begin{array}{lll} 0&{} 0&{} 1 \\ \end{array} }} \right\} ^{T}$, and $d$ is the distance between point $A$ and $G$. In the next section, Eq. (8) will be used to construct the Gibbs’ function for the platform.

As is shown in [20], the angular velocities for the right and left driving wheels $(\dot{\theta }_R, \dot{\theta }_L)$ in terms of $v_A$ and $\dot{\varphi }$ are obtained as

$$\begin{aligned} \dot{\theta }_{R/L} =\frac{1}{r_a }\left( {v_A \pm b\dot{\varphi }} \right) \end{aligned}$$

(9)

where $r_a$ is the radius of the driving wheels and $b$ is the distance between point $A$ and the center of the driving wheels. In the next two sections, Eq. (9) will be used to calculate the Gibbs’ function of the driving wheels and also the generalized forces due to the torques exerted on the right and left driving wheels.

3 Dynamics of the system

3.1 The system’s acceleration energy and its derivatives

The G–A method uses a scalar function in terms of accelerations to derive the equations of motion. The acceleration energy of the mobile manipulator arises from three sources: (1) acceleration energy due to links motion, (2) acceleration energy due to platform motion and (3) acceleration energy due to the rotation of the driving wheels. The Gibbs’ function (acceleration energy) of the manipulator, based on TBT, can be represented as

$$\begin{aligned} S_\mathrm{M} \!=\! \sum _{i=1}^n \int _0^{ l_i } \frac{1}{2} \left[ \mu _i \left( \eta \right) \left( {{ }^i\ddot{\vec {r}}_Q^T \cdot { }^i\ddot{\vec {r}}_Q } \right) \!+\!{ }^i\ddot{\vec {\theta }}_i^T \cdot J_i \left( \eta \right) { }^i\ddot{\vec {\theta }}_i \right] d\eta \nonumber \\ \end{aligned}$$

(10)

where $n$ is the total number of links; $l_i$ is the length of the $i$th link; and $\mu _i \left( \eta \right)$ and $J_i \left( \eta \right)$ are the mass per unit length and mass moment of inertia matrix per unit length of the $i$th link, respectively. By using Eqs. (5) and (6), the total acceleration energy of the manipulator can be evaluated as

$$\begin{aligned} S_\mathrm{M}&= \sum _{i=1}^n {\frac{1}{2}B_{0i} { }^i\ddot{\vec {r}}_{O_i }^T } \cdot { }^i\ddot{\vec {r}}_{O_i } +{ }^i\ddot{\vec {r}}_{O_i }^T \cdot { }^i\vec {B}_{1i} \nonumber \\&\quad -2{ }^i\ddot{\vec {r}}_{O_i }^T \cdot B_{2i} { }^i\vec {\omega }_i -{ }^i\ddot{\vec {r}}_{O_i }^T \cdot B_{3i} { }^i\dot{\vec {\omega }}_i \nonumber \\&\quad -{ }^i\ddot{\vec {r}}_{O_i }^T \cdot { }^i\tilde{\omega }_i B_{3i} { }^i\vec {\omega }_i +\frac{1}{2}B_{4i} -2{ }^i\vec {\omega }_i^T \cdot { }^i\vec {B}_{5i} \nonumber \\&\quad +{ }^i\dot{\vec {\omega }}_i^T \cdot { }^i\vec {B}_{6i} -{ }^i\vec {\omega }_i^T \cdot B_{7i} { }^i\vec {\omega }_i +2{ }^i\dot{\vec {\omega }}_i^T \cdot B_{8i} { }^i\vec {\omega }_i \nonumber \\&\quad +\frac{1}{2}{ }^i\dot{\vec {\omega }}_i^T \cdot B_{9i} { }^i\dot{\vec {\omega }}_i +{ }^i\dot{\vec {\omega }}_i^T \cdot { }^i\tilde{\omega }_i B_{9i} { }^i\vec {\omega }_i \nonumber \\&\quad +\frac{1}{2}B_{10i} +irrelevant\,terms \end{aligned}$$

(11)

where ${ }^i\tilde{\omega }_i$ is the skew-symmetric tensor associated with vector ${ }^i\vec {\omega }_i$. Also, the other variables that appeared in Eq. (11) can be represented as

$$\begin{aligned}&B_{0i} = \int _0^{ l_i } {\mu _i d\eta }\end{aligned}$$

(12)

$$\begin{aligned}&{ }^i\vec {B}_{1i} = \sum _{j=1}^{m_i } {\ddot{\delta }_{ij} } \vec {C}_{1ij}\end{aligned}$$

(13)

$$\begin{aligned}&B_{2i} = \sum _{j=1}^{m_i } {\dot{\delta }_{ij} } \tilde{C}_{1ij}\end{aligned}$$

(14)

$$\begin{aligned}&B_{3i} = C_{2i} +\sum _{j=1}^{m_i } {\delta _{ij} } \tilde{C}_{1ij}\end{aligned}$$

(15)

$$\begin{aligned}&B_{4i} = \sum _{j=1}^{m_i } {\sum _{k=1}^{m_i } {\ddot{\delta }_{ij} \ddot{\delta }_{ik} C_{3ijk} } }\end{aligned}$$

(16)

$$\begin{aligned}&{ }^i\vec {B}_{5i} = \sum _{j=1}^{m_i } {\sum _{k=1}^{m_i } {\ddot{\delta }_{ij} \dot{\delta }_{ik} \vec {C}_{4ijk} } }\end{aligned}$$

(17)

$$\begin{aligned}&{ }^i\vec {B}_{6i} = \sum _{j=1}^{m_i } {\ddot{\delta }_{ij} \vec {\alpha }_{ij} }\end{aligned}$$

(18)

$$\begin{aligned}&B_{7i} = \sum _{j=1}^{m_i } {\ddot{\delta }_{ij} } \beta _{ij}\end{aligned}$$

(19)

$$\begin{aligned}&B_{8i} = \sum _{j=1}^{m_i } {\dot{\delta }_{ij} } \beta _{ij}\end{aligned}$$

(20)

$$\begin{aligned}&B_{9i} = C_{5i} +\sum _{j=1}^{m_i } {\delta _{ij} \left( {C_{6ij}^T +\beta _{ij} } \right) }\end{aligned}$$

(21)

$$\begin{aligned}&B_{10i} = \sum _{j=1}^{m_i } {\sum _{k=1}^{m_i } {\ddot{\delta }_{ij} \ddot{\delta }_{ik} } } C_{7ijk} \end{aligned}$$

(22)

In Eq. (11), there is a term which is called “irrelevant terms.” In fact, in the Gibbs’ function, the terms that are not functions of quasi-accelerations can be ignored, because the partial derivatives of these terms with respect to $\ddot{q}_j$ and $\ddot{\delta }_{jf}$ are equal to zero. In the above equations, $\tilde{C}_{1ij}$ is the skew-symmetric tensor associated with vector $\vec {C}_{1ij}$. This vector and all the other variables appearing in Eqs. (12) through (22) can be expressed as

$$\begin{aligned}&\vec {C}_{1ij} = \int _0^{ l_i } {\mu _i \vec {r}_{ij} d\eta }\end{aligned}$$

(23)

$$\begin{aligned}&C_{2i} = \int _0^{ l_i } {\mu _i \tilde{\eta }d\eta }\end{aligned}$$

(24)

$$\begin{aligned}&C_{3ijk} = \int _0^{ l_i } {\mu _i \vec {r}_{ij}^T \cdot \vec {r}_{ik} d\eta }\end{aligned}$$

(25)

$$\begin{aligned}&\vec {C}_{4ijk} = \int _0^{ l_i } {\mu _i \tilde{r}_{ij} \vec {r}_{ik} d\eta }\end{aligned}$$

(26)

$$\begin{aligned}&C_{5i} = \int _0^{ l_i } {\mu _i \tilde{\eta }^{T}\tilde{\eta }d\eta }\end{aligned}$$

(27)

$$\begin{aligned}&C_{6ij} = \int _0^{ l_i } {\mu _i \tilde{\eta }^{T}\tilde{r}_{ij} d\eta }\end{aligned}$$

(28)

$$\begin{aligned}&C_{7ijk} = \int _0^{l_i } {\vec {\theta }_{ij}^T \cdot J_i \vec {\theta }_{ik} d\eta }\end{aligned}$$

(29)

$$\begin{aligned}&\vec {C}_{8ij} = \int _0^{ l_i } {\mu _i \tilde{\eta } \vec {r}_{ij} d\eta }\end{aligned}$$

(30)

$$\begin{aligned}&C_{9ijk} = \int _0^{ l_i } {\mu _i \tilde{r}_{ij}^T \tilde{r}_{ik} d\eta }\end{aligned}$$

(31)

$$\begin{aligned}&\vec {\alpha }_{ij}= \vec {C}_{8ij} +\sum _{k=1}^{m_i } {\delta _{ik} } \vec {C}_{4ikj}\end{aligned}$$

(32)

$$\begin{aligned}&\beta _{ij} = C_{6ij} +\sum _{k=1}^{m_i } {\delta _{ik} } C_{9ikj} \end{aligned}$$

(33)

where $\tilde{\eta }$ and $\tilde{r}_{ij}$ are the skew-symmetric tensors associated with vectors $\vec {\eta }$ and $\vec {r}_{ij}$, respectively. Now, the Gibbs’ function (acceleration energy) of the platform and driving wheels will be presented as

$$\begin{aligned} S_\mathrm{P} +S_\mathrm{W}&= \frac{1}{2}M_\mathrm{pw} \left[ {\left( {\dot{v}_A -d\dot{\varphi }^{2}} \right) ^{2}+\left( {v_A \dot{\varphi }+d\ddot{\varphi }} \right) ^{2}} \right] \nonumber \\&\quad \quad +\frac{1}{2}I_\mathrm{pw} \ddot{\varphi }^{2}+\frac{1}{2}I_\mathrm{w} \left( {\ddot{\theta }_R^2 +\ddot{\theta }_L^2 } \right) \end{aligned}$$

(34)

where $M_\mathrm{pw}$ is the total mass of the platform and driving wheels; $I_\mathrm{pw}$ is the total moment of inertia of the platform and driving wheels about a vertical axis passing through the center of mass $G$; and $I_\mathrm{w}$ is the moment of inertia of the right and left driving wheels about the wheels’ axis of revolution. The summation of Eqs. (11) and (34) gives the acceleration energy of the whole system $\left( {S=S_\mathrm{M} +S_\mathrm{P} +S_\mathrm{W}} \right)$. Using the G–A method, the motion equations of the system are achieved by differentiating the Gibbs’s function with respect to quasi-accelerations. Therefore, a set of appropriate independent quasi-velocities should be selected. In this paper, the generalized velocities of joints (i.e., $\dot{q}_i$) modal generalized velocities of the links (i.e., $\dot{\delta }_{ij}$), velocity of point $A$ (i.e., $v_A$) and the platform’s angular velocity (i.e., $\dot{\varphi }$) are selected as quasi-velocities. So,

• Partial derivative of Gibbs’ function with respect to $\ddot{q}_j$:

  $$\begin{aligned} \frac{\partial S}{\partial \ddot{q}_j }&= \sum _{i=j+1}^n {\frac{\partial { }^i\ddot{\vec {r}}_{O_i }^T }{\partial \ddot{q}_j }} \cdot \left( B_{0i} { }^i\ddot{\vec {r}}_{O_i } +{ }^i\vec {B}_{1i} \right. \nonumber \\&\quad \left. -2B_{2i} { }^i\vec {\omega }_i -B_{3i} { }^i\dot{\vec {\omega }}_i -{ }^i\tilde{\omega }_i B_{3i} { }^i\vec {\omega }_i \right) \nonumber \\&\quad +\sum _{i=j}^n {\frac{\partial { }^i\dot{\vec {\omega }}_i^T }{\partial \ddot{q}_j }\cdot } \left( B_{3i} { }^i\ddot{\vec {r}}_{O_i } +{ }^i\vec {B}_{6i} \right. \nonumber \\&\quad \left. +2B_{8i} { }^i\vec {\omega }_i +B_{9i} { }^i\dot{\vec {\omega }}_i +{ }^i\tilde{\omega }_i B_{9i} { }^i\vec {\omega }_i \right) \nonumber \\ \end{aligned}$$

  (35)

• Partial derivative of Gibbs’ function with respect to $\ddot{\delta }_{jf}$:

  $$\begin{aligned} \frac{\partial S}{\partial \ddot{\delta }_{jf} }&= \sum _{i=j+1}^n \frac{\partial { }^i\ddot{\vec {r}}_{O_i }^T }{\partial \ddot{\delta }_{jf} }\cdot \left( B_{0i} { }^i\ddot{\vec {r}}_{O_i } +{}^i\vec {B}_{1i} \right. \nonumber \\&\qquad \left. -2B_{2i} { }^i\vec {\omega }_i -B_{3i} { }^i\dot{\vec {\omega }}_i -{ }^i\tilde{\omega }_i B_{3i} { }^i\vec {\omega }_i \right) \nonumber \\&\quad + \sum _{i=j+1}^n \frac{\partial { }^i\dot{\vec {\omega }}_i^T }{\partial \ddot{\delta }_{jf} }\cdot \left( B_{3i} { }^i\ddot{\vec {r}}_{O_i } +{ }^i\vec {B}_{6i}\right. \nonumber \\&\qquad \left. +2B_{8i} { }^i\vec {\omega }_i +B_{9i} { }^i\dot{\vec {\omega }}_i +{ }^i\tilde{\omega }_i B_{9i} { }^i\vec {\omega }_i \right) \nonumber \\&\quad + \sum _{k=1}^{m_j } \ddot{\delta }_{jk} \left( {C_{3jfk} +C_{7jfk} } \right) \nonumber \\&\quad -\,2 { }^j\vec {\omega }_j^T \cdot \sum _{k=1}^{m_j } \dot{\delta }_{jk} \vec {C}_{4jfk} -{ }^j\vec {\omega }_j^T \cdot \beta _{jf} { }^j\vec {\omega }_j \nonumber \\&\quad +\,{ }^j\ddot{\vec {r}}_{O_j }^T \cdot \vec {C}_{1jf} +{ }^j\dot{\vec {\omega }}_j^T \cdot \vec {\alpha }_{jf} \end{aligned}$$

  (36)

• Partial derivative of Gibbs’ function with respect to $\dot{v}_A$:

  $$\begin{aligned} \frac{\partial S}{\partial \dot{v}_A }&= \sum _{i=1}^n \frac{\partial { }^i\ddot{\vec {r}}_{O_i }^T }{\partial \dot{v}_A }\cdot \left( B_{0i} { }^i\ddot{\vec {r}}_{O_i } +{ }^i\vec {B}_{1i} \right. \nonumber \\&\left. -\,2B_{2i} { }^i\vec {\omega }_i -B_{3i} { }^i\dot{\vec {\omega }}_i -{ }^i\tilde{\omega }_i B_{3i} { }^i\vec {\omega }_i \right) \nonumber \\&-\,M_\mathrm{pw} d\dot{\varphi }^{2}+\left( {M_\mathrm{pw} +\frac{2I_\mathrm{w} }{r_a^2 }} \right) \dot{v}_A \end{aligned}$$

  (37)

• Partial derivative of Gibbs’ function with respect to $\ddot{\varphi }$:

  $$\begin{aligned} \frac{\partial S}{\partial \ddot{\varphi }}&= \sum _{i=1}^n \frac{\partial { }^i\ddot{\vec {r}}_{O_i }^T }{\partial \ddot{\varphi }}\cdot \left( B_{0i} { }^i\ddot{\vec {r}}_{O_i } +{ }^i\vec {B}_{1i} \right. \nonumber \\&\left. -2B_{2i} { }^i\vec {\omega }_i -B_{3i} { }^i\dot{\vec {\omega }}_i -{ }^i\tilde{\omega }_i B_{3i} { }^i\vec {\omega }_i \right) \nonumber \\&+\,M_\mathrm{pw} d\left( {d\ddot{\varphi }+v_A \dot{\varphi }} \right) \nonumber \\&+\,\sum _{i=1}^n \frac{\partial { }^i\dot{\vec {\omega }}_i^T }{\partial \ddot{\varphi }}\cdot \left( B_{3i} { }^i\ddot{\vec {r}}_{O_i } +{ }^i\vec {B}_{6i} \right. \nonumber \\&\left. +\,2B_{8i} { }^i\vec {\omega }_i +B_{9i} { }^i\dot{\vec {\omega }}_i +{ }^i\tilde{\omega }_i B_{9i} { }^i\vec {\omega }_i \right) \nonumber \\&+\,\left( {I_\mathrm{pw} +2I_\mathrm{w}\frac{b^{2}}{r_a^2 }} \right) \ddot{\varphi } \end{aligned}$$

  (38)

3.2 The system’s potential energy and its derivatives

The sources of the potential energy of the system can be classified as (1) gravity and (2) elastic deformations. The effect of gravity on manipulator can be obtained by inserting ${ }^0\ddot{\vec {r}}_{O_0 } =g{ }^0\vec {y}_0$, where $g$ is the acceleration of gravity. To obtain the strain potential energy for an n-viscoelastic-link robotic manipulator, based on TBT, one may refer to [19], where this function has been represented as

$$\begin{aligned}&V_{ei} = \frac{1}{2}\int _0^{l_i } \left[ kA_i G_i \left( {\phi _{yi}^2 +\phi _{zi}^2 } \right) +E_i I_{yi} \left( {\frac{\partial \theta _{yi} }{\partial \eta }} \right) ^{2} \right. \nonumber \\&\quad \left. +\,E_i I_{zi} \left( {\frac{\partial \theta _{zi} }{\partial \eta }} \right) ^{2} {+E_i A_i \left( {\frac{\partial u_i }{\partial \eta }} \right) ^{2}\!+\!G_i I_{xi} \left( {\frac{\partial \theta _{xi} }{\partial \eta }} \right) ^{2}} \right] d\eta \nonumber \\ \end{aligned}$$

(39)

where $E_i$ and $G_i$ are the Young’s modulus and shear modulus, respectively; $I_{xi}$, $I_{yi}$ and $I_{zi}$ are the area moments of inertia about the $O_i x_i$, $O_i y_i$ and $O_i z_i$ axes, respectively; $A_i$ is the cross-sectional area of the $i$th link, and $k$ is the shear correction factor. By substituting Eqs. (2) and (5) into Eq. (39), the strain potential energy for the whole system will be obtained as

$$\begin{aligned} V_e =\frac{1}{2}\sum _{i=1}^n {\sum _{j=1}^{m_i } {\sum _{k=1}^{m_i} {\delta _{ij} \left( t \right) \delta _{ik} \left( t \right) K_{ijk}}}} \end{aligned}$$

(40)

where

$$\begin{aligned} K_{ijk}&= \int _0^{l_i } \left[ kA_i G_i \left( {\phi _{yij} \phi _{yik} +\phi _{zij} \phi _{zik} } \right) \right. \nonumber \\&\quad +\,E_i I_{yi} \frac{\partial \theta _{yij} }{\partial \eta }\frac{\partial \theta _{yik} }{\partial \eta }+E_i I_{zi} \frac{\partial \theta _{zij} }{\partial \eta }\frac{\partial \theta _{zik} }{\partial \eta }\nonumber \\&\quad \left. {+\,E_i A_i \frac{\partial x_{ij} }{\partial \eta }\frac{\partial x_{ik} }{\partial \eta }+G_i I_{xi} \frac{\partial \theta _{xij} }{\partial \eta }\frac{\partial \theta _{xik} }{\partial \eta }} \right] d\eta \nonumber \\ \end{aligned}$$

(41)

For deriving the equations of motion of this robotic system, the partial derivatives of strain potential energy with respect to quasi-coordinates are needed.

$$\begin{aligned} \frac{\partial V_e }{\partial q_j }&= \frac{\partial V_e }{\partial x_A }=\frac{\partial V_e }{\partial \varphi }=0\end{aligned}$$

(42)

$$\begin{aligned} \frac{\partial V_e }{\partial \delta _{jf} }&= \sum _{k=1}^{m_j } {\delta _{jk} \left( t \right) K_{jkf} } \end{aligned}$$

(43)

It should be noted that $x_A$ is a quasi-coordinate that has no specific physical meaning.

3.3 Rayleigh’s dissipation function of the system and its derivatives

Using the Rayleigh’s dissipation function is an appropriate way of considering the viscous damping forces. For viscous air damping (as external damping), and structural viscoelasticity effect (as internal damping), the Rayleigh’s dissipation function can be obtained from [19] as

$$\begin{aligned}&D_i = \frac{1}{2}\int _0^{l_i } {\gamma \left[ {\left( {\frac{\partial v_i }{\partial t}} \right) ^{2}+\left( {\frac{\partial w_i }{\partial t}} \right) ^{2}} \right] } d\eta \nonumber \\&\quad +\frac{1}{2}\int _0^{l_i } {K_{vi} \left[ {I_{zi} \left( {\frac{\partial ^{3}v_i }{\partial \eta ^{2}\partial t}} \right) ^{2}+I_{yi} \left( {\frac{\partial ^{3}w_i }{\partial \eta ^{2}\partial t}} \right) ^{2}} \right] } d\eta \nonumber \\ \end{aligned}$$

(44)

where $K_{vi}$ is the Kelvin–Voigt damping coefficient of the $i$th link, and $\gamma$ is the air damping coefficient. Again by inserting Eq. (2) into Eq. (44), the Rayleigh’s dissipation function for the whole system will be obtained as

$$\begin{aligned} D=\frac{1}{2}\sum _{i=1}^n {\sum _{j=1}^{m_i } {\sum _{k=1}^{m_i } {\dot{\delta }_{ij} \left( t \right) \dot{\delta }_{ik} \left( t \right) D_{ijk} } } } \end{aligned}$$

(45)

where

$$\begin{aligned}&D_{ijk} = \int _0^{l_i } \gamma \left( {y_{ij} y_{ik} +z_{ij} z_{ik}} \right) d\eta \nonumber \\&\quad +\int _0^{l_i } {K_{vi} } \left( {I_{zi} \frac{\partial ^{2}y_{ij} }{\partial \eta ^{2}}\frac{\partial ^{2}y_{ik} }{\partial \eta ^{2}}+I_{yi} \frac{\partial ^{2}z_{ij} }{\partial \eta ^{2}}\frac{\partial ^{2}z_{ik} }{\partial \eta ^{2}}} \right) d\eta \nonumber \\ \end{aligned}$$

(46)

By taking the partial derivatives of this function with respect to quasi-velocities, the generalized forces due to the internal and external damping will be obtained.

$$\begin{aligned} \frac{\partial D}{\partial \dot{q}_j }&= \frac{\partial D}{\partial v_A }=\frac{\partial D}{\partial \dot{\varphi }}=0\end{aligned}$$

(47)

$$\begin{aligned} \frac{\partial D}{\partial \dot{\delta }_{jf} }&= \sum _{k=1}^{m_j } {\dot{\delta }_{jk} \left( t \right) D_{jkf} } \end{aligned}$$

(48)

3.4 Governing equations of the system

The generalized force $\left( {U_k } \right)$ associated with the $k$th quasi-velocity $\left( {u_k } \right)$ can be calculated as

$$\begin{aligned} U_k&= \sum _{i=1}^n {\frac{\partial \dot{q}_i }{\partial u_k } \tau _i } +\frac{\partial \dot{\theta }_R }{\partial u_k } \tau _R +\frac{\partial \dot{\theta }_L }{\partial u_k } \tau _L \nonumber \\ u_k&= \dot{q}_1, \dot{\delta }_{11}, \ldots , \dot{\delta }_{1m_1 }, \ldots , \dot{q}_n , \dot{\delta }_{n1} , \ldots , \dot{\delta }_{nm_n } , v_A ,\dot{\varphi }\nonumber \\ \end{aligned}$$

(49)

where $\tau _i$ is the external torque exerted on the $i$th joint of the robotic manipulator, and $\tau _R$ and $\tau _L$ are the external torques that applied to the right and left driving wheels, respectively. Now, the complete dynamic equations of motion for mobile robotic manipulators with viscoelastic links, obtained by G–A formulation, can be presented as

• 1. The equation of motion of $j{th}$ joint

  $$\begin{aligned} \frac{\partial S}{\partial \ddot{q}_j }+\frac{\partial D}{\partial \dot{q}_j }+\frac{\partial V_e }{\partial q_j }=\tau _j \quad j=1,2,\ldots \ldots ,n\nonumber \\ \end{aligned}$$

  (50)

• 2. The deflection equation of motion

  $$\begin{aligned}&\frac{\partial S}{\partial \ddot{\delta }_{jf} }+\frac{\partial D}{\partial \dot{\delta }_{jf} }+\frac{\partial V_e }{\partial \delta _{jf} }=0 \nonumber \\&\quad j=1,2,\ldots \ldots ,n;f=1,2,\ldots \ldots ,m_j \end{aligned}$$

  (51)

• 3. The translational motion equation of the platform

  $$\begin{aligned} \frac{\partial S}{\partial \dot{v}_A }+\frac{\partial D}{\partial v_A }+\frac{\partial V_e }{\partial x_A }=\frac{1}{r_a }\left( {\tau _R +\tau _L } \right) \end{aligned}$$

  (52)

• 4. The rotational motion equation of the platform

  $$\begin{aligned} \frac{\partial S}{\partial \ddot{\varphi }}+\frac{\partial D}{\partial \dot{\varphi }}+\frac{\partial V_e }{\partial \varphi }=\frac{b}{r_a }\left( {\tau _R -\tau _L } \right) \end{aligned}$$

  (53)

The above equations are in the inverse dynamic form. In this case, the torques applied by the actuators will be evaluated algebraically, knowing the configuration (position, velocity and acceleration) of the system.

4 Motion equations in forward dynamic form

In the forward dynamic form, the equations of motion should be presented as

$$\begin{aligned} I\left( \Theta \right) \ddot{\vec {\Theta }}=\overrightarrow{Re} \end{aligned}$$

(54)

where $I\left( \Theta \right)$ is the inertia matrix of the whole system, and $\ddot{\vec {\Theta }}$ is the vector of quasi-accelerations. $\overrightarrow{Re}$ denotes the vectors of gravitational, Coriolis, centrifugal forces and also the generalized torques applied to the joints of the robotic manipulator and to the right and left driving wheels. These two vectors can be represented as

$$\begin{aligned} \ddot{\vec {\Theta }}&= \left\{ {\ddot{q}_1 } \quad {\ddot{\delta }_{11} } \quad \cdots \quad {\ddot{\delta }_{1m_1 } } \quad {\ddot{q}_2 } \quad {\ddot{\delta }_{21} } \right. \nonumber \\&\quad \cdots \quad {\ddot{\delta }_{2m_2 } } \quad \cdots \nonumber \\&\quad {\ddot{q}_j } \quad {\ddot{\delta }_{j1} } \quad \cdots \quad {\ddot{\delta }_{jm_j } } \quad \cdots \quad {\ddot{q}_n } \nonumber \\&\quad \left. {\ddot{\delta }_{n1} } \quad \cdots \quad {\ddot{\delta }_{nm_n } } \quad {\dot{v}_A } \quad {\ddot{\varphi }} \right\} ^{T} \end{aligned}$$

(55)

$$\begin{aligned} \overrightarrow{Re}&= \left\{ {Re_{q_1 } } \quad {Re_{\delta _{11}}} \quad \cdots \quad {Re_{\delta _{1m_1 } } } \quad {Re_{q_2}} \quad {Re_{\delta _{21} } } \right. \nonumber \\&\quad \cdots \quad {Re_{\delta _{2m_2 }}} \quad \cdots \nonumber \\&\quad { Re_{q_j } } \quad {Re_{\delta _{j1} } } \quad \cdots \quad {Re_{\delta _{jm_j } } } \quad \cdots \quad {Re_{q_n } } \quad {Re_{\delta _{n1} } } \nonumber \\&\quad \left. \cdots \quad {Re_{\delta _{nm_n } } } \quad {Re_{v_A } } \quad {Re_\varphi }\right\} ^{T} \end{aligned}$$

(56)

where $Re_{q_j}$, $Re_{\delta _{jf}}$, $Re_{v_A}$ and $Re_\varphi$ will be obtained after excluding all the terms in Eqs. (50) through (53) that contain quasi-accelerations.

To accomplish the aims of this section, ${ }^i\ddot{\vec {r}}_{O_i}$ and ${ }^i\dot{\vec {\omega }}_i$ must be written in summation form as

$$\begin{aligned}&{ }^i\ddot{\vec {r}}_{O_i } = { }^i\ddot{\vec {r}}_{O_{s,i} } +{ }^i\ddot{\vec {r}}_{O_{v,i} }\end{aligned}$$

(57)

$$\begin{aligned}&{ }^i\dot{\vec {\omega }}_i = { }^i\dot{\vec {\omega }}_{s,i} +{ }^i\dot{\vec {\omega }}_{v,i} \end{aligned}$$

(58)

where ${ }^i\ddot{\vec {r}}_{O_{s,i}}$ and ${ }^i\dot{\vec {\omega }}_{s,i}$ are those components of ${ }^i\ddot{\vec {r}}_{O_i}$ and ${ }^i\dot{\vec {\omega }}_i$ that contain $\ddot{q}_j$, $\ddot{\delta }_{jf}$, $\dot{v}_A$ and $\ddot{\varphi }$ as quasi-accelerations; while ${ }^i\ddot{\vec {r}}_{O_{v,i}}$ and ${ }^i\dot{\vec {\omega }}_{v,i}$ are those components of ${ }^i\ddot{\vec {r}}_{O_i}$ and ${ }^i\dot{\vec {\omega }}_i$ that do not contain quasi-accelerations. These terms can be represented as

$$\begin{aligned} { }^i\ddot{\vec {r}}_{O_{s,i} }&= \sum _{k=1}^{i-1} {{ }^iR_k \left( {{ }^k\ddot{\vec {r}}_{O_{k+1} /O_k } +{ }^k\dot{\vec {\omega }}_{s,k} \times { }^k\vec {r}_{O_{k+1} /O_k } } \right) } \nonumber \\&\quad \quad +{ }^iR_0 \left( {\dot{v}_A { }^0\vec {x}_0 -d\ddot{\varphi }{ }^0\vec {z}_0 } \right) \end{aligned}$$

(59)

$$\begin{aligned} { }^i\ddot{\vec {r}}_{O_{v,i} }&= \sum _{k=1}^{i-1} {{ }^iR_k } \left( { }^k\vec {\omega }_k \times \left( 2{ }^k\dot{\vec {r}}_{O_{k+1} /O_k } +{ }^k\vec {\omega }_k \right. \right. \nonumber \\&\quad \left. \left. \times { }^k\vec {r}_{O_{k+1} /O_k } \right) +{}^k\dot{\vec {\omega }}_{v,k}\times { }^k\vec {r}_{O_{k+1}/O_k } \right) \nonumber \\&\quad +\,{ }^iR_0 \left( {-d\dot{\varphi }^{2}{ }^0\vec {x}_0 \!+\! g_y { }^0\vec {y}_0 \!-\!v_A \dot{\varphi }{ }^0\vec {z}_0 } \right) \qquad \end{aligned}$$

(60)

$$\begin{aligned} { }^i\dot{\vec {\omega }}_{s,i}&= { }^iR_0 { }^0\vec {y}_0 \ddot{\varphi }+\sum _{k=1}^i {{ }^iR_k } { }^k\vec {z}_k \ddot{q}_k \nonumber \\&+\sum _{k=1}^{i-1} {{ }^iR_k { }^k\ddot{\vec {\theta }}_k } \left( {l_k } \right) \end{aligned}$$

(61)

$$\begin{aligned} { }^i\dot{\vec {\omega }}_{v,i}&= \sum _{k=0}^{i-1} {{ }^iR_k } \left( {{ }^k\vec {\omega }_k +{ }^k\dot{\vec {\theta }}_k \left( {l_k } \right) } \right) \nonumber \\&\times { }^iR_{k+1} { }^{k+1}\vec {z}_{k+1} \dot{q}_{k+1} \nonumber \\&+\sum _{k=1}^{i-1} {{ }^iR_k } \left( {{ }^k\vec {\omega }_k \times { }^k\dot{\vec {\theta }}_k \left( {l_k } \right) } \right) \end{aligned}$$

(62)

where ${ }^jR_i$ is a compound rotation matrix which shows the orientation of the $i$th body’s local reference system $(x_i y_i z_i)$ with respect to the $j$th one $(x_j y_j z_j)$. This compound rotation matrix can be recursively represented as

$$\begin{aligned} { }^jR_i ={ }^jR_{i-1} {E}'_{i-1} {A}'_i \end{aligned}$$

(63)

where ${A}'_i$ is the rotation matrix of the $i$th joint, which indicates the orientation of the $x_i y_i z_i$ coordinate system with respect to the $\hat{{x}}_{i-1} \hat{{y}}_{i-1} \hat{{z}}_{i-1}$. This matrix can be represented by dot products of pairs of unit vectors as

$$\begin{aligned} {A}'_i =\left[ {{\begin{array}{l@{\quad }l@{\quad }l} {x_i \cdot \hat{{x}}_{i-1} }&{} {y_i \cdot \hat{{x}}_{i-1} }&{} {z_i \cdot \hat{{x}}_{i-1} } \\ {x_i \cdot \hat{{y}}_{i-1} }&{} {y_i \cdot \hat{{y}}_{i-1} }&{} {z_i \cdot \hat{{y}}_{i-1} } \\ {x_i \cdot \hat{{z}}_{i-1} }&{} {y_i \cdot \hat{{z}}_{i-1} }&{} {z_i \cdot \hat{{z}}_{i-1} } \\ \end{array} }} \right] \end{aligned}$$

(64)

Also, ${E}'_i$ is the rotation matrix of the $i$th link, which shows the orientation of the $\hat{{x}}_i \hat{{y}}_i \hat{{z}}_i$ coordinate system with respect to the $x_i y_i z_i$. Like ${A}'_i$, this matrix is also composed of dot products of pairs of unit vectors; but because of the small angles between these vectors ($\theta _{xi}$, $\theta _{yi}$ and $\theta _{zi})$, ${E}'_i$ can be exactly represented as

(65)

where $C\theta =\cos \theta$ and $S\theta =\sin \theta$. Now, the partial derivatives of ${ }^i\ddot{\vec {r}}_{O_i}$ and ${ }^i\dot{\vec {\omega }}_i$ with respect to quasi-accelerations can be expressed as

$$\begin{aligned} \frac{\partial { }^i\dot{\vec {\omega }}_i }{\partial \ddot{q}_j }&= { }^iR_j { }^j\vec {z}_j\end{aligned}$$

(66)

$$\begin{aligned} \frac{\partial { }^i\ddot{\vec {r}}_{O_i } }{\partial \ddot{q}_j }&= { }^iR_j { }^j\vec {z}_j \times { }^i\vec {r}_{O_i/O_j }\end{aligned}$$

(67)

$$\begin{aligned} \frac{\partial { }^i\dot{\vec {\omega }}_i }{\partial \ddot{\delta }_{jf} }&= { }^iR_j \vec {\theta }_{jf} (l_j )\end{aligned}$$

(68)

$$\begin{aligned} \frac{\partial { }^i\ddot{\vec {r}}_{O_i } }{\partial \ddot{\delta }_{jf} }&= { }^iR_j \vec {r}_{jf} (l_j )+{ }^iR_j \vec {\theta }_{jf} (l_j )\times { }^i\vec {r}_{O_i /O_{j+1} }\end{aligned}$$

(69)

$$\begin{aligned} \frac{\partial { }^i\dot{\vec {\omega }}_i }{\partial \ddot{\varphi }}&= { }^iR_0 { }^0\vec {y}_0\end{aligned}$$

(70)

$$\begin{aligned} \frac{\partial { }^i\ddot{\vec {r}}_{O_i } }{\partial \ddot{\varphi }}&= -{ }^iR_0 d{ }^0\vec {z}_0 +{ }^iR_0 { }^0\vec {y}_0 \times { }^i\vec {r}_{O_i /O_1 }\end{aligned}$$

(71)

$$\begin{aligned} \frac{\partial { }^i\ddot{\vec {r}}_{O_i } }{\partial \dot{v}_A }&= { }^iR_0 { }^0\vec {x}_0 \end{aligned}$$

(72)

4.1 Inertia matrix

To obtain the coefficients of the inertia matrix, Eqs. (66) through (72) and also Eqs. (57) and (58) should be substituted into Eqs. (50) through (53). Keeping all the terms, which have quasi-accelerations ($\ddot{q}_k$, $\ddot{\delta }_{kt}$, $\dot{v}_A$ and $\ddot{\varphi }$) as their coefficients on the left-hand side, and arranging them in a matrix form, will yield to the inertia matrix of the whole system. The details of the above procedure will be explained in the following.

The coefficients of quasi-accelerations in the joint equations of motion: In Eq. (50), all the terms that have $\ddot{q}_k$, $\ddot{\delta }_{kt}$, $\dot{v}_A$ and $\ddot{\varphi }$ as their coefficients can be grouped as

$$\begin{aligned}&\left( \sum _{k=1}^n {{ }^j\vec {z}_j^T \cdot \left( {{ }^j\sigma _k -{ }^j\psi _k } \right) { }^k\vec {z}_k }\right. \nonumber \\&\quad \left. -\sum _{k=1}^{n-1} {{ }^j\vec {z}_j^T \cdot { }^jU_k { }^k\vec {z}_k } \right) \ddot{q}_k\nonumber \\&\quad +\left( \begin{array}{l} \sum \limits _{k=1}^{n-1} {\sum \limits _{t=1}^{m_k } {{ }^j\vec {z}_j^T \cdot \left( {{ }^j\sigma _{k^{+}} -{ }^j\psi _{k^{+}} } \right) \vec {\theta }_{kt} }} \\ +\sum \limits _{k=1}^{n-1} {\sum \limits _{t=1}^{m_k } {{ }^j\vec {z}_j^T \cdot \left( {{ }^j\xi _{k^{+}} +{ }^j\gamma _k } \right) \vec {r}_{kt}} } \\ -\sum \limits _{k=1}^{n-2} {\sum \limits _{t=1}^{m_k } {{ }^j\vec {z}_j^T \cdot { }^jU_{k^{+}} \vec {\theta }_{kt} } }\\ +\sum \limits _{k=j+1}^n \sum \limits _{t=1}^{m_k } { }^j\vec {z}_j^T \cdot { }^j\tilde{r}_{O_k /O_j } { }^jR_k \vec {C}_{1kt} \\ +\sum \limits _{k=j}^n {\sum \limits _{t=1}^{m_k } {{ }^j\vec {z}_j^T \cdot { }^jR_k \vec {\alpha }_{kt} } } \\ \end{array}\right) \ddot{\delta }_{kt} \nonumber \\&\quad +\left( {{ }^j\vec {z}_j^T \cdot \left( {{ }^j\xi _{0^{+}} +{ }^j\gamma _0 } \right) { }^0\vec {x}_0 } \right) \dot{v}_A \nonumber \\&\quad +\left( { }^j\vec {z}_j^T \cdot \left( {{ }^j\sigma _{0^{+}} -{ }^j\psi _{0^{+}} -{ }^jU_{0^{+}} } \right) { }^0\vec {y}_0 \right. \nonumber \\&\quad \left. -\,{ }^j\vec {z}_j^T \cdot d\left( {{ }^j\xi _{0^{+}} +{ }^j\gamma _0 } \right) { }^0\vec {z}_0 \right) \ddot{\varphi } \end{aligned}$$

(I)

where

$$\begin{aligned} { }^j\sigma _k&= \sum _{i=\max (k,j)}^n {{ }^jR_i B_{9i} { }^iR_k }\end{aligned}$$

(73)

$$\begin{aligned} { }^j\psi _k&= \sum _{i=\max (k,j+1)}^n {{ }^j\tilde{r}_{O_i /O_j } { }^jR_i B_{3i} { }^iR_k }\end{aligned}$$

(74)

$$\begin{aligned} { }^jU_k&= \sum _{t=k}^{n-1} {\left( {{ }^j\gamma _t +{ }^j\xi _{t^{+}} } \right) { }^t\tilde{r}_{O_{t+1} /O_t } { }^tR_k}\end{aligned}$$

(75)

$$\begin{aligned} { }^j\sigma _{k^{+}}&= \sum _{i=\max (k+1,j)}^n {{ }^jR_i B_{9i} { }^iR_k }\end{aligned}$$

(76)

$$\begin{aligned} { }^j\psi _{k^{+}}&= \sum _{i=\max (k+1,j+1)}^n {{ }^j\tilde{r}_{O_i /O_j } { }^jR_i B_{3i} { }^iR_k }\end{aligned}$$

(77)

$$\begin{aligned} { }^jU_{k^{+}}&= \sum _{t=k+1}^{n-1} {\left( {{ }^j\gamma _t +{ }^j\xi _{t^{+}} } \right) { }^t\tilde{r}_{O_{t+1} /O_t } { }^tR_k }\end{aligned}$$

(78)

$$\begin{aligned} { }^j\xi _{k^{+}}&= \sum _{i=\max (k+1,j)}^n {{ }^jR_i B_{3i} { }^iR_k }\end{aligned}$$

(79)

$$\begin{aligned} { }^j\gamma _t&= \sum _{i=\max (t+1,j+1)}^n {{ }^j\tilde{r}_{O_i /O_j } B_{0i} { }^jR_t } \end{aligned}$$

(80)

In Fig. 2, that part of the inertia matrix of the whole system, constructed by Exp. (I), is determined by 1, 2, 3 and 4 for $\ddot{q}_k$, $\ddot{\delta }_{kt}$, $\dot{v}_A$ and $\ddot{\varphi }$, respectively. By writing Exp. (I) in matrix form, we can see that a symmetric matrix is generated. This fact can be used to more quickly build the inertia matrix of the whole system.

Fig. 2

The inertia matrix of n-viscoelastic-link robotic manipulator on a mobile base

The coefficients of quasi-accelerations in the deflection equations of motion: Since the inertia matrix of the whole system is symmetric, the coefficient of $\ddot{q}_j$ in Eq. (51) is the same as the coefficient of $\ddot{\delta }_{jf}$ in Exp. (I). But the coefficients of the other quasi-accelerations can be represented as

$$\begin{aligned}&\left( {\begin{array}{l} \sum _{k=1}^{n-1} {\sum _{t=1}^{m_k } {\vec {\theta }_{jf}^T \cdot \left( {{ }^{j^{+}}\sigma _{k^{+}} -{ }^{j^{+}}\psi _{k^{+}} } \right) \vec {\theta }_{kt} } } \\ -\sum _{k=1}^{n-2} {\sum _{t=1}^{m_k } {\vec {\theta }_{jf}^T \cdot { }^{j^{+}}U_{k^{+}} \vec {\theta }_{kt}} }\\ -\sum _{k=1}^{n-2} {\sum _{t=1}^{m_k } {\vec {r}_{jf}^T \cdot { }^jV_k \vec {\theta }_{kt} } } \\ -\sum _{k=1}^{n-1} \sum _{t=1}^{m_k } \vec {r}_{jf}^T \cdot { }^{j^{+}}\xi _{k^{+}} \vec {\theta }_{kt} \\ -\sum _{k=1}^{j-2} {\sum _{t=1}^{m_k } {\vec {C}_{1jf}^T \cdot { }^jW_k \vec {\theta }_{kt} } } \\ +\sum _{k=1}^{j-1} {\sum _{t=1}^{m_k } {\vec {\alpha }_{jf}^T \cdot { }^jR_k \vec {\theta }_{kt} } } \\ +\sum _{k=1}^{n-1} \sum _{t=1}^{m_k } \vec {\theta }_{jf}^T \cdot \left( {{ }^{j^{+}}\gamma _k +{ }^{j^{+}}\xi _{k^{+}} } \right) \vec {r}_{kt} \\ +\sum _{k=1}^{n-1} \sum _{t=1}^{m_k } \vec {r}_{jf}^T \cdot { }^j\lambda _k \vec {r}_{kt}\\ +\sum _{k=1}^{j-1} {\sum _{t=1}^{m_k } {\vec {C}_{1jf}^T \cdot { }^jR_k \vec {r}_{kt} } } \\ +\sum _{k=j+1}^n \sum _{t=1}^{m_k } \vec {r}_{jf}^T \cdot { }^jR_k \vec {C}_{1kt} \\ +\sum _{k=j+2}^n \sum _{t=1}^{m_k } \vec {\theta }_{jf}^T \cdot { }^j\tilde{r}_{O_k /O_{j+1} } { }^jR_k \vec {C}_{1kt}\\ +\sum _{k=j+1}^n {\sum _{t=1}^{m_k } {\vec {\theta }_{jf}^T \cdot { }^jR_k \vec {\alpha }_{kt} } } \\ +\sum _{t=1}^{m_k } {\left( {C_{3kft} +C_{7kft} } \right) } \\ \end{array}} \right) \ddot{\delta }_{kt} \nonumber \\&\quad +\,\left( \vec {r}_{jf}^T \cdot { }^j\lambda _0 { }^0\vec {x}_0 +\vec {\theta }_{jf}^T \cdot \left( {{ }^{j^{+}}\gamma _0 +{ }^{j^{+}}\xi _{0^{+}} } \right) { }^0\vec {x}_0 \right. \nonumber \\&\qquad \left. +\,\vec {C}_{1jf}^T \cdot { }^jR_0 { }^0\vec {x}_0 \right) \dot{v}_A \nonumber \\&\quad +\,\left( {\begin{array}{l} \vec {\theta }_{jf}^T \cdot \left( {{ }^{j^{+}}\sigma _{0^{+}} -{ }^{j^{+}}\psi _{0^{+}} -{ }^{j^{+}}U_{0^{+}} } \right) { }^0\vec {y}_0\\ -\vec {\theta }_{jf}^T \cdot \left( {{ }^{j^{+}}\gamma _0 +{ }^{j^{+}}\xi _{0^{+}} } \right) d{ }^0\vec {z}_0 -\vec {r}_{jf}^T \cdot { }^j\lambda _0 d{ }^0\vec {z}_0 \\ -\vec {C}_{1jf}^T \cdot { }^jR_0 d{ }^0\vec {z}_0 -\vec {C}_{1jf}^T \cdot { }^jW_0 { }^0\vec {y}_0 \\ +\vec {\alpha }_{jf}^T \cdot { }^jR_0 { }^0\vec {y}_0 -\vec {r}_{jf}^T \cdot \left( {{ }^jV_0 +{ }^{j^{+}}\xi _{0^{+}} } \right) { }^0\vec {y}_0 \\ \end{array}} \right) \ddot{\varphi }\nonumber \\ \end{aligned}$$

(II)

where

$$\begin{aligned}&{ }^{j^{+}}\sigma _{k^{+}} = \sum _{i=\max (k+1,j+1)}^n {{ }^jR_i B_{9i} { }^iR_k }\end{aligned}$$

(81)

$$\begin{aligned}&{ }^{j^{+}}\xi _{k^{+}} = \sum _{i=\max (k+1,j+1)}^n {{ }^jR_i B_{3i} { }^iR_k }\end{aligned}$$

(82)

$$\begin{aligned}&{ }^jV_k = \sum _{t=k+1}^{n-1} {{ }^j\lambda _t { }^t\tilde{r}_{O_{t+1} /O_t } { }^tR_k }\end{aligned}$$

(83)

$$\begin{aligned}&{ }^{j^{+}}\psi _{k^{+}} = \sum _{i=\max (k+1,j+2)}^n {{ }^j\tilde{r}_{O_i /O_{j+1} } { }^jR_i B_{3i} { }^iR_k }\end{aligned}$$

(84)

$$\begin{aligned}&{ }^{j^{+}}\gamma _k = \sum _{i=\max (k+1,j+2)}^n {{ }^j\tilde{r}_{O_i /O_{j+1} } B_{0i} { }^jR_k }\end{aligned}$$

(85)

$$\begin{aligned}&{ }^jW_k = \sum _{t=k+1}^{j-1} {{ }^jR_t { }^t\tilde{r}_{O_{t+1} /O_t } { }^tR_k }\end{aligned}$$

(86)

$$\begin{aligned}&{ }^{j^{+}}U_{k^{+}} = \sum _{t=k+1}^{n-1} {\left( {{ }^{j^{+}}\gamma _t +{ }^{j^{+}}\xi _{t^{+}} } \right) { }^t\tilde{r}_{O_{t+1} /O_t } { }^tR_k }\end{aligned}$$

(87)

$$\begin{aligned}&{ }^j\lambda _k = \sum _{i=\max (k+1,j+1)}^n {B_{0i} { }^jR_k } \end{aligned}$$

(88)

The position of Exp. (II) in the inertia matrix of the whole system is, respectively, determined by 5, 6 and 7 for $\ddot{\delta }_{kt}$, $\dot{v}_A$ and $\ddot{\varphi }$ (Fig. 2).

The coefficients of quasi-accelerations in the translational motion equation of the platform: Again, by using the symmetric feature of the whole system’s inertia matrix, we can realize that the coefficient of $\ddot{q}_j$ in Eq. (52) is identical to the coefficient of $\dot{v}_A$ in Exp. (I) and also the coefficient of $\ddot{\delta }_{jf}$ in Eq. (52) is the same as the coefficient of $\dot{v}_A$ in Exp. (II). But the coefficients of $\dot{v}_A$ and $\ddot{\varphi }$ can be expressed as

$$\begin{aligned}&\left( {M_\mathrm{tot} +M_\mathrm{pw} +\frac{2I_\mathrm{w} }{r_a^2 }} \right) \dot{v}_A\nonumber \\&\quad -\left( {{ }^0\vec {x}_0^T \cdot \left( {{ }^0V_0 +{ }^0\xi _{0^{+}} } \right) { }^0\vec {y}_0 } \right) \ddot{\varphi } \end{aligned}$$

(III)

where

$$\begin{aligned} M_\mathrm{tot} =\sum _{i=1}^n {B_{0i} } \end{aligned}$$

(89)

Exp. (III) should be written in matrix form. The position of this expression in the inertia matrix of the whole system is shown by 8 and 9 for $\dot{v}_A$ and $\ddot{\varphi }$, respectively.

The coefficients of quasi-accelerations in the rotational motion equation of the platform: In a manner similar to the previous three steps, the below expression will be obtained after grouping all the terms in Eq. (53) that have $\ddot{\varphi }$ as their coefficients.

$$\begin{aligned} \left( {\begin{array}{l} { }^0\vec {z}_0^T \cdot d\left( {{ }^0V_0 +{ }^{0^{+}}\xi _{0^{+}} } \right) { }^0\vec {y}_0 \\ +\,{ }^0\vec {y}_0^T \cdot \left( {{ }^{0^{+}}\sigma _{0^{+}} -{ }^{0^{+}}U_{0^{+}} -{ }^{0^{+}}\psi _{0^{+}} } \right) { }^0\vec {y}_0 \\ -\,{ }^0\vec {y}_0^T \cdot d\left( {{ }^{0^{+}}\gamma _0 +{ }^{0^{+}}\xi _{0^{+}} } \right) { }^0\vec {z}_0 \\ +\,d^{2}\left( {M_\mathrm{pw} +M_\mathrm{tot} } \right) +I_\mathrm{pw} +2I_\mathrm{w} \left( {\frac{b^{2}}{r_a^2 }} \right) \\ \end{array}} \right) \ddot{\varphi } \end{aligned}$$

(IV)

It should be noted that the coefficients of $\ddot{q}_j$, $\ddot{\delta }_{jf}$ and $\dot{v}_A$ in Eq. (53) are the same as the coefficients of $\ddot{\varphi }$ in Exp. (I), Exp. (II) and Exp. (III), respectively. But the position of Exp. (IV) in the inertia matrix of the whole system is determined by 10 for $\ddot{\varphi }$.

As was mentioned above, because of the symmetry of the whole system’s inertia matrix, it is not necessary to evaluate the gray regions of this matrix. This makes the reduction in required mathematical operations for constructing the inertia matrix of the whole system.

4.2 Right-hand side of motion equations

Now, the right-hand side of the governing equations will be obtained in recursive form. To this end, in Eq. (50), all the terms without $\ddot{q}_j$, $\ddot{\delta }_{jf}$, $\dot{v}_A$ and $\ddot{\varphi }$ should be transferred to the right-hand side as

$$\begin{aligned} Re_{q_j }&= \tau _j -\sum _{i=j+1}^n {\frac{\partial { }^i\ddot{\vec {r}}_{O_i }^T }{\partial \ddot{q}_j }} \cdot { }^i\vec {S}_i \nonumber \\&\quad -\sum _{i=j}^n {\frac{\partial { }^i\dot{\vec {\omega }}_i^T }{\partial \ddot{q}_j } \cdot { }^i}\vec {T}_i \end{aligned}$$

(90)

where

$$\begin{aligned} { }^i\vec {S}_i&= B_{0i} { }^i\ddot{\vec {r}}_{O_{v,i} } -2B_{2i} { }^i\vec {\omega }_i \nonumber \\&- \,B_{3i} { }^i\dot{\vec {\omega }}_{v,i} -{ }^i\tilde{\omega }_i B_{3i} { }^i\vec {\omega }_i\end{aligned}$$

(91)

$$\begin{aligned} { }^i\vec {T}_i&= B_{3i} { }^i\ddot{\vec {r}}_{O_{v,i} } +2B_{8i} { }^i\vec {\omega }_i \nonumber \\&+\,B_{9i} { }^i\dot{\vec {\omega }}_{v,i} +{ }^i\tilde{\omega }_i B_{9i} { }^i\vec {\omega }_i \end{aligned}$$

(92)

Substituting Eqs. (66) and (67) into Eq. (90) and converting the obtained equation to a recursive form yields:

$$\begin{aligned} Re_{q_j } =\tau _j -{ }^j\vec {z}_j^T \cdot { }^j\vec {\chi }_j \end{aligned}$$

(93)

where

$$\begin{aligned} { }^j\vec {\chi }_j&= { }^j\vec {T}_j +{ }^j\tilde{r}_{O_{j+1} /O_j } { }^j\vec {\varPhi }_j +{ }^jR_{j+1} { }^{j+1}\vec {\chi }_{j+1}\end{aligned}$$

(94)

$$\begin{aligned} { }^j\vec {\varPhi }_j&= { }^jR_{j+1} \left( {{ }^{j+1}\vec {S}_{j+1} +{ }^{j+1}\vec {\varPhi }_{j+1} } \right) \end{aligned}$$

(95)

In Eq. (51), if the terms that do not have quasi-accelerations as their coefficients are transferred to the right-hand side, the below expression will be obtained.

$$\begin{aligned} Re_{\delta _{jf} }&= Q_{jf} -\sum _{i=j+1}^n {\frac{\partial { }^i\ddot{\vec {r}}_{O_i }^T }{\partial \ddot{\delta }_{jf} }\cdot } { }^i\vec {S}_i \nonumber \\&-\sum _{i=j+1}^n {\frac{\partial { }^i\dot{\vec {\omega }}_i^T }{\partial \ddot{\delta }_{jf} } \cdot { }^i\vec {T}_i } \end{aligned}$$

(96)

where

$$\begin{aligned} Q_{jf}&= -\sum _{k=1}^{m_j } {\left( {\delta _{jk} K_{jkf} +\dot{\delta }_{jk} D_{jkf} } \right) } \nonumber \\&+\, 2{ }^j\vec {\omega }_j^T \cdot \sum _{k=1}^{m_j } {\dot{\delta }_{jk} \vec {C}_{4jfk} } +{ }^j\vec {\omega }_j^T \cdot \beta _{jf} { }^j\vec {\omega }_j \nonumber \\&- \,{ }^j\ddot{\vec {r}}_{O_{v,j} }^T \cdot \vec {C}_{1jf} -{ }^j\dot{\vec {\omega }}_{v,j}^T \cdot \vec {\alpha }_{jf} \end{aligned}$$

(97)

Substituting Eqs. (68) and (69) into Eq. (96) and converting it to a recursive form yields:

$$\begin{aligned} Re_{\delta _{jf} } =Q_{jf} -\vec {r}_{jf}^T \cdot { }^j\vec {\varPhi }_j -\vec {\theta }_{jf}^T \cdot { }^jR_{j+1} { }^{j+1}\vec {\chi }_{j+1} \end{aligned}$$

(98)

In Eq. (52), all the terms that do not have $\ddot{q}_j$, $\ddot{\delta }_{jf}$, $\dot{v}_A$ and $\ddot{\varphi }$ as their coefficients can be grouped as

$$\begin{aligned} Re_{v_A }&= \frac{1}{r_a }\left( {\tau _R +\tau _L } \right) +M_\mathrm{pw} d\dot{\varphi }^{2}\nonumber \\&\quad -\sum _{i=1}^n {\frac{\partial { }^i\ddot{\vec {r}}_{O_i }^T }{\partial \dot{v}_A }\cdot { }^i\vec {S}_i } \end{aligned}$$

(99)

Substituting Eq. (72) into Eq. (99) and changing the obtained equation to a recursive form yields:

$$\begin{aligned} Re_{v_A } =\frac{1}{r_a }\left( {\tau _R +\tau _L } \right) +M_\mathrm{pw} d\dot{\varphi }^{2}-{ }^0\vec {x}_0^T \cdot { }^0\vec {\varPhi }_0 \end{aligned}$$

(100)

And finally in Eq. (53), if all the terms that do not have quasi-accelerations as their coefficients are moved to the right- hand side the following expression will be obtained.

$$\begin{aligned} Re_\varphi&= \frac{b}{r_a }\left( {\tau _R -\tau _L } \right) -M_\mathrm{pw} d\dot{\varphi }v_A \nonumber \\&\quad -\sum _{i=1}^n {\frac{\partial { }^i\ddot{\vec {r}}_{O_i }^T }{\partial \ddot{\varphi }}\cdot { }^i\vec {S}_i } -\sum _{i=1}^n {\frac{\partial { }^i\dot{\vec {\omega }}_i^T }{\partial \ddot{\varphi }}\cdot { }^i\vec {T}_i } \end{aligned}$$

(101)

Inserting Eqs. (70) and (71) into Eq. (101) and changing the resulting equation to a recursive form yields:

$$\begin{aligned} Re_\varphi&= \frac{b}{r_a }\left( {\tau _R -\tau _L } \right) -M_\mathrm{pw} d\dot{\varphi }v_A \nonumber \\&\quad -{ }^0\vec {y}_0^T \cdot { }^0R_1 { }^1\vec {\chi }_1 +d{ }^0\vec {z}_0^T \cdot { }^0\vec {\varPhi }_0 \end{aligned}$$

(102)

Equations (93), (98), (100) and (102) show the recursive form of the right-hand side of the governing equations.

5 Computational complexity of the proposed method

Based on the formulations developed in previous sections, the required mathematical operations for deriving the motion equations by the G–A method for the two dynamic systems, i.e., the n-viscoelastic-link robotic manipulator with fixed base (Ref. [19]), and the one with mobile base (this work), are presented in Table 1.

Table 1 Required mathematical operations based on recursive G–A for two dynamic systems

To compare the computational complexities of these two robotic systems, first, the effect of increasing the number of mode shapes on the mathematical operations needed for deriving the equations of motion will be studied. In this comparison, it is assumed that both of these robotic systems have two links that each of them is flexible $(n=n_f =2)$.

As is shown in Fig. 3, with the increase in the number of mode shapes, the number of mathematical operations needed for deriving the motion equations of both fixed and mobile robotic systems increase. Now, we consider the conditions in which the number of mode shapes is constant $(m=2)$, but the number of flexible links increases.

Fig. 3

Computational complexities of fixed and mobile bases with a constant number of flexible links

Again, as seen in Fig. 4, by increasing the number of flexible links, the number of mathematical operations required for deriving the motion equations increases. Moreover, the number of required mathematical operations for mobile robotic manipulators with viscoelastic links is expected to be higher than that for systems with fixed bases. However, it is shown in [19] that the number of mathematical operations in the recursive G–A method is less than in the recursive Lagrangian method. It is emphasized that even a few savings in multiplications or additions may have a significant effect on the efficiency of the algorithm. As a result, one can satisfactorily apply the algorithm in real-time applications or use less advanced, less expensive computing systems to perform the same work.

Fig. 4

Computational complexities of fixed and mobile bases with constant number of mode shapes

6 Computer simulation

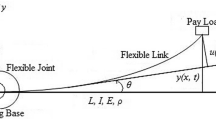
In this section, a simulation is performed according to the proposed formulation. The simulation involves a two-link robotic manipulator with viscoelastic links mounted on a mobile platform (Fig. 5).

Fig. 5

Two-link mobile robotic manipulator with viscoelastic links

To model the elastic properties of each link, the AMM is applied, which has an advantage over the finite element method, because in the latter, a lot of boundary conditions should be considered in order to solve a large set of differential equations. In the mathematical modeling of elastic robotic manipulators by the AMM, the proper selection of mode shapes is an important step for improving the results. In this paper, the eigenfunctions with clamped-free boundary conditions based on the TBT (in which the mode shapes of deflections and rotations are independently obtained) have been adopted [21]. In all the previous works that have considered multiple flexible links, the eigenfunctions are obtained on the basis of the Euler–Bernoulli beam theory in which the rotational mode shapes are acquired by simply differentiating the bending eigenfunctions. These translational and rotational mode shapes are expressed as

$$\begin{aligned} y_{ij}&= C_1 \sin \left( {a \cdot \eta } \right) +C_2 \cos \left( {a \cdot \eta } \right) \nonumber \\&\quad +C_3 \sinh \left( {b \cdot \eta } \right) +C_4 \cosh \left( {b \cdot \eta } \right) \end{aligned}$$

(103)

$$\begin{aligned} \theta _{zij}&= \alpha .C_2 \sin \left( {a \cdot \eta } \right) -\alpha \cdot C_1 \cos \left( {a \cdot \eta } \right) \nonumber \\&\quad +\beta \cdot C_4 \sinh \left( {b \cdot \eta } \right) +\beta \cdot C_3 \cosh \left( {b \cdot \eta } \right) \nonumber \\ \end{aligned}$$

(104)

where $a, b, \alpha , \beta , C_1 , C_2 , C_3 , C_4$ can be found in Table 2.

To explain computational procedure for the simulation clearly, we rewrite Eq. (54) as (Ref. [22]):

$$\begin{aligned} \ddot{\vec {\Theta }}=I^{-1}\left( {\vec {\Theta }} \right) \overrightarrow{Re} \end{aligned}$$

(105)

Converting Eq. (105) in state form yields:

$$\begin{aligned} \dot{\vec {X}}_1&= \vec {X}_2\end{aligned}$$

(106)

$$\begin{aligned} \dot{\vec {X}}_2&= I^{-1}\left( {\vec {X}_1 } \right) \overrightarrow{Re} \end{aligned}$$

(107)

where $\vec {X}_1 =\vec {\Theta }$ and $\vec {X}_2 =\dot{\vec {\Theta }}$. Also the initial conditions are given as

$$\begin{aligned}&q_1 =\dot{q}_1 =\delta _{11} =\dot{\delta }_{11} =q_2 =\dot{q}_2 =\delta _{21} \\&\quad =\dot{\delta }_{21} =x_A =v_A =\varphi =\dot{\varphi } |_{t=0} =0 \end{aligned}$$

All the other necessary parameters for the numerical simulation can be found in Table 3. The time responses of the system are obtained by solving a set of twelve differential equations.

Table 2 The coefficients of translational and rotational mode shapes

Table 3 Required parameters for the simulation of a two-flexible-link mobile robotic manipulator

Figure 6 illustrates the end effector trajectories for both the rigid and flexible links. This figure shows that the time response of the flexible robotic manipulator fluctuates around the time response of its rigid counterpart. This time response can be used to prove the correctness of the obtained recursive formulations in generating the governing equations for these kinds of robotic systems.

Now, to study the effects of damping coefficients, the time response results of the system including the hub angular positions (Figs. 7, 11), hub angular velocities (Figs. 8, 12), modal generalized coordinates (Figs. 9, 13) and the variations of those coordinates with respect to time (Figs. 10, 14) and also the trajectory of the platform in the XY plane (Fig. 15) are presented for each link, and for different values of air damping coefficients and Kelvin–Voigt damping coefficients.

As is observed, with the increase in the value of damping coefficient, vibration amplitude diminishes. In other words, damping coefficient has a negligible effect on the time responses of the system’s large motions, but it greatly influences the time responses of small deflections. To quantitatively analyze this effect, the root-of-mean-square (RMS) value of each joint’s variation (as large motions) and each link’s variation (as small deflections) should be evaluated. The RMS value can be interpreted as the power of a signal. So, as expected, by increasing the damping coefficient, this value decreases for small deflections of links, but it remains almost unchanged for the large motions of joins (Table 4).

Table 4 RMS of the small deflections and large motions of two-viscoelastic-link mobile manipulator

Here, the numerical stability of the proposed method is investigated by using different modulus of elasticity in the simulation of the above-mentioned robotic system. To avoid the loss in accuracy of simulation results, no stabilization method is employed and the simulation results are obtained using the “ode45” function in Matlab v. R2007b software. The time response of the first joint is selected as the representative of the time response of the whole system.

Fig. 6

End effector trajectory in the XYZ Plane

As is observed in Fig. 16, with the reduction in the Young’s modulus of the links, the time response of the system becomes unstable and the numerical stability fails at $E_1 =E_2 =2\times 10^{7}$. Finally, to see whether different Matlab ODE solvers get different results, the governing equations were solved by ODE45, ODE23, ODE23t, ODE23s and ODE15s, but no significant discrepancy was observed.

Fig. 7

Angular position of the first joint

Fig. 8

Angular velocity of the first joint

Fig. 9

Modal generalized coordinate of the first link

Fig. 10

Modal generalized velocity of the first link

Fig. 11

Angular position of the second joint

Fig. 12

Angular velocity of the second joint

Fig. 13

Modal generalized coordinate of the second link

Fig. 14

Modal generalized velocity of the second link

Fig. 15

Platform trajectory in XY plane (point A)

Fig. 16

Angular position of the first joint with different values of Young’s modulus

7 Summery and conclusion

Dynamic modeling of viscoelastic-link robotic arms becomes a complex and challenging task when the number of these robotic arms increases or when the system’s dynamic model is upgraded, which makes the manual derivation of the motion equations practically impossible. Thus, recursive algorithms should be sought that can automatically and systematically derive the equations of motion. In this manuscript, by employing the G–A formulation, a recursive formulation is presented for the automatic and systematic derivation of motion equation of n-viscoelastic-link robotic manipulators that mounted on a mobile platform. The most important characteristic of the recursive formulations presented in this manuscript is the use of the $3\times 3$ rotational matrices instead of the $4\times 4$ transformation matrices, which reduces the computational complexity of the mentioned algorithm. To improve the mathematical modeling of elastic robotic arms, Timoshenko’s beam theory with considering the effects of internal and external damping has been developed. Also, the dynamic interactions between the manipulator and the mobile platform, both nonholonomic constraints associated with no-slipping and no-skidding conditions, and the simultaneous large motion and small deflections of the elastic arms have been considered. So, the proposed formulation can be prepared in the form of a software package to be used in designing and analyzing these robotic systems.