Tamper detection and self-recovery scheme by DWT watermarking

Abstract

We present a tamper detection algorithm based on cat map and discrete wavelet decomposition. The algorithm is fragile to any tampering modification, but it is robust to harmless common image processing operations like JPEG compression, resizing, noising and filtering. The detection algorithm generates a witness image showing the tampered regions based on the blind analysis made on the tampered image. The embedding algorithm uses the approximation coefficient of a $m \times m$ block image as the watermark to be inserted in the details coefficients of another block. The blocks pairs are associated using a cat map permutation of $m \times m$ blocks. Moreover, we have been able to recover most of the original watermarked image based on a threshold depicted from the witness image. Simulations results demonstrate the efficiency of the tamper detection and recovery algorithm. We use many metrics to quantify the imperceptibility level like the PSNR, wPSNR, UIQ and SSIM. Also sensitivity and false alarm levels of the detection algorithm are measured and reported.

1 Introduction

Nowadays with the rapid growth of internet and the popularity of low-cost and high-resolution digital cameras, digital media is playing more and more important role in our daily life whatever it was for personal use or military use in surveillance or spying. In these days, digital media is used even as evidence in court law. However, with the presence of powerful and easy for use editing softwares (as Photoshop), digital media can be easily manipulated without leaving significant clues. So the need of protecting the integrity of these information became more urgent. That is why various authentication schemes have been recently proposed for verifying the integrity of images content. Theses schemes can be classified into three categories: (1) digital signature schemes, (2) image forensic techniques and (3) digital watermarking schemes.

Digital signature schemes can detect whether or not the image has been tampered. They use hash functions combined with public encryption algorithms. However, these schemes cannot locate the exact tampered areas.

Digital image forensic aims at providing tools to support blind investigation. These techniques exploit image processing and analysis tools to recover information about the history of an image. For example, the acquisition process and the tampering techniques leave subtle traces in the image. The task of forensics experts is to expose these traces by exploiting existing knowledge on digital imaging mechanisms, being aided by consolidated results in multimedia security research [13]. Digital image forensic techniques like in [16–19] are often referred to as passive methods since they do not insert any additional information in the image. However, these techniques need a huge database of images captured by different cameras to be able to distinguish between different camera models. It is also needed to distinguish between different exemplars of the same camera model to be able to identify the image source device. And in a second level, it is needed to expose traces of forgeries by studying inconsistencies in natural image statistics. The field of digital image forensic is still growing and seems to be a promising alternative for image authentication and integrity verification.

Digital watermarking schemes like in [4, 7, 8] embed some information in the host image to be protected. The information, called a watermark, can be extracted from the marked image in order to test the integrity of the image.

Many watermarking-based schemes have been proposed. Digital watermarking can be classified into several categories depending on the requirements set forward by a given application type. The main classification is perhaps the one according to the working domain : spatial domain watermarking and transform domain watermarking. Another main classification deals with watermarking algorithm type: robust or fragile or semi-fragile watermarking schemes. Robust watermarking is designed to resist any editing operations or attacks in order to reserve copyright. In the other hand, fragile watermarking is designed to be fragile and sensible to any changes or fraud in order to detect any possible tamper. But in this type of watermarking, several practical problems emerge, for example, its high sensibility even to accidental changes or innocent image editing like compression. The solution remains in using the semi-fragile watermarking instead of fragile one. The semi-fragile watermarking schemes are designed to survive innocent image editing and accidental tamper like noise, but they should be sensible to any possible attacks or attempt of forgery. We can also classify the watermarking techniques according to the extraction technique. Blind detection where the extraction process needs only the watermarked image to extract the embedded mark. Other extraction schemes needs besides the watermarked image the original watermark to extract the embedded one which is called semi-blind detection. We see in this technique a weakness due to the fact that the watermark has to be sent along with the watermarked image.

Chaos theory was used for two decades now in many aspects of security like cryptographic techniques design, watermarking algorithm and data hiding algorithms. The random appearance, the ergodicity, the mixing property and the high sensibility of the chaotic system to initial conditions and parameters are the main properties that attracted researchers to use chaos in the design of their security aspect algorithms. In this paper, we propose a semi-fragile watermark for tamper detection and partial recovery for digital images. We consider the approximation coefficient of the discrete wavelet decomposition as the watermark to be inserted in the remaining detail coefficients. Our scheme uses several chaotic schemes, and it is protected by private keys to embed and extract the watermark. The scheme is totally blind in the detection process, and it gave a great results to locate tampered areas.

The rest of the paper is organized as follows: Sect. 2 presents a brief mathematical preliminary about the cat map and the discrete wavelet transform. The embedding scheme and the tamper detection process are described in Sect. 3. In Sect. 4, we analyze the robustness of the scheme to most common image processing operations. The conclusions are drawn in Sect. 5.

2 Mathematical preliminary

2.1 The generalized cat map

In our experiment, we used the generalized cat map [2, 6, 12] defined by:

$$\begin{aligned} \left[ \begin{array}{c} x_{i+1} \\ y_{i+1} \end{array}\right] = \left( \begin{array}{cc} 1 &{} a \\ b &{} ab+1 \end{array}\right) \left[ \begin{array}{c} x_i \\ y_i \end{array}\right] \, {\hbox {mod}} \, N \end{aligned}$$

(1)

where $\left[ \begin{array}{c} x_{i} \\ y_{i} \end{array}\right]$ is the state vector at index i. $a$ and $b$ are control parameters $\in \mathbb {N}$. The parameter $N\, \in \mathbb {N}$ is the modulo of the map. The cat map has a period $T$ for given parameters $a, b$ and $N$ meaning that

$$\begin{aligned} \left( \begin{array}{cc} 1 &{} a \\ b &{} ab+1 \end{array}\right) ^T \, \equiv \, \left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} 1 \end{array}\right) \, ({\mathrm {mod}} \, N). \end{aligned}$$

In [3], there is a study on finding the period $T$ of the cat map (when $a=b=1$) and on the generalized cat map ($(a,b)\ne (1,1)$). Notations in the article [3] note the period of the cat map as $P(N)$ and the minimal period as ${\varPi }(N)$. Because we need the cat map in our scheme to be used in the permutation processes, we need to avoid weak keys leading to undesirable effect where two valid keys lead to the same results. Hence, we mean by period $T$ the minimal period ${\varPi }(N)$. When we apply the cat map or its variant to images, typical values of $N$ are 512, 256, 128 and 64 because it is related to the size of the image which is often square. In other cases when we deal with non-squared image, we can split it to the desired sized sub-images and apply the permutation via cat map.

The cat map can be used also on blocks of the images rather than pixels like in our proposed algorithm. For example, if we divide a $256 \times 256$ image $P$ on $4 \times 4$ blocks, we generate a matrix $P_b$ of size $64 \times 64$ formed by these blocks. We can apply the cat map on this matrix to permute these blocks. We take as parameters $a=b=1$, and hence $T=48$. We show in Fig. 1 the evolution of this permutation from $k=1$ to $k=T=48$ iterations of the cat map on the $4 \times 4$ blocks of the image Jet.

Fig. 1

Evolution of the cat map iteration on the $4 \times 4$ blocks of the $256 \times 256$ Jet image

2.2 Discrete wavelet transform

The DWT performs a two-dimensional wavelet decomposition with respect to a given wavelet (for example the wavelet $db1$) [5, 9, 10]. The DWT applied to an image leads to an approximation coefficient $cA$ and to three details: horizontal, vertical and diagonal coefficients $cH, cV$ and $cD$. The decomposition algorithm of an image P uses a low decomposition filter Low_D, a high decomposition filter high_D and a downsampling process of the rows and columns of the image.

The inverse discrete wavelet transform (idwt) reconstructs the original image from its coefficients by using an upsampling process and two filters: a low reconstruction filter Low_R and a high reconstruction filter High_R. We have putted in Table 1 some statistics on the coefficient $cA, cH, cV$ and $cD$ for 68 gray scale images from the image database of the Computer Vision Group (CVG) of the University of Granada [1]. The statistics report the mean, the standard deviation (std), of the relative DWT coefficient of 20 selected images from that set. We have plotted the dynamics of these coefficients for 12 different images in Fig. 3. Both Table 1 and Fig. 3 show that the dynamic of the approximation coefficient is wider than the other coefficients. Maximum of the image energy is also concentrated on the approximation coefficient $cA$. The horizontal detail coefficient $cH$ comes second in dynamics and energy. The vertical detail coefficient $cV$ comes third, and the diagonal detail coefficient $cD$ is the last in dynamic and energy. We conclude that the approximation coefficient $cA$ of the image $P$ contains the maximum energy concentration because it was produced from the result of two low filters for rows and columns. And because the information is usually concentrated in low-frequency components, the approximation coefficient is a minimized copy of the original image P. That is why any modification on the approximation coefficient $cA$ will harm the reconstruction of the original image using the idwt.

Fig. 2

12 test images from [1]

Fig. 3

Plot of the dwt coefficients of the images in Fig. 2

Table 1 Statistics of the DWT coefficients for 20 images from [1]

Our watermarking algorithm will take into account these observations about the dwt coefficients. In the next section, we will present the embedding algorithm where we choose to insert a scrambled copy of the approximation coefficient into the detail coefficients.

3 Proposed semi-fragile watermarking and recovery scheme

3.1 Embedding scheme

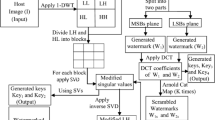
The embedding scheme is graphically described by Fig. 4. Given a gray scale image $P$ of size $M \times M$. Let us say that P is an image of size $M \times M=256 \times 256$. The steps leading to embed the watermark in the details coefficients are described as follows:

• 1. Image decomposition: The image P is decomposed to blocks of size $m\times m$. The number of blocks size is then $\frac{M \times M}{m\times m}$. The result of this decomposition should be a Matrix $P_b$ formed by these blocks with size $\frac{M}{m} \times \frac{M}{m}$. For example, if the size of the original image $P$ is $M \times M=256 \times 256$ and the blocks size is $m\times m= 4 \times 4$, then we will obtain a blocks matrix $P_b$ of size $64 \times 64$.

  Fig. 4

  

  Embedding scheme

• 2. Block permutation: Use the generalized cat map to permute the matrix blocks $P_b$ of size $\frac{M}{m} \times \frac{M}{m}$ to obtain a matrix block $J_b$ with the same size. Hence, the permutation is done as follows:

  $$\begin{aligned} \left[ \begin{array}{c} i' \\ j' \end{array}\right] = \left( \begin{array}{cc} 1 &{} a \\ b &{} ab+1 \end{array}\right) ^k \left[ \begin{array}{c} i \\ j \end{array}\right] \, {\mathrm {mod}} \, \frac{M}{m} \end{aligned}$$

  (2)

  for every $i,j=1,\ldots , \frac{M}{m}$, where $(i,j)$ is the block coordinates of $P_b$ and $(i',j')$ is the permuted block coordinates of $J_b$, for example, for $a=b=1$ and a blocks matrix of size $64 \times 64$ have as period $T=48$. If we choose $k =20$, then the permutation is done as follows :

  $$\begin{aligned} \left[ \begin{array}{c} i' \\ j' \end{array}\right] = \left( \begin{array}{cc} 1 &{} 1 \\ 1 &{} 2 \end{array}\right) ^{20} \left[ \begin{array}{c} i \\ j \end{array}\right] \, {\mathrm {mod}} \, 64 \end{aligned}$$

• 3. DWT decomposition of $P_b$ and $J_b$: For every block in $P_b$ and $J_b$, make a discrete wavelet transform (DWT) decomposition to obtain the approximation coefficient $cA$ and three details coefficients $cH, cV$ and $cD$. In our experiment, we used the Haar wavelet $db1$ to make the DWT. The decomposition can be described as follows:

  $$\begin{aligned}&[cAP,cHP,cVP,cDP] = dwt(P_b(i,j),db1) \\&[cAJ,cHJ,cVJ,cDJ] = dwt(J_b(i,j),db1) \end{aligned}$$

• 4. Embedding each block approximation in the detail coefficients of another block: For each block, We chose to embed the image characteristics contained in the approximation coefficient $cAP$ of each block $P_b(i,j)$ in the detail coefficients $cHJ, cVJ, cDJ$ of the permuted block $J_b(i,j)$. But because the dynamics of $cAP$ is very large compared to the dynamics of the details coefficients and to not degrade the perceptual quality of the image, we need to shrink the dynamic of $cAP_b$ by inserting a minimized copy of $cAP$. This is done as follows:

  $$\begin{aligned} cHJ'&= cHJ+ \frac{cAP-{\mathrm {mean}}(cAP)}{32}-\frac{cDJ}{16} \nonumber \\ cVJ'&= cVJ+ \frac{cAP-{\mathrm {mean}}(cAP)}{32}-\frac{cDJ}{16} \nonumber \\ cDJ'&= cDJ/32 + \frac{{\mathrm {mean}}(cAP)}{64} \cdot Id \nonumber \\&-\frac{16 \cdot cHJ + 16 \cdot cVJ}{64} \end{aligned}$$

  (3)

  with $Id$ is the identity matrix of size $m/2 \times m/2$. And $mean(cAJ)$ is the mean value of the matrix $cAJ$.

• 5. IDWT transformation: For each block, perform the inverse discrete wavelet Transform on the approximation coefficient $cAJ$ of the permuted block $J_b$ and their modified detail coefficients $cHJ', cVJ', cDJ'$ to obtain the corresponding block $J_b'(i,j)$ as follows:

  $$\begin{aligned} J_b'(i,j)=idwt(cAJ,cHJ',cVJ',cDJ',db1) \end{aligned}$$

  (4)

• 6. Inverse cat map permutation: Use the generalized cat map to permute the matrix blocks $J_b'$ of size $\frac{M}{m} \times \frac{M}{m}$ to obtain a matrix block $P_b'$ with the same size. Hence, the permutation is done as follows:

  $$\begin{aligned} \left[ \begin{array}{c} i' \\ j' \end{array}\right]&= \left( \begin{array}{cc} 1 &{} a \\ b &{} ab+1 \end{array}\right) ^{T-k} \left[ \begin{array}{c} i \\ j \end{array}\right] \, {\mathrm {mod}} \, \frac{M}{m} \end{aligned}$$

  (5)

  where $(i,j)$ is the block coordinates of $J_b'$ and $(i',j')$ is the permuted block coordinates of $P_b'$. As an example, $k=20, T=48$ and $\frac{M}{m}=64$, then:

  $$\begin{aligned} \left[ \begin{array}{c} i' \\ j' \end{array}\right]&= \left( \begin{array}{cc} 1 &{} 1 \\ 1 &{} 2 \end{array}\right) ^{28} \left[ \begin{array}{c} i \\ j \end{array}\right] \, {\mathrm {mod}} \, 64 \end{aligned}$$

• 7. Image reconstruction: From the blocks $P_b'(i,j)$ for every $i,j=1,\ldots ,\frac{M}{m}$, reconstruct the watermarked image P’ by combining all the blocks together to form again an image of size $M \times M$.

3.2 Tamper detection and recovery process

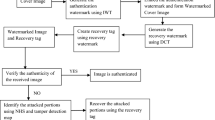
Suppose we have a suspected tampered image $R$ which was previously watermarked by our embedding scheme. If there is no tampering, then $R=P'$. If there is tampering, the next steps describe the tamper detection process and the localization of the tampered regions. The tamper detection and the self-recovery scheme are graphically described by Fig. 5.

• 1. Image decomposition: The image R is decomposed to blocks of size $m\times m$. The number of blocks size is then $\frac{M \times M}{m\times m}$. The result is a $\frac{M}{m} \times \frac{M}{m}$ Matrix $R_b$ formed by blocks of size $m \times m$. For example, if the size of the tampered image $R$ is $M \times M=256 \times 256$ and the blocks size is $m\times m= 4 \times 4$, then we will obtain a blocks matrix $R_b$ of size $64 \times 64$.

• 2. Block permutation: Use the generalized cat map to permute k times the matrix blocks $R_b$ of size $\frac{M}{m} \times \frac{M}{m}$ to obtain a matrix block $I_b$ with the same size. Hence, the permutation is done as follows:

  $$\begin{aligned} \left[ \begin{array}{c} i' \\ j' \end{array}\right]&= \left( \begin{array}{cc} 1 &{} a \\ b &{} ab+1 \end{array}\right) ^k \left[ \begin{array}{c} i \\ j \end{array}\right] \, {\mathrm {mod}} \, \frac{M}{m} \end{aligned}$$

  (6)

  where $(i,j)$ is the block coordinates of $R_b$ and $(i',j')$ is the permuted block coordinates of $I_b$. For example for $a=b=1$ and a blocks matrix of size $64 \times 64$, the cat map have as period $T=48$. $k$ should have the same value as in the embedding process which is 20:

  $$\begin{aligned} \left[ \begin{array}{c} i' \\ j' \end{array}\right]&= \left( \begin{array}{cc} 1 &{} 1 \\ 1 &{} 2 \end{array}\right) ^{20} \left[ \begin{array}{c} i \\ j \end{array}\right] \, {\mathrm {mod}} \, 64 \end{aligned}$$

• 3. DWT decomposition of $R_b$ and $I_b$: For every block in $R_b$ and $I_b$, make a Discrete Wavelet Transform (DWT) decomposition to obtain the approximation coefficient $cA$ and three details coefficients $cH, cV$ and $cD$ as in the embedding process :

  $$\begin{aligned}&[cAR,cHR,cVR,cDR] = dwt(R_b(i,j),db1) \\&[cAI,cHI,cVI,cDI] = dwt(I_b(i,j),db1) \end{aligned}$$

• 4. Estimation of the approximation coefficient $cAP$: For every block, Reconstruct an approximation of $cAP$ noted $\widehat{cAP}$ from the extracted detail coefficients $cHI, cVI, cDI$ as follows:

  $$\begin{aligned} \widehat{cAP}=16 \times cHI + 16 \times cVI + 64 \times cDI \end{aligned}$$

  (7)

  If there is no tampering, then $cHI=cHJ', cVI=cVJ'$ and $cDI=cDJ'$ and consequently,

  $$\begin{aligned} \widehat{cAP}\!=\!cAP\!=\!16 \!\!\times cHJ' \!+\! 16 \times cVJ' \!+\! 64 \times cDJ' \end{aligned}$$

• 5. Construct the approximation coefficient error for each block:

  $$\begin{aligned} cE=\widehat{cAP}- cAR \end{aligned}$$

  (8)

  with $cAR$ is the approximation coefficient of the tampered block $R_b(i,j)$ derived from the third step of the tamper detection process.

• 6. Construction of the error image block: For every block, the error blocks matrix $E_b$ localizing the tampered regions is generated as follows for every $i,j=1,\ldots , \frac{M}{m}$:

  $$\begin{aligned} E_b(i,j)=idwt(cE,[\,],[\,],[\,],db1) \end{aligned}$$

  (9)

  which means performing an inverse discrete wavelet transform from only the approximation coefficient $cE$ and without the details coefficients (horizontal or vertical or diagonal one).

• 7. Inverse cat map permutation: Use the generalized cat map to permute the matrix blocks $E_b$ of size $\frac{M}{m} \times \frac{M}{m}$ to obtain a matrix block $W_b$ with the same size. Hence, the permutation is done as follows:

  $$\begin{aligned} \left[ \begin{array}{c} i' \\ j' \end{array}\right]&= \left( \begin{array}{cc} 1 &{} a \\ b &{} ab+1 \end{array}\right) ^{T-k} \left[ \begin{array}{c} i \\ j \end{array}\right] \, {\mathrm {mod}} \, \frac{M}{m} \end{aligned}$$

  (10)

  where $(i,j)$ is the block coordinates of $E_b$ and $(i',j')$ is the block coordinates of $W_b$. following the example given in the embedding process, $k$ was taken as $20, T=48$ and $\frac{M}{m}=64$, then:

  $$\begin{aligned} \left[ \begin{array}{c} i \\ j \end{array}\right]&= \left( \begin{array}{cc} 1 &{} 1 \\ 1 &{} 2 \end{array}\right) ^{28} \left[ \begin{array}{c} i' \\ j' \end{array}\right] \, {\mathrm {mod}} \, 64 \end{aligned}$$

• 8. Witness image reconstruction: From the blocks $W_b(i,j)$ for every $i,j=1,\ldots ,\frac{M}{m}$, reconstruct the witness image $W$ by combining all the blocks together to form an image of size $M \times M$.

• 9. Recovery of the original watermarked image blocks: For every $W_b(i,j)$ for $i,j=1,\ldots ,\frac{M}{m}$

$$\begin{aligned} \widehat{P_b'(i,j)} \!=\!\left\{ {\begin{array}{ll} idwt(\widehat{cAP},[\,],[\,],[\,],db1) \quad {\mathrm {if}} &{} \sum _{p=1}^m \sum _{r=1}^m W_b(i,j)[p,r] \!\ge \! 255 \!\times \! m \\ R_b(i,j) \quad {\mathrm {if}} &{} \sum _{p=1}^m \sum _{r=1}^m W_b(i,j)[p,r] < 255 \times m \end{array}} \right. \end{aligned}$$

(11)

• 10. Reconstruction of the recovered image: From the blocks $\widehat{P_b'(i,j)}$ for every $i,j=1,\ldots , \frac{M}{m}$, reconstruct the recovered $M\times M$ image $\widehat{P'}$ which constitutes an estimation of the watermarked image $P'$.

Fig. 5

Tamper detection and partial recovery scheme

4 Simulation results

4.1 Imperceptibility evaluation

To evaluate the imperceptibility of the inserted mark in the host image, we experimented the embedding algorithm on the image database in [1]. In Fig. 6, we show the watermarked images of those of Fig. 2 using the embedding algorithm. As can be seen, no visual degradation can be detected by the naked eye. Objective metrics also should be used to confirm this subjective statement. These metrics are as follows:

• 1. PSNR metrics:

  • The peak signal-to-noise ratio (PSNR) evaluates the ratio between the maximum possible power of a signal and the power of corrupting noise that affects this signal. The PSNR is defined as:

    $$\begin{aligned} {\mathrm {PSNR}}=10 \, {\mathrm {log}}_{10} \left( \frac{255^2}{\mathrm {MSE}} \right) \, \, [{\mathrm {dB}}] \end{aligned}$$

    (12)

    with MSE is the mean squared error measured between the original image $x$ and the watermarked image $y$:

    $$\begin{aligned} {\mathrm {MSE}}(x,y)&= \frac{1}{M \times M}\sum _{i=1}^{M}\sum _{j=1}^{M}\nonumber \\&\times \left[ x(i,j)-y(i,j) \right] ^2 \end{aligned}$$

    (13)

    Typical values of PSNR for good quality watermarked images are between 30 and 40 dB (Table 2).

  • The weighted PSNR (wPSNR) : The usual PSNR penalizes the visibility of the inserted mark in all regions of the image in the same way. However, the visibility of noise in flat regions is higher than that in textures and edges [14]. The wPSNR is an adaptation of the usual PSNR because it emulates the human visual system (HVS). wPSNR uses different weights for perceptually different regions instead of the PSNR where all the regions are treated equivalently. wPSNR is given by:

    $$\begin{aligned} w{\mathrm {PSNR}}(x,y)=10 \, {\mathrm {log}}_{10} \left( \frac{255^2}{\mathrm {NVF} \times \mathrm {MSE}} \right) \, \, [{\mathrm {dB}}] \end{aligned}$$

    (14)

    where x and y are the original and the watermarked images and MSE is the mean square error between them defined by Eq. (13) and NVF is the Noise visibility function (NVF) which is used by the wPSNR as a weighting matrix. For flat regions, NVF is close to 1 while for edge or textured regions is more close to 0. Noise visibility function was first proposed in [15], and it is given by:

    $$\begin{aligned} {\mathrm {NVF}}(i,j)= \frac{1}{1+\sigma _x^2(i,j)} \end{aligned}$$

    (15)

    where $\sigma _x^2(i,j)$ denotes the local variance of the image in a window of size $(2L+1)\times (2L+1)$ centered on the pixel with coordinates $(i,j)$:

    $$\begin{aligned} \sigma _x^2(i,j) =\frac{1}{(2L+1)^2}\sum _{k=-L}^{L}\sum _{l=-L}^{L}\nonumber \\ \times \left[ x(i+k,j+l)-\overline{x}(i,j) \right] ^2 \end{aligned}$$

    (16)

    and $\overline{x}(i,j)$ is the mean of that window:

    $$\begin{aligned} \overline{x}(i,j) =\frac{1}{(2L+1)^2}\sum _{k=-L}^{L}\sum _{l=-L}^{L} x(i+k,j+l) \end{aligned}$$

    (17)

    wPSNR value is generally higher than the PSNR value. This is due to the fact that for flat and smooth areas NVF $\simeq$1 hence wPSNR $\simeq$ PSNR. And for textured areas or edges NVF $<$1 then wPSNR $>$ PSNR. And this reflects the fact that HVS will have less sensitivity to modifications in textured areas than smooth areas.

• 2. Watson metric: The Watson model has been adopted in the “Checkmark” [11] and consists on weightening the errors for each DCT coefficient in each block by its corresponding sensitivity threshold which is a function of the contrast sensitivity, luminance masking and contrast masking [14]. The Watson model outputs a total perceptual error (TPE) and two block numbers NB1 and NB2.

  • TPE: The total perceptual error is calculated by pooling errors in the DCT coefficients over space and frequency. The errors are weighted by the corresponding sensitivity threshold of its block. A global threshold $GT$ = 4.1 was adopted to decide whether (TPE $>$ GT) or not (TPE $<$ GT) the watermarked images are as good quality.

  • NB1 : A local perceptual error threshold LT1$=$ 7.6 for blocks of size $16 \times 16$ has been adopted. Blocks that have greater perceptual errors than LT1 may be locally visible. We count the number of these affected blocks and put them in the variable NB1. The lower NB1 will be, the good will be the perceptual quality of the image.

  • NB2: a second local perceptual error threshold LT2 = 30 for blocks of size $16 \times 16$ is also adopted. Blocks that have perceptual error greater than LT2 are potentially affected and they are clearly visible. NB2 contains the numbers of these blocks. If NB2 $>$ 1, the watermarked image is systematically rejected.

• 3. Structural similarity:

  • The Universal Image Quality index (UIQ) [20] measures the structural similarity between two images (original x and watermarked y) and is defined by:

    $$\begin{aligned} {\mathrm {UIQ}}(x,y) =\frac{\sigma _{xy}}{\sigma _x \, \sigma _y} \, \frac{2 \, \overline{x} \, \overline{y}}{\overline{x}^2 + \overline{y}^2} \, \frac{2 \, \sigma _x \, \sigma _y}{\sigma _x^2 + \sigma _y^2} \end{aligned}$$

    (18)

    where $\overline{x}$ and $\overline{y}$ are the mean of x and y respectively. $\sigma _x$ and $\sigma _y$ are the variance of x and y respectively. And $\sigma _{xy}$ is the covariance between x and y. The closer UIQ to 1, the more similar the images x and y.

  • The Structural Similarity Index Measure (SSIM) [21] is an enhanced version of the UIQ and it is defined by :

    $$\begin{aligned} {\mathrm {SSIM}}(x,y) \!=\! \frac{2 \, \overline{x} \, \overline{y} \!+\! C_1}{\overline{x}^2 \!+\! \overline{y}^2\!+\!C_1} \, \frac{2 \, \sigma _x \, \sigma _y \!+\! C_2}{\sigma _x^2 \!+\! \sigma _y^2 \!+\! C_2} \, \frac{\sigma _{xy}\!+\!C_3}{\sigma _x \, \sigma _y \!+\! C_3}\nonumber \\ \end{aligned}$$

    (19)

    where $C_1, C_2$ and $C_3$ are constants parameters. Again the closer is SSIM to 1, the more similar the images x and y will be.

Fig. 6

Watermarked versions of the images in Fig. 2

Table 2 Perceptual similarity between original and watermarked images using various metrics for 20 images

4.2 Tamper detection performance

Tampering modification and Tamper detection performance can be measured using many metrics. Let us define the following quantities:

• True-Positive pixels (TP): the number of tampered pixels correctly identified as tampered.

• False-Positive pixels (FP): the number of unmodified pixels incorrectly identified as tampered.

• True-Negatives pixels (TN): the number of unmodified pixels correctly identified as unmodified.

• False-Negative pixels (FN): the number of tampered pixels incorrectly identified as unmodified.

Then, to quantify the tampering made on the watermarked image, the tampering ratio $\rho$ is defined as :

$$\begin{aligned} \rho =\frac{\textit{FN}+\textit{TP}}{M\times M} \times 100\,\% \end{aligned}$$

The tampering detection accuracy can be measured through two metrics :

• The detection sensitivity or the true-positive rate (TPR): this metric relates to the test’s ability to identify positive results. It is a way to express the probability of correctly identifying the tampered regions. The higher be the TPR, the better will be the result. The TPR is defined as :

  $$\begin{aligned} \textit{TPR}=\frac{\textit{TP}}{\textit{TP}+\textit{FN}} \times 100\,\% \end{aligned}$$

• The false alarm metric or the false-positive rate (FPR): this metric relates to the errors of incorrectly identify unmodified pixels as tampered. It express the probability of the test’s false alarm. The lower be the FPR, the better will be the result. The FPR can be expressed as:

  $$\begin{aligned} \textit{FPR}=\frac{\textit{FP}}{\textit{FP}+\textit{TN}} \times 100\,\% \end{aligned}$$

In Table 3, we give some tamper detection results (FPR and TPR) for six tampered images with different tampering ratios. As been expected, the proposed algorithm should have a moderate (not high nor low: $40\,\% < \textit{TPR} < 80\,\%$) level of TPR because it should be a semi-fragile algorithm and have resilience to some operations. This means that it should have a moderate sensitivity to any modification. In the same time, it should have a low level of FPR (meaning $\textit{FPR} <1\,\%$) giving the minimum false alarm errors.

Table 3 Detection performance of the proposed scheme tested for various images

In Fig. 7, we show in the first column the watermarked images. In the second column we show the manipulated (tampered) images with different tampering ratio $\rho$, we give also the PSNR and SSIM between the watermarked/manipulated images. In the third column, we show the witness images results of the tamper detection made on the manipulated images where we give the TPR and the FPR measuring the accuracy of the detection algorithm. And in the last column, we show the recovered images where we give the PSNR and SSIM compared to the watermarked ones.

Fig. 7

Tamper detection performance

We compare our proposed scheme with others tamper detection schemes in terms of PSNR of the watermarked image, FPR and TPR results of the witness image. Many images were taken to make this experience where the average value of $\rho$ is 8.24 % for the four algorithms. The comparison is made between the following algorithms:

• 1. The proposed algorithm

• 2. Hsu and Tu algorithm presented in [7]

• 3. Chang et al. algorithm presented in [4]

• 4. Lin et al. algorithm presented in [8]

The comparison is made by averaging the resulted values of PSNR, FPR and TPR. The comparison results are drawn in Table 4, and they show that although the proposed algorithm has the worst PSNR of the watermarked image, it has the minimal false alarm rate (FPR) demonstrating the best detection performance. It has also a moderate TPR compared to the other three algorithms. A moderate TPR shows that the proposed algorithm is less sensitive to modifications than the others algorithms which is a desired property for semi-fragile watermarking for tamper detection.

Table 4 Performance comparisons between the proposed scheme and three others algorithms in term of PSNR of the watermarked image, FPR and TPR

4.3 Robustness to most common image processing operations

Although the watermarking algorithm should be fragile to any harmful operation which has as goal to manipulate the image, it should be robust to most common image processing operations which have as goal to fit the image in the user application like resizing, rotating, filtering, compression JPEG or noising in case of noisy transmission channel. These operations can be described as “innocent” operations which do not intend to tamper the image.

We have compressed the watermarked image Lena with different levels of JPEG quality from 100 to 70 %. And every time, the algorithm shows a resilience to this operation which is a very destructive manipulation. For example, a compression JPEG 80 % is equivalent to a tamper modification of ratio $\rho = 79.1\,\%$ compared to the watermarked image. And the algorithm still does not detect a pattern or show an all white image. The recovered image shows no other pattern that does not exist in the compressed image. Of course, in this case, the quality of the compressed image is better than the recovered image. But we made this experience to show that the detection algorithm will not find any pattern showing that the image was illegally modified. This result of this experience is shown in Fig. 8. We have tested the robustness of our algorithm against other common operations showed in Fig. 9, and we found that our algorithm survives most of them. We should mention that before running the detection algorithm on the manipulated image, a pre-treatment on the manipulated image is done to refit the image to the same size or orientation of the watermarked image. For example, if the watermarked image is resized from $256 \times 256$ to $200 \times 200$ then before running the detection algorithm on this image, we should resize it to $256 \times 256$.

Fig. 8

Resilience to JPEG compression. The first column images are the JPEG compresses watermarked images with different qualities, the second column show the corresponding witness images and the third column show the corresponding recovered images

Fig. 9

Resilience to Common Image Processing “innocent” attacks on the watermarked image. The first column shows the attacked watermarked images, the second column shows the corresponding witness images, and the last column shows the corresponding recovered images

5 Conclusion

In this paper, we have presented a tamper detection algorithm which can localize the tampered region by highlighting it for a subjective human recomposition. The algorithm can also regenerate the watermarked image before forgery. The main characteristics of an image block are concentrated in the approximation coefficients $cA$ of its Discrete wavelet decomposition. That is why we choose to consider it as the watermark to be inserted because it will preserve these original characteristics even if the image has been tampered. And because the other remaining coefficients ($cH, cV, cD$) are considered as detail coefficients, they would be the best place were we should insert the watermark $cA$. The insertion of each block approximation coefficient $cA$ is inserted in the detail coefficients of another block. A cat map is used to find this association between each two blocks. The algorithm resist most common image processing operations which cannot be considered as a forgery attack. Users can manipulate some watermarked images to fit their screens and applications, that is why the algorithm should be robust to these “innocent” operations.