1 Introduction

In the past few decades, the study of fractional differential equations [1, 2] attracts many scientists and engineers. For example, He and Luo [3] studied the dynamic behaviors of fractional order Duffing system, and the synchronization of the fractional non-autonomous is obtained based on the stability of linear fractional systems. In Refs. [4, 5], the periodic oscillation of the fractional order nonlinear systems is investigated via the residue harmonic balance method, and the effects of the fractional order and system parameter on the vibration frequency and amplitude are revealed.

Cao et al. [6] used the fourth-order Runge–Kutta method along with tenth-order continued fraction expansion-Euler method to study the nonlinear dynamics of Duffing system with fractional order damping. Recently, the dynamic behaviors of the fractional damped crack rotor system are also simulated in Ref. [7], and the significant effects of fractional order damping and crack on the system dynamic behaviors are confirmed.

Based on the averaging method, Kovacic and Miodrag [8] studied the free oscillators with a power-form restoring and fractional derivative damping. In Refs. [9, 10], the averaging method is also applied to investigate the primary resonance of Duffing oscillator with fractional order derivatives. The equivalent damping and stiffness coefficients are proposed to characterize the influence of fractional order derivatives on the frequency amplitude response behavior. From the above literatures, it can be seen that seeking periodic solutions of nonlinear fractional differential equations remains a significant problem that needs new techniques to develop exact and approximate solutions.

The stability problem of periodic solution is very essential and crucial for nonlinear dynamical system. There are two category approaches to analyze the stability of periodic solutions: time and frequency approaches [11]. A deeper comparison of these stability methods is available in Ref. [12]. Recently, stability analysis is extended to fractional order systems. In Ref. [13], the stability of a linear fractional vibration system of single degree of freedom is analyzed by using the ideal of stability switch. Some other stability results in fractional order systems can be found in Ref. [14].

In structural dynamics, taking into account, uncertainty is important for various reasons: To increase the robustness of design, to ensure the compliance of vibration levels to standards, to assess worst case behavior and so on. In many instances, simulating solutions using a deterministic model may lead to inaccurate computational results. Therefore, any realistic analysis of nonlinear systems must take the uncertainties into account.

Uncertainties are usually described following two different points of view, known as probabilistic and non-probabilistic approaches [15]. The polynomial chaos expansion mixed with the harmonic balance method is used in Ref. [16] to investigate the stochastic stability of a self-excited nonlinear system with friction. Among non-probabilistic methods, the so-called interval analysis method (see e.g., [17]) may be considered as the most attractive analytical tool due to its simplicity.

Sensitivity analysis for the determination of the gradients of objective and constraints is the dominant process in the accuracy and computational time of many optimization problems. In Ref. [18], finite difference technique has been used to determine the gradients of the objective and constraints function. However, finite difference evaluation of gradients may result in inaccurate optimum solution and is also computationally expensive. Therefore, an efficient analytical evaluation of sensitivity gradients is required. The purpose of the present paper was to extend the proposed method to nonlinear fractional differential equations where the derivatives of the objective and constraints function are given.

The rest of this paper is organized as follows: The general formulation of the developed method for determining the periodic solutions is presented in Sect. 2. Demonstrations of the proposed method are then conducted in Sect. 3. Numerical examples are given to validity the effectiveness of the proposed method. Finally, concluding remarks are presented and discussed in Sect. 4.

2 The proposed method

In this section, the constrained optimization harmonic balance method [18] is extended to deal with Duffing oscillator with fractional derivatives. The analytical formulation of the nonlinear equality constraints is derived, and the gradients of the nonlinear equality constraints and the object function are therefore obtained. The deterministic eigenvalue problem and interval eigenvalue problem for assessing the stability of periodic solutions are constructed. In addition, the sensitivity of the Fourier coefficients with respect to the influence parameters can also be calculated. By virtue of the sensitivity information, the bounds of the peak response can be computed by using the interval analysis method.

2.1 System equation of motion

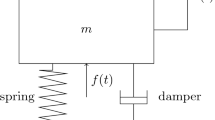
The following equation of motion for the Duffing oscillator with the Caputo fractional derivative terms is considered [9]:

$$\begin{aligned} m\ddot{u}+c\dot{u}+ku+\alpha u^{3}+ {K}_{1} {D}^{p_1 }u+{K}_2 {D}^{p_2 }u=F \hbox {cos}(\omega t) \end{aligned}$$
(1)

where \(m, c, k, \alpha F\) and \(\omega \) are the mass, damping, linear stiffness, nonlinear stiffness, harmonic forcing amplitude and the excitation frequency of oscillation; \(K_{1} ,K_2 \) are the coefficients of the fractional derivative terms with the orders \(p_{1}\) and \(p_{2,}\) respectively; \(u,\dot{u}\) and \(\ddot{u}\) are, respectively, the displacement, velocity, acceleration; the dot denotes differentiation with respect to \(t\).

2.2 Analytical derivations of the nonlinear equality constraints

2.2.1 The evaluation of the nonlinear equality constraints

To derive the proposed method, the harmonic balance method is adopted. In the HBM, \(u(t)\) is represented by a truncated Fourier series:

$$\begin{aligned} u(t)=\mathbf{T}(t)\mathbf{U} \end{aligned}$$
(2)

where \(\mathbf{T}(t)=[1\quad {\hbox {cos}(\omega t)}\quad {\hbox {sin}(\omega t)}\quad \cdots \quad {\hbox {cos}(k\omega t)} {\hbox {sin}(k\omega t)}\!\!\quad \cdots \!\!\quad {\cos (N_\mathrm{H} \omega t)}\!\!\quad {\sin (N_\mathrm{H} \omega t)}]_{1\times (1+2*N_\mathrm{H} )} \) and \(\mathbf{U}=\left[ {{\begin{array}{lllllllll} {U_0 }&{} {U_1^c }&{} {U_1^s }&{} \cdots &{} {U_k^c }&{} {U_k^s }&{} \cdots &{} {U_{N_\mathrm{H} }^c }&{} {U_{N_\mathrm{H} }^s } \\ \end{array} }} \right] ^\mathrm{T}\) represents the Fourier coefficients. Upon introducing the new independent variable \(\tau =\omega t\), the dimensionless form of \(u(t)\) can be written as \(u(\tau )=\mathbf{T}(\tau )\mathbf{U}\) by replacing \(\tau \) with \(\omega t\) in \(\mathbf{T}(t)\).

  1. (1)

    General formula of \(D_t^\ell u(t)\)

The aim in this part is to derive the expression of \(D_t^\ell u(t)\) with any order of \(\ell >0\).

Lemma

The following statements hold for all \(\ell >0\)

$$\begin{aligned} D_t^\ell u(t)=\mathbf{T}(t){\varvec{\nabla }}^{\ell }\mathbf{U} \end{aligned}$$
(3)

where

$$\begin{aligned} {\varvec{\nabla }}^{\ell }&= \mathbf{diag}\left( {0,{\varvec{\nabla }} _1^\ell ,\ldots ,{\varvec{\nabla }}_k^\ell ,\ldots ,{\varvec{\nabla }} _{N_\mathrm{H}}^\ell } \right) , \nonumber \\ {\varvec{\nabla }} _k^\ell&= \left( {k\omega } \right) ^{\ell }\mathbf{R}(\vartheta ),\quad \vartheta =\frac{\ell {\varvec{\uppi }} }{2},\nonumber \\ \quad \mathbf{R}(\theta )&= \left[ {{\begin{array}{ll} {\hbox {cos}(\theta )}&{} {\hbox {sin}(\theta )} \\ {-\hbox {sin}(\theta )}&{} {\hbox {cos}(\theta )} \\ \end{array} }} \right] \end{aligned}$$
(4)

If \(\ell >0\) is an integer, Eq. (3) becomes \(\dot{u}\) and \(\ddot{u}\) which are widely examined.

Proof

The fractional derivatives of \( \hbox {cos}(k\omega t)\) and \( \hbox {sin}(k\omega t)\) are given by [19]

$$\begin{aligned} D_t^{\ell } \left[ {\hbox {cos}(k\omega t)} \right]&= \left( {k\omega } \right) ^{\ell }\hbox {cos}\left( k\omega t+\frac{\ell \pi }{2}\right) ,\nonumber \\ D_t^{\ell } \left[ {\hbox {sin}(k\omega t)} \right]&= \left( {k\omega } \right) ^{\ell }\hbox {sin}\left( k\omega t+\frac{\ell \pi }{2}\right) \end{aligned}$$
(5)

\(\square \)

Then, \(D_t^{\ell } u(t)\) is transformed into the following matrix form:

$$\begin{aligned}&D_t^\ell u(t) \nonumber \\&\quad =\sum \limits _{k=1}^{N_\mathrm{H} } {\left\{ {{U}_k^{c} D_{t}^{\ell } \left[ {\hbox {cos}(k\omega t)} \right] +U_k^{s} D_t^{\ell } \left[ {\hbox {sin}(k\omega t)} \right] } \right\} } \nonumber \\&\quad =\sum \limits _{k=1}^{N_\mathrm{H} } {\left\{ {\left[ {{\begin{array}{ll} {\hbox {cos}(k\omega t)}&{} {\hbox {sin}(k\omega t)} \\ \end{array} }} \right] \left[ {\left( {k\omega } \right) ^{\ell }\mathbf{R}(\vartheta )} \right] \left[ {{\begin{array}{l} {U_k^c } \\ {U_k^s } \\ \end{array} }} \right] } \right\} } \nonumber \\&\quad =\mathbf{T}(t){\varvec{\nabla }} ^{\ell }\mathbf{U} \end{aligned}$$
(6)
  1. (2)

    General formula of \(u^{k}\)

Let \({v}(t)=\mathbf{T}(t)\mathbf{V}\) with \(\mathbf{V}=[ {{V}_0 }\,\, {V_1^c }\,\, {V_1^s }\, \cdots \, {V_k^c }\,\, {V_k^s }\, \cdots {V_{N_\mathrm{H}}^c }\, {V_{N_\mathrm{H} }^s }]^\mathrm{T}\). Using the trigonometric identities, \(u(t)v(t)\) is given as below

$$\begin{aligned} u(t)v(t)&= \left[ {\mathbf{T}(t)\mathbf{U}} \right] ^\mathrm{T}\left[ {\mathbf{T}(t)\mathbf{V}} \right] \nonumber \\&= \left\{ {\mathbf{U}^{T}\left[ {\mathbf{T}(t)} \right] ^\mathrm{T}\left[ {\mathbf{T}(t)} \right] } \right\} \mathbf{V} \nonumber \\&= \left\{ {\mathbf{T}(t)\mathbf{E}(\mathbf{U})} \right\} \mathbf{V} \end{aligned}$$
(7)

where \( \mathbf{E}(\mathbf{U})\) is called operational matrix given as follows

$$\begin{aligned} \mathbf{E}(\mathbf{U})=\left[ {{\begin{array}{lllllllll} {U_0 }&{} {{\varvec{\Upsilon }}_1 }&{} {{\varvec{\Upsilon }}_2 }&{} \ddots &{} {{\varvec{\Upsilon }}_k }&{} \ddots &{} {{\varvec{\Upsilon }}_{{ N}_\mathrm{H} -2} }&{} {{\varvec{\Upsilon }}_{{ N}_\mathrm{H} -1} }&{} {{\varvec{\Upsilon }}_{{ N}_\mathrm{H} } } \\ {\mathbf{H}_1 }&{} {U_0 \mathbf{I}+\mathbf{Q}_2 }&{} {\mathbf{N}_1 +\mathbf{Q}_3 }&{} {\mathbf{N}_2 +\mathbf{Q}_4 }&{} \ddots &{} \ddots &{} \ddots &{} {\mathbf{N}_{{ N}_\mathrm{H} -2} +\mathbf{Q}_{{ N}_\mathrm{H} } }&{} {\mathbf{N}_{{ N}_\mathrm{H} -1} } \\ {\mathbf{H}_2 }&{} {\mathbf{L}_1 +\mathbf{Q}_3 }&{} {U_0 \mathbf{I}+\mathbf{Q}_4 }&{} {\mathbf{N}_1 +\mathbf{Q}_5 }&{} \ddots &{} \ddots &{} {\mathbf{N}_k +\mathbf{Q}_{{ N}_\mathrm{H} } }&{} \ddots &{} {\mathbf{N}_{{ N}_\mathrm{H} -2} } \\ \ddots &{} {\mathbf{L}_2 +\mathbf{Q}_4 }&{} {\mathbf{L}_1 +\mathbf{Q}_5 }&{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} {\mathbf{N}_k }&{} \ddots \\ {\mathbf{H}_k }&{} \ddots &{} \ddots &{} \ddots &{} {U_0 \mathbf{I}+\mathbf{Q}_{{ N}_\mathrm{H} } }&{} {\mathbf{N}_1 }&{} {\mathbf{N}_2 }&{} \ddots &{} {\mathbf{N}_k } \\ \ddots &{} \ddots &{} \ddots &{} {\mathbf{L}_2 +\mathbf{Q}_{{ N}_\mathrm{H} } }&{} {\mathbf{L}_1 }&{} {U_0 \mathbf{I}}&{} {\mathbf{N}_1 }&{} {\mathbf{N}_2 }&{} \ddots \\ {\mathbf{H}_{{ N}_\mathrm{H} -2} }&{} \ddots &{} {\mathbf{L}_k +\mathbf{Q}_{{ N}_\mathrm{H} } }&{} \ddots &{} {\mathbf{L}_2 }&{} {\mathbf{L}_1 }&{} {U_0 \mathbf{I}}&{} {\mathbf{N}_1 }&{} {\mathbf{N}_2 } \\ {\mathbf{H}_{{ N}_\mathrm{H} -1} }&{} {\mathbf{L}_{{ N}_\mathrm{H} -2} +\mathbf{Q}_{{ N}_\mathrm{H} } }&{} \ddots &{} {\mathbf{L}_k }&{} \ddots &{} {\mathbf{L}_2 }&{} {\mathbf{L}_1 }&{} {U_0 \mathbf{I}}&{} {\mathbf{N}_1 } \\ {\mathbf{H}_{{ N}_\mathrm{H} } }&{} {\mathbf{L}_{{ N}_\mathrm{H} -1} }&{} {\mathbf{L}_{{ N}_\mathrm{H} -2} }&{} \ddots &{} {\mathbf{L}_k }&{} \ddots &{} {\mathbf{L}_2 }&{} {\mathbf{L}_1 }&{} {U_0 \mathbf{I}} \\ \end{array} }} \!\right] \end{aligned}$$
(8)

with

$$\begin{aligned} \mathbf{H}_{k}&= \left[ {{\begin{array}{l} {U_k^{c} } \\ {U_k^{s} } \\ \end{array} }} \right] , \quad {\varvec{\Upsilon }}_k =\frac{1}{2}\left[ {{\begin{array}{ll} {U_k^{c} }&{} {U_k^{s} } \\ \end{array} }} \right] ,\\ \mathbf{L}_k&= \frac{1}{2}\left[ {{\begin{array}{ll} {U_k^{c} }&{} {-U_k^{s} } \\ {U_k^{s} }&{} {U_k^{c} } \\ \end{array} }} \right] , \quad \mathbf{N}_k =\frac{1}{2}\left[ {{\begin{array}{ll} {U_k^{c} }&{} {U_k^{s} } \\ {-U_k^{s} }&{} {U_k^{c} } \\ \end{array} }} \right] ,\\ \mathbf{Q}_k&= \frac{1}{2}\left[ {{\begin{array}{ll} {U_k^{c} }&{} {U_k^{s} } \\ {U_k^{s} }&{} {-U_k^{c} } \\ \end{array} }} \right] . \end{aligned}$$

Thus, the polynomial nonlinear terms satisfies the recurrence relation

$$\begin{aligned} u^{k}=\left[ {\mathbf{T}(t)\mathbf{U}} \right] ^\mathrm{T}u^{k-1}=\mathbf{T}(t)\left\{ {[\mathbf{E}(\mathbf{U})]}^{k-1}\mathbf{U} \right\} \end{aligned}$$
(9)

Substituting Eqs. (3) and (9) into Eq. (1) gets

$$\begin{aligned} \mathbf{C}_\mathrm{E} (\mathbf{U})&= \left\{ {\left[ {m{\varvec{\nabla }} ^{2}\mathbf{U}} \right] +\left[ {c{\varvec{\nabla }} \mathbf{U}} \right] +k\mathbf{U}+\alpha [\mathbf{E}(\mathbf{U})]}^{2}\mathbf{U}\right. \nonumber \\&\quad \left. +\,\left[ {K_{1} {\varvec{\nabla }} ^{p_1 }\mathbf{U}} \right] +\left[ {K_2 {\varvec{\nabla }} ^{p_2 }\mathbf{U}} \right] \right\} -\mathbf{F}=0 \end{aligned}$$
(10)

where

$$\begin{aligned} \mathbf{F}=\left[ {{\begin{array}{lllllllll} 0&{} 1&{} 0&{} \cdots &{} 0&{} 0&{} \cdots &{} 0&{} 0 \\ \end{array} }} \right] ^\mathrm{T} \end{aligned}$$
(11)

The nonlinear algebraic equations in Eq. (10) are used to construct the nonlinear equality constraints of the optimization problem.

2.2.2 Gradients of the nonlinear equality constraints

In the following, the gradients of the nonlinear equality constraints are estimated analytically through direct differentiation of Eq. (10) with respect to each influence parameter.

Based on Eq. (10), the gradient of \(\mathbf{C}_\mathrm{E} (\mathbf{U})\) with respect to \(\mathbf{U}\) is calculated as follows:

$$\begin{aligned} \mathbf{J}&= \frac{{\varvec{\partial }} \mathbf{C}_\mathrm{E} (\mathbf{U})}{{\varvec{\partial }}\mathbf{U}} =\left( {k\mathbf{I}+c{\varvec{\nabla }} +m{\varvec{\nabla }} ^{2}} \right) \nonumber \\&\quad +\,\left( {K_{1} {\varvec{\nabla }} ^{p_1 }+K_2 {\varvec{\nabla }} ^{p_2 }} \right) \nonumber \\&\quad +\,\alpha \frac{{\varvec{\partial }} \left\{ {[\mathbf{E}(\mathbf{U})]}^{2}\mathbf{U} \right\} }{{\varvec{\partial }}\mathbf{U}} \end{aligned}$$
(12)

The partial derivative of the composite function \(\frac{\varvec{\partial } \left\{ {\mathbf{E}(\mathbf{U})\mathbf{U}} \right\} }{\varvec{\partial } \mathbf{U}}\) can be expressed by the formula

$$\begin{aligned} \frac{\varvec{\partial }\left\{ {\mathbf{E}(\mathbf{U})\mathbf{U}} \right\} }{\varvec{\partial } \mathbf{U}}=\frac{\varvec{\partial } \mathbf{E}(\mathbf{U})}{\varvec{\partial } \mathbf{U}}\mathbf{U}+\mathbf{E}(\mathbf{U}) \end{aligned}$$
(13)

Using the expression in Eq. (8), each column of the matrix \(\frac{\varvec{\partial } \mathbf{E}(\mathbf{U})}{\varvec{\partial } \mathbf{U}}\mathbf{U}\) can be derived rather than calculating the individual elements. Therefore, the following recurrence relation allows to calculate \(\frac{\varvec{\partial } \left\{ {[\mathbf{E}(\mathbf{U})]^{k}\mathbf{U}} \right\} }{\varvec{\partial } \mathbf{U}}\) for \(k>2\):

$$\begin{aligned} \frac{\varvec{\partial } \left\{ {[\mathbf{E}(\mathbf{U})]^{k}\mathbf{U}} \right\} }{\varvec{\partial } \mathbf{U}}&= \frac{\varvec{\partial } \left\{ {\mathbf{E}(\mathbf{U})\left[ {\left( {\mathbf{E}(\mathbf{U})} \right) ^{k-1}\mathbf{U}} \right] } \right\} }{\varvec{\partial } \mathbf{U}} \nonumber \\&= \frac{\varvec{\partial } \mathbf{E}(\mathbf{U})}{\varvec{\partial } \mathbf{U}}\left[ {\left( {\mathbf{E}(\mathbf{U})} \right) ^{k-1}\mathbf{U}} \right] \nonumber \\&\quad +\,\mathbf{E}(\mathbf{U})\frac{\varvec{\partial } \left[ {\left( {\mathbf{E}(\mathbf{U})} \right) ^{k-1}\mathbf{U}} \right] }{\varvec{\partial } (\mathbf{U})} \end{aligned}$$
(14)

Following an analogous methodology, calculating the gradients of \(\mathbf{C}_\mathrm{E} (\mathbf{U})\) with \(\omega ,\ell ,m,c,k,\alpha \) are generally straight forward.

2.2.3 General scheme for calculation of vibration response sensitivity

The sensitivity of the Fourier coefficients with respect to the influence parameters can easily be determined by analytical gradients. Taking the inverse of the \(\mathbf{J}\) matrix in Eq. (12), the sensitivity can be expressed as a first order explicit form:

$$\begin{aligned} \frac{\varvec{\partial } \mathbf{U}}{\varvec{\partial } b_k }=-\mathbf{J}^{-1}\frac{\varvec{\partial } \mathbf{C}_\mathrm{E} (\mathbf{U})}{\varvec{\partial } b_k }. \end{aligned}$$
(15)

2.3 Stability analysis for nonlinear systems with fractional order derivatives

The approaches to be outlined in this section seek to solve the stability problem for deterministic system and uncertainty system. Two detailed methods are formulated. The first approach directly deals with the deterministic generalized eigenvalue problem. The second approach described in Sect. 2.3.2 is an interval eigenvalue problem.

2.3.1 Deterministic stability analysis by solving the generalized eigenvalue problem

In this part, using the concept of superimposing a small disturbance around a periodic solution, the stability analysis is performed. With the aid of Taylor expansion method, the generalized eigenvalue problem is formed to determine the stability of periodic solution.

Let \(\mathbf{T}(t){\hbox {e}}^{\lambda t}\mathbf{Z}\) with \(\mathbf{Z}=[ {\hbox {Z}_0 }\,\, {\hbox {Z}_1^c } \,\, {\hbox {Z}_1^s } \,\, \cdots \,\, {\hbox {Z}_k^c } \,\, {\hbox {Z}_k^s }\,\, \cdots \,\, {\hbox {Z}_{N_\mathrm{H} }^c }\,\, {\hbox {Z}_{N_\mathrm{H} }^s } ]^\mathrm{T}\) be a small perturbation for the equilibrium \(\mathbf{T}(t)\mathbf{Y}\) of Eq. (1). Introducing perturbation \(\mathbf{T}(t)\hbox {e}^{\lambda t}\mathbf{Z}\) into Eq. (1) yields the stability criterion. In the following, fractional term \(D_t^\ell u(t)\) in Eq. (1) is evaluated by using \(\mathbf{U}=\mathbf{T}(t)\left[ {\mathbf{Y}+\hbox {e}^{\lambda t}\mathbf{Z}} \right] \) to derive the stability method.

Utilizing the property \(D_x^\ell \left[ {\hbox {e}^{ax}} \right] =a^{\ell }\hbox {e}^{ax}\) and the Euler transformation, \(\hbox {Z}_k^c D_t^\ell \left[ {\hbox {e}^{\lambda t}\hbox {cos}(k\omega t)} \right] +\hbox {Z}_k^s D_t^\ell \left[ {\hbox {e}^{\lambda t}\hbox {sin}(k\omega t)} \right] \) can be reformulated:

$$\begin{aligned}&\hbox {Z}_k^c D_t^\ell \left[ {\hbox {e}^{\lambda t}\hbox {cos}(k\omega t)} \right] +\hbox {Z}_k^s D_t^\ell \left[ {\hbox {e}^{\lambda t}\hbox {sin}(k\omega t)} \right] \nonumber \\&\quad =\hbox {e}^{\lambda t}\left[ {{\begin{array}{ll} {\hbox {cos}(k\omega t)}&{} {\hbox {sin}(k\omega t)} \\ \end{array} }} \right] \mathbf{S}^{\ell }(\lambda ,k\omega )\left[ {{\begin{array}{l} {\hbox {Z}_k^c } \\ {\hbox {Z}_k^s } \\ \end{array} }} \right] \end{aligned}$$
(16)

where

$$\begin{aligned}&\mathbf{S}^{\ell }(\lambda ,k\omega )\nonumber \\&=\frac{1}{2}\left[ {{\begin{array}{ll} {\left( {\lambda +\sqrt{-1}k\omega } \right) ^{\ell }+\left( {\lambda -\sqrt{-1}k\omega } \right) ^{\ell }}&{} {\sqrt{-1}\left[ {\left( {\lambda -\sqrt{-1}k\omega } \right) ^{\ell }-\left( {\lambda +\sqrt{-1}k\omega } \right) ^{\ell }} \right] } \\ {\sqrt{-1}\left[ {\left( {\lambda +\sqrt{-1}k\omega } \right) ^{\ell }-\left( {\lambda -\sqrt{-1}k\omega } \right) ^{\ell }} \right] }&{} {\left( {\lambda +\sqrt{-1}k\omega } \right) ^{\ell }+\left( {\lambda -\sqrt{-1}k\omega } \right) ^{\ell }} \\ \end{array} }} \right] \end{aligned}$$
(17)

and \(\sqrt{-1}\) is an imaginary unit.

In order to calculate \(\left( {\lambda \pm \sqrt{-1}k\omega } \right) ^{\ell }\), let \(h_c (x)=(x\hbox {+}c)^{\ell },c=\pm \sqrt{-1}k\omega \). Then, \(h_{\pm \sqrt{-1}k\omega } (\lambda )\) can be calculated by expanding \(h_c (x)\) as a second order Taylor series. With use of \(h_{\pm \sqrt{-1}k\omega } (\lambda )\), Eq. (16) can be expressed in matrix form as

$$\begin{aligned} D^{\ell }\left[ {\hbox {e}^{\lambda t}\mathbf{T}(t)\mathbf{Z}} \right]&= \hbox {e}^{\lambda t}\mathbf{T}(t)\tilde{{\varvec{\nabla }} }_\mathbf{S}^\ell \mathbf{Z} \nonumber \\&= \hbox {e}^{\lambda t}\mathbf{T}(t)\left\{ {\tilde{{\varvec{\nabla }} }_0^\ell \!+\!\tilde{{\varvec{\nabla }} }_1^\ell \lambda \!+\!\tilde{{\varvec{\nabla }} }_2^\ell \lambda ^{2}} \right\} \mathbf{Z} \end{aligned}$$
(18)

where

$$\begin{aligned} \tilde{{\varvec{\nabla }} }_j^\ell&= \mathbf{diag}\left( h_j^\ell (x_0 ,0),\mathbf{S}_j^\ell (x_0 ,\omega ),\cdots ,\mathbf{S}_j^\ell (x_0 ,k\omega ),\right. \nonumber \\&\quad \left. \ldots ,\mathbf{S}_j^\ell (x_0 ,N_H \omega ) \right) ,\quad j=0,1,2 \end{aligned}$$
(19)

with

$$\begin{aligned} \mathbf{S}_j^\ell (x_0 ,k\omega )=\left[ {{\begin{array}{cc} {h_j^\ell (x_0 ,\sqrt{-1}k\omega )+h_j^\ell (x_0 ,-\sqrt{-1}k\omega )}&{} {-\sqrt{-1}\left[ {h_j^\ell (x_0 ,\sqrt{-1}k\omega )-h_j^\ell (x_0 ,-\sqrt{-1}k\omega )} \right] } \\ {\sqrt{-1}\left[ {h_j^\ell (x_0 ,\sqrt{-1}k\omega )-h_j^\ell (x_0 ,-\sqrt{-1}k\omega )} \right] }&{} {h_j^\ell (x_0 ,\sqrt{-1}k\omega )+h_j^\ell (x_0 ,-\sqrt{-1}k\omega )} \\ \end{array} }} \right] ; \end{aligned}$$
$$\begin{aligned} h_0^\ell (x_0 ,c)&= h_c (x_0 )-{h}'_c (x_0 )x_0 +\frac{{h}''_c (x_0 )}{2}x_0^2 ,h_1^\ell (x_0 ,c)\nonumber \\&= {h}'_c (x_0 )-{h}''_c (x_0 )x_0 ,h_2^\ell (x_0 ,c)=\frac{{h}''_c (x_0 )}{2}\nonumber \\ \end{aligned}$$
(20)

By plugging \(\mathbf{U}=\mathbf{T}(t)\left[ {\mathbf{Y}+\hbox {e}^{\lambda t}\mathbf{Z}} \right] \) and Eqs. (18) into Eq. (1), the stability analysis problem is transformed into the following generalized eigenvalue problem:

$$\begin{aligned}&{\mathbf{A}\psi _{j} =\lambda _{j} \mathbf{B}\psi _{j} }\nonumber \\&\left( {\phi _j } \right) ^\mathrm{T}\mathbf{A}=\lambda _{j} \left( {\phi _j } \right) ^\mathrm{T}\mathbf{B} \end{aligned}$$
(21)

where \(\phi _j \) and \(\psi _j \) are the \(j\)th left and right eigenvectors associated with eigenvalue \(\lambda _j \). The matrices A and B are given by

$$\begin{aligned} \mathbf{A} \!&= \!\left[ {{\begin{array}{cc} \mathbf{0}&{} {\left( {mI\!+\!\tilde{{\varvec{\nabla }} }_2 } \right) } \\ {\!-\!\left( {m{\varvec{\nabla }} ^{2}\!+\!c{\varvec{\nabla }} \!+\!k\mathbf{I}\!+\!3\alpha \mathbf{E}(\mathbf{V})\!+\!\tilde{{\varvec{\nabla }} }_0 } \right) }&{} \mathbf{0} \\ \end{array} }} \right] , \nonumber \\ \mathbf{B}&= \left[ {{\begin{array}{cc} {\left( {m\mathbf{I}+\tilde{{\varvec{\nabla }} }_2 } \right) }&{}\mathbf{0} \\ {\left( {c\mathbf{I}+2m{\varvec{\nabla }} +\tilde{{\varvec{\nabla }} }_1 } \right) }&{} {\left( {m\mathbf{I}+\tilde{{\varvec{\nabla }} }_2 } \right) } \\ \end{array} }} \right] \end{aligned}$$
(22)

Following the approach in Ref. [20], the eigenvalues \(\bar{{\lambda }}_j \) used for stability analysis correspond to the eigenvector with the most symmetrical shape. Therefore, the periodic solution to be stable requires:

$$\begin{aligned} {\varvec{\mathfrak {R}}}\left( {\bar{{\lambda }}_j } \right) \le 0 \end{aligned}$$
(23)

The stability condition in Eq. (23) is used to form the nonlinear inequality constraint of the optimization problem.

2.3.2 Uncertain stability analysis by calculating the interval eigenvalue problem

When dynamical systems are subjected to parameter uncertainties, the periodic solution should be assessed in the way of robust stability. With the help of the perturbation theory and the interval analysis method, the interval eigenvalues are then obtained to determine the robust stability of periodic solution.

Applying the interval analysis method with the interval matrices \(\mathbf{A}^{\hbox {I}}=\mathbf{A}^{\hbox {C}}+\Delta \mathbf{A}^{\hbox {I}},\mathbf{B}^{\hbox {I}}=\mathbf{B}^{\hbox {C}}+{\varvec{\Delta }} \mathbf{B}^{\hbox {I}}\) to the eigenvalue problem in Eq. (21), the stability of periodic solution of Eq. (1) is then transformed into the following interval eigenvalue problem

$$\begin{aligned}&{\left( {\mathbf{A}^{{\mathrm{C}}}+{\varvec{\Delta }}\mathbf{A}^{\mathrm{I}}} \right) \psi _j^\mathrm{I} =\lambda _j^\mathrm{I} \left( {\mathbf{B}^{{\mathrm{C}}}+{\varvec{\Delta }}\mathbf{B}^{{\mathrm{I}}}} \right) \psi _j^\mathrm{I} } \nonumber \\&\quad \left( {\phi _j^\mathrm{I} } \right) ^\mathrm{T}\left( {\mathbf{A}^{{\mathrm{C}}}\!+\! {\varvec{\Delta }} \mathbf{A}^{{\mathrm{I}}}} \right) \!=\!\lambda _j^\mathrm{I} \left( {\phi _j^\mathrm{I} } \right) ^\mathrm{T}\left( {\mathbf{B}^{\mathrm{C}}\!+\!{\varvec{\Delta }}\mathbf{B}^{\mathrm{I}}} \right) \end{aligned}$$
(24)

where

$$\begin{aligned} \lambda _j^\mathrm{I} ={\varvec{\mathfrak {R}}} \left( {\lambda _j^\mathrm{I} } \right) +{\varvec{\mathfrak {I}}} \left( {\lambda _j^\mathrm{I} } \right) \sqrt{-1} \end{aligned}$$
(25)

According to the perturbation theory and interval expansion, the nominal eigenvectors \(\phi _j^\mathrm{C} ,\psi _j^\mathrm{C} \) and eigenvalues \(\lambda _j^\mathrm{C} \) related to \(\mathbf{A}^\mathrm{C}\) and \(\mathbf{B}^\mathrm{C}\) are then used to calculate the interval eigenvalue \(\lambda _j^\mathrm{I} \) as follows [21]:

$$\begin{aligned}&\left\{ {{\begin{array}{l} {{\varvec{\mathfrak {R}}} \left( {\lambda _j^\mathrm{I} } \right) } \\ {{\varvec{\mathfrak {I}}} \left( {\lambda _j^\mathrm{I} } \right) } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{l} {{\varvec{\mathfrak {R}}} \left( {\lambda _j^\mathrm{C} } \right) } \\ {{\varvec{\mathfrak {I}}} \left( {\lambda _j^\mathrm{C} } \right) } \\ \end{array} }} \right\} +\left\{ {{\begin{array}{l} {{\varvec{\mathfrak {R}}} \left[ {\varvec{\Delta } \lambda _j^\mathrm{C} (\varvec{\Delta } \mathbf{A}^{{\mathrm{I}}})} \right] } \\ {{\varvec{\mathfrak {I}}} \left[ {\varvec{\Delta } \lambda _j^\mathrm{C} (\varvec{\Delta } \mathbf{A}^{{\mathrm{I}}})} \right] } \\ \end{array} }} \right\} \nonumber \\&\,\,+\left[ {{\begin{array}{ll} {{\varvec{\mathfrak {R}}} \left( {\lambda _j^\mathrm{C} } \right) }&{} {-{\varvec{\mathfrak {I}}} \left( {\lambda _j^\mathrm{C} } \right) } \\ {{\varvec{\mathfrak {I}}} \left( {\lambda _j^\mathrm{C} } \right) }&{} {{\varvec{\mathfrak {R}}} \left( {\lambda _j^\mathrm{C} } \right) } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {{\varvec{\mathfrak {R}}} \left[ {\varvec{\Delta } \lambda _j^\mathrm{C} (-\varvec{\Delta } \mathbf{B}^{{\mathrm{I}}})} \right] } \\ {{\varvec{\mathfrak {I}}} \left[ {\varvec{\Delta } \lambda _j^\mathrm{C} (-\varvec{\Delta } \mathbf{B}^{{\mathrm{I}}})} \right] } \\ \end{array} }} \right\} \end{aligned}$$
(26)

where

$$\begin{aligned}&\varvec{\Delta }\lambda _j^\mathrm{C} (\mathbf{X})=\left\{ {{\begin{array}{ll} {\left[ {{\varvec{\mathfrak {R}}} \left( {\phi _j^\mathrm{C} } \right) } \right] ^\mathrm{T}}&{} {\left[ {{\varvec{\mathfrak {I}}} \left( {\phi _j^\mathrm{C} } \right) } \right] ^\mathrm{T}} \\ \end{array} }} \right\} \nonumber \\&\quad \left\{ {\left[ {{\begin{array}{ll} 1&{} {\sqrt{-1}} \\ {\sqrt{-1}}&{} {-1} \\ \end{array} }} \right] {{\otimes }} \left( \mathbf{X} \right) } \right\} \left\{ {{\begin{array}{l} {{\varvec{\mathfrak {R}}} \left( {\psi _j^\mathrm{C} } \right) } \\ {{\varvec{\mathfrak {I}}} \left( {\psi _j^\mathrm{C} } \right) } \\ \end{array} }} \right\} \end{aligned}$$
(27)

This section gathers the theoretical derivations of the proposed approach for stability analysis of periodic solution. By employing the harmonic balance formulation with the Taylor expansion technology, a new stability method for fractional nonlinear systems is derived. Further treatments of the stability of interval uncertainty systems are derived based on the estimation of the eigenvalue boundary.

2.4 Calculation of the bounds using the interval analysis method

Assume that \(u({{\tau }})\) attains its maximum over the interval [0, 2\({\varvec{\uppi }}\)] at the point \({{\tau }}_{{\mathrm{max}}} \). By means of natural interval extension, the interval responses of the maximum vibration displacement \(u(\mathbf{a}^{\mathrm{I}},{\varvec{\tau }}_{{\mathrm{max}}} )\) with interval parameter \(\mathbf{a}^{\mathrm{I}}\) can be determined straightforward as follows [22]:

$$\begin{aligned}&u(\mathbf{a}^{\mathrm{I}},{\varvec{\tau }}_{\mathrm{max}} )=u(\mathbf{a}^{\mathrm{C}},{\varvec{\tau }}_{\mathrm{max}} ) \nonumber \\&\qquad +\,\sum _j{\left. {\frac{\varvec{\partial } u(\mathbf{a},{\varvec{\tau }}_{\mathrm{max}} )}{\varvec{\partial } a_j }} \right| _{a_j =a_j^\mathrm{C} } } \left( {a_j^\mathrm{I} -a_j^\mathrm{C} } \right) \nonumber \\&\quad \!=\!u(\mathbf{a}^{\mathrm{C}},{\varvec{\tau }}_{\mathrm{max}} )\!+\!\sum _j{\mathbf{T}({\varvec{\tau }}_{\mathrm{max}} )\left. {\frac{\varvec{\partial } \mathbf{U}}{\varvec{\partial } a_j }} \right| _{a_j =a_j^{\mathrm{C}} } {\varvec{\Delta }} a_j^\mathrm{I} } \end{aligned}$$
(28)

It is obvious that the interval response depends on the sensitivity \({\varvec{\partial } \mathbf{U}}/{\varvec{\partial } a_j }\) and interval width \(\varvec{\Delta } a_j^\mathrm{I} \). The above explicit expression of the interval response provides useful information on the influence of uncertainties on the range of the interval response.

2.5 Optimization problem formulation

Within the framework of the proposed method [18], the nonlinear algebraic equations in Eq. (10) and the stability criterion in Eq. (23) are treated as the generally nonlinear constraints. Therefore, the following nonlinear optimization problem can be formulated:

$$\begin{aligned} \begin{array}{l} f({{\varvec{x}}})=f(\mathbf{U},\omega ,{{\varvec{v}}}_u )=\max u(\tau ) \\ {\begin{array}{lll} &{} \mathrm{s.t}&{} {\left\{ {{\begin{array}{l} {{\varvec{g}}}({{\varvec{x}}})=\mathbf{C}_\mathrm{E} (\mathbf{U})=\mathbf{0} \\ {{\varvec{g}}}_{{\varvec{s}}} ({{\varvec{x}}})={{\mathfrak {R}}} \left( {\bar{{\lambda }}_j } \right) \le 0 \\ \end{array} }} \right. } \\ \end{array} } \\ \end{array} \end{aligned}$$
(29)

where \({{\varvec{x}}}=\left\{ {\mathbf{U},{\varvec{\omega }},{{\varvec{v}}}_u } \right\} ^\mathrm{T}\) and \({{\varvec{v}}}_u \) is a set of design parameters and/or uncertainty parameters. \({{\varvec{g}}}({{\varvec{x}}})\) and \({{\varvec{g}}}_{{\varvec{s}}} ({{\varvec{x}}})\) represent the nonlinear equality and inequality constraints, respectively.

There are three major advantages to derive the analytical gradients of the nonlinear constrained optimization problem. First, the analytical gradients can be used to accelerate the convergence of the optimization algorithm, thus reducing the computational costs. Second, the stability analysis of the periodic solution can be determined by virtue of the analytical derivation of the nonlinear equality constraints. Furthermore, the interval eigenvalue problem is solved to identify the robust stability region. Third, based on the analytical gradients of the nonlinear equality constraints, the sensitivity of the Fourier coefficients with respect to influence parameters can be derived, and the bounds of periodic solution are calculated with the help of the interval analysis method.

3 Numerical results

In order to demonstrate the effectiveness of the proposed method, numerical examples which have been taken from recent publication [9] are considered. The dynamic behaviors of the Duffing oscillator without and with fractional derivative terms are compared. Parameter studies about the fractional derivative terms are also conducted. The sensitivity of the Duffing oscillator is analyzed. The explicit stability and response bounds for the Duffing system with parameter uncertainty are given.

3.1 The dynamical behaviors of the Duffing oscillator without fractional order derivative terms

3.1.1 The frequency response curve of the Duffing oscillator

To align with the computational study in Ref. [9], the following structural parameters were chosen: \(m=5, c=0.1, k=10, \alpha =15,K_{1}=0.8,K_{2}=1,p_1 =0.6,p_2 =1.4,F=5\). In order to highlight the influence of the fractional derivative terms, the frequency response function of the standard Duffing oscillator without the fractional derivative terms is plotted in Fig. 1 where the stable and unstable segments of the frequency responses are shown by the solid and dashed line, respectively.

Fig. 1
figure 1

Frequency–response curve of the Duffing oscillator without the fractional derivative terms

Full size image

It can be seen from Fig. 1 that the system reaches the top amplitude at resonant peak \(P\). The unstable region is located between two bifurcation points \({B}_{1}\) and \(B_{2}\). Three periodic solutions of which the upper and lower response bounds are \({F}_{1}\) and \({F}_{3}\), respectively, coexist at the excitation frequency \(\omega =2.2\). The solution \({F}_{2 }\) is unstable. In the following, three cases are investigated by utilizing the proposed method:

  1. (1) Case 1

    searching the resonant peak P

As explained previously, the unknown variables that have to be determined are the unknown Fourier coefficients U and the resonant frequency of the periodic solution \(P\).

  1. (2) Case 2

    seeking the bifurcation points

In order to seek the bifurcation points \(B_{1}\) and \(B_{2}\), the object function shown in Eq. (29) is set as \(\min \left| {{{\mathfrak {R}}} \left( {\bar{{\lambda }}_j } \right) } \right| \) and only the nonlinear equality constraints are considered.

  1. (3) Case 3

    finding the multi-solutions at a given frequency

While looking for multiple solutions at a given frequency, the excitation frequency is not included as an optimization variable, and the Fourier coefficients U are the only unknown variables. It should be noted that the objective function in Eq. (29) is changed as the minimization of the vibration displacement for searching the periodic solution \(F_{3}\), while the sign of inequality stability constraint is reversed to locate the solution \(F_{2}\).

3.1.2 The numerical results of the proposed method

When the Duffing oscillator has no fractional derivatives, the numerical results are presented in Fig. 2. As shown in Fig. 2, there is one main harmonic term in the system response, and the presence of several higher harmonic components can be detected.

Fig. 2
figure 2

Numerical optimization results of the Duffing oscillator without the fractional derivative terms

Full size image

Table 1 summarizes the stability results that were evaluated at these optimal solutions. In Table 1, \(\bar{{\rho }}_j \) represents the Floquet multipliers obtained using the proposed stability method. For the purpose of comparison, stability results using the Runge–Kutta method are also listed in Table 1 where the corresponding Floquet multipliers are denoted by \(\hat{{\rho }}_j \). It can be seen from Table 1 that the stability results obtained in this paper are consistent with the results calculated by the conventional stability method in the time domain. Regions of stable and unstable periodic response appear to be correctly predicted. In particular, there is always one multiplier 1 for \({B}_{1}\) and \({B}_{2}\), which the optimization algorithm intends to find. Overall, comparing to the known stability method, the proposed stability method in Sect. 2.3.1 is verified.

Table 1 Numerical results of the Duffing oscillator without the fractional derivative terms
Full size table

3.1.3 Sensitivity information

Sensitivity analysis can be used as a useful design tool to evaluate the system response to changing parameters. One advantage of the proposed method over previous ones (such as the method in Ref. [18]) is the sensitivity information which provides the trends of variation of the objective and constraint functions versus system parameters efficiently.

Sensitivities of the Fourier coefficients with respect to the influence parameters are displayed in Fig. 3. As shown in Fig. 3, the dominant contribution of the sensitivity is the first harmonic content with negligible contributions from other higher terms. For all points studied, the Fourier coefficients appear to be very sensitive to the variation of frequency \({\omega }\). It should be noted that for the periodic solutions with higher vibration amplitude, such as \(P, {B}_{2}\) and \({F}_{1}\), the Fourier coefficients are seen to be in general much more sensitive to changes of damping, whereas the sensitivity of \({\varvec{\partial } \mathbf{U}}/{\varvec{\partial } {m}}\) seems to be greater than \({\varvec{\partial } \mathbf{U}}/{\varvec{\partial } {c}}\) for solutions \({B}_{1}, {F}_{2}, {F}_{3}\) and \(U\). The sensitivity results show that the sensitivities of U with respect to the stiffness parameters \({k}\) and \({\alpha }\) have the lowest sensitivity. The sensitivity of linear stiffness \({k}\) is more significant than \({\alpha }\) in the region of low vibration amplitude, while the contribution by the nonlinear stiffness parameter \({\alpha }\) becomes large for high vibration amplitude solutions \(P\), \({B}_{2}\) and \({F}_{1}\). In addition, it is indicated that the bifurcation points show the highest sensitivity. The level of the sensitivity of the bifurcation points implies that the Jacobian matrix may be close to singularity.

Fig. 3
figure 3

Sensitivities of the Duffing oscillator without the fractional derivative terms. a Resonance peak solution P. b Bifurcation solution \({B}_{1 }\). c Solution \({F}_{3}\). d Solution L

Full size image

3.1.4 The interval boundaries in the presence of uncertainty

Obtaining stability boundaries is vital to study the effects of structural parameters. One of the merits of the proposed method is that the robust stability boundaries and response intervals can be obtained using the presented method when some of the structural parameters are subjected to uncertainties. In the following, the stability boundaries and interval responses of uncertain dynamic systems are estimated. The interval parameters of the uncertain structural parameters are described by

$$\begin{aligned} m\in m^{I}&= \left[ {m^{\mathrm{C}}-{\varvec{\Delta }} m,m^{\mathrm{C}}+{\varvec{\Delta }} m} \right] ,\quad c\in c^{\mathrm{I}} \nonumber \\&= \left[ {c^{\mathrm{C}}-{\varvec{\Delta }} c,c^{\mathrm{C}}+{\varvec{\Delta }} c} \right] ,\quad k\in k^{\mathrm{I}} \nonumber \\&= \left[ {k^{\mathrm{C}}-{\varvec{\Delta }} k,k^{\mathrm{C}}+{\varvec{\Delta }} k} \right] \end{aligned}$$
(30)

where \(m^{\mathrm{C}}=5,c^{\mathrm{C}}=0.1,k^{\mathrm{C}}=10\) and \({\varvec{\Delta }} m,{\varvec{\Delta }} c\) and \({\varvec{\Delta }} k\) are the uncertainty degree.

Table 2 shows the comparisons when one of the structural parameters \(m,c,\) and \(k\) is assumed to be uncertain while the other two parameters are kept fixed. In Table 2, the real and imaginary parts of the interval eigenvalues \(\bar{{\lambda }}_j^\mathrm{I} \) are presented to estimate stability bounds of periodic solutions. As it can be noticed in Table 2 that for \({\varvec{\Delta }} k=0.01\), all the upper bounds of the real parts of the interval eigenvalues are negative for solutions \(P\) and \(U\) which are robust asymptotically stable while other solutions are not robust stable. The stability boundaries are not sensitive to the variation of \(c\). On the contrary, the uncertainty of \(m\) has strong effects on the stability boundaries. Even for small uncertainty \({\varvec{\Delta }} m=0.01\), all the solutions except \(U\) lose stability.

Table 2 Stability boundaries with different uncertainty parameters
Full size table

When both the coefficients \(m, c\) and \(k\) vary, the combined effects of the uncertainty in \(m, c, k\) are given in Tables 3 and 4 in which \(m, c\) and \(k\) vary between 1, 3, 5 % of the nominal values. Compared with the results obtained in Tables 2 and 3 clearly shows that the dominated term in the system’s stability boundaries is the mass \(m\) term, whereas the terms \(k\) and \(c\) have small contributions. In Table 4, the response bounds with positive upper bound of \({\varvec{\mathfrak {R}}} \left( {\bar{{\lambda }}_j^\mathrm{I} } \right) \) are not reliable and should be considered as the only validation of the method in Sect. 2.4.

Table 3 Stability boundaries with different \({\varvec{\Delta }} m,{\varvec{\Delta }} c,{\varvec{\Delta }} k\)
Full size table
Table 4 Response intervals with different \({\varvec{\Delta }} m,{\varvec{\Delta }} c,{\varvec{\Delta }} k\)
Full size table

It is worth emphasizing that high interval sensitivity to a selected uncertain parameter means a strong influence of this parameter on the width of the interval response. Such information may be useful to identify the most crucial uncertain parameters.

3.2 The dynamic behaviors of the Duffing oscillator with two kinds of fractional derivative terms

The method in Ref. [18] cannot deal with the fractional order nonlinear systems. Moreover, the stability Hill method is not able to identify the periodic solution stability of fractional order nonlinear systems. Integer order Duffing system validation in Sect. 3.1 shows that the proposed method in Sect. 2 is correct. In this section, based on the proposed method, the vibration characters of fractional order Duffing oscillator are studied to show the advantage of the developed method for finding the periodic solutions and its stability in fractional order nonlinear systems.

3.2.1 The numerical results of the proposed method

Using the developed method, the numerical optimization results of the Duffing Oscillator with fractional derivatives are shown in Table 5. As shown in Table 5, all the moduli of the Floquet multipliers are \(<\)1 except for the periodic solution \(F_{2}\), and the bifurcation solutions \(B_{1 }\)and \(B_{2}\) and these solutions obtained by the proposed method are stable. For the bifurcation solution \(B_{1}\), the moduli of a pair of complex conjugate Floquet multipliers 0.6988 \(\pm \) 0.7153i is equal to 1. This indicates that a Hopf bifurcation occurs at \(B_{1}\).

Table 5 Numerical results of the Duffing oscillator with fractional derivative terms
Full size table

The difference between the numerical results obtained with and without fractional derivatives is apparent. When analyzed in the absence of fractional derivatives, as demonstrated in Fig. 2 and Table 1, \(u\) has its maximum value 5.8773 at resonance frequency 8.7446. When fractional derivatives are taken into account, the vibration amplitude in resonance is 1.2941 where the resonance frequency is located at 2.3172. The maximum vibration amplitude without fractional derivatives is 4.5416 times larger than that with fractional derivatives. Therefore, the fractional derivatives can remarkably influence the vibration responses of the nonlinear systems. It should be noted that the vibration amplitude and vibration frequency of all these solutions in Table 5 are identical to those presented in Fig. 1 of Ref. [9], which validates the proposed method.

In order to fully validate the stability approach, direct numerical integrations have been carried out. Numerical simulations are performed using the Grunwald–Letnikov method (see Eq. (38) in Ref. [9]). The initial conditions can be readily supplied by the results of the presented method. In order to eliminate the transient part of the responses, the initial responses are discarded from the stored responses and results are plotted only for 350–400. The phase portraits of the Duffing system at these optimal solutions are presented in Fig. 4 using the time integration method (denoted by TIM)and the proposed method (denoted by COHBM). For the unstable solution \(F_{2}\), the temporal evolution of numerical integration solution is displayed in Fig. 5. As demonstrated in Fig. 5, the unstable solution \(F_{2 }\) jumps to the stable solution \(F_{1}\) after a finite period of time, thus confirms the unstable of solution \(F_{2}\). From Figs. 4 and 5, it is evident that the present approach solutions match well with the numerical integration solutions. Therefore, the validity of the presented stability method is confirmed.

Fig. 4
figure 4

Comparison of these solutions between the time integration method (TIM) and the proposed method (COHBM)

Full size image
Fig. 5
figure 5

The time evolution of the unstable solution \(F_{2}\)

Full size image

3.2.2 The sensitivity information

In Fig. 6, the sensitivities of the Fourier coefficients with respect to the structural parameters are depicted. For the Duffing oscillator with fractional derivatives, the dynamic behaviors of the structural parameters \({\omega },{c},{m},{k}\) and \({\alpha }\) are similar to that of the Duffing oscillator without fractional derivatives. For the high vibration amplitude solutions \(P, B_{2},F_{1},F_{2}\) and \(L\), these two parameters \(K_{2}\) and \(p_{1 }\) have a significant impact on the sensitivity results. Conversely, the Fourier coefficients are more sensitive to \(p_{2}\) and \({m}\) for the low vibration amplitude points \(B_{1}, F_{3}\) and \(U\). It should be noted that the bifurcation points \(B_{1 }\) and \(B_{2}\) have great difference between the sensitivity. The bifurcation point \(B_{2 }\) has very large sensitivity values, which approaches to infinity. However, the sensitivities of bifurcation point \(B_{1}\) are relatively very small. Therefore, it can be concluded that in the fractional nonlinear systems, bifurcation periodic solution may not be sensitive to the variation of structural parameters.

Fig. 6
figure 6

Sensitivities of the Duffing oscillator with fractional derivative terms. a Resonance peak solution P. b Bifurcation solution \(B_{1 }\). c Solution \(F_{3 }\). d Solution \(L\)

Full size image

3.2.3 The interval boundaries in the presence of uncertainty

For several values of \({\varvec{\Delta }} m,{\varvec{\Delta }} c,{\varvec{\Delta }} k\), the computed stability and response bounding intervals are listed in Tables 6 and 7. Generally, the smaller the uncertainty is, the tighter the interval results is. With the increase of \({\varvec{\Delta }} m,{\varvec{\Delta }} c,{\varvec{\Delta }} k\), the width of \({\varvec{\mathfrak {R}}} \left( {\bar{{\lambda }}_j^\mathrm{I} } \right) \) increases gradually. The upper bounds of \({\varvec{\mathfrak {R}}} \left( {\bar{{\lambda }}_j^\mathrm{I} } \right) \) for the solution P with \({\varvec{\Delta }} m,{\varvec{\Delta }} c,{\varvec{\Delta }} k=0.03,0.05\) are 0.0070 and 0.1253, respectively, which are greater than 0. According to the Floquet theorem, it can be concluded that the periodic solution \(P\) is not robust asymptotically stable. Similarly, the cases of 3 and 5 % uncertainty for solution \(F_{1}\) show that the solution \(F_{1}\) does not robust asymptotically stable for this relative high uncertainty. On the contrary, the maximal stability margins for solutions \(F_{3}, L\) and \(U\) indicate that these low vibration amplitude solutions are not sensitive to the uncertainty. In particularly, the lower and upper bounds of the stability interval for solution \(U\) are the same for the three levels of uncertainty.

Table 6 Stability boundaries with different \({\varvec{\Delta }} m,{\varvec{\Delta }} c,{\varvec{\Delta }} k\)
Full size table
Table 7 Response intervals with different \({\varvec{\Delta }} m,{\varvec{\Delta }} c,{\varvec{\Delta }} k\)
Full size table

To consider the stability of bifurcation solutions \(B_{1}\) and \(B_{2}\), the solutions \(B_{1}\) and \(B_{2}\) become unstable in the presence of uncertainty. The smallest deviations for \({\varvec{\mathfrak {R}}} \left( {\bar{{\lambda }}_j^\mathrm{I} } \right) \) of solution \(B_{2}\) are null. It is obvious that the interval response results for solution \(B_{2}\) in Table 7 shows no meaning. It should be noted that the first order Taylor expansion based interval approach is to over estimate the structural response of bifurcation solutions with high sensitivity especially when the magnitudes of the parameter uncertainty are relatively large. A further study in future work is needed to tight the interval bounds.

The proposed method, based on the joint application of the proposed stability method and the interval analysis method, provides general estimates of the range of the stability regions and response bounds even when relatively large uncertainties are involved. Compared with the direct Monte Carlo simulation for calculating the stability and response boundaries, the presented approach enables to drastically reduce the computational costs.

3.3 The effects of \(K_1, K_2, {p}_1 \) and \({p}_2 \) on the maximum vibration amplitude

The combined effects of structural parameters on the vibration response can be investigated via the proposed approach when all the influence parameters vary simultaneously. In order to demonstrate the superiority of the proposed method, the influence of structural parameters \(K_{1}, K_{2}, p_{1}\) and \(p_{2}\) on the maximum vibration amplitude are illustrated in this section.

3.3.1 The numerical results of the proposed method

A first simulation is carried out to obtain the worst case resonance. Using the proposed method in Eq. (29), the structural parameters taking into account are included as optimization variables in Eq. (29), i.e., \(v_u= \{K_{1}, K_{2}, p_{1}, p_{2}\}\). The optimization bounds of the optimization variables are \(K_{1}\in [0, 1.6], K_{2}\in [0.5, 1.5], p_{1}\in [0.2, 0.8], p_{2}\in [1.2, 1.8]\). Optimization results demonstrate that the solution attains its positive maximum at \(K_{1}=0,K_{2}=0.5,p_{1}=0.2\) and \(p_{2}=1.8\), which is located at the boundary of the domain \(\Omega (K_1 ,K_2 ,p_1 ,p_2 )\). It can be seen that the maximum vibration amplitude strongly depends on the parameters of fractional derivatives, and the parameter \(p_{2}\) has a significant effect on the vibration response.

To demonstrate the above results, a set of data points in the domain \(\Omega (K_1 ,K_2 ,p_1 ,p_2 )\) is selected to gain more insight of the influence of these structural parameters. These data points are listed in Table 8.

The optimization results with the mentioned method are presented in Table 9. Observe in Table 9 that these optimal solutions are stable because all the moduli of the Floquet multiplier are \(<\)1.

Table 8 The selected parameter sets
Full size table
Table 9 Numerical results of the eight cases
Full size table

Obviously, the maximum vibration amplitudes and the corresponding resonance frequencies are monotonically decreasing function about \(K_{1},K_{2}\) and \(p_{1}\), that is to say, decreasing \(K_{1}, K_{2}\) and \(p_{1}\) could increase \(u(\tau _{{\mathrm{max}}} )\) and resonance frequency. On the contrary, increasing \(p_{2}\) leads to the decrease of \(u(\tau _{\mathrm{max}} )\) and its resonance frequency. This means that \(p_{2}\) plays a key effect on the present results and increasing \(p_{2}\) could suppress the worst resonance.

3.3.2 The sensitivity information

The variations of the sensitivity for the eight cases are illustrated in Fig. 7. It is shown that, among the nine influence parameters, the sensitivities of U with \(p_{2}, c, K_{2}\) and \(\omega \) are significantly higher than the other five. From Fig. 7, it can be realized that the sensitivity values of the Fourier coefficients decrease dramatically with increasing \(K_{1}, K_{2}\) and \(p_{1}\) and decreasing \(p_{2}\). For \({\varvec{\partial } U}/{\varvec{\partial } {p}_1 }\), the sensitivity magnitude of \({\varvec{\partial } U}/{\varvec{\partial } {p}_1}\) increases to a maximum value at DP2 and then begins to decrease. The case DP1 shows the highest sensitivity and the DP8 case the lowest one.

Fig. 7
figure 7

Sensitivity curves for different parameters of the fractional derivative terms

Full size image

By inspection of Fig. 7, the influence of these structural parameters on the maximum vibration amplitude can be detected. In particular, it is observed that the maximum vibration displacement and its sensitivity turn out to be mainly affected by the structural parameters \(p_{2}, c\) and \(K_{2}\). The influence of \(\omega \) is comparatively less significant, while the structural parameters \(K_{1}, p_{1}, m, \alpha \) and \(k\) have almost negligible effects on the sensitivity.

3.3.3 The interval boundaries in the presence of uncertainty

Following the developed method, the upper and lower bounds of \(\bar{{\lambda }}_j^\mathrm{I} \) for the eight cases with three different values of the deviation amplitude of the interval parameters, say \({\varvec{\Delta }} m,{\varvec{\Delta }} c,{\varvec{\Delta }} k=0.01,0.03\) and 0.05, are illustrated in Table 10. The response bounds estimated are given in Table 11. A close inspection of Tables 10 and 11 show that, for small level of uncertainty (\({\varvec{\Delta }} m,{\varvec{\Delta }} c,{\varvec{\Delta }} k= 0.01\)), the upper bounds of \({\varvec{\mathfrak {R}}} \left( {\bar{{\lambda }}_j^\mathrm{I} } \right) \) for all cases are negative. Therefore, the interval responses listed in the second column of Table 11, which associate with stable periodic solutions, are credible.

Table 10 Stability boundaries with different \({\varvec{\Delta }} m,{\varvec{\Delta }} c,{\varvec{\Delta }} k\)
Full size table
Table 11 Responses intervals with different \({\varvec{\Delta }} m,{\varvec{\Delta }} c,{\varvec{\Delta }} k\)
Full size table

Notice that the stability boundaries for cases DP3, DP7 and DP8 are less sensitive to the fluctuation of the uncertainty parameters than other cases. The upper bounds of \({\varvec{\mathfrak {R}}} \left( {\bar{{\lambda }}_j^\mathrm{I} } \right) \) for cases DP3,DP7 and DP8 with three different values of \({\varvec{\Delta }} m,{\varvec{\Delta }} c,{\varvec{\Delta }} k\) are \({<}\)0, which demonstrate that these periodic solutions are still stable even for relatively large uncertainty. Indeed, the stability bounds which are characterized by a wider region imply a greater deviation of the dynamical behavior from the periodic solution pertaining to the nominal system.

4 Conclusions

The improved method in Ref. [18] is used to solve the Duffing oscillator with two kinds of fractional order derivative terms. The fractional operation matrix and the polynomial nonlinear operation matrix are derived analytically, and the gradients of the nonlinear equality constraints and objective function with respect to optimization variables are therefore obtained. Then, a generalized eigenvalue problem is constructed to analyze the stability of periodic solution, and the uncertainty stability boundary is determined by the interval eigenvalue problem. Moreover, the response bounds of periodic solution are calculated by using the interval analysis method along with the sensitivity information. Finally, the validity of the proposed approach is demonstrated on the Duffing oscillator without and with fractional derivative terms. Parameter studies for the fractional derivative terms are performed. It is illustrated that the fractional derivative terms have an evident influence on the dynamic behaviors of Duffing oscillator, and the bifurcation solution in fractional nonlinear systems may not be sensitive to the change of the influence parameter.

It is worth mentioning that the proposed approach in this paper can be used as the robust design optimization method. The basic idea of the potential robust design method is given as follows: To reduce the undesired vibration response for the given frequency interval, the objective function is to minimize the upper bound of vibration response given in Eq. (29), while the inequality stability criterion in Eq. (29) is replaced with \({\varvec{\mathfrak {R}}} \left( {\bar{{\lambda }}_j^\mathrm{I} } \right) <0\). The corresponding examples will appear in the near future.