New globally asymptotical synchronization of chaotic systems under sampled-data controller

Abstract

This paper investigates the robust synchronization problem of chaotic Lur’e systems with external disturbance using sampled-data $H_{\infty }$ controller. The new method is based on a novel construction of piecewise differentiable Lyapunov–Krasovskii functional (LKF) in the framework of an input delay approach. Compared with existing works, the new LKF makes full use of the information on the nonlinear part of the system and introduces the novel terms, which guarantees the positive of the whole LKF. The output feedback $H_{\infty }$ synchronization controller is presented to not only guarantee stable synchronization, but also reduce the effect of external disturbance to an $H_{\infty }$ norm constraint. The proposed controller can be obtained by solving the linear matrix inequality problem. The effectiveness of the proposed method is demonstrated by the numerical simulations of Chua’s circuit.

1 Introduction

Since the pioneering work was introduced by Pecora and Carroll [1], chaos synchronization has been a very hot topic in the nonlinearity community and has attracted much interest of scientists and engineers due to its potential applications in various fields, include chaos generator design, secure communication, chemical reaction, biological systems, and information science [2–6]. It is well known that a large class of nonlinear systems, such as Chua’s circuit, n-scroll attractors, and hyperchaotic attractors [7], can be modeled as Lur’e systems which consist of a linear dynamical system and a feedback nonlinearity satisfying sector bound constraints. For this reason, a lot of attention have been devoted to the study of the master–slave synchronization of Lur’e systems [8–12]. From the control strategy point of view, a number of methods have been proposed for the master–slave synchronization of Lur’e systems. These methods are almost implemented by analog circuits (such as observer-based control [13], adaptive control [14], and feedback control [15, 16]). During working in high-quality and high-speed communication channels, the controllers based on these methods can provide well control performance, since they can use continuous feedback signals to tune the optimal control output in real time. However, it may be difficult to obtain the accuracy feedback signal in real time due to the noise corruption [17], especially for the communication channels are occupied all the time for such type of control strategies. With the rapid advances in data communication networks and high-speed computers, it is preferable to use digital controllers instead of analog circuits, particularly in aerospace systems and industries [18]. These control systems can be modeled by sampled-data systems, whose control signals are kept constant during the sampling period and are allowed to change only at the sampling instant. These samples are used by sampled-data controllers to control the slave chaotic system and result in synchronization between the master and the slave chaotic systems. This drastically reduces the amount of synchronization information transmitted from the master chaotic system to the slave chaotic system and increases the efficiency of bandwidth usage, which makes this method more efficient and useful in real-life applications.

During using a sampled-data controller to synchronize the chaotic systems, how to choose the sampling period is an important issue to be considered. It is clear that a bigger sampling period will lead to lower communication channel occupying, fewer actuation of the controller, and less signal transmission [19, 20]. Therefore, it is an important objective to design a controller which can achieve the synchronization under a bigger sampling period. In the sampled-data control literature, a popular analysis approach is the so-called input delay approach proposed in [21]. This approach is based on modeling the sampled-and-hold with a delayed control input. Then, the Lyapunov–Krasovskii functional (LKF) method can be applied to establish the stability conditions. Note that recent improvements of the input delay approach have been obtained in [22]. The work in [23] and [24] introduced a discontinuous LKF to study the sampled-data control problem for master–slave synchronization schemes. The authors in [25] introduced a new LKF for the synchronization of Lur’e systems with time delays, which was positive definite at sampling times but not necessarily positive definite inside the sampling intervals.

On the other hand, in the real-world situation, parameter uncertainties are unavoidable mainly due to the modeling inaccuracies, variations of the operating point, aging of the devices, etc. Therefore, the issue of robustness analysis has been taken into account in all sorts of systems by many researchers [26–29]. Hou et al. [30] firstly adopted the $H_{\infty }$ control concept for chaotic synchronization problem of a class of chaotic systems. In [31], a dynamic controller for the $H_{\infty }$ synchronization was proposed. Choon [32] proposes a new output feedback $H_{\infty }$ synchronization method for delayed chaotic neural networks with external disturbance. Very recently, Lee et al. [33] have investigated the robust synchronization problem for uncertain nonlinear chaotic systems using stochastic sampled-data control. To the best of our knowledge, however, for the robust synchronization of chaotic systems using sampled-data $H_{\infty }$ control, there is no result in the literature so far, which still remains open and challenging.

In this paper, a discontinuous Lyapunov functional approach is proposed to discuss the robust master–salve synchronization for Lur’e systems by use of a sampled-data $H_{\infty }$ control in the present of a constant input delay. In order to make full use of the available information about the actual sampling pattern, a novel LKF is proposed. The positive definitiveness of the given LKF can be guaranteed by only requiring the sum of several terms of the LKF to be positive. Different from the LKF introduced in [34], our delay-dependent LKF adopts some useful information of the nonlinear function, which makes it possible to deduce less conservative stability conditions. By means of the numerical simulations of Chua’s circuit it is shown that the proposed results are effective and can significantly improve the existing ones.

Throughout this paper, $\mathbb {R}^{n}$ is the n-dimensional Euclidean space, $\mathbb {R}^{m\times n}$ denotes the set of $m\times n$ real matrix. $X_{ij}$ denotes the element in row $i$ and column $j$ of matrix $X$. $I$ is the identity matrix. The notation $*$ always denotes the symmetric block in one symmetric matrix. Matrices, if not explicitly stated, are assumed to have compatible dimensions.

2 Problem statement and preliminary

Consider the following general master–slave type of time-delay Lur’e systems with parameter uncertainties using sampled-data feedback controller:

$$\begin{aligned}&M:\left\{ \begin{array}{l} \dot{x}(t)=(A+\varDelta A(t))x(t)\\ \quad \,\,\,\qquad +(H+\varDelta H(t))\sigma (D^\mathrm{T}x(t)) \\ y(t)=Cx(t) \end{array} \right. \nonumber \\&S:\left\{ \begin{array}{l} \dot{z}(t)=(A+\varDelta A(t))z(t)\\ \quad \,\,\,\qquad +(H+\varDelta H(t))\sigma (D^\mathrm{T}z(t))+u(t)+E\omega (t) \\ \hat{y}(t)=Cz(t) \end{array} \right. \nonumber \\&C:u(t)=K(y(t_{k})-\hat{y}(t_{k})),\quad t_{k}\le t<t_{k+1} \end{aligned}$$

(1)

which consists of the master system $M$, the slave system $S$, and the sampled-data feedback controller $C$. $x(t)$ and $z(t)\in \mathbb {R}^{n}$ are the state vectors of master and slave systems, respectively, $y(t)$ and $\hat{y}(t)\,\,\in \mathbb {R} ^{l}$ are the ouput vectors. $u(t)\in \mathbb {R}^{n}$ is the control input, $\omega (t)\in \mathbb {R}^{k}$ is the external disturbance which belongs to $L_{2}[0,\infty )$. $A\in \mathbb {R}^{n\times n},C\in \mathbb {R}^{l\times n},D\in \mathbb {R}^{n_{h}\times n},E\in \mathbb {R}^{n\times k}$, and $H\in \mathbb {R}^{n\times n_{h}}$ are known constant matrices. $K\in \mathbb {R}^{n\times l}$ is the sampled-data feedback control gain matrix to be designed. $\varDelta A(t)$ and $\varDelta H(t)$ are unknown matrices representing time-varying parameter uncertainties. In this paper, the admissible parameter uncertainties are assumed to be of the following form.

$$\begin{aligned}{}[\varDelta A(t) \quad \varDelta H(t)]=NF(t)[N_{a} \quad N_{h}] \end{aligned}$$

(2)

in which $N, N_{a}, N_{h}$ are known constant matrices, and the time-varying nonlinear function $F(t)$ satisfies

$$\begin{aligned} F^\mathrm{T}(t)F(t)\le I, \quad \forall t\ge 0. \end{aligned}$$

(3)

It is assumed that all the elements of $F(t)$ are Lebesgue measurable. We assume that $\sigma (\cdot )$:$\mathbb {R} ^{n_{h}}\longmapsto \mathbb {R} ^{n_{h}}$ is a diagonal nonlinearity with $\sigma _{i}(\cdot )$ satisfying the following inequality:

$$\begin{aligned}{}[\sigma _{i}(\xi )-\varpi _{i}^{+}\xi ][\sigma _{i}(\xi )-\varpi _{i}^{-}\xi ]\le 0,\quad \forall \xi , \end{aligned}$$

(4)

for all $i=1,2,\ldots ,n_{h}.$ Thus, the nonlinear function satisfies sector bounding condition and $\sigma _{i}(\cdot )$ is said to belong in the sector $[\varpi _{i}^{-},\varpi _{i}^{+}].$ Denote the updating instant time of the ZOH by $t_{k}$. For sampled-data feedback synchronization, only discrete measurements of $y(t)$ and $\hat{y}(t)$ can be used for synchronization purposes, that is, we only have the measurement $y(t_{k})$ and $\hat{y}(t_{k})$ at the sampling instant $t_{k}.$ Suppose that the updating signal (successfully transmitted signal from the sampler to the controller and to the ZOH) at the instant $t_{k}$ has experienced a constant signal transmission delay $\eta .$ It is assumed that the sampling intervals are bounded and satisfy

$$\begin{aligned}&0=t_{0}<t_{1}<\cdots <t_{k}<\cdots <\underset{k\rightarrow \infty }{\lim } t_{k}=+\infty ,\\&t_{k+1}-t_{k}\le h_\mathrm{max},\quad \forall k\ge 0, \end{aligned}$$

where $h_\mathrm{max}$ is a positive scalar and represents the largest sampling interval.

Thus, we have

$$\begin{aligned} t_{k+1}-t_{k}+\eta \le h_\mathrm{max}+\eta \triangleq h_{M} \end{aligned}$$

(5)

Here, $h_{M}$ denotes the maximum time span between the time $t_{k}-\eta$ at which the next update arrives at the destination. The main aim of this study is to design the sampled-data controller $C$ for the synchronization between master $M$ and slave $S$. That is the error between two dynamics must be equal to zero asymptotically. Let the error between master and slave systems be $e(t)=x(t)-z(t).$ Moreover, based on the above sampled-data controller design formulation, the feedback controller takes the following form:

$$\begin{aligned} u(t)=Ke(t_{k}-\eta ),\quad t_{k}\le t < t_{k+1},\quad k=0,1,2,\ldots \end{aligned}$$

(6)

with $t_{k+1}$ being the next updating instant time of the ZOH after $t_{k}.$ Then we obtain the closed loop synchronization error system

$$\begin{aligned} \dot{e}(t)&= Ae(t)+Hf(D^\mathrm{T}e(t))-KCe(t_{k}-\eta )\nonumber \\&-E\omega (t)+Np(t),\nonumber \\ p(t)&= F(t)q(t),\nonumber \\ q(t)&= N_{a}e(t)+N_{h}f(D^\mathrm{T}e(t)). \end{aligned}$$

(7)

where $f(D^\mathrm{T}e(t))=\sigma (D^\mathrm{T}e(t)\!+\!D^\mathrm{T}z(t))\!-\!\sigma (D^\mathrm{T}z(t)).$ Defining $\tau (t)=t-t_{k}+\eta ,$ $h_{\tau }(t)=h_{M} -\tau (t),$ thus we have $\eta \le \tau (t)<t_{k+1}-t_{k}+\eta \le h_{M},$ and $\dot{ \tau }(t)=1,$ for $t\ne t_{k}.$ It can be easily checked that $f_{i}(0)=0$, and the nonlinearity $f_{i}(\cdot )$ belongs to the sector [$\varpi _{i}^{+},\varpi _{i}^{-}$] for all $i=1,2,\ldots ,n_{h},$ and

$$\begin{aligned}{}[f_{i}(\xi )\!-\!\varpi _{i}^{+}\xi ][f_{i}(\xi )\!-\!\varpi _{i}^{-}\xi ]\le 0,\quad i\!=\!1,2,\ldots ,n_{h} \end{aligned}$$

(8)

Also, consider $K_{1}=\mathrm{diag}\{\varpi _{1}^{+},\varpi _{2}^{+},\ldots ,\varpi _{n_{k}}^{+}\},$ and $K_{2}=\mathrm{diag}\{\varpi _{1}^{-},\varpi _{2}^{-},\ldots ,\varpi _{n_{k}}^{-}\}.$ It is implied from the above formulation that the synchronization problem between $M$ and $S$ is converted into an equivalent absolute stability problem of the error dynamical systems (7). In this paper, we aim at establishing easily computable yet less conservative synchronization criteria by finding maximum sampling time $h_{\max }.$ Since a bigger sampling period leads to lower communication channel occupying, fewer behaviors of the controller, and less signal transmission, we aim to design a sampled-data controller $C$ to make slave system $S$ synchronize with master system $M$ under a sampling period as big as possible.

Now we state the following definitions and lemmas which will be used in the sequel.

Definition 2.1

The master system $M$ and slave system $S$ are said to be asymptotically synchronized if and only if the error dynamical systems (7) are globally asymptotically stable for the equilibrium point $e(t)\equiv 0.$ That is, $e(t)\rightarrow 0$ as $t\rightarrow \infty .$

Definition 2.2

The error system (7) is $H_{\infty }$ synchronized if the synchronization error $e(t)$ satisfies

$$\begin{aligned} \int _{0}^{\infty }e^\mathrm{T}(s)Se(s)\mathrm{d}s < \gamma ^2\int _{0}^{\infty }\omega ^\mathrm{T}(s)\omega (s)\mathrm{d}s \end{aligned}$$

for a given level $\gamma >0$ under zero initial condition, where $S$ is a positive symmetric matrix. The parameter $\gamma$ is called the $H_{\infty }$ norm bound or the disturbance attenuation level.

Lemma 2.3

[34] For any constant matrix $X\in \mathbb {R} ^{n\times n},X=X^\mathrm{T}>0$, there exist positive scalar $h$ such that $0\le h(t)\le h,$ and a vector-valued function $\dot{x}:[-h,0]\rightarrow \mathbb {R} ^{n},$ the integration $-h\int _{t-h}^{h}\dot{x}^\mathrm{T}(s)X\dot{x} (s)\mathrm{d}s$ is well defined,

$$\begin{aligned}&-h\int _{t-h}^{t}\dot{x}^\mathrm{T}(s)X\dot{x}(s)\mathrm{d}s\\&\quad \le \left[ \begin{array}{c} x(t) \\ x(t-h(t)) \\ x(t-h) \end{array} \right] ^\mathrm{T}\left[ \begin{array}{ccc} -X &{} X &{} 0 \\ *&{} -2X &{} X \\ *&{} *&{} X \end{array} \right] \left[ \begin{array}{c} x(t) \\ x(t-h(t)) \\ x(t-h) \end{array} \right] . \end{aligned}$$

Lemma 2.4

[22] Let there exist positive numbers $\alpha ,\beta ,$ and a functional $V:\mathbb {R}\times W[-\tau _{M},0]\times L_{2}[-\tau _{M},0]\rightarrow \mathbb {R}$ such that

$$\begin{aligned} \alpha \left| \phi (0)\right| ^{2}\le V(t,\phi ,\dot{\phi })\le \beta \left\| \phi \right\| _{W}^{2}. \end{aligned}$$

Let the function $\bar{V}(t)=V(t,x_{t},\dot{x}_{t}),$ where $x_{t}(\theta )=x(t+\theta ),$ and $\dot{x}_{t}(\theta )=\dot{x}(t+\theta )$ with $\theta \in [-\tau _{M},0]$ is continuous from the right for $x(t)$ satisfying the system , absolutely continuous for $t\ne t_{k}$ and satisfies $\lim \limits _{t\rightarrow t_{k}^{-}}\bar{V}(t)\ge \bar{V} (t_{k}).$ Through (7), $\overset{\cdot }{\bar{V}}(t)\le -\epsilon \left| e(t)\right| ^{2}$ for $t\ne t_{k}$ and for some scalar $\epsilon >0,$ hence (7) is asymptotically stable.

The purpose of this paper is to design the output feedback controller $u(t)$ guaranteeing the $H_{\infty }$ synchronizationif there exists the external disturbance $\omega (t)$. In addition, this controller $u(t)$ will be shown to guarantee the asymptotical synchronization when the system uncertainty and external disturbance $\omega (t)$ disappear.

3 Main results

In this section, sufficient conditions will be established to assure the synchronization between the master–slave system (1) by employing a new LKF, which captures the characteristic of sampled-data systems. For simplicity, the following notations are given:

$$\begin{aligned}&e_{i}=[0_{n\times (i-1)n} \ I_{n\times n}\! \ 0_{n\times (7-i)n}], i\!=\!1,2,3,4,5,6,7\\&\zeta (t)=[e^\mathrm{T}(t) \ e^\mathrm{T}(t-\eta )\ \ e^\mathrm{T}(t_{k}-\eta ) \ e^\mathrm{T}(t-h_{M})\\&\ f^\mathrm{T}(D^\mathrm{T}e(t)) \ \dot{e}^\mathrm{T}(t) \ p(t)]^\mathrm{T}. \end{aligned}$$

Theorem 3.1

For given positive scalars $h_{M}$, $\eta$, $\epsilon$, $\mu$, and $\gamma$, the master system $M$ and the slave system $S$ in (1) are synchronous if there exist matrices $P > 0, Q_{1}> 0, Q_{2}> 0, S > 0, S_{1} > 0, S_{2}$, $\varLambda =\mathrm{diag} (\lambda _{1}, \lambda _{2},\ldots , \lambda _{n_{h}}) > 0, \varDelta =\mathrm{diag}(\delta _{1}$, $\delta _{2},\ldots , \delta _{n_{h}})>0, K_{1}= \mathrm{diag}(\varpi _{1}^{+},\varpi _{2}^{+},\ldots ,\varpi _{n_{k}}^{\!+\!})$, $K_{2}=\mathrm{diag}(\varpi _{1}^{-},\varpi _{2}^{-},\ldots ,\varpi _{n_{k}}^{-}), T_{i}\ge 0,i=1,2$, $\bar{W}=\left[ \begin{array}{cc} W_{11} &{} W_{12}\\ *&{} W_{22} \end{array} \right] >0, \bar{R}=\left[ \begin{array}{cc} R_{11} &{} R_{12}\\ *&{} R_{22} \end{array} \right] >0,$ and any appropriately dimensioned matrices $\bar{X}=\left[ \begin{array}{cc} X_{1}+X_{1}^\mathrm{T} &{} -X_{1}-X_{2}\\ *&{} X_{2}+X_{2}^\mathrm{T} \end{array} \right] , G,L$, and $M=[M_{1}^\mathrm{T},M_{2}^\mathrm{T},M_{3}^\mathrm{T},M_{4}^\mathrm{T},M_{5}^\mathrm{T},M_{6}^\mathrm{T},M_{7}^\mathrm{T}]^\mathrm{T},$ such that

$$\begin{aligned} \varPhi =\left[ \begin{array}{cc} P+h_{M}(X_{1}+X_{1}^\mathrm{T}) &{} -h_{M}(X_{1}+X_{2})\\ *&{} h_{M}(X_{2}+X_{2}^\mathrm{T}) \end{array} \right] >0, \end{aligned}$$

(9)

$$\begin{aligned} \left[ \begin{array}{ccc} \varXi _{1} &{} \mu \varUpsilon _{1}^\mathrm{T} &{} \varPi _{1}^\mathrm{T}\\ *&{} -\mu I &{} 0\\ *&{} *&{} -\gamma ^{2}I \end{array} \right] <0, \end{aligned}$$

(10)

$$\begin{aligned} \left[ \begin{array}{ccc} \varXi _{2} &{} \mu \varUpsilon _{2}^\mathrm{T} &{} \varPi _{2}^\mathrm{T}\\ *&{} -\mu I &{} 0\\ *&{} *&{} -\gamma ^{2}I \end{array} \right] <0, \end{aligned}$$

(11)

where

$$\begin{aligned} \varXi _{1}&=\left[ \begin{array}{ccccccc} \varXi _{11}+\varPi _{11} &{} \varXi _{12} &{} \varXi _{13} &{} M_{4}^\mathrm{T} &{} \varXi _{15}+\varPi _{12} &{} \varXi _{16}+\varPi _{13} &{} \varXi _{17}\\ *&{} \varXi _{22} &{} \varXi _{23} &{} 0 &{} 0 &{} 0 &{} 0 \\ *&{} *&{} \varXi _{33}+h_{M}R_{11} &{} \varXi _{34} &{} \varXi _{35} &{} \varXi _{36}+\varPi _{14}&{}\varXi _{37}\\ *&{} *&{} *&{} \varXi _{44} &{} 0 &{} 0 &{} 0 \\ *&{} *&{} *&{} *&{} -2T_{2} &{} \varXi _{56} &{}0\\ *&{} *&{} *&{} *&{} *&{}\varXi _{66}+h_{M}R_{22}&{}\epsilon GN\\ *&{} *&{} *&{} *&{} *&{}*&{}-\mu I \end{array} \right] ,\\ \varXi _{2}&=\left[ \begin{array}{cccccccc} \varXi _{11}+\varPi _{21} &{} \varXi _{12} &{} \varXi _{13} &{} M_{4}^\mathrm{T} &{} \varXi _{15}+\varPi _{22} &{} \varXi _{16} &{}\varXi _{17}&{} -h_{M}M_{1} \\ *&{} \varXi _{22} &{} \varXi _{23} &{} 0 &{} 0&{}0 &{}0&{} -h_{M}M_{2} \\ *&{} *&{} \varXi _{33}-h_{M}R_{11} &{} \varXi _{34} &{} \varXi _{35} &{}\varXi _{36} &{}\varXi _{37}&{} \varPi _{23} \\ *&{} *&{} *&{} \varXi _{44} &{} 0 &{}0 &{}0&{} -h_{M}M_{4} \\ *&{} *&{} *&{} *&{} -2T_{1} &{}\varXi _{56} &{}0&{} -h_{M}M_{5} \\ *&{} *&{} *&{} *&{} *&{}\varXi _{66} &{}\epsilon GN&{} -h_{M}M_{6} \\ *&{} *&{} *&{} *&{} *&{} *&{} -\mu I&{}-h_{M}M_{7}\\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} -h_{M}R_{22} \end{array} \right] , \end{aligned}$$

$$\begin{aligned}&\varUpsilon _{1}=[N_{a} 0 0 0 N_{h} 0 0],\\&\varUpsilon _{2}=[\varUpsilon _{1} 0],\\&\varPi _{1}=[E^\mathrm{T}G^\mathrm{T} 0 E^\mathrm{T}G^\mathrm{T} 0 0 \epsilon E^\mathrm{T}G^\mathrm{T} 0],\\&\varPi _{2}=[\varPi _{1} 0],\\&\varPi _{11}=-2D^\mathrm{T}K_{1}T_{2}K_{2}D,\\&\varPi _{12}=D^\mathrm{T}(K_{1}+K_{2})T_{2},\\&\varPi _{13}=h_{M}(X_{1}+X_{1}^\mathrm{T}), \\&\varPi _{14}=h_{M}(R_{12}-X_{1}^\mathrm{T}-X_{2}^\mathrm{T}),\\&\varPi _{21}=-2D^\mathrm{T}K_{1}T_{1}K_{2}D,\\&\varPi _{22}=D^\mathrm{T}(K_{1}+K_{2})T_{1},\\&\varPi _{23}=-h_{M}(M_{3}+R_{12}),\\&\varXi _{11}=-(X_{1}+X_{1}^\mathrm{T})+S+S_{1}-S_{2}\\&\qquad \quad +M_{1}+M_{1}^\mathrm{T}+GA+A^\mathrm{T}G^\mathrm{T},\\&\varXi _{12}=S_{2}+M_{2}^\mathrm{T},\\&\varXi _{13}=X_{1}+X_{2}+M_{3}^\mathrm{T}-M_{1}-LC+A^\mathrm{T}G^\mathrm{T},\\&\varXi _{15}=M_{5}^\mathrm{T}+GH,\\&\varXi _{16}=M_{6}^\mathrm{T}+D^\mathrm{T}K_{1}\varLambda D -D^\mathrm{T}K_{2}\varDelta D\\&\qquad \quad +P-G+\epsilon A^\mathrm{T}G^\mathrm{T},\\&\varXi _{17}=M_{7}^\mathrm{T}+GN,\\&\varXi _{22}=-S_{1}-S_{2}+Q_{1}-Q_{2}+W_{22},\\&\varXi _{23}=W_{12}^\mathrm{T}+Q_{2}-M_{2},\\&\varXi _{33}=-(X_{2}+X_{2}^\mathrm{T})+W_{11}-Q_{2} -Q_{2}^\mathrm{T}\\&\qquad \quad -M_{3}-M_{3}^\mathrm{T}-LC-C^\mathrm{T}L^\mathrm{T},\\&\varXi _{34}=Q_{2}-M_{4}^\mathrm{T}, \end{aligned}$$

$$\begin{aligned} \varXi _{35}&= -M_{5}^\mathrm{T}+GH,\\ \varXi _{36}&= -M_{6}^\mathrm{T}-G-\epsilon C^\mathrm{T}L^\mathrm{T},\\ \varXi _{37}&= -M_{7}^\mathrm{T}+GN,\\ \varXi _{44}&= -Q_{1}-Q_{2},\\ \varXi _{56}&= -D\varLambda +D\varDelta +\epsilon H^\mathrm{T}G^\mathrm{T},\\ \varXi _{66}&= \eta ^{2}S_{2}+(h_{M}-\eta )^{2}Q_{2}-\epsilon G-\epsilon G^\mathrm{T}.\\ \end{aligned}$$

Moreover, the sampled-data controller gain matrix in (1) is given by $K=G^{-1}L$.

Proof

Consider the following LKF for the synchronization error system (7):

$$\begin{aligned}&V(t)=\underset{i=1}{\overset{6}{ {\displaystyle \sum }}}V_{i}(t),\quad t\in [t_{k},t_{k+1}), \end{aligned}$$

(12)

where

$$\begin{aligned}&V_{1}(t)=2\displaystyle \sum \limits _{i=1}^{n_{h}}\int _{0}^{d_{i}^\mathrm{T}e}[\lambda _{i}(\varpi _{i}^{+}s -f_{i}(s))\\&\qquad \quad +\delta _{i}(f_{i}(s)-\varpi _{i}^{-}s)]\mathrm{d}s,\\&V_{2}(t)=e^\mathrm{T}(t)Pe(t)+h_{\tau }(t)\varepsilon ^\mathrm{T}(t)\bar{X}\varepsilon (t),\\&V_{3}(t)=\int _{t-\eta }^{t}e^\mathrm{T}(s)S_{1}e(s)\mathrm{d}ds\\&\qquad \quad +\eta \int _{-\eta }^{0}\int _{t+\theta }^{t}\dot{e}^\mathrm{T}(s)S_{2} \dot{e}(s)\mathrm{d}s\mathrm{d}\theta ,\\ {}&V_{4}(t)=\int _{t-h _{M}}^{t-\eta }e^\mathrm{T}(s)Q_{1}e(s)\mathrm{d}s\\&\qquad \quad +(h _{M}-\eta )\int _{-h _{M}}^{-\eta }\int _{t+\theta }^{t} \dot{e}^\mathrm{T}(s)Q_{2}\dot{e}(s)\mathrm{d}s\mathrm{d}\theta ,\\&V_{5}(t)=\int _{t_{k}-\eta }^{t-\eta }\left[ \begin{array}{c} e(t_{k}-\eta ) \\ e(s) \end{array} \right] ^\mathrm{T}\bar{W} \left[ \begin{array}{c} e(t_{k}-\eta ) \\ e(s) \end{array} \right] \mathrm{d}s,\\&V_{6}(t)=h_{\tau }(t)\int _{t_{k}-\eta }^{t}\left[ \begin{array}{c} e(t_{k}-\eta ) \\ \dot{e}(s) \end{array} \right] ^\mathrm{T}\bar{R} \left[ \begin{array}{c} e(t_{k}-\eta ) \\ \dot{e}(s) \end{array} \right] \mathrm{d}s,\\&\varepsilon (t)=\left[ \begin{array}{c} e(t) \\ e(t_{k}-\eta ) \end{array} \right] . \end{aligned}$$

From the assumption, we know that $V_{1}(t),V_{3}(t),V_{4}(t),V_{5}(t)$, and $V_{6}(t)$ are positive. If $V_{2}(t)$ is positive, we can guarantee the positive of the LKF $V(t)$. We can get

$$\begin{aligned} V_{2}(t)&= \left( \frac{\tau (t)}{h _{M}}+\frac{h_{\tau }(t)}{h _{M}}\right) e^\mathrm{T}(t)Pe(t)\\&+\frac{h_{\tau }(t)}{h _{M} } \varepsilon ^\mathrm{T}(t)h _{M}\bar{X }\varepsilon (t) \\&= \frac{\tau (t)}{h _{M}}e^\mathrm{T}(t)Pe(t)+\frac{h_{\tau }(t)}{h _{M} } \int _{t_{k}-\eta }^{t}\varepsilon ^\mathrm{T}(t)\frac{\varPhi }{t-t_{k}+\eta }\varepsilon (t). \end{aligned}$$

If the LMI(9) holds, then $V_{2}(t)>0$, and the LKF(12) is positive. Then calculating the derivatives of $V(t)$. It is noted that the $V(t)$ is continuous on $[0,\infty )$ except the sampling instants $t_{k}$ $(k=0,1,2,\ldots ).$ When $t=t_{k},V_{5}(t)$ vanishes. Hence, the condition

$$\begin{aligned} \lim _{t\rightarrow t_{k}^{-}}V(t,e_{t},\dot{e}_{t})\ge V(t_{k}) \end{aligned}$$

holds. Calculating the time derivation of $V(t)$ along the trajectories of (7), we have

$$\begin{aligned}&\dot{V}_{1}(t)=2[(e^\mathrm{T}(t)D^\mathrm{T}K_{1}-f^\mathrm{T}(D^\mathrm{T}e(t)))\varLambda D\dot{e}(t)\nonumber \\&\qquad \qquad +(f^\mathrm{T}(D^\mathrm{T}e(t))-e^\mathrm{T}(t)D^\mathrm{T}K_{2})\varDelta D\dot{e}(t)], \end{aligned}$$

(13)

$$\begin{aligned}&\dot{V}_{2}(t)=2e^\mathrm{T}(t)P\dot{e}(t)-\varepsilon ^\mathrm{T}(t)\bar{X}\varepsilon (t)\nonumber \\&\qquad \qquad +2h_{\tau }(t)\varepsilon ^\mathrm{T}(t)\bar{X} \left[ \begin{array} [c]{c} \dot{e}(t) \\ 0 \end{array} \right] , \end{aligned}$$

(14)

$$\begin{aligned}&\dot{V}_{3}(t)=e^\mathrm{T}(t)S_{1}e(t)-e^\mathrm{T}(t-\eta )S_{1}e(t-\eta )\nonumber \\&\qquad \qquad +\eta ^{2} \dot{e}^\mathrm{T}(t)S_{2}\dot{e}(t)-\eta \int _{t-\eta }^{t}\dot{e} ^\mathrm{T}(s)S_{2}\dot{e}(s)\mathrm{d}s, \end{aligned}$$

(15)

$$\begin{aligned} \dot{V}_{4}(t)&= e^\mathrm{T}(t-\eta )Q_{1}e(t-\eta )-e^\mathrm{T}(t-h _{M})\nonumber \\&Q_{1}e(t-h_{M})+(h_{M}-\eta )^{2}\dot{e}^\mathrm{T}(t)Q_{2}\dot{e}(t)\nonumber \\&-(h_{M}-\eta )\int _{t-h_{M}}^{t-\eta }\dot{e} ^\mathrm{T}(s)Q_{2}\dot{e}(s)\mathrm{d}s, \end{aligned}$$

(16)

$$\begin{aligned} \dot{V}_{5}(t)=\left[ \begin{array}{c} e(t_{k}-\eta ) \\ e(t-\eta ) \end{array} \right] ^\mathrm{T}\bar{W}\left[ \begin{array}{c} e(t_{k}-\eta ) \\ e(t-\eta ) \end{array} \right] , \end{aligned}$$

(17)

$$\begin{aligned} \dot{V}_{6}(t)=&-\int _{t_{k}-\eta }^{t}\left[ \begin{array}{c} e(t_{k}-\eta ) \\ \dot{e}(s) \end{array} \right] ^\mathrm{T}\bar{R} \left[ \begin{array}{c} e(t_{k}-\eta ) \\ \dot{e}(s) \end{array} \right] \mathrm{d}s\nonumber \\&+h_{\tau }(t)\left[ \begin{array}{c} e(t_{k}-\eta ) \\ \dot{e}(t) \end{array} \right] ^\mathrm{T}\bar{R} \left[ \begin{array}{c} e(t_{k}-\eta ) \\ \dot{e}(t) \end{array} \right] . \end{aligned}$$

(18)

By using Lemma 2.2 to (15) and (16) , we have

$$\begin{aligned}&-\eta \int _{t-\eta }^{t}\dot{e}^\mathrm{T}(s)S_{2}\dot{e}(s)\mathrm{d}s\nonumber \\&\quad \le - \left[ \begin{array}{c} e(t) \\ e(t-\eta ) \end{array} \right] ^\mathrm{T}\left[ \begin{array}{cc} S_{2} &{} -S_{2} \\ *&{} S_{2} \end{array} \right] \left[ \begin{array}{c} e(t) \\ e(t-\eta ) \end{array} \right] , \end{aligned}$$

(19)

$$\begin{aligned}&-(h_{M}-\eta )\int _{t-h_{M}}^{t-\eta }\dot{e}^\mathrm{T}(s)Q_{2} \dot{e}(s)\mathrm{d}s\nonumber \\&\quad \!\le \! -\!\left[ \begin{array}{c} e(t\!-\!\eta ) \\ e(t\!-\!\tau (t)) \\ e(t\!-\!h _{M}) \end{array} \right] ^\mathrm{T}\left[ \begin{array}{ccc} Q_{2} &{} \!-Q_{2} &{} 0 \\ *&{} 2Q_{2} &{} -Q_{2} \\ *&{} *&{} Q_{2} \end{array} \right] \left[ \begin{array}{c} e(t\!-\!\eta ) \\ e(t\!-\!\tau (t)) \\ e(t\!-\! h _{M}) \end{array} \right] .\nonumber \\ \end{aligned}$$

(20)

Applying (19) and (20) to (15) and (16), we can get

$$\begin{aligned} \dot{V}_{3}(t)&=e^\mathrm{T}(t)S_{1}e(t) -e^\mathrm{T}(t-\eta )S_{1}e(t-\eta )\nonumber \\&\quad +\eta ^{2} \dot{e}^\mathrm{T}(t)S_{2}\dot{e}(t)\nonumber \\&\quad - \left[ \begin{array}{c} e(t) \\ e(t-\eta ) \end{array} \right] ^\mathrm{T}\left[ \begin{array}{cc} S_{2} &{} -S_{2} \\ *&{} S_{2} \end{array} \right] \left[ \begin{array}{c} e(t) \\ e(t-\eta ) \end{array} \right] , \end{aligned}$$

(21)

$$\begin{aligned} \dot{V}_{4}(t)&=e^\mathrm{T}(t-\eta )Q_{1}e(t-\eta )-e^\mathrm{T}(t-h_{M})Q_{1}e(t-h _{M})\nonumber \\&+(h _{M}-\eta )^{2}\dot{e}^\mathrm{T}(t)Q_{2}\dot{e}(t)\nonumber \\&-\left[ \begin{array}{c} e(t-\eta ) \\ e(t-\tau (t)) \\ e(t-h _{M}) \end{array} \right] ^\mathrm{T}\left[ \begin{array}{ccc} Q_{2} &{} -Q_{2} &{} 0 \\ *&{} 2Q_{2} &{} -Q_{2} \\ *&{} *&{} Q_{2} \end{array} \right] \left[ \begin{array}{c} e(t-\eta ) \\ e(t-\tau (t)) \\ e(t-h _{M}) \end{array} \right] . \end{aligned}$$

(22)

For any appropriately dimensioned matrix $M$, the following equation is true:

$$\begin{aligned} 0=2\zeta ^\mathrm{T}(t)M[e(t)-e(t_{k}-\eta )-\int _{t_{k}-\eta }^{t}\dot{e} (s)\mathrm{d}s].\nonumber \\ \end{aligned}$$

(23)

On the other hand, according to (7), for any appropriately dimensioned matrices $G$ and scalar $\epsilon ,$ the following equation is true:

$$\begin{aligned} 0&=2[e^\mathrm{T}(t)+e^\mathrm{T}(t_{k}-\eta )+\epsilon \dot{e}^\mathrm{T}(t)] [-G\dot{e}(t)\nonumber \\&\quad +GAe(t) +GHf(D^\mathrm{T}e(t))-GKCe(t_{k}-\eta ) \nonumber \\&\quad -GE\omega (t)+GNp(t)]\nonumber \\&=2[e^\mathrm{T}(t)+e^\mathrm{T}(t_{k}-\eta )+\epsilon \dot{e}^\mathrm{T}(t)] [-G\dot{e}(t)\nonumber \\&\quad +GAe(t)+GHf(D^\mathrm{T}e(t))\nonumber \\&\quad -GKCe(t_{k}-\eta )+GNp(t)]-2[e^\mathrm{T}(t)\nonumber \\ {}&\quad +e^\mathrm{T}(t_{k}-\eta )+\epsilon \dot{e}^\mathrm{T}(t)]GE\omega (t). \end{aligned}$$

(24)

If we use the inequality $-2X^\mathrm{T}Y\le X^\mathrm{T}\varLambda X+Y^\mathrm{T}\varLambda ^{-1} Y$, which is valid for any matrices $X\in \mathbb {R}^{n\times m}$, $Y\in \mathbb {R}^{n\times m}$, $\varLambda =\varLambda ^\mathrm{T}>0, \varLambda \in \mathbb {R}^{n\times n}$, we have

$$\begin{aligned}&-2[e^\mathrm{T}(t)+e^\mathrm{T}(t_{k}-\eta )+\epsilon \dot{e}^\mathrm{T}(t)]GE\omega (t)\nonumber \\&\le \frac{1}{\gamma ^{2}}\zeta ^\mathrm{T}(t)\varPi _{1}^\mathrm{T}\varPi _{1}\zeta (t)+\gamma ^{2}\omega ^\mathrm{T}(t)\omega (t). \end{aligned}$$

(25)

Also, from (2) and (3), we have

$$\begin{aligned} p^\mathrm{T}(t)p(t)\le q^\mathrm{T}(t)q(t). \end{aligned}$$

(26)

Then, there exists a positive constant, $\mu$, satisfying the following equation:

$$\begin{aligned} \mu [\zeta ^\mathrm{T}\varUpsilon _{1}^\mathrm{T}\varUpsilon _{1}\zeta -p^\mathrm{T}(t)p(t)]\ge 0. \end{aligned}$$

(27)

Moreover, for any $T_{i}=\mathrm{diag}(t_{1i},t_{2i},\ldots ,t_{n_{h}i})\ge 0,i=1,2,$ it follows form (8) that

$$\begin{aligned} g(i,t)&= 2[e^\mathrm{T}(t)D^\mathrm{T}K_{1}-f(D^\mathrm{T}e(t))]\\&T_{i}[f(D^\mathrm{T}e(t))-e(t)D^\mathrm{T}K_{2}]\ge 0 \end{aligned}$$

then

$$\begin{aligned} \frac{\tau (t)}{h _{M}}g(1,t)+\frac{h_{\tau }(t)}{h _{M}}g(2,t)\ge 0. \end{aligned}$$

(28)

By using (13), (14), (17), (18), and (21)–(28), letting $L=GK$, we obtain

$$\begin{aligned} \dot{V}(t)=\dot{\hat{V}}(t)-e^\mathrm{T}(t)Se(t)+\gamma ^{2}\omega ^\mathrm{T}(t)\omega (t), \end{aligned}$$

where

$$\begin{aligned} \dot{\hat{V}}(t)&=\zeta ^\mathrm{T}(t)\left[ \varPhi _{0}+\frac{\tau (t)}{h_{M}}\varPhi _{1}+\frac{h_{\tau }(t)}{h_{M}}(\varPhi _{2}+h_{M}\varPhi _{3})\right] \\&\quad \ \zeta (t)-\int _{t_{k}-\eta }^{t}\left[ \begin{array} [c]{c} \zeta (t)\\ \dot{e}(s) \end{array} \right] ^\mathrm{T}\varPhi _{4}\left[ \begin{array} [c]{c} \zeta (t)\\ \dot{e}(s) \end{array} \right] \mathrm{d}s\\&=\frac{h_{\tau }(t)}{h_{M}}\zeta ^\mathrm{T}(t)(\varXi _{1}+\mu \varUpsilon _{1}^\mathrm{T}\varUpsilon _{1}+ \gamma ^{-2}\varPi _{1}^\mathrm{T}\varPi _{1})\zeta (t)\\&\quad +\frac{1}{h_{M}} \int _{t_{k}-\eta }^{t}\left[ \begin{array} [c]{c} \zeta (t)\\ \dot{e}(s) \end{array} \right] ^\mathrm{T}(\varXi _{2}+\mu \varUpsilon _{2}^\mathrm{T}\varUpsilon _{2}\\&\quad + \gamma ^{-2}\varPi _{2}^\mathrm{T}\varPi _{2})\left[ \begin{array}{c} \zeta (t)\\ \dot{e}(s) \end{array} \right] \mathrm{d}s. \end{aligned}$$

$\varXi _{1},\varXi _{2}$ are given in (10) and (11), and

$$\begin{aligned} \varPhi _{0}=\varPhi _{11}+\varPhi _{12}+\varPhi _{12}^\mathrm{T}, \end{aligned}$$

$$\begin{aligned} \varPhi _{11}&=e_{1}^\mathrm{T}Se_{1}-\mu e_{7}^\mathrm{T}e_{7}+e_{1}^\mathrm{T}S_{1}e_{1}-e_{2}^\mathrm{T}S_{1}e_{2}\\&\quad +\eta ^{2}e_{6}^\mathrm{T}S_{1}e_{2} +e_{2}^\mathrm{T}Q_{1}e_{2}-e_{4}^\mathrm{T}Q_{1}e_{4}\\&\quad +(h_{M}-\eta )^{2}e_{6}^\mathrm{T}Q_{2}e_{6} -\left[ \begin{array} [c]{c} e_{1}\\ e_{3} \end{array} \right] ^\mathrm{T}\bar{X}\left[ \begin{array} [c]{c} e_{1}\\ e_{3} \end{array} \right] \\&\quad -\left[ \begin{array} [c]{c} e_{1}\\ e_{2} \end{array} \right] ^\mathrm{T}\left[ \begin{array} [c]{cc} S_{2} &{} -S_{2} \\ *&{} S_{2} \end{array} \right] \left[ \begin{array} [c]{c} e_{1}\\ e_{2} \end{array} \right] +\left[ \begin{array} [c]{c} e_{3}\\ e_{2} \end{array} \right] ^\mathrm{T}\\&\qquad \ \bar{W} \left[ \begin{array} [c]{c} e_{3}\\ e_{2} \end{array} \right] -\left[ \begin{array} [c]{c} e_{2}\\ e_{3}\\ e_{4} \end{array} \right] ^\mathrm{T}\left[ \begin{array} [c]{ccc} Q_{2} &{} -Q_{2}&{}0 \\ *&{} 2Q_{2}&{} -Q_{2}\\ *&{}*&{} Q_{2} \end{array} \right] \left[ \begin{array} [c]{c} e_{2}\\ e_{3}\\ e_{4} \end{array} \right] \!\!,\\ \end{aligned}$$

$$\begin{aligned} \varPhi _{12}&=e_{1}^\mathrm{T}Pe_{6}+(e_{1}^\mathrm{T}D^\mathrm{T}K_{1}-e_{5}^\mathrm{T})\varLambda De_{6}\\&\quad +(e_{5}^\mathrm{T}-e_{1}^\mathrm{T}D^\mathrm{T}K_{2})\varDelta De_{6}\\&\quad +(e_{1}^\mathrm{T}M_{1}+e_{2}^\mathrm{T}M_{2}+e_{3}^\mathrm{T}M_{3}+e_{4}^\mathrm{T}M_{4}\\&\quad +e_{5}^\mathrm{T}M_{5}+e_{6}^\mathrm{T}M_{6}+e_{7}^\mathrm{T}M_{7})(e_{1}-e_{3})\\&\quad +(e_{1}^\mathrm{T}+e_{3}^\mathrm{T}+\epsilon e_{6}^\mathrm{T})(-Ge_{6}+GAe_{1}\\&\quad +GHe_{5}-LCe_{3}+GNe_{7}), \end{aligned}$$

$$\begin{aligned} \varPhi _{i}&=\left[ \begin{array} [c]{c} e_{1}\\ e_{5} \end{array} \right] ^\mathrm{T}\left[ \begin{array} [c]{cc} -2D^\mathrm{T}K_{1}T_{i}K_{2}D &{} D^\mathrm{T}(K_{1}+K_{2})T_{i}\\ *&{} -2T_{i} \end{array} \right] \\ {}&\quad \left[ \begin{array} [c]{c} e_{1}\\ e_{5} \end{array} \right] ,i=1,2 \end{aligned}$$

$$\begin{aligned} \varPhi _{3}&=\left[ \begin{array} [c]{c} e_{3}\\ e_{6} \end{array} \right] ^\mathrm{T}\bar{R}\left[ \begin{array} [c]{c} e_{3}\\ e_{6} \end{array} \right] +\left[ \begin{array} [c]{c} e_{1}\\ e_{3} \end{array} \right] ^\mathrm{T}\bar{X}\left[ \begin{array} [c]{c} e_{6}\\ 0 \end{array} \right] \\ {}&\quad +\left[ \begin{array} [c]{c} e_{6}\\ 0 \end{array} \right] ^\mathrm{T}\bar{X}\left[ \begin{array} [c]{c} e_{1}\\ e_{3} \end{array} \right] , \end{aligned}$$

$$\begin{aligned} \varPhi _{4}=\left[ \begin{array} [c]{ccccccccc} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} &{} 0 &{} M_{1}\\ *&{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} &{} 0 &{} M_{2}\\ *&{} *&{} R_{11}&{} 0 &{} 0 &{} 0 &{} &{} 0 &{} R_{12}+M_{3}\\ *&{} *&{} *&{} 0 &{} 0 &{} 0 &{} &{} 0 &{} M_{4}\\ *&{} *&{} *&{} *&{} 0 &{} 0 &{} &{} 0 &{} M_{5}\\ *&{} *&{} *&{} *&{} *&{} 0 &{} &{} 0 &{} M_{6}\\ *&{} *&{} *&{} *&{} *&{} *&{} &{} 0 &{} M_{7}\\ *&{} *&{} *&{} *&{} *&{} *&{} &{} *&{} R_{22} \end{array} \right] . \end{aligned}$$

If $\dot{\hat{V}}(t)<0$, we have

$$\begin{aligned} \dot{V}(t)<-e^\mathrm{T}(t)Se(t)+\gamma ^{2}\omega ^\mathrm{T}(t)\omega (t). \end{aligned}$$

(29)

Integrating both sizes of (29) from 0 to $\infty$ gives

$$\begin{aligned}&V(\infty )-V(0)<-\int _{0}^{\infty }e^\mathrm{T}(s)Se(s)\mathrm{d}s\\&\quad +\gamma ^{2}\int _{0}^{\infty }\omega ^\mathrm{T}(s)\omega (s)\mathrm{d}s. \end{aligned}$$

From Schur complement, $\dot{\hat{V}}(t)<0$ is equivalent to the LMI (10) and (11), since $V(\infty )>0$ and $V(0)=0$, then, by Definition 2.2, the error systems (7) are $H_{\infty }$ synchronized. This implies that the synchronization between the master and slave systems is achieved by the designed controller (6), and the sampled-data controller gain matrix is given by $K=G^{-1}L$. This completes the proof.

Remark 3.2

It is noted that the characteristic of sampling instants has been considered for the construction of the LKF, which makes full use of the available information about the actual sampling pattern. Compared with the LKF used in [35], $\ V_{2}(t)$ and $V_{6}(t)$ are introduced to take the fact into account. As a consequence, the proposed synchronization criterion has less conservatism.

Remark 3.3

Through introducing Lyapunov matrices $\bar{X}$-dependent term, the constraint conditions of the matrices in the LKF have been relaxed. In the above criterion, this constraint is replaced by a more relaxable condition (9) to keep $V_{2}(t)$ positive.

Remark 3.4

The information of the slope of the nonlinear function has been used. The slope $\omega _{i}^{+},\omega _{i}^{-}$ is applied to construct the first term of the LKF, while the LKFs used in [34] ignore this information.

To the end of this section, when the system uncertainty and external disturbance disappear, letting $\eta =0$, by using the method employed in the proof of Theorem 3.1, we have the following corollary.

Corollary 3.5

For given scalars $h_{\max }>0$,and $\epsilon$, the master system $M$ and the slave system $S$ in (1) are synchronous if there exist matrices $P>0, Q_{1}>0, Q_{2}>0, \varLambda =\mathrm{diag}(\lambda _{1}, \lambda _{2},\ldots , \lambda _{n_{h}})>0, \varDelta =\mathrm{diag}(\delta _{1},\delta _{2},\ldots , \delta _{n_{h}})>0, K_{1}=\mathrm{diag}(\varpi _{1}^{+}, \varpi _{2}^{+},\ldots ,\varpi _{n_{k}}^{+}), K_{2}=\mathrm{diag}(\varpi _{1}^{-}, \varpi _{2}^{-},\ldots ,\varpi _{n_{k}}^{-}), T_{i}\ge 0,i=1,2, \bar{W}=\left[ \begin{array} [c]{cc} W_{11} &{} W_{12}\\ *&{} W_{22} \end{array} \right] >0, \bar{R}=\left[ \begin{array} [c]{cc} R_{11} &{} R_{12}\\ *&{} R_{22} \end{array} \right] >0,$ and any appropriately dimensioned matrices $\bar{X}=\left[ \begin{array} [c]{cc} X_{1}+X_{1}^\mathrm{T} &{} -X_{1}-X_{2}\\ *&{} X_{2}+X_{2}^\mathrm{T} \end{array} \right] , G,L$ and $M=[M_{1}^\mathrm{T},M_{2}^\mathrm{T},M_{3}^\mathrm{T},M_{4}^\mathrm{T},M_{5}^\mathrm{T}]^\mathrm{T},$ such that

$$\begin{aligned} \varPhi =\left[ \begin{array} [c]{cc} P+h_{\max }(X_{1}+X_{1}^\mathrm{T}) &{} -h_{\max }(X_{1}+X_{2})\\ *&{} h_{\max }(X_{2}+X_{2}^\mathrm{T}) \end{array} \right] >0, \end{aligned}$$

(30)

$$\begin{aligned} \varXi _{3}&= \left[ \begin{array}{ccccc} \hat{\varXi } _{11}+\varPi _{11} &{} \hat{\varXi } _{12}&{} M_{3}^\mathrm{T} &{} \hat{\varXi } _{14}+\varPi _{12} &{} \hat{\varXi }_{15}+\hat{\varPi } _{13} \\ *&{} \hat{\varXi } _{22}+h_{\max }R_{11} &{} \hat{\varXi }_{23} &{} -M_{4}^\mathrm{T} &{}\hat{\varPi } _{14}-M_{5}^\mathrm{T}\\ *&{} *&{} \hat{\varXi } _{33} &{} 0 &{} 0 \\ *&{} *&{} *&{} -2T_{2} &{}\hat{ \varXi } _{45} \\ *&{} *&{} *&{} *&{} \hat{\varXi } _{55}+h_{\max }R_{22} \\ \end{array} \right] <0,\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \,\, \end{aligned}$$

(31)

$$\begin{aligned} \varXi _{4}&= \left[ \begin{array}{cccccc} \hat{\varXi } _{11}+\varPi _{21} &{} \hat{\varXi } _{12} &{} M_{3}^\mathrm{T} &{} \hat{\varXi } _{14}+\varPi _{22} &{} \hat{\varXi }_{15} &{} -h_{\max }M_{1} \\ *&{} \hat{\varXi } _{22}-h_{\max }R_{11} &{} \hat{\varXi } _{23} &{} -M_{4}^\mathrm{T} &{} -M_{5}^\mathrm{T} &{} \hat{\varPi }_{23} \\ *&{} *&{} \hat{\varXi } _{33} &{} 0 &{} 0 &{} -h_{\max }M_{3}\\ *&{} *&{} *&{} -2T_{1} &{} \hat{\varXi } _{45} &{} -h_{\max }M_{4}\\ *&{} *&{} *&{} *&{} \hat{\varXi } _{55} &{} -h_{\max }M_{5}\\ *&{} *&{} *&{} *&{} *&{}-h_{\max }R_{22} \end{array} \right] <0,\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \,\, \end{aligned}$$

(32)

where

$$\begin{aligned} \hat{\varPi }_{13}&= h_{\max }(X_{1}+X_{1}^\mathrm{T}),\\ \hat{\varPi }_{14}&= h_{\max }(R_{12}-X_{1}^\mathrm{T}-X_{2}^\mathrm{T}),\\ \hat{\varPi }_{23}&= -h_{\max }(M_{2}+R_{12}),\\ \hat{\varXi }_{11}&= -(X_{1}+X_{1}^\mathrm{T})+M_{1}+M_{1}^\mathrm{T}+GA+A^\mathrm{T}G^\mathrm{T}\\&+Q_{1}-Q_{2}+W_{22},\\ \hat{\varXi }_{12}&= X_{1}+X_{2}+W_{12}^\mathrm{T}+Q_{2}-M_{1}-LC\\&+A^\mathrm{T}G^\mathrm{T}+M_{2}^\mathrm{T},\\ \hat{\varXi }_{14}&= M_{4}^\mathrm{T}+GH,\\ \hat{\varXi }_{15}&= M_{5}^\mathrm{T}+D^\mathrm{T}K_{1}\varLambda D-D^\mathrm{T}K_{2}\varDelta D+P-G\\&+\epsilon A^\mathrm{T}G^\mathrm{T},\\ \hat{\varXi }_{22}&= -(X_{2}+X_{2}^\mathrm{T})+W_{11}-Q_{2}-Q_{2}^\mathrm{T}\\&-M_{2}-M_{2}^\mathrm{T}-LC-C^\mathrm{T}L^\mathrm{T},\\ \hat{\varXi } _{23}&= Q_{2}-M_{3}^\mathrm{T},\\ \hat{\varXi } _{33}&= -Q_{1}-Q_{2},\\ \hat{\varXi } _{45}&= -D\varLambda +D\varDelta +\epsilon H^\mathrm{T}G^\mathrm{T},\\ \hat{\varXi } _{55}&= h_{\max }^{2}Q_{2}-\epsilon G-\epsilon G^\mathrm{T}. \end{aligned}$$

and the other parameters are given in Theorem 3.1. Moreover, the sampled-data controller gain matrix in (1) is given by $K=G^{-1}L$.

Remark 3.6

Corollary 3.5 provides a new synchronization criterion for the master system $M$ and the slave system $S$ in (1). It should be pointed out that the term $V_{1}(t),V_{2}(t),$ and $V_{6}(t)$ are neglected in [34], which will reduce the conservatism of the LKF.

The objective of this paper is to calculate the maximum admissible sampling period and the corresponding control gains based on the conditions given in Theorem 3.1 and Corollary3.5 for the preset $\epsilon .$ The major difference lies in $V_{2}(t)$ and $V_{6}(t)$ by making use of the actual pattern of the sampling time and delay induced in ZOH.

4 Numerical examples

In this section, we provide one illustrative example to show the validity and reduced conservatism of the proposed new synchronization scheme.

Example 4.1

Consider the following time-delay Chua’s circuit via sampled-data feedback control. The equation of Chua’s circuit can be expressed as

$$\begin{aligned}&\dot{x}_{1}(t)=a(x_{2}(t)-m_{1}x_{1}(t)+\sigma (x_{1}(t)))-cx_{1}(t)\\&\dot{x}_{2}(t)=x_{1}(t)-x_{2}(t)+x_{3}(t)-cx_{1}(t)\\&\dot{x}_{3}(t)=-bx_{2}(t)+c(2x_{1}(t)-x_{3}(t)) \end{aligned}$$

with the nonlinear characteristics

$$\begin{aligned} \sigma (x_{1}(t))=\frac{1}{2}(m_{1}-m_{0})(\left| x_{1}(t)+1\right| -\left| x_{1}(t)-1\right| ) \end{aligned}$$

belonging to sector $[0,1]$, and parameters $m_{0}=-1/7,m_{1} =2/7,a=9,b=14.28,c=0.1$.

Obviously, the system can be rewritten as the Lur’e form with the following parameters:

$$\begin{aligned} A&= \left[ \begin{array} [c]{ccc} -am_{1} &{} a &{} 0\\ 1 &{} -1 &{} 1\\ 0 &{} -b &{} 0 \end{array} \right] ,H=\left[ \begin{array} [c]{c} -a(m_{0}-m_{1})\\ 0\\ 0 \end{array} \right] ,\\ C&= D=\left[ \begin{array} [c]{ccc} 1&0&0 \end{array} \right] , \end{aligned}$$

The initial conditions of the master and slave systems are chosen as $x(t)=\left[ 0.2\,\, 0.3\,\, 0.2\right] ^\mathrm{T} \hbox {and} z(t)=\left[ -0.3\,\, -0.1 \,\,0.4 \right] ^\mathrm{T},$ respectively.

By setting $\eta =0,\epsilon =2$ using Matlab LMI Toolbox, we obtain the maximum values of the sampling period $h_{\max }=0.5147$ using Corollary 3.5 given in this paper, the maximum value of the sampling period that allows the synchronization of the master and slave systems is 0.5147 and the corresponding gain matrix is $K=\left[ 3.1272\,\,0.0982\,\,-2.9132 \right] ^\mathrm{T}.$ Our result and some other results are listed in Table 1.

Table 1 Maximum value of sampling period for Chua system with $\eta =0$

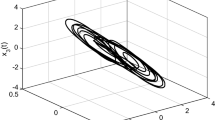
The responses of the states $x(t)$ and $z(t),$ the error signal $e(t),$ for the system under the controller $K$ with the sampling period of 0.5147 are shown in Figs. 1 and 2, which show that the controller can effectively achieve the master–slave synchronization. For different values of $\eta$ and $\epsilon$, the obtained $h_{M}$ results are listed in Table 2. The results shows that the controller obtained by the proposed criterion can achieve the master–slave synchronization under a bigger sampling period.

Fig. 1

Response of x(t) and z(t) with the sampling period of 0.5147

Fig. 2

Response of e(t) with the sampling period of 0.5147

5 Conclusion

It this paper, a sampled-data $H_{\infty }$ control approach is proposed for the robust synchronization problem of chaotic Lur’e system. A new discontinuous LKF is introduced for the synchronization error system, which takes the information of the nonlinear function into account. A new term has been applied to guarantee the non-negative of the LKF by making the sum of several terms be positive. The explicit expression of the desired sampled-data controller obtained via the proposed criterion can provide a bigger value of the upper bound in achieving synchronization compared with the published results.

Table 2 Maximum value of the sampling period with different $\eta$