Particle filtering for nonlinear dynamic state systems with unknown noise statistics

Abstract

In this paper, we provide a tutorial for the applications of cost-reference particle filter (CRPF) to problems in signal processing disciplines. CRPF works in particle filtering (PF) framework although it may not be viewed as a Bayesian approach because the estimation is not based on the expected posterior function. CRPF has an interesting feature, i.e., the information of the noise statistics is not needed in its applications as opposed to the cases of the Kalman filter and standard PF approaches that work in dynamic state systems. Therefore, it is highly effective when the noise information is not available; nevertheless, it may not show optimal performance in general. In this paper, we introduce and disseminate this useful approach that is not known to many researchers even in related fields, and show how to effectively apply to problems which we provide as examples.

1 Introduction

We introduce the Kalman filter (KF) and particle filter (PF) before we discuss cost-reference particle filter (CRPF) because the CRPF is a variant of PF and PF is developed based on the KF. In many problems of signal processing disciplines, the estimate of a “targeted state” is obtained based on some measurement which is a function of the state. Particularly, if the state system can be described by the discrete time-varying states in a stochastic process, we can estimate the targeted state sequentially by probabilistic approaches. Probabilistic approaches are also called Bayesian methods which are modern approaches compared to classical maximum likelihood (ML) methods. ML methods assume that the target to be estimated is a deterministic variable rather than random variable. Therefore, based on Bayesian methods, the target is estimated to be an expected value rather than a definite value, which is a prominent difference between the two approaches. The dynamic state system that describes the hidden state $\varvec{s}$ and observed measurement $\varvec{m}$ with zero mean and additive noise processes of $\varvec{u}$ and $\varvec{w}$ at time step $k$ are expressed as follows:

$$\begin{aligned}&\varvec{s}_k = g\left(\varvec{s}_{k-1} \right)+ \varvec{u}_k, \end{aligned}$$

(1)

$$\begin{aligned}&\varvec{m}_k = h\left(\varvec{s}_k \right)+ \varvec{w}_k, \end{aligned}$$

(2)

where boldface denotes a vector representation, $g(\cdot )$ and $h(\cdot )$ are the given state transition function and the measurement function, respectively, which are possibly nonlinear. Based on this system model, we can estimate the time-varying state $\varvec{s}_k$ sequentially by using the obtained measurement $\varvec{m}_k$ at each time step via the dynamic filters, e.g., the Kalman filter, particle filter, and their variants. The minimum mean squared error (MMSE) estimate can be obtained as follows (see [23], Ch. 11 for detailed derivation of MMSE estimator):

$$\begin{aligned} \hat{\varvec{s}}^{\mathrm{MMSE}}_k = \int \varvec{s}_k p(\varvec{s}_{0:k} | \varvec{m}_{1:k}) d\varvec{s}_k, \end{aligned}$$

(3)

where “$1:k$” indicates the time indices from 1 to $k, \hat{}$ denotes a estimated version, and $p (\varvec{s}_{0:k} | \varvec{m}_{1:k})$ is the posterior density. In the particular case, both $g(\cdot )$ and $h(\cdot )$ are linear functions; and $\varvec{u}_k$ and $\varvec{w}_k$ are Gaussian distributed, the Kalman filter (KF) is the optimal MMSE estimator [21]. The KF estimates the state sequentially in a closed form as follows:

$$\begin{aligned} \hat{\varvec{s}}^{\mathrm{KF}}_k = \bar{\varvec{s}}_k + \mathcal {K}_k \left[\varvec{m}_k - h(\bar{\varvec{s}}_k) \right], \end{aligned}$$

(4)

where $\mathcal {K}_k$ is the Kalman gain that is computed by the algorithm at each time step, and $\bar{\varvec{s}}_k = g\left(\hat{\varvec{s}}^{\mathrm{KF}}_{k-1} \right)$ (see [23], Ch. 13 and [19], Ch. 7 for details of KF).

In general cases, i.e., other than the linear and Gaussian case, there exist a number of sub-optimal approaches such as particle filtering (PF) [2, 40]. The Kalman filter also can be applied as a sub-optimal approach to nonlinear model by extending it using Taylor series (in this case, still Gaussian noise is assumed) [1, 17, 22, 27, 37]. Readers can be referred to [19, 24] for more details about Kalman filtering and extended Kalman filtering. Particle filtering generates random particles (which represent the possible states) according to a proposal density (or importance function) based on the posterior function. The weight of each particle is computed based on the relation of the proposal density to the posterior function, and normalized. Therefore, the posterior function is approximated by particles as follows:

$$\begin{aligned} p(\varvec{s}_{0:k}|\varvec{m}_{1:k}) \approx \sum ^{N}_{i_p=1} \omega ^{i_p}_k \delta (\varvec{s}_{0:k} - \varvec{s}^{i_p}_{0:k}), \end{aligned}$$

(5)

where $i_p$ is the particle index, $N$ is the number of employed particles, $\omega ^{i_p}_k$ is the weight of the particle $i_p$ at the time step $k$, and $\delta (\cdot )$ denotes the Dirac delta function that has the following property:

$$\begin{aligned} \delta (\varvec{s}_{k} - \varvec{s}^{i_p}_k) = \left\{ \begin{array}{ll} +\infty ,\quad \; \varvec{s}_{k} = \varvec{s}^{i_p}_k, \\ 0, \qquad \,\,\,\, \varvec{s}_{k} \ne \varvec{s}^{i_p}_k. \end{array} \right. \end{aligned}$$

The estimate is obtained in two criteria: i.e., MMSE and maximum a posteriori (MAP) estimates as follows:

$$\begin{aligned}&\hat{\varvec{s}}^{\mathrm{PF}}_k = \nonumber \\&\quad \left\{ \begin{array}{ll} \hat{\varvec{s}}^{\mathrm{MMSE}}_k =\sum \limits ^N_{i_p=1} \omega ^{i_p}_k \varvec{s}^{i_p}_k \\ \hat{\varvec{s}}^{\mathrm{MAP}}_k = \arg \max _{\varvec{s}_k \in \big \{ \varvec{s}^{i_p}_k \big \}^N_{i_p=1}} \left[\sum \limits ^N_{i_p=1} \delta \left(\varvec{s}^{i_p}_k - \varvec{s}_k \right)\omega ^{i_p}_k \right]. \end{array} \right. \nonumber \\ \end{aligned}$$

(6)

There are variants of the extended KF (EKF) and those of PF approaches: e.g., unscented KF (UKF), Gaussian PF, auxiliary PF, likelihood PF, etc. Although PF approaches require high computational cost, they outperform EKF and its variants in most highly nonlinear problems; furthermore, the noise does not have to be assumed Gaussian.

Incidently, all these approaches require the knowledge of noise statistics in their applications. Therefore, it is assumed that the means and the variances of $\varvec{u}$ and $\varvec{w}$ are assumed to be known in their applications. However, we may encounter the situation when we need to solve the problem with unknown noise statistics in practice. Therefore, in this paper, we introduce the approach, i.e., CRPF that we can apply in that situation. This approach was initially developed in [34], and is still not known to many researchers even in signal processing disciplines. CRPF is highly effective in the scenario when the problem is highly nonlinear and the information of the noise statistics is unknown. In this paper, we explain the step-by-step algorithm of CRPF with a number of example problems where CRPF has been successfully applied. Readers can be referred to [8, 44] for further reading for better understanding of CRPF.

For readability facilitation, the list of abbreviations used in this paper is provided as follows:

Abbreviations

• ACK: acknowledgement

• BER: bit error rate

• CIR: channel impulse response

• CFO: carrier frequency offset

• CTS: clear-to-send

• CRB: Cramer–Rao bound

• CRPF: cost-reference particle filter

• CSMA/CA: carrier sense multiple access with the collision avoidance

• CUSUM: cumulative summary

• DCF: distributed coordination function

• DIFS: distributed inter-frame space

• DSSS: direct sequence spread spectrum

• EHIF: extended H infinity filter

• EKF: extended Kalman filter

• $\frac{E_b}{N_0}$: bit energy to noise ratio

• GMM: Gaussian mixture model

• GMSPPF: Gaussian mixture sigma point particle filter

• GPF: Gaussian particle filter

• HF: extended H infinity filter

• KF: Kalman filter

• MAC: medium access control

• MAP: maximum a posteriori

• MMSE: minimum mean squared error

• MSE: mean squared error

• OFDM: orthogonal frequency division multiplexing

• PF: particle filter

• PHY: physical layer

• PMF: probability mass function

• RLS: recursive least squares

• RMSE: root mean squared error

• PI: particle impoverishment

• RTS: request-to-send

• SIFS: short inter-frame space

• SNR: signal to noise ratio

• SIR-PF: sequential importance resampling particle filter

• UKF: unscented Kalman filter

• WLAN: wireless local area network

2 Cost-reference particle filter

Since the 1990s, the so-called sequential Monte Carlo filtering or sequential importance sampling technique was developed, which is also addressed “particle filtering.” Standard particle filtering works well for the problems that are modeled by nonlinear functions of the state and/or the measurement. Furthermore, the noise does not have to be Gaussian; nonetheless, the noise information is required in its application. Recently, CRPF algorithm was developed [8, 30, 34, 44], which works in PF framework although it may not be reasonable to view it as a Bayesian approach due to the reason that the estimation is not based on the posterior function as opposed to the case of standard PF. CRPF does not need the information of statistics of both the state process noise and measurement noise [46, 47]. In CRPF algorithm, we need to define a couple of important functions, i.e., the cost function and the risk function. These functions are adopted as the measure of the quality of particles in the algorithm. The cost function needs to satisfy strictly convex with respect to $\varvec{s}_k$ to avoid the ambiguities in estimates and in the resampling step. The risk function needs to be simple and highly tractable in computation for practical implementation of the algorithm

The cost function in CRPF is a measure of “particle quality” including past particles, which is defined by

$$\begin{aligned} \mathcal {C}(\varvec{s}_{0:k}^{i_p} | \varvec{m}_{1:k}, \lambda ) \!=\! \lambda \mathcal {C} (\varvec{s}_{0:k-1}^{i_p} | \varvec{m}_{1:k-1}, \lambda )\! +\! \Delta \mathcal {C} (\varvec{s}_k^{i_p} | \varvec{m}_k),\nonumber \\ \end{aligned}$$

(7)

and can be simply expressed as

$$\begin{aligned} \mathcal {C}_k^{i_p}=\lambda \mathcal {C}_{k-1}^{i_p}+\Delta \mathcal {C}_k^{i_p}, \end{aligned}$$

(8)

where $i_p$ denotes the particle index, and $\lambda$ is the forgetting factor ($0\le \lambda \le 1$) which is the amount of contributions of past particles to evaluating the cost function. $\Delta \mathcal {C}^{i_p}_k$ is the “incremental cost function” which indicates the accuracy of $\varvec{s}_k^{i_p}$ given the measurement $\varvec{m}_k$, and is computed by $\parallel \varvec{m}_k - h(\varvec{s}_k^{i_p})\parallel ^q$ with $q \ge 1$. The cost-based random measure is represented by a set of “particles and associated costs” as

$$\begin{aligned} \varXi _k = \big \{ \varvec{s}_k^{i_p}, \mathcal {C}_k^{i_p} \big \}_{i_p=1}^N, \end{aligned}$$

(9)

where $N$ is the number of employed particles. The risk function is also defined by

$$\begin{aligned} \mathcal {R}(\varvec{s}_{k-1}^{i_p}|\varvec{m}_k) \!=\! \Delta \mathcal {C} (E[ \varvec{s}_k^{i_p}] | \varvec{m}_k) \!= \!\Delta \mathcal {C} (\varvec{s}_{k-1}^{i_p} | \varvec{m}_k). \end{aligned}$$

(10)

The risk function represents the adequacy of $\varvec{s}_{k-1}^{i_p}$ given the measurement $\varvec{m}_k$. In addition, the risk function is a prediction of the cost increment $\Delta \mathcal {C}_k^{i_p}$. Then, the predictive cost function is defined as follows:

$$\begin{aligned} \mathcal {R}^{i_p}_k = \lambda \mathcal {C}_{k-1}^{i_p} + \mathcal {R}(\varvec{s}_{k-1}^{i_p}|\varvec{m}_k). \end{aligned}$$

(11)

The probability mass function (PMF) is computed by using the risk function as follows:

$$\begin{aligned} { \tilde{ \pi } }_{ k }^{ i_p }\!\propto \! { \mu }_{ 1 }({ \mathcal {R} }_{ k }^{ i_p })\!=\!1/( { \mathcal {R} }_{ k }^{ i_p }\!-\!\min { { \{ { \mathcal {R} }_{ k }^{ i_p } \} }_{ i_p=1 }^{ N } } \!+\!\delta ) ^{ \beta }, \end{aligned}$$

(12)

where $\delta , \beta >0$.

With the parameters defined above, the sequential algorithm recursively repeats the steps of risk evaluation, selection, particle propagation, and updating the cost with time. The detailed steps for the sequential estimation of $\varvec{s}$ are given as follows:

• 1. Initialization for $i_p=1, \dots , N$ (number of particles), generate $\varvec{s}_0^{i_p} \sim p_0(\varvec{s}_0)$ which is a known prior density, and assign the cost $\mathcal {C}_0^{i_p} = 0$, and initialize the variance of the propagation density $\varvec{\sigma }^{2,i_p}_0$. In simulations, usually an uniform distribution or a Gaussian distribution is employed for the prior density.

• 2. Recursive update for $k=1, \dots , K$ (total time steps)

  • (a) Compute (for $i_p=1, \dots , N$) $\mathcal {R}^{i_p}_k = \lambda \mathcal {C}_{k-1}^{i_p} + \parallel \varvec{m}_k - h[g(\varvec{s}^{i_p}_{k-1})] \parallel ^q$ for $q \ge 1$, and probability mass function (PMF), $\tilde{\pi }_k^{i_p} \propto \mu _1(\mathcal {R}^{i_p}_k) = \frac{1}{\left(\mathcal {R}^{i_p}_k - \min \big \{ \mathcal {R}^{i_p}_k \big \}^N_{i_p=1} +\delta \right)^{\beta }}$, where $\delta , \beta >0$: small value of $\delta$ is to ensure the denominator is not zero.

  • (b) Do the selection (resampling) $\check{\varXi }_{k-1} = \big \{ \check{\varvec{s}}_{k-1}^{i_p}, \check{\mathcal {C}}_{k-1}^{i_p} \big \}^N_{i_p=1}$ according to $\tilde{\pi }_k^{i_p}$, where “ $\check{}$ ” denotes the resampled version. Resampling process is performed by randomly reselecting $N$ particles based on PMF; therefore, some particles are reselected to multiply depending on the PMF. See [2] for pseudocode of resampling algorithm.

  • (c) Particle propagation (for $i_p=1, \dots , N$) $\varvec{s}_k^{i_p} \sim p_k(\varvec{s}_k|\check{\varvec{s}}^{i_p}_{k-1})= \mathcal {N} \left(g(\check{\varvec{s}}^{i_p}_{k-1}), \varvec{\sigma }^{2,i_p}_{k-1} \varvec{I} \right)$, which is a Gaussian density, where $\varvec{\sigma }^{2,i_p}_{k} = \frac{k-1}{k} \varvec{\sigma }^{2,i_p}_{k-1} + \frac{\parallel \varvec{s}_k^{i_p} - g(\check{\varvec{s}}^{i_p}_{k-1}) \parallel ^2 }{k\times \text {dim}[\varvec{s}]}$, and $\varvec{I}$ is the identity matrix with the dimension of $\varvec{s}$. Therefore, the variance of the propagation density is adjusted online in the CRPF algorithm although we need to determine the initial one.

  • (d) Compute the cost (for $i_p=1, \dots , N$), $\mathcal {C}_k^{i_p} = \lambda \check{\mathcal {C}}_{k-1}^{i_p} + \parallel \varvec{m}_k - h(\varvec{s}_k^{i_p}) \parallel ^q$, and normalized PMF, $\pi ^{i_p}_k \!\sim \! \mu _2\left(\mathcal {C}_k^{i_p}\right)\!=\! \frac{1}{\left(\mathcal {C}_k^{i_p} \!-\! \min \big \{ \mathcal {C}_k^{i_p} \big \}^N_{i_p=1} \!+\!\delta \right)^{\beta }}$.

  • (e) Estimate $\hat{\varvec{s}}_k = \hat{\varvec{s}}_k^{\mathrm{CRPF}} = \sum _{i_p=1}^N \pi ^{i_p}_k \varvec{s}_k^{i_p}$.

As described in the above algorithm, there is not any usage of information regarding $\varvec{u}$ and $\varvec{w}$.

2.1 Discussion

Generally, $0.1$ and $2$ are successfully employed for $\delta$ and $\beta$, respectively, for satisfactory performance of CRPF. Apart from $\delta$ and $\beta$, we need to perform preliminary tuning process for the initial variance of the propagation density ($\varvec{\sigma }^2_0$), the forgetting factor ($\lambda$), and $q$ based on the size of the variances of the system noise $\varvec{u}$ and $\varvec{w}$. Well-tuned parameters enhance the performance of CRPF. Particularly, $\varvec{\sigma }^2_0$ needs to be carefully selected while $\lambda$ and $q$ are usually selected from $\{ 0, 0.95\}$ and $\{ 1, 2\}$, respectively. The values of $\lambda$ and $q$ need to satisfy: $0 \le \lambda \le 1$ and $q \ge 1$. The value of zero is also considered for $\lambda$ because the mean state estimate ($s^{\mathrm{mean}}_k$) becomes asymptotically optimal in terms of its incremental cost when $\lambda = 0$ [34]. The selections of $q$ and $\lambda$ affect the risk and the cost functions that consequently affect the performance of CRPF.

This tuning process is a tedious work if we want to obtain perfectly and optimally tuned CRPF for every parameter although we do not need to plug in the exact information of noise statistics. Among the all parameters, the initial variance of the propagation density is the most impactive factor for satisfactory performance of CRPF, and we will show the result of the difference of the performance made by the different selections of $\varvec{\sigma }^2_0$ in the following example problems.

3 Applications of CRPF

Via the following example problems, we explain the step-by-step algorithm of CRPF, and show how to obtain satisfactory performance. The main measure for the assessed performance is mean squared error (MSE) which can be obtained as follows:

$$\begin{aligned} \text {MSE} = \frac{ \sum _{i_S=1}^{S} \left(n-\hat{\varvec{s}}_{i_S} \right)^2 }{S}, \end{aligned}$$

(13)

where $S$ is the number of simulations, $i_S$ denotes the simulation index, $\varvec{s}$ is the state of interest to be estimated, and $\hat{\varvec{s}}_{i_S}$ is the estimate in the $i_S$-th simulation.

3.1 Carrier frequency offset estimation in OFDM systems

In data communication systems, by employing orthogonal frequency division multiplexing (OFDM) scheme, we can eliminate intersymbol interference problem based on additionally inserted prefix codes. On the other hand, this system has unavoidable defect of intercarrier interference problem caused by carrier frequency offset (CFO). Therefore, estimating CFO is important in OFDM systems [16, 18, 32].

The binary bits are mapped to data symbols $\left(A(r) \right)$ on the complex signal constellation space. Grouped symbols (i.e., an OFDM symbol) are modulated onto subcarriers in the form of inverse fast Fourier transform (IFFT) as follows:

$$\begin{aligned} a(k) \!=\! \frac{1}{K} \sum _{r=0}^{K-1} A(r) e^{j\frac{2\pi r k}{K}}, \quad \quad k=0,1, \ldots , K-1,\nonumber \\ \end{aligned}$$

(14)

where $A(r)$ is a data symbol (for example, $1+j, -1+j, -1-j$, and $1-j$ in the case of quadrature phase shift keying), and $K$ is the number of subcarriers. The cyclic prefix is added up to the signal to mitigate the intersymbol interference, and is removed at the receiver. Then, the received signal is expressed in the time domain as follows:

$$\begin{aligned} m(k) = e^{j\frac{2\pi k \varepsilon }{K}} \sum _{l=0}^{L-1} a_{k-l} f_l \!+\! w_k \quad \!\quad \! k\!=\!0,1, \ldots , K\!-\!1,\nonumber \\ \end{aligned}$$

(15)

where $\varepsilon$ is a normalized CFO (meaning the relative offset from a carrier frequency); $f_l\,(l\!=\!0,1, \ldots , L\!-\!1)$ is the $L$-tap channel impulse response; and $w_k$ is unknown additive noise. We want to estimate $\varepsilon$ based on the received signals, and then decode the symbols.

The corresponding dynamic state system and the measurement equations for the problem can be modeled as follows:

$$\begin{aligned}&\varepsilon _k = \varepsilon _{k-1}, \end{aligned}$$

(16)

$$\begin{aligned}&m(k) = h_k(\varepsilon ) + w_k, \end{aligned}$$

(17)

where we can assume CFO $\varepsilon$ is a constant within the data frame ($k$ is from $0$ to $K-1$) since each OFDM frame is short enough. In this example, the measurement function $h(\cdot )$ is time varying, i.e., $h_k(\cdot )$. Then, from (15), we obtain

$$\begin{aligned} h_k(\varepsilon )= e^{j\frac{2\pi k \varepsilon }{K}} \sum _{l=0}^{L-1}, a_{k-l} f_l. \end{aligned}$$

(18)

Now, we are ready to apply CRPF to the problem of estimating CFO with known preamble symbols “$A(r)$”; we also assume the channel impulse response “$f_l$” is given. The state noise $\varvec{u}$ is assumed known and zero while the measurement noise $\varvec{w}$ is non-zero and initially unknown in this system model. We apply CRPF to this problem under the above-noted noise scenario: although the state noise is known, we do not take advantage of it in the algorithm. On the other hand, perfectly known noise information is given to all the other approaches that are compared with CRPF in this example. Table 1 describes the steps of the CRPF algorithm for estimating CFO.

Table 1 CRPF algorithm for estimating CFO

We consider that a single antenna, 64 subcarrier OFDM system and the quadrature-phase shift keying (QPSK) scheme is employed for the simulation. Various additive Gaussian noise power levels are applied to the measurement for different ratios of $\frac{E_b}{N_0}$ (bit energy to noise ratio). The normalized CFO $\varepsilon$ is uniformly and randomly generated from the range between $-0.9$ and $0.9$ that we estimate. The employed parameters for the application of CRPF are $q=1$; $\lambda =0$; $\delta = 0.1$; and $\beta = 2$. The initial 500 particles for CRPF are generated as the way the true CFO is generated. 3,000 independent, 64 preamble data symbols, which are known at the receiver, are generated for the MSE performance evaluation of the methods.

In Figs. 1 and 2, examples of single tracking trajectories are depicted, where the performance is affected depending on how well $\sigma ^{2,(i_p)}_0$ is selected. Figure 1 shows the result of the scenario when a badly selected $\sigma ^{2,(i_p)}_0$ is employed with a high $\frac{E_b}{N_0}$, where CRPF diverges at the end of the tracking. If we employ a well-selected $\sigma ^{2,(i_p)}_0$, the tracking performance is greatly improved as shown in Fig. 2. Figure 3 shows the result of tuning of $\sigma ^{2,(i_p)}_0$, where the dotted line with no mark shows the performance when we employ $\sigma ^{2,(i_p)}_0 = 0.0006$. Therefore, we use $\sigma ^{2,(i_p)}_0 = 0.0006$ for the assessment of MSE performance of CRPF. Figure 4 shows the MSE performance of the various approaches, where 10 particles are employed for particle filtering approaches. It shows that CRPF outperforms sequential importance resampling PF (SIR-PF) and Gaussian PF (GPF) when only 10 particles are employed. Extended H infinity filter (EHIF) shows good performance at 15dB and above while extended KF shows bad performance in this range. EKF does not show a stable performance for highly nonlinear problems. Standard PF such as SIR-PF has a drawback for estimating a static parameter due to particle impoverishment (PI) phenomenon, particularly when the number of particles is small and/or the frequency offset is large. PI is caused by the resampling process which results in the particles that have high weights statistically selected many times; consequently, resultant particles contain many repeated particles. Usually, PI is severe when the state process noise is very small or zero in the dynamic state equation, and hence all particles may turn into an identical particles within a few iterations [2]. In this example problem, the state process noise is zero. PI phenomenon degrades the performance since the left identical particles do not converge to the true value, and it may not be eliminated unless sufficiently many particles are employed. CRPF does not undergo the PI problem because new particles are generated based on a Gaussian distribution rather than a posterior function. Nonetheless, we do not obtain optimal performance by CRPF when highly increased number of particles are employed for PF approaches as shown in the following.

Fig. 1

Tracking example with $\sigma ^{2,(i_p)}_0 = 0.8$ and $\frac{E_b}{N_0}=40$dB

Fig. 2

Tracking example with $\sigma ^{2,(i_p)}_0 = 0.0006$ and $\frac{E_b}{N_0}=40$dB

Fig. 3

Tuning the initial variance of particles, i.e., $\sigma ^{2,(i_p)}_0$

Fig. 4

MSE performance of the approaches, only 10 particles were employed for PF approaches

Figure 5 shows the MSE performance of the various approaches, where $500$ particles are employed for particle filtering approaches. Overall, GPF shows optimal performance when we increase the number of particles [31]. CRPF shows similar performance regardless of the number of employed particles.

Fig. 5

MSE performance of the approaches, only 10 particles were employed for PF approaches

3.2 Estimating the number of competing terminals in WLAN

In IEEE 802.11 systems, the system throughput performance is affected by the back-off window size of terminals that try to transmit packets. The optimal back-off window size needs to be selected based on the number ($n$) of competing terminals in the system. In this example, we apply CRPF for estimating $n$ in IEEE 802.11 systems. Contrary to previously proposed approaches, CRPF does not require extra computational cost, and furthermore, tracking latency is avoided as well, due to the nonnecessity of additional state detection algorithm. Prompt tracking performance is obtained by avoiding tracking latency, which results in accurate estimate of $n$. Based on estimated $n$, we apply optimally selected back-off window to obtain enhanced throughput performance.

Following [4, 6], we consider a scenario of the fixed number of $n$ competing terminals. Each terminal operates in the saturated network and ideal channel conditions: the saturated network condition means that all terminals always have a packet waiting for transmission. $\zeta$ denotes the collision probability that a packet is transmitted on a collided channel. Then, $n$ can be expressed as the function of $\zeta$ as follows [6]:

$$\begin{aligned} n=F(\zeta )=1+\frac{ \log { (1-\zeta ) } }{ \log { \left( 1-\frac{ 2(1-2\zeta ) }{ (1-2\zeta )(D_{\mathrm{min}}+1)+\zeta D_{\mathrm{min}}(1-{ (2\zeta ) }^{ \kappa })} \right) } },\nonumber \\ \end{aligned}$$

(19)

where $\kappa$ and $D_{\mathrm{min}}$ denote the maximum back-off stage and the minimum contention window size, respectively. After a collision, each terminal doubles its contention window size up to the maximum value $D_{\mathrm{max}}={2}^{\kappa }D_{\mathrm{min}}$, where $\kappa =\log _{ 2 }{ (D_{\mathrm{max}}/D_{\mathrm{min}}) }$. In order to maximize the saturation throughput, $D_{\mathrm{min}}$ is optimally selected, which satisfies the following [4, 5]:

$$\begin{aligned} D_{\mathrm{min}} = n\sqrt{2T}, \end{aligned}$$

(20)

where $T$ is the packet transmission time. From (19), we can estimate $n$ by measuring collision probability $\zeta$. $\zeta$ is measured by each terminal at the time step $k$ (each time step comprises $B$ slots) as follows:

$$\begin{aligned} \zeta _{ k }=\frac{ 1 }{ B } \sum _{ i=(k-1)B }^{ kB-1 }{ { C }_{ i } }, \end{aligned}$$

(21)

where ${C}_{i}=0$ if the corresponding slot is empty or the transmission is successful during the slot $i$ while ${C}_{i}=1$ if the slot is busy or collided. As shown in Fig. 6, one slot can be either one actual slot or a packet length depending on the channel state. If the packet length or $n$ increases, then the actual observation time increases even if $B$ remains the same. This will degrade the prompt tracking performance.

Fig. 6

Model time and actual time of the observation slots $B$

The discrete time dynamic state system model for the number of competing terminals is defined as follows [6]:

$$\begin{aligned} { n }_{ k }={ n }_{ k-1 }+{ w }_{ k }, \end{aligned}$$

(22)

where $w_k$ is the state process noise; determine the varying pattern of $n$ which is hard to be known. The obtained measurement (21) is related with the state $n_k$ based on (19) as follows:

$$\begin{aligned} { \zeta }_{ k }={F}^{-1}({ n }_{ k })+{v }_{ k }={h}({ n }_{ k })+{v }_{ k }, \end{aligned}$$

(23)

where $h(\cdot )$ is the inverse function of (19), $v_k$ is the measurement noise that follows the binomial distribution with zero mean, and the variance can be computed as follows [7]:

$$\begin{aligned} \text {Var} [{ v }_{ k }]=\frac{ h({ n }_{ k })\cdot [1-h({ n }_{ k })] }{ B }. \end{aligned}$$

(24)

Therefore, the system model of the problem is nonlinear and non-Gaussian.

Table 2 describes the step-by-step algorithm for estimating $n$ by the CRPF approach.

Table 2 CRPF algorithm for estimating $n$

We apply the CRPF approach and compare its performance with that of the existing methods by simulations. The packet transmission by each terminal follows basic access mode, and direct sequence spread spectrum (DSSS) is adopted for physical layer (PHY). In DSSS, $32$ for $D_{\min }, 1,024$ for $D_{\max }$ are employed, respectively. The packet format and simulation parameters are described in Table 3. This is the same as that adopted in [6] except for the packet payload size. We adopt 2,000 for observation slots $B$, the given initial estimate of ${\hat{n}}_{0}$ is $5$, and the given initial error variance $P_0$ is $10$ for all filtering methods. The CUSUM algorithm is employed for the EKF and Gaussian mixture sigma point particle filter (GMSPPF) [26, 35] for the state variation detection. GMSPPF is a variant of particle filtering that demands high computational complexity [25, 49]. The number of employed particles, $N=300$ for GMSPPF and CRPF. We select the parameters for CRPF by training, which are $\lambda =0.95$; $\delta =0.1$; $q=2$; and $\beta =2$. The experiment is performed by using MATLAB 7.11.0. We employ some ReBEL Toolkit functions (e.g., GMM, expectation maximization algrorithm) for GMSPPF as employed in [35].

Table 3 Packet format and parameters

We assess the performance of the approaches in the respect of MSE of estimates and the saturation throughput of the system. Figure 7 shows how $D_{\min }$ affects the saturation throughput performance depending on its size. In the middle of simulation, $n$ changes from $10$ to $25$. At that time, $D_{\min }$ is adjusted based on true $n$ and the estimated $\hat{n}$ by the EKF, respectively, and we compare the performance to that with non-adjusted $D_{\min }$. Whereas the throughput degrades with non-adjusted $D_{\min }$ as $n$ varies, the throughput degradation is not observed with adjusted $D_{\min }$ as shown in Fig. 7.

Fig. 7

Saturation throughput performance depending on $D_{\min }$

We perform the simulation in the scenario of non-saturated network condition. In the non-saturated network condition, all terminals randomly send packets whose lengths are also random. It is close to the real internet network scenario where users’ random requests make random data traffic. We assume that the data traffic length and the transmission period follow the exponential distribution with the rates of $0.11/$s and $0.7/$s, respectively, in simulations. To describe large changes of the total number of terminals, e.g., as in subways or hot spot area, we change the total number of terminals every 20 s in the pattern of 15, 25, 15, 30, and 20 terminals.

Figure 8 shows tracking $n$ by the EKF which employs the CUMSUM algorithm for the state variation detection, where $n$ varies less drastically and more dynamically compared to the varying pattern in the saturated network condition.

Fig. 8

Tracking $n$ by the EKF in non-saturated network condition

We assess MSE and the saturation throughput performance by running 200 simulations of the scenario that generates a result of Fig. 8. The MSE result of Fig. 9 shows that CRPF outperforms the EKF and GMSPPF during the entire simulation period. This result shows the critical disadvantage of the CUSUM algorithm: the CUSUM algorithm is set to detect relatively large variation of $n$; therefore, algorithms that employ the CUSUM are not good at tracking small changes of $n$ promptly. Furthermore, CRPF shows far better performance compared to the other approaches especially during the periods of drastic variations of $n$. Figure 10 shows the result of the saturation throughput performance. In the non-saturated network condition, CRPF performs better than in the saturated network condition, and it outperforms the other approaches, especially during the period of the state variation as shown in Fig. 10. The non-saturated network condition is close to real conditions; therefore, CRPF is more effective and useful for real scenarios.

Fig. 9

Mean square error in the non-saturated network condition

Fig. 10

Saturation throughput in the non-saturated network condition

We summarized the performance results of the non-saturated network condition in Table 4, where we highlight the result of throughput during the period of drastic variations of $n$. CRPF clearly shows outperforming result over the entire simulation period. The degradation ratio shows that the performance degradation is reduced by $77~\%$ for CRPF compared to that of the EKF approach. According to the degradation ratio result, we clearly observe that the performance of CRPF is highly enhanced in the non-saturated network condition.

Table 4 Performance in non-saturated network condition

In summary, CRPF does not need the additional state variation detector in the algorithms, whereas most of the previously proposed approaches require the state variation detector that incurs the latency in tracking $n$. Furthermore, CRPF avoids the extra computational cost which results from the adoption of the state variation detector. By using the CRPF approach, we showed enhanced system throughput performance by selecting the optimal minimum contention window based on the estimated $n$ which is time varying. CRPF outperformed the existing methods that additionally employ the state variation detection algorithm, especially in the non-saturated network condition. The non-saturated network condition is closer to the real internet scenario, where $n$ changes with the pattern less drastically, rapidly, and more dynamically compared to the saturated network condition. This tracking performance results from the nonnecessity of the state variation detector. The prompt tracking results in accurate estimation of $n$, and the accurately estimated $n$ is reflected to the selection of optimal back-off window size.

3.3 Target tracking based on bearing and range

In this example, we track a single target’s location and velocity in two-dimensional space, where a target is moving with random noise perturbation [36, 45, 48]. We apply the EKF and H infinity filter based on observations, i.e., the range and the bearing of the target measured at the origin of the coordinate system. Figure 11 describes the range and the bearing of the target measured at the origin of the coordinate. When we apply the EKF, the noise information of the problem is perfectly known. The moving direction of the target is subject to the noise perturbation, which is determined by the process noise in the state equation. In this example, we denote the state and the measurement by $\varvec{s}$ and $\varvec{m}$, respectively.

Fig. 11

The range ($R$) and the bearing ($\beta$) measurements of a target in motion

The state equation is expressed as follows if we assume that the sampling period is short enough for the velocity to be assumed a constant during the sampling period, the profile of the velocity with discrete time steps follows the shape of a staircase rather than the ramp shape:

$$\begin{aligned} \underbrace{\left[\begin{array}{c} r_{x,k} \\ r_{y,k} \\ v_{x,k} \\ v_{y,k} \end{array}\right]}_{\varvec{s}_k} = \underbrace{\left[\begin{array}{cccc} 1 &{} 0 &{} T &{} 0 \\ 0 &{} 1 &{} 0 &{} T \\ 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \end{array}\right]}_{\varvec{A}} \underbrace{\left[\begin{array}{c} r_{x,k-1} \\ r_{y,k-1} \\ v_{x,k-1} \\ v_{y,k-1} \end{array}\right]}_{\varvec{s}_{k-1}} + \underbrace{\left[\begin{array}{c} 0 \\ 0 \\ u_{x,k} \\ u_{y,k} \end{array}\right]}_{\varvec{u}_k}, \end{aligned}$$

(25)

where $r, v, u$, and $(x,y)$ denote the location, the velocity, the noise perturbation, and coordinates, respectively. $T$ is the sampling period, and $k$ is the time index. Therefore, the dynamically time-varying state is composed of four elements, i.e., $2$-D location and $2$-D velocity coordinates. The state noise of the location coordinate is zero, whereas that of the velocity is subjected to a random process of $\varvec{u}_k$. The range and the bearing compose the measurement equation, which is highly non-linear, and described as follows:

$$\begin{aligned} \varvec{m}_k = h[\varvec{s}_k] + \varvec{w}_k= \left[R_k \; \beta _k \right]^{\top } + \varvec{w}_k, \end{aligned}$$

(26)

where the range

$$\begin{aligned} R_k = \sqrt{ r^2_{x,k} + r^2_{y,k} } , \end{aligned}$$

(27)

the bearing

$$\begin{aligned} \beta _k = \arctan \left(\frac{ r_{y,k} }{ r_{x,k} }\right), \end{aligned}$$

(28)

and the measurement noise $\varvec{w}_k = [w_{R,k} \; w_{\beta ,k}]^{\top }$, respectively. Therefore, the state $\varvec{s}_k$ is sequentially estimated based on the observed information $\varvec{m}_k$.

CRPF can be easily adopted for the target tracking problem based on (1) and (2). The function $g(\cdot )$ is linear, and is equal to $\varvec{A}$ in this example. The steps of the CRPF algorithm for tracking a target is described in Table 5.

Table 5 Cost-reference particle filter algorithm for target tracking

We apply CRPF and the EKF for tracking a target in a two-dimensional space for performance assessment. Sampling period, $T=1$, and the initial true state of the target is $\varvec{s}_0 = [10 \;-5\; -0.2\; 0.2]^{\top }$. The given initial estimate of the state for all methods is $\hat{\varvec{s}}_0 = [5\; 5\; 0\; 0]^{\top }$. Diverse variance scenarios of uncorrelated noises for perturbations (in both directions), the range, and the bearing are investigated when a single Gaussian is applied. We also simulate for the scenario that a mixture Gaussian noise is applied. The first Gaussian noise is adopted (which is wrong information) for the application of the EKF, while the noise information is unknown for CRPF in the mixture Gaussian noise scenario. When a mixture Gaussian is applied, $u_{x,y} \sim 0.1\mathcal {N}(0,1) + 4\times 10^{-4}\cdot \mathcal {N}(0,1) + 10^{-6}\cdot \mathcal {N}(0,1), w_{R} \sim \sqrt{0.1}\mathcal {N}(0,1) + 0.04\mathcal {N}(0,1) + 2.5\times 10^{-5}\cdot \mathcal {N}(0,1)$, and $w_{\beta } \sim 0.1\mathcal {N}(0,1) + 4\times 10^{-4}\mathcal {N}(0,1) + 1.6\times 10^{-7}\cdot \mathcal {N}(0,1)$, where $\mathcal {N} \left(a, b^2 \right)$ denotes the Gaussian distribution with the mean of $a$ and the variance of $b^2$. The given initial covariance for the EKF is diag($1\;1\;1\;1$), where “diag” denotes the diagonal matrix with the diagonal elements in the parenthesis, and the noise statistics are perfectly known when we apply the EKF. We perform preliminary tuning process for CRPF. The performance of CRPF highly relies on the initial variance of propagation density $\varvec{\sigma }^{2, i_p}_0 = \left[{\sigma }^{2,i_p}_{0, (1)}\; {\sigma }^{2,i_p}_{0, (2)}\; {\sigma }^{2,i_p}_{0, (3)}\; {\sigma }^{2,i_p}_{0, (4)}\right]^{\top }$. We run $500$ simulations with various values of $\varvec{\sigma }^{2,i_p}_0$ and diverse noise scenarios: ${\sigma }^{2,i_p}_{0, (1,2)} =1, 5, 10$; ${\sigma }^{2,i_p}_{0, (3,4)} =0.1, 1, 5$; variances of $w_{\beta } = 0.01, 0.1$; variances of $w_R = 0.1, 1$; and variances of $u_{x,y} = 0.001, 0.01$. Moreover, $q$ and $\lambda$ are tuned for diverse parameter scenarios based on narrowed selection of $\varvec{\sigma }^{2,i_p}_0$. The tuning process for this example problem is highly extensive due to the high dimension of the state, i.e., four. Although we do not specify the detailed tuned values of $\varvec{\sigma }^{2,i_p}_0$ corresponding to specific scenarios, we assess the MSE performance based on extensive tuning process. For other parameters, the number of particles is 500; $\delta = 0.1$; $\beta = 2$, respectively.

In Fig. 12, the root mean squared error (RMSE) of the methods are depicted when we run 300 times for an identical trajectory with a single Gaussian noise, and there was no diverging tracking for any methods during the simulations for this particular trajectory. The applied noise variances are 0.01, 0.1, and 0.001 for $w_{\beta }, w_R$, and $u_{x,y}$, respectively. The result shows that the EKF outperforms CRPF, slightly. EKF tracks well when the true trajectory is not highly nonlinear in this particular scenario. When we apply the mixture Gaussian noise for the identical trajectory over 300 simulations, the result is very similar to Fig. 12 although we do not show the result here. To obtain more various simulation results with a single Gaussian noise, we perform simulations with various noise variance scenarios: applied variances of $w_{\beta }, w_R$, and $u_{x,y}$ are (0.01, 0.1), (0.1, 1), and (0.001, 0.01), respectively. In Figs. 13 and 14, the RMSEs are depicted when a single Gaussian was applied over 300 simulations, where the true target trajectory is randomly generated at each run, and some tracking of highly nonlinear trajectories are diverging. In these cases, CRPF outperforms the EKF which takes advantage of the noise information of the system. Although we do not show results here, all the other scenarios produce similar results with Figs. 13 and 14. Figure 15 shows a similar result to that of a single Gaussian case when we apply a mixture Gaussian noise to the problem. Figure 16 shows an example of target tracking by the methods when a mixture Gaussian noise is applied. CRPF shows robust tracking performance, while the EKF does not. The MATLAB code for this simulation is available in Appendix, where “selection” function that is included in the middle of m-file is also provided.

Fig. 12

RMSE in X coordinate by 300 runs for the same trajectory when a single Gaussian noise was applied

Fig. 13

RMSE in X coordinate by 300 runs of randomly different traces when a single Gaussian noise was applied. The noise variance scenario is (0.01, 0.1, 0.001) in the order of $w_{\beta }, w_R$, and $u_{x,y}$

Fig. 14

RMSE in X coordinate by 300 runs of randomly different traces when a single Gaussian noise was applied. The noise variance scenario is (0.1, 1, 0.01) in the order of $w_{\beta }, w_R$, and $u_{x,y}$

Fig. 15

RMSE in X coordinate by 300 runs of randomly different traces when a mixture Gaussian noise was applied

Fig. 16

A target tracking by the methods when a mixture Gaussian noise is applied

Under the noise variance scenario of ($w_{\beta }=0.01, w_R = 0.1$, and $u_{x,y} = 0.001$), the numbers of diverging or deviating tracking from the true target tracks during the simulations are summarized in Table 6. We set the threshold of divergence or deviation to $\pm 5$ m for both the EKF and CRPF, in any direction and at any time step when we count the number of times the trackers deviate from the true tracks. CRPF never crosses over the threshold while the EKF does dozens of times, which shows the robustness of CRPF in this non-linear problem. Therefore, CRPF showed a good outperforming result over traditional well-known EKF in this example problem.

Table 6 The number of diverging or considerable deviating tracking from the true target tracks out of 300 runs

3.4 High-bandwidth tilt estimation

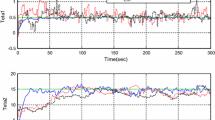
The tilt of a vehicle attitude is determined in the inertial reference frame on the earth. The tilt can be either “roll,” “pitch,” or “yaw,” and the combination of three elements compose the attitude of a vehicle in three-dimensional space as shown in Fig. 17. The estimation of the “tilt” of vehicles has been of much interest, especially in the areas such as aerospace or control systems [11, 12, 28, 29, 43]. For instance, controlling “unmanned aerial vehicle [3, 9, 10, 13, 33, 39]” or “walking robot [13–15]” are the practical issues related with tilt estimation. Numerous approaches have been proposed in order to estimate the attitude of vehicles: attitude estimation is of interest in the integration of global positioning system (GPS) and inertial navigation system (INS) as well [20, 41, 42].

Fig. 17

Attitude (roll, pitch, and yaw) of a vehicle

Inclinometer sensor is mainly used for tilt estimation; however, it may not be appropriate for measuring high rate data (greater than 1 Hz). Gyroscope is complementarily employed to overcome the drawback of the inclinometer; but gyroscope also has a disadvantage that its error keeps increasing with time unless supplement for the tilt estimation system is provided. Therefore, we consider an accelerometer in addition to the gyroscope for estimating the tilt of a vehicle attitude. We employ both “accelerometer” and “gyroscope” for the observations measurement which are relatively cost effective compared to the inclinometer.

It is assumed that “piezoelectrical vibrating gyroscope (Murata ENV-05DB)” for measuring the angular velocity, and its measurement equation as a function of time $t$ are modeled as

$$\begin{aligned} m_1(t) = \tau _1 \dot{\theta } (t) + w_1(t), \end{aligned}$$

(29)

where $\dot{\theta }$ is the rate of the tilt; $\tau _1$ is the scaling coefficient; and $w_1$ is the gyroscope measurement noise, and it is assumed that $w_1$ includes the scaling factor error and gyrodrift [38]. Note that $m_1$ is a linear function of $\dot{\theta }$. Micromechanical accelerometer (Analog Devices ADXL 202) is employed for measuring the acceleration of the vehicle: it measures the accelerations in two perpendicular directions to each other; one is perpendicular to the direction of the gravitational field, and the other in the opposite direction of the gravitational field; therefore, the position is computed by measuring the accelerations in two directions. Therefore, the observed output of the accelerometer can be modeled as follows:

$$\begin{aligned} m_2(t)&= \tau _2 \sin \theta (t) + w_2(t), \end{aligned}$$

(30)

$$\begin{aligned} m_3(t)&= -\tau _2 \cos \theta (t) + w_3(t), \end{aligned}$$

(31)

where $\tau _2$ is a scaling coefficient; $w_2$ and $w_3$ are additive noises which are mainly caused by the vibration of the object. It is assumed that the variances of $w_1, w_2$, and $w_3$ are time varying. Contrary to $m_1$ case, equations for $m_2$ and $m_3$ are nonlinear functions of $\theta$ which are not tractable measurements.

The discrete-time state-space model, where the parameter of interest is dynamically varying with time, is described as follows if it is assumed that the sampling period is short enough for the tilt rate to be a constant during a sampling period; consequently, the profile of the tilt rate with discrete-time steps follows the shape of a staircase rather than the ramp shape:

$$\begin{aligned} \underbrace{\left[\begin{array}{c} \theta _k \\ \dot{\theta }_k \end{array}\right]}_{\varvec{\theta }_k} = \underbrace{\left[\begin{array}{c c} 1 &{} T \\ 0 &{} 1 \end{array}\right]}_{\varvec{A}} \cdot \underbrace{\left[\begin{array}{c} \theta _{k-1} \\ \dot{\theta }_{k-1} \end{array}\right]}_{\varvec{\theta }_{k-1}} + \underbrace{\left[\begin{array}{c} 0 \\ u_k \end{array}\right]}_{\varvec{u}_k}, \end{aligned}$$

(32)

where $k$ is the time index; $\theta$ is the tilt; $\dot{\theta }$ is the rate of the tilt; $T$ is the sampling time period; $\varvec{A}$ is a known $2 \times 2$ state transition matrix; and $\varvec{u}_k$ is the state process noise, respectively. The state noise is the perturbing random noise in the dynamic system.

The measurement equation, as already described in (29) and (30), is expressed as follows:

$$\begin{aligned} \underbrace{\left[\begin{array}{c} m_{1, k} \\ m_{2, k} \end{array} \right]}_{\varvec{m}_k} = \underbrace{\left[\begin{array}{c} \tau _1 \dot{\theta }_{k} \\ \tau _2 \sin \theta _{k} \end{array} \right]}_{h[\varvec{\theta }_k]} + \underbrace{ \left[\begin{array}{c} w_{1, k} \\ w_{2, k} \end{array} \right]}_{\varvec{w}_k}, \end{aligned}$$

(33)

where $h(\cdot )$ is the measurement function, and we use only $m_1$ and $m_2$ as the measurements.

CRPF can be easily adopted to the tilt estimation problem based on the system model (1) and (2), where the function $g(\varvec{\theta }^{}_{k-1})$ is linear and is equal to $\varvec{A}\cdot \varvec{\theta }^{}_{k-1}$ in the problem. The detailed steps for tilt estimation are given by

• 1. Initialization for $i_p=1, \dots , N$ generate $\varvec{\theta }_0^{i_p}=[\theta ^{i_p}_0 \; \dot{\theta }^{i_p}_0]^{\top } \sim p_0(\varvec{\theta _0})$, which is a known prior density, and assign the cost $\mathcal {C}_0^{i_p} = 0$, and initialize the variance of the propagation density $\varvec{\sigma }^{2,i_p}_0$. In simulations, the same initial values are given to the respective approaches.

• 2. Recursive update for $k=1, \dots , K$,

  • (a) Compute (for $i_p=1, \dots , N$) $\mathcal {R}^{i_p}_k = \lambda \mathcal {C}_{k-1}^{i_p} + \parallel \varvec{m}_k - h[\varvec{A}\cdot \varvec{\theta }^{i_p}_{k-1}] \parallel ^q$ for $q > 0$, and probability mass function (PMF), $\tilde{\pi }_k^{i_p} \propto \mu _1(\mathcal {R}^{i_p}_k) = \frac{1}{\left(\mathcal {R}^{i_p}_k - \min \{ \mathcal {R}^{i_p}_k \}^N_{i_p=1} +\delta \right)^{\beta }}$, where $\delta , \beta >0$: small value of $\delta$ is to ensure the denominator is not zero.

  • (b) Do the selection, or resampling $\check{\varXi }_{k-1} = \{ \check{\varvec{\theta }}_{k-1}^{i_p}, \check{\mathcal {C}}_{k-1}^{i_p} \}^N_{i_p=1}$ according to $\tilde{\pi }_k^{i_p}$, where “ $\check{}$ ” denotes the resampled version.

  • (c) Particle propagation (for $i_p=1, \dots , N$) $\varvec{\theta }_k^{i_p} \sim p_k(\varvec{\theta }_k|\check{\varvec{\theta }}^{i_p}_{k-1})= \mathcal {N} \left(\varvec{A}\cdot \check{\varvec{\theta }}^{i_p}_{k-1}, \varvec{\sigma }^{2,i_p}_{k-1} \varvec{I} \right)$, which is a Gaussian density, where $\varvec{\sigma }^{2,i_p}_{k} = \frac{k-1}{k} \varvec{\sigma }^{2,i_p}_{k-1} + \frac{\parallel \varvec{\theta }_k^{i_p} - \varvec{A}\cdot \check{\varvec{\theta }}^{i_p}_{k-1} \parallel ^2 }{k\times \mathrm{dim}[\varvec{\theta }]}$, and $\varvec{I}$ is the identity matrix with the dimension of $\varvec{\theta }$. In the studied problem, taking advantage of knowing that the state noise is zero for the tilt $\theta$, only the particles of tilt rate are generated with their propagation variances, i.e., $\dot{\theta }_k^{i_p} \sim p_k(\dot{\theta }_k|\check{\dot{\theta }}^{i_p}_{k-1})= \mathcal {N} \left(\check{\dot{\theta }}^{i_p}_{k-1}, \sigma ^{2,i_p}_{k-1} \right)$, where $\sigma ^{2,i_p}_{k} = \frac{k-1}{k} \sigma ^{2,i_p}_{k-1} + \frac{\parallel \dot{\theta }_k^{i_p} - \check{\dot{\theta }}^{i_p}_{k-1} \parallel ^2 }{k}$, which is not a vector value anymore but is a scalar value. Then, ${\theta }_k^{i_p}$ is computed based on $\check{\dot{\theta }}^{i_p}_{k-1}$ according to (16).

  • (d) Compute the cost (for $i_p=1, \dots , N$), $\mathcal {C}_k^{i_p} = \lambda \check{\mathcal {C}}_{k-1}^{i_p} + \parallel \varvec{m}_k - h(\varvec{\theta }_k^{i_p}) \parallel ^q$, and normalized PMF, $\pi ^{i_p}_k \sim \mu _2\left(\mathcal {C}_k^{i_p}\right)= \frac{1}{\left(\mathcal {C}_k^{i_p} - \min \{ \mathcal {C}_k^{i_p} \}^N_{i_p=1} +\delta \right)^{\beta }}$.

  • (e) Estimate $\hat{\varvec{\theta }}_k = \varvec{\theta }_k^{\mathrm{mean}} = \sum _{i_p=1}^N \pi ^{i_p}_k \varvec{\theta }_k^{i_p}$.

We compare the performance of the EKF and CRPF via MATLAB simulations for the problem of estimating the tilt of a vehicle attitude. The performance in estimating the tilt rate is also investigated. The total number of time steps with which the tilt and the tilt rate vary is 100. 5,000 simulations are run for each method, and MSE of the estimates is evaluated. According to the discrete-time system model (32), the sampling frequency $T=0.5$ (s) is considered. The initial true state $\varvec{\theta }_0 = [10 \text { rad}\; -0.2 \text { rad/s}]^{\top }$. The scaling coefficients $\tau _1$ and $\tau _2$ are equal to $10$, respectively. The given initial estimate of the state for both methods is $\hat{\varvec{\theta }}_0 = [7 \text { rad}\; 0 \text { rad/s}]^{\top }$. Three different values of “state process noise power spectral density (equivalently the variance for a zero mean white noise process)” $v$ are considered: the applied variances ($v$) of additive Gaussian noise ($u_k$) are $0.001, 0.1$, and 1, respectively; they are assumed to be time invariant as opposed to the case of measurement noise variance. The variance of the measurement noise is assumed to be time variant: at every discrete-time step, the variance is randomly selected from a uniform distribution; then, zero-mean and additive Gaussian noise with the selected variance is applied; two uniform distributions are considered for the selection of measurement noise variance; one variance is uniformly distributed from $0$ to $0.1$ , and the other is distributed from 0 to 10. These parameters ($0.1$ and $10$) are denoted by $r_v$.

The initial variance of the propagation density $\sigma ^2_0$ for the tilt rate of CRPF is tuned by extensive preliminary simulations. The parameters for CRPF are $q=1$; $\lambda =0.95$; $\delta = 0.1$; $\beta = 2$; and the initial variance for the Gaussian propagation density $\varvec{\sigma }^{2,i_p}_0$ is selected depending on $v$ and $r_v$. The identical $N$ initial particles of estimates are generated for CRPF.

Simulation results are shown in Figs. 18 and 19 for estimating $\theta$ and $\dot{\theta }$ with various scenarios of $v$ and $r_v$. As can be seen in (29), (30), and (32), the state function and one measurement function are linear, and only (30) is a nonlinear function of tilt. Therefore, this example problem is not a highly nonlinear problem. CRPF and the EKF show similar performance for the tilt estimation, while the EKF outperforms CRPF for tilt rate estimation as shown in Figs. 18 and 19. CRPF performs more effectively in nonlinear problem (tilt) rather than in linear problem (tilt rate) compared to the EKF performs.

Fig. 18

MSE performance of estimated tilt $\theta$ for various $v$ and $r_v$. $300$ and 10 denote the number of employed particles for CRPF

Fig. 19

MSE performance of estimated tilt rate $\dot{\theta }$ for various $v$ and $r_v$. $300$ and 10 denote the number of employed particles for CRPF

4 Summary and conclusion

In this paper, we provided a tutorial for the applications of CRPF, in multiple fields of signal processing. CRPF works in particle filtering framework that has the generic character of the advantage for highly nonlinear problems. This particle filtering has an advantageous feature that the noise information is not needed in its applications although we need preliminary tuning process mainly based on the size of the variances of the system noise. CRPF is particularly useful when the statistical noise information of the problem is not available. We explained the detailed steps of its employment with example problems of various fields in signal processing. Particularly, the CRPF approach showed the optimal performance in the problem of estimating the number of competing terminals in IEEE 802.11 WLAN systems. As shown in the example problems, CRPF can be applied to diverse fields in signal processing besides the examples, e.g., speech recognition, bio-medical image processing, estimating the attitude and trajectory of launch vehicles, channel estimation/equalization, etc. Based on the contribution of this tutorial, we expect disseminative applications of CRPF to problems where, particularly, the EKF could have been successfully applied if noise statistics were known.

Appendix

1.1 MATLAB m-files for tracking a target by CRPF with Gaussian mixture noise

In this appendix section, we provide m-files for MATLAB simulations as shown in Figs. 20–21. The m-file generates the result that CRPF tracks a target in 2-D space, and the measurement noise is a mixture Gaussian. Three MATLAB figures are generated: the first one shows the track of a target and the estimated tracking by CRPF, and next two figures show the error with respect to each coordinate (Fig. 21).

Fig. 20

A MATLAB m-file for tracking a target by CRPF with Gaussian mixture noise

Fig. 21

A MATLAB m-file function, “resampling 2” in Fig. 20, a selection (resampling) algorithm