1 Introduction

In general, sliding mode control (SMC) follows two main steps: a switching surface is defined first such that the closed-loop system exhibits desired dynamic behavior during sliding mode, and then sliding mode controller is employed to derive the system states to remain on the sliding surface [1, 2]. It is a powerful robust method which has been successfully used for the control of linear and nonlinear systems [3, 4]. In the conventional sliding mode control, during the reaching phase-controlled system is not robust and even matched disturbances can affect the system. For solving this problem, integral sliding mode (ISM) concept is proposed in [5]. In this method, an integral-type term is added in sliding surface, and then, it guarantees that the reaching phase is eliminated and the system trajectories start in the surface right from the beginning.

The composite nonlinear feedback (CNF) control law was first proposed by Lin et al. [6] to improve the transient performance for the tracking control of second-order linear systems with input saturations. This technique consists of linear and nonlinear feedback laws without any switching element [7, 8]. The linear portion yields small damping ratio of the closed-loop system for a quick response and the nonlinear portion is used to tune the damping ratio of the closed-loop system gradually as the system output approaches the output of the reference model to reduce the overshoot caused by the linear portion [9, 10]. In the recent years, this method is developed for more general class of linear and nonlinear systems. Besides developments in theory, the CNF method is applied to design various servo control systems, such as HDD servo system [7, 11], helicopter flight control system [12], and position servo system [9].

Though the CNF control law is fully investigated for normal linear and nonlinear systems, the CNF technique for time-delayed systems is seldom addressed. The reason may be that the control problems for time-delayed systems are in general more challenging and time-delays are sources of instability and poor performance for a control system [13, 14]. To the best of the author’s knowledge, there is little work undertaken on the problem of stabilization and attaining high performance and robustness for a class of uncertain dynamical systems with multiple time-delays, which is still open in the literature.

In this paper, we aim to design a nonlinear integral-type sliding mode controller combined with CNF control method for uncertain multi-input multi-output (MIMO) linear systems with multiple state-delays and external disturbances such that the resulting controlled output would track a target reference as fast as possible without any steady-state bias. The proposed control method retains the actual structure of CNF controller in following the reference trajectory within a given accuracy and the invariance property of ISM method in rejecting disturbances.

The paper is organized as follows: The design procedure of the robust composite nonlinear feedback controller for guaranteeing the robust tracking and performance improvement is developed in Sect. 2. The selection procedure of the nonlinear function is proposed in Sect. 3. In Sect. 4, simulation results are illustrated. Finally, conclusions are provided in Sect. 5.

2 Robust composite nonlinear feedback control

Consider an uncertain MIMO linear system with multiple time-delays and external disturbances as

$$\begin{aligned} \dot{x}(t)&= \left[ {A+\Delta A(r(t))} \right] x(t)\nonumber \\&+\sum _{i=1}^{N_1 } {\Delta A_{di} (v(t))x(t-\tau _i (t))}\nonumber \\&+\left[ {B+\Delta B(p(t))} \right] u(t)+W(q(t))\\ y(t)&= Cx(t),\nonumber \end{aligned}$$
(1)

where \(t\in [t_0 , \infty )\), \(x(t)\in R^{n}\) is the measurable state vector, \(u(t)\in R^{m}\) is the control input, \(A\), \(B\), \(C\) are constant matrices of appropriate dimensions, \(y(t)\in R^{p}\) is the output vector, and the matrices \(\Delta A(.)\), \(\Delta B(.)\), and \(\Delta A_{di} (.), i=1,\ldots , N_1 \) denote the time-varying matched uncertainties and are continuous in all their arguments. Moreover, \(\tau _i (t)\in R^{+}\) is the time-varying delay and the vector \(W(q(t))\in R^{n}\) is the external disturbance. The uncertain functions \(r(t), p(t), v(t)\), and \(q(t)\) are Lebesgue measurable functions which belong to a compact bounding set \(\Omega \).

Assumption 1

There exist continuous and bounded matrix functions \(N(.)\), \(E(.)\), \(N_{di} (.)\), and \(\tilde{W}(.)\) of appropriate dimensions such that [14]

$$\begin{aligned}&\Delta A(r(t))=BN(r(t)),\nonumber \\&\Delta B(p(t))=BE(p(t)),\nonumber \\&\Delta A_{di} (v(t))=BN_{di} (v(t)),\nonumber \\&W(q(t))=B\tilde{W}(q(t)). \end{aligned}$$
(2)

This assumption is known as the matching condition on the uncertainties. For convenience, the following notations which represent the bounds of the uncertainties are introduced:

$$\begin{aligned}&\rho _r = \mathop {\max }\limits _{r\in \Omega } \left\| {N(r(t))} \right\| ,\nonumber \\&\mu = \mathop {\max }\limits _{p\in \Omega } \left\| {E(p(t))} \right\| ,\nonumber \\&\rho _{vi} = \mathop {\max }\limits _{v\in \Omega } \left\| {N_{di} (v(t))} \right\| ,\nonumber \\&\rho _q = \mathop {\max }\limits _{q\in \Omega } \left\| {\tilde{W}(q(t))} \right\| . \end{aligned}$$
(3)

The objective is to design a feedback control law such that the controlled output \(y(t)\) can track step command input \(r\), in the presence of matched uncertainties and multiple time-delays without experiencing large overshoot. To design a state-feedback CNF law, the following assumptions are required [15]:

  1. (1)

    Pair \((A,B)\) is stabilizable;

  2. (2)

    \((A,B,C)\) is invertible and has no zeros as \(s=0\).

In the first step of CNF state-feedback law procedure, a linear feedback control law is designed [7]. In the second step, the design of nonlinear feedback control is carried out, and lastly, in the final step, the linear and nonlinear feedback laws are combined to form the CNF control law.

The linear feedback control law for system (1) is designed as [7, 8]

$$\begin{aligned} u_L =Fx(t)+G_l r, \end{aligned}$$
(4)

where \(r\) is the step command input and \(F\) is designed such that \((A+BF)\) is an asymptotically stable matrix and the closed-loop system \(C\left( {sI-A-BF} \right) ^{-1}B\) has small damping ratio. Furthermore, by calculating \(d.c.\) gain from \(y(t)\) to \(r\), the matrix \(G_l\) is given by

$$\begin{aligned} G_l =-\left[ {C\left( {A+BF} \right) ^{-1}B} \right] ^{-1}. \end{aligned}$$
(5)

Moreover, by finding \(d.c.\) gain between \(x(t)\) and \(r\), new steady state value \(x_e \) is given as

$$\begin{aligned} x_e =-\left( {A+BF} \right) ^{-1}BG_l r. \end{aligned}$$
(6)

The nonlinear feedback control law \(u_N\) is given by

$$\begin{aligned} u_N =\psi (r,y)B^{T}P(x-x_e ), \end{aligned}$$
(7)

where \(\psi (r,y)\) is any nonpositive function locally Lipschitz in \(y(t)\), which is used to change the damping ratio of the closed-loop system as the controlled output approaches the step command input to reduce the overshoot caused by the linear part [10]. The real symmetric matrix \(P>0\) in (7) is the solution of the following Lyapunov equation:

$$\begin{aligned} (A+BF)^{T}P+P(A+BF)=-W, \end{aligned}$$
(8)

for some positive definite matrix \(W\). Note that such a \(P\) exists, since \(A+BF\) is asymptotically stable.

The linear and nonlinear feedback control laws obtained in (4) and (7) are now combined to form a CNF controller as follows:

$$\begin{aligned} \kappa (x,t)&= u_L +u_N\nonumber \\&= Fx(t)+G_l r+\psi (r,y)B^{T}P(x-x_e ), \end{aligned}$$
(9)

where this controller does not provide robust performance. To achieve a robust CNF controller, the following nonlinear integral-type sliding surface is proposed:

$$\begin{aligned} s(x,t)=G\left\{ {x(t)-x(0)-\int \limits _0^t {(Ax(\tau )+B\kappa (x,\tau ))d\tau } } \right\} , \end{aligned}$$
(10)

where \(G\in R^{m\times n}\) is a constant matrix, \(GB\) is uniformly invertible, and the additional integral term provides one more degree of freedom in design than the linear sliding surface. Furthermore, this sliding surface provides a general framework to eliminate the reaching phase such that the sliding mode exists from the beginning, and then the system response is completely invariant against uncertainties and multiple time-delays.

Taking the derivative of the sliding surface (10) along the trajectories of system (1) yields

$$\begin{aligned}&\dot{s}(x,t)\nonumber \\&\quad = G\left\{ {\dot{x}(t)-Ax(t)-B\kappa (x,t)} \right\} \nonumber \\&\quad = GB\left\{ N(r(t))x(t)+\sum _{i=1}^{N_1 } {N_{di} (v(t))x(t-\tau _i (t))}\right. \nonumber \\&\qquad \left. +\left[ I+E(p(t)) \right] u(t)+\tilde{W}(q(t))-\kappa (x,t) \right\} .\nonumber \\ \end{aligned}$$
(11)

The control law using the sliding surface (10) can be designed as

$$\begin{aligned} u(t)=\left\{ {\begin{array}{l@{\quad }l} \kappa (x,t)-\rho (x,t)\frac{(GB)^{T}s}{\left\| {(GB)^{T}s} \right\| }, &{} \textit{if} \ s\ne 0\\ \kappa (x,t), &{} \textit{if} \ s=0 \end{array}}\right. \end{aligned}$$
(12)

where the switching function \(\rho (x,t)\) satisfies that

$$\begin{aligned}&\rho (x,t) \nonumber \\&\quad >\frac{\rho _r \left\| {x(t)} \right\| \!+\!\sum _{i=1}^{N_1 } {\rho _{vi} \left\| {x(t-\tau _i (t))} \right\| } \!+\!\rho _q \!+\!\mu \left\| {\kappa (x,t)} \right\| }{1+\mu }.\nonumber \\ \end{aligned}$$
(13)

Theorem 1

Consider the uncertain time-delay system (1) and suppose that Assumption 1 is satisfied. Applying the control law (12) with the switching function \(\rho (x,t)\) chosen as (13), the trajectory of the system (1) is guaranteed to be kept on the nonlinear integral-type sliding surface (10) from any initial condition.

Proof

Consider the Lyapunov function candidate as

$$\begin{aligned} V(x,t)=\frac{1}{2}s^{T}(x,t)s(x,t). \end{aligned}$$
(14)

Differentiating the Lyapunov function (14) with respect to time and using (11)–(13) yields

$$\begin{aligned}&\dot{V}(x,t) = s^{T}(x,t)\dot{s}(x,t)\nonumber \\&\quad = s^{T}GB\left[ N(r(t))x(t)+\sum _{i=1}^{N_1 } {N_{di} (v(t))x(t-\tau _i (t))} \right. \nonumber \\&\qquad +\,\tilde{W}(q(t)) -\rho (x,t)\frac{(GB)^{T}s}{\left\| {(GB)^{T}s} \right\| }\nonumber \\&\qquad \left. +\, E(p(t))\left\{ {\kappa (x,t)-\rho (x,t)\frac{(GB)^{T}s}{\left\| {(GB)^{T}s} \right\| }} \right\} \right] .\nonumber \\&\quad \le \, \left\| {(GB)^{T}s} \right\| \left\{ \left\| {N(r(t))} \right\| \left\| {x(t)} \right\| \right. \nonumber \\&\quad \quad +\, \sum _{i=1}^{N_1 } \left\| {N_{di} (v(t))} \right\| \left\| {x(t-\tau _i (t))} \right\| +\left\| {\tilde{W}(q(t))} \right\| \nonumber \\&\quad \quad \left. +\left\| {E(p(t))} \right\| \left\| {\kappa (x,t)} \right\| -\rho (x,t)\left\{ {1+\left\| {E(p(t))} \right\| } \right\} \right\} \nonumber \\&\quad \quad \le \left\| {(GB)^{T}s} \right\| \left\{ \rho _r \left\| {x(t)} \right\| +\sum _{i=1}^{N_1 } {\rho _{vi} \left\| {x(t-\tau _i (t))} \right\| }\right. \nonumber \\&\qquad \left. +\,\rho _q +\mu \left\| {\kappa (x,t)} \right\| -\rho (x,t)\left\{ {1+\mu } \right\} \right\} <0. \end{aligned}$$
(15)

Therefore, the controller (12) using the switching gain function (13) guarantees that the sliding mode can be maintained for \(t\ge t_0\). \(\square \)

3 Selection of the nonlinear function \(\psi (r,y)\)

The selection procedure of nonlinear function \(\psi (r,y)\) is the same as that given in [7]. The freedom of choosing the nonlinear function \(\psi (r,y)\) is used to tune the control law so as to improve the closed-loop system performance as the output approaches the command input and should be a smooth nonpositive function of \(\left| {r-y} \right| \). The main purpose of adding the nonlinear term to the CNF control law is to speed up the settling time, or equivalently to contribute an important value to the linear control input when the tracking error, \(r-y\), is small. This function needs to be chosen such that it has the following properties:

  1. (I)

    When the controlled output \(y(t)\) is far away from the command input, \(\left| {\psi (r,y)} \right| \) becomes small, and, therefore, the effect of the nonlinear part of CNF control law will be very limited.

  2. (II)

    When the controlled output \(y(t)\) approaches the command input, \(\left| {\psi (r,y)} \right| \) becomes large, and thus the nonlinear part of the CNF control law will become effective.

The closed-loop system comprising the uncertain linear system (1) and the CNF control law (12) can be expressed as follows:

$$\begin{aligned}&\dot{x}(t) = \left[ {A+BF} \right] x(t)+BG_l r+B\psi (r,y)B^{T}P(x-x_e )\nonumber \\&\qquad \qquad +\,\Delta A(r(t))x(t)+\sum _{i=1}^{N_1 } {\Delta A_{di} (v(t))x(t-\tau _i (t))}\nonumber \\&\qquad \qquad +\,\Delta B(p(t))u(t)+W(q(t))\nonumber \\&\qquad = \left[ {A+BF+B\psi (r,y)B^{T}P} \right] x(t)\nonumber \\&\qquad +\,\left[ {I_n +B\psi (r,y)B^{T}P(A+BF)^{-1}} \right] BG_l r\nonumber \\&\qquad +\,B\left[ N(r(t))x(t)+\sum _{i=1}^{N_1 } {N_{di} (v(t))x(t-\tau _i (t))} \right. \nonumber \\&\qquad \left. +\,E(p(t))u(t)+\tilde{W}(q(t)) \right] . \end{aligned}$$
(16)

The eigenvalues of the closed-loop system (16) can be changed by the nonlinear function \(\psi (r,y)\). The poles of the closed-loop system (16), which are the functions of the tuning parameter \(\psi (r,y)\), start from the open loop poles, i.e., the eigenvalues of \(A+BF\), when \(\psi (r,y)=0\), and end up at the open loop zeros, as \(\left| {\psi (r,y)} \right| \) becomes larger. The nonlinear function \(\psi (r,y)\) is defined in a diagonal form as [16, 17]

$$\begin{aligned} \psi (r,y)=diag\left[ {\psi _1 (r,y), \cdots , \psi _m (r,y)} \right] , \end{aligned}$$
(17)

where its elements, i.e., \(\psi _i (r,y), i=1, \cdots , m\) are nonunique and defined in various forms. For example, in [6], \(\psi _i (r,y)\) is of the form of an exponential function

$$\begin{aligned} \psi _i (r,y)=-\beta _i e^{-\alpha _i \left\| {y-r} \right\| }, i=1, \cdots ,m, \end{aligned}$$
(18)

where \(\beta _i >0\) and \(\alpha _i >0\) are tuning parameters. \(\left| {\psi _i (r,y)} \right| \) tends to zero as \(\left| {y-r} \right| \) tends to infinity and \(\left| {\psi _i (r,y)} \right| \) reaches its maximum value \(\beta _i \) when \(\left| {y-r} \right| \) tends to zero. Another possible choice is as follows [18]:

$$\begin{aligned} \psi _i (r,y)=-\beta _i e^{-k(y-r)^{2}}, \end{aligned}$$
(19)

where \(k\) is a positive scalar which should be large to ensure a small initial value of \(\psi _i (r,y)\).

4 Simulation results

In this section, the proposed method of this paper is illustrated to apply on an uncertain system with multiple time-varying delays. The numerical example is given by the following differential equations:

$$\begin{aligned}&\dot{x}(t)=\left( {\left[ {{\begin{array}{l@{\quad }l@{\quad }l} 1&{} {-2}&{} 3\\ {-4}&{} 5&{} -6\\ 7&{} {-8}&{} 9 \end{array}}}\right] +\Delta A(r(t))} \right) x(t)\nonumber \\&\quad \qquad \quad +\,\sum _{i=1}^3 {\Delta A_{di} (v(t))x(t-\tau _i (t))}\nonumber \\&\qquad +\,\left( {\left[ {{\begin{array}{l@{\quad }l} 1&{} {-2}\\ {-3}&{} 4\\ 5&{} 6 \end{array} }} \right] +\Delta B(p(t))} \right) u(t)+W(q(t)),\nonumber \\&y=\left[ {{\begin{array}{l@{\quad }l@{\quad }l} 1&{} 0&{} 0\\ 0&{} 0&{} 1 \end{array}}}\right] x(t), \end{aligned}$$
(20)

where \(\tau _i (t)\)’s are time-delays. The disturbances and uncertainties have the following bounds: \(\left| {r_1 (t)} \right| \le 0.5\), \(\left| {r_2 (t)} \right| \le 1\), \(\left| {p(t)} \right| \le 0.5\), \(\left| {q(t)} \right| \le 0.5\), \(\left| {v(t)} \right| \le 1.5\), and \(\Delta A(r(t))=\left[ {{\begin{array}{l@{\quad }l@{\quad }l} {r_1 (t)}&{} {-2r_2 (t)}&{} {r_3 (t)}\\ {-3r_1 (t)}&{} {4r_2 (t)}&{} {-3r_3 (t)}\\ {5r_1 (t)}&{} {6r_2 (t)}&{} {5r_3 (t)} \end{array} }} \right] \), \(\Delta B(p(t))=\left[ {{\begin{array}{l@{\quad }l} {p(t)}&{} {-2p(t)}\\ {-3p(t)}&{} {4p(t)}\\ {5p(t)}&{} {6p(t)} \end{array} }} \right] \), \(\Delta A_{d1} (v(t))=\left[ {{\begin{array}{l@{\quad }l@{\quad }l} 0&{} {v(t)}&{} {-2v(t)}\\ 0&{} {-3v(t)}&{} {4v(t)}\\ 0&{} {5v(t)}&{} {6v(t)} \end{array} }} \right] \), \(\Delta A_{d2} (v(t))=\left[ {{\begin{array}{l@{\quad }l@{\quad }l} {v(t)}&{} {-2v(t)}&{} {v(t)}\\ {-3v(t)}&{} {4v(t)}&{} {-3v(t)}\\ {5v(t)}&{} {6v(t)}&{} {5v(t)} \end{array} }} \right] \), \(\Delta A_{d3} (v(t))=\left[ {{\begin{array}{l@{\quad }l@{\quad }l} {-2v(t)}&{} 0&{} {v(t)}\\ {4v(t)}&{} 0&{} {-3v(t)}\\ {6v(t)}&{} 0&{} {5v(t)}\\ \end{array} }} \right] \), \(W(q(t))=\left[ {{\begin{array}{l} {q(t)}\\ {-3q(t)}\\ {5q(t)} \end{array} }} \right] \).

From (2) and (20), one can obtain: \(N(r(t))=\left[ {{\begin{array}{l@{\quad }l@{\quad }l} {r_1 }(t)&{} 0&{} {r_3 }(t)\\ 0&{} {r_2 }(t)&{} 0\\ \end{array}}} \right] \), \(E(p(t))=p(t)\), \(\tilde{W}(q(t))=\left[ {{\begin{array}{l} {q(t)}\\ 0\end{array} }} \right] \), \(N_{d1} (v(t))=\left[ {{\begin{array}{l@{\quad }l@{\quad }l} 0&{} {v(t)}&{} 0\\ 0&{} 0&{} {v(t)} \end{array} }} \right] \), \(N_{d2} (v(t))=\left[ {{\begin{array}{l@{\quad }l@{\quad }l} {v(t)}&{} 0&{} {v(t)}\\ 0&{} {v(t)}&{} 0 \end{array} }} \right] \), \(N_{d3} (v(t))=\left[ {{\begin{array}{l@{\quad }l@{\quad }l} 0&{} 0&{} {v(t)}\\ {v(t)}&{} 0&{} 0 \end{array} }} \right] \). Then, from (3), the following parameters are calculated: \(\rho _r =1\), \(\mu =0.5\), \(\rho _q =0.5\), \(\rho _{v1} =\rho _{v3} =1.5\), \(\rho _{v2} =2.12\). The constant parameters are selected as \(G=\left[ {{\begin{array}{l@{\quad }l} {0.3}&{} {-0.6}\\ {-0.3}&{} {0.8} \end{array} }} \right] \) and \(\alpha _i =\beta _i =2, i=1, 2\). For the simulation purposes, the uncertain parameters \(r_j (t), j=1,2,3\), \(p(t)\), \(q(t)\), \(v(t)\), and initial conditions are set as follows:

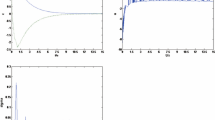
\(r_1 (t)=0.5\sin (3t), \quad r_2 (t)=\cos (3t), \quad r_3 (t)=0.5\sin (2t), p(t)=0.5\cos (2t), q(t)=0.5\sin (3t), v(t)=1+0.5\sin (2t), x(0)=\left[ {{\begin{array}{l@{\quad }l@{\quad }l} {-1}&0&0 \end{array} }} \right] ^{T}\). The time-varying delays \(\tau _1 (t)\), \(\tau _2 (t)\), and \(\tau _3 (t)\) are chosen as shown in Fig. 1, where \(\tau _1 (t)=\tau _3 (t)=1+0.5\sin (\pi t)\).

Fig. 1
figure 1

The time-varying delays \(\tau _1 (t)\) (dashed) and \(\tau _2 (t)\) (solid)

Full size image

The sampling time is set to 10 ms. The eigenvalues of the system are selected as \(\lambda _{1,2,3} \!=\![-0.29, -0.1,-0.2]\), where the gain matrix \(F\) is determined as \(F=\left[ {{\begin{array}{l@{\quad }l@{\quad }l} {1.363}&{} {-1.673}&{} {1.955}\\ {0.033}&{} {0.068}&{} {-0.127} \end{array} }} \right] .\) The solution of the Lyapunov equation (8) with \(W=I_3 \) is \(P=\left[ {{\begin{array}{l@{\quad }l@{\quad }l} {28.18}&{} {11.39}&{} {12.69}\\ {11.39}&{} {7.51}&{} {5.84}\\ {12.69}&{} {5.84}&{} {7.44} \end{array} }} \right] .\) The nonlinear function elements \(\psi _i (r,y)\) are defined in the form of (18). The final eigenvalues of the system by applying the nonlinear function \(\psi (r,y)\) are \(\lambda _{1,2,3} \!=\!\left[ {-787.47, -2.2, -129.9} \right] \). Figure 2 shows the controlled outputs using the linear feedback control law and the proposed controller. It demonstrates significantly the importance of adding the nonlinear function \(\psi (r,y)\) for improving the controlled output. Also, control inputs are shown in Fig. 3. As it can be seen from the results, the proposed method provides faster and better transition responses over those of other method.

Fig. 2
figure 2

Responses of the controlled outputs using a the linear feedback controller, b the CNF controller

Full size image
Fig. 3
figure 3

Control inputs \(u(t)\). a linear feedback control law, b CNF controller

Full size image

The integral of absolute-value of error (IAE) and integral of time multiplied by absolute-value of error (ITAE) for the controlled outputs using the proposed controller in comparison with linear feedback controller are shown in Table 1. As it can be seen, the IAE and ITAE performance indices values are much better when using the proposed controller compared with the other one.

Table 1 Performance indices values using proposed controller compared with linear controller (without nonlinear function)
Full size table

Furthermore, simulations are performed for different values of \(\tau _i (t)\) with 20% enhancement. As illustrated in Fig. 4, it is clear that increasing the time-delay values causes the instabilities and bad performance of the controlled system. Figure 5 shows that for the time-delay values 1.15 times bigger than the previous ones, the control input goes to infinity and system becomes unstable.

Fig. 4
figure 4

Responses of the controlled outputs with 20 % increment in time-delay values

Full size image
Fig. 5
figure 5

Responses of the control inputs with 20 % increment in time-delay values

Full size image

In the following, the simulation results of the proposed controller are illustrated in comparison with the results of [2]. To compare the results with those of [2], the system is also simulated with the adaptive controller given in [2]. Figure 6 demonstrates the trajectory of the controlled outputs. As it can be seen from the results, the proposed method provides faster and better transition responses over those of other method. The comparison of the control inputs is illustrated in Fig. 7 which shows that the control signals of the proposed method have much better behavior in comparison with those of the controller in [2]. However, Fig. 7 shows that the control signal introduced in [2] contains high frequency oscillations which are undesirable in practice.

Fig. 6
figure 6

The trajectories of the controlled outputs

Full size image
Fig. 7
figure 7

The responses of the control signals

Full size image

5 Conclusion

This paper discusses robustness and high performance for matched uncertain MIMO linear systems with multiple state-delays and external disturbances. For this purpose, the theory of the combination of CNF and ISM techniques is presented. The simulation results demonstrate that the new technique has better IAE and ITAE performance indices values than the conventional linear feedback control method. The proposed method is effective and feasible and can be considered as a promising way for controlling similar nonlinear systems.