Bifurcation analysis of a piecewise-linear impact oscillator with drift

Abstract

We investigate the complex bifurcation scenarios occurring in the dynamic response of a piecewise-linear impact oscillator with drift, which is able to describe qualitatively the behaviour of impact drilling systems. This system has been extensively studied by numerical and analytical methods in the past, but its intricate bifurcation structure has largely remained unknown. For the bifurcation analysis, we use the computational package TC-HAT, a toolbox of AUTO 97 for numerical continuation and bifurcation detection of periodic orbits of non-smooth dynamical systems (Thota and Dankowicz, SIAM J Appl Dyn Syst 7(4):1283–322, 2008) The study reveals the presence of co-dimension-1 and -2 bifurcations, including fold, period-doubling, grazing, flip-grazing, fold-grazing and double grazing bifurcations of limit cycles, as well as hysteretic effects and chaotic behaviour. Special attention is given to the study of the rate of drift, and how it is affected by the control parameters.

1 Introduction

Various drifting oscillator models [2–6] have been extensively studied in the past due to their effectiveness for predicting overall dynamics and progressive motion in engineering applications, such as percussive drilling and vibro-impact moling [7]. In these studies, the impacted media was represented by so-called sliders, which modelled the contact force acting on the drill-bit during the interactions, and the Kelvin–Voigt model was frequently used to represent the contact force generated during the impact. To facilitate the comprehensive analysis of the drifting system [3], in the previous work the drift was separated from the bounded dynamics in [8], and a five-dimensional flow was reduced to a two-dimensional map [9] first and later to an approximate one-dimensional iterative map [10]. Finding the optimum characteristics of the applied static and dynamics forces for maximising the progression rates was an important focus of these investigations, and the special attention was paid to period-1 motion [11]. These models were developed further in [12, 13] to take into account the influence of contact geometries and the governing force–displacement relationship during all stages of the interactions. In [12], the influence of different force contact models on the global and local dynamics has been investigated for three different models of the contact force: Kelvin–Voigt, Hertz stiffness and nonlinear stiffness and damping, while in [13], a power-law relationship between the force and penetration was assumed, with a power-law exponent which depends on the impactor geometry (conical or spherical) and on the contact phase (loading or unloading). The conducted analysis revealed that despite the obtained differences given by all these models, the drifting oscillator [3] with a simple linear visco-elastic slider based on the Kelvin–Voigt model provides a good approximation to study and predict the behaviour of the real systems in the appropriate parameters’ ranges.

To support the development of mathematical models capable of describing the main phenomena occurring during impact drilling, a number of experimental studies were also conducted. Wiercigroch et al. [14] presented extensive studies of ultrasonic percussive drilling with diamond-coated tools in laboratory conditions on rocks such as sandstone, limestone, granite and basalt. Franca [15] carried out a series of experiments on an in-house designed rotary-percussive drilling rig and proposed a phenomenological bit-rock interaction model for rotary-percussive drilling aiming to obtain quantitative information from drilling data related to rock properties, bit conditions and drilling efficiency. More recently, Franca and Weber [16] conducted experimental and numerical studies of a new resonance hammer drilling model with drift and showed that the behaviour of the system may vary significantly from simple periodic regimes to chaos. In all these cases, simple drifting oscillators were useful in describing certain phenomena observed in the experiments.

Inspired by the impact-induced effects occurring in percussive drilling, an extensive research programme has been conducted at the Centre for Applied Dynamics Research of Aberdeen University in the last few years to develop a novel drilling technology known as Resonance Enhanced Drilling (RED) [17]. The main idea behind this technology is to apply an adjustable high-frequency dynamic stress (generated by an axially vibrating tool through intermittent impacts), in combination with rotary action in order to enhance the penetration rates by creating resonance conditions between the drill-bit and the drilled formation. This resonance needs to be maintained for varying drilling conditions by adjusting the static force (weight on bit) together with the frequency and amplitude of the dynamic stress, so as to produce a steadily propagating fracture zone, which is particularly beneficial while drilling hard rocks. A recent investigation [18] shows that the drifting oscillator model [3] is capable of giving good estimates of the optimal values of the static force and the amplitude of the dynamic stress, which can be used for the operational control of RED-based systems while drilling through different rock formations. However, the complete picture of the dynamics of the drifting oscillator [3] under parameter variations is still to be developed, and the present paper aims precisely to fill this gap in order to assist the optimization of the next-generation drilling operations.

From the mathematical point of view, the drifting oscillator [3] belongs to the class of piecewise-smooth systems, and the presence of nonlinearities of two different types: dry friction and soft impact (see also [19]), makes its dynamics especially interesting. As is well known, the fundamental bifurcations occurring in this type of systems are still a subject of ongoing research, and a growing literature has concerned itself with the classification and local description of the dynamics in the vicinity of limit cycles interacting with discontinuity boundaries in a degenerate manner [20–22]. Practical examples where these phenomena are observed can be found e.g. in [23] and [24], which focus on the mathematical modelling of cam-follower devices and the dynamics of gear rattling, respectively. The present paper aims also to contribute in this area. For this purpose, we will conduct a detailed bifurcation analysis of the periodic response of the drifting system [3] using path-following (numerical continuation) techniques. Here, our interest in the periodic motion is motivated by its practical implications on the system performance (e.g. penetration rates) [25]. As most of the mathematical models of drifting oscillators are piecewise-smooth, the numerical continuation of their periodic solutions requires the assembly of multiple boundary-value problems, resulting in a continuation problem of large dimension, whose implementation requires involved programming and mathematical manipulation. These complications can be overcome by means of a suitable software application such as TC-HAT [1], a driver of AUTO 97 for path-following and bifurcation detection of periodic solutions of non-smooth dynamical systems. Therefore, we will make intensive use of this toolbox in order to unveil the intricate bifurcation structure of the drifting oscillator considered in this paper.

The organization of the paper is as follows. In the next section, we explain the physical model of the drifting oscillator and present its equations of motion describing the different modes of operation in a compact manner. In Sect. 3, the mathematical description of the system is appropriately adopted in order to carry out the numerical analysis of the system by means of TC-HAT. The outcome of this analysis is presented in Sect. 4. First, we carry out an extensive study of the system response under one-parameter variations, thus, obtaining precise values of several co-dimension-1 bifurcations. Then, this information is used to conduct a two-parameter study of the system response, for which we use TC-HAT to trace the co-dimension-1 bifurcations previously found, which allows us to detect several bifurcations of co-dimension 2. Finally, we present some conclusions and closing remarks concerning our study.

2 Physical model

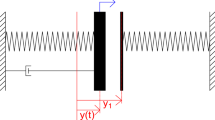
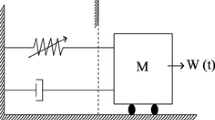
Consider a drifting impact oscillator modelled as an oscillating mass $m$ (impactor) driven by an external force $f(t)$, as shown in Fig. 1, where three physical models with increasing complexity are shown in panels a–c. All these models have been developed and extensively studied at the University of Aberdeen (Krivtsov and Wiercigroch [2], Pavlovskaia et al. [3] and Ajibose et al. [12]). The interactions between the impactor and the impacted media are represented by a frictional, visco-elastic slider with negligible mass. The slider moves downwards in stick-slip phases, where the progression takes place when the force acting on the mass from the slider exceeds the threshold force $f_{r}=1$. The variables $x$, $z$ and $v$ stand for the positions of the mass, slider top and slider bottom, respectively. We assume that the gravity loads are included in the static term $b$ of the driving force $f(t)$. During operation, the difference $(z+g)-x$ is monitored in order to detect an impact between the slider top and the impactor. The system can operate under one of three modes at any time: No contact, Contact without progression or Contact with progression. We refer the reader to [3, 7, 8] for a detailed description of these modes. The nondimensionalised equations of motion of the system can be written in compact form as follows:

$$\begin{aligned} p'&=y-P_{1}P_{3}\left( y+\frac{1}{2\xi }(q-1)\right) ,\nonumber \\ y'&=a\cos (\omega t+\varphi _{0})+b-P_{1}P_{2}(1-P_{3})(2\xi y+q)\nonumber \\&\qquad -P_{1}P_{3},\nonumber \\ q'&=-\frac{1}{2\xi }q+P_{1}P_{2}(1-P_{3})\left( y+\frac{1}{2\xi }q\right) +\frac{P_{1}P_{3}}{2\xi },\\ v'&=P_{1}P_{3}\left( y+\frac{1}{2\xi }(q-1)\right) ,\nonumber \end{aligned}$$

(1)

with $P_{1}{:=}H(p-q-g)$, $P_{2}{:=}H(2\xi y+q)$ and $P_{3}{:=}H(2\xi y+q-1)$, where $H(\cdot )$ stands for the Heaviside step function. In (1), the linear transformation

$$\begin{aligned} p=x-v,q=z-v, \end{aligned}$$

has been introduced. The new variables $p$ and $q$ represent the displacements of the mass and the slider top, respectively, relative to the position of the slider bottom $v$. This linear change of coordinates allows to decouple the oscillatory motion of the system captured by the variables $(p,y,q)$ from the drift $v$, see [8].

Fig. 1

Physical models of drifting impact oscillators: a without elasticity of the slider as introduced in [2]; b with linear visco elastic characteristics of the slider as proposed in [3]; and c with nonlinear visco-elastic properties of the slider as studied in [12]

3 Mathematical modelling with TC-HAT

The mathematical model of the piecewise-linear system (1) can be formulated as a hybrid dynamical system [1], which is characterized by continuous-time behaviour interrupted by discrete-time events. In this context, a solution trajectory is divided into a sequence of segments, each of which comprises a smooth vector field describing the evolution of the segment, a smooth event function whose zeroes define the terminal point of the segment and a smooth jump function which maps the terminal point of the current segment to the initial point of the next one. Each segment is associated with an index $I_{i}$, $i\in {{\mathrm{\mathbb {N}}}}$, in such a way that any periodic trajectory of the hybrid dynamical system is fully described by its solution signature $\left\{ I_{i}\right\} ^l_{i=1}$, $l\in {{\mathrm{\mathbb {N}}}}$ being the length of the signature.

This mathematical formulation allows us to study numerically the bifurcation structure of a hybrid dynamical system by means of TC-HAT [1]. This is a FORTRAN-based toolbox for the numerical continuation and bifurcation detection of periodic orbits of non-smooth dynamical systems. It exploits the pseudo-arclength numerical continuation applied to boundary-value problems implemented in AUTO 97. Specifically, TC-HAT uses this boundary-value problem formulation for the one-parameter continuation of periodic trajectories composed of multiple segments and two-parameter continuation of fold, period-doubling and grazing bifurcations of such trajectories. A detailed explanation of the functionality and usage of this toolbox is available in [1, 26]. A recent application of TC-HAT can be found in [27], where the authors use this path-following software to unveil the bifurcation structure of a non-smooth model of a Jeffcott rotor.

3.1 Basic framework

Let us introduce the vector fields, event functions and jump functions characterizing the periodic trajectories of the drifting oscillator (1). Let $\alpha {:=}(b,\omega ,a,\xi ,g,\varphi _{0})$ $\in {{\mathrm{\mathbb {R}}}}^+_{0}\times \left( {{\mathrm{\mathbb {R}}}}^+\right) ^4 \times {{\mathrm{\mathbb {S}}}}^1$ be the parameters of the system, with ${{\mathrm{\mathbb {R}}}}^+_{0}$ being the set of nonnegative numbers. Denote by $u{:=}(p,y,q,s)_{\mathrm{T}}\in W_{g}\times {{\mathrm{\mathbb {S}}}}^1$ the state variables of the system, with the invariant set $W_{g}{:=}\left\{ (p,y,q)\in {{\mathrm{\mathbb {R}}}}^3:\right.$ $\left. 0\le q\le 1 \text{ and } p\le q+g\right\}$.

The periodic trajectories described by Eq. (1) will consist of the following segments:

No contact (NC). This segment occurs when the impactor ($m$) and the slider top move separately (see Fig. 1b), i.e. $p-q-g<0$. The dynamics of the system during this regime is governed by the equation (cf. Eq. (1))

$$\begin{aligned} u'=f_{\mathrm{NC}}(u,\alpha ){:=}\left( \begin{array}{c} y\\ a\cos (s+\varphi _{0})+b\\ -\dfrac{1}{2\xi }q\\ \omega \end{array}\right) . \end{aligned}$$

(2)

This segment terminates when a crossing with the discontinuity boundary

$$\begin{aligned} \Pi {:=}\left\{ (p,y,q)\in {{\mathrm{\mathbb {R}}}}^3:h_{\mathrm{C}}(u,\alpha ){:=}p-q-g=0\right\} \end{aligned}$$

(3)

is detected. The initial point of the next segment is given by the jump function $g_{\mathrm{id}}(u){:=}u$.

No contact 2 $\pi (NC2\pi )$. This segment is introduced to keep the angular variable $s$ within the interval $[0,2\pi )$. The dynamics of the system is governed by Eq. (2), and the segment terminates when $h_{2\pi }(u,\alpha )\,{:=}\,s-2\pi =0$, with the corresponding jump function

$$\begin{aligned} g_{2\pi }(u)=\left( \begin{array}{c} p\\ y\\ q\\ s-2\pi \end{array}\right) . \end{aligned}$$

The initial phase $\varphi _{0}$ will be chosen in such a way that the event $h_{2\pi }(u,\alpha )=0$ occurs during this segment only.

Contact without progression 1 (CwoP-1). In this segment, the impactor is in contact with the slider top (i.e. $p-q-g=0$), and consequently they move together. The behaviour of the system is described by the equation (cf. Eq. (1))

$$\begin{aligned} u'&= f_{\mathrm{CwoP}}(u,\alpha )\nonumber \\&:= \left( \begin{array}{c} y\\ a\cos (s+\varphi _{0})+b-(2\xi y+q)\\ y\\ \omega \end{array}\right) . \end{aligned}$$

(4)

This segment is characterized by the fact that the force acting on the mass from the slider is positive but less than the threshold of the dry friction $f_{r}=1$ (i.e. $0<2\xi y+q<1$); hence, no progression occurs. The terminal point of the segment corresponds to a crossing with the discontinuity boundary

$$\begin{aligned} \ell _{1}&:= \{(p,y,q)\in {{\mathrm{\mathbb {R}}}}^3:h_{\mathrm{CwoP-}1}(u,\alpha )\nonumber \\&:= 2\xi y+q-1=0,p-q-g=0\} \end{aligned}$$

(5)

with the jump function $g_{\mathrm{id}}$ previously defined.

Contact without progression 2 (CwoP-2). This segment is the same as the one introduced above, except for its terminal point, which is defined by the discontinuity boundary

$$\begin{aligned} \ell _{2}{:=}\{&(p,y,q)\in {{\mathrm{\mathbb {R}}}}^3:h_{\mathrm{CwoP-}2}(u,\alpha ){:=}2\xi y+q=0,\nonumber \\&p-q-g=0\}. \end{aligned}$$

(6)

Contact with progression (CwP). This segment occurs when the force acting on the mass from the slider is large enough to move the slider bottom downwards, i.e. $2\xi y+q\ge 1$, and $p-q-g=0$. The dynamics of the drifting oscillator during this phase is governed by the following system of ODEs:

$$\begin{aligned} u'=f_{\mathrm{CwP}}(u,\alpha ){:=}\left( \begin{array}{c} -\dfrac{1}{2\xi }(q-1)\\ a\cos (s+\varphi _{0})+b-1\\ -\dfrac{1}{2\xi }(q-1)\\ \omega \end{array}\right) . \end{aligned}$$

(7)

The segment ends when the trajectory hits the discontinuity boundary $\ell _{1}$, with the initial point for the next segment given by the jump function $g_{\mathrm{id}}$ defined above.

Near grazing (NG). This segment is introduced to detect a grazing contact with the event surfaces $\ell _{1}$ or $\ell _{2}$, during the Contact without progression mode of operation. The dynamics during this segment is described by the vector field $f_{\mathrm{CwoP}}$, and the terminal point is defined by the condition (cf. [1], Sect. 3.2])

$$\begin{aligned} h_{\mathrm{NG}}(u,\alpha )&:= \partial _{u} h_{\mathrm{CwoP-}1}(u,\alpha )\cdot f_{\mathrm{CwoP}}(u,\alpha )\\&= \partial _{u} h_{\mathrm{CwoP-}2}(u,\alpha )\cdot f_{\mathrm{CwoP}}(u,\alpha )\\&= y(1-4\xi ^2)+2\xi (a\cos (s+\varphi _{0})\\&+b-q)=0, \end{aligned}$$

with the jump function $g_{\mathrm{id}}$ previously defined. Adding the auxiliary boundary conditions $h_{\mathrm{CwoP-}1}(u,\alpha )=0$, $h_{\mathrm{CwoP-}2}(u,\alpha )=0$, allows to locate the parameter values at which the trajectory makes grazing contact with the event surfaces $\ell _{1}$ and $\ell _{2}$, respectively.

The segments defined above along with the corresponding vector fields, event functions and jump functions are summarized in Table 1. Here, we also assigned an index to each segment. In Fig. 2, we present a period-1 trajectory of the drifting oscillator illustrating some of the segments introduced in this section. Finally, the equations of motion of the system can be written in terms of the vector fields defined above as follows:

$$\begin{aligned}&u'\nonumber \\&\quad ={\left\{ \begin{array}{ll}f_{\mathrm{NC}}(u,\alpha ), &{} p<q+g \text{ or } 2\xi y+q\le 0,\\ f_{\mathrm{CwoP}}(u,\alpha ), &{} p=q+g \text{ and } 0<2\xi y+q<1,\\ f_{\mathrm{CwP}}(u,\alpha ), &{} p=q+g \text{ and } 2\xi y+q\ge 1. \end{array}\right. }\nonumber \\ \end{aligned}$$

(8)

Fig. 2

Period-1 orbit of the drifting oscillator computed for $a=0.3$, $\omega =0.1$, $\xi =0.05$, $b=0.15$, $g=0.02$ and $\varphi _{0}=0$. The trajectory is plotted using different colours to distinguish each segment $I_{1}$–$I_{5}$. The figure also includes a number of subspaces that are used to study the system dynamics by means of low-dimensional maps, as published in a previous work [10]. For the current numerical implementation, we will make use of the discontinuity boundaries $\Pi =X_{2}\bigcup X_{3}$, $\ell _{1}=\Sigma _{2}\bigcup \Sigma _{3}$ and $\ell _{2}=\Sigma _{4}$, as defined in (3), (5) and (6)

Table 1 Segments defined for the numerical analysis using TC-HAT.

3.2 Solution measures

In order to construct a bifurcation diagram of a certain invariant set, a measure of the invariant set is usually plotted against a single control parameter. In many path-following packages (e.g. AUTO 97 [28]), the $L_{2}$-norm is set by default as the principal solution measure. In the present work, however, we will use solution measures related to physical phenomena occurring in the system. In the case that a periodic trajectory is studied for which progression takes place (i.e. those whose solution signature includes the index $I_{3}$), we will use the average rate of progression (drift) per period (rate of progression, for short) as solution measure, which is computed as follows. Consider a periodic solution $(p(t),y(t),q(t))$ of Eq. (8) with period $T>0$. We, thus, define the rate of drift

$$\begin{aligned} ROP{:=}\frac{1}{T}\int \limits _{0}^{T}v'(t)\,dt, \end{aligned}$$

(9)

where

$$\begin{aligned} v'(t)={\left\{ \begin{array}{ll} y(t)+\dfrac{1}{2\xi }(q(t)-1), &{} p(t)=q(t)+g \text{ and } \\ &{} 2\xi y(t)+q(t)\ge 1,\\ 0, &{} \text{ otherwise. } \end{array}\right. } \end{aligned}$$

Thus, the solution measure defined by (9) gives us the average velocity of the slider bottom during one period of oscillation.

In our analysis, we will also deal with periodic trajectories where no progression is observed, i.e. their solution signature does not contain the index $I_{3}$. In this case, the ROP is not a suitable measure, as the progression per period is always zero. For this type of motion we will use the average power dissipated by the damper $c$ (see Fig. 1b) per period as solution measure, which can be calculated as follows:

$$\begin{aligned} P_{c}{:=}\frac{1}{T}\int \limits _{0}^{T}w'(t)\,dt, \end{aligned}$$

(10)

with

$$\begin{aligned} w'(t)={\left\{ \begin{array}{ll} \dfrac{1}{2\xi }q(t)^2, &{} p(t)<q(t)+g \text{ or } \\ &{} 2\xi y(t)+q(t)\le 0,\\ 2\xi y(t)^2, &{} p(t)=q(t)+g \text{ and } \\ &{} 0<2\xi y(t)+q(t)<1,\\ \dfrac{1}{2\xi }(q(t)-1)^2, &{} p(t)=q(t)+g \text{ and } \\ &{} 2\xi y(t)+q(t)\ge 1. \end{array}\right. } \end{aligned}$$

Here, $w'(t)$ gives us the instantaneous rate at which the damper $c$ dissipates energy along the periodic motion $(p(t),y(t),q(t))$. With this mathematical formulation we are now ready to show the main results of the present work.

4 Bifurcation analysis of the drifting oscillator

In [3], the authors discovered that, within a certain interval of the static force $b$ with the remaining parameters fixed, the rate of progression achieves a local maximum for period-1 motion. Thus, in the present work we will study this type of periodic response of the system in detail. In Fig. 2 we show the initial period-1 trajectory that will be analysed by means of path-following techniques. In the next section, we will begin our analysis with a detailed one-parameter study of the drifting oscillator in order to understand the effect of the control parameters on its response and also to determine their optimal values yielding the highest rate of progression. In this analysis, several co-dimension-1 bifurcations will be detected and then continued in two control parameters in Sect. 4.2, thus, yielding a two-parameter bifurcation diagram where co-dimension-2 phenomena will be observed and discussed.

4.1 One-parameter analysis

One of the main concerns from a practical point of view is to maximise the rate of progression (ROP), for which a careful analysis of the system response under parameter variations is essential. To this end, we will first perform the numerical continuation of the periodic orbit shown in Fig. 2 with respect to the static force $b$, using the rate of progression as solution measure. The result is depicted in Fig. 3 (red curve). Here, we show how the ROP varies with the static force. In this way, we found that for $b\approx 0.1638$ the ROP achieves a maximum value $\approx 0.5387$. This optimal point lies within the interval of stability of the period-1 motion, which is bounded by period-doubling and fold bifurcations located at $b\approx 0.11$ and $b\approx 0.1671$, respectively. For parameter values below the period-doubling point, the period-1 trajectory is unstable and undergoes a grazing bifurcation at $b\approx 0.0277$ (grazing with the discontinuity boundary $\ell _{1}$), where the ROP becomes zero. In Fig. 3, we also depict continuation curves for the cases $a=0.28$ (green) and $a=0.32$ (black). As can be seen, the bifurcation scenario just described persists under perturbations in the amplitude $a$.

Fig. 3

One-parameter continuation of the periodic orbit shown in Fig. 2 with respect to the static force. The solid and dashed lines mark stable and unstable solutions, respectively. In what follows, this convention is used to denote stability. The green, red and black curves correspond to the cases $a=0.28$, $a=0.3$ and $a=0.32$, respectively. Bifurcations and points of maximal ROP are marked by X’s and dots, respectively. (Color figure online)

In order to study the period-1 orbits for values of static force below the grazing bifurcation, we will use the average dissipated power as solution measure [see (10)], as these orbits never operate under the Contact with progression mode; hence, the ROP is always zero. In Fig. 4a we show the continuation of the period-1 solution for values of $b$ both above and below the grazing bifurcation found previously. The performed continuation reveals a second grazing bifurcation at $b=0$ (grazing with the discontinuity boundary $\Pi$). Figure 4b shows different unstable period-1 orbits for values of static force between and including the grazing points.

Fig. 4

a Continuation of the period-1 orbit shown in Fig. 2 with respect to $b$; b unstable period-1 orbits of (8) for values of static force between the grazing bifurcations shown in a, with $b_{1}=0.0277$, $b_{2}=0.0192$, $b_{3}=0.0119$, $b_{4}=0.0048$ and $b_{5}=0$

Fig. 5

a Bifurcation diagram of the piecewise-linear system (8) for the parameter values $a=0.3$, $\omega =0.1$, $\xi =0.05$, $g=0.02$ and $\varphi _{0}=0$. The picture shows the periodic window $(\epsilon _{n},\rho _{n})$ belonging to a reverse period-adding cascade. b–d show a sequence of fingered strange attractors computed along the period-adding cascade, computed for the static force values $b_{1}$, $b_{2}$, $b_{3}$ shown in a

Now let us investigate the steady-state attractors of the drifting oscillator for values of static force below the period-doubling bifurcation found before, where the period-1 motion is unstable. For this purpose, we will construct a bifurcation diagram computed by means of direct numerical integration. We set initially $b=0.12$ where a stable period-1 trajectory exists (see Fig. 3). Then we choose suitable initial values (which can be obtained from the continuation results described above) and integrate (8) over 500 periods of external forcing to allow for the decay of transients. Next we continue the flow for another interval of 100 periods and plot samples of the solution at the times $t=\frac{2i\pi }{\omega }$, $i=1,2,\ldots ,100$. Subsequently, $b$ is decreased by a small amount and the same procedure is repeated, where now the final sample of the previous step is used as initial value. This is done, until the grazing point $b=0$ is reached. This procedure allows us to visualize the qualitative changes in the $\omega$-limit sets of the iterations of a Poincaré map under parameter perturbation, which in turn provides relevant information about the changes in the long-time dynamics of the drifting oscillator. The outcome of this numerical procedure is shown in Fig. 5. The bifurcation diagram (panel a) shows a large interval of period-1 motion $0.11\le b\le 0.1671$, which corresponds to the solid segment of the curve bounded by the period-doubling and fold bifurcations shown in Fig. 4a. For parameter values slightly greater than the fold point, the motion becomes chaotic. In the parameter range, $0\le b\le 0.1671$, the bifurcation diagram reveals the presence of a reverse period-adding cascade with bands of chaos appearing between periodic intervals. This cascade consists of a sequence of parameter windows $(\epsilon _{n},\rho _{n})$ where stable period-$n$ orbits exist, $n=1,2,\ldots$, with one impact with the plane $p-q=g$ per orbital period. This type of orbit is called a maximal periodic orbit, cf. [29–31]. The period of these orbits increases in an arithmetic sequence as $b$ is decreased, in such a way that each period increment is due to the appearance of an additional excursion of the periodic orbit through the No contact regime. According to the numerical observations, the periodic windows seem to accumulate on the grazing bifurcation $b=0$, with the period going to infinity and the width of the windows decreasing to zero as $b\rightarrow 0^+$.

It can also be observed that the transitions between adjacent periodic windows involve further bifurcations and chaotic behaviour. Let us explain this in more detail. Assume $b\in (\epsilon _{n},\rho _{n})$ for some fixed $n\ge 1$. For this parameter value a stable period-$n$ orbit exists, and it disappears when $b$ is increased beyond $b=\rho _{n}$ via a fold bifurcation. Moreover, the period-$n$ orbit looses stability at $b=\epsilon _{n}$, where a period-doubling cascade is born, thus leading to chaos, which is manifested as a strange attractor with a fingered structure, see Fig. 5b–d. The number of fingers of this attractor increases in an arithmetic sequence, as the static force is decreased, following the increment of the period of the orbits in the window $(\epsilon _{n},\rho _{n})$. The phenomena described above have been shown to be universal in the sense that, qualitatively, this system response has been observed in a wide variety of impact oscillators for near-grazing conditions [29, 30, 32].

Now let us study the behaviour of the system when the parameter $a$ is varied. As in the previous case, we will perform the one-parameter continuation of the initial periodic orbit shown in Fig. 2, using the ROP as solution measure. Furthermore, the same procedure described before will be employed to generate a bifurcation diagram based on direct numerical integration, this time taking $a$ as the varying parameter. The result is shown in Fig. 6. As can be seen, the initial period-1 orbit ($a=0.3$) disappears via a fold bifurcation $a\approx 0.2717$, at which value there is a sudden jump to impacting chaotic behaviour. On the other hand, if the value of $a$ is increased, the periodic orbit looses stability at a period-doubling bifurcation $a\approx 0.4576$, where a period-doubling cascade leading to chaos is born, as shown in the blue diagram of Fig. 6. The unstable period-1 motion regains stability at a reverse supercritical period-doubling bifurcation located at $a\approx 1.7845$. For $0.6498<a<0.6723$, a significant window of period-2 motion exists, culminating in a period-doubling cascade. After this cascade, a long interval of chaotic behaviour interrupted by small periodic windows is observed. The co-dimension-1 bifurcations described above are confirmed by the red curve shown in Fig. 6 computed via numerical continuation.

Fig. 6

Bifurcation diagram of the drifting oscillator with respect to $a$. The red curve represents the continuation of the period-1 motion shown in Fig. 2, while the diagram in blue corresponds to the bifurcation picture generated via direct numerical integration. The diagrams were computed for the parameter values $b=0.15$, $\omega =0.1$, $\xi =0.05$, $g=0.02$ and $\varphi _{0}=0$. (Color figure online)

To finish this section, we will analyse the effect of the frequency of the driving force. As in the previous cases, we begin the study with the numerical continuation of the period-1 solution shown in Fig. 2, this time with respect to $\omega$. In Fig. 7 we depict the resulting bifurcation diagram using the rate of progression (panel a) and the average dissipated power (panel b) as solution measures. By decreasing the frequency from the starting point $\omega =0.1$, we found a fold bifurcation at $\omega \approx 0.0622$, where a pair of stable and unstable period-1 orbits collide and then disappear for lower frequency values. Close to this fold point, the ROP achieves a maximum value $\approx 0.7614$ at $\omega \approx 0.0628$. If the frequency is now increased, the orbit looses stability at a period-doubling point $\omega \approx 0.2697$ and then undergoes a grazing bifurcation at $\omega \approx 0.5088$ (grazing with the discontinuity boundary $\ell _{1}$), where the ROP becomes zero. In Fig. 7b we show further bifurcations of the period-1 orbit for $\omega$ values greater than the grazing point found before. As can be seen in the picture, the period-1 orbit recovers stability via a reverse supercritical period-doubling bifurcation at $\omega \approx 1.6257$, and then another grazing bifurcation takes place at $\omega \approx 1.7385$ (grazing with the discontinuity boundary $\ell _{2}$). After this point, the period-1 solution remains on the plane $p-q=g$, centred at the point $(b+g,0,b)$, with decreasing amplitude as $\omega$ grows. This behaviour can be observed in the phase diagram shown in Fig. 8 for different values of $\omega$.

Fig. 7

One-parameter continuation of the periodic orbit shown in Fig. 2 with respect to the excitation frequency $\omega$. a Behaviour of the rate of progression as $\omega$ is varied. The point of maximal ROP is marked by a dot. b Average power dissipated by the damper $c$ (see Fig. 1b). The labels $\omega _{1}$–$\omega _{5}$ define the frequency values at which the corresponding periodic solutions are plotted in Fig. 8

Fig. 8

Period-1 orbits of the drifting oscillator for the frequency values $\omega _{1}=0.5088$, $\omega _{2}=0.6741$, $\omega _{3}=0.9544$, $\omega _{4}=1.7385$ and $\omega _{5}=3.1043$ (see Fig. 7b). The orbits computed at $\omega _{4}$ and $\omega _{5}$ are stable while the rest are unstable

In the parameter window limited by the period-doubling bifurcations found before, the long-time dynamics of the drifting oscillator is remarkably complex. This fact can be observed from the bifurcation diagram plotted in Fig. 9. From the starting point $\omega =0.2$, we observe a period-1 attractor that bifurcates at the period-doubling point, $\omega \approx 0.2697$, found earlier. Here, a typical period-doubling cascade is born, followed by small windows of chaotic behaviour and further cascades. For frequency values between $0.4212$ and $0.5499$, we find a larger band of chaotic response interrupted by small periodic windows, and after that a significant interval of period-2 motion is observed, which bifurcates at $\omega \approx 0.6341$, giving rise to a period-doubling cascade leading to chaos. For $\omega \in I_{1}{:=}[0.9163,$ $0.9672]$, Fig. 9 reveals parameter hysteresis in the system, produced by the co-existence of a band of intermittent chaotic motion and periodic attractors. A bigger interval of hysteresis can observed for $\omega \in I_{2}{:=}[1.5096,1.9026]$, where different stable periodic motions co-exist.

Fig. 9

Bifurcation diagram computed for the parameter values $b=0.15$, $a=0.3$, $\xi =0.05$, $g=0.02$ and $\varphi _{0}=0$. The red and blue colours mark the frequency sweeps in the increasing and decreasing directions, respectively. The intervals $I_{1}$, $I_{2}$ represent the frequency windows at which hysteretic effects can be observed. The red diagram is depicted at these windows only, where different attractors co-exist. (Color figure online)

In this section we have carried out a careful numerical study of the system dynamics changing one parameter at the time, and considering $a$, $b$ and $\omega$ as the main control variables, i.e. the parameters governing the external forcing of the drifting oscillator. This analysis is fundamental for gaining a deeper insight into the role played by each of the control parameters, in particular, how they affect the rate of progression during period-1 motion. Specifically, Figs. 3, 6 and 7 show the behaviour of the ROP, as the control parameters are adjusted.

Let us discuss these remarks in more detail. As can be seen in Fig. 3, the stable period-1 motion survives within an interval bounded by a period-doubling and a fold point, which reveals the crucial role of the static force in the operation of the system. Between these two bifurcations, we find a point where the ROP achieves a maximum value, which is the optimal operation condition from a practical point of view. Moreover, Fig. 7a reveals that, qualitatively speaking, the influence of the frequency of external excitation on the system operation and that of the static force are analogous. On the other hand, the variation of the amplitude $a$ affects the system response in a slightly different way, as can be observed in Fig. 6. The stability of the period-1 motion depends again on this parameter, but in this case the highest ROP within the interval of stability bounded by the fold and period-doubling bifurcations is found at its end. Thus, one might be tempted to set the amplitude as close as possible to the period-doubling bifurcation; however, in practical terms the aim could be compromised, as the period-1 motion may lose stability under small perturbations. All of these aspects must be taken into account for a suitable adjustment of the control parameters to achieve the best ROP.

4.2 Two-parameter analysis

In the previous section, a detailed one-parameter analysis of the dynamical response of the piecewise-linear system (8) was undertaken. Generically, one expects co-dimension-1 bifurcations to occur, i.e. qualitative changes in the system behaviour produced by the variation of a single parameter. In our particular case, the following co-dimension-1 bifurcations of limit cycles were found: fold, period-doubling and grazing. As has been extensively explored over the past decades, these bifurcations can be traced in a two-parameter space, giving rise to bifurcation curves that often intersect at isolated co-dimension-2 points. The presence of such points deeply influences the qualitative behaviour of the system, as they play the role of organizing centres for the nearby dynamics, giving rise to intricate bifurcation scenarios. In this section, our focus will be on searching for co-dimension-2 bifurcations, where a smooth and a discontinuity-induced bifurcation (DIB, [31]) occur together, i.e. when an orbit undergoing grazing contact with a discontinuity boundary can be characterized by a nontrivial Floquet multiplier on the unit circle.

In what follows, we will leave the value of the static force fixed at $b=0.15$ and consider $\omega$ and $a$ as the bifurcation parameters. This is motivated by the fact that in practical applications the static force is kept constant, whereas $\omega$ and $a$ are usually varied. In other words, we will focus on studying the effect of the harmonic component of the external forcing on the system dynamics. In Fig. 10a we show a global extension of the two-parameter continuation of the fold (blue), period-doubling (red) and grazing (black, green) bifurcations in the $\omega$-$a$ plane. As can be seen in this picture, the region of stability (grey area) of period-1 orbits of the type shown in Fig. 2 is bounded from below, above and the right side by a fold, period-doubling and grazing bifurcation curves, respectively. This gives us critical information regarding the parameter region from which the control parameters must be chosen for the system to operate under period-1 motion, taking also into account suitable rates of progression which can be controlled by these parameters (see Sect. 4.1). For instance, if $\omega$ and $a$ are chosen from the grey area, close to the grazing curve, then the ROP will be close to zero (see e.g. Fig. 7a), which is undesirable from a practical point of view.

Fig. 10

a Two-parameter continuation computed for $b=0.15$, $\xi =0.05$, $g=0.02$ and $\varphi _{0}=0$, showing the bifurcation curves: fold (blue), period-doubling (red), grazing with the discontinuity boundary $\ell _{1}$ (black) and grazing with $\ell _{2}$ (green). Co-dimension-2 bifurcations are denoted by cod-2. The dotted vertical and horizontal lines correspond to the one-parameter bifurcation diagrams shown in Figs. 6 and 7b, respectively. The grey area represents the parameter region in which stable period-1 orbits of the type shown in Fig. 2 exist. b, c show enlargements of the bifurcation diagram around cod-2 points. In addition to the period-doubling (red) and grazing (black) curves, we computed a curve (brown) of grazing bifurcations of period-2 orbits that emanates from the co-dimension-2 point (see also Fig. 11 below). (Color figure online)

Fig. 11

Period-2 orbits of system (8) for parameter values along the grazing curve (brown) depicted in Fig. 10c: $\omega =0.4733$, $a=0.1616$, ($O_{1}$, red); $\omega =0.4644$, $a=0.2044$, ($O_{2}$, grey) and $\omega =0.43$, $a=0.4065$, ($O_{3}$, blue). This last orbit corresponds to a double grazing bifurcation (co-dimension 2) for which grazing contacts with the discontinuity boundaries $\ell _{1}$ and $\ell _{2}$ occur simultaneously. (Color figure online)

The numerical continuation of the co-dimension-1 bifurcations found before allows us to detect three co-dimension-2 points: two flip-grazing ($\omega \approx 1.3946$, $a\approx 6.7289$; $\omega \approx 0.4733$, $a\approx 0.1616$) and one fold-grazing ($\omega \approx 0.4292$, $a\approx 0.0277$) bifurcations, all of which lie on the black grazing curve. In Fig. 10b–c we show a blow-up of the parameter space near two of the co-dimension-2 bifurcations shown in Fig. 10a. In the left panel, two branches of the grazing curve are depicted, corresponding to stable (solid line) and unstable (dashed line) grazing orbits, which are joined together at the fold-grazing bifurcation. From this point, a branch of fold bifurcations emanates tangentially to the grazing curve. In the right panel, we plot an enlargement of the parameter region around the flip-grazing bifurcation $(\omega ,a)\approx (0.4733,0.1616)$, where a period-doubling and a grazing curve of period-1 solutions intersect each other. In addition, we computed a grazing curve of period-2 orbits that emanates from this co-dimension-2 point. In Fig. 11, three period-2 orbits along this grazing curve are depicted. The orbit labelled $O_{1}$ corresponds to the flip-grazing point, where the period-1 trajectory is traced twice. This point is detected as a branching point during the continuation of the grazing curve of period-2 orbits. The global extension of this curve terminates at $(\omega ,a)\approx (0.43,0.4065)$, where a double grazing bifurcation occurs, as can be seen in the plot of the orbit $O_{3}$.

As pointed out in [20, 22], the systematic study of co-dimension-2 bifurcations occurring in non-smooth dynamical systems is far from being complete. One of the main reasons for this is the possibility that a classical (smooth) and a discontinuity-induced bifurcation occur simultaneously upon parameter variations, e.g. when a non-hyperbolic cycle makes tangential contact with a discontinuity boundary in the phase space. In such cases, the particular geometry of the involved boundary can play a significant role in the bifurcation scenario, hence making an exhaustive classification of bifurcations occurring in non-smooth systems almost hopeless.

Nevertheless, there are certain geometric features that are common in many applications. For instance, the fold-grazing bifurcation found in the present drifting oscillator clearly belongs to the class described in [22], Sect. 3], where this type of co-dimension-2 point appears in an impacting model for forest fires [33]. Similarly, the flip-grazing bifurcation encountered in our study shares some common features with that analysed in [22], Sect.4]. An analogous two-parameter bifurcation picture can also be found in [24], where the authors exploit the existence of explicit solutions in order to compute bifurcations curves in a mathematical model used to describe gear rattle.

Before finishing this section, it is worth mentioning another type of non-smooth bifurcation that has recently received significant attention. Consider a parameter-dependent impacting system with a moving obstacle whose motion is described by a non-smooth function in time. Upon parameter variations, it is generally possible that the impacts occur exactly at the points where the motion of the obstacle loses smoothness. This phenomenon is referred to as a corner event [34], and it can cause significant changes in the system dynamics, including period-adding cascades, also observed in the drifting oscillator analysed in the present paper. A well-known practical example where corner events are observed is the cam-follower device studied in [35]. It consists of a cam rotating at a constant speed, which provides a harmonic excitation to a follower that may, for instance, open and close a valve. Owing to the possibility of cam profiles being characterized by a non-smooth geometry, corner events appear naturally in cam-follower systems, typically at high rotational speeds [23]. This is a good example to illustrate the wide range of bifurcation scenarios that can appear in non-smooth engineering applications.

5 Conclusions

In the present work, for the first time a detailed bifurcation analysis of the periodic response of a piecewise-linear impact oscillator with drift has been carried out. The model considered here operates under one of the three regimes: No contact, Contact without progression and Contact with progression, each of which governed by a separate set of ordinary differential equations.

The system was studied in the context of hybrid dynamical systems, for which we used the AUTO 97 toolbox TC-HAT [1]. Specifically, we applied the toolbox to carry out the numerical continuation of period-1 and -2 solutions of the drifting oscillator, using the ROP as the main solution measure. This study enabled us not only to locate co-dimension-1 bifurcations (fold, period-doubling, grazing) but also to investigate the effect of the control parameters on the ROP and thus, determine the points where the ROP achieves a maximum value, which is one of the main concerns from a practical point of view. Specifically, we have carried out a careful numerical study of the periodic response of the system under one-parameter perturbations, considering $a$, $b$ and $\omega$ as the main control parameters, i.e. the parameters governing the driving force of the drifting oscillator. This study allowed us to gain a deeper insight into the role played by each of the control parameters and how they affect the ROP.

A particular contribution of this work is the numerical continuation of the detected co-dimension-1 points in two control parameters, thus, yielding a detailed stratification of the parameter space where the topologically different system behaviours can be identified. This study revealed the presence of co-dimension-2 bifurcations, such as flip-grazing, fold-grazing and double grazing, which serve as organizing centres of the co-dimension-1 bifurcations occurring in the system. Moreover, we also computed bifurcation diagrams based on direct numerical integration showing the rich spectrum of the possible system responses, including period-adding cascades, chaotic behaviour and hysteretic effects. The bifurcation analysis presented in this paper may provide fundamental knowledge for understanding the dynamical behaviour of systems with nonlinearities similar to those of the drifting oscillator considered in this work.