1 Introduction

The choice of the geometry description used in the large displacement analysis can be a challenge, particularly in the case of finite rotations. An example of a large displacement analysis formulation is the floating frame of reference (FFR) formulation, which is widely used when the bodies experience finite rigid-body rotation and small deformation. This formulation leads to a local linear elasticity problem that allows for exploiting model-order reduction techniques [1]. Because of the need for the simulation of rigid-body motion and large deformation, several non-linear theories were proposed in the two fields of computational mechanics and flexible multibody system (MBS) dynamics. In the co-rotational formulations, a coordinate system is used for each finite element (FE) to define both the elastic and inertia forces [2]. In the absolute nodal coordinate formulation (ANCF), on the other hand, the rigid and flexible body motion is defined using global coordinates including Cartesian position and gradient coordinates [3–5]. Another FE formulation used for the description of large rotation and large deformation problems is the large rotation vector formulation (LRVF), which is supposed to be a non-incremental procedure intended mostly for beam and plate applications [6]. Simo and Vu-Quoc developed this formulation by describing the geometrically exact beam dynamics based on the Kirchhoff–Love model developed by Reissner [7, 8]. Reissner’s work represents the foundation of the large-displacement finite-strain theory of shear-deformable beams [9]. Reissner formulated a one-dimensional large-strain beam theory for plane deformations by first deriving the local equations of beam equilibrium with the assumption of a plane and undistorted cross-section. He then developed generalized constitutive relations at the beam-theory level based on generalized strain measures such as the bending, axial force, and shear force strains. The virtual work of the internal, external, and boundary forces was then derived to obtain the governing equations. Simo and Vu-Quoc expanded upon this static theory to dynamics with the essence of this approach leading to accomplishing a fully non-linear plane beam theory that can account for finite rotations as well as finite strains. Absolute positions and absolute finite angles are used as generalized coordinates. The position and rotation fields are interpolated independently in the LRVF, giving rise to questions with regard to the redundancy in the geometric description. The rotation field can be used to define a tangent vector that defines a space curve which possesses geometric properties, such as curvature and torsion, which can significantly differ from those obtained using the position field [10]. In fact, the nodes of the position-based (PB) interpolation can occupy positions in space, which are different from the positions occupied by the nodes of the rotation-based (RB) interpolation. Furthermore, as will be shown in this paper, the rotation mesh can define a beam that is inextensible, leading to an additional inconsistency in the LRVF geometry representation.

Several notable contributions by other authors were based on Simo and Vu-Quoc’s geometrically exact beam theory, such as the work of Romero [11] who examined the use of interpolation types for the rotation field. The interpolations types were discussed in terms of advantages and drawbacks using non-linear rod models to provide qualitative and quantitative evaluation of four interpolation techniques with the goal to assess each method. The best overall properties were obtained with models using an orthogonal interpolation in the rotation group, where the objectivity of the continuum model was preserved. This method was originally proposed by Crisfield and Jelenic [12], where it was also shown that the application of linear interpolation techniques to finite rotation fields of either incremental or iterative rotations is non-objective and is path-dependent. Objectivity is achieved when the geometry is invariant under rigid-body transformation. When this condition is met, the formulation is said to be objective, otherwise it is non-objective. In order to address this problem, simple algorithms that achieve objectivity were developed to test finite rotation formulations to help identifying the source of the problems and deal with the unavoidable singularities associated with the use of some finite rotation parameters [13]. Although the algorithms can handle the finite rotations through a rescaling operation, the separation of displacement and rotation fields still exists.

The objective of this paper is to analytically and numerically examine and demonstrate the fundamental LRVF redundancy problem. It is shown in this paper that the use of two independent interpolations for the position and rotation leads to two independent meshes with nodes that occupy different positions in space in the deformed configuration. As a consequence, the material points of the rotation mesh are different from the material points of the position mesh. Furthermore, the space curve resulting from the rotation mesh is inextensible regardless of the axial load applied. Another contribution of this paper is to show that, while shear is an independent mode of deformation, the independent position and rotation interpolations cannot, in general, lead to the same geometric representation. As a consequence, the use of curvature defined using the rotation mesh to describe the bending of the position mesh cannot be justified. Numerical examples are presented for the first time in this paper to shed light on these fundamental issues and concepts. This paper is organized as follows. Section 2 demonstrates using a simple example that two independent kinematic descriptions cannot be used, in general, to obtain the same geometry. The brief discussion presented in Sect. 2 is necessary in order to clearly understand the LRVF kinematic assumptions and the potential problems which can develop from using independent interpolations for the position and rotation. Section 3 shows that a rotation mesh implicitly defines another space curve whose geometric properties may differ from an independently interpolated position mesh in a three-dimensional case. The LRVF kinematic description and equations of motion are presented in Sect. 4 for the planar case, where the definitions of the strains are also included. Section 5 compares the curvatures obtained using the PB and RB interpolations and shows how they can vary significantly. This section will also show additional complications resulting from using an independent RB interpolation such as the rotation field’s inextensibility when some assumptions related to the definition of the tangent vector are made. Section 6 presents numerical results obtained using the LRVF, including a robot arm subjected to a specified angular motion and an axial load. The numerical results obtained, which demonstrate that the nodes of the two meshes occupy different positions in space, shed light on the fundamental redundancy issue in the definition of inertia and strains. Conclusions are presented in Sect. 7.

2 Background

In this section, a simple example is used to demonstrate that two independent kinematic descriptions can possess significantly different geometries. This issue is fundamental in understanding the basic assumptions and the redundancy problem associated with the use of some large displacement FE formulations. There are two types of redundancies; one which can be eliminated systematically using a constraint or penalty approach, while the other cannot be eliminated and this second type can pose fundamental problems since it is in violation of basic mechanics motion description principles.

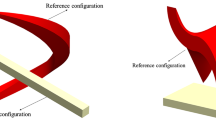
In order to explain the second type of redundancy which cannot be resolved, the two modes of deformation shown in Fig. 1 are considered. Figure 1a shows an example of a simple mode shape that defines a displacement field \(u_1 \left( {x,t} \right) =\left( {\hbox {sin}\left( {\frac{\pi x}{L}} \right) } \right) q_1 \left( t \right) \), while Fig. 1b shows a second mode shape that defines another displacement field \(u_2 \left( {x,t} \right) =\left( {\hbox {sin}\left( {\frac{2\pi x}{L}} \right) } \right) q_2 \left( t \right) \) with \(q_1 \) and \(q_2 \) being the amplitudes of the first and second independent mode shapes, respectively, for an element of length \(L\) with \(x\) as the axial coordinate of the beam, and \(t\) as time. Even in this simple case, the two independent fields \(u_1 \) and \(u_2 \) have significantly different geometric properties. By applying forces or constraints, \(u_1 \) and \(u_2 \) cannot be brought to be the same. As a consequence, the material points of the curve defined by the field \(u_1 \) will occupy positions that are different from the positions occupied by the material points of the curve defined by the field \(u_2 \) regardless of the forces and the constraints used. For example, the constraint condition that \(u_1 \left( {x,t} \right) =u_2 \left( {x,t} \right) \) leads to the trivial solution \(q_1 \left( t \right) =q_2 \left( t \right) =0\) which corresponds to the undeformed reference configuration.

Fig. 1
figure 1

Mode shape displacement and curvature

Full size image

One can also show, using the simple example of this section, that the geometric properties of two independent fields can be significantly different. As a consequence, it cannot be justified to assume that the geometric properties, obtained using one field, are the same as those of the other field. For example, using the assumption of small change in the length of the beam, the curvatures of the curves defined by the two fields \(u_1 \left( {x,t} \right) \) and \(u_2 \left( {x,t} \right) \) can be approximated by differentiating twice with respect to the parameter \(x\) as \(\left( {{\partial ^{2}u_1 }/{\partial x^{2}}} \right) =-\left( {{\pi ^{2}}/{L^{2}}} \right) \left( {\hbox {sin}\left( {\frac{\pi x}{L}} \right) } \right) q_1 \left( t \right) \) and \(\left( {{\partial ^{2}u_2 }/{\partial x^{2}}} \right) =-\left( {{4\pi ^{2}}/{L^{2}}} \right) \left( {\hbox {sin}\left( {\frac{2\pi x}{L}} \right) } \right) q_2 \left( t \right) \). These two equations show that for the same amplitudes, the values of the curvature of \(u_2 \) are different from the values of the curvature of \(u_1 \). The differences in curvature can be seen clearly in Fig. 1c where the same coordinate amplitude \(q\) is used for the two fields.

The concept discussed in this section is important to understand when nodes in the position and rotation meshes as shown in later sections of this paper occupy different positions in space. While the displacement solution obtained using the position mesh in the LRVF may compare favorably with the solution obtained using other formulations, further investigation into derived geometric properties such as curvature and torsion can show greater geometric inconsistency that sheds light on more fundamental formulation issues.

3 RB geometric representation

In the preceding section, it was shown, using a simple example, that in general two different shapes cannot be brought together perfectly regardless of the magnitude of the forces or type of constraints applied. In the LRVF, two independent interpolations are used for the position and finite rotation fields. The curve defined using the rotation field has geometric properties different from those of the curve defined by the position field. This section explains how the rotation field can be used to define a space curve (another position field) expressed in terms of finite rotations.

A three-dimensional space curve can be systematically defined in a global coordinate system \(XYZ\) by introducing a rotation field that defines the orientation of coordinate systems at points on the space curve. One can then choose an appropriate sequence of the three Euler angle successive rotations to reach any orientation in space. For example, if \(s\) is the space curve arc length parameter, one can use the interpolated rotation vector \({\varvec{\uptheta }}\left( s \right) =\left[ {{\begin{array}{lll} {\psi \left( s \right) }&{} {\phi \left( s \right) }&{} {\theta \left( s \right) } \\ \end{array} }} \right] ^\mathrm{T}\) to define the orientation of coordinate systems with origins attached to material points on the space curve. If \(X^{i}Y^{i}Z^{i}\) is the coordinate system at an arbitrary material point \(i\) defined by the arc length parameter \(s\) on the space curve, one can use the Euler angle sequence defined by an angle \(\psi \) (yaw) about the \(Z^{i}\) axis, followed by a second rotation \(\phi \) (roll) about the \(-Y^{i}\) axis, followed by a third and final rotation \(\theta \) (pitch) about the \(-X^{i}\) axis [14]. Using this sequence of rotations, the transformation matrix that defines the orientation of the coordinate system at \(s\) can be written as [15]

$$\begin{aligned} \mathbf{A}=\!\left[ \! {{\begin{array}{lll} {\hbox {cos}\psi \hbox {cos}\theta }&{} {-\hbox {sin}\psi \hbox {cos}\phi +\hbox {cos}\psi \hbox {sin}\theta \hbox {sin}\phi }&{} {-\hbox {sin}\psi \hbox {sin}\phi -\hbox {cos}\psi \hbox {sin}\theta \hbox {cos}\phi } \\ {\hbox {sin}\psi \hbox {cos}\theta }&{} {\hbox {cos}\psi \hbox {cos}\phi +\hbox {sin}\psi \hbox {sin}\theta \hbox {sin}\phi }&{} {\hbox {cos}\psi \hbox {sin}\phi -\hbox {sin}\psi \hbox {sin}\theta \hbox {cos}\phi } \\ {\hbox {sin}\theta }&{} {-\hbox {cos}\theta \hbox {sin}\phi }&{} {\hbox {cos}\theta \hbox {cos}\phi } \end{array} }} \!\right] \!. \end{aligned}$$
(1)

In order to construct a curve using the rotation field, the first column of the transformation matrix can be considered as the unit tangent to the space curve at \(s\). Let \(\mathbf{r}(s)=\left[ {{\begin{array}{lll} x&{} y&{} z \\ \end{array} }} \right] ^\mathrm{T}\) be the vector that defines the space curve. The location of an arbitrary point on the space curve as a function of the arc length can be determined by integrating the equation \({\text{ d }}\mathbf{r}=\mathbf{t}{\text{ d }}s\). This equation with the use of (1) can be written as \(\mathbf{r}(s)=\mathbf{r}_0 +\int {\mathbf{t}{\text{ d}}s} \). Substituting the tangent vector \(\mathbf{t}\) into this equation leads to

$$\begin{aligned} \mathbf{r}\left( s \right) =\mathbf{r}_0 +\int \limits _{s_0 }^s {\left[ {{\begin{array}{l} {\hbox {cos}\psi \left( s \right) \hbox {cos}\theta \left( s \right) } \\ {\hbox {sin}\psi \left( s \right) \hbox {cos}\theta \left( s \right) } \\ {\hbox {sin}\theta \left( s \right) } \\ \end{array} }} \right] \text {d}s}, \end{aligned}$$
(2)

where subscript 0 refers to an initial value, and \(\mathbf{t}=\left[ {{\begin{array}{lll} {\hbox {cos}\psi \hbox {cos}\theta }&{} {\hbox {sin}\psi \hbox {cos}\theta }&{} {\hbox {sin}\theta } \\ \end{array} }} \right] ^\mathrm{T}\) is the unit tangent vector at the arbitrary point \(i\) on the space curve. The preceding equation can be used to define a curve based on the rotation field without resorting to a PB interpolation. It is important to note that, even in the case of using a linear rotation field, the space curve of (2) is a highly non-linear function since it contains trigonometric functions.

Differentiating the tangent vector with respect to the parameter \(s\) defines the curvature vector as

$$\begin{aligned} \frac{{\text{ d}}\mathbf{t}}{{\text{ d}}s}=\left[ {{\begin{array}{l} {-{\psi }'\sin \psi \cos \theta -{\theta }'\cos \psi \sin \theta } \\ {{\psi }'\cos \psi \cos \theta -{\theta }'\sin \psi \sin \theta } \\ {{\theta }'\cos \theta } \\ \end{array} }} \right] , \end{aligned}$$
(3)

where \({\psi }'=\partial \psi /\partial s\) and \({\theta }'=\partial \theta /\partial s\). The norm of this vector defines the curve curvature as

$$\begin{aligned} \kappa =\left| {\frac{{\text{ d}}\mathbf{t}}{{\text{ d}}s}} \right| =\sqrt{({\psi }'\cos \theta )^{2}+({\theta }')^{2}}. \end{aligned}$$
(4)

Furthermore, the normal vector can be defined using (3) and (4) as

$$\begin{aligned} \mathbf{n}&= \frac{\left( {{\text{ d}}\mathbf{t}/{\text{ d}}s} \right) }{\left| {{\text{ d}}\mathbf{t}/{\text{ d}}s} \right| }\nonumber \\&= \frac{1}{\kappa }\left[ {{\begin{array}{l} {-{\psi }'\sin \psi \cos \theta -{\theta }'\cos \psi \sin \theta } \\ {{\psi }'\cos \psi \cos \theta -{\theta }'\sin \psi \sin \theta } \\ {{\theta }'\cos \theta } \\ \end{array} }} \right] \!. \end{aligned}$$
(5)

The curve torsion can then be evaluated by differentiating the curvature vector of (3) with respect to \(s\) one more time. Therefore, the geometric properties of the curve can be uniquely defined. Furthermore, if the angles are functions of time, the curvature will also change as function of the angles, and therefore, an arbitrary large deformation can be captured.

The curvature and torsion, obtained using the finite rotation interpolation, are often used to formulate the strains in the LRVFs. It is implicitly assumed that the RB curvature and torsion are the same as the curvature and torsion of another space curve obtained using an independent position interpolation. This important issue will be discussed in more detail in later sections of this paper.

4 Large rotation vector formulation

While in the preceding section, general three-dimensional analysis is used to define a space curve using the finite rotation interpolation, the LRVF considered in this paper can be clearly addressed without delving into the details of the spatial analysis. The LRVF incorporates two independent interpolations, one PB and one RB; this brings up the issue of redundancy despite the fact that shear is an independent deformation mode. As previously shown, two independent meshes cannot be brought together regardless of the constraints and forces used. In this section, the kinematics and dynamic equations of the LRVF are explained using planar analysis in order to better understand and interpret the results of the examples that will be presented in later sections of this paper. To this end, consider a two-dimensional flexible beam of length \(L\), with one end at the origin of the inertial frame \(XY\). The beam is allowed to rotate about the \(Z\) axis, but the entire motion of the beam is constrained to the \(XY\) plane.

4.1 LRVF kinematics

In the LRVF, two independent interpolations are used for the position and finite rotations. These two independent fields can be written, respectively, as \(\mathbf{r}_0 \left( {x,t} \right) =\mathbf{S}_r \left( x \right) \mathbf{e}_r \left( t \right) \) and \(\theta \left( {x,t} \right) =\mathbf{S}_\theta \left( x \right) \mathbf{e}_\theta \left( t \right) \), where \(x\) is the axial coordinate, \(t\) is time, subscript 0 refers to the beam centerline, \(\mathbf{S}_r \) and \(\mathbf{S}_\theta \) are shape function matrices, and \(\mathbf{e}_r \) and \(\mathbf{e}_\theta \) are vectors of nodal coordinates. The position vector of an arbitrary point \(P\) on a FE \(j\) may be defined as follows

$$\begin{aligned} \mathbf{r}_P^j (x,t)=\mathbf{r}_0 (x,t)+y\mathbf{t}_2 (x,t), \end{aligned}$$
(6)

where \(\mathbf{r}_0 (x,t)=\left[ {{\begin{array}{ll} {x+u}&{} v \\ \end{array} }} \right] ^\mathrm{T}\) denotes the deformed position of the beam axis (see Fig. 2), \(y\) is a coordinate that defines the locations of points on the planar cross-sections, and \(\mathbf{t}_2 \) is a vector in the direction of the cross-section. Scalars \(u\) and \(v\) represent the displacements of the beam material points along the global axes \(X\) and \(Y\), respectively. The position vector \(\mathbf{r}_0 \) and the moving vectors \(\mathbf{t}_1 \) and \(\mathbf{t}_2 \) are defined with respect to the inertial frame. The moving vectors are parameterized by means of the time-dependent finite angle \(\theta \) as

$$\begin{aligned} \mathbf{A}=\left[ {{\begin{array}{ll} {\mathbf{t}_1 }&{} {\mathbf{t}_2 } \\ \end{array} }} \right] , \quad \mathbf{t}_1 =\left[ {{\begin{array}{ll} {\cos \theta } \\ {\sin \theta } \\ \end{array} }} \right] ,\quad \mathbf{t}_2 =\left[ {{\begin{array}{l} {-\sin \theta } \\ {\cos \theta } \\ \end{array} }} \right] . \end{aligned}$$
(7)

In Eq. (7), A is the orientation matrix defined at a point on the beam centerline. The orientation of the cross-section is therefore kinematically uncoupled from the position field in order to allow accounting for the shear.

Fig. 2
figure 2

Kinematic definition of a beam in the LRVF

Full size image

It is important to point out that while the LRVF kinematic description accounts for the shear deformation, the beam cross-section in this description is assumed to be rigid and planar. An axial force or stretch of the beam does not lead to a change in the cross-section dimensions. This formulation is, therefore, conceptually different from the ANCF which allows for the shear and warping using fully parameterized elements. The two formulations capture different modes of deformation, and therefore, the LRVF and the ANCF can be compared only when using very specific and simplified examples.

4.2 Energy expressions

For the most part, the LRVF implementation is based on the co-rotational approach. Following the work presented in [6] and using the co-rotational procedure description, no distinction is made in most LRVF investigations between the spatial coordinate \(x\) and the beam centerline arc length \(s\). It is important, however, to point out that in the case of large deformation and when non-incremental solution procedure is used, one must distinguish between \(x\) and \(s\) in order to accurately define the beam geometry. Based on the kinematic description in Eq. (6), the kinetic energy of a beam can be written as [6]

$$\begin{aligned} T=\frac{1}{2}\int \limits _0^L {(A_\rho {\dot{\mathbf{r}}}_0 ^\mathrm{T}{\dot{\mathbf{r}}}_0 +I_\rho \dot{\theta }^{2}){\text{ d }}x}, \end{aligned}$$
(8)

where \(L\) is the length of the element in the longitudinal direction, and the inertia constants are defined as \(A_\rho =\int _{-h/2}^{h/2} {\rho (x,y){\text{ d }}y} \) and \(I_\rho =\int _{-h/2}^{h/2} {\rho (x,y)y^{2}{\text{ d }}y} \), respectively, where \(\rho \) is the mass density and \(h\) is the beam height. The resulting LRVF mass matrix is constant only in the case of planar analysis. In the case of three-dimensional analysis, the resulting LRVF mass matrix is highly non-linear. This is another fundamental difference between the LRVF and ANCF since ANCF FEs always lead to a constant mass matrix.

The LRVF potential energy, however, becomes non-linear and is defined by the axial, bending, and shear components as

$$\begin{aligned} V=\frac{1}{2}\int \limits _0^L {\left( {\mathrm{EA}\varepsilon _{xx}^2 +\mathrm{GA}_s \varepsilon _{xy}^2 +\mathrm{EI}\left( {\frac{{\text{ d}}\theta }{{\text{ d}}x}} \right) ^{2}} \right) {\text{ d }}x}, \end{aligned}$$
(9)

where EA, \(\mathrm{GA}_\mathrm{s}\), and EI are the axial, shear, and flexural stiffnesses of the beam, and \(\varepsilon _{xx} \) and \(\varepsilon _{xy} \) are the axial and shearing strains, respectively, which can be defined as

$$\begin{aligned} \varepsilon _{xx} ={\begin{array}{ll} {\mathbf{t}_1^\mathrm{T} \mathbf{{r}'}_0 -1,}&{} \quad {\varepsilon _{xy} =\mathbf{t}} \\ \end{array} }_2^\mathrm{T} \mathbf{{r}'}_0, \end{aligned}$$
(10)

where \(\mathbf{{r}'}_0 =\partial \mathbf{r}_0 /\partial x=\left( {\partial \mathbf{r}_0 /\partial s} \right) \left( {\partial s/\partial x} \right) \), in which \(s\) is the arc length of the beam centerline. From Eq. (10), it is clear that the strains are defined using both interpolation meshes which can have very different geometry. If the independent rotation mesh is used with the assumption that \(x\approx s\), then \(\mathbf{{r}'}_0 =\mathbf{t}_1 \) and when \(\mathbf{{r}'}_0 \) is substituted into (10), the axial and shearing strains become \(\varepsilon _{xx} =\mathbf{t}_1^\mathrm{T} \mathbf{t}_1 -1=0\) and \(\varepsilon _{xy} =\mathbf{t}_2^\mathrm{T} \mathbf{t}_1 =0\), respectively, and are therefore constant. For a consistent geometry description, the two meshes should yield the same location for the material points at which the strains are computed. This presents a brief proof of the inextensibility of a beam when using independent angular coordinates and can easily be generalized to the three-dimensional case, leading to an inconsistency in the LRVF geometry representation. Further analysis into beam inextensibility, as well as other issues associated with independent rotation interpolations, will be shown in greater detail in Sect. 5.

4.3 Equations of motion

The equations of motion of a planar body in the LRVF utilize uncoupled inertia terms and can be systematically obtained by means of Hamilton’s principle [6]. Accordingly, it is required that

$$\begin{aligned} L=\int \limits _{t_1 }^{t_2 } {(T-V){\text{ d }}t} \end{aligned}$$
(11)

be stationary for arbitrary paths connecting two points at time \(t_1 \) and \(t_2 \) in the configuration space. Substituting the kinetic and potential energies previously defined in (8) and (9), respectively, into (11) with standard manipulations yields the following equations for the planar case

$$\begin{aligned} {\begin{array}{l} {A_\rho {\ddot{\mathbf{r}}}_0 -\left[ {\mathbf{ACA}^\mathrm{T}\left[ {{\begin{array}{l} {1+{u}'-\cos \theta } \\ {{v}'-\sin \theta } \\ \end{array} }} \right] } \right] ^{\prime }-{\bar{\mathbf{n}}}=0} \\ I_\rho \ddot{\theta }-\mathrm{EI}{\theta }''-\left[ {{\begin{array}{l} {-{v}'} \\ {1+{u}'} \\ \end{array} }} \right] ^\mathrm{T}\mathbf{ACA}^\mathrm{T}\left[ {{\begin{array}{l} {1+{u}'-\cos \theta } \\ {{v}'-\sin \theta } \\ \end{array} }} \right] \\ \quad -\bar{{m}}=0, \\ \end{array} } \end{aligned}$$
(12)

where

$$\begin{aligned} \mathbf{C}=\left[ {{\begin{array}{ll} \mathrm{EA}&{} 0 \\ 0&{} {\mathrm{GA}_\mathrm{s} } \\ \end{array} }} \right] , \end{aligned}$$
(13)

and EA and \(\mathrm{GA}_\mathrm{s}\) are the axial and shear stiffness of the beam, respectively, \(A_\rho \) and \(I_\rho \) are the respective inertia constants defined in the previous subsection, and \(({\bullet }{)}'={\text{ d }}({\bullet })/{\text{ d }}x\). The external force vector and external moment acting on the deformed cross-section of the beam are represented in these equations as \({\bar{\mathbf{n}}}=\left[ {{\begin{array}{ll} {\bar{{n}}_1 }&{} {\bar{{n}}_2 } \\ \end{array} }} \right] ^\mathrm{T}\) and \({\bar{m}}\), respectively, while the transformation matrix A is defined previously in (7). Note that the equations shown in (12) constitute the system of non-linear partial differential equations governing the response of the system and neglect the effects of viscous friction.

5 Comments on the rotation interpolation

The interpolation of angles with application to the analysis of large displacement of beams and plates has posed a number of challenges with regard to its use in computer simulations. This section intends to provide discussions on some limitations and difficulties which are characteristic of the interpolation of large rotations in flexible MBSs.

The LRVF uses two independent meshes which can cause redundancy in the geometric definition. This issue especially affects the definition of the strains of the beam, which is at the core of the formulation and its applicability. Another issue, even though algorithmically avoidable, is the singularity that appears when parameterizing rotations using a minimal set of angular parameters. The mesh defined by these angular parameters is, in this section, shown to be inextensible, which makes it unsuitable to capture axial deformation. Other methods that employ linearized angles, such conventional beams used with the co-rotational formulation, do not face some of the problems discussed in this section. Nonetheless, the use of linearized angles entails approximations that can burden the computational efficiency and accuracy and limits the applicability of the method in the case of high rotational speeds [16]. The subsections presented hereafter discuss these problems in more detail either by deriving simple proofs or including state-of-the-art solutions to the aforesaid problems.

5.1 Redundancy of the strain definition

The use of two independent meshes to describe the same geometry causes redundancy in the definition of strains since two independent shapes cannot be brought together, as shown in Sect. 2. This issue can be easily exemplified using the strains by deriving the expressions for the curvature using both FE meshes. In the case of planar beam elements, the tangent vector along the space curve \(\mathbf{t}_1 \), defined in Eq. (7), can be differentiated with respect to parameter \(s\) to determine the curvature vector as

$$\begin{aligned} \frac{{\text{ d}}\mathbf{t}_1 }{{\text{ d}}s}=\left[ {{\begin{array}{l} {-{\theta }'\sin \theta } \\ {{\theta }'\cos \theta } \\ \end{array} }} \right] , \end{aligned}$$
(14)

where \({\theta }'={\partial \theta }/{\partial s}\). The norm of this vector defines the RB curvature as

$$\begin{aligned} \kappa ^\mathrm{rot}=\left| {\frac{{\text{ d}}\mathbf{t}_1 }{{\text{ d}}s}} \right| ={\theta }'. \end{aligned}$$
(15)

The preceding definition of the curvature is based on the rotation mesh. If an independent position field is used, there exists, however, a different definition of the geometry invariants that depend on the assumed field of the position mesh. The geometric curvature based on the position mesh may be defined by the following equation

$$\begin{aligned} \kappa ^\mathrm{pos}=\left| {\mathbf{r}_{ss} } \right| =\frac{\left| {\mathbf{r}_x \times \mathbf{r}_{xx} } \right| }{\left| {\mathbf{r}_x } \right| ^{3}}, \end{aligned}$$
(16)

where the subscript \(x\) denotes a spatial derivative with respect to the beam longitudinal coordinate. The definition in (16) requires the computation of second spatial derivatives, which are geometrically unrelated to the expression in Eq. (15), based on the rotation mesh. Equations (15) and (16) are an example of the redundancy in the geometry definition that results from the use of two independent meshes. The preceding two equations demonstrate that the use of two independent meshes leads to two different sets of geometry invariants (curvature and torsion). In the LRVF, the curvature shown in (15) is commonly used to define the elastic forces.

5.2 Singularities in the three-dimensional analysis of beams

The study of the three-dimensional body rotation requires addressing the known problem of singularities. Flexible multibody formulations that use angles to describe large deformation can make use of minimal (e.g., Euler angles) or non-minimal (e.g., Euler parameters) rotation parameters to this end. When singularities occur, the simulation of the motion of the system does not proceed smoothly and this often causes the simulation to stop. Romero [11] discussed different rotation interpolation strategies in four different methods in a series of tests for geometrically exact rods. Romero found in his work that two of his interpolation strategies (orthogonal interpolation by local rotation updates and non-orthogonal interpolation) possess singularities. The purpose of these investigations and several others was to cut down on extra computational costs and avoid any potential error accumulation. Within the context of the LRVF, rescaling operations of a minimal set of rotation parameters have been suggested in order to avoid the singularities associated with the interpolation of rotation [13]. In the latter publication, Bauchau et al. [13] analyzed the interpolation of finite rotations by developing and testing two algorithms dealing with geometrically exact beams. The first algorithm interpolated the rotation field by its rotation parameters at the nodes of each FE and removed any possible effects of rescaling from the interpolation process. The second algorithm interpolated the rotation field by incremental nodal rotations defined by the rotation parameters at the nodes of each finite element. In both algorithms, the task of rescaling is mandatory to avoid simulation failure.

In summary, the treatment of the interpolation of rotations requires the use of algorithms specifically devised to avoid the accumulation of error and the well-known singularities associated with minimal sets of rotation parameters. This problem can be avoided using non-RB FE formulations such as the ANCF.

5.3 Inextensibility of the rotation field

The LRVF relies on both the rotation and position mesh for the calculation of strains. When calculating the strains, both meshes contribute to the geometric definition of strains (see (10) or [6]). In the large deformation analysis of beams, a consistent description of geometry is necessary since strains can reach high values. However, RB meshes can be inextensible, which adds a significant anomaly in the LRVF description of the large deformation. Another issue with regard to the use of a RB position representation is its inability to capture accurately axial and shearing strains in various applications. This can be especially problematic in situations where the beam stiffness is particularly low. Beam inextensibility when using a rotation mesh can be proven in multiple ways using a two-dimensional beam element example. For a RB mesh \(\theta \left( {x,t} \right) \) that employs the axial coordinate \(x\) as a parameter, one can write \({\text{ d }}\mathbf{r}_0 =\left( {{\partial \mathbf{r}_0 }/{\partial x}} \right) {\text{ d }}x\) and use this equation to define a space curve. If \({\partial \mathbf{r}_0 }/{\partial x}\) is assumed to be the first column of a rotation matrix based on the assumed rotation field, the position vector of an arbitrary point can be defined by rotation parameters instead of the previously defined position coordinates \(u \)and \(v\) as

$$\begin{aligned} \mathbf{r}_0 \left( {x,t} \right) =\left[ {{\begin{array}{l} {x+\int \limits _0^x {\left( {\hbox {cos}\theta \left( {\bar{{x}},t} \right) -1} \right) {\text{ d }}\bar{{x}}} } \\ {\int \limits _0^x {\hbox {sin}\theta \left( {\bar{{x}},t} \right) {\text{ d }}\bar{{x}}} } \\ \end{array} }} \right] , \end{aligned}$$
(17)

where \(x\) is the axial parameter of the beam, and \(t\) is time. Note that in Eq. (7), it is assumed that \({\partial \mathbf{r}_0 }/{\partial x}\) is a unit tangent. Figure 2 shows that \({u}'=\cos \theta -1\) and \({v}'=\sin \theta \) in the rotation mesh, which leads to \(\mathbf{{r}'}_0 \left( {x,t} \right) =\left[ {{\begin{array}{ll} {1+\left( {\hbox {cos}\theta \left( {x,t} \right) -1} \right) }&{} {\hbox {sin}\theta \left( {x,t} \right) } \\ \end{array} }} \right] ^\mathrm{T}=\left[ {{\begin{array}{ll} {\hbox {cos}\theta \left( {x,t} \right) }&{} {\hbox {sin}\theta \left( {x,t} \right) } \\ \end{array} }} \right] ^\mathrm{T}=\mathbf{t}_1 \), where \(\mathbf{{r}'}_0 =\partial \mathbf{r}_0 /\partial x\). The strain measures of a beam using a RB mesh can then be defined as

$$\begin{aligned} \left. {{\begin{array}{ll} {\varepsilon _{xx}^\mathrm{rot} =\mathbf{t}_1^\mathrm{T} \mathbf{{r}'}_0 -1=\left[ {{\begin{array}{ll} {\cos \theta }&{} {\sin \theta } \\ \end{array} }} \right] \left[ {{\begin{array}{ll} {\cos \theta }&{} {\sin \theta } \\ \end{array} }} \right] ^\mathrm{T}-1=0} \\ {\varepsilon _{xy}^\mathrm{rot} =\mathbf{t}_2^\mathrm{T} \mathbf{{r}'}_0 =\left[ {{\begin{array}{ll} {-\sin \theta }&{} {\cos \theta } \\ \end{array} }} \right] \left[ {{\begin{array}{ll} {\cos \theta }&{} {\sin \theta } \\ \end{array} }} \right] ^\mathrm{T}=0} \\ {\kappa ^\mathrm{rot}=\frac{{\text{ d}}\theta (x,t)}{{\text{ d}}x}={\theta }'} \\ \end{array} }} \right\} , \end{aligned}$$
(18)

where \(\varepsilon _{xx}^\mathrm{rot} \) and \(\varepsilon _{xy}^\mathrm{rot} \) are the axial and shearing strains, respectively, and \(\kappa ^\mathrm{rot}\) is the RB curvature. The moving vectors \(\mathbf{t}_1 \) and \(\mathbf{t}_2 \) are defined in (7) with respect to the inertial frame and shown in Fig. 2. Equation (18) shows that the axial and shearing strains are constant throughout.

A second proof of beam inextensibility when using the rotation mesh can be shown by defining the current length of a beam as \({\text{ d }}l^{2}={\text{ d }}\mathbf{r}_0^\mathrm{T} {\text{ d }}\mathbf{r}_0 ={\text{ d }}x\left[ {{\begin{array}{ll} \hbox {cos}\theta (x,t)&{} {\hbox {sin} \theta }(x,t) \\ \end{array} }} \right] \left[ \! {{\begin{array}{ll} {\hbox {cos}\theta }(x,t)&{} {\hbox {sin}\theta }(x,t) \\ \end{array} }} \!\right] ^\mathrm{T} {\text{ d }}x= \left( {{\text{ d}}x} \right) ^{2}=\left( {{\text{ d}}l_0 } \right) ^{2}\). This shows that, when using the RB mesh parameter to define a unit tangent as the first column of the rotation matrix, the current length of a beam \(l\) will be equal to its initial length. Therefore, the described beam cannot be stretched and will retain its original length, which leads to inaccuracy when capturing the precise deformation of a beam. A specific example highlighting beam inextensibility of the rotation mesh will be shown in the numerical results section to better shed light on this fundamental issue.

The fact that a RB interpolation leads to an inextensible beam can be also demonstrated in the case of spatial analysis. Using the rotation coordinates, the tangent vector can always be defined as the first column of a rotation matrix. This column of the rotation matrix is always a unit vector regardless of the parameterization used (\(x\) or \(s\)). The angles at an arbitrary point on the beam centerline can be defined in terms of any parameter; coordinates in the reference configuration are often used as parameters to define the rotation mesh (Lagrangian description). The use of parameters defined in the current deformed configuration will require a different treatment and different solution procedure. Nonetheless, the first column of the rotation matrix expressed in terms of these angles remains a unit vector, and in the reference configuration without any loss of generality \(s=x\).

5.4 Energy conservation

One widespread field of research within the context of flexible multibody dynamics is linked to the study of energy and momentum preserving schemes. The total energy of a non-dissipative system must remain constant throughout the simulation. When the LRVF description was systematically incorporated into flexible multibody systems codes, the use of constraints became mandatory. These constraints cause non-physical high-frequency oscillations in the solution. These oscillations, in turn, together with the conservation of energy and momentum of the integration algorithms, have been studied in numerous investigations. One such investigation using beams was presented by Bauchau et al. [17]. In their work, it was discussed that high-frequency oscillations hindered the convergence of the equations of motion and that a smaller time step did not necessarily help this problem. The higher frequency oscillations also made strict total energy preservation strenuous to accomplish. Bauchau and Theron [18] later discussed an energy-decaying scheme for non-linear beam models with the main focus being on the derivation of an algorithm presenting with high-frequency dissipation. The derived energy decay algorithms followed the parameter that the total energy at a time step must be equal to or less than that of the previous time step. It was also mentioned that this approach could be used as a time-step control parameter with the concept that if the total energy was larger than it was at the previous time step, then a smaller time step would be used. Some of this theory was used by Romero and Armero [19] when they developed a FE formulation using geometrically exact rods. These rods used a time-stepping algorithm which improved the rod’s dynamics using the preservation of total linear and angular momentum, as well as the conservation of the total mechanical energy \(H\) (or Hamiltonian \(H=T+V\), where \(T\) and \(V\) are the kinetic and potential energy, respectively).

Besides the challenge of an energy and momentum preserving numerical integration, the definition of the strains using two independent meshes can lead to an inconsistent definition of the strain energy, which utilizes strain measures defined by the two meshes, when large deformation occurs. This can be attributed to the inextensibility of the rotation field in the way presented in the preceding subsection. According to the axial and shearing stresses defined in (10), the potential energy definition uses independently interpolated position and rotation meshes. As shown earlier, these meshes should describe the same geometry. However, the beam material points using LRVF cannot be properly and uniquely associated with the rotation and position meshes, and the same material point can greatly differ in location between the two meshes. This can cause inaccuracies in the definition of the strain energy. As a beam moves during a simulation, the differences in the position and rotation meshes can become considerably large and this may cause some sort of energy drift. While the kinematics used in the LRVF, as traditionally used by the FE community, can be accurate for the description of small deformation, the study of the geometry of large deformation on the basis of two independent meshes can lead to inconsistency.

6 Numerical examples

A flexible robot arm rotating about one end is considered to illustrate the effect of the use of the rotation interpolation in the large rotation–large deformation analysis of beams. To this end, the LRVF is used, as detailed in by Simo and Vu-Quoc [6]. The robot arm is represented by a beam whose first node is connected to the ground by a revolute joint. Several cases of an angle-driven flexible robot arm are considered to better demonstrate the redundancy of the geometry definition. For the figures in this section, Eq. (2) is used to obtain the space curve from the rotation mesh. The dimensions of the beam are assumed to be the same as reported by [6], while the axial, shear, and flexural stiffnesses of the arm for each case are shown in Table 1. The FE mesh consists of ten elements of equal length with linear interpolation functions for both displacement and rotation. The equations of motion are obtained using selective Gauss quadrature.

Table 1 Model parameters
Full size table

In the first case, the robot arm is repositioned to an angle of 1.5 rad from its initial position by prescribing the rotation angle as a linear function of time, as shown in Fig. 3a. The sequence of motion during this repositioning stage is depicted in Fig. 4, where one snapshot of the beam is depicted at each second. This figure shows that when the stiffness is high and the angular velocity is low, the material point position results obtained using the position and rotation meshes can be in a good agreement. In the second case, the same prescribed rotational displacement is used with lower element stiffness. More significant differences may be observed between the two curves in this case, as shown in Fig. 5: The differences between geometry representations can be observed from the first steps of the simulation. The third case involves the robot arm repositioning to an angle of 1.5 rad from its initial position in 4.5 s, as shown in Fig. 3b, with the elemental stiffness being the same as in the previous simulation model. Figure 6 shows that the increased angular velocity with a low stiffness leads to the meshes differing greatly in terms of curvature and nodal position. Figure 7 shows further differences between the position and RB meshes when incorporating an axial load at the tip of the flexible arm. The tip load of 100 kN is applied in the axial direction of the last element of the arm at each time step. The results presented in this last figure show that the RB interpolation cannot capture the stretch in the elements, whereas the independent PB interpolation is actually stretched.

Fig. 3
figure 3

Rotation angle at the revolute joint

Full size image
Fig. 4
figure 4

Repositioning sequence in LRVF: high stiffness (thick blue line PB curve and dashed red line RB curve). (Color figure online)

Full size image
Fig. 5
figure 5

Repositioning sequence in LRVF: medium stiffness (thick blue line PB curve and dashed red line RB curve). (Color figure online)

Full size image
Fig. 6
figure 6

Repositioning sequence in LRVF: low stiffness (thick blue line PB curve and dashed red line RB curve). (Color figure online)

Full size image
Fig. 7
figure 7

Repositioning sequence in LRVF: axial load (thick blue line PB curve and dashed red line RB curve). (Color figure online)

Full size image

Another example using the same beam model is depicted in Fig. 8. In this second example, the clamped boundary conditions are assumed at the first node. A constant external moment of 30 kN m is applied at the free tip of the beam. The generalized moment is applied on the rotation coordinate of the node at the tip. The definition of axial and shear strains (10) involves both position and rotation meshes. For this reason, the applied moment can generate axial and shear stresses. However, this aforesaid coupling is not sufficient to bring the two meshes together, as shown in Fig. 8. It is clear from the results presented in this figure that the curvature obtained using the RB mesh is not a good representative of the curvature of the PB mesh. Figure 9 displays the values of the RB curvature at 20 s. When using the RB mesh, the curvature is non-zero and constant within the elements. However, because of the linear interpolation, the PB mesh always yields null curvature at every point within the element, which is in contrast to the large values obtained from the other mesh. It can also be seen in Fig. 9 that the curvature used to account for bending deformation in the LRVF does not possess inter-elemental continuity. More specifically, the use of independent position and the rotation meshes in the LRVF makes it difficult to create strategies to enforce higher-order derivatives continuity.

Fig. 8
figure 8

Cantilever beam with a moment applied at the tip (thick blue line PB curve and dashed red line RB curve). (Color figure online)

Full size image
Fig. 9
figure 9

Curvature of RB mesh at t = 20 s (the PB curvature remains zero for all the simulation due to the linear interpolation of the displacements)

Full size image

7 Summary and conclusions

This paper highlights some issues on the interpolation of rotations in the analysis of large deformation of bodies in flexible multibody system dynamics and presents results of the large rotation vector formulation. The focus of this paper is on the geometry issues arising from the use of two interpolation meshes: the position mesh and the rotation mesh. These two meshes lead to different space curves that can differ by an arbitrary rigid-body displacement and have different geometric properties. The examples demonstrate the fact that the rotation mesh of the LRVF can be inextensible and that the material points of a RB position mesh occupy different positions from the material points of the position mesh. The consequences of the redundancy in the geometry definition can negatively affect the accuracy of the strain energy and the inertia of the bodies. These inconsistencies become more apparent in the case of larger deformations and are not circumvented by the inclusion of elastic forces or imposing kinematic constraints. This is mainly due to the fact that two different assumed displacement fields cannot, in general, be brought to the same configuration as illustrated in this paper.

It is important to point out that this paper is focused on a fundamental issue related to the use of the large rotation vector formulation. This study is not intended to provide a comparison of the LRVF with other formulations. Nonetheless, it is worth mentioning that several other approaches have been used in the large displacement analysis of structural systems. These formulations include the ANCF and methods based on B-spline representation. For example, a more recent approach for flexible beams in MBSs employs elastic beams modeled using dynamic splines [20, 21]. This approach is based on the Qin and Terzopoulos’s work with D-NURBS [22], which is a physics-based generalization of non-uniform rational B-Splines. D-NURBS combines physics-based constraint equations with spline geometry to improve the overall design process. Theetten et al. [20] used this concept to develop geometrically exact dynamic splines (GEDS), which extends the mechanical accuracy with the use of geometrically exact formal expressions along with analytical spline expressions for real-time, computer-aided models. Valentini and Pennestri [21] further advanced this approach by developing a dynamic spline formulation which could be suitable for MBS dynamics implementation of flexible beams undergoing large displacement.