Suppression of harmonic perturbations and bifurcation control in tracking objectives of a boiler–turbine unit in power grid

Abstract

In the presence of harmonic disturbances, boiler–turbine units may demonstrate quasi-periodic behaviour due to the occurrence of various types of bifurcation. In this article, a nonlinear model of boiler–turbine unit is considered in which drum pressure, electric output and drum water level are controlled via manipulation of valve positions for fuel, steam and feed-water flow rates. For bifurcation control in tracking problem, two controllers are designed based on gain scheduling and feedback linearization (FBL). To investigate the efficiency of control strategies, three cases are considered for desired tracking objectives (a sequence of steps, ramps/steps, and a combination of them). According to the results, FBL controller works successfully in suppression of harmonic perturbations and consequently bifurcation control. As it is implemented, quasi-periodic solutions (caused by Hopf bifurcation) are vanished; leading to the appearance of periodic solutions with low amplitudes. Consequently, appropriate tracking performance with less oscillatory behaviour is observed for the drum pressure, electric output, and drum water level (desirable for the power grid). In addition, when FBL controller is used, less control efforts are predicted for the bifurcation control.

1 Introduction

Boiler–turbine unit is one of the critical components of the power plants; responsible for producing the steam with desirable quality. Due to dynamic interaction between the various components, these units constitute complex nonlinear systems. Although the steam production is varied during the plant operation, output variables such as steam pressure, electric output, and water level of drum must be maintained at their respected values [1]. Simplification of nonlinear models of boiler–turbine units [2], dynamic modelling of a boiler–turbine unit based on parameter estimation [3], system identification using neural networks [4] and modelling based on data logs [5] have been done as the early works.

Recently, simple dynamic modelling and stability analysis of a steam boiler drum [6]; development of various simulation packages for steam plants with natural and controlled recirculation (e.g., [7]) and using a computational model for analysis and minimizing the fuel and environmental costs of a 310-MW fuel oil fired boiler has been studied [8].

Dynamic nonlinear modelling of power plants has been investigated through neural networks (e.g., [9]). Also, other various nonlinear models of boiler–turbine units, based on data logs and parameter estimation [10] and identification of boiler–turbine system based on T–S fuzzy method [11] have been presented. Recently, using fuzzy-neural network methods, modelling of a 1000-MW power plant including ultra super-critical boiler system [12] and numerical simulations of a small-scale biomass boiler unit [13] have been presented.

Various control methods have been used for boiler or boiler–turbine units. In this area, optimal control [14], decoupling control [15], predictive control based on local model networks [16], fuzzy-predictive control based on genetic algorithm [17], pure fuzz-based control systems [18] and neuro-fuzzy network modelling with PI control [19] have been presented. In some other works, model nonlinearity is avoided by selecting the appropriate operating zones such that the linear controller can perform effectively. By constituting a linear parameter varying model, gain-scheduled optimal control have been used [20].

In addition, tracking control based on approximate feedback linearization [21] and its comparison with gain scheduling [22] have been applied. For robust performance, adaptive–predictive algorithm [23], backstepping-based nonlinear control [24], adaptive control with fuzzy-interpolated model [25], multivariable robust control [26] and a comparison between sliding mode and $H_{\infty }$ techniques [27] have been presented. Also, for robust state estimation of the process, an optimum minimum-order observer has been designed [28].

According to the reviewed literature, dynamic modelling and performance control of boiler–turbine units have been extensively investigated; while linear theories have been used to predict the approximate dynamic system response. In industrial world, without a comprehensive pre-knowledge of these nonlinear units behaviour against possible disturbances, the designed controllers may lead to the aggressive response of output variables and also increase in energy consumption.

In the previous recent research [29], nonlinear dynamics of the boiler–turbine unit was investigated through the concepts of bifurcation and limit cycles behaviour. To improve the aperiodic and quasi-periodic behaviour of the system to the stable periodic one, a regulator was designed based on feedback linearization approach. However, this controller guarantees the regulation of the system around the fixed points; i.e., the controller only keeps the system around its operating points (set-points), in the presence of harmonic disturbances.

In this paper, tracking of desired set-paths is investigated in the presence of harmonic perturbations; which is essentially demanded by the power grid. For this purpose, two controllers are designed based on gain scheduling (GS) and feedback linearization (FBL). Such investigation has not been studied in any of previous works in the power-plant industry. To simulate realistic conditions, three desired tracking objectives including a sequence of steps, ramps-steps and a combination of them are considered. For the sake of brevity, results are presented for drum pressure and electric output (not shown for drum water level). For the control of output variables, valve positions of the fuel, steam and feed-water flow rates are manipulated. Performance of the GS and FBL controllers in tracking of desired set-paths, bifurcation control and consequently changing the unstable quasi-periodic solutions into the stable periodic ones is investigated and compared. In addition, GS and FBL control efforts, required for keeping the system around the desired tracking objectives are compared.

2 Nonlinear dynamics of the boiler–turbine unit and its performance

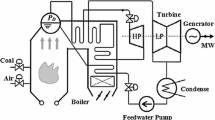
Figure 1 shows the schematic of a water-tube boiler in which preheated water is fed into the steam drum and flows through the down-comers into the mud drum. Passing through the risers, water is heated and changed into the saturation condition. The saturated mixer of steam and water enters the steam drum, where the steam is separated from water and flows into the primary and secondary super-heaters. Then, steam is more heated and is fed into the header. There is a spray attemperator between two super-heaters that regulates the steam temperature by mixing low temperature water with the steam.

Fig. 1

Schematic of a boiler–turbine unit

As a real case study, nonlinear dynamic model of the boiler–turbine unit presented by Bell and Astrom is considered here [10]. This practical model has been used in many of previous works, especially to investigate control aspects of the problem. Parameters of this model were estimated by data measurement from the Synvendska Kraft AB Plant in Malmo, Sweden. As shown in Fig. 2 [20], output variables are denoted by $y_{1}$ for drum pressure (${\hbox {kg}} {\hbox {f}}/{\hbox {cm}}^{2}), y_{2}$ for electric output (MW) and $y_{3}$ for drum water level (m). Input variables are denoted by $u_{1}, u_{2}$, and $u_{3}$ for valves position of the fuel, steam, and feed-water flows, respectively. Dynamics of this $160\,\hbox {MW}$ oil-fired unit is given in the state-space as [10]:

$$\begin{aligned} \!\!\!\left\{ {\begin{array}{l} \dot{x}_1 =-\alpha _1 u_2 x_1 ^{9/8}+\alpha _2 u_1 -\alpha _3 u_3 \\ \dot{x}_2 =(\beta _1 u_2 -\beta _2) x_1 ^{9/8}-\beta _3 x_2 \\ \dot{x}_3 =[\gamma _1 u_3 -(\gamma _2 u_2 -\gamma _3 ) x_1 ]/\gamma _4 \\ \end{array}} \right. ;~ \left\{ {\begin{array}{l} y_1 =x_1 \\ y_2 =x_2 \\ \end{array}} \right. \end{aligned}$$

(1)

where $x_{3}$ denotes the fluid density $({\hbox {kg/m}}^{3})$ and coefficients $\alpha _{i}, \beta _{i}, \gamma _{j}\,i =1...3,\,j= 1...4$ are given in Table 1. The output vector is defined as $\mathbf{y}=[x_1\, x_2\,y_3 ]^{T}$, while the drum water level $(y_{3})$ is given in terms of steam quality $a_\mathrm{cs}$ and evaporation rate $q_\mathrm{e}({\hbox {kg/s}})$ as:

$$\begin{aligned} y_3&= 0.05 (0.13073 x_3 +100 a_\mathrm{cs} +{q_\mathrm{e} }/9-67.975)\nonumber \\ a_\mathrm{cs}&= \frac{(1-0.001538 x_3 )(0.8 x_1 -25.6)}{x_3 (1.0394{-}0.0012304 x_1 )} ;\nonumber \\ q_\mathrm{e}&= (0.854 u_2 -0.147) x_1 +45.59 u_1 -2.514 u_3\nonumber \\&-2.096 \end{aligned}$$

(2)

Fig. 2

a Multivariable model of the boiler–turbine unit [20]. b Structure of the closed-loop control system

Table 1 Dynamic coefficients of the boiler–turbine model by Bell and Astrom [10]

and due to actuator limitations, control inputs and their rates are limited as:

$$\begin{aligned}&0\le u_i \le 1, -0.007\le \dot{u}_1 \le 0.007, -2\le \dot{u}_2 {\le } 0.02,\nonumber \\&-0.05\le \dot{u}_3 \le 0.05 \ (i=1,2,3). \end{aligned}$$

(3)

Some typical operating points of the Bell and Astrom model are given in Table 2; where the nominal model coincides with the operating point # 4 [10]. In this paper, $y_{i}^{j}$ denotes the output $y_{i}$ at operating point $j$ while $y_{i}^{(j)}$ represents the differentiation of $y_{i}$ of order $j$.

Table 2 Typical operating points of Bell and Astrom model [10]

3 Why the bifurcation control in tracking objectives of boiler–turbine units?

Due to varying operating conditions and load demands by the power grid, control systems must be able to satisfy some requirements. Electric output must be followed by the variation in demands from a power network while the steam pressure of the collector must be maintained constant. The amount of water in the steam drum must be kept constant to prevent over-heating of drum components or flooding of steam lines. On the other hand, to avoid over-heating of the super-heaters and to prevent wet steam entering turbines, the steam temperature must be maintained at the desired level [20]. In addition, the physical constraints exerted on the actuators must be satisfied by the control signals.

Under the above expectations and constraints, various types of perturbations are one of the major hindrances to achieve appropriate performance of the boiler–turbine units. In addition, in the presence of perturbations, changing some model parameters may lead to the occurrence of bifurcation and consequently unstable quasi-periodic behaviour. Such phenomenon was observed in the previous investigation [29]. To provide an overview of that investigation, some brief results adopted from [29] are presented in Fig. 3.

Fig. 3

The quasi-periodic behavior of electric output (MW) after the occurrence of secondary Hopf (Neimark) bifurcation at: a $\alpha _1 =0.0005$ and, b $\beta _3 =0.9$ (adopted from the source [29])

When the value of coefficient $\alpha _{1}$ decreases, at the critical value of $\alpha _{\hbox {1crit}} =0.00093$, secondary Hopf bifurcation occurs (for more details on bifurcation, see e.g., [30]). Figure 3a shows the unstable quasi-periodic orbit of the electric output for $\alpha _1 =0.0005$, which is located far from the nominal operating point $x_2^4 =66.65\,{\hbox {MW}}$. Similarly, as the value of $\beta _{3}$ increases, at the critical value of $\beta _{\hbox {3crit}} =0.84$, Hopf bifurcation occurs (e.g., see Fig. 3b for $\beta _{3}=0.9$).

In research [29], a FBL controller was designed to regulate the dynamic system around its fixed points by improving the quasi-periodic limit cycles into the periodic ones. However, both regulation and tracking of the load variation commands for the output variables are important when the controller is designed to overcome the hindrance of perturbations. Therefore, besides the regulation of dynamic system, its performance in tracking of desired set-paths (determined by the power grid), is another important objective.

4 Controller design based on gain scheduling & feedback-linearization approaches for tracking objectives

The general structure of the closed-loop control system is shown in Fig. 2b. In this section and for the purpose of desired tracking in the presence of perturbations, two controllers are designed based on gain scheduling (GS) and feedback linearization (FBL) methods. In these approaches, the nonlinear system is transferred into a fully or partly linear one. Then, various powerful linear control techniques can be applied to complete the control design process. It is assumed that all state variables are available for construction of feedback control law, either by direct measurement or by using a state observer. The procedure of a robust observer design has been presented in the previous research [28].

Detailed formulation of the FBL controller design was presented in the previous research [29] (also, it is presented briefly in Appendix 1). It should be mentioned that in the previous research [22], this approach was implemented for tracking objectives in the absence of perturbations (for a nominal model without disturbance). In this section, design of GS controller is presented.

Dynamic model given by Eq. (1) is considered. To maintain the system around each operating point of Table 2 at state vector $\bar{{x}}^{0}=[x_1^0\;x_2^0\;x_3^0 ]$, a constant input vector $\bar{{u}}^{0}=[u_1^0\;u_2^0\;u_3^0 ]$ must be imposed. For math simplicity, let’s define the new variables as

$$\begin{aligned} \xi _1&= x_1 ^{0}, \xi _2 =x_2 ^{0}, \xi _3 =x_3 ^{0} \nonumber \\ \eta _1&= u_1 ^{0}, \eta _2 =u_2 ^{0},\eta _3 =u_3 ^{0} \end{aligned}$$

(4)

Linearizing the Eq. (1) around any operating points of Table 2, yields

$$\begin{aligned} \dot{\bar{{x}}}_\delta&= A(\xi _i ,\eta _i ) \bar{{x}}_\delta +B(\xi _i ,\eta _i ) \bar{{u}}_\delta \quad i=1,2,3 \nonumber \\ \bar{{x}}_\delta&= \bar{{x}}-\bar{{x}}^{0},\quad \bar{{u}}_\delta =\bar{{u}}-\bar{{u}}^{0} \end{aligned}$$

(5)

where

(6)

In state feedback control scheme, to achieve desired locations of closed-loop control system and consequently desired performance of the system, the control vector $\bar{{u}}_\delta$ is constructed as:

$$\begin{aligned} \bar{{u}}_\delta&= -K (\xi _i ,\eta _i ) \bar{{e}}, \nonumber \\ \bar{{e}}&= \bar{{x}}_\delta -\bar{{r}}_\delta , \bar{{r}}_\delta =\bar{{y}}_R -\bar{{y}}^{0} \end{aligned}$$

(7)

where $K(\xi _{i}, \eta _{i})$ is the variable gain matrix adjusted according to the monitored scheduling variables, $\bar{{e}}$ is the error vector, $\bar{{y}}_R$ is the command vector signal that must be tracked. $\bar{{y}}^{0}=[y_1^0\;y_2^0\;y_3^0 ]$ is the output vector, defined by Eqs. (1) and (2), at each operating point of Table 2. Substituting Eqs. (6) and (7) in the first derivative of Eq. (5), yields

$$\begin{aligned} \dot{\bar{{x}}}_\delta&= [A(\xi _i ,\eta _i )-B(\xi _i ,\eta _i ) K (\xi _i ,\eta _i )] \bar{{x}}_\delta \nonumber \\&\quad + B(\xi _i ,\eta _i ) K (\xi _i ,\eta _i ) \bar{{r}}_\delta . \end{aligned}$$

(8)

The procedure of designing the feedback gain matrix for the MIMO system is given in Appendix 2. It is assumed that a maximum overshoot of $M_{p} = 10\,\%$ and settling time of about $t_{s}$ = 200 s in tracking behaviour of all output variables is desired. To achieve this, closed-loop poles of the system (including a far non-dominant pole, $\mu _{3}=-0.2$) must be assigned as:

$$\begin{aligned} \mu _{1,2} = -0.02\pm 0.0266 j, \quad \mu _3 =-0.2. \end{aligned}$$

Finding transformation $\mathfrak {R}$ and matrices $A_{d}, F, P$ and $\Gamma$ (as given in Appendix 2), and using Eq. (29), feedback gain matrix $K(\varphi _{i}, \psi _{i})$ is found.

5 Simulation results and discussion

5.1 Characteristics of the simulation conditions

In this section, the effect of controllers in desired tracking objectives of the boiler–turbine unit is investigated in the presence of the harmonic perturbations and bifurcations. In general, perturbations are caused by the environmental factors affecting the boiler–turbine units or by the occurrence of mismatches in the model parameters of the units. As it is well known, any transient function can be mathematically expanded through its Fourier series components. Therefore, if dynamic behaviour of the system is identified against harmonic perturbations, its behaviour will be also recognized against any other transient perturbation.

Fig. 4

Desired set-paths for tracking objectives in switching between the operating points #1 to #7 for: a a sequence of steps, b ramps-steps, and c a combination of them (drum pressure left column, electric output right column)

Simulation results are obtained via Simulink Toolbox of Matlab (based on ODE45 algorithm). For the sake of brevity, time responses and limit cycles behaviour are presented for the drum pressure and electric output. Due to similarity, it is not shown for water level of drum. As a case study, real harmonic disturbances in state variables are considered as:

$$\begin{aligned} \Delta x_1&= 10 \sin 0.021 t;\quad \Delta x_2 =6 \sin 0.021 t;\nonumber \\ \Delta x_3&= 40 \sin 0.021 t. \end{aligned}$$

(9)

For instance, $\Delta x_{2}=6 \sin 0.021t$ physically means a harmonic variation of the electric output $(x_{2})$ with amplitude of 6 (MW) around the nominal value of $x_{2}^{4}=66.65\,({\hbox {MW}})$; during the interval time of $\tau =2 \pi /0.021\!=\!300\,\mathrm{s}=5\,{\hbox {min}}$. It should be mentioned that the magnitudes of disturbances (Eq. 9) are chosen arbitrarily around 10 % of the magnitudes of nominal operating point # 4, (i.e., $\Delta x_{1} \approx 0.1x_{1}^{4} \approx 10$, $\Delta x_{2} \approx 0.1 x_{2}^{4} \approx 6$, $\Delta x_{3} \approx 0.1 x_{3}^{4} \approx 40)$; with arbitrary frequency of $\omega =0.021{\hbox {rad}}/\hbox {s}$. Similarly, all the simulation results can be presented in a straightforward manner for other values of disturbance magnitudes and frequency. Therefore, the following analysis can be accomplished for other harmonic disturbances.

To investigate the efficiency of designed controllers in switching between various operating points # 1 to # 7 (Table 2), three arbitrary cases of desired set-paths are considered for the drum pressure and electric output (as shown in Fig. 4). A sequence of steps, ramps-steps and a combination of them are considered as cases ‘a’, ‘b’, and ‘c’, respectively.

5.2 Implementation of GS & FBL controllers for bifurcation control in tracking

5.2.1 Case ‘a’

In the following simulations, it is assumed that Hopf bifurcation occurs either by a small value of $\alpha _1$ or a large value of $\beta _3$. Figure 5 shows time response of the drum pressure $(x_{1} = y_{1})$ and electric output $(x_{2} = y_{2})$ in tracking a desired sequence of steps (case ‘a’ in Fig. 4), after the implementation of GS and FBL controllers. As it is observed, both controllers satisfy the tracking objective. But the GS controller cannot guarantee the suppression of unstable quasi-periodic solutions, arisen by Hopf bifurcation occurrence. As FBL controller is implemented, unstable quasi-periodic solutions with large oscillations are changed to the stable periodic solutions with low oscillations, around the desired operating points # 1–7.

Fig. 5

Time response of the: a drum pressure (kg f/cm$^{2}$) and b electric output (MW) in tracking a sequence of steps (case ‘a’ of Fig. 4) after implementation of GS controller (light blue line) and FBL controller (thick black line); in the presence of Hopf bifurcation. (Color figure online)

Related limit cycles’ behaviour (in correlation with Fig. 5) are shown in Fig. 6. As it is observed, FBL controller acts efficiently in transferring the large quasi-periodic limit cycles into the small periodic ones. It should be noticed that in all next plots, fixed points #1–#7, i.e., operating points of the system given in Table 2, are depicted by red stars. In addition, the size of small diameter of elliptical limit cycles indicates the amount of oscillations around the operating points. As Fig. 6 shows, FBL controller is successful in maintaining the system around its operating points with small oscillatory behaviour. It should be mentioned that the rough appearance of quasi-periodic limit cycles, e.g., for electric output in Fig. 6b, is due to the type of algorithm used (ODE45). Using other types of ODE solvers, it is possible to obtain smooth limit cycles; but for consistency, all simulations are presented with ODE45 solver.

Fig. 6

Periodic and quasi-periodic orbits of: a drum pressure (kg f/cm$^{2})$ and b electric output (MW) in tracking a sequence of steps (case “a”); after implementation of GS controller (light blue line) and FBL controller (thick black line). (Color figure online)

Required variation of valve positions for fuel $(u_{1})$, steam $(u_{2})$, and feed-water $(u_{3})$ flow rates for the purpose of bifurcation control in tracking of case “a”, is shown in Fig. 7. As it is observed, less amount of control efforts is required when the FBL controller is used (in comparison with GS controller). Moreover, the required control efforts by FBL controller satisfies the constrain condition $(0~\le u_{i} \le 1)$, given by Eq. (3).

Fig. 7

Time response of the required a fuel flow rate, $u_{1}$, b steam flow rate, $u_{2}$ (c) feed-water flow rate, $u_{3}$ for the Hopf bifurcation control in tracking a sequence of steps (case “a”); when GS controller (light blue line) and FBL controller (thick black line) are used. (Color figure online)

Finally, the effect of perturbations intensity on dynamic system behaviour is shown in Fig. 8 (it is shown only for FBL controller due to its effectiveness). Figure 8a shows the time response of drum pressure in the presence of nominal values of perturbations, i.e., $\Delta x_i =\Delta \bar{{x}}_i$ as given by Eq. (9), and the values of $\Delta x_i =4 \Delta \bar{{x}}_i$ (due to similarity, it is not shown for electric output). Related limit cycles’ behaviour is shown in Fig. 8b. As it is physically expected, when the perturbations increase, relatively more oscillatory behaviour (but still acceptable periodic values) is observed in tracking objectives. Required variation of control efforts for the nominal case of perturbation $(\Delta x_i =\Delta \bar{{x}}_i )$ and the case of $(\Delta x_i =4 \Delta \bar{{x}}_i )$ is shown in Fig. 9. Again, as physically expected, more control actuation is required when the amplitude of perturbations increases. Due to similar conclusions, this investigation on the intensity of perturbations is not presented next for cases “b” and “c”.

Fig. 8

a Time response of the drum pressure (kg f/cm$^{2})$ and b its related periodic orbits in tracking a sequence of steps (case “a”) after implementation of FBL controller; with nominal values of perturbation amplitudes $\Delta x_i =\Delta \bar{{x}}_i$ (black solid line), $\Delta x_i =2 \Delta \bar{{x}}_i$ (green dot line/circles) and $\Delta x_i =4 \Delta \bar{{x}}_i$ (blue dashed line/squares). (Color figure online)

Fig. 9

Time response of the required a fuel flow rate, $u_{1}$ (b) steam flow rate, $u_{2}$ (c) feed-water flow rate, $u_{3}$ for the Hopf bifurcation control in tracking a sequence of steps (case “a”) after implementation of FBL controller; for nominal values of perturbation amplitudes $\Delta x_i =\Delta \bar{{x}}_i$ (black solid line) and $\Delta x_i =4 \Delta \bar{{x}}_i$ (blue dashed line). (Color figure online)

5.2.2 Cases “b” and “c”

Time responses and corresponding limit cycles of the drum pressure and electric output in tracking desired paths of ramps-steps (case “b” in Fig. 4) are shown in Figs. 10 and 11, respectively. To be obvious, inside area of periodic limit cycles is gray-shaded. As it is observed, FBL controller is able to change the unstable quasi-periodic behaviour of the system into a stable periodic one (around the fixed points). Required control efforts for bifurcation control and maintaining the system around the desired set-path of case “b” is shown in Fig. 12. It is observed that when FBL controller is implemented, less amount of control efforts is required (in comparison with the GS approach).

Fig. 10

Time response of the a drum pressure (kg f/cm$^{2}$) and b electric output (MW) in tracking ramps-steps (case “b” of Fig. 4) after implementation of GS controller (light blue line) and FBL controller (thick black line); in the presence of Hopf bifurcation. (Color figure online)

Fig. 11

Periodic and quasi-periodic orbits of: a drum pressure (kg f/cm$^{2}$) and b electric output (MW) in tracking ramps-steps (case “b”); after implementation of GS controller (light blue line) and FBL controller (thick black line). (Color figure online)

Fig. 12

Time response of the required a fuel flow rate, $u_{1}$ b steam flow rate, $u_{2}$ c feed-water flow rate, $u_{3}$ for the Hopf bifurcation control in tracking ramps-steps (case “b”); when GS controller (light blue line) and FBL controller (thick black line) are used. (Color figure online)

Dynamic behaviour of the boiler–turbine unit, in tracking a desired combination of ramps and steps (case “c” of Fig. 4), is shown in Fig. 13 through 15. As it is shown in Figs. 13 and 14, similar to the previous cases “a” and “b”; implementation of FBL controller leads to the suppression of unstable quasi-periodic orbits. Moreover, less manipulation of valves position for fuel, steam and feed-water flow rates is required when FBL controller is applied (Fig. 15). As another remark in all three cases, when FBL controller is used, less oscillatory behaviour is observed for the electric output, in comparison with the drum pressure (as shown in Figs. 5, 10, and 13). This is more desirable for the power grid where less oscillations of electric output around the desired operating points is expected.

Fig. 13

Time response of the: a drum pressure (kg f/cm$^{2}$) and b electric output (MW) in tracking a combination of ramps/steps (case “c” of Fig. 4) after implementation of GS controller (light blue line) and FBL controller (thick black line); in the presence of Hopf bifurcation. (Color figure online)

Fig. 14

Periodic and quasi-periodic orbits of: a drum pressure (kg f/cm$^{2}$) and b electric output (MW) in tracking a combination of ramps/steps (case “c”); after implementation of GS controller (light blue line) and FBL controller (thick black line). (Color figure online)

Fig. 15

Time response of the required a fuel flow rate, $u_{1}$ b steam flow rate, $u_{2}$ c feed-water flow rate, $u_{3}$ for the Hopf bifurcation control in tracking a combination of ramps/steps (case “c”); when GS controller (light blue line) and FBL controller (thick black line) are used. (Color figure online)

In summary, according to the results of previous research [29], where the regulation problem around the desired set-points was discussed; and presented results of this research, where the tracking problem around the desired set-paths is studied, it can be concluded that feedback linearization controller works efficiently in suppression of perturbations and bifurcation control of boiler–turbine units.

6 Conclusions

In this paper, the performance of two controllers based on gain scheduling (GS) and feedback linearization (FBL) in tracking problem of a boiler–turbine unit is investigated. Their influence on suppression of perturbations and bifurcation control is predicted and compared. In the considered nonlinear model of boiler–turbine unit, drum pressure, electric output, and water level of drum are controlled via manipulation of valve positions for fuel, steam, and feed-water flow rates. To simulate the realistic conditions that may demanded in the real world, three arbitrary desired tracking objectives including a sequence of steps, ramps-steps and a combination of them are considered (nominated as case studies “a”, “b” and “c”, respectively). For the sake of brevity, results are presented for drum pressure and electric output (not shown for water level of drum, due to similarity). According to the results obtained, the following conclusions can be obtained:

• 1. Both GS and FBL controllers satisfy the tracking objective. But the GS controller cannot guarantee the suppression of unstable quasi-periodic solutions, arisen by Hopf bifurcation occurrence. Consequently (unlike the GS controller), when the FBL controller is implemented, a more stable physical response can be obtained for the electric output and drum pressure, even in the presence of perturbations/bifurcations.

• 2. For all three cases of desired tracking objectives and in the presence of bifurcation, FBL controller acts efficiently in improving the unstable quasi-periodic solutions into the stable periodic ones. Consequently, small oscillations of drum pressure and electric output, around the desired set-paths and operating points #1–# 7, are obtained in practice. This stable behaviour is especially observed for the electric output. It physically means that a more smooth (while desired) behaviour can be obtained for the electric output, which is essentially demanded by the power grid.

• 3. For the purpose of bifurcation control and suppression of perturbations, less amount of control efforts is required when the FBL controller is used; in comparison with the GS controller (in all three cases). Therefore, less amount of input energy is invested for the actuators when the FBL controller is implemented (for instance, less amount of motor torque is required to move the valve positions for the fuel, steam and feed-water flow rates). In addition, FBL controller satisfies the constraint condition $(0 \le u_{i} \le 1)$. Accordingly, with FBL controller, it is physically possible to prevent the saturation and fatigue of actuators and consequently increasing their working life.

• 4. When the intensity of perturbations is increased, relatively more oscillatory behaviour (but still acceptable values) is observed in tracking objectives (with FBL controller). Moreover, higher control efforts are required to suppress quasi-periodic solutions into the stable periodic ones. It physically means that as the perturbations amplitude increases, more oscillatory behaviour (but still acceptable) is observed for both of the drum pressure and electric output. Also, more actuator efforts must be expensed to overcome the intense perturbations. It should be mentioned that the existence of very large values of perturbations amplitude is a mathematical assumption which may not occur in practice. But, to evaluate the controller efficiency, this case was also investigated.

Finally, it should be mentioned that the procedure used in this research can be extended in a straight-forward manner to any other industrial boiler–turbine unit; which its dynamic model has been extracted from experimental data logs.

Appendices

Appendix 1: Design of controller based on feedback linearization

In feedback linearization (FBL) approach, the nonlinear terms of the dynamic system are eliminated by means of state variables feedback. Then a suitable controller is designed to stabilize the desired trajectories of the system [31]. In this section, a brief overview on the design of FBL controller is presented. More details of this approach were discussed in [29]. Consider a square MIMO system in the neighbourhood of the operating point $\bar{{x}}^{0}$ as [31]

$$\begin{aligned} \dot{\bar{{x}}}=\Phi (\bar{{x}})+\Psi (\bar{{x}}) \bar{{u}}; \bar{{y}}=\mathrm{H}(\bar{{x}}) \end{aligned}$$

(10)

where $\bar{{x}}$ is $n \times 1$ the state vector, $\bar{{u}}$ is $r \times 1$ control input vector,$\bar{{y}}$ is $m \times 1$ outputs vector; $\Phi$ and H are smooth vector fields and $\Psi$ is a $n \times r$ smooth matrix (in this paper, $m = r =3$). Assume that $\delta _{i}$ is the smallest integer that at least one of the inputs appears in $y_i ^{(\delta _i )}$, then (in this paper, $y_{i}^{(j)}$ represents the $j$ order differentiation of $y_{i}$):

$$\begin{aligned} y_i ^{(\delta _i )}=L_{\Phi ^{\delta _i }} \mathrm{H}_i +\sum _{j=1}^r {L_{\Psi _j } L_{\Phi ^{\delta _i -1}} \mathrm{H}_i u_j } \end{aligned}$$

(11)

with repeated Lie derivatives $L_{\Psi _j } L_{\Phi ^{\delta _i -1}} \mathrm{H}_i (x)\ne 0$ for at least one $j$ in the vicinity of $\bar{{x}}^{0}$; while Lie derivative of H with respect to $\Phi$ is a scalar function defined as:

$$\begin{aligned} L_\Phi \mathrm{H}&= \nabla \mathrm{H} \cdot \Phi ; L_{\Phi ^{0}} \mathrm{H}=\mathrm{H}\nonumber \\ L_{\Phi ^{i}} \mathrm{H}&= L_\Phi (L_{\Phi ^{i-1}} \mathrm{H})=\nabla (L_{\Phi ^{i-1}} \mathrm{H})\cdot \Phi . \end{aligned}$$

(12)

Similarly, if $\Psi$ is another vector field, then the scalar function $L_{\Psi }L_{\Phi }$H$(x)$ is

$$\begin{aligned} L_\Psi L_\Phi \hbox {H}=\nabla (L_\Phi \mathrm{H})\cdot \Psi . \end{aligned}$$

(13)

Applying the same procedure for each output $y_{i}$, yields

$$\begin{aligned} \left[ {y_1 ^{(\delta _1 )}\ldots y_m ^{(\delta _m )}} \right] ^{T}&= \left[ {L_{\Phi ^{\delta _1 }} \mathrm{H}_1 (\bar{{x}})}\quad {L_{\Phi ^{\delta _2 }} \mathrm{H}_2 (\bar{{x}})}\right. \nonumber \\&\quad \left. \ldots {L_{\Phi ^{\delta _m }} \mathrm{H}_m (\bar{{x}})} \right] ^{T}+\mathrm{N}(\bar{{x}}) \bar{{u}}.\nonumber \\ \end{aligned}$$

(14)

If $\mathrm{N} (\bar{{x}})$ is invertible over the region $\Omega$, the input transformation

$$\begin{aligned} \bar{{u}}&= \mathrm{N}^{-1} \left[ {v_1 -L_{\Phi ^{\delta _1}} \mathrm{H}_1}\quad {v_2 -L_{\Phi ^{\delta _2 }} \mathrm{H}_2}\right. \nonumber \\&\qquad \quad \left. \cdots \, {v_m -L_{\Phi ^{\delta _m }} \mathrm{H}{ }_m}\right] ^{T} \end{aligned}$$

(15)

yields a simpler form of $m$equations as

$$\begin{aligned} y_i ^{(\delta _i )}=v_i. \end{aligned}$$

(16)

In this research, it is assumed that the third state variable $(x_{3})$ is measured either directly or by estimation through a robust state observer (with a general design as presented in the previous research [28]). To avoid tedious computations caused by differentiation of $y_{3}$ as given in Eq. (2), third state variable is chosen as the third output (instead of water level of drum, the fluid density is considered as the third output,$y_{3} = x_{3}$). Through simulations, it can be shown that this definition of $y_{3}$ will not affect the control of real output (i.e., drum water level) represented by Eq. (2). The validity of this assumption was discussed in [29]. Following the same procedure given above (while $\delta _{i}=1$), FBL control laws are determined for the dynamic system of Eq. (1) as [29]:

$$\begin{aligned}&\!\!\!\left[ {{\begin{array}{ccc} {u_1 }&{} {u_2 }&{} {u_3 } \\ \end{array} }} \right] ^{T}\nonumber \\&\quad =\mathrm{N}^{-1}\left[ {{\begin{array}{ccc} {v_1 }&{} {v_2 +\beta _3 x_2 +\beta _2 x_1 ^{9/8}}&{} {v_3 -\frac{\gamma _3 }{\gamma _4 }x_1 } \nonumber \\ \end{array} }} \right] ^{T} ; \\&\qquad \mathrm{N}=\;\left[ {{\begin{array}{c@{\quad }c@{\quad }c} {\alpha _2 }&{} {-\alpha _2 x_1 ^{9/8}}&{} {-\alpha _3 } \\ 0&{} {\beta _1 x_1 ^{9/8}}&{} 0 \\ 0&{} {-({\gamma _2 }/{\gamma _4 }) x_1 }&{} {({\gamma _1 }/{\gamma _4 })} \\ \end{array} }} \right] \end{aligned}$$

(17)

after decoupling the outputs dynamics (Eq. 16), a PI controller is designed as:

$$\begin{aligned} v_i =-K_{1i} e_i -K_{2i} \sigma _i ,\quad \dot{\sigma }_i =e_i =y_i -r_i \end{aligned}$$

(18)

where $r_{i}$ is the command input signal that is desired to be tracked (Fig. 4). Differentiating from Eq. (16), using Eq. (18), and transforming the result into the Laplace domain, yields

$$\begin{aligned} \frac{Y_i (s)}{R_i (s)}=\frac{K_{1i} s+K_{2i} }{s^{2}+K_{1i} s+K_{2i}}. \end{aligned}$$

(19)

To have a characteristic equation similar to the standard second-order system as:

$$\begin{aligned} s^{2}+2\zeta \omega _n s+\omega _n ^{2}=0,\,\omega _n >0,\,0<\zeta <1. \end{aligned}$$

(20)

Control signal gains must be adjusted as

$$\begin{aligned} K_{1i} =2\zeta _i \omega _i , \; K_{2i} =\omega _i ^{2}. \end{aligned}$$

(21)

Appendix 2: Structure of the feedback control law in MIMO system

Dynamic model of boiler–turbine unit is of rank $n=3$. Since the controllability matrix

$$\begin{aligned} {\mathbb {C}}= [B\quad AB\quad A^{2}B \ldots \quad A^{n-1}B]\quad \end{aligned}$$

is of rank 3, dynamic system is completely state controllable. Using the similarity transformation $\mathfrak {R}$ as $\bar{{x}}= \mathfrak {R}\bar{{z}}$, Eq. (5) is represented as:

$$\begin{aligned}&\dot{\bar{{z}}}_\delta = \hat{{A}}_G \bar{{z}}_\delta + \hat{{B}}_G \bar{{u}}_\delta \nonumber \\&\hat{{A}}_G = \mathfrak {R}^{-1}A \mathfrak {R}, \hat{{B}}_G = \mathfrak {R}^{-1} B \end{aligned}$$

(22)

where $\bar{{z}}_\delta$ is the new introduced state vector. Also, using the following transformations:

$$\begin{aligned} \bar{{u}}_\delta = F \bar{{w}}_\delta ; \bar{{w}}_\delta = \bar{{v}}_\delta - P \bar{{z}}_\delta . \end{aligned}$$

(23)

Equation (22) is described as:

$$\begin{aligned}&\dot{\bar{{z}}}_\delta = A_G \bar{{z}}_\delta +B_G \bar{{v}}_\delta \nonumber \\&A_G =\hat{{A}}_G - \hat{{B}}_G FP, B_G =\hat{{B}}_G F \end{aligned}$$

(24)

where $\bar{{v}}_\delta$ is the new control input vector and $A_{G}, B_{G}$ has the general canonical form with elements of $[A_i ]_{\gamma _i \times \gamma _i }\, , \,[B_i ]_{\gamma _i \times 1} ,\,i =1,2,..,r$ and $\sum _{i=1}^{r} \gamma _{i} = n$ as [32]:

$$\begin{aligned} A_G&= \left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} [A_1 ]&{}0&{} \ldots &{}0 \\ 0&{}[A_2 ]&{}\ldots &{}0 \\ &{}&{}.&{} \\ 0&{}0&{}\ldots &{}[A_r ] \\ \end{array}} \right] _{n\times n},\nonumber \\ B_G&= \left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} [B_1 ]&{}0&{}\cdots &{}0 \\ 0&{}[B_2 ]&{}\cdots &{}0 \\ &{}&{}.&{} \\ 0&{}0&{} \cdots &{} [B_r ] \\ \end{array}} \right] _{n\times r}, \nonumber \\ \left[ A_i\right]&= \left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0&{}1&{}0&{}\cdots &{}0 \\ 0&{}0&{}1&{}\cdots &{}0 \\ &{}&{}&{}.&{} \\ 0&{}0&{}0&{}\cdots &{}1 \\ 0&{}0&{}0&{}\cdots &{}0 \\ \end{array}} \right] _{\gamma _i \times \gamma _i }, [B_i ]=\left[ {\begin{array}{l} 0 \\ 0 \\ . \\ . \\ 1 \\ \end{array}} \right] _{\gamma _i \times 1} \end{aligned}$$

(25)

where $r$ is the number of input variables (in this case, $r=3$). Introducing the modified controllability matrix as:

$$\begin{aligned} \bar{{\mathbb {C}}}&= [b_1 b_2\,...\,b_\mathrm{r} \vdots Ab_1 Ab_2\,...\,Ab_\mathrm{r}\vdots \, \ldots \,\vdots A^{n-r}b_1\\&\quad A^{n-r}b_2\,...\,A^{n-r}b_\mathrm{r}] \end{aligned}$$

where $b_{i}$ are the columns of matrix $B$ given by Eq. (6); regular basis of $\bar{{\mathbb {C}}}$ is developed as

$$\begin{aligned} \hat{{ \mathbb {C}}}&= [b_1\,Ab_1\,...\,A^{\gamma _1 -1}b_1\vdots \,b_2\,Ab_2\,...\,A^{\gamma _2-1}b_2\vdots \,...\,\vdots b_r\nonumber \\&\quad Ab_\mathrm{r}\,...\,A^{\gamma _r -1}b_\mathrm{r} ] \end{aligned}$$

(26)

where each column, $A^{j}b_{i}, i = 1,...,r, j = 0,..., r$, is independent from its previous columns. Inverse of $\hat{{\mathbb {C}}}$ given by Eq. (26) is displayed as ([]$^{\prime }$ stands for transpose of the [] quantity):

$$\begin{aligned} \hat{{\mathbb {C}}}^{-1}=\left[ {{e}'_{11}\,..\,{e}'_{1\gamma _1 } \vdots {e}'_{21}\,...\,{e}'_{2\gamma _2 } \vdots \,...\,\vdots {e}'_{r1}\,...\,{e}'_{r\gamma _r } } \right] ^{\prime }. \end{aligned}$$

Similarity transformation $\mathfrak {R}$ is defined as [32]:

$$\begin{aligned} \mathfrak {R}&= \left( \left[ {e}'_{1\gamma _1 } {e}'_{1\gamma _1 } A,\,...\,{e}'_{1\gamma _1 } A^{\gamma _1 -1} \vdots {e}'_{2\gamma _2 } {e}'_{2\gamma _2 } A\,...\,{e}'_{2\gamma _2 } \right. \right. \nonumber \\&\quad \left. \left. A^{\gamma _2 -1} \,\vdots \ldots \vdots \, {e}'_{r\gamma _r } {e}'_{r\gamma _r } A\,...\, {e}'_{r\gamma _r } A^{\gamma _r -1}\right] ^{\prime }\right) ^{-1}.\nonumber \\ \end{aligned}$$

(27)

Considering again Eq. (24) and constructing the feedback control law as $v_{\delta }=-\Gamma z_{\delta }$, yields:

$$\begin{aligned} \dot{\bar{{z}}}_\delta = A_d \bar{{z}}_\delta , A_d =A_G -B_G \Gamma \end{aligned}$$

(28)

where $A_{d}$ is the desired state matrix including coefficients representing desired closed loop poles $({\vert }{ sI}-A_{d}{\vert }=(s-\mu _{1})(s-\mu _{2})\ldots (s-\mu _{n}))$; having the general form of $A_{G}$ as given by Eq. (25). Considering Eqs. (7), (B-2) and similarity transformation $\bar{{x}}_\delta = \mathfrak {R}\bar{{z}}_\delta$, yields the feedback control law of the system as:

$$\begin{aligned}&\bar{{u}}_\delta =- K (\xi _i ,\eta _i ) \bar{{x}}_\delta \nonumber \\&K (\xi _i ,\eta _i )= F [ \Gamma + P] \mathfrak {R}^{-1} \end{aligned}$$

(29)

where $F, P$, and $\Gamma$ are obtained using Eqs. (23), (24), and (28) as follows:

$$\begin{aligned} F&= (B_G ^{\prime }\hat{{B}}_G )^{-1}, P= B_G ^{\prime } (A_G -\hat{{A}}_G ),\nonumber \\ \Gamma&= B_G ^{\prime } (A_G -A_d). \end{aligned}$$

(30)