Synchronization analysis of directed complex networks with time-delayed dynamical nodes and impulsive effects

Abstract

In this paper, the effect of impulses on the synchronization of a class of general delayed dynamical networks is analyzed. The network topology is assumed to be directed and weakly connected with a spanning tree. Two types of impulses occurred in the states of nodes are considered: (i) synchronizing impulses meaning that they can enhance the synchronization of dynamical networks; and (ii) desynchronizing impulses defined as the impulsive effects can suppress the synchronization of dynamical networks. For each type of impulses, some novel and less conservative globally exponential synchronization criteria are derived by using the concept of average impulsive interval and the comparison principle. It is shown that the derived criteria are closely related with impulse strengths, average impulsive interval, and topology structure of the networks. The obtained results not only can provide an effective impulsive control strategy to synchronize an arbitrary given delayed dynamical network even if the original network may be asynchronous itself but also indicate that under which impulsive perturbations globally exponential synchronization of the underlying delayed dynamical networks can be preserved. Numerical simulations are finally given to demonstrate the effectiveness of the theoretical results.

1 Introduction

Complex dynamical networks consisting of a large set of interacting dynamical nodes connected by links have recently received increasing attention from various fields of science and engineering [1–3]. The main reason is that many real systems can be described as complex dynamical networks, such as Internet, ecosystems, biological neural networks, biomolecular networks, and social networks. As one of the most interesting emergent phenomena in dynamical networks, synchronization of all dynamical nodes has been a hot research topic due to its potential engineering applications, such as secure communication, parallel image processing, and pattern recognition. From the literature, there exist two common phenomena in many dynamical networks: delay effects and impulsive effects [4–9]. Time delay is a very familiar phenomenon in various systems [4–6]. Due to the finite speeds of transmission and spreading as well as traffic congestion, a signal or influence traveling through a network often is associated with time delays [5, 6]. It is known that time delays can result in oscillatory behavior or network instability (periodic oscillation and chaos). On the other hand, the states of nodes in many realistic networks are often subject to instantaneous perturbations and experience abrupt changes at certain instants, which may be caused by switching phenomenon, frequency change, or other sudden noise; that is, they exhibit impulsive effects [7–9]. Impulsive effects can also be found in many evolutionary processes and biological systems [7, 8]. Recently, impulsive dynamical systems have drawn increasing attention for their various applications in information science, economic systems, automated control systems, etc [7–10]. Since time delays and impulses can heavily affect the dynamical behaviors of the networks, it is imperative to investigate both effects of time delays and impulses on the synchronization of dynamical networks.

In general, there are two types of impulses in dynamical networks: synchronizing impulses and desynchronizing impulses [10]. An impulsive sequence is said to be synchronizing if it can enhance the synchronization of dynamical networks. Conversely, an impulsive sequence is said to be desynchronizing if the impulsive effects can suppress the synchronization of dynamical networks. In the past decades, much progress has been made in the study of the synchronization of complex dynamical networks with synchronizing or desynchronizing impulses [10–21]. For instance, in [10–17], the synchronization dynamics of complex dynamical networks with synchronizing impulses was investigated. In [18–21], the synchronization problem of complex dynamical networks with desynchronizing impulses was addressed.

When the network dynamics are desynchronizing and the impulsive effects are synchronizing, in order to ensure synchronization, intuitively, there should not be overly long intervals between impulses. Hence, a requirement that the upper bound of the impulse intervals should be smaller than a certain positive constant is imposed in [11–17] to guarantee the frequency of synchronizing impulses should not be too low. Conversely, when the network dynamics are synchronizing and the impulsive effects are desynchronizing, the impulses should not occur too frequently in order to guarantee synchronization. Thus, there exists a requirement that the lower bound of the impulse intervals should be larger than a certain positive constant in [18–20] to ensure that the desynchronizing impulses do not occur too frequently. However, using the upper bound or lower bound of the impulsive intervals to characterize the frequency of impulses would lead the obtained results to be rather conservative [10]. Recently, Lu et al. [10] introduced a concept of average impulsive interval to describe the impulses sequences and then established a less conservative unified synchronization criterion for impulsive dynamical networks subject to synchronizing impulses or desynchronizing impulses. In addition, using the average impulsive interval approach, Lu et al. [21] also investigated the exponential synchronization of linearly coupled neural networks with impulsive disturbances. Unfortunately, the authors of [10] did not consider time delays, the results in [21] only investigated coupled delayed neural networks with desynchronizing impulses. Moreover, both the results in [10, 21] only considered the case of dynamical networks with impulses occurred in the processes of coupling. They cannot be directly extended to the case of delayed dynamical networks with impulsive effects on the nodes’ states; another common phenomenon occurred in many realistic networks [7, 8, 19, 20]. Hence, the aim of this paper is to study the synchronization problem of general delayed dynamical networks with impulsive effects on the nodes’ states using the average impulsive interval approach.

In practice, there usually exist two types of time delays in complex networks [5, 13, 22–25]. One is coupling delays caused by exchange of information between nodes [5]. The other is internal delays occurring inside the system [13, 22–25]. In view of the fact that internal delays occurring inside the system are more complex than time delays in the couplings [13, 22–25], time delays in the dynamical nodes will be considered in this paper.

Motivated by the above discussions, this paper is concerned with synchronization of general complex networks with time-varying delays dynamical nodes and impulsive effects. The directed and weakly connected topology of networks is focused on. Two types of impulses occurred in the states of nodes are considered: synchronizing impulses and desynchronizing impulses. By using the concept of average impulsive interval and the comparison principle, some novel and less conservative globally exponential synchronization criteria are derived for each type of impulses. It is shown that besides impulse strengths and average impulsive interval, the obtained criteria are also closely related with topology structure of the networks. Our results not only can provide an effective impulsive control strategy to synchronize an arbitrary given delayed dynamical network even if the original network may be asynchronous itself but also indicate that under which impulsive perturbations globally exponential synchronization of the underlying delayed dynamical networks can be preserved. Numerical examples are also provided to illustrate the effectiveness of the theoretical analysis.

2 Problem formulation and preliminaries

Consider a general complex network consisting of $N$ identical time-delayed dynamical nodes. Each node of the network is an $n$-dimensional nonautonomous dynamical system with time-varying delays, which is described by:

$$\begin{aligned} \dot{x}_{i}(t)&= f(t,x_{i}(t),x_i(t-\tau (t)))\nonumber \\&+c\sum \limits _{j=1}^{N} b_{ij}\varGamma x_j(t),\quad i=1,\ldots ,N, \end{aligned}$$

(1)

where $x_i(t)=(x_{i1}(t),x_{i2}(t),\ldots ,x_{in}(t))^{\top }\in \mathbb {R}^{n}$ is the state vector of node $i,\,f:\mathbb {R}\times \mathbb {R}^{n} \times \mathbb {R}^{n}\rightarrow \mathbb {R}^{n}$ is a continuously vector-valued function governing the dynamics of isolated nodes. The time delay $\tau (t)$ may be unknown (constant or time-varying) but is bounded by a known constant, i.e., $0\le \tau (t)\le \tau$. The positive constant $c$ is the coupling strength, and $\varGamma >0$ is the inner connecting matrix describing the individual coupling between nodes. $B=(b_{ij})_{N\times N}$ is the coupling matrix representing the underlying topological structure of the network, and $b_{ij}$ is defined as follows: if there is a link from node $j$ to node $i$ ($j\ne i$), then $b_{ij}>0$; otherwise, $b_{ij}=0$. This implies that the network is directed, and the coupling matrix $B$ is asymmetric. In addition, it is assumed that $B$ satisfies the following properties: $\sum _{j=1}^{N} b_{ij}=0$ and $\mathrm{rank}(B)=N-1$ [13, 26]. As indicated in [27, 28], the coupling matrix $B$ can be regarded as the Laplacian matrix of a weighted graph with a spanning tree, and $B$ has an eigenvalue 0 with multiplicity 1. Note that the coupling matrix $B$ is not restricted to be symmetric or irreducible, and the inner coupling matrix $\varGamma$ is not assumed to be diagonal or symmetric.

Due to switching phenomenon, frequency change, or other sudden noise, the states of nodes in many realistic networks are often subject to instantaneous perturbations and experience abrupt changes at certain instants [8, 9, 19, 20]. Without loss of generality, we assume that at time instants $t_k$, there are “sudden changes” (or “jumps”) in the state variable such that

$$\begin{aligned}&U(k,x_i)=\Delta x_i |_{t=t_k}\mathop {=}\limits ^\mathrm{\triangle }x_i(t_k^{+})-x_i(t_k^{-}),\quad \nonumber \\&\quad i=1,2,\ldots ,N, \end{aligned}$$

(2)

where $\{t_1,t_2,t_3,\ldots \}$ is an impulsive sequence satisfying $t_{k-1}<t_k$ and $\lim _{k\rightarrow \infty }t_{k}=+\infty ,\,x_i(t_k^+)=\lim _{t\rightarrow t_k^+}x_i(t)$ and $x_i(t_k^-)=\lim _{t\rightarrow t_k^-}x_i(t).$ Let $U(k,x_i)$ $=d_{k} x_i,$ where $d_{k} \in \mathbb {R}$ represents the strength of impulses, then we obtain the following impulsive-delayed dynamical network:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_{i}(t)=f(t,x_{i}(t),x_i(t-\tau (t)))\\ \qquad \qquad +\,\,c\sum _{j=1}^{N} b_{ij}\varGamma x_j(t),\,t\ne t_k,\\ \Delta x_i=x_i(t_k^{+})-x_i(t_k^{-})\\ \qquad \qquad =d_{k} x_i(t_k^-), t= t_k,\, k\in Z^+,\\ x_i(t_0+s)=\varphi _i(s),\, s\in [-\tau ,0], \\ \quad \qquad \qquad i=1,2,\ldots ,N,\;t\ge t_0, \end{array} \right. \end{aligned}$$

(3)

where $Z^+=\{1,2,\ldots \}$ denotes the set of positive integer numbers. Without loss of generality, it is assumed that $x_i(t)$ is right continuous at $t=t_k$, i.e., $x_i(t_k)=x_i(t_k^+)$. The initial conditions $\varphi _i(s)\in PC([-\tau ,0],\mathbb {R}^n)$, in which $PC([-\tau , 0],\mathbb {R}^n)$ denotes the set of all functions of bounded variation and right-continuous on any compact subinterval of $[-\tau , 0]$. We always assume that Eq. (3) has a unique solution with respect to initial conditions.

Remark 1

Taking into account that the coupled states $x_j(t)-x_i(t)$ between connected nodes $j$ and $i$ can suddenly change in the form of impulses at discrete times $t_k$ in the process of signal transmission, the impulses occurred in the process of coupling were studied in [10, 21]. Hence, $x_i(t_k^+)-x_j(t_k^+)=S_k \big (x_i(t_k^-)-x_j(t_k^-)\big )$ was assumed in [10, 21]. In this paper, another common phenomenon that the states of nodes in many realistic networks are often subject to instantaneous perturbations and experience abrupt changes at certain instants [7, 8, 19, 20] is considered, and so $x_i(t_k^{+})-x_i(t_k^{-})=d_{k} x_i(t_k^-)$ is assumed here. In addition, here the coupling matrix $B$ is not necessarily to be symmetric or irreducible, and the inner coupling matrix $\varGamma$ is not assumed to be diagonal or symmetric. A general structure of the network is discussed here, that is, the corresponding graph generated by matrix $B$ can be directed and weakly connected. However, the coupling matrix $B$ in [10, 21] is required to be irreducible, and the inner coupling matrix $\varGamma$ is also restricted to be diagonal in [21].

Assumption 1

[26] For the vector-valued function $f(t,x(t),x(t-\tau (t)))$, suppose the uniform semi-Lipschitz condition with respect to the time $t$ holds, i.e., for any $x(t),\,y(t)\in \mathbb {R}^n$, there exist positive constants $L_1>0$ and $L_2>0$ such that

$$\begin{aligned}&\!\!\!\!\big (x(t)-y(t)\big )^{\top }\big (f(t,x(t),x(t-\tau (t)))\\&\!\!\!\!\quad -f(t,y(t),y(t-\tau (t)))\big )\\&\le L_1\,\big (x(t)-y(t)\big )^{\top }\big (x(t)-y(t)\big )\\&\!\!\!\!\quad +L_2 \big (x(t-\tau (t))-y(t-\tau (t)) \big )^{\top }\big (x(t-\tau (t))\\&\!\!\!\!\quad -y(t-\tau (t))\big ).\\ \end{aligned}$$

Remark 2

Assumption 1 gives some requirements for the dynamics of isolated node in network (1). If the function describing each node in network (1) satisfies uniform Lipschitz condition with respect to the time $t$ [13], i.e., $\Vert f(t,x(t),x(t-\tau (t)))-f(t,y(t),y(t-\tau (t)))\Vert \le K_1\Vert x(t)-y(t)\Vert +K_2\Vert x(t-\tau (t))-y(t-\tau (t)) \Vert$, one can choose $L_1=K_1+ \omega K_2/2$ and $L_2=K_2/(2\omega )$ to satisfy Assumption 1, where $\omega$ is a positive constant. Moreover, it is easy to check that almost all the well-known chaotic systems with delays or without delays, such as the Lorenz system, Rössler system, Chen system, and Chua’s circuit as well as the delayed Ikeda equations, delayed Hopfield neural networks and delayed cellular neural networks, and so on (see [13, 26], and the references therein) also satisfy Assumption 1.

Definition 1

The impulsive-delayed dynamical network (3) is said to be globally exponentially synchronized if there exist constants $\lambda _0>0$ and $M_0>0$ such that for any initial conditions $\varphi _i(s)\in PC([-\tau ,0],\mathbb {R}^n)\,$ $(i=1,2,\ldots ,N)$

$$\begin{aligned} \Vert x_i(t)-x_j(t) \Vert \le M_0 e^{-\lambda _0 (t-t_0)},\quad \forall t\ge t_0. \end{aligned}$$

Definition 2

[10] (Average Impulsive Interval) The average impulsive interval of the impulsive sequence $\zeta =\{t_1,t_2,t_3,\ldots \}$ is equal to $(N_0,T_\mathrm{a})$ if there exist positive integer $N_0$ and positive number $T_\mathrm{a}$, such that

$$\begin{aligned}&\frac{T-t}{T_\mathrm{a}}-N_0\le N_\zeta (T,t)\le \frac{T-t}{T_\mathrm{a}}+N_0,\quad \nonumber \\&\quad \forall T\ge t \ge 0, \end{aligned}$$

(4)

where $N_\zeta (T,t)$ denotes the number of impulsive times of the impulsive sequence $\zeta$ on the interval $(t,T)$.

Let $s(t)=\frac{1}{N}\sum \nolimits _{l=1}^{N}x_l(t)$ and $e_i(t)=x_i(t)-s(t)\,(1\le i\le N)$ be synchronization errors, then we have

$$\begin{aligned}&\!\!\!\!\dot{e}_i(t)=\dot{x}_i(t) - \dot{s}(t)\\&\!\!\!\!\quad =\tilde{f}(t,e_{i}(t),e_i(t-\tau (t)))\\&\!\!\!\!\qquad +\,c\sum \limits _{j=1}^{N} b_{ij}\varGamma e_j(t)+J,\quad t\ne t_k,\\&\!\!\!\!\quad \Delta e_i(t_k)=e_i(t_k^+)-e_i(t_k^-)= x_i(t_k^+)-x_i(t_k^-)\\&\!\!\!\!\qquad -\, \big (s(t_k^+)-s(t_k^-)\big ) \\&\!\!\!\!\quad =x_i(t_k^+)-x_i(t_k^-)- \frac{1}{N}\sum \limits _{l=1}^{N}\big (x_l(t_k^+)-x_l(t_k^-)\big ) \\&\!\!\!\!\quad =d_k x_i(t_k^-)-\frac{d_k}{N}\sum \limits _{l=1}^{N} x_l(t_k^-)=d_k e_i(t_k^-),\quad t=t_k,\\&\!\!\!\!\quad \sum \limits _{i=1}^N e_i(t)=\sum \limits _{i=1}^N \Big (x_i(t)-s(t) \Big )=\sum \limits _{i=1}^N x_i(t)-N s(t)\nonumber \\&\quad =\sum \limits _{i=1}^N x_i(t)-\sum \limits _{l=1}^{N}x_l(t)=0, \end{aligned}$$

where $\tilde{f}(t,e_{i}(t),e_i(t-\tau (t)))\!=\!f(t,e_{i}(t)+s(t),e_i(t-\tau (t)) +s(t-\tau (t)))-f(t,s(t),s(t-\tau (t)))$, and $J=f(t,s(t),s(t-\tau (t))) -\frac{1}{N}\sum \nolimits _{l=1}^{N}f(t,x_{l}(t),x_l(t-\tau (t))) -\frac{c}{N}\sum \nolimits _{l=1}^{N}\sum \nolimits _{j=1}^{N} b_{lj}\varGamma x_j(t)$. Note that $x_i(t)$ is right continuous at $t=t_k$, i.e., $x_i(t_k)=x_i(t_k^+)$, the error dynamical system then can be written as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \dot{e}_{i}(t)=\tilde{f}(t,e_{i}(t),e_i(t-\tau (t)))\\ \qquad \qquad +c\sum _{j=1}^{N} b_{ij}\varGamma e_j(t)+J,\; t\ne t_k,\; t\ge t_0,\\ e_i(t_k)=(1+d_k) e_i(t_k^-),\\ \quad \quad t= t_k,\, k\in Z^+,\,i=1,2,\ldots ,N. \end{array} \right. \end{aligned}$$

(5)

It is easy to see that globally exponential synchronization of the dynamical network (3) is achieved if the zero solution of the error dynamical system (5) is globally exponentially stable.

Remark 3

When $| (1+d_k) |<1$, i.e., the impulsive strengths $-2<d_k<0$, the impulses are beneficial for the synchronization of the impulsive- delayed dynamical network (3), since the absolute values of the synchronization errors are reduced. Thus, the impulses are synchronizing impulses if $-2<d_k<0$. Conversely, when $| (1+d_k) |>1$, i.e., the impulsive strengths $d_k>0$ or $d_k<-2$, the impulses are desynchronizing impulses, since the absolute values of the synchronization errors are enlarged. In addition, when $|(1+d_k)|=1$, i.e., the impulsive strengths $d_k=0$ or $d_k=-2$, the impulses are neither beneficial nor harmful for the synchronization of the impulsive-delayed dynamical network (3), since the absolute values of the synchronization errors are unchanged. This type of impulses are called inactive impulses [10]. We will not discuss this trivial case in this paper because they have no effect on the synchronization dynamics of the impulsive-delayed dynamical network (3).

Lemma 1

[29] Let $0\le \tau (t) \le \tau$ and $F(t,x,y):[t_0,\infty )\times \mathbb {R}\times \mathbb {R}\rightarrow \mathbb {R}$ be nondecreasing in $y$ for each fixed $(t,x),$ and $I_k(x):\mathbb {R}\rightarrow \mathbb {R}$ be nondecreasing in $x$. Suppose that $u(t),\,v(t)\in PC([t_0-\tau ,\infty ),\mathbb {R})$ satisfy

$$\begin{aligned}&\!\!\!\!\left\{ \!\! \begin{array}{l} D^{+}u(t)\le F(t,u(t),u(t-\tau (t)),\, t\ge t_0,\\ u(t_{k})\le I_{k}(u(t_k^{-})), \quad k\in Z^+, \end{array} \right. \\&\!\!\!\!\left\{ \!\! \begin{array}{l} D^{+}v(t)> F(t,v(t),v(t-\tau (t)),\, t\ge t_0,\\ v(t_{k})\ge I_{k}(v(t_k^{-})), \quad k\in Z^+. \end{array} \right. \end{aligned}$$

If $u(t)\le v(t)$, for $t_0-\tau \le t \le t_0$, then $u(t)\le v(t),\, t\ge t_0$.

3 Main results

Hereafter, let the matrix $\tilde{B}$ be defined as $\tilde{B}\mathop {=}\limits ^\mathrm{\Delta }(B+B^{\top })-\Delta ,$ where $\Delta =\mathrm{diag}(\delta _1,\delta _2,\ldots ,\delta _N)$ with $\delta _j=\sum _{k=1}^N b_{kj}$. Then the matrix $\tilde{B}$ is a symmetrical irreducible matrix with zero-sum and nonnegative off-diagonal elements. This implies that zero is an eigenvalue of $\tilde{B}$ with multiplicity $1,$ and all the other eigenvalues of $\tilde{B}$ are strictly negative [27, 28]. Its eigenvalues can be ordered as $0=\tilde{\lambda }_1>\tilde{\lambda }_2\ge \cdots \ge \tilde{\lambda }_N.$

3.1 Synchronization criteria for synchronizing impulses

In this subsection, some less conservative globally exponential synchronization criteria for the impulsive-delayed dynamical network (3) with synchronizing impulses will be derived. It will be shown that an appropriate sequence of impulses can make an unsynchronized delayed dynamical network (1) globally exponentially synchronous.

Theorem 1

Consider the impulsive-delayed dynamical network (3) with synchronizing impulses. Suppose that Assumption 1 holds, and the average impulsive interval of impulsive sequence $\zeta =\{t_1,t_2,t_3,\ldots \}$ is equal to $(N_0,T_\mathrm{a})$. Then the impulsive-delayed dynamical network (3) is globally exponentially synchronized if there exists a positive constant $0<d<1$ such that

• (i) $(1+d_k)^2\le d$,   $k\in Z^+$,

• (ii) $\varpi \mathop {=}\limits ^\mathrm{\Delta }\frac{\ln d}{T_\mathrm{a}}+2L_1+r\lambda (r)+2d ^{-N_0}L_2<0$

where

$$\begin{aligned} r&= c\Big (\tilde{\lambda }_2+\max _{1\le k\le N} \delta _k\Big ) \;\mathrm{with}\; \lambda (r)\\&= \left\{ \begin{array}{ll} \displaystyle \lambda _{\max }(\varGamma ), &{} \quad \mathrm{if}\;r>0,\\ 0,&{}\quad \mathrm{if}\;r=0,\\ \displaystyle \lambda _{\min }(\varGamma ), &{}\quad \mathrm{if} \; r<0. \end{array} \right. \end{aligned}$$

Proof

Let $e(t)=(e_1^{\top }(t),e_2^{\top }(t),\ldots ,e_N^{\top }(t))^{\top }$, consider the following Lyapunov function:

$$\begin{aligned} V(t)\!=\!\frac{1}{2}e^{\top }(t)(I_N\otimes I_n)e(t)=\frac{1}{2}\sum _{i=1}^{N}e_i^{\top }(t)e_i(t).\qquad \end{aligned}$$

(6)

Calculating the upper Dini derivative of $V(t)$ along the solution of Eq. (3), by using Assumption 1 and note that $\sum \nolimits _{i=1}^{N}e_i(t)=0$, we get

$$\begin{aligned} D^+ V(t)&= \sum \limits _{i=1}^{N} e_i^{\top }(t)\Big [\tilde{f}(t,e_{i}(t),e_i(t-\tau (t)))\nonumber \\&+\,c\sum \limits _{j=1}^{N} b_{ij}\varGamma e_j(t)+J \Big ]\nonumber \\&= \sum \limits _{i=1}^{N} e_i^{\top }(t)\tilde{f}(t,e_{i}(t),e_i(t-\tau (t)))\nonumber \\&+\,c e^{\top }(t)(B\otimes \varGamma )e(t)+\sum \limits _{i=1}^{N} e_i^{\top }(t) J\nonumber \\&= \sum \limits _{i=1}^{N} e_i^{\top }(t)\tilde{f}(t,e_{i}(t),e_i(t-\tau (t)))\nonumber \\&+\,c e^{\top }(t)(B\otimes \varGamma )e(t)\nonumber \\&\le \sum \limits _{i=1}^{N} L_1 e_i^{\top }(t) e_i(t)\!+\!\sum \limits _{i=1}^{N} L_2 e_i^{\top }\nonumber \\&\times (t\!-\!\tau (t)) e_i(t-\tau (t))\!+\!c e^{\top }(t)(B\!\otimes \! \varGamma )e(t)\nonumber \\&\le 2 L_1 V(t)+2 L_2 V(t-\tau (t))\nonumber \\&+\,c e^{\top }(t)(B\otimes \varGamma )e(t)\nonumber \\&= 2 L_1 V(t)+2 L_2 V(t-\tau (t))\nonumber \\&+\,\frac{c}{2} e^{\top }(t)\Big ((B+B^{\top })\otimes \varGamma \Big )e(t)\nonumber \\&= 2 L_1 V(t)+2 L_2 V(t-\tau (t))\nonumber \\&+\,\frac{c}{2} e^{\top }(t)\Big ((\tilde{B}+\Delta )\otimes \varGamma \Big )e(t), t\ne t_k. \end{aligned}$$

(7)

On the other hand, since $\tilde{B}$ is a symmetrical matrix, there exists a unitary matrix $U=(u_1,\ldots ,u_N)$ with $UU^{\top }=I_N$ such that $\tilde{B}=U \mathrm{diag} (\tilde{\lambda }_1,\tilde{\lambda }_2,\ldots ,\tilde{\lambda }_N)U^{\top }$. Introduce a transformation $Z(t)=(U^{\top }\otimes I_n)e(t)$, where $Z(t)=(z_1^{\top }(t),z_2^{\top }(t),\ldots ,z_N^{\top }(t))^{\top },\,z_k\in \mathbb {R}^n$, then one has

$$\begin{aligned} Z^{\top }(t)Z(t)=\sum \limits _{i=1}^{N}e_i^{\top }(t)e_i(t). \end{aligned}$$

(8)

Note that $\tilde{\lambda }_1=0$ is an eigenvalue of the matrix $\tilde{B}$, and its corresponding eigenvector is $u_1=(\frac{1}{\sqrt{N}},\frac{1}{\sqrt{N}},$ $\ldots ,\frac{1}{\sqrt{N}})^{\top }$, then we get

$$\begin{aligned} z_1(t)=(u_1^{\top }\otimes I_n)e(t)=\frac{1}{\sqrt{N}}\sum \limits _{i=1}^{N}e_i(t)=0. \end{aligned}$$

(9)

From Eqs. (8) and (9), we have

$$\begin{aligned}&\!\!\!\!ce^{\top }(t)\Big ((\tilde{B}+\Delta )\otimes \varGamma \Big )e(t)\nonumber \\&\!\!\!\!\quad =ce^{\top }(t)(U\otimes I_n)\Big (\Big (\mathrm{diag} (\tilde{\lambda }_1,\tilde{\lambda }_2,\ldots ,\tilde{\lambda }_N)\nonumber \\&\!\!\!\!\qquad +\,\,U^{\top }\Delta U\Big )\otimes \varGamma \Big )(U^{\top }\otimes I_n)e(t)\nonumber \\&\!\!\!\!\quad \le cZ^{\top }(t)\Big (\Big (\mathrm{diag} (\tilde{\lambda }_1,\tilde{\lambda }_2,\ldots ,\tilde{\lambda }_N)\nonumber \\&\qquad +\,\,\lambda _{\max }(U^{\top }\Delta U)I_N\Big )\otimes \varGamma \Big )Z(t)\nonumber \\&\!\!\!\!\quad \le cZ^{\top }(t)\Big (\Big (\mathrm{diag} (\tilde{\lambda }_1,\tilde{\lambda }_2,\ldots ,\tilde{\lambda }_N)\nonumber \\&\!\!\!\!\qquad +\,\,\max _{1\le k \le N}\delta _k I_N\Big )\otimes \varGamma \Big )Z(t)\nonumber \\&\!\!\!\!\quad =c\sum _{i=1}^{N} (\tilde{\lambda }_i+ \max _{1\le k \le N}\delta _k) z_i^{\top }(t) \varGamma z_i(t)\nonumber \\&\!\!\!\!\quad =c\sum _{i=2}^{N} (\tilde{\lambda }_i+ \max _{1\le k \le N}\delta _k) z_i^{\top }(t) \varGamma z_i(t)\nonumber \\&\!\!\!\!\quad \le c\sum _{i=2}^{N} (\tilde{\lambda }_2+ \max _{1\le k \le N}\delta _k) z_i^{\top }(t) \varGamma z_i(t)\nonumber \\&\!\!\!\!\quad = \sum _{i=1}^{N}c(\tilde{\lambda }_2+\max _{1\le k \le N}\delta _k) z_i^{\top }(t)\varGamma z_i(t)\nonumber \\&\!\!\!\!\quad \le r \lambda (r)\sum _{i=1}^{N}e_i^{\top }(t)e_i(t)=2r\lambda (r)V(t). \end{aligned}$$

(10)

Substituting (10) into (7) gives

$$\begin{aligned} D^+V(t)&\le \big (2L_1+r\lambda (r)\big )V(t)\nonumber \\&+2L_2 V(t-\tau (t)),\quad t\ne t_k. \end{aligned}$$

(11)

When $t=t_k$, we have

$$\begin{aligned}&V(t_k)=\frac{1}{2}\sum _{i=1}^{N}e_i^{\top }(t_k)e_i(t_k)\nonumber \\&\quad =\frac{1}{2}\sum _{i=1}^{N}(1+d_k)^2 e_i^{\top }(t_k^-)e_i(t_k^-)\le d V(t_k^-). \end{aligned}$$

(12)

Denote $p=2L_1+r\lambda (r)$ and $q=2L_2$. For any $\epsilon >0$, let $\mu _{\epsilon }(t)$ be a unique solution of the following impulsive- delayed dynamical system:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \dot{\mu }_{\epsilon }(t)\!=\!p \mu _{\epsilon }(t)+q \mu _{\epsilon }(t\!-\!\tau (t)){+}\epsilon , t{\ne } t_k,\,t\ge t_0, \\ \displaystyle \mu _{\epsilon }(t_k)=d \mu _{\epsilon }(t_k^-),\quad \,k\in Z^{+},\\ \mu _{\epsilon }(t)=\sup \nolimits _{t_0-\tau \le s \le t_0} \Vert V(s) \Vert ,\quad t_0-\tau \le t \le t_0. \end{array} \right. \end{aligned}$$

(13)

Let $M_0=d^{-N_0}\sup _{t_0-\tau \le s \le t_0} \Vert V(s) \Vert$ and $\eta =-(\ln d)$/${T_\mathrm{a}}-p$. In the following, we shall prove that condition (ii) implies

$$\begin{aligned} \mu _{\epsilon }(t)<M_0 e^{-\lambda (t-t_0)}+\frac{\epsilon }{(\eta -d^{-N_0}q) d^{N_0}}, \quad t\ge t_0,\nonumber \\ \end{aligned}$$

(14)

where $\lambda >0$ is a unique positive solution of

$$\begin{aligned} \lambda +\frac{\ln d}{T_\mathrm{a} }+p+d^{-N_0}q e^{\lambda \tau }=0. \end{aligned}$$

(15)

Denote $H(\lambda )=\lambda -\eta +d^{-N_0}q\exp ^{\lambda \tau }$. From condition (ii), we have $\eta -d^{-N_0}q>0,\,d^{\,-N_0}q\ge 0,$ and so $H(0)<0,\,H(+\infty )>0$, and $\frac{\text {d} H(\lambda )}{\text {d} \lambda }>0.$ Using the continuity and the monotonicity of $H(\lambda ),$ the equation (15) has an unique positive solution $\lambda >0.$ By the formula for the variation of parameters [29, 30], we obtain

$$\begin{aligned} \mu _{\epsilon }(t)&= W(t,t_0)\mu _{\epsilon }(t_0)\nonumber \\&+\int _{t_0}^{t}W(t,s)\Big [q \mu _{\epsilon }(s-\tau (s))+\epsilon \Big ] \text {d}s,\,\, t\ge t_0,\nonumber \\ \end{aligned}$$

(16)

where $W(t,s),t,s\ge t_0$ is the Cauchy matrix of linear system [29, 30]

$$\begin{aligned} \left\{ \!\! \begin{array}{ll} \dot{\psi }(t)= p\, \psi (t),\quad t\ne t_k, \,t\ge t_0,\\ \psi (t_{k})= d\psi (t_k^-),\quad \,k\in Z^{+}. \end{array} \right. \end{aligned}$$

(17)

Let $N_\zeta (t,t_0)$ be the number of impulsive times of the impulsive sequence $\zeta$ in the interval $(t_0,t)$, according to the representation of the Cauchy matrix [29, 30], we have

$$\begin{aligned} W(t,s)&= \left( \prod \limits _{s<t_k\le t } d\right) e^{p\, (t-s)}\nonumber \\&= d^{N_\zeta (t,s)}e^{p\, (t-s)}, \quad t > s\ge t_0. \end{aligned}$$

(18)

Since the average impulsive interval of the impulsive sequence $\zeta =\{t_1,t_2,\ldots \}$ is equal to $(N_0,T_\mathrm{a})$, we have $N_\zeta (t,s)\ge \frac{t-s}{T_\mathrm{a}}-N_0,\,\forall t>s\ge t_0$. Notice that $0<d<1$, we obtain

$$\begin{aligned} W(t,s)&= d^{N_\zeta (t,s)}e^{p\, (t-s)}\nonumber \\&\le d^{-N_0}d^{\frac{t-s}{T_\mathrm{a}}}e^{(-\eta -\frac{\ln d}{T_\mathrm{a}})(t-s)}\nonumber \\&= d^{-N_0}e^{\frac{(t-s)}{T_\mathrm{a}} \ln d}e^{(-\eta -\frac{\ln d}{T_\mathrm{a}})(t-s)}\nonumber \\&= d^{-N_0}e^{-\eta (t-s)}, \quad t> s\ge t_0. \end{aligned}$$

(19)

Substituting (19) into (16) gives

$$\begin{aligned} \mu _{\epsilon }(t)&\le d^{-N_0}e^{-\eta (t-t_0)} \mu _{\epsilon }(t_0)\nonumber \\&+\int _{t_0}^{t}d^{-N_0}e^{-\eta (t-s)}\Big [ q\mu _{\epsilon }(s-\tau (s))+\epsilon \Big ] \text {d}s\nonumber \\&= M_0 e^{-\eta (t-t_0)}+\int _{t_0}^{t} e^{-\eta (t-s)}\Big [d^{-N_0} q \mu _{\epsilon }(s\nonumber \\&-\tau (s))+d^{-N_0}\epsilon \Big ] \text {d}s, \, t\ge t_0. \end{aligned}$$

(20)

Since $\epsilon , \lambda , \eta -d^{-N_0}q >0,$ and $0<d<1,$ we have

$$\begin{aligned}&\mu _{\epsilon }(t)\le d^{\,-N_0} \sup _{t_0-\tau \le s\le t_0}\Vert V(s)\Vert < M_0 e^{-\lambda (t-t_0)}\nonumber \\&\quad +\frac{\epsilon }{(\eta -d^{-N_0}q) d^{N_0}}, \,\quad t_0-\tau \le t \le t_0. \end{aligned}$$

(21)

Now, we show that (14) holds. If it is not true, from (21), then there must exist a $t^{*}>t_0$ satisfying

$$\begin{aligned}&\mu _{\epsilon }(t^{*})\ge M_0 e^{-\lambda (t^{*}-t_0)}+\frac{\epsilon }{(\eta -d^{-N_0}q) d^{N_0}},\end{aligned}$$

(22)

$$\begin{aligned}&\mu _{\epsilon }(t)< M_0 e^{-\lambda (t-t_0)}+\frac{\epsilon }{(\eta -d^{-N_0}q) d^{N_0}}, \nonumber \\&\quad t_0-\tau \le t<t^{*}. \end{aligned}$$

(23)

By (15), (20) and (23), we have

$$\begin{aligned}&\!\!\!\!\mu _{\epsilon }(t^{*})\le M_0 e^{-\eta (t^{*}-t_0)}\nonumber \\&\!\!\!\!\qquad +\,\int _{t_0}^{t^{*}}e^{-\eta (t^{*}-s)}\Big [d^{-N_0}q \displaystyle \mu _{\epsilon }(s-\tau (s))+d^{-N_0}\epsilon \Big ] \text {d}s\nonumber \\&\!\!\!\!\quad \le e^{-\eta (t^{*}-t_0)}\Bigg \{M_0\nonumber \\&\!\!\!\!\qquad +\,\int _{t_0}^{t^{*}}e^{\eta (s-t_0)}\Big [d^{-N_0}q M_0 e^{-\lambda \big (s-\tau (s)-t_0\big )}\nonumber \\&\!\!\!\!\qquad +\,\frac{\epsilon d^{-N_0}q }{(\eta -d^{-N_0}q) d^{N_0}}+d^{-N_0}\epsilon \Big ] \text {d}s\Bigg \}\nonumber \\&\!\!\!\!\quad \le e^{-\eta (t^{*}-t_0)}\Bigg \{M_0+d^{-N_0}q M_0 e^{\lambda \tau }\int _{t_0}^{t^{*}} e^{(\eta -\lambda ) (s-t_0)}\text {d}s \nonumber \\&\!\!\!\!\qquad +\,\frac{\epsilon \eta }{(\eta -d^{-N_0}q) d^{N_0}}\int _{t_0}^{t^{*}} e^{\eta (s-t_0)}\text {d}s \Bigg \}\nonumber \\&\!\!\!\!\quad < M_0 e^{-\lambda (t^*-t_0)} + \frac{\epsilon }{(\eta -d^{-N_0}q) d^{N_0}}. \end{aligned}$$

(24)

This contradicts (22), and so (14) holds. Denote $F(t,x,y)=p\, x+ q y$ with $x(t)=V(t)$ and $y(t)=V(t-\tau (t))$, and $I_k(x)=d x$ with $x(t)=V(t)$, then the function $F$ and $I_k$ satisfy the monotonicity given in Lemma 1. Since $V(t)\le \displaystyle \sup _{t_0-\tau \le s \le t_0}\Vert V(s)\Vert =\mu _{\epsilon }(t),$ for $t_0-\tau \le t \le t_0,$ it follows from (11)–(13) and Lemma 1 that

$$\begin{aligned}&V(t)\le \mu _{\epsilon }(t)<M_0 e^{-\lambda (t-t_0)}+\frac{\epsilon }{(\eta -d^{-N_0}q)d^{N_0}}, \nonumber \\&\quad t\ge t_0. \end{aligned}$$

Letting $\epsilon \rightarrow 0^{+},$ then we have

$$\begin{aligned} V(t)\le M_0 e^{-\lambda (t-t_0)}, \, t\ge t_0. \end{aligned}$$

This means the zero solution of the error system (5) is globally exponentially stable. The proof of Theorem 1 is thus completed. $\square$

Remark 4

When $d<1$, i.e., the impulsive effects are synchronizing, condition (ii) still holds if $T_\mathrm{a}$ is replaced by $\sup _{k\in Z^+}\{t_k-t_{k-1} \}$; then condition (ii) in Theorem 1 becomes:

$$\begin{aligned} \displaystyle \varpi _{\sup }&\mathop {=}\limits ^\mathrm{\Delta } \frac{\ln d}{\sup _{k\in Z^+}\{t_k-t_{k-1} \} }\nonumber \\&+2 L_1+ r\lambda (r)+2d^{-N_0}L_2<0. \end{aligned}$$

(25)

Note that $\ln d<0$ and $T_\mathrm{a}< \sup _{k\in Z^+}\{t_k-t_{k-1} \}$, condition (ii) derived by using $T_\mathrm{a}$ is thus easier to be satisfied and less conservative than inequality (25) obtained by using $\sup _{k\in Z^+}\{t_k-t_{k-1} \}$. This point will be further verified by numerical examples.

Remark 5

Theorem 1 indicates that globally exponential synchronization of the impulsive-delayed dynamical network (3) with synchronizing impulses depends mainly on the impulsive strengths $d_k$, the average impulsive interval $T_\mathrm{a}$, and the eigenvalue $\tilde{\lambda }_2$. Just as stated in [31–33], the synchronizability of the dynamical network can also be characterized by the second largest eigenvalue $\tilde{\lambda }_2$ of the specific matrix $\tilde{B}$. Therefore, the results show that the network topology also has a great impact on synchronization dynamics of the impulsive- delayed dynamical network.

Remark 6

From the proof of Theorem 1, we can see that the condition $-p>q\ge 0$, that is, $L_1+r\lambda (r)/2<-L_2$, is not required here. This means that the underlying delayed dynamical network (1) without impulsive effects can be asynchronous [34]. Theorem 1 can thus be used to synchronize an unsynchronized delayed dynamical network via impulses. Consequently, Theorem 1 provides an effective impulsive control strategy to synchronize an arbitrary given delayed dynamical network even if the original networks may be asynchronous itself.

For simplicity, we consider the impulsive strengths $d_k\equiv d_0,\,k\in Z^+$. Then, the following result can be obtained readily from Theorem 1.

Corollary 1

Consider the impulsive-delayed dynamical network (3) with synchronizing impulses. Suppose that Assumption 1 holds, and the average impulsive interval of impulsive sequence $\zeta =\{t_1,t_2,t_3,\ldots \}$ is equal to $(N_0,T_\mathrm{a})$. Then the impulsive-delayed dynamical network (3) is globally exponentially synchronized if the following condition holds

$$\begin{aligned} \varpi&\mathop {=}\limits ^\mathrm{\Delta } \frac{2\ln |1+d_0|}{ T_\mathrm{a} }+2L_1+r\lambda (r)\nonumber \\&+2(1+d_0)^{-2N_0} L_2<0,\quad -2<d_0<0. \end{aligned}$$

(26)

3.2 Synchronization criteria for desynchronizing impulses

In this subsection, globally exponential synchronization of the impulsive-delayed dynamical network (3) with desynchronizing impulses will be studied. In this case, the impulses can potentially destroy the synchronization. Thus it is necessary to have some criteria under which the synchronization of a delayed dynamical network can be preserved under impulsive perturbations. The main results are stated as follows.

Theorem 2

Consider the impulsive-delayed dynamical network (3) with desynchronizing impulses. Suppose that Assumption 1 holds, and the average impulsive interval of impulsive sequence $\zeta =\{t_1,t_2,t_3,\ldots \}$ is equal to $(N_0,T_\mathrm{a})$. Then the impulsive-delayed dynamical network (3) is globally exponentially synchronized if there exists a positive constant $d> 1$ such that

• (iii)  $(1+d_k)^{2}\le d$,   $k\in Z^+$,

• (iv)   $\displaystyle \varpi ^*\mathop {=}\limits ^\mathrm{\Delta }\frac{\ln d }{T_\mathrm{a} }+2L_1+r\lambda (r)+2d ^{N_0}L_2<0$

where

$$\begin{aligned} r&= c\Big (\tilde{\lambda }_2+\max _{1\le k\le N} \delta _k\Big ) \;\mathrm{with}\; \lambda (r)\nonumber \\&= \left\{ \begin{array}{ll} \displaystyle \lambda _{\max }(\varGamma ), &{} \quad \mathrm{if}\;r>0,\\ 0,&{}\quad \mathrm{if}\;r=0,\\ \displaystyle \lambda _{\min }(\varGamma ), &{}\quad \mathrm{if} \; r<0. \end{array} \right. \end{aligned}$$

Proof

Consider the following Lyapunov function:

$$\begin{aligned} V(t)=\frac{1}{2}e^{\top }(t)(I_N\otimes I_n)e(t)=\frac{1}{2}\sum \limits _{i=1}^{N}e_i^{\top }(t)e_i(t). \end{aligned}$$

Then, similar to the proof of Theorem 1, we can prove that condition (iv) implies

$$\begin{aligned} V(t)\le M_0 e^{-\lambda (t-t_0)}, \, t\ge t_0, \end{aligned}$$

where $\lambda >0$ is an unique positive solution of the equation $\lambda +\displaystyle \frac{\ln d}{T_\mathrm{a} }+p+d^{\,N_0}q e^{\lambda \tau }=0$, if we note that when $d>1$

$$\begin{aligned} W(t,s)&= \left( \prod \limits _{s<t_k\le t} d\right) e^{p (t-s)}=d^{N_\zeta (t,s)}e^{p (t-s)}\nonumber \\&\le d^{N_0}d^{\frac{t-s}{T_\mathrm{a}}}e^{(-\eta -\frac{\ln d}{T_\mathrm{a}})(t-s)}\nonumber \\&= d^{N_0}e^{-\eta (t-s)}, \quad t> s\ge t_0. \end{aligned}$$

$\square$

Remark 7

When impulsive effects are desynchronizing, i.e., $|(1+d_k)|>1$, condition (iv) is still true if $T_\mathrm{a}$ is replaced by $\inf _{k\in Z^+}\{t_k-t_{k-1} \}$; then condition (iv) in Theorem 2 becomes:

$$\begin{aligned} \displaystyle \varpi ^*_{\inf }&\mathop {=}\limits ^\mathrm{\Delta } \frac{\ln d}{ \inf _{k\in Z^+}\{t_k-t_{k-1}\}}\nonumber \\&+\,2 L_1+ r\lambda (r)+2d^{N_0}L_2<0. \end{aligned}$$

(27)

It is easy to see that condition (iv) derived by using $T_\mathrm{a}$ can be satisfied more easily and less conservative than inequality (27) obtained by using $\inf _{k\in Z^+}\{t_k-t_{k-1} \}$ because $\ln d>0$ and $T_\mathrm{a}> \inf _{k\in Z^+}\{t_k-t_{k-1} \}$. Such statement will be further verified through numerical examples.

Remark 8

From condition (iv), one has $L_1+r\lambda (r)/2+d ^{N_0}L_2<0$ since $(\ln d)/T_\mathrm{a}>0$, that is, $p+q d^{N_0}<0$. This results in $-p>q>0$, which implies that the underlying delayed dynamical network (1) in fact is globally exponential synchronization itself in this case [7, 18]. Thus, Theorem 2 indicates that under which desynchronizing impulses globally exponential synchronization of the original-delayed dynamical network (1) can be preserved. In addition, similar to Theorem 1, Theorem 2 also shows that globally exponential synchronization of the impulsive-delayed dynamical network (3) with desynchronizing impulses is closely related with impulse strengths, average impulsive interval, and topology structure of the networks.

Let the impulsive strengths $d_k\equiv d_0,\,k\in Z^+$. Then, we can derive the following result from Theorem 2.

Corollary 2

Consider the impulsive-delayed dynamical network (3) with desynchronizing impulses. Suppose that Assumption 1 holds, and the average impulsive interval of impulsive sequence $\zeta =\{t_1,t_2,t_3,\ldots \}$ is equal to $(N_0,T_\mathrm{a})$. Then the impulsive-delayed dynamical network (3) is globally exponentially synchronized if the following condition holds

$$\begin{aligned} \varpi ^*&\mathop {=}\limits ^\mathrm{\Delta } \frac{2 \ln |1+d_0|}{ T_\mathrm{a} }+2L_1+r\lambda (r)+2(1+d_0)^{2N_0}\nonumber \\&L_2 <0,\quad d_0>0\;\mathrm{or}\; d_0<-2. \end{aligned}$$

(28)

Remark 9

In [11–17], the synchronization problem with synchronizing impulses was investigated. In order to ensure synchronization, a requirement that $\sup _{k\in Z^+}\{t_k-t_{k-1} \}\le \varepsilon _1$ for a certain positive constant $\varepsilon _1$ is needed in [11–17] to guarantee the frequency of synchronizing impulses should not be too low. In [18–20], the synchronization dynamics with desynchronizing impulses was studied. In order to guarantee synchronization, there exists a requirement that $\inf _{k\in Z^+}\{t_k-t_{k-1} \}\ge \varepsilon _2$ for a certain positive constant $\varepsilon _2$ in [18–20] to ensure that the desynchronizing impulses do not occur too frequently. In this paper, the synchronization problem of impulsive dynamical networks with time-varying delays dynamical nodes is considered, and two types of impulses occurred in the sates of nodes are discussed. Different from the results in [11–20], here the average impulsive interval $T_\mathrm{a}$ is used to derive synchronization criteria. Since $\sup _{k\in Z^+}\{t_k-t_{k-1}\}>T_\mathrm{a}$, our synchronization criteria increase the impulses distances of synchronizing impulses than the results obtained in [11–17] by using the upper bound of the impulsive intervals. Similarly, due to $\inf _{k\in Z^+}\{t_k-t_{k-1} \}<T_\mathrm{a}$, our synchronization criteria decrease the impulses distances of desynchronizing impulses than the results derived in [18–20] by using the lower bound of the impulsive intervals. Hence, results of this paper are less conservation than those in [11–20]. Recently, synchronization of impulsive dynamical networks was investigated in [10, 21] by using the average impulsive interval approach. However, the authors of [10] did not consider time delays; the results in [21] only investigated coupled delayed neural networks with desynchronizing impulses. Moreover, both the results in [10, 21] only considered the case of dynamical networks with impulses occurred in the processes of coupling. They cannot be directly extended to the case of delayed dynamical networks with impulsive effects on the nodes’ states; another common phenomenon occurred in many realistic networks [7, 8, 19, 20]. Hence, our results are new and extend those in [10–21]. Furthermore, as shown in [10, 21], impulsive signals with a wider range of impulsive interval can also be described by utilizing the concept of average impulsive interval. Therefore, our synchronization criteria can be applicable to a wider range of impulsive signals.

Remark 10

In this paper, for simplicity’s sake, the network model is assumed to be time-invariant. However, in reality, complex networks are more likely to be time-varying networks, that is, the coupling coefficients $b_{ij}$ and the coupling matrix $\varGamma$ are time-varying [2]. By referring to [2, 16, 29], the results in this paper can actually be generalized to the case of general time-varying dynamical network model. We will give a detailed analysis for this case and present it elsewhere.

4 Numerical examples

4.1 The examples of simulations

In this subsection, two simulation examples, one for synchronizing impulses and the other for desynchronizing impulses, are given to illustrate the effectiveness of our theoretical results. The Chua oscillator with time-delayed nonlinearity is used as uncoupled node in network (1). A single time-delayed Chua oscillator is given by [26]

$$\begin{aligned} \dot{x}(t)&= f(t,x(t),x(t-\tau (t)))\nonumber \\&= Ax(t)+g_1(x(t))+g_2(x(t-\tau (t))), \end{aligned}$$

(29)

where $x(t)=(x_{1}(t),x_{2}(t),x_{3}(t))^{\top }\in \mathbb {R}^3,\,g_1(x(t))=\big (-\frac{1}{2}\alpha (m_1-m_2)(|x_1(t)+1|-|x_1(t)-1|), 0, 0\big )^{\top }\in \mathbb {R}^3,\,g_2(x(t-\tau (t)))=\big (0, 0, -\beta \varrho \sin (vx_1(t-\tau (t)))\big )^{\top }$ $\in \mathbb {R}^3$,

$$\begin{aligned} A=\left[ \begin{array}{ccc} -\alpha (1+m_2)&{}\quad \alpha &{}\quad 0\\ 1 &{}\quad -1 &{}\quad 1\\ 0 &{}\quad -\beta &{}\quad - \omega \end{array} \right] , \end{aligned}$$

(30)

and $\alpha =10,\,\beta =19.53,\,\omega =0.1636,\,m_1 =-1.4325,\,m_2=-0.7831,\,v=0.5,\,\varrho =0.2$, and $\tau (t)=0.02$. Figure 1 shows the chaotic attractor of the time-delayed Chua oscillator (29). It is easy to check that

$$\begin{aligned}&\!\!\!\!\Big (x(t)-y(t)\Big )^{\top }\Big (f(t,x(t),x(t-\tau (t)))\nonumber \\&\!\!\!\!\qquad -\,f(t,y(t),y(t-\tau (t))) \Big )\nonumber \\&\!\!\!\!\quad \le \frac{1}{2} \Big (x(t)-y(t)\Big )^{\top }(A+A^{\top })\Big (x(t)-y(t)\Big )\nonumber \\&\!\!\!\!\qquad +\,|\alpha (m_1-m_2)|\Big (x_{1}(t)-y_1(t)\Big )^2\nonumber \\&\!\!\!\!\qquad +\,\beta \varrho v|x_{3}(t)-y_3(t)||x_{1}(t-\tau (t))-y_1(t-\tau (t))|\nonumber \\&\!\!\!\!\quad \le \lambda _{\max }(\tilde{A})\Big (x(t)-y(t)\Big )^{\top }\Big (x(t)-y(t)\Big )\nonumber \\&\!\!\!\!\qquad +\,(\beta \varrho v)/(2 \omega )\Big (x(t-\tau (t))\nonumber \\&\!\!\!\!\qquad -\,y(t-\tau (t))\Big )^{\top }\Big (x(t-\tau (t))\nonumber \\&\!\!\!\!\qquad -\,y(t-\tau (t))\Big )\nonumber \\&\!\!\!\!\quad = L_1\Big (x(t)-y(t)\Big )^{\top }\Big (x(t)-y(t)\Big )\nonumber \\&\!\!\!\!\qquad +\,L_2\Big (x(t-\tau (t))-y(t-\tau (t))\Big )^{\top }\Big (x(t\nonumber \\&\!\!\!\!\qquad -\,\tau (t))-y(t-\tau (t))\Big ). \end{aligned}$$

where $\tilde{A}=\Big ((A+A^{\top })/{2}+\mathrm{diag}\big (|\alpha (m_1-m_2)|,0,\omega$ $({\beta \, \varrho \, v})/2\big )\Big ),\,L_1=\lambda _{\max }(\tilde{A}),\,L_2=(\beta \varrho v)/(2 \omega )$, and $\omega$ is a positive constant. Thus, the condition of Assumption 1 is satisfied.

Fig. 1

Chaotic attractor of the time-delayed Chua oscillator (29) with initial conditions $x_1(0)=0.5$, $x_2(0)=0.1$, $x_3(0)=1.2$

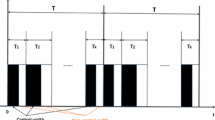
For most real-world impulsive signals, the occurrence of impulses is not uniformly distributed. In the following, we consider a special nonuniformly distributed impulsive signal $\overline{\zeta }=\{t_1,t_2,t_3,\ldots \}$ described by [10]

$$\begin{aligned}&\!\!\!\!t_k-t_{k-1}\nonumber \\&\!\!\!\!\quad =\left\{ \begin{array}{ll} \epsilon _0, &{}\quad \mathrm{if}\; \mathrm{mod} (k,N_0)\ne 0,\\ N_0(T_\mathrm{a}-\epsilon _0)+\epsilon _0, &{}\quad \mathrm{if}\; \mathrm{mod} (k,N_0)= 0, \end{array} \right. \end{aligned}$$

(31)

where $\epsilon _0$ and $T_\mathrm{a}$ are positive numbers satisfy $\epsilon _0<T_\mathrm{a}$, and $N_0$ is a positive integer. It follows from Definition 2 that the average impulsive interval of impulsive signal $\overline{\zeta }$ in (31) is equal to $(T_\mathrm{a}, N_0)$. From the structure of the impulsive signal $\overline{\zeta }$, we can obtain that $\inf _{k\in Z^+}\{t_k-t_{k-1} \} =\epsilon _0$ and $\sup _{k\in Z^+}\{t_k-t_{k-1} \} =N_0(T_\mathrm{a}-\epsilon _0)+\epsilon _0$. When $\epsilon _0$ is small and $N_0$ is large, the quantity $\inf _{k\in Z^+}\{t_k-t_{k-1} \} =\epsilon _0$ will be small, and the quantity $\sup _{k\in Z^+}\{t_k-t_{k-1} \} =N_0(T_\mathrm{a}-\epsilon _0)+\epsilon _0$ will be large. In such case, the results in [11–20] may not be applicable.

Example 1

In this example, we consider a nearest-neighbor unidirectional coupled delayed dynamical network (3) with synchronizing impulses. The coupling matrix $B$ of this network is of the form

$$\begin{aligned} B=\left( \begin{array}{ccccc} -1 &{}\quad 1 &{}\quad 0 &{}\quad \cdots &{}\quad 0 \\ 0 &{}\quad -1 &{}\quad 1 &{}\quad \cdots &{}\quad 0\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \vdots \\ 0 &{}\quad \cdots &{} 0 &{} -1 &{} 1\\ 1&{}\quad 0 &{}\quad \cdots &{}\quad 0 &{}\quad -1 \end{array}\right) _{N\times N}. \end{aligned}$$

Clearly, the coupling matrix $B$ is an asymmetrical Laplacian matrix of a weighted graph with a spanning tree. In this simulation, choosing $N$=100, then one has $\tilde{\lambda }_2=-0.0039$ and $\max _{1\le k\le N} \delta _k=0$. Let the coupling strength $c=5$, and the inner coupling matrix $\varGamma =I_3$. By simple calculation, one can obtain that $r\lambda (r)=-0.0195$.

Let the synchronizing impulsive strengths $d_k\equiv d_0=-0.30,\,k\in Z^+$, and the impulsive signal $\overline{\zeta }$ satisfy (31) with average impulsive interval $T_\mathrm{a}=0.02,\,\epsilon _0=0.005$, and $N_0=4$. Select $\omega =10$, one has $L_1=15.7098$ and $L_2=0.0977$. Then, we can obtain that $\varpi =-0.8779$. According to Corollary 1, it can be concluded that the delayed dynamical network with synchronizing impulses is globally exponentially synchronized. Figure 2 shows the synchronizing impulses sequence, and Fig. 3 visualizes the change process of the sate variables of the nearest-neighbor unidirectional coupled delayed dynamical network with impulsive strength $d_0=0$, which clearly shows desynchronization of the underlying delayed dynamical network without impulses. Error trajectories of the nearest-neighbor unidirectional coupled delayed dynamical network with synchronizing impulses $d_0=-0.30$ are plotted in Fig. 4. We can see that the network achieves quickly synchronization under the synchronizing impulses.

Fig. 2

Synchronizing impulsive sequence with $T_\mathrm{a}=0.02,\,\epsilon _0=0.005,\,N_0=4$, and $d_0=-0.30$ in time interval [0  1]

Fig. 3

Change process of the sate variables of the nearest-neighbor unidirectional coupled delayed dynamical network with impulsive strength $d_0=0$ in time interval [0  100]

Fig. 4

Error trajectories of the nearest-neighbor unidirectional coupled delayed dynamical network with synchronizing impulses $d_0=-0.30$ in time interval [0  1]

For the impulsive signal shown in Fig. 2, the upper bound of the impulsive interval is 0.0650. If we use $\sup _{k\in Z^+}\{t_k-t_{k-1} \}=0.0650$ instead of $T_\mathrm{a}$, then we get $\varpi _{\sup }=23.8150$, and so inequality (25) is not satisfied. Hence, for this example, inequality (25) fails to judge whether the impulsive-delayed dynamical network can be synchronized if $\sup _{k\in Z^+}\{t_k-t_{k-1} \}$ is utilized. Consequently, condition (ii) is less conservative than the results in [11–17], which are obtained by using $\sup _{k\in Z^+}\{t_k-t_{k-1}\}$.

Example 2

A BA scale-free [35] coupled delayed dynamical network (3) with desynchronizing impulses is taken as the second example. The parameters of the BA model are given by $m_0=m=4$ and $N=100$. In this simulation, one obtains that $\tilde{\lambda }_2=-4.5003$ and $\max _{1\le k\le N} \delta _k=0$. Let the coupling strength $c=6$ and the inner coupling matrix $\varGamma =I_3$. Select $\omega =1$, one has $L_1=11.3931$ and $L_2=0.9765$. Then, $2L_1+r\lambda (r)+2L_2= -2.2624<0$, that is, $-p>q> 0$. Thus, the underlying delayed dynamical network without impulses is globally exponentially synchronized itself in this example, as shown in Fig. 5.

Fig. 5

Change process of the sate variables of the scale-free coupled delayed dynamical network without impulses in time interval [0  50]

Let the desynchronizing impulsive strengths $d_k\equiv d_0=0.10,\,k\in Z^+$, and the impulsive signal $\overline{\zeta }$ satisfy (31) with average impulsive interval $T_\mathrm{a}=0.03,\,\epsilon =0.025$, and $N_0=3$. Then, one has $\varpi ^*=-0.1203$. By Corollary 2, globally exponential synchronization of the scale-free coupled delayed dynamical network with the desynchronizing impulses is maintained. Figure 6 depicts the desynchronizing impulsive sequence, and corresponding trajectories of the impulsive-delayed dynamical network are displayed in Fig. 7.

Fig. 6

Desynchronizing impulsive sequence with $T_\mathrm{a}=0.30$, $\epsilon _0=0.025$, $N_0=3$, and $d_0=0.1$ in time interval [0  5]

Fig. 7

Synchronization of the scale-free coupled delayed dynamical network with desynchronizing impulses $d_0=0.10$ in time interval [0  5]

For the impulsive signal shown in Fig. 6, the lower bound of the impulsive interval is 0.025. If we utilize $\inf _{k\in Z^+}\{t_k-t_{k-1} \}=0.025$ instead of $T_\mathrm{a}$, then $\varpi ^*_{\inf }=6.8691$, and so inequality (27) is not satisfied. Hence, inequality (27) fails to judge whether the impulsive delayed dynamical network can maintain globally exponential synchronization if $\inf _{k\in Z^+}\{t_k-t_{k-1} \}$ is used. Consequently, condition (iv) is less conservative than the results in [18–20], which are derived by utilizing $\inf _{k\in Z^+}\{t_k-t_{k-1} \}$.

4.2 The example of application

In the following, we provide one example to show some potential real-world application of our theoretical results.

As we know now, many real-world complex networks contain several significantly recurring nontrivial patterns of interconnections, termed network motifs [40, 41]. Network motifs were suggested to be elementary building blocks that carry out key functions in the networks [40, 41]. As typical network motifs, the feed-forward loops (FFLs) have been intensively investigated in various fields over the last decade [41, 42]. The FFLs, depending on the nature of the regulating interactions, can be of eight different types which can again be classified into two categories: coherent FFLs (CFFLs) and incoherent FFLs (ICFFLs) [41]. Moreover, extensive research shows most biological networks are complex networks with scale-free characteristic [43, 44]. Therefore, we take FFLs as basic elements to synthesize a complex network, and consider a BA scale-free [35] coupled genetic networks consisting of $N$ FFLs motifs. In this subsection, we just discuss the type-1 CFFL with SUM logic [41], other types of FFLs with different logics can be similarly analyzed. A typical mathematical model of the type-1 CFFL with SUM logic is described by [41, 42]

$$\begin{aligned} \dot{x}(t)=f(t,x(t))=Ax(t)+g_1(x(t)), \end{aligned}$$

(32)

where $x(t)=(x_{1}(t),x_{2}(t),x_{3}(t))^{\top }\in \mathbb {R}^3,\,A=\mathrm{diag}\big (\beta _1,\beta _2,\beta _3\big ),\,g_1(x(t))=\big (\alpha _1 x_1, \alpha _2 x_1^n/(K_1^n+x_1^n),$ $\alpha _3 x_1^n/(K_2^n+x_1^n)+\alpha _4 x_2^n/(K_3^n+x_2^n)\big )^{\top }\in \mathbb {R}^3$. The parameters $\beta _1=-0.2,\,\beta _2=-0.05,\,\beta _3=-0.07,\,\alpha _1 =0.2,\,\alpha _2=0.9,\,\alpha _3=1.2,\,\alpha _4=1.2,\,K_1 =10,\,K_2=20,\,K_3=10$, and $n=2$. The biological meaning of these parameters can be founded in [41, 42]. By using mean value theorem [45], Assumption 1 is obviously satisfied with $L_1=0.0375$ and $L_2=0$. In this example, the parameters of the BA model are given by $m_0=m=3$ and $N=100$, then we get $\tilde{\lambda }_2=-2.8634$ and $\max _{1\le k\le N} \delta _k=0$. Let the coupling strength $c=1$ and the inner coupling matrix $\varGamma =I_3$. Through simple calculation, one can obtain that $2L_1+r\lambda (r)+2L_2= -2.7884<0$. Hence, the scale-free coupled genetic networks are globally exponentially synchronized, as indicated in Fig. 8.

Fig. 8

Trajectories of the state variables of the scale-free coupled genetic networks in time interval [0  20]

Since the states of biological networks often exhibit impulsive effects [9, 10, 21], we consider the scale-free coupled genetic networks with desynchronizing impulses. Let the desynchronizing impulsive strengths $d_k\equiv d_0=0.10,\,k\in Z^+$, and the impulsive signal $\overline{\zeta }$ satisfy (31) with average impulsive interval $T_\mathrm{a}=0.2,\,\epsilon =0.05$, and $N_0=3$, as depicted in Fig. 9. Then, one has $\varpi ^*=-1.0853$. By Corollary 2, globally exponential synchronization of the scale-free coupled genetic networks with the desynchronizing impulses is preserved, as shown in Fig. 10. The synchronization of genetic networks is essential for the understanding of living organisms at both molecular and cellular levels [45]. Our result shows that under some impulsive disturbances the synchronization of genetic networks can be preserved . It sheds some light on the potential real-world applications of our theoretical results.

Fig. 9

Desynchronizing impulsive sequence with $T_\mathrm{a}=0.20$, $\epsilon _0=0.05$, $N_0=3$, and $d_0=0.1$ in time interval [0  4]

Fig. 10

Synchronization of the scale-free coupled genetic networks with desynchronizing impulses $d_0=0.10$ in time interval [0  4]

5 Conclusion and future research issues

In this paper, a detailed analysis has been carried out for the synchronization of directed complex networks with time-varying delays dynamical nodes and impulsive effects. Two types of impulses occurred in the states of nodes have been discussed. Without assuming symmetry and irreducibility of coupling structure, some globally exponential synchronization criteria for general impulsive- delayed dynamical networks with weakly connected topology have been established for each type of impulses by using the concept of average impulsive interval and the comparison principle. The derived results not only can provide an effective impulsive control strategy to synchronize an arbitrary given delayed dynamical network even if the original network may be asynchronous itself but also indicate that under which impulsive perturbations globally exponential synchronization of the underlying delayed dynamical networks can be preserved. Numerical examples and their simulations have been given to verify the effectiveness of the theoretical results. According to theoretical analysis and numerical examples, our results have been proved to be less conservative.

Recently, the consensus problem for multi-agent systems has attracted much attention due to its extensive applications in real-world distributed computation, rendezvous tasks, flocking, swarming, biological systems, sensor networks, and so on [36–39]. For example, in [38], the flocking of multi-agent nonholonomic systems with proximity graphs was studied. In [39], the consensus of a discrete-time multi-agent system with transmission nonlinearity and time-varying delays was investigated. As the authors of [36] pointed out, the topic of synchronization of coupled nonlinear oscillators is closely related to the consensus of multi-agent systems. Hence, it would be of great interest to extend the recent results of consensus in [38, 39] to the case of synchronization discussed in this paper. Moreover, it is worth mentioning that applying the analysis method presented in this paper to the synchronization problem of complex-switched dynamical networks with impulsive effects also presents an interesting and important topic for future research.