Bifurcation and chaos analysis of multistage planetary gear train

Abstract

A nonlinear time-varying dynamic model for a multistage planetary gear train, considering time-varying meshing stiffness, nonlinear error excitation, and piece-wise backlash nonlinearities, is formulated. Varying dynamic motions are obtained by solving the dimensionless equations of motion in general coordinates by using the varying-step Gill numerical integration method. The influences of damping coefficient, excitation frequency, and backlash on bifurcation and chaos properties of the system are analyzed through dynamic bifurcation diagram, time history, phase trajectory, Poincaré map, and power spectrum. It shows that the multi-stage planetary gear train system has various inner nonlinear dynamic behaviors because of the coupling of gear backlash and time-varying meshing stiffness. As the damping coefficient increases, the dynamic behavior of the system transits to an increasingly stable periodic motion, which demonstrates that a higher damping coefficient can suppress a nonperiodic motion and thereby improve its dynamic response. The motion state of the system changes into chaos in different ways of period doubling bifurcation, and Hopf bifurcation.

1 Introduction

Multistage planetary gear trains are widely used in various applications including automotive transmission, rotorcraft, wind and gas turbine gearboxes, and other industrial power transmission systems, owing to their advantages such as less space requirement, larger transmission ratio, greater load sharing, and providing multiple speed reduction (gear) ratios. Multistage planetary trains consist of a number of single-stage planetary gear sets whose central members are connected according to a given power flow configuration. Input, output, and a fixed (stationary) member are assigned to certain central members to achieve a given gear ratio.

Most of the published planetary gear train dynamic models were limited to single-stage planetary gear sets. Early models were of linear time-invariant type, and the eigen solutions and model summation techniques were used to predict the natural modes and the forced responses [1–4]. The gear systems in the advanced mechanical systems often undergo startups and brakes interactively or run at high speed and under light load. Current studies have shown that it would be likely for a gear to lose contact and the tooth separations to occur due to the unavoidable backlash. Moreover, experimental and theoretical studies on varying-form gear trains dynamics [5–7] clearly indicate that the gear trains should be modeled as nonlinear systems including periodically varying parameters and backlash. In recent years, the research on nonlinear dynamic of planetary gear sets has been developed. Al-shyyab and Kahraman [8] developed a torsional single-stage nonlinear dynamic model of a simple planetary gear set and provided a semi-analytical forced response solution by using the multiterm harmonic balance method (HBM). They also showed that these HBM solutions matched well with the numerical integration (NI) and deformable body finite-element-based solutions. Tao and Yan [9] investigated the frequency response of nonlinear planetary set with multiple clearances by means of a single-term HBM focusing on a single power flow configuration in which the ring gear was held stationary. Parker et al. [10] employed a unique finite element-contact analysis method to simulate the nonlinear dynamics of a spur gear system and verified the numerical predictions experimentally. Studies on the bifurcation and chaos characteristics of the gear systems started more than ten years ago. In 2001, Vaishya and Singh [11] used a sliding friction method to simulate the nonlinear dynamics of a gear system in order to obtain insights into the relative effects of sliding friction and mesh damping, respectively. Litak and Friswell [12] examined the effect of adding an additional degree of freedom to a simple model of gear vibration and presented the evolution of attractor Poincaré sections with respect to the shaft stiffness showing a number of chaotic and regular attractors. They [13] also examined the dynamics of gear systems with various faults in meshing stiffness, and the analysis of various types of errors and tooth faults highlights the presence of dynamic jumping phenomenon. Such jumps between different types of motions, namely chaotic and regular, can be crucial for the system reliability. Recently, Chang-Jian and Chen [14–17] presented a series of investigations on nonperiodic and chaotic responses of flexible rotors supported by various bearings. The results provided a useful source of reference for engineers in specifying suitable operating parameters to prevent an undesirable motion of the rotor and therefore to reduce the vibrations within the rotor-bearing system. The nonlinear dynamics of a multistage planetary compared with a single-stage one is much more complicated, and the related published papers are very limited. Al-shyyab [18] built a nonlinear, torsional dynamic model of a multistage planetary train. A case study of a two-stage planetary train was used to demonstrate the effectiveness of the model and multiterm HBM solution methods. The nonlinear dynamic behaviors and bifurcation and chaos characteristics of a multistage planetary train need further research.

This study establishes a nonlinear dynamic model of a two-stage planetary gear train. This model includes time-varying meshing stiffness, nonlinear error excitation, and piece-wise backlash nonlinearities. Equations of motion in general coordinates are obtained in a matrix form and solved by using the varying-step Gill numerical integration method. The nonlinear dynamic behavior of the two-stage planetary gear train is analyzed as a function of the damping coefficient, the dimensionless excitation frequency, and the dimensionless backlash. The bifurcation and chaos traits of the system are illustrated by calculating dynamic bifurcation diagrams, time histories, phase trajectories, Poincaré maps, and power spectra.

2 Dynamic model

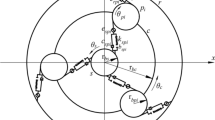
A schematic of a two-stage compound planetary gear train is shown in Fig. 1. The system consists of two single-stage 2K-H type planetary gear trains in series. A particular stage n (n=1,2) is comprised of four elements, the sun gear s ⁽ⁿ⁾, the ring gear r ⁽ⁿ⁾, the carrier c ⁽ⁿ⁾, and several planet gears $p^{(n)}_{i}$ ($N^{(n)}_{p}$ is the number of the planet gears of stage n, and $N^{(1)}_{p} = 3, N^{(2)}_{p} = 4$). The ring gear of each stage is a part of the gearbox, thus, its displacement is insignificant, and the center of ring gear is assumed to be stationary. In each stage, the central component sun gear and carrier are identified as input and output members of the gear train. The planet gears of each stage are free to rotate with respect to the carrier. All the gears are mounted on their flexile shafts supported by rolling element bearings. T _in and T _out are representatives of input and output torques. The torsional spring stiffnesses K ^(1,2) represents the coupling between the central member carrier of stage 1 and the central member sun gear of stage 2.

Fig. 1

Structure diagram of two-stage planetary gear train

To establish the mathematical model of the system, a number of assumptions are employed as follows:

• 1. Each gear body is assumed to be rigid, and the flexibilities of the gear teeth at each gear mesh interface are modeled by a spring with periodically time-varying stiffness acting along the gear line of action. This mesh stiffness is subject to a clearance element representing gear backlash.

• 2. Each gear and the planet carrier are assumed to move in the torsional direction only.

• 3. Each planet gear on the planet carrier distributes uniformly with the same parameters.

• 4. Gears and carriers are considered to be free of any eccentricities or run-out, roundness errors, and meshing friction on tooth surface.

The torsional dynamic model of the planetary gear train of stage n is shown in Fig. 2. The central elements s, r, and c are constrained by torsional linear springs of stiffness magnitudes $k_{st}^{(n)}$, $k_{rt}^{(n)}$, and $k_{ct}^{(n)}$, respectively. The magnitudes of these stiffness constraints can be chosen according to simulated different power flow arrangements with different fixed central members. A particular central member is held stationary by assigning a very large constraint stiffness value to it. Likewise, a zero value for the constraint stiffness indicates that this central member is not connected to the gearbox. Each gear body $j\ (j = s^{(n)},p_{i}^{(n)},c^{(n)},r^{(n)},i = 1,2,\ldots,N_{p}^{(n)},n = 1,2)$ is modeled as a rigid disc of polar mass moment of inertia $I_{j}^{(n)}$, base radius $r_{\mathrm{b}j}^{(n)}$, and angular displacement $\theta_{j}^{(n)}$. Here, $\theta_{j}^{(n)}$ is the nominal rigid body rotation of the gear. External torques $T_{j}^{(n)}\ (j = s^{(n)},c^{(n)},r^{(n)},n = 1,2)$ are applied to the central members that are identified as the input and the output members of the gear train.

Fig. 2

Dynamics model of multistage planetary gear train

The mesh of gear j (s or r) with a planet p _i is represented by a periodically time-varying stiffness element $k_{jpi}^{(n)}$ subjected to a piecewise-linear backlash function $g_{jpi}^{(n)}$ that includes a backlash of amplitude $2b_{jpi}^{(n)}$. A periodic displacement function $e_{jpi}^{(n)}$ is applied along the line of action of account for intentional gear tooth profile modifications and deviations because of surface wear and manufacturing errors. The dissipation on the lubricated gear mesh interface is represented by the constant viscous damping $c_{jpi}^{(n)}$. Here, for each stage, $k_{jpi}^{(n)}$, $e_{jpi}^{(n)}$, $b_{jpi}^{(n)}$, $g_{jpi}^{(n)}$, and $c_{jpi}^{(n)}$ are the same for all jpi ⁽ⁿ⁾ meshes, except the phase angles of $k_{jpi}^{(n)}$ and $e_{jpi}^{(n)}$, which differ since that the particular planet phasing condition is considered.

3 Equations of motion

3.1 Equivalent displacements

Regarding the angular displacement $\theta_{j}^{(n)}$ of each gear body in driving $j\ (j = s^{(n)},p_{i}^{(n)},c^{(n)},r^{(n)},i = 1,2,\ldots,N_{p}^{(n)},n = 1,2)$, the direction of the revolution caused by the driving torque is assumed to be positive. The equivalent gear mesh displacements $u_{j}^{(n)}$ in the pressure line direction are defined as

$$ \begin{aligned} &u_{\mathrm{s}}^{(n)} = r_{\mathrm{bs}}^{(n)} \theta_{\mathrm{s}}^{(n)},\qquad u_{\mathrm{p}i}^{(n)} = r_{\mathrm{bp}i}^{(n)}\theta_{\mathrm{p}i}^{(n)}, \\ & u_{\mathrm{r}}^{(n)} = r_{\mathrm{br}}^{(n)} \theta_{\mathrm{r}}^{(n)}, \qquad u_{\mathrm{c}}^{(n)} = r_{\mathrm{bc}}^{(n)}\theta_{\mathrm{c}}^{(n)}, \end{aligned} $$

(1)

where $r_{\mathrm{b}j}^{(n)}(j = s,pi,r)$ are the base circle radii of gears, and $r_{\mathrm{bc}}^{(n)}$ is the nominal base circle radius of the carrier defined as $r_{\mathrm{bc}}^{(n)} = r_{\mathrm{bs}}^{(n)} + r_{\mathrm{bp}i}^{(n)}$.

According to the meshing relation, the relative gear mesh displacements $x_{jpi}^{(n)}(j = s,r)$ in the direction of the pressure line of stage n are expressed as

$$ \left \{ \begin{array}{l} x_{\mathrm{sp}i}^{(n)} = u_{\mathrm{s}}^{(n)} - u_{\mathrm{p}i}^{(n)} - u_{\mathrm{c}}^{(n)} - e_{\mathrm{sp}i}^{(n)} \\ x_{\mathrm{rp}i}^{(n)} = u_{\mathrm{p}i}^{(n)} - u_{\mathrm{c}}^{(n)} - u_{\mathrm{r}}^{(n)} - e_{\mathrm{rp}i}^{(n)} \end{array} \right .. $$

(2)

It should be pointed out that the angular displacement of the ring gear r in the two-stage compound planetary gear train as shown in Fig. 1 is set to be zero because the ring gear is fixed on gearbox, that is, $\theta_{\mathrm{r}}^{(n)} = 0$.

The relative displacement $x_{\mathrm{cs}}^{(1,2)}$ between the output member carrier c of stage 1 and input member sun gear s of stage 2 is defined as

$$ x_{\mathrm{cs}}^{(1,2)} = u_{\mathrm{c}}^{(1)} - u_{\mathrm{s}}^{(2)}. $$

(3)

3.2 Excitations of the system

The mesh cycle of each gear pair in the same stage is identical because of the continuous rotation of the planetary gear train. As the ring gear of each stage is fixed on the gearbox, according to the transmission of the planetary gear, the meshing frequency of stage n can be derived as

$$ \omega_{m}^{(n)} = \frac{\omega_{\mathrm{s}}^{(n)}Z_{\mathrm{s}}^{(n)}Z_{\mathrm{r}}^{(n)}}{Z_{\mathrm{s}}^{(n)} + Z_{\mathrm{r}}^{(n)}} = \omega_{\mathrm{c}}^{(n)}Z_{\mathrm{r}}^{(n)}, $$

(4)

where $\omega_{m}^{(n)}$ is the meshing frequency of stage-n, $\omega_{\mathrm{s}}^{(n)}$ and $\omega_{\mathrm{c}}^{(n)}$ are the rotational frequency of the sun gear and the carrier in stage n, respectively, and $Z_{\mathrm{s}}^{(n)}$ and $Z_{\mathrm{r}}^{(n)}$ are the numbers of teeth of the sun gear and the ring gear in stage n, respectively.

The nonlinear time-varying meshing stiffness $k_{jpi}^{(n)}$(j=s,r) of stage n can be represented as a rectangular wave with a fundamental time period [19]. They can be written in the form of Fourier series

$$ k_{jpi}^{(n)} = k_{mjpi}^{(n)} + k_{ajpi}^{(n)}\cos \bigl(\omega_{m}^{(n)}t + \varphi_{kjpi}^{(n)}\bigr), $$

(5)

where $k_{mjpi}^{(n)}$, $k_{aspi}^{(n)}$, and $\varphi_{kjpi}^{(n)}(j = s,r)$ are the average amplitude, the varying amplitude, and the initial phase angle of the jpi ⁽ⁿ⁾ meshing stiffness in stage n, respectively.

The periodic meshing error function $e_{jpi}^{(n)}(j = s,r)$ of stage n can be simplified in the sine function form [20] as

$$ e_{jpi}^{(n)} = E_{jpi}^{(n)}\sin \bigl( \omega_{m}^{(n)}t + \varphi_{ejpi}^{(n)}\bigr), $$

(6)

where $E_{jpi}^{(n)},\varphi_{ejpi}^{(n)}\ (j = s,r)$ are the amplitude and the initial phase angle of comprehensive meshing error in stage n, respectively.

The piecewise-linear backlash functions $g_{jpi}^{(n)}(j = s,r)$ of stage n are defined as

$$ g\bigl(x_{l}^{(n)}\bigr) = \left \{ \begin{array}{l@{\quad }l} x_{l}^{(n)} - b_{l}^{(n)}& x_{l}^{(n)} > b_{l}^{(n)} \\ 0 & \vert x_{l}^{(n)} \vert \le b_{l}^{(n)} \\ x_{l}^{(n)} + b_{l}^{(n)}& x_{l}^{(n)} < - b_{l}^{(n)} \end{array} \right ., $$

(7)

where $2b_{l}^{(n)}(l = spi,rpi)$ is the gear backlash in stage n.

3.3 Dynamic equations of the system

The equations of motion for the two-stage compound planetary gear train shown in Fig. 1 can be established by using the Lagrange principle as

$$\begin{aligned} &I_{\mathrm{s}}^{(1)}\ddot{\theta}_{\mathrm{s}}^{(1)} + \sum _{i = 1}^{N_{1}} c_{\mathrm{sp}i}^{(1)}r_{\mathrm{bs}}^{(1)} \dot{x}_{\mathrm{sp}i}^{(1)} + \sum_{i = 1}^{N_{1}} k_{\mathrm{sp}i}^{(1)}r_{\mathrm{bs}}^{(1)}g \bigl(x_{\mathrm{sp}i}^{(1)} \bigr) \\ &\quad = T_{\mathrm{s}}^{(1)}, \end{aligned}$$

(8a)

$$\begin{aligned} &\begin{aligned}[b] &I_{\mathrm{p}i}^{(1)}\ddot{\theta}_{\mathrm{p}i}^{(1)} - c_{\mathrm{sp}i}^{(1)}r_{\mathrm{bp}i}^{(1)} \dot{x}_{\mathrm{sp}i}^{(1)} + c_{\mathrm{rp}i}^{(1)}r_{\mathrm{bp}i}^{(1)} \dot{x}_{\mathrm{rp}i}^{(1)} \\ &\quad - k_{\mathrm{sp}i}^{(1)}r_{\mathrm{bp}i}^{(1)}g \bigl(x_{\mathrm{sp}i}^{(1)} \bigr) + k_{\mathrm{rp}i}^{(1)}r_{\mathrm{bp}i}^{(1)}g \bigl(x_{\mathrm{rp}i}^{(1)} \bigr) = 0, \end{aligned} \end{aligned}$$

(8b)

$$\begin{aligned} &\begin{aligned}[b] & I_{\mathrm{ce}}^{(1)}\ddot{\theta}_{\mathrm{c}}^{(1)} - \sum_{i = 1}^{N_{1}} c_{\mathrm{sp}i}^{(1)}r_{\mathrm{bc}}^{(1)} \dot{x}_{\mathrm{sp}i}^{(1)} - \sum_{i = 1}^{N_{1}} c_{\mathrm{rp}i}^{(1)}r_{\mathrm{bc}}^{(1)}\dot{x}_{\mathrm{rp}i}^{(1)} \\ &\quad - \sum_{i = 1}^{N_{1}} k_{\mathrm{sp}i}^{(1)}r_{\mathrm{bc}}^{(1)}g \bigl(x_{\mathrm{sp}i}^{(1)}\bigr) - \sum_{i = 1}^{N_{1}} k_{\mathrm{rp}i}^{(1)}r_{\mathrm{bc}}^{(1)}g \bigl(x_{\mathrm{rp}i}^{(1)}\bigr) \\ &\quad + K^{(1,2)}r_{\mathrm{bc}}^{(1)} \bigl[ u_{\mathrm{c}}^{(1)} - u_{\mathrm{s}}^{(2)} \bigr] = - T_{\mathrm{c}}^{(1)} , \end{aligned} \end{aligned}$$

(8c)

$$\begin{aligned} &\begin{aligned}[b] &I_{\mathrm{s}}^{(2)}\ddot{\theta}_{\mathrm{s}}^{(2)} + \sum_{i = 1}^{N_{2}} c_{\mathrm{sp}i}^{(2)}r_{\mathrm{bs}}^{(2)} \dot{x}_{\mathrm{sp}i}^{(2)} + \sum_{i = 1}^{N_{2}} k_{\mathrm{sp}i}^{(2)}r_{\mathrm{bs}}^{(2)}g \bigl(x_{\mathrm{sp}i}^{(2)} \bigr) \\ &\quad - K^{(1,2)}r_{\mathrm{bs}}^{(2)} \bigl[ u_{\mathrm{c}}^{(1)} - u_{\mathrm{s}}^{(2)} \bigr] = T_{\mathrm{s}}^{(2)}, \end{aligned} \end{aligned}$$

(8d)

$$\begin{aligned} &\begin{aligned}[b] &I_{\mathrm{p}i}^{(2)}\ddot{\theta}_{\mathrm{p}i}^{(2)} - c_{\mathrm{sp}i}^{(2)}r_{\mathrm{bp}i}^{(2)} \dot{x}_{\mathrm{sp}i}^{(2)} + c_{\mathrm{rp}i}^{(2)}r_{\mathrm{bp}i}^{(2)} \dot{x}_{\mathrm{rp}i}^{(2)} \\ &\quad - k_{\mathrm{sp}i}^{(2)}r_{\mathrm{bp}i}^{(2)}g \bigl(x_{\mathrm{sp}i}^{(2)} \bigr) + k_{\mathrm{rp}i}^{(2)}r_{\mathrm{bp}i}^{(2)}g \bigl(x_{\mathrm{rp}i}^{(2)} \bigr) = 0, \end{aligned} \end{aligned}$$

(8e)

$$\begin{aligned} &\begin{aligned}[b] &I_{\mathrm{ce}}^{(2)}\ddot{\theta}_{\mathrm{c}}^{(2)} - \sum_{i = 1}^{N_{2}} c_{\mathrm{sp}i}^{(2)}r_{\mathrm{bc}}^{(2)} \dot{x}_{\mathrm{sp}i}^{(2)} - \sum_{i = 1}^{N_{2}} c_{\mathrm{rp}i}^{(2)}r_{\mathrm{bc}}^{(2)}\dot{x}_{\mathrm{rp}i}^{(2)} \\ &\qquad - \sum_{i = 1}^{N_{2}} k_{\mathrm{sp}i}^{(2)}r_{\mathrm{bc}}^{(2)}g \bigl(x_{\mathrm{sp}i}^{(2)} \bigr) - \sum_{i = 1}^{N_{2}} k_{\mathrm{rp}i}^{(2)}r_{\mathrm{bc}}^{(2)}g \bigl(x_{\mathrm{rp}i}^{(2)} \bigr) \\ &\quad = - T_{\mathrm{c}}^{(2)}, \end{aligned} \end{aligned}$$

(8f)

where $I_{\mathrm{ce}}^{(n)} = I_{\mathrm{c}}^{(n)} + \sum_{i = 1}^{N_{p}^{(n)}} m_{\mathrm{p}i}^{(n)}[r_{\mathrm{c}}^{(n)}]^{2}$ is the equivalent mass moment of inertia of the carrier assembly of stage n, $m_{\mathrm{p}i}^{(n)}$ is the mass of the planet $p_{i}^{(n)}$, and $r_{\mathrm{c}}^{(n)}$ is the radius of the carrier in stage n.

The dynamic model derived above is a semi-definite system. It can be changed into a definite system by using the equivalent relative displacements defined in Eqs. (2) and (3). New general coordinates q are introduced in order to eliminate the rigid body movement in Eqs. (8a)–(8f) as

$$\begin{aligned} \boldsymbol{q} = \bigl\{& x_{\mathrm{sp}1}^{(1)},x_{\mathrm{sp}2}^{(1)},x_{\mathrm{sp}3}^{(1)},x_{\mathrm{rp}1}^{(1)},x_{\mathrm{rp}2}^{(1)},x_{\mathrm{rp}3}^{(1)}, x_{\mathrm{sp}1}^{(2)},x_{\mathrm{sp}2}^{(2)}, \\ &x_{\mathrm{sp}3}^{(2)},x_{\mathrm{sp}4}^{(2)},x_{\mathrm{rp}1}^{(2)},x_{\mathrm{rp}2}^{(2)},x_{\mathrm{rp}3}^{(2)},x_{\mathrm{rp}4}^{(2)},x_{\mathrm{cs}}^{(1,2)} \bigr\}^{\mathrm{T}}. \end{aligned}$$

(9)

The equations of motion in the general coordinates q can be derived as

$$\begin{aligned} & \ddot{x}_{\mathrm{sp}i}^{(1)} + \biggl( \frac{1}{M_{\mathrm{s}}^{(1)}} + \frac{1}{M_{\mathrm{c}}^{(1)}}\biggr)\sum_{i = 1}^{N_{1}} c_{\mathrm{sp}i}^{(1)}\dot{x}_{\mathrm{sp}i}^{(1)} \\ &\qquad + \biggl( \frac{1}{M_{\mathrm{s}}^{(1)}} + \frac{1}{M_{\mathrm{c}}^{(1)}}\biggr)\sum_{i = 1}^{N_{1}} k_{\mathrm{sp}i}^{(1)}g\bigl(x_{\mathrm{sp}i}^{(1)}\bigr) \\ &\quad + \frac{1}{M_{\mathrm{p}i}^{(1)}}c_{\mathrm{sp}i}^{(1)}\dot{x}_{\mathrm{sp}i}^{(1)} + \frac{1}{M_{\mathrm{p}i}^{(1)}}k_{\mathrm{sp}i}^{(1)}g\bigl(x_{\mathrm{sp}i}^{(1)} \bigr) \\ &\qquad - \frac{1}{M_{\mathrm{p}i}^{(1)}}c_{\mathrm{rp}i}^{(1)}\dot{x}_{\mathrm{rp}i}^{(1)} - \frac{1}{M_{\mathrm{p}i}^{(1)}}k_{\mathrm{rp}i}^{(1)}g\bigl(x_{\mathrm{rp}i}^{(1)} \bigr) \\ &\qquad + \frac{1}{M_{\mathrm{c}}^{(1)}}\sum_{i = 1}^{N_{1}} c_{\mathrm{rp}i}^{(1)}\dot{x}_{\mathrm{rp}i}^{(1)} + \frac{1}{M_{\mathrm{c}}^{(1)}} \\ &\qquad \times\sum_{i = 1}^{N_{1}} k_{\mathrm{rp}i}^{(1)}g\bigl(x_{\mathrm{rp}i}^{(1)}\bigr) - \frac{1}{M_{\mathrm{c}}^{(1)}}K^{(1,2)}x_{\mathrm{cs}}^{(1,2)} \\ &\quad = \frac{r_{\mathrm{bs}}^{(1)}}{I_{\mathrm{s}}^{(1)}}T_{\mathrm{s}}^{(1)} + \frac{r_{\mathrm{bc}}^{(1)}}{I_{\mathrm{ce}}^{(1)}}T_{\mathrm{c}}^{(1)} - \ddot{e}_{\mathrm{sp}i}^{(1)}, \end{aligned}$$

(10a)

$$\begin{aligned} &\ddot{x}_{\mathrm{rp}i}^{(1)} - \frac{1}{M_{\mathrm{p}i}^{(1)}}c_{\mathrm{sp}i}^{(1)} \dot{x}_{\mathrm{sp}i}^{(1)} - \frac{1}{M_{\mathrm{p}i}^{(1)}}k_{\mathrm{sp}i}^{(1)}g \bigl(x_{\mathrm{sp}i}^{(1)}\bigr) \\ &\qquad + \frac{1}{M_{\mathrm{p}i}^{(1)}}c_{\mathrm{rp}i}^{(1)} \dot{x}_{\mathrm{rp}i}^{(1)} + \frac{1}{M_{\mathrm{p}i}^{(1)}}k_{\mathrm{rp}i}^{(1)}g \bigl(x_{\mathrm{rp}i}^{(1)}\bigr) + \frac{1}{M_{\mathrm{c}}^{(1)}} \\ &\qquad\times\sum_{i = 1}^{N_{1}} c_{\mathrm{sp}i}^{(1)}\dot{x}_{\mathrm{sp}i}^{(1)} + \frac{1}{M_{\mathrm{c}}^{(1)}}\sum_{i = 1}^{N_{1}} k_{\mathrm{sp}i}^{(1)}g\bigl(x_{\mathrm{sp}i}^{(1)}\bigr) + \frac{1}{M_{\mathrm{c}}^{(1)}} \\ &\qquad \times\sum_{i = 1}^{N_{1}} c_{\mathrm{rp}i}^{(1)}\dot{x}_{\mathrm{rp}i}^{(1)} + \frac{1}{M_{\mathrm{c}}^{(1)}}\sum_{i = 1}^{N_{1}} k_{\mathrm{rp}i}^{(1)}g\bigl(x_{\mathrm{rp}i}^{(1)}\bigr) \\ &\qquad - \frac{1}{M_{\mathrm{c}}^{(1)}}K^{(1,2)}x_{\mathrm{cs}}^{(1,2)} \\ &\quad = \frac{r_{\mathrm{bc}}^{(1)}}{I_{\mathrm{ce}}^{(1)}}T_{\mathrm{c}}^{(1)} - \ddot{e}_{\mathrm{rp}i}^{(1)}, \end{aligned}$$

(10b)

$$\begin{aligned} &\ddot{x}_{\mathrm{sp}i}^{(2)} + \biggl( \frac{1}{M_{\mathrm{s}}^{(2)}} + \frac{1}{M_{\mathrm{c}}^{(2)}}\biggr)\sum_{i = 1}^{N_{2}} c_{\mathrm{sp}i}^{(2)}\dot{x}_{\mathrm{sp}i}^{(2)} \\ &\qquad + \biggl( \frac{1}{M_{\mathrm{s}}^{(2)}} + \frac{1}{M_{\mathrm{c}}^{(2)}}\biggr)\sum_{i = 1}^{N_{2}} k_{\mathrm{sp}i}^{(2)}g\bigl(x_{\mathrm{sp}i}^{(2)}\bigr) \\ &\qquad + \frac{1}{M_{\mathrm{p}i}^{(2)}}c_{\mathrm{sp}i}^{(2)}\dot{x}_{\mathrm{sp}i}^{(2)} + \frac{1}{M_{\mathrm{p}i}^{(2)}}k_{\mathrm{sp}i}^{(2)}g\bigl(x_{\mathrm{sp}i}^{(2)} \bigr) \\ &\qquad - \frac{1}{M_{\mathrm{p}i}^{(2)}}c_{\mathrm{rp}i}^{(2)}\dot{x}_{\mathrm{rp}i}^{(2)} - \frac{1}{M_{\mathrm{p}i}^{(2)}}k_{\mathrm{rp}i}^{(2)}g\bigl(x_{\mathrm{rp}i}^{(2)} \bigr) + \frac{1}{M_{\mathrm{c}}^{(2)}} \\ &\qquad \times\sum_{i = 1}^{N_{2}} c_{\mathrm{rp}i}^{(2)}\dot{x}_{\mathrm{rp}i}^{(2)} + \frac{1}{M_{\mathrm{c}}^{(2)}}\sum_{i = 1}^{N_{2}} k_{\mathrm{rp}i}^{(2)}g\bigl(x_{\mathrm{rp}i}^{(2)}\bigr) \\ &\qquad - \frac{1}{M_{\mathrm{s}}^{(2)}}K^{(1,2)}x_{\mathrm{cs}}^{(1,2)} \\ &\quad = \frac{r_{\mathrm{bs}}^{(2)}}{I_{\mathrm{s}}^{(2)}}T_{\mathrm{s}}^{(2)} + \frac{r_{\mathrm{bc}}^{(2)}}{I_{\mathrm{ce}}^{(2)}}T_{\mathrm{c}}^{(2)} - \ddot{e}_{\mathrm{sp}i}^{(2)}, \end{aligned}$$

(10c)

$$\begin{aligned} &\ddot{x}_{\mathrm{rp}i}^{(2)} - \frac{1}{M_{\mathrm{p}i}^{(2)}}c_{\mathrm{sp}i}^{(2)} \dot{x}_{\mathrm{sp}i}^{(2)} - \frac{1}{M_{\mathrm{p}i}^{(2)}}k_{\mathrm{sp}i}^{(2)}g \bigl(x_{\mathrm{sp}i}^{(2)}\bigr) \\ &\qquad + \frac{1}{M_{\mathrm{p}i}^{(2)}}c_{\mathrm{rp}i}^{(2)} \dot{x}_{\mathrm{rp}i}^{(2)} + \frac{1}{M_{\mathrm{p}i}^{(2)}}k_{\mathrm{rp}i}^{(2)}g \bigl(x_{\mathrm{rp}i}^{(2)}\bigr) \\ &\qquad + \frac{1}{M_{\mathrm{c}}^{(2)}}\sum_{i = 1}^{N_{2}} c_{\mathrm{sp}i}^{(2)}\dot{x}_{\mathrm{sp}i}^{(2)} + \frac{1}{M_{\mathrm{c}}^{(2)}}\sum_{i = 1}^{N_{2}} k_{\mathrm{sp}i}^{(2)}g\bigl(x_{\mathrm{sp}i}^{(2)}\bigr) \\ &\qquad + \frac{1}{M_{\mathrm{c}}^{(2)}}\sum_{i = 1}^{N_{2}} c_{\mathrm{rp}i}^{(2)}\dot{x}_{\mathrm{rp}i}^{(2)} + \frac{1}{M_{\mathrm{c}}^{(2)}}\sum_{i = 1}^{N_{2}} k_{\mathrm{rp}i}^{(2)}g\bigl(x_{\mathrm{rp}i}^{(2)}\bigr) \\ &\quad = \frac{r_{\mathrm{bc}}^{(2)}}{I_{\mathrm{ce}}^{(2)}}T_{\mathrm{c}}^{(2)} - \ddot{e}_{\mathrm{rp}i}^{(2)} , \end{aligned}$$

(10d)

$$\begin{aligned} &\ddot{x}_{\mathrm{cs}}^{(1,2)} - \frac{1}{M_{\mathrm{p}i}^{(1)}}c_{\mathrm{rp}i}^{(1)} \dot{x}_{\mathrm{rp}i}^{(1)} - \frac{1}{M_{\mathrm{p}i}^{(1)}}k_{\mathrm{rp}i}^{(1)}g \bigl(x_{\mathrm{rp}i}^{(1)}\bigr) \\ &\qquad - \frac{1}{M_{\mathrm{c}}^{(1)}}\sum _{i = 1}^{N_{1}} c_{\mathrm{rp}i}^{(1)} \dot{x}_{\mathrm{rp}i}^{(1)} - \frac{1}{M_{\mathrm{c}}^{(1)}}\sum _{i = 1}^{N_{1}} k_{\mathrm{rp}i}^{(1)}g \bigl(x_{\mathrm{rp}i}^{(1)}\bigr) \\ & \qquad - \frac{1}{M_{\mathrm{s}}^{(2)}}\sum_{i = 1}^{N_{2}} c_{\mathrm{sp}i}^{(2)}\dot{x}_{\mathrm{sp}i}^{(2)} - \frac{1}{M_{\mathrm{s}}^{(2)}}\sum_{i = 1}^{N_{2}} k_{\mathrm{sp}i}^{(2)}g\bigl(x_{\mathrm{sp}i}^{(2)}\bigr) \\ &\qquad + \biggl(\frac{1}{M_{\mathrm{c}}^{(1)}} + \frac{1}{M_{\mathrm{s}}^{(2)}}\biggr)K^{(1,2)}x_{\mathrm{cs}}^{(1,2)} \\ &\quad = - \frac{r_{\mathrm{bc}}^{(1)}}{I_{\mathrm{ce}}^{(1)}}T_{\mathrm{c}}^{(1)} - \frac{r_{\mathrm{bs}}^{(2)}}{I_{\mathrm{s}}^{(2)}}T_{\mathrm{s}}^{(2)} . \end{aligned}$$

(10e)

Here $M_{j}^{(n)} = \frac{I_{j}^{(n)}}{[r_{\mathrm{b}j}^{(n)}]^{2}}(j = s,r,pi)$, $M_{\mathrm{c}}^{(n)} = \frac{I_{\mathrm{ce}}^{(n)}}{[r_{\mathrm{bc}}^{(n)}]^{2}}$, $c_{\mathrm{sp}i}^{(n)} = 2\xi_{1}\sqrt{k_{m\mathrm{sp}i}^{(n)}/(1/M_{\mathrm{s}}^{(n)} + 1/M_{\mathrm{p}i}^{(n)})}$, and $c_{\mathrm{rp}i}^{(n)} = 2\xi_{2}\sqrt{k_{m\mathrm{rp}i}^{(n)}(1/M_{\mathrm{r}}^{(n)} + 1/M_{\mathrm{p}i}^{(n)})}$, where ξ ₁ and ξ ₂ are the damping coefficients of the meshes spi ⁽ⁿ⁾ and rpi ⁽ⁿ⁾ in stage n, respectively.

Equations (10a)–(10e) can be further simplified by using a number of dimensionless parameters. The dimensionless time parameter is introduced by setting τ=ω _d t, where $\omega_{\mathrm{d}} = \sqrt{k_{m\mathrm{sp}i}^{(1)}/m_{\mathrm{eq}1}}$, and $m_{\mathrm{eq}1} = M_{\mathrm{s}}^{(1)}M_{\mathrm{c}}^{(1)}M_{\mathrm{p}i}^{(1)}/(M_{\mathrm{c}}^{(1)}M_{\mathrm{p}i}^{(1)} + M_{\mathrm{s}}^{(1)}M_{\mathrm{p}i}^{(1)} + M_{\mathrm{s}}^{(1)}M_{\mathrm{c}}^{(1)})$. The nominal dimension b _c is employed, and the dimensionless displacement, velocity, and acceleration are representatives of $\bar{x} = x/b_{\mathrm{c}}$, $\dot{\bar{x}} = \dot{x}/\omega_{\mathrm{d}}b_{\mathrm{c}}$, and $\ddot{\bar{x}} = \ddot{x}/\omega_{\mathrm{d}}^{2}b_{\mathrm{c}}$. Other dimensionless parameters are defined as

$$ \bar{e}_{j\mathrm{p}i}^{(n)} = \frac{E_{j\mathrm{p}i}^{(n)}}{b_{\mathrm{c}}}\sin \bigl( \varOmega_{m}^{(n)}\tau + \varphi_{ej\mathrm{p}i}^{(n)} \bigr), $$

(11)

where $\varOmega_{m}^{(n)} = \frac{\omega_{m}^{(n)}}{\omega_{\mathrm{d}}}$.

$$\begin{aligned} &g\bigl(\bar{x}_{l}^{(n)}\bigr) = \left \{ \begin{array}{l@{\quad }l} \bar{x}_{l}^{(n)} - \bar{b}_{l}^{(n)}& \bar{x}_{l}^{(n)} > \bar{b}_{l}^{(n)} \\ 0& \vert \bar{x}_{l}^{(n)} \vert \le \bar{b}_{l}^{(n)} \\ \bar{x}_{l}^{(n)} + \bar{b}_{l}^{(n)}& \bar{x}_{l}^{(n)} < - \bar{b}_{l}^{(n)} \end{array} \right ., \\ &\quad \bar{b}_{l} = b_{l}/b_{\mathrm{c}}(l = spi,rpi). \end{aligned}$$

(12)

Thus, the dimensionless equation of motion in the general coordinates can be derived in the matrix form as

$$ \bar{\boldsymbol{M}}\ddot{\bar{\boldsymbol{q}}}(\tau ) + \bar{\boldsymbol{C}}\dot{\bar{\boldsymbol{q}}}(\tau ) + \bar{\boldsymbol{K}}\boldsymbol{g}\bigl(\bar{\boldsymbol{q}}(\tau )\bigr) = \bar{\boldsymbol{F}}(\tau ). $$

(13)

Here the mass matrix $\bar{\boldsymbol{M}}$, the stiffness matrix $\bar{\boldsymbol{K}}$, the damping matrix $\bar{\boldsymbol{C}}$, and the force vector $\bar{\boldsymbol{F}}(\tau )$ could be obtained from the dimensionless method mentioned above.

4 Results and discussion

As an example, the two-stage compound planetary gear train as shown in Fig. 1 is studied. The system parameters are listed in Table 1, and the calculation parameters are given in Table 2. The excitations are associated with the mesh stiffness fluctuation and the errors expressed by Eqs. (5) and (6). The different stages have different mesh frequencies with the relationship of $\omega_{m}^{(1)} = \varLambda \omega_{m}^{(2)}$, where Λ=5.571 is the transmission ratio of the planetary gear train of the first stage.

Table 1 System parameters of the two-stage planetary gear train

Table 2 Calculation parameters of the two-stage planetary gear train

The nonlinear dynamic equations presented in Eq. (13) are solved by using the varying-step Gill numerical integration method, and the termination criterion is specified to an error tolerance of less than 0.0001. The time series data corresponding to the first 800 revolutions of the dynamic system are deliberately excluded from the results in order to discard the transient solutions and ensure that the analyzed data approaches to steady-state solution [21, 22]. The sampled data were used to generate the bifurcation diagrams, time histories, phase trajectories, Poincaré maps, and power spectra of the two-stage compound planetary gear train in order to obtain a basic understanding of its dynamic behaviors based on the nonlinear dynamic model.

The bifurcation diagram [23] could be obtained by quasi-static increasing of the dimensionless displacement and the bifurcation parameter, and the continuation of solutions could be achieved by substitution of final to initial conditions for the next new parameter value. Figure 3 presents the dimensionless displacement $\bar{x}_{\mathrm{rp}i}^{(1)}$ of the two-stage compound planetary gear train using the damping coefficient ξ as a bifurcation parameter at the dimensionless excitation frequency of stage 1 Ω _m =1.06 and the dimensionless backlash b _a=1, and the initial conditions $\bar{x}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0.1$ and $\dot{\bar{x}}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0$. It shows that the two-stage compound planetary gear train has rich nonlinear dynamic behavior because of the coupling of gear backlash and time-varying meshing stiffness. The bifurcation diagrams of other mesh pairs of planetary gear train in each stage can be obtained in the same way. The plots are not provided here in order to be brief. The results show that other solutions have the same variation tendency.

Fig. 3

Bifurcation diagram for $\bar{x}_{\mathrm{rp}i}^{(1)}$ versus ξ with $\varOmega_{m}^{(1)} = 1.06$, b _a=1, $\bar{x}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0.1$, and $\dot{\bar{x}}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0$ obtained by the varying-step Gill numerical integration method

According to Fig. 3, the system exhibits nonperiodic motion at low values of the damping coefficient ξ, i.e., ξ≤0.0524. Specifically, when the damping coefficient ξ=0.03, the system experiences a chaotic motion, as shown in Fig. 4. The time history in Fig. 4(c) shows that the chaos is characterized by obvious irregular fluctuations of the amplitude from cycle to cycle. The phase trajectories in Fig. 4(a) are highly disordered and spread through almost the entire phase area, which indicates the chaotic motion. The strange attractor of the chaotic motion is illustrated in the Poincaré map as shown in Fig. 4(b). The power spectrum in Fig. 4(d) reveals the continuous power spectrum that has numerous excitation frequencies. The chaotic motion transits to an unstable quasi-periodic motion when the damping coefficient ξ reaches 0.035. When the damping coefficient ξ=0.045, the system experiences a three quasi-periodic motion as shown in Fig. 5. The phase trajectories are similar to 3T-periodic motion and repeat themselves every three periods but have differences between adjacent trajectories. There are three closed loops in the Poincaré map in Fig. 5(b). This quasi-periodic solution consists of three frequencies Ω _B1, Ω _B2, and Ω _B3, which are relatively prime. There are peaks existing in the linear combination of the three fundamental frequencies on the power spectrum as shown in Fig. 5(d).

Fig. 4

Chaotic motion at ξ=0.03 with $\varOmega_{m}^{(1)} = 1.06$, b _a=1, $\bar{x}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0.1$, and $\dot{\bar{x}}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0$: (a) the time history, (b) the phase trajectory, (c) the Poincaré map, (d) the power spectrum

Fig. 5

Quasi-periodic motion at ξ=0.045 with $\varOmega_{m}^{(1)} = 1.06$, b _a=1, $\bar{x}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0.1$, and $\dot{\bar{x}}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0$: (a) the time history, (b) the phase trajectory, (c) the Poincaré map, (d) the power spectrum

At higher values of the damping coefficient, the dynamic behavior of the system is found to be a subharmonic 3T-periodic motion at ξ=0.0524–0.0736. Letting the damping coefficient ξ be equal to 0.06, for example, the numerical solutions are shown in Fig. 6. The trajectories repeat themselves every three periods, and there are three discrete points on the Poincaré map. The corresponding power spectrum has peaks at the point of hΩ _B /3, where Ω _B is the fundamental frequency, and h is a positive integer.

Fig. 6

3T-periodic motion at ξ=0.06 with $\varOmega_{m}^{(1)} = 1.06$, b _a=1, $\bar{x}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0.1$ and $\dot{\bar{x}}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0$: (a) the time history, (b) the phase trajectory, (c) the Poincaré map, (d) the power spectrum

As the damping coefficient ξ further increases, the dynamic behavior of the system reverts to a one quasi-periodic motion at ξ=0.0738–0.0878. When the damping coefficient ξ=0.075, the numerical solutions are shown in Fig. 7. The time history in Fig. 7(c) shows that there is only small, irregular fluctuation of the amplitude from cycle to cycle. The phase trajectories repeat themselves every period and have the differences between adjacent trajectories, which look like a closed curve belt with a certain width. The Poincaré map in Fig. 7(b) appears as a closed loop, and the power spectrum has peaks at iΩ _B1+jΩ _B2 (i, j=0, ±1, ±2,…), where Ω _B1 and Ω _B2 are two relatively prime fundamental frequencies. When the damping coefficient ξ is at [0.0738, 0.0878] area, there are some periodic motion windows. For example, when the damping coefficient ξ=0.081, a 17T-periodic motion shows up, as shown in Fig. 8. There are 17 discrete points on the Poincaré map. The phase trajectory of this long periodic motion is similar to that of the quasi-periodic motion.

Fig. 7

Quasi-periodic motion at ξ=0.075 with $\varOmega_{m}^{(1)} = 1.06$, b _a=1, $\bar{x}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0.1$, and $\dot{\bar{x}}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0$: (a) the time history, (b) the phase trajectory, (c) the Poincaré map, (d) the power spectrum

Fig. 8

17T-periodic motion at ξ=0.081 with $\varOmega_{m}^{(1)} = 1.06$, b _a=1, $\bar{x}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0.1$, and $\dot{\bar{x}}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0$: (a) the time history, (b) the phase trajectory, (c) the Poincaré map, (d) the power spectrum

Finally, for the damping coefficient ξ>0.088, the system performs a stable 1T-periodic motion. An example is presented in Fig. 9, which illustrates the situation where the damping coefficient ξ is equal to 0.1. The solutions have a noncircular phase plane plots, and there is a single point on the Poincaré map. The time history illustrates that the motion repeats itself during each period and the corresponding power spectrum has peaks at the point of hΩ _B , where h is a positive integer.

Fig. 9

1T-periodic motion at ξ=0.1 with $\varOmega_{m}^{(1)} = 1.06$, b _a=1, $\bar{x}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0.1$, and $\dot{\bar{x}}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0$: (a) the time history, (b) the phase trajectory, (c) the Poincaré map, (d) the power spectrum

It can be seen that the nonlinear behavior of the compound multistage planetary gear system is very sensitive to the damping coefficient ξ. In practical multistage compound planetary gear trains, the rotational speed is commonly used as a bifurcation parameter. Accordingly, the dynamic behavior of the two-stage compound planetary gear train is also examined using the dimensionless excitation frequency Ω _m as a bifurcation parameter. Figure 10 presents the corresponding bifurcation diagrams of the dynamic system at the dimensionless backlash b _a=1, the initial conditions $\bar{x}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0.1$ and $\dot{\bar{x}}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0$, and different damping coefficients of ξ=0.07, 0.1, 0.12, and 0.15. By comparing Figs. 10(a)–(d), the results show that at low values of the damping coefficient ξ, the two-stage compound planetary gear train exhibits a nonperiodic response at most values of the dimensionless excitation frequency Ω _m . However, the dynamic behavior of the system transits to an increasingly stable periodic motion as the value of the damping coefficient increases. In other words, the results demonstrate the effectiveness of a higher damping coefficient in suppressing nonperiodic motions of the multistage planetary gear train, thereby improving its dynamic response.

Fig. 10

Bifurcation diagrams for $\bar{x}_{\mathrm{rp}i}^{(1)}$ versus $\varOmega_{m}^{(1)}$ for various ξ with b _a=1, $\bar{x}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0.1$, and $\dot{\bar{x}}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0$ obtained by the varying-step Gill numerical integration method: (a) ξ=0.07, (b) ξ=0.1, (c) ξ=0.12, (d) ξ=0.15

The damping coefficient in tooth meshing is related to the structure parameter and the physical parameters of the gear train. By on-purpose designing, the proper damping coefficient could be acquired through adjusting the structure and the physical parameters of the gear train. As a result of that, the system is expected to have narrow interval of the chaotic motion, extended life time, enhanced reliability, and lower noise.

The bifurcation diagram, as shown in Fig. 11, using the dimensionless backlash b _a as a bifurcation parameter at the dimensionless excitation frequency Ω _m =0.85 and the damping coefficient ξ=0.07, and the initial conditions $\bar{x}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0.1$ and $\dot{\bar{x}}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0$. According to Figs. 3, 10, and 11, it can be revealed that the motion state of the system changes into chaos in many different ways. As the dimensionless excitation frequency and the dimensionless backlash increase, the motion state of the system changes into chaos through Hopf bifurcation and period doubling bifurcation, respectively. Take the parameter of the dimensionless excitation frequency Ω _m for example, Fig. 12 presents the corresponding Poincaré maps at various values of the dimensionless excitation frequency in the range of Ω _m =1.45–1.55 from Fig. 10(a). It reveals the bifurcation and chaos properties of the system, which changes into chaos through Hopf bifurcation. It is found that the Poincaré map corresponding to Ω _m =1.45 has two points, and thus it can be inferred that the system behavior is in a subharmonic 2T-periodic motion. As the dimensionless excitation frequency increases, the two stable points lose their stability and become two unstable points through Hopf bifurcation, and then, the unstable points expand into two closed-loop surfaces. This indicates that the system comes into a two quasi-periodic motion. As the dimensionless excitation frequency further increases, the two smooth closed-loop surfaces start oscillating, twisting, winding, and phase locking. Finally the two closed-loop surfaces become fracture, and the presence of the strange attractor in the Poincaré map indicates a chaotic motion. That is a complete process for a stable subharmonic 2T-periodic motion transiting into a chaotic motion. It is a kind of common evolution path that changes a stable periodic motion into a chaotic motion.

Fig. 11

Bifurcation diagram for $\bar{x}_{\mathrm{rp}i}^{(1)}$ versus b _a with $\varOmega_{m}^{(1)} = 0.85$, ξ=0.07, $\bar{x}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0.1$, and $\dot{\bar{x}}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0$ obtained by the varying-step Gill numerical integration method

Fig. 12

Poincáre maps for various Ω _m ∈[1.45,1.55] with ξ=0.07, b _a=1, $\bar{x}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0.1$, and $\dot{\bar{x}}_{\mathrm{rp}i}^{(1)}(\tau = 0) = 0$

Chaos happened in the transmission system means that the system works in a state of unpredictability and nonrepeatability. According to the Figs. 4 and 9, the amplitudes in the chaotic motion are almost double than that in the stable periodic motion. For the actual mechanical equipments, chaos is partly detrimental to the working performance and causes noises. According to the bifurcation diagram, the rotational speeds that probably cause the chaotic motion should be avoided in order to ensure the stability and reliability of the system.

5 Conclusions

This study presented a numerical analysis of the nonlinear dynamic response of a typical two-stage planetary gear train. The main conclusions are:

• (1) A discrete nonlinear, time-variant, torsional dynamic model for a typical two-stage planetary gear train, considering time-varying meshing stiffness, nonlinear error excitation, and backlash, is formulated. Dimensionless equations of motion in general coordinates are obtained in a matrix form and solved by using the varying-step Gill numerical integration method.

• (2) The nonlinear dynamics of the two-stage planetary gear train are analyzed by reference to its dynamic bifurcation diagrams, time histories, phase trajectories, Poincaré maps, and power spectra. The dynamic response of the system is investigated as a function of the dimensionless damping coefficient. The numerical results reveal that the system exhibits a nonperiodic motion at low values of the damping coefficient ξ, i.e., ξ≤0.0524. The chaotic motion transits to an unstable quasi-periodic motion when the damping coefficient ξ reaches 0.035. The dynamic behavior of the system is found to be a subharmonic 3T-periodic motion at ξ=0.0524–0.0736. As the damping coefficient ξ further increases, the dynamic behavior of the system reverts to a one quasi-periodic motion at ξ=0.0738–0.0878. Finally, for the damping coefficient ξ>0.088, the system performs stable 1T-periodic motion.

• (3) The dynamic system is very sensitive to the damping coefficient and the backlash. The dynamic behavior of the system transited to an increasingly stable periodic motion as the value of the damping coefficient increased. This demonstrates the effectiveness of a higher damping coefficient in suppressing nonperiodic motion, thereby improving its dynamic response. On the contrary, a higher backlash would result in a chaotic motion of the system.

• (4) The motion state of the system changes into chaos through Hopf bifurcation and period doubling bifurcation as the dimensionless excitation frequency and the dimensionless backlash increase, respectively. Results enable suitable values of the damping coefficient, the rotational speed ratio, and the backlash to be specified so that chaotic behavior can be avoided, thus reducing the amplitude of vibration within the system and extending the system life.