1 Introduction

A neuron is a nerve cell that is the basic building block of the nervous system, e.g., a one-year old human has about 100 billion neurons. The electric activities of neurons could be reproduced in biological neuron models such as the Hodgkin–Huxley neuron model, which explained the ionic mechanisms underlying the initiation and propagation of action potentials in the squid giant axon [1], integrate-and-fire model [2], leaky integrate-and-fire model [3], exponential integrate-and-fire model [4], FitzHugh–Nagumo model [5–7], Morris–Lecar model [8–10], and Hindmarsh–Rose model [11]. Most of these neuron modes could be a simplified version of the original Hodgkin–Huxley model and each neuron model is a mathematical description of the properties of nerve cells (or neurons), which can predict biological processes accurately. The motivation for designing the FitzHugh–Nagumo model (FHN) [6] was to isolate conceptually the essentially mathematical properties of excitation and propagation from the electrochemical properties of sodium and potassium ion flow. The model suggested by FitzHugh in 1961 was ever called as “Bonhoeffer–van der Pol model,” and then this model was investigated in an equivalent circuit by Nagumo et al. [7]. The FHN model consists of a voltage-like variable having cubic nonlinearity that allows regenerative self-excitation via a positive feedback, and a recovery variable having a linear dynamics that generates a slower negative feedback. Catherine Morris and Harold Lecar developed a biological neuron model [8–10] to reproduce the variety of oscillatory behavior in relation to Ca2+ and K+ conductance in the giant barnacle muscle fiber, which is called the Morris–Lecar model (ML). The Morris–Lecar neurons exhibit both class I and class II neuron excitability, and the experiments relied on the current clamp method were established by Keynes et al. in 1973. The Hindmarsh–Rose model (HR) of neuronal activity is aimed to study the spiking-bursting behavior of the membrane potential observed in experiments made with a single neuron [11].

Various dynamic behaviors can be observed in many nonlinear systems under appropriate parameter regions, and electric circuits are designed to reproduce some dominant properties such as chaos/hyperchaos in these systems [12–18]. For example, an electric circuit is proposed to realize an unidirectional coupling between two cells, and the chemical synaptic coupling is also mimicked [12]. Ge et al. [13] designed an electric circuit to generate trichaos attractors with three positive Lyapunov exponents. Li et al. [14] performed an experimental study of the ultrahigh-frequency chaotic dynamics generated in an improved Colpitts oscillator. Mogo et al. [15] investigated the dynamics of a nonlinear electromechanical system including a cantilever robot arm manipulator. Liu et al. [17] studied the implementation of an electronic circuit and the finite-time synchronization for the 4D (four-dimensional) Rabinovich hyperchaotic system. [18] demonstrated chaotic performance of the colpitts oscillator in the ultrahigh frequency (300–1000 MHz) range by using PSpice. Rocha et al. [19] presented an experimental characterization of the behavior of an analogous version of the Chua’s circuit. On the other hand, some theoretical models can reproduce main properties of biological neurons, for example, Wang et al. [20] confirmed that an arbitrary signal can be transmitted reliably through spontaneous and highly irregular spike trains, and then be reconstructed downstream in the information transmission pathway. The electric activity of neuron often shows regularity due to noise-induced coherence resonance [21–25] and/or stochastic resonance [26, 27] induced by noise and periodic pacing. Furthermore, the dynamic evolution in neuronal circuits [28–34] were also investigated, and these results could be useful to detect the collective behaviors in networks or coupled electric oscillators. For example, Crotty et al. [28] simulated the neuronal activities with two coupled Josephson junctions. Wagemakers et al. [33] proposed a method for the design of electronic bursting neurons based on a simple conductance neuron model. Within the neuronal circuit [33], it uses mainly linear components except for the analog multipliers and diodes. The Josephson junction shows superconductivity when the operating temperature is far below the critical temperature, and it plays like a nonlinear inductor in circuit. The coupled Josephson-junction resonator can show complex nonlinear dynamics, and it is useful to design a signal generator with high frequency about terahertz. For example, Li et al. [35] confirmed that the coupled Josephson-junction resonator can synchronize a neuron model and generated similar electric activity of neurons based on an adaptive synchronization scheme. Dana et al. [36] reported neuron-like spiking and bursting in the resistive-capacitive-inductive shunted Josephson-junction (RCLSJ) model. It is found that spiking oscillations, intrinsically bursting (IB) and fast spiking (FS), which are usually seen in a rat’s motor cortex, are observed in a single junction under external DC bias. Particularly, Coomans et al. [37] confirmed that coupled asymmetric SRLs are able to excite pulses in each other, mimicking neuron functionality as optical spiking neurons. A reliable neuron circuit does generate spiking, bursting series under different parameter regions, and the circuit should be practical in circuit experiments.

In this paper, the design and realization of neuronal circuits will be checked by using a Personal Simulation Program with Integrated Circuit Emphasis (PSpice) [38]. The device of Josephson junction is replaced by an equivalent nonlinear circuit, the coupled Josephson-junction resonator, and the circuit for Morris–Lecar model are designed. The output signals from the neuronal circuits can emerge spiking, bursting series in appropriate parameter region, and these results are consistent with the numerical studies.

2 Model

The dynamics of Morris–Lecar (ML) neuron is described as follows:

$$\begin{aligned} &C \frac{dV}{dt}=\bar{g}_K N(V) (V_K-V)+ \bar{g}_{\mathrm{Ca}}M_{\infty}(V) (V_{\mathrm{Ca}}-V) \\ &\phantom{C \frac{dV}{dt}=\,}+g_L(V_L-V)+I; \end{aligned}$$
(1)
$$\begin{aligned} &\frac{dN(V)}{dt}=\lambda _{N}(V)\bigl[N_{\infty}(V)-N(V) \bigr]; \\ &M_{\infty}(V)=0.5\biggl(1+\tanh\biggl(\frac{V-V_{1}}{V_{2}}\biggr)\biggr); \\ &N_{\infty}(V)=0.5\biggl(1+\tanh\biggl(\frac{V-V_{3}}{V_{4}} \biggr)\biggr); \\ &\lambda _{N}(V)=\overline{\lambda _{N}}\cosh\biggl( \frac{V-V_{3}}{2V_{4}}\biggr), \end{aligned}$$
(2)

where the variable V, N, I denotes the membrane potential (mV), variable for gate channel, and intensity of external injected current (μA/cm2) on the neuron, respectively. The capacitance of the membrane (μF/cm2), conductance of potassium, conductance of calcium, and conductance of leakage current is represented by C, \(g_{K} (\leq \bar{g}_{K}^{\max})\), \(g_{\mathrm{Ca}} (\leq \bar{g}_{\mathrm{Ca}}^{\max})\), \(\bar{g}_{L}\), respectively. The physiological parameters for reversal potentials are denoted as V K , V Ca, and V L , while M ∞(V), N ∞(V) defines the stable value of opening probability for calcium, potassium, where \(\overline{\lambda_{N}}, V_{1}, V_{2}, V_{3}, V_{4}\) are parameters of the system as shown in Eqs. (1), (2), and the values for these parameters are associated with the cell and temperature.

3 Numerical results and discussion

In this section, firstly, the theoretical Morris–Lecar (ML) model and Josephson junction coupled with resonator are simulated in a numerical way, respectively. Then the corresponding equivalent circuit is designed to generate similar dynamic properties of the theoretical model, and the critical parameter regions are detected in experiments. In Sect. 3.1, the dynamic properties of the ML model are discussed in numerical way and PSpice platform, respectively. In Sect. 3.2, the dynamics of the Josephson junction coupled with a resonator are also investigated in a theoretical model and PSpice platform, respectively.

3.1 Realization of circuit for the Morris–Lecar model

The schematic diagram of ML model is often illustrated in Fig. 1, which is composed of a capacitor to measure the fluctuation of membrane potentials, and three subbranches are used to describe the effect of ion channels.

Fig. 1
figure 1

Schematic diagram for the Morris–Lecar model

Full size image

According to the theoretical model as shown in Eq. (1), it is important to detect the stable value of opening probability for calcium, potassium (M ∞(V), N ∞(V)). In a numerical way, the curves for M ∞(V), N ∞(V) are plotted in Fig. 2.

Fig. 2
figure 2

The characteristic curve for M ∞(V), N ∞(V) defined in Eq. (2). The parameters are selected as V 1=−1.2, V 2=18, V 3=12, V 4=17.4 (mV)

Full size image

The numerical results in Fig. 2 show that the appearances for M ∞(V), N ∞(V) are like a ‘S’ shaped curves, and these characteristic curves could be reproduced by adjusting the voltage fluctuation and stable threshold of voltage of device based on the unidirectional continuity of diodes. Then the circuit unit is designed by using PSpice, and the results are shown in Fig. 3.

Fig. 3
figure 3

Appropriate circuits are designed to generate “S” shaped curves, the upper part is for N ∞(V) and the one below is for M ∞(V)

Full size image

The operational amplifier (U4) in Fig. 3 is injected feedback from two diodes; the feedback resistance and enlargement factor are decreased when the diodes are unblocked. Otherwise, the feedback resistance and enlargement factor are increased. As a result, the input–output series show two distinct different slopes, and a continuous nonlinear characteristic curve is approached in experiments. The experimental results confirm that a bigger slope emerges in the region about −0.7 mV≤V≤0.7 mV and the slope is decreased when other diodes are unblocked completely. Two diodes are connected to the input end of operational amplifier (U3), thus the input voltage for operational amplifier (U3) is adjusted from −0.7 mV to 0.7 mV. It is also confirmed that the input voltage in the operational amplifier (U3) varies from −0.7 mV to 0.7 mV, and the output voltage from the operational amplifier (U3, U1) is shown in Fig. 4.

Fig. 4
figure 4

The fluctuation of output voltages from the operational amplifier U3 (blue), U1 (red) (Color figure online)

Full size image

Compared to the output series in Fig. 4 with the curve as shown in Fig. 2, it is confirmed that our designed circuits in Fig. 3 can generate similar characteristic curves for M ∞(V), N ∞(V). In the PSpice platform, multiplying units are often packaged, thus the detailed units seldom appear in a combination units of an operational amplifier other electronic components. Furthermore, an equivalent Morris–Lecar neuron circuit could be designed by using the integrators, multiplying units, and the circuit diagram is shown in Fig. 5.

Fig. 5
figure 5

The design of an equivalent Morris–Lecar neuron circuit plotted in PSpice

Full size image

Furthermore, it is important to check the output series in the equivalent Morris–Lecar neuron circuit and compare these results with the output series from the theoretical model in a numerical way. In the numerical studies, the parameters for the Morris–Lecar neuron are selected as follows. g L =2.0, g Ca=4.0, g K =8.0, V L =−60.0, V Ca=120.0, V K =−80.0, V 1=−1.2, V 2=18.0, V 3=12.0, V 4=17.4, C=5.0, \(\overline{\lambda_{N}} =1/15\). The fourth-order Runge–Kutta algorithm is used with time step about 0.01 being used. To give a clear illustration for the electric activity of the neuron, the evolution for a membrane of potentials under different forcing currents and phase diagram are calculated, and the results are shown in Fig. 6.

Fig. 6
figure 6

The discharge series of neuron and phase diagram are plotted when different external forcing currents are imposed for I=20 (a1), I=45 (b1), I=90 (c1), I=120 (d1), and the corresponding phase portraits for I=20 (a2), I=45 (b2), I=90 (c2), I=120 (d2). The inserted subgraph in Fig. 6(a1) (and Fig. 6(d1)) is an enlarged series from t=0 to t=500 time units

Full size image

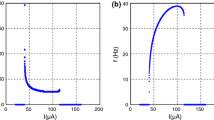
The results in Fig. 6 show that the electric activities of neurons are much more dependent on the external forcing current. The membrane potential of the neuron is close to a stable value with little fluctuation about an order 10−3, and intermittent bursting emerges with increasing the intensity of the external forcing current to a value about 120. Then it gives the bifurcation diagram by calculating the interspike interval (ISI) vs. the injected current, and the results are shown in Fig. 7.

Fig. 7
figure 7

Bifurcation diagram: the averaged interspike interval (ISI) for membrane potentials of the neuron vs. external forcing current

Full size image

The results in Fig. 7 confirm that the ISI of an excited neuron can vary in a large range when the appropriate forcing current (I>40) is imposed on the neuron; then the ISI is decreased to be close to a smaller value below 30 when the external forcing current is increased to 85 mA. It is understood that distinct regular spiking emerges with increasing the intensity of forcing current, which is consistent with the results as shown in Fig. 6(a1, b1, c1). The bursting state begins to appear with further increasing the intensity of forcing the current and multiperiodic solution for the ML model could be detected in the output series vs. time. Now, it is important to reproduce these characteristic prosperities in the ML circuit, and the experimental results are shown in Figs. 8 (spiking) and 9 (bursting).

Fig. 8
figure 8

Spiking state in the simplified ML circuit in PSpice when the circuit is forced by different currents, for I=10 μA (a), for I=50 μA (b), for I=3 mA (c), for I=4 A (d)

Full size image
Fig. 9
figure 9

Bursting state in the simplified ML circuit in PSpice (below row), periodic forcing current (upper row), and the external forcing current is i=50 μA+50sin(ωt), ω=25

Full size image

The results in Fig. 8 confirm that the ML circuit in PSpice can reproduce a similar spiking series by changing the external forcing current, and they are similar to the results from the theoretical model in a numerical way. It is found that transition of electric activities for neuron circuit in PSpice could be induced by changing the external forcing current completely. Furthermore, bursting like outputs are generated by imposing an appropriate forcing current on the circuit in PSpice, and the results in the experiment are shown in Fig. 9.

The results in Fig. 9 confirm that bursting series can also be observed in the ML circuit in PSpice as well, and the series for voltage are similar to the results in a numerical way within the theoretical model. In other words, the improved ML circuit in PSpice can reproduce different electric activities for neurons, and it could be used as a practical tool to study the transition of electric activities in neurons.

3.2 Realization of circuit for Josephson junction coupled with resonator

Josephson-junction devices have been investigated due to the discovery of the quantum-mechanical tunneling of carriers through an insulator sandwiched between two superconducting metals (Josephson effect) [39]. As a result, many different models [40] were presented to investigate the dynamics in Josephson-junction circuits [41]. For example, the shunted linear resistive-capacitive junction (RCSJ) [42], shunted nonlinear resistive-capacitive junction (SNRCJ), and shunted linear resistive-capacitive-inductance junction (RCLSJ) [43, 44]. It is found that the RCLSJ model is useful in high-frequency applications [45] and the author of this paper even confirmed that the chaotic circuit of resistive-capacitive-inductive-shunted Josephson junction is effective to simulate behaviors of the Hindmarsh–Rose neuronal discharges based synchronization scheme [46]. In a nonlinear circuit, the Josephson junction is often used as a sensitive inductor, and it is often coupled with other electronic components (inductor, capacitor, resistor) to generate an oscillating series from the circuit. The two basic equations for the Josephson junction are often described as follows:

$$\begin{aligned} \begin{aligned} &\frac{d \theta}{d t}=\frac{2\pi e}{h}V ; \\ &I=I_{C}\sin(\theta), \end{aligned} \end{aligned}$$
(3)

where h denotes the Planck constant, and V,I C ,θ is the voltage, critical current of the Josephson junction, phase difference of the superconductor pair, respectively. The schematic diagram of the RCLSJ circuit, which is shown as Fig. 1(a) in [36], is reproduced in Fig. 10, where R(V), C, R S , I S ,I ext denotes a nonlinear resistance, junction capacitance, leakage resistance, the current through shunt inductance L, and the external forcing current, respectively. The RCLSJ circuit [36] after dimensionless transformation (τ=ω 0 t, ω 0=2πeI c R s /h, \(\beta_{c}=2\pi eI_{c}CR_{s}^{2}/h\), β L =2πeI c L/h, g(v)=R S /R(v), v=V/I C R s , i s =I s /I C , i ext=i 0+i 1sin(ωt)) is replaced by

$$\begin{aligned} \begin{aligned} &\beta _{C}\frac{d ^{2}\theta}{d \tau^{2}}+g(v)\frac{d \theta}{d \tau}+\sin( \theta)+i_{s}\\ &\quad{}=i_{0}+i_{1}\sin\biggl( \frac{\omega \tau}{\omega _{0}}\biggr); \\ &\beta _{L}\frac{d i_{s}}{d \tau}= v-i_{s}; \\ &\frac{d \theta}{d \tau}=v, \end{aligned} \end{aligned}$$
(4)

where the external current i 0=I 0/I C presents the DC bias current and i 1=I 1/I C denotes the amplitude of the sinusoidal forcing of angular frequency ω. And the step function g(v) approximates the I–V characteristic of the junction and it is defined as follows:

$$\begin{aligned} g(v)= \left \{ \begin{array}{l@{\quad}l} \frac{R_{S}}{R_{n}}=0.366, & \vert v \vert > \frac{V_{g}}{I_{C}R_{S}}=2.9; \\ \frac{R_{S}}{R_{sg}}=0.061, & \vert v \vert \leq \frac{V_{g}}{I_{C}R_{S}}=2.9.\\ \end{array} \right . \end{aligned}$$
(5)
Fig. 10
figure 10

RCLSJ model of Josephson junction is shown as the schematic diagram in Fig. 1(a) of [36]

Full size image

The nonlinear function could be realized in PSpice by using unidirectional continuity of diodes, and the equivalent circuit is shown in Fig. 11, where the triangle in the schematic circuit denotes the amplifier, and the switched threshold 2.9 is decreased to 0.7. The total resistance is decreased to approach an equivalent nonlinear resistance when the diodes are unblocked completely. According to the basic equations as shown in Eq. (3), it gets

$$ I=I_{C}\sin\biggl(\frac{2\pi e}{h}\int V dt +\theta _{0} \biggr). $$
(6)
Fig. 11
figure 11

The realization for nonlinear function g(v) in circuit in PSpice

Full size image

For simplicity, but without loss of generality, it is considered θ 0=0 and the equivalent circuit for the ideal Josephson junction is given in Fig. 12,

Fig. 12
figure 12

The equivalent circuit for the ideal Josephson junction

Full size image

where EPOLY denotes Voltage controlled voltage source (VCVS), which is used to transmit the voltage to the integrator; INTEG is an ideal integrator. GAIN is an ideal amplifier, SIN is sine function; GPOLY is a Voltage Controlled Current Source (VCCS), which is used to transmit the voltage to current. As a result, the equivalent circuit for RCLSJ after normalization is illustrated in Fig. 13.

Fig. 13
figure 13

The schematic diagram for equivalent circuit for RCLSJ after normalization

Full size image

Within the diagram in Fig. 13, an equivalent circuit for RCLSJ is constructed by replacing the ideal Josephson junction with an equivalent circuit. In the following, the numerical results from the theoretical RCLSJ model will compare with the outputs from the circuit in PSpice. In the numerical studies for the RCLSJ model, β c =0.005, time step 0.01, and different parameters for β L forcing currents are selected to generate spiking, bursting series, respectively.

The results in Fig. 14 show that the output voltages begin to oscillate with increasing the intensity of external forcing DC currents, and continuous spiking series are generated. Then an equivalent circuit in PSpice is used to detect the output series, and the results are shown in Fig. 15.

Fig. 14
figure 14

The time series for voltages in the RCLSJ model, β c =0.005, β L =20, i 1=0, for i 0=1 (a), i 0=1.5 (b), i 0=2 (c), i 0=3 (d). (e) Bifurcation diagram: the averaged interspike interval (ISI) for membrane potentials of neuron vs. external forcing current

Full size image
Fig. 15
figure 15

The output voltages from the RCLSJ circuit in PSpice, β c =0.005, β L =20, i 1=0, for i 0=1 (a), i 0=1.5 (b), i 0=2 (c), i 0=3 (d)

Full size image

The results in Fig. 15 show that the output voltage keeps a stable rhythm when the external forcing current is below the threshold. There are diodes in the equivalent circuit; a downgrade about 0.7V occurs when the diode is turned on, and thus the amplitudes of outputs in the circuit are in certain difference from the numerical results but the spiking rhythm is synchronous. Furthermore, it also checks the case for bursting, and the numerical results for bursting are shown in Figs. 16 and 18, while experimental results for bursting are from PSpice are shown in Figs. 17 and 19.

Fig. 16
figure 16

Bursting series from the RCLSJ model in numerical way, β c =0.05, β L =100, i 1=0, i 0=2.5 (a). (b) Bifurcation diagram: the averaged interspike interval (ISI) for membrane potentials of neuron vs. external forcing current

Full size image
Fig. 17
figure 17

Bursting-like output voltage from the circuit in PSpice, β c =0.01, β L =100, i 1=0, i 0=3.2

Full size image

The results in Fig. 16(a) show that stable bursting series are generated when appropriate parameters and forcing current are used. The bifurcation diagram confirms that transition of electric activity in RCLSJ model can go through from stable state, spiking to bursting with increasing the intensity of forcing currents. Then the circuit is checked in PSpice and the results are shown in Fig. 17.

The results in Fig. 17 confirm that the circuit in PSpice can generate stable bursting series similar to the numerical results in Fig. 18 by selecting bigger parameters β c , β L (conductance, inductance). Furthermore, it investigates another way to induce bursting series by imposing periodic currents on the model and circuit, and the results in numerical way and experimental circuit are plotted in Figs. 18 and 19, respectively.

Fig. 18
figure 18

Bursting series from the RCLSJ model in numerical way, β c =0.01, β L =5, i 1=0.35, i 0=1.25, i=i 0+i 1sin(ω′t),ω′=0.05

Full size image
Fig. 19
figure 19

Bursting series from the RCLSJ circuit in PSpice, β c =0.01, β L =5, i 1=0.35, i 0=1.25, i=i 0+i 1sin(ω′t),ω′=0.05

Full size image

The results in Fig. 18 confirm that perfect bursting series could be generated when periodic forcing current is introduced into the RCLSJ model, and then the problem is investigated in circuit in PSpice, and the results are shown in Fig. 19.

The results in Fig. 19 confirm that similar bursting series can be generated in the circuit in PSpice when an appropriate periodic forcing current is imposed on the circuit in PSpice.

In a summary, circuits for the Morris–Lecar neuron model and RCLSJ model are designed in PSpice, similar wave profile (spiking, bursting series) could be generated in the equivalent circuits, and these results are consistent with the numerical results. Within the circuit for the Morris–Lecar neuron, the integrator is updated and an equivalent small-circuit (packaged unit) is used to replace the ideal Josephson junction in RCLSJ circuit. The bifurcation diagrams for the two neuronal models give us a clear way to understand the excitability dependence on the external forcing current. The designed circuits are controllable and could be useful to simulate collective behaviors of neurons in network of circuits.

4 Conclusions

In this paper, two types of improved circuits are presented to reproduce the electric activities of neurons, and the dynamics are investigated by analyzing the time series, phase portraits, and bifurcation diagram. Within the Morris–Lecar neuron circuit, a new operational amplifier is constructed, and the experimental results show that distinct transition in electric activities can be switched from quiescent state to type I, then type II, and return to quiescent state. These results in an experimental way based on PSpice are consistent with the results from the theoretical way. In the Josephson-junction coupled resonator, an equivalent circuit is designed to measure the Josephson-junction effect, and it is found that different kinds of electric activities could be reproduced in the circuit designed from PSpice. It could be useful to construct a network of neuronal circuits in a large scale so that the collective behaviors of neurons could be detected and investigated in a practical way.