Introduction

Neurons are the basic functionality unit of the human brain, which possesses the most complex neural network in the world (Ison et al. 2015; Zyarah et al. 2020). The neuronal dynamics can influence the brain’s functionalities, i.e., associate memory and cognitive behavior (Grewe et al. 2017; Wang et al. 2023; Shine et al. 2019; Andalman et al. 2019). The neurons act as signal receptors and processors with the firing patterns triggered by the changes in the electrophysiological environment (Lv et al. 2016; Li et al. 2024). The diversity of neuron firing patterns is crucial for realizing the brain’s functionality and providing the basis for exploring brain-like applications (Sun et al. 2024; Wu et al. 2021). The bionic circuit is the hardware-bearing platform of the applications. Therefore, it is important to explore the production of abundant firing patterns and deduce their forming mechanism in the bionic circuit, which can effectively reproduce various firing patterns or emulate the dynamical behaviors of neurons (Huang et al. 2019; Xu et al. 2024). In the literature, the bionic circuits were mainly constructed by considering the neuron functionality or neuronal microstructure. Some other bionic circuits were derived from neuron models by employing commercially available components, e.g., resistor, inductor, capacitor, and newly proposed circuit component, e.g., memristor (Xie et al. 2024a, b). In this paper, a bionic circuit is constructed by considering the micro-structure of the neuronal membrane, for which abundant firing patterns, e.g., fast-slow dynamics, related to external stimulus are revealed.

In 1952, Hodgkin and Huxley conducted a biometric experiment and acquired the membrane potential of the North Atlantic squid by current-clamp technique, and then built the first bionic circuit, aka, Hodgkin–Huxley (H–H) circuit, by the membrane theory (Hodgkin and Huxley 1952). Meanwhile, the ion transport mechanism for generating the membrane potential was elaborated (Hodgkin 1951). That is, the conductance of the sodium ion channel has a transient increase when sodium ions move inwards and the conductance of the potassium ion channel has a transient increase when potassium ions move outwards. The ion transport mechanism based on membrane theory declared that the action potential mainly depends on a rapid sequence of changes in the permeability to the sodium and potassium ions. They have declared that the conductances of the ion channels are time-varying and can be equivalent to time-varying resistors (Hodgkin and Huxley 1952). Following the pioneer’s work, Professor Chua theoretically deduced that two time-varying resistors meet the definition of locally active memristor (LAM) (Jin et al. 2023; Lin et al. 2020).

The memristor was postulated in 1971 and widely deployed to construct memristive neuron models, neural networks (Li et al. 2024; Wang et al. 2024), and the echo state network (Deng et al. 2024). The concept of a LAM was introduced by Chua in 2014, which is associated with a device showing a negative differential resistance or negative differential conductance in its DC \(V-I\) curve (Dong et al. 2020). LAM has the feature of amplifying small fluctuations in its locally active domain and triggering an action potential (Liang et al. 2020; Ying et al. 2023), which has natural advantages in constructing bionic circuits. According to the shapes of DC \(V-I\) curves, the LAMs can be named voltage-controlled N-type LAM (Dong et al. 2022), current-controlled S-type LAM (Liang et al. 2020), voltage-controlled Chua corsage LAM (CCM) (Chua 2023), and CCM-like LAM (Xu et al. 2024). From the perspective of circuit modeling, N-type LAMs usually connect to a capacitor in parallel and S-type LAMs connect to an inductor in series. To date, LAMs were used to characterize the potassium ion and sodium ion channels in H–H circuits, from which the memristor parameters were adjusted to make the memristive H–H circuits exhibit periodic and chaotic firing patterns (Xu et al. 2024, 2019). Besides, LAM can be deployed to construct a bionic circuit via small signal analysis, which constructs Hopf bifurcation to make the bionic circuit lose its stability and generate spiking behaviors (Jin et al. 2021; Ascoli et al. 2022; Mannan et al. 2017).

Hardware implementation of the bionic circuits can verify the existence of firing patterns and provide the feasibility of applications. There are mainly three categories of physical implementation technologies, including the MCU- and FPGA-based digital platforms (Xu et al. 2023; Lin et al. 2023), CMOS-based VLSI circuits (Kumar et al. 2024; Guo et al. 2023), and commercially available component-based analog circuits (Xu et al. 2022, 2024). Each of these technologies possesses its features. The digital platforms can be flexibly modified by rewriting and updating code, but accuracy and adaptability should be considered. The CMOS-based VLSI circuit can provide high integration and energy efficiency but lacks the abilities of modification and universality. The commercially available component-based analog circuit has high design flexibility and good real-time performance, but it brings inevitable discreteness of circuit components. Besides, general researchers can perform commercially available component-based analog hardware measurements since there is a low requirement for experimental equipment.

Inspired by the above literature, this paper proposes a memristive ion channel-based bionic circuit, which involves an N-type LAM to characterize the ion channels, a capacitor to represent the membrane capacitor, a DC voltage to represent the reversal potential, and an AC current to emulate the external stimulus. The dynamical effect of the external stimulus is numerically and experimentally explored, since the firing pattern of a biological neuron is intimately related to changes in the electrophysiological environment (Yang et al. 2021; Wouapi et al. 2020; Ouyang et al. 2023). The most significant is that the bionic circuit can generate spiking behavior under the external stimulus with high-frequency and bursting behavior under low-frequency one. We name the dynamical effect of high- and low-frequency stimuli as fast-slow dynamics. Besides, the memristive ion channel-based bionic circuit might be more suitable to depict the firing patterns of a biological neuron.

The rest of this paper is arranged as follows. Section 2 deduces the modeling for the memristive ion channel-based bionic circuit and analyzes the equilibrium trajectory and its stability. In Section 3, bursting behaviors and their bifurcation mechanism are numerically revealed under the low-frequency stimulus, and then spiking behaviors and coexisting behaviors under the high-frequency stimulus are numerically disclosed. Section 4 performs the hardware experiments to verify the numerical results. Section 5 summarizes the paper.

Memristive ion channel-based bionic circuit

This section proposes an N-type second-order LAM and displays its memristive property and locally active domain. After that, the circuit schematic of the proposed bionic circuit is presented and the circuit state equation is built. Then, the equilibrium trajectory and the stability are studied.

An N-type second-order LAM

The commercially available component-based emulator of an N-type second-order LAM contains a floating ground module composed of current feedback operational amplifiers (C-FOAs) \(U_1\) to \(U_4\), two reverse integration circuit modules realized by two operational amplifiers (op-amps) \(U_\text {A}\) and \(U_\text {B}\), an inverting adder module \(-(+)\), and four analog multiplier modules \(M_1\) to \(M_4\), as shown in Fig. 1 The floating module enables that the N-type LAM can connect to a DC voltage in series, which can ensure the LAM operating in its LAD. The N-type LAM includes two integration capacitor \(C_1\) and \(C_2\), where \(v_{\varphi 1}\) is the state variable of \(C_1\) and \(v_{\varphi 2}\) is the state variable of \(C_2\), and then its circuit state equation can be built as

$$\begin{aligned} \left\{ \begin{aligned}&{i_M} = \frac{{{g_2}({g_1}{v_{\varphi 1}}{v_{\varphi 2}} + {v_{\varphi 2}}){v_M}}}{{{R_M}}} \\&{C_1}\frac{{{\text {d}}{v_{\varphi 1}}}}{{{\text {d}}t}} = \frac{{{g_3}{v_{\varphi 1}}{v_M}}}{{{R_1}}} - \frac{{{v_{\varphi 1}}}}{{{R_2}}} - \frac{{{v_M}}}{{{R_3}}} \\&{C_2}\frac{{{\text {d}}{v_{\varphi 2}}}}{{{\text {d}}t}} = \frac{{{g_4}{v_{\varphi 2}}{v_M}}}{{{R_4}}} - \frac{{{v_{\varphi 2}}}}{{{R_5}}} - \frac{{{v_M}}}{{{R_6}}} \\ \end{aligned}\right. \end{aligned}$$
(1)

where \(i_M\) represents the current through the memristor and \(v_M\) denotes the input voltage of the memristor. \(g_1\) to \(g_4\) are the gains of the multipliers \(M_1\) to \(M_4\). Additionally, typical circuit parameters for the N-type LAM are chosen as

\(C_1 = C_2 = {50}\,\text {nF}\), \(R_{1} {\text{ }} = {\text{ }}R_{6} {\text{ }} = {\text{ }}1{\text{k}}\Omega\), \(R_{2} = R_{5} = 2{\text{k}}\Omega\), \(R_{4} {\text{ }} = {\text{ }}10\;{\text{k}}\Omega\), \(R_{3} = 20{\kern 1pt} {\text{k}}\Omega\), \(g_1 = g_2 = g_3 = g_4 = 1~\mathrm V^{-1}\), \(R_{{\text{W}}} = R_{{{\text{W1}}}} = R_{{{\text{W2}}}} = 10\;{\text{k}}\Omega\), \(R_{M} = 1\;{\text{k}}\Omega\).

Fig. 1
figure 1

Commercially available component-based emulator of the N-type second-order LAM

Full size image

The DC \(V-I\) curve can obviously display the locally active property of a LAM (Chua 2022; Mannan et al. 2016). Herein, \(i_M\) and \(v_M\) are respectively denoted as \(I_M\) and \(V_M\), and d\(v_{\varphi 1}/{\text d}t\) = 0, d\(v_{\varphi 2}/{\text d}t\) = 0 in Eq. (1) are set. By numerically calculating the relation between \(V_M\) and \(I_M\), the DC \(V-I\) curve is obtained, as shown in Fig. 2a. The DC \(V-I\) curve exhibits a negative slope within the range of \({0\,\mathrm{\text {V}}} \le V_M \le {0.4181\,\mathrm{\text {V}}}\) and has an N-shaped. The LAM can work in its LAD when series connecting to a DC voltage within this range. Figure 2b depicts frequency-dependent pinched hysteresis loops of the memristor, where \(v_M=\sin (2 \pi F t)\) is applied to the input terminal and the frequency F is set as 2, 5, and 10 kHz. It is demonstrated that the pinched hysteresis loops pass through the origin and the lobe area decreases with the increase of frequency, which meets the definition of a memristor (Chua 2015).

Fig. 2
figure 2

Inner properties of the second-order LAM: a The DC V-I curve of the LAM; b Frequency-dependent pinched hysteresis loops of the LAM

Full size image

Circuit modeling and stability analysis

The memristive ion channel-based bionic circuit is newly constructed and its circuit scheme is figured out in the right of Fig. 3. The bionic circuit consists of an N-type second-order LAM W, a DC voltage E, a capacitor C, and a current stimulus \(I_{{{\text{ext}}}}\). Herein, the concept of ion channel transport in membrane theory is employed to establish the memristive ion channel-based bionic circuit. The N-type LAM is a voltage-controlled one, which possesses an inner state variable with its resistance controlled by the input voltage and inner state variable. This can reflect the regulation of resistance in the interaction process of ion transport and membrane potential variation. Our aim is not to characterize the membrane structure of any specific biological neuron but to deploy the consideration of the membrane structure. Additionally, the relationship can be equivalently represented as parallel, since the ion channels of neurons are protein channels embedded in lipid bilayer membrane, as shown in the middle of Fig. 3. The mathematical state equation of the bionic circuit shown in Fig. 3 can be established as

$$\begin{aligned} \left\{ \begin{aligned}&C\frac{{{\text {d}}v}}{{{\text {d}}t}} = {I_{{\text {ext}}}} - \frac{{{g_2}({g_1}{v_{\varphi 1}}{v_{\varphi 2}} + {v_{\varphi 2}})(v - E)}}{{{R_M}}} \\&{C_1}\frac{{{\text {d}}{v_{\varphi 1}}}}{{{\text {d}}t}} = \frac{{{g_3}{v_{\varphi 1}}(v - E)}}{{{R_1}}} - \frac{{{v_{\varphi 1}}}}{{{R_2}}} - \frac{{(v - E)}}{{{R_3}}} \\&{C_2}\frac{{{\text {d}}{v_{\varphi 2}}}}{{{\text {d}}t}} = \frac{{{g_4}{v_{\varphi 2}}(v - E)}}{{{R_4}}} - \frac{{{v_{\varphi 2}}}}{{{R_5}}} - \frac{{(v - E)}}{{{R_6}}} \\ \end{aligned} \right. \end{aligned}$$
(2)

Here, C = 100 nF and the external stimulus is given as \(I_{{{\text{ext}}}} = I_{{\text{m}}} \sin (2 \pi f t)\), where \(I_{{{\text{ext}}}}\) is the amplitude and f is the frequency. The DC voltage E is set to 0.3 V to push the LAM work in the LAD. Note that the bionic circuit has the natural frequency in about 1 kHz. This is a benefit for commercially available component-based hardware measurement. Certainly, we can regulate the natural frequency of the bionic circuit by adjusting the resistances and capacitances.

Fig. 3
figure 3

Memristive ion channel-based bionic circuit

Full size image

To analyze the equilibrium trajectory and its stability of the bionic circuit, we set the left side of Eq. (2) to 0 and the equilibrium trajectory \(E_S\) of the bionic circuit can be yielded as

$$\begin{aligned} {E_S} = [\eta ,\frac{{\eta - 0.3}}{{20(\eta - 0.8)}},\frac{{10(\eta - 0.3)}}{{\eta - 5.3}}] = [\eta ,{\chi _1},{\chi _2}] \end{aligned}$$
(3)

where the value of the \(\eta\) can be solved by

$$\begin{aligned} I_{\text {m}}\sin (2\pi ft) - \frac{{({\chi _1}{\chi _2} + {\chi _2})(\eta - 0.3)}}{{{R_M}}} = 0 \end{aligned}$$
(4)

Then, the Jacobian matrix at \(E_S\) can be expressed as

$$\begin{aligned} \textbf{J}_{S}=\left( {\begin{array}{*{20}{c}} {{m_{11}}}& {{m_{12}}}& {{m_{13}}} \\ {{m_{21}}}& {{m_{22}}}& 0 \\ {{m_{31}}}& 0& {{m_{33}}} \end{array}} \right) \end{aligned}$$
(5)

where

$$\begin{aligned} \begin{aligned}&{m_{11}} = - 10000000({\chi _1}{\chi _2} + {\chi _2})/{R_M} \\&{m_{12}} = 10000000{\chi _2}(0.3 - \eta )/{R_M} \\&{m_{13}} = 10000000(0.3 - \eta )({\chi _1} + 1)/{R_M} \\&{m_{21}} = 20000{\chi _1} - 1000 \\&{m_{22}} = 20000\eta - 16000 \\&{m_{31}} = 2000{\chi _2} - 20000 \\&{m_{33}} = 2000\eta - 10600 \\ \end{aligned} \end{aligned}$$
(6)

Thus, the characteristic polynomial of the Jacobian matrix is

$$\begin{aligned} {\lambda ^3} + {m_1}{\lambda ^2} + {m_2}\lambda + {m_3} = 0 \end{aligned}$$
(7)

Here

$$\begin{aligned} \begin{aligned}&{m_1} = - {m_{11}} - {m_{22}} - {m_{33}} \\&{m_2} = {m_{11}}{m_{22}} - {m_{12}}{m_{21}} + {m_{11}}{m_{33}} - {m_{13}}{m_{31}} + {m_{22}}{m_{33}} \\&{m_3} = {m_{12}}{m_{21}}{m_{33}} - {m_{11}}{m_{22}}{m_{33}} + {m_{13}}{m_{22}}{m_{31}} \\ \end{aligned} \end{aligned}$$
(8)

A dynamical system can be regarded as slow variables modulating the fast variables when there exist more than two time scales (Han and Bi 2023). Herein, we set frequency f, which is much lower than the natural frequency of the bionic circuit. In this context, \(I_{{{\text{ext}}}}\) can be seen as a slow variable. That is, \(I_{{{\text{ext}}}}\) can be considered as a constant changing in \([- I_{{\text{m}}} , I_{{\text{m}}} ]\). Here, we demonstrate the equilibrium trajectory and stability of the bionic circuit for \(R_{M} = 0.5\;{\text{k}}\Omega\), \(I_{{\text{m}}} = {0.05\,\mathrm{\text {m}\text {A}}}\) and \(f = {220\,\mathrm{\text {Hz}}}\) as a paradigm. Figure 4 illustrates the equilibrium trajectory of \({\eta }\) value and its stability for the variation of current stimulus \(I_{{{\text{ext}}}}\), within which different colors are deployed to represent different kinds of stability. One can see that there exist stable node focus (SNF) for \(I_{{{\text{ext}}}} < {{-}0.5682\,\mathrm{\text {m}\text {A}}}\) and \(I_{{{\text{ext}}}} > {{-}0.000006\,\mathrm{\text {m}\text {A}}}\); unstable saddle point (USP) and SNF for \({{-}0.5682\,\mathrm{\text {m}\text {A}}}< I_{{{\text{ext}}}} < {{-}0.4949\,\mathrm{\text {m}\text {A}}}\); unstable saddle focus (USF), USP, and SNF for \({{-}0.4949\,\mathrm{\text {m}\text {A}}}< I_{{{\text{ext}}}} < {{-}0.0180\,\mathrm{\text {m}\text {A}}}\); SNF and USP for \(- 0.0180\;{\text{A < }}I_{{{\text{ext}}}} < - 0.0078\;{\text{mA}}\); SNF, USP, and stable node (SNP) for \(- 0.0078\;{\text{mA < }}I_{{{\text{ext}}}} < - 0.000006\;{\text{mA}}\); fold bifurcation points (FBP) for \(I_{{{\text{ext}}}} = - 0.000006\;{\text{mA}}\) and \(I_{{{\text{ext}}}} = - 0.5682\;{\text{mA}}\); Hopf bifurcation point (HBP) for \(I_{{{\text{ext}}}} = - 0.0180\;{\text{mA}}\). In summary, the bionic circuit has three state variables possessing a similar time-scale, e.g., high-frequency, and fold/Hopf bifurcations for the variation of current stimulus. Thus, we can set the current stimulus with low-frequency to govern the bionic circuit having fast-slow time-scale, which can trigger bursting behaviors.

Fig. 4
figure 4

Equilibrium trajectory and its stability with respect to \(I_{{{\text{ext}}}}\)

Full size image

Fast-slow dynamical behaviors

External stimulus can effectively influence the electrophysiological activity of biological neurons (Kim et al. 2019; Yu et al. 2022; Sachdeva et al. 2020; Yao and Ma 2018). This section uses numerical simulations to explore the dynamical behavior of the memristive ion channel-based bionic circuit under high-frequency and low-frequency stimuli. In the numerical simulations, the MATLAB-based ODE45 algorithm with a total-time \(0.1 \rm{s}\) and a fixed time-step \(10^{-6} \rm{s}\) are used to obtain the bifurcation diagram and time-domain waveform. Total-time 2 s and fixed time-step \(10^{-4} \rm{s}\) are set to calculate the Lyapunov exponent spectrum (LEs) by using the Jacobi matrix-based Wolf’s method (Xu et al. 2023). The circuit parameters used in the dynamical analysis for low-frequency analysis are the same as those in the paradigm in Sect. 2. Additionally, the initial states are set to \([v(0), v_{\varphi 1}(0), v_{\varphi 2}(0)]= [{0\,\mathrm{\text {V}}}, {0\,\mathrm{\text {V}}}, {0\,\mathrm{\text {V}}}]\) to eliminate the dynamical influence of initial states.

Dynamical effect of low-frequency stimulus

The bifurcation diagram in a two-parameter plane can effectively reveal the dynamical distribution for the two parameters. By detecting the periodicity of state variable v, a two-parameter bifurcation diagram in the \(I_{{\text{m}}} -f\) plane is plotted. Figure 5a shows the two-parameter bifurcation diagram in the interval of \({0\,\mathrm{\text {m}\text {A}}} \le I_{{\text{m}}} \le {0.6\,\mathrm{\text {m}\text {A}}}\), \({150\,\mathrm{\text {Hz}}} \le f \le {350\,\mathrm{\text {Hz}}}\) with \(R_{M} = 0.5\;{\text{k}}\Omega\), in which different states are distinguished by different colors. These are, red for chaotic behavior(CH), yellow for multiple periodic behavior (MP) with its periodicity more than 8, and other colors for period-1 (P1) to period-8 (P8). Many stripe regions exist in the two-parameter bifurcation diagram, indicating the generation of rich dynamical behaviors. Figure 5b illustrates a two-parameter Lyapunov exponent plot in the \(I_{{\text{m}}} -f\) parameter plane, which is described by the largest Lyapunov exponent. The colors are classified according to the values of the largest Lyapunov exponent. For a non-autonomous circuit, a positive Lyapunov exponent presents the chaotic state and a negative Lyapunov exponent stands for periodic states with different periodicities. One can observe that the Lyapunov exponent plot well confirms the dynamical behaviors revealed by the two-parameter bifurcation diagram. Note that the largest Lyapunov exponent is large in absolute value since the numerical simulation employs the state equation of a physical circuit with small time-scale (Chen et al. 2018).

Fig. 5
figure 5

Two-parameter dynamical distribution in the \(I_{{\text{m}}} -f\) parameter plane, where \(R_{M} = 0.5\;{\text{k}}\Omega\): a Two-parameter bifurcation diagram by checking the periodicity of v; b Two-parameter Lyapunov exponent plot described by the largest Lyapunov exponent

Full size image

Besides, the one-parameter bifurcation diagram and LEs plot are figured out to illustrate the bifurcation effects for one parameter, as shown in Fig. 6. The local maximum values of the state variable v is used to describe the one-parameter bifurcation diagram and the largest Lyapunov exponent is deployed in LEs plot. The upper of Fig. 6a displays the one-parameter bifurcation diagram as \(I_{{\text{m}}}\) varies in the interval \([{0\,\mathrm{\text {m}\text {A}}}, {0.6\,\mathrm{\text {m}\text {A}}}]\) with \(f={220\,\mathrm{\text {Hz}}}\) and \(R_{M} = 0.5\;{\text{k}}\Omega\). One can observe that period-adding bifurcation behaviors appear with the increase of \(I_{{\text{m}}}\) (Kafraj et al. 2020). Additionally, several narrow ranges of chaotic behavior exist within the parameter range \({0.32\,\mathrm{\text {m}\text {A}}} \le I_{{\text{m}}} \le {0.36\,\mathrm{\text {m}\text {A}}}\), which is confirmed by the LE larger than zero, as shown in the bottom. Figure 6b illustrates the one-parameter bifurcation diagram and LEs plot by f varying in the interval \([{150\,\mathrm{\text {Hz}}}, {350\,\mathrm{\text {Hz}}}]\) with \(I_{{\text{m}}} = {0.05\,\mathrm{\text {m}\text {A}}}\) and \(R_{M} = 0.5\;{\text{k}}\Omega\). The one-parameter bifurcation diagram and LEs plot in Fig. 6b demonstrate that reverse period-adding bifurcation behaviors are triggered with the increase of f and some narrow parameter ranges for chaos are generated, e.g., near \(f = {215\,\mathrm{\text {Hz}}}\), \({310\,\mathrm{\text {Hz}}}\), and \({348\,\mathrm{\text {Hz}}}\).

Fig. 6
figure 6

One-parameter bifurcation diagrams(up) and LEs plot (bottom) for low-frequency stimulus, respectively: a For the variation of \(I_{{\text{m}}}\); b For the variation of f

Full size image

The one-parameter bifurcation diagrams shown in Fig. 6 demonstrate that the bionic circuit can generate abundant periodic and chaotic firing patterns. To further disclose these firing patterns, we select some values of \(I_{{\text{m}}}\) from Fig. 6a and plot the time-domain waveforms of \(I_{{\text{m}}}\), as shown in Fig. 7. The time-domain waveforms are P3 bursting, P4 bursting, P5 bursting, P6 bursting and P5 bursting, for \(I_{{\text{m}}} ={0.02\,\mathrm{\text {m}\text {A}}}\), \(I_{{\text{m}}} ={0.03\,\mathrm{\text {m}\text {A}}}\), \(I_{{\text{m}}} ={0.04\,\mathrm{\text {m}\text {A}}}\), \(I_{{\text{m}}} ={0.055\,\mathrm{\text {m}\text {A}}}\), and \(I_{{\text{m}}} ={0.58\,\mathrm{\text {m}\text {A}}}\), respectively. As \(I_{{\text{m}}}\) increases, the number of spikes in each burster increases, which verifies the period-adding bifurcation behavior. Note that period-5 bursting behaviors for \(I_{{\text{m}}} ={0.04\,\mathrm{\text {m}\text {A}}}\) and \(I_{{\text{m}}} ={0.58\,\mathrm{\text {m}\text {A}}}\) are different, which should be formed by different bifurcation mechanisms. Furthermore, these time-domain waveforms demonstrate that the memristive ion channel-based bionic circuit can effectively generate bursting behavior under the low-frequency stimulus. The membrane potential is not less than zero since the existence of DC voltage E. The DC voltage \(E = {0.3\,\mathrm{\text {V}}}\) raises the membrane potential to positive values. Note that our aim is not to replicate the firing patterns of any specific biological neuron. Instead, we are focusing on investigating the diverse firing patterns generated by the memristive ion channel-based bionic circuit.

Fig. 7
figure 7

Time-domain waveforms for different \(I_{{\text{m}}}\) with \(f={220\,\mathrm{\text {Hz}}}\): a Period-3 bursting for \(I_{{\text{m}}} ={0.02\,\mathrm{\text {m}\text {A}}}\); b Period-4 bursting for \(I_{{\text{m}}} ={0.03\,\mathrm{\text {m}\text {A}}}\); c Period-5 bursting for \(I_{{\text{m}}} ={0.04\,\mathrm{\text {m}\text {A}}}\); d Period-6 bursting for \(I_{{\text{m}}} ={0.055\,\mathrm{\text {m}\text {A}}}\); e Period-5 bursting for \(I_{{\text{m}}} ={0.58\,\mathrm{\text {m}\text {A}}}\)

Full size image

Bifurcation mechanism for bursting behavior

Herein, we reveal the bifurcation mechanism of bursting behaviors by deducing the fold bifurcation (FB) and Hopf bifurcation (HB) sets of the bionic circuit. The polynomial equation in Eq. 7 has zero eigenvalue indicating the appearance of FB (Wouapi et al. 2021) and a pair of pure conjugate imaginary roots manifesting the occurrence of HB (Huang and Bi 2023). Thus, FB happens with \(m_3=0\) and HB occurs with \(m_3 = 0\) and \(m_1 m_2-m_3 = 0\). The FB and HB sets are figured out in Fig. 8. One can see that there is one FB for \({0.000006\,\mathrm{\text {m}\text {A}}}< I_{{\text{m}}} < {0.018\,\mathrm{\text {m}\text {A}}}\), one FB and one HB for \({0.018\,\mathrm{\text {m}\text {A}}}< I_{{\text{m}}} < {0.5682\,\mathrm{\text {m}\text {A}}}\), two FBs and one HB for \({0.5682\,\mathrm{\text {m}\text {A}}}< I_{{\text{m}}} < {0.6\,\mathrm{\text {m}\text {A}}}\) respectively. This means that FB and HB happen two times with the number of them in a period of the stimulus, e.g., FB happens two times and HB happens two times in a period of the stimulus for \(I_{{\text{m}}} ={0.04\,\mathrm{\text {m}\text {A}}}\)

Fig. 8
figure 8

FB and HB sets in the \(\sin (2 \pi f t)- I_{{\text{m}}}\) parameter plane

Full size image

To more intuitively reveal the bifurcation mechanism of bursting behaviors, time-domain waveforms of v along with the value of \(\eta\) of the equilibrium trajectory for \(I_{{\text{m}}} ={0.04\,\mathrm{\text {m}\text {A}}}\) and \(I_{{\text{m}}} ={0.58\,\mathrm{\text {m}\text {A}}}\) are selected as paradigms, as shown in Fig. 9. We describe the bifurcation mechanism for the bursting behaviors in a period of the stimulus marked by T and the period is defined by starting at an HB point.

In Fig. 9a, the circuit trajectory initially operates along the lower SNF forming a resting state, then the HB 1 occurs. After that, the circuit trajectory only slightly deviates from the \(\eta\)-trajectory due to the coexistence of USP and SNP. The circuit trajectory transmits to the upper SNF and forms the spikes via FB 1, and the amplitude of the spikes decreases since they oscillate along the upper SNF. Then, the amplitude of the spike increases when FB 2 happens along with the generation of USP. The amplitude of the spike further increases when HB 2 happens and the circuit trajectory transmits to the lower SNF exhibiting a resting state when the circuit trajectory passes through the SNF. Finally, the circuit trajectory enters into the next period T. In Fig. 9b, the bifurcation mechanism is the same as the first case at the beginning and then the amplitude of the spike decreases to the upper SNF. After that, the circuit trajectory directly transmits to the lower SNF after the HB 2 happens. Then, the circuit trajectory falls into the lower SNF forming the resting state. In this process, the FB 2, 3 and 4 do not affect the circuit trajectory.

Fig. 9
figure 9

Time-domain waveforms and equilibrium trajectories over the time: a \(I_{{\text{m}}} ={0.04\,\mathrm{\text {m}\text {A}}}\); b \(I_{{\text{m}}} ={0.58\,\mathrm{\text {m}\text {A}}}\)

Full size image

Dynamical effect of high-frequency stimulus

In this section, dynamical behaviors of the bionic circuit under high-frequency stimulus are investigated. The circuit parameters are set to \(I_{{\text{m}}} ={0.27\,\mathrm{\text {m}\text {A}}}\), \(f={1600\,\mathrm{\text {Hz}}}\) and \(R_{M} = 1\;{\text{k}}\Omega\) and the other circuit parameters are the same as the ones deployed in Sect. 3.1.

Fig. 10
figure 10

Two-parameter dynamical distribution in the \(I_{{\text{m}}} -f\) parameter plane with \(R_{M} = 1\;{\text{k}}\Omega\): a Bifurcation diagram by checking the periodicity of v; b Lyapunov exponent plot

Full size image

Two-parameter bifurcation diagram and Lyapunov exponent plot in the \(I_{{\text{m}}} -f\) parameter plane are plotted. The adjustable parameter are set to \([{0.2\,\mathrm{\text {m}\text {A}}}, {0.6\,\mathrm{\text {m}\text {A}}}]\) and \([{1100\,\mathrm{\text {Hz}}}, {2100\,\mathrm{\text {Hz}}}]\) for \(I_{{\text{m}}}\) and f, respectively. The colormap setting for the bifurcation diagram is the same as the one employed in Fig. 5. In Fig. 10a, there are extensive regions of chaotic behaviors and periodic behaviors blending into each other in the upper left parameter range. One can see that the memristive ion channel-based bionic circuit can exhibit various periodic and chaotic behaviors under different stimulus parameters. The two-parameter Lyapunov exponent plot in Fig. 10b further confirms the dynamical behaviors revealed by the bifurcation diagram.

Afterward, one-parameter bifurcation diagrams and LEs plots for \(I_{{\text{m}}}\) and f under high-frequency stimulus are numerically simulated, as shown in Fig. 11. In Fig. 11a, the bifurcation diagram shows a transition from MP to P2, then follows period-doubling bifurcations (Xu et al. 2023) demonstrating the dynamical transition of P4-P8-CH (Xu et al. 2023). Afterward, the reverse period-doubling bifurcation route happens, leading to the circuit trajectory running in P1. These dynamical transition behaviors are further confirmed by the corresponding one-parameter LEs plot. In Fig. 11b, the circuit trajectory starts with P1 and undergoes the period-doubling bifurcation route, leading the the occurrence of chaos. Then, the circuit trajectory falls into P1 via the reverse period-doubling bifurcation route. Notably, several sharp transitions occur during this evolution process, which might lead to the generation of coexisting behaviors related to memristor initial states. These sharp transitions are confirmed by the one-parameter LEs plot exhibiting several peaks above zero beyond the normal evolutionary trend.

Fig. 11
figure 11

One-parameter bifurcation diagram (up) and LEs plot (bottom) for high-frequency stimulus: a For the variation of amplitude \(I_{{\text{m}}}\); b For the variation of frequency f

Full size image

To illustrate the firing patterns under the high-frequ-ency stimulus, we selected some specific values of \(I_{{\text{m}}}\) to plot the time-domain waveforms of v, as shown in Fig. 12. They are chaotic spiking for \(I_{{\text{m}}} ={0.27\,\mathrm{\text {m}\text {A}}}\), period-8 spiking for \(I_{{\text{m}}} ={0.29\,\mathrm{\text {m}\text {A}}}\), period-4 spiking for \(I_{{\text{m}}} ={0.3\,\mathrm{\text {m}\text {A}}}\), period-2 spiking for \(I_{{\text{m}}} ={0.4\,\mathrm{\text {m}\text {A}}}\), and period-1 spiking for \(I_{{\text{m}}} ={0.5\,\mathrm{\text {m}\text {A}}}\). These time-domain waveforms display chaotic and periodic spiking behaviors, which are different from the bursting behaviors under the low-frequency stimulus. Besides, these firing patterns have a transition of CH-P8-P4-P2-P1, which further reflects the reverse period-doubling bifurcation route with the increase of \(I_{{\text{m}}}\). These spiking firing patterns might hold the promise to provide high energy efficiency implementations of spike-based neuromorphic hardware for spiking neural networks (Abderrahmane et al. 2020).

Fig. 12
figure 12

Time-domain waveforms of v for different \(I_{{\text{m}}}\) with \(f={1600\,\mathrm{\text {Hz}}}\): a Chaotic spiking for \(I_{{\text{m}}} ={0.27\,\mathrm{\text {m}\text {A}}}\); b Period-8 spiking for \(I_{{\text{m}}} ={0.29\,\mathrm{\text {m}\text {A}}}\); c Period-4 spiking for \(I_{{\text{m}}} ={0.3\,\mathrm{\text {m}\text {A}}}\); d Period-2 spiking for \(I_{{\text{m}}} ={0.4\,\mathrm{\text {m}\text {A}}}\); e Period-1 spiking for \(I_{{\text{m}}} ={0.5\,\mathrm{\text {m}\text {A}}}\)

Full size image

The coexistence of firing patterns is an interesting phenomenon in biological neurons, which might play an unknown functionality in realizing biological information processing (Lin et al. 2021). In Fig. 11b, the single-parameter bifurcation diagram shows sharp transitions of dynamical behaviors, which implies the potential existence of coexisting firing patterns related to the initial states (Xu et al. 2024; Gu et al. 2015). Thus, we select four sets of circuit parameters in the sharp transition parameter ranges, e.g., \(f={1530\,\mathrm{\text {Hz}}}\), \(f={1588\,\mathrm{\text {Hz}}}\), \(f={1858\,\mathrm{\text {Hz}}}\), and \(f={2070\,\mathrm{\text {Hz}}}\) as paradigms to display the coexisting firing patterns. Phase trajectories in the \(v-v_{\varphi 1}\) plane for the four sets of circuit parameters under different memristor initial states are figured out, as shown in Fig. 13. Figure 13a displays the coexisting P4 and CH firing patterns for \(f={1530\,\mathrm{\text {Hz}}}\) under initial states \([v(0), v_{\varphi 1}(0), v_{\varphi 2}(0)] = [{0\,\mathrm{\text {V}}}, {1\,\mathrm{\text {V}}}, {1\,\mathrm{\text {V}}}]\) and \([{0\,\mathrm{\text {V}}}, {0\,\mathrm{\text {V}}}, {0\,\mathrm{\text {V}}}]\). Figure 13b demonstrates the coexisting CH firing patterns for \(f={1558\,\mathrm{\text {Hz}}}\) under the initial states \([v(0), v_{\varphi 1}(0), v_{\varphi 2}(0)] = [{0\,\mathrm{\text {V}}}, {1\,\mathrm{\text {V}}}, {1\,\mathrm{\text {V}}}]\) and \([{0\,\mathrm{\text {V}}}, {0\,\mathrm{\text {V}}}, {0\,\mathrm{\text {V}}}]\). The two CH attractors have different top-ologies. Figure 13c demonstrates the coexisting P1, P3, and CH firing patterns for \(f={1858\,\mathrm{\text {Hz}}}\) under the initial states \([v(0), v_{\varphi 1}(0), v_{\varphi 2}(0)] = [{0\,\mathrm{\text {V}}}, {1\,\mathrm{\text {V}}}, {1\,\mathrm{\text {V}}}]\), \([{0\,\mathrm{\text {V}}}, {-1\,\mathrm{\text {V}}}, {-1\,\mathrm{\text {V}}}]\), and \([{0\,\mathrm{\text {V}}}, {0\,\mathrm{\text {V}}}, {0\,\mathrm{\text {V}}}]\). Figure 13d gives the coexisting P1 and P5 firing patterns for \(f={2070\,\mathrm{\text {Hz}}}\) for initial states \([v(0), v_{\varphi 1}(0), v_{\varphi 2}(0)] = [{0\,\mathrm{\text {V}}}, {-1\,\mathrm{\text {V}}}, {-1\,\mathrm{\text {V}}}]\) and \([{0\,\mathrm{\text {V}}}, {1\,\mathrm{\text {V}}}, {1\,\mathrm{\text {V}}}]\). Actually, these are periodic and chaotic spiking behaviors.

Fig. 13
figure 13

Phase trajectories in the \(v-v_{\varphi 1}\) plane for different f: a Coexisting P4 and CH for \(f={1530\,\mathrm{\text {Hz}}}\); b Coexisting CHs for \(f={1588\,\mathrm{\text {Hz}}}\); c Coexisting P1, P3 and CH for \(f={1858\,\mathrm{\text {Hz}}}\); d Coexisting P1 and P5 for \(f={2070\,\mathrm{\text {Hz}}}\)

Full size image

Hardware circuit and experiment

The hardware experiment is crucial for confirming the dynamical behavior of a bionic circuit and verifying the feasibility of the bionic circuit. The hardware circuit using commercially available components is one of the feasible ways, which can offer some advantages, such as better real-time performance and design flexibility. In this section, we implement the memristive ion channel-based bionic circuit by discrete circuit components and execute hardware experiments to validate the numerical simulation results.

Fig. 14
figure 14

Discrete circuit component-based hardware circuit (left) and hardware experimental platform (right)

Full size image

A discrete circuit component-based bionic circuit is made by referring to the equivalent circuit in Figs. 1 and 3, as depicted in the left of Fig. 14. In the hardware circuit, \(U_1\) to \(U_5\) are CFOA AD844AN, \(M_1\) to \(M_4\) are analog multiplier AD633JN, and \(U_\text {A}\), \(U_\text {B}\), \(U_6\), and \(U_7\) are operational amplifiers AD711JN. Among them, \(U_6\) and \(R_7\) to \(R_9\) constitute an inverting adder module corresponding to the \(-(+)\) module. \(U_7\), \(R_{10}\), and \(R_{11}\) are used to generate a DC voltage 0.3 V, \(R_{12}\) to \(R_{19}\) respectively control the gain of their connected multiplier to \(1~\mathrm V^{-1}\). \(U_5\) and \(R_{20}\) constitute a voltage-current conversion module, which converts the input AC voltage into AC current. Note that two \({100\,\mathrm{\text {n}\text {F}}}\) capacitors are connected in series to obtain the two capacitors \(C_1 = {50\,\mathrm{\text {n}\text {F}}}\) and \(C_2 = {50\,\mathrm{\text {n}\text {F}}}\). The DC voltage is connected to the LAM emulator in series to confirm the LAM working in its LAD. The right of Fig. 14 shows the hardware experimental platform. In hardware experiments, a TPS5420 voltage regulator module provides the \(\pm {15\,\mathrm{\text {V}}}\) operating voltage. A function generator is employed to supply a sinusoidal AC voltage \(V_{{{\text{ext}}}} = V_{{\text{m}}} \sin (2\pi ft)\). Then, the AC voltage is converted to AC current by using the voltage-current conversion module, and the conversion relationship is obtained as \(I_{{{\text{ext}}}} = V_{{{\text{ext}}}} /10\;{\text{k}}\Omega\). An oscilloscope is connected to display the voltage of capacitor C.

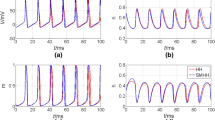
Some circuit parameters are slightly adjusted to offset the parasitic parameters of discrete circuit components and the influence of the external environment (Wang et al. 2023; Cai et al. 2022; Xu et al. 2021). The other circuit parameters are set to the typical ones in numerical simulations. For low-frequency stimulus, \(I_\text {m}\), \(R_{M}\), \(R_1\), \(R_2\), and \(R_5\) are finely adjusted to capture the time-domain waveforms for bursting behaviors, as shown in Fig. 15. The time-domain waveforms are shifted down by \({2\,\mathrm{\text {V}}}\) on the oscilloscope, except that P5 bursting behavior (\(I_{{\text{m}}} ={0.58\,\mathrm{\text {m}\text {A}}}\)) is shifted down by \({1.875\,\mathrm{\text {V}}}\) for better visualization. For high-frequency stimulus, \(R_{M}\), \(R_1\), \(R_2\), \(R_4\), and \(R_5\) are finely adjusted to capture the time-domain waveforms for spiking behaviors, as shown in Fig. 16. The time-domain waveforms are shifted down by \({1.125\,\mathrm{\text {V}}}\) on the oscilloscope.

Fig. 15
figure 15

Hardware measured time-domain waveforms of v for different \(I_{{\text{m}}}\) with \(f={220\,\mathrm{\text {Hz}}}\): a Period-3 bursting for \(I_{{\text{m}}} ={0.02\,\mathrm{\text {m}\text {A}}}\); b Period-4 bursting for \(I_{{\text{m}}} ={0.03\,\mathrm{\text {m}\text {A}}}\); c Period-5 bursting for \(I_{{\text{m}}} ={0.04\,\mathrm{\text {m}\text {A}}}\); d Period-6 bursting for \(I_{{\text{m}}} ={0.055\,\mathrm{\text {m}\text {A}}}\); e Period-5 bursting for \(I_{{\text{m}}} ={0.58\,\mathrm{\text {m}\text {A}}}\)

Full size image
Fig. 16
figure 16

Hardware measured time-domain waveforms of v for different \(I_{{\text{m}}}\) with \(f={1600\,\mathrm{\text {Hz}}}\): a Chaotic spiking for \(I_{{\text{m}}} ={0.27\,\mathrm{\text {m}\text {A}}}\); b Period-8 spiking for \(I_{{\text{m}}} ={0.29\,\mathrm{\text {m}\text {A}}}\); c Period-4 spiking for \(I_{{\text{m}}} = 0.3{\kern 1pt} {\text{mA}}\); d Period-2 spiking for \(I_{{\text{m}}} ={0.4\,\mathrm{\text {m}\text {A}}}\); e Period-1 spiking for \(I_{{\text{m}}} ={0.5\,\mathrm{\text {m}\text {A}}}\)

Full size image

Here, we assess the deviation of circuit parameters between hardware experiment and numerical simulation by the mean absolute percentage error (MAPE) (De Myttenaere et al. 2016), which can be written as

$$\begin{aligned} {\text {MAPE}} = \frac{1}{N}\sum \limits _{k = 1}^N {\frac{{\left| {{P_{{\text {desired}}k}} - {P_{{\text {measured}}k}}} \right| }}{{{P_{{\text {desired}}k}}}}} \times 100\% \end{aligned}$$
(9)

where \(P_\mathrm{{desiredk}}\) is the circuit parameters in numerical simulation and \(P_{ \rm{measuredk}}\) is the circuit parameters in hardware experiment. N is the number of finely adjusted circuit parameters.

The finely adjusted circuit parameters and corresponding MAPEs for low-frequency and high-frequency stimuli are listed in Tables 1 and 2, respectively. They display that the MAPEs for low-frequency and high-frequency stimuli are all smaller than \(10 \%\), which is acceptable in analog circuit-based hardware experiments.

Table 1 Circuit parameters in hardware experiments and MAPEs for bursting behaviors
Full size table
Table 2 Circuit parameters in hardware experiments and MAPEs for spiking behaviors
Full size table

At low and high frequency stimulus, the MAPE values are respectively shown in Tables 1 and 2, with common fine-tunned parameters \(R_M\), \(R_1\), \(R_2\), and \(R_5\). The difference lies in the fact that for low frequency, fine-tunned parameters was done on the \(I_{{\text{m}}}\), due to its smaller amplitude, whereas for high frequency, fine-tunned parameters was done on \(R_4\). Seen from two tables, in the low-frequency experiments, as the number of periodicity for bursting behavior increases, the MAPE values exhibit a decreasing trend. However, in the high-frequency experiments, from P1 to CH spiking activities, the MAPE values show an increasing trend. The reason for this phenomenon can be found in the single-parameter bifurcation diagram with \(I_{{\text{m}}}\), where wider ranges of \(I_{{\text{m}}}\) corresponding to the adjusted periodic behavior make hardware experiments relatively easier, and vice versa. This is also why period-8 spiking has the largest MAPE.

Conclusion

This paper proposed an N-type second-order LAM to characterize the ion channel of a neuronal membrane, thereby a memristive ion channel-based bionic circuit was constructed. The equilibrium trajectory and its stability of the bionic circuit have complex evolutions over time, which involve FBP and HBP. Numerical simulations and hardware experiments were performed to reveal the fast-slow dynamics in the bionic circuit. It is displayed that the bionic circuit can generate chaotic and periodic bursting behaviors when applying a low-frequency current stimulus. The FB/HB sets were numerically simulated and the bifurcation mechanisms for bursting behaviors were qualitatively deduced. Besides, chaotic/periodic spiking behaviors and coexisting firing patterns were disclosed when applying a high-frequency stimulus. These numerical simulations and hardware experiments verify the memristive ion channel-based bionic circuit can effectively generate chaotic/periodic busting and spiking behaviors.

The done work let us know that the N-type LAM is effective in characterizing ion channels to construct bionic circuits and generate firing patterns. We can deploy N-type LAMs with different mathematical models to extend the design of bionic circuits with this topology. In other words, the topology of the bionic circuit is extendable. Besides, ion channel blockage can affect the firing patterns (Zhou et al. 2020). How to characterize the ion channel blockage effect by an N-type LAM? These deserve our concern in future work.