Dissipativity of a class of cellular neural networks with proportional delays

Abstract

In this paper, the problem of dissipativity is investigated for cellular neural networks with proportional delays. Without assuming monotonicity, differentiability, and boundedness of activation functions, two new delay-independent criteria for checking the dissipativity of the addressed neural networks are established by using inner product properties and matrix theory. Two examples and their simulation results are given to show the effectiveness and less conservatism of the proposed criteria.

1 Introduction

In recent years, neural networks (NNs) and delayed neural networks (DNNs) have been widely investigated because of their extensive applications in classification, parallel computation and optimization and many other fields. In such applications, it is of prime importance to ensure that the designed NNs be stable. Therefore, the stability of NNs and DNNs have received much attention [1, 4]. At the same time, others dynamics properties of NNs and DNNs, such as dissipativity, bifurcation, chaos etc, are better studied [2, 3, 5, 6, 9].

The concept of dissipativity in dynamical systems, introduced in the 1970s, generalizes the idea of a Lyapunov stability and there have been found applications in diverse areas such as stability theory, chaos and synchronization theory, system norm estimation, and robust control. Therefore, it is a very interesting issue to investigate the dissipativity of dynamical systems. In recent years, the dissipativity of the DNNs has recently begun to receive initial research interest and many results have been obtained [2, 7–19]. At present, in research on the dissipativity of DNNs, only a few papers, such as [15, 16], have not been applied to Lyapunov functionals or Lyapunov–Krasovskii functionals and linear matrix inequality (LMI). By utilizing the delay partitioning technique combined with the stochastic integral inequalities, some sufficient conditions ensuring mean-square exponential stability and dissipativity of stochastic neural networks with time delay are derived in [15]. [16] is concerned with the problems of stability and dissipativity analysis for static NNs with time delay by using the delay partitioning technique. Most dissipativity results for DNNs studied in [2, 7, 8, 10, 11, 13, 14, 17, 18] are mainly based on such approaches as Lyapunov functionals or Lyapunov–Krasovskii functionals and LMI. It is well known that Lyapunov functional and Lyapunov–Krasovskii functionals have not been fixed construction method, and the construction of a new Lyapunov functional or Lyapunov–Krasovskii functionals is very difficult. The feature of LMI-based result is that it can consider the neuron’s inhibitory and excitatory effects on neural networks, and LMI can be solved numerically very efficiently. However, in the general case, the matrix was structured in terms of the linear matrix inequality method, which is relatively large, complicated, not easy to be observe directly, such as [8, 10, 11, 13, 14, 17, 18]. In this paper, the dissipativity results obtained for NNs with proportional delays are not based on Lyapunov functional or Lyapunov–Krasovskii functionals and LMI, which is important, as did for NNs model studied in [19–21].

So far, most studied models of dynamic behavior are NNs with constant delay [2, 5, 7, 12, 15], time-varying and bounded delay [8–11, 14, 17, 18], distributed delay [1, 13]. Proportional delay is one of many delay types and objective existence, such as in Web quality of service (QoS) routing decision, proportional delay usually is required. Few results of dynamic behavior of NNs with proportional delays have been reported [19–21]. One of the most important reasons, a NNs with proportional delays is a kind of proportional delay differential equation, while the analytical solution of differential equation with proportional delays is very difficult to be obtained, many scholars dedicated to the research on numerical solution of differential equations with proportional delays [29]. But still it attracted many scholars’ interest [22–28]. The engineering background of proportional delay systems was described in [22, 23]. Iserles [24, 25] had investigated the asymptotic behavior of certain difference equation with proportional delays. Asymptotic behavior of functional differential equations with proportional time delays was studied by Liu in [26]. Van [27] had studied holomorphic solutions to pantograph type equation with neutral fixed points. The feedback stabilization problem of linear systems with proportional delays was analyzed in [28]. The proportional delay system as an important mathematical model often rises in some fields such as physics, biology systems and control theory. Another reason: the time delay function of NNs with proportional delays, is time-varying and unbounded, and previous research methods, such as Lyapunov functional, Halanay-type inequality and LMI, etc., cannot easily deal with such a delay function. So that the study on the dynamic properties of NNs with proportional delays is relatively slow. Nonetheless, some results can be obtained by using the pantograph delay differential equation theory and combining with neural networks’s own characteristics [19–21]. In [19], the global dissipativity of a class of cellular neural networks (CNNs) with multi-pantograph delays is discussed by constructing the Lyapunov functional. The exponential stability of a class of CNNs with multi-pantograph delays is studied by nonlinear measure in [20]. Delay-dependent sufficient conditions ensuring global exponential stability for a class of CNNs with multi-proportional delays is investigated in [21], by employing matrix theory and Lyapunov functional.

Time delays in practical implementation of NNs may not be constants, but time-varying delays with time proportional, that is, proportional delays. Since a neural network usually has a spatial nature due to the presence of an amount of parallel pathways of a variety of axon sizes and lengths, it is desired to model by introducing continuously proportional delay over a certain duration of time. Proportional delay [19–29] is time-varying and unbounded, a delay which is different from constant delay, bounded time-varying delay, and distributed delay, etc. This is because of the pantograph delay function τ(t)=(1−q)t→+∞ as, t→+∞, where q is a constant and satisfies 0<q<1. Although proportional delay and distributed delay are all unbounded time-varying delay, there is a big difference between the two. For distributed delay [1, 13], the delay kernels k _ij :R ⁺→R ⁺ are real valued nonnegative continuous functions that satisfy $\int_{0}^{\infty}k_{ij}(s)\,ds=1$, $\int_{0}^{\infty}sk_{ij}(s)\,ds<\infty$, and there exist a positive number μ such that $\int_{0}^{\infty}\mathrm{e}^{\mu S}k_{ij}(s)\,ds<\infty$. Thus in the use of inequality, distributed delay is easier to handle (see [1, 13]). Compared with distributed delay, due to the pantograph delay function τ(t)=(1−q)t→+∞ as t→+∞ and there being no other conditions, proportional delay is not easy to deal with in the derivation of dynamic behavior of neural networks. Even unbounded time-varying delay was mentioned in the literature [1], which is also a distributed delay. At present, in addition to the distributed delays, in the discussion on the dynamic behavior of NNs with delays, the delay function τ(t) is mostly bounded, we rarely see only general unbounded delay τ(t)≥0. The results in [8–11, 14, 17, 18] are required for the delay function τ(t) to satisfy 0≤τ(t)≤τ and other conditions. The pantograph delay function τ(t)=(1−q)t (pantograph delay factor q is a constant and satisfies 0<q<1) is a monotonically increasing function with the increase of time t>0, thus it may be convenient to control the network’s running time according to the network allowed delays. It is important to ensure that the designed network be stable in the presence of proportional delay. Therefore, it has important theoretical importance to study dynamic behavior of NNs with proportional delays.

Motivated by the discussion above, the previous criteria for checking the dissipativity of the addressed NNs are somewhat conservative due to the construction of constructed Lyapunov functionals and the technicality of the mathematical method used. Hence, it is our intention in this paper to reduce the possible conservatism. Delayed cellular neural networks (DCNNs) have been widely investigated and there have been found many important applications in the fields of pattern recognition, signal processing, optimization and associative memories, detecting speed of moving objects. To the best of our knowledge, few authors have considered dynamical behavior for the CNNs with proportional delays [19–21]. In this paper, the dissipativity of cellular neural networks with proportional delays is discussed, inspired by [29]. Consider that activation function is Lipschitz continuous. By using inner product properties and matrix theory, but it has not been constructed a proper Lyapunov functional or Lyapunov–Krasovskii functionals and LMI, two new delay-independent sufficient conditions of dissipativity of cellular neural networks with proportional delays are obtained. So far, this paper is the first to use the inner product properties to study the dissipativity of neural networks. The main contributions of this paper include the derivations of new global attractive sets and characterization of global dissipativity. These properties play an important role in the design and applications of global dissipative DCNNs, and may be of great interest in many applications, such as chaos and synchronization theory, robust control. The rest of the paper is organized as follows. Model description and preliminary knowledge will be given in Sect. 2. Main results and proofs will be presented and discussed in Sect. 3. Illustrative examples and their simulation results for dissipativity will be given in Sect. 4.

2 Preliminaries and model

Let H be a complex Hilbert space with the inner product 〈⋅,⋅〉 and corresponding norm ∥⋅∥, X be a dense continuously imbedded subspace of H in [29]. Consider the pantograph differential equation

$$ \left\{ \begin{aligned} &\dot{x}(t)=g\bigl(x(t),x(qt)\bigr),\quad t>0, \\ &x(0)=x_0, \end{aligned} \right. $$

(2.1)

where q is a constant with 0<q<1, and g satisfies

(2.2)

with γ,α,β denoting real constants.

By the change of the independent variable y(t)=x(e^t) (see [26, 29]), (2.1) can be transformed into the constant delay differential equation

$$\left\{ \begin{aligned} & \dot{y}(t)=f\bigl(t,y(t),y(t-\tau)\bigr),\quad t>0, \\ &y(t)=\varphi(t),\quad -\tau\leq t\leq 0, \end{aligned} \right. $$

where τ=−logq>0, and

$$ f\bigl(t,y(t),y(t-\tau)\bigr)=\mathrm{e}^tg \bigl(y(t),y(t-\tau)\bigr). $$

(2.3)

It follows from (2.2) and (2.3) that

(2.4)

Definition 2.1

[29]

System (2.1) is said to be dissipative in H if there is a bounded set B⊂H, such that for all bounded sets Φ⊂H there is a time t ₀=t ₀(Φ). such that for all initial values x ₀ contained in Φ, the corresponding solution x(t) is contained in B for all t≥t ₀. B is called an absorbing set in H.

Lemma 2.2

[29]

Suppose

$$V'(t)\leq 2 \mathrm{e}^t\bigl(\gamma+\alpha V(t)+\beta V(t-\tau)\bigr),\quad t>0, $$

with α+β<0 and β>0,γ>0. Then

$$V(t)\leq-\frac{\gamma}{\alpha+\beta}+G\mathrm{e}^{-\mu^{*}t},\quad t>0, $$

where G=2sup_{−τ≤t≤0} V(t)>0, and μ ^∗>0 is defined as

$$\mu^{*}=\inf_{t\geq0}\bigl\{\mu(t):\mu(t)+2 \mathrm{e}^t\bigl(\alpha+\beta \mathrm{e}^{\mu(t)\tau}\bigr)=0\bigr \}. $$

Lemma 2.3

[4]

For any a,b∈R ⁿ and any positive σ>0, the inequality

$$2a^{T}b\leq \sigma a^{T}Xa+\sigma^{-1}b^{T}X^{-1}b $$

holds, in which X is any matrix with X>0.

In this paper, let $\mathbb{R}^{n}$ be a Euclidean Space with the inner product 〈x,y〉=y ^T x and corresponding norm $\Vert x \Vert_{2}=\sqrt{\langle x,x\rangle}$, x=(x ₁,x ₂,…,x _n )^T, y=(y ₁,y ₂,…,y _n )^T∈R ⁿ. Vector norm ∥x∥₂ induced matrix norm $\|A\|_{2}=\sup_{\|x\|_{2}=1}\|Ax\|_{2}=\sqrt{\rho(A^{T}A)}= \sqrt{\lambda_{\max}(A^{T}A)}$, for A∈R ^n×n, where λ _max(A ^T A) denotes the maximum eigenvalue of A ^T A. λ _min(A) denotes the minimum eigenvalue of A.

Consider the system of cellular neural networks with proportional delays described by the following functional differential equations:

$$ \left\{ \begin{aligned} &\dot{u}(t)=-Du(t)+Af\bigl(u(t)\bigr) \\ &\phantom{\dot{u}(t)=\,}+Bf\bigl(u(qt)\bigr)+I,\quad{}t\geq1, \\ &u(t)=u_0,\quad t\in[q,1], \end{aligned} \right. $$

(2.5)

where $D=\operatorname{diag}(d_{1},d_{2},\ldots,d_{n})$, in which d _i >0 represents the rate with which the ith neuron will rest its potential to the resting state in isolation when disconnected from the networks and external inputs; $u(t)=(u_{1}(t),u_{2}(t),\ldots,u_{n}(t))^{T}\in \mathbb{R}^{n}$ denotes the state of the networks at time t; A=(a _ij ) _n×n , B=(b _ij ) _n×n , in which a _ij and b _ij denote the constant connection weight of the jth neuron on the ith neuron at time t and qt, respectively; $f(u(t))=(f_{1}(u_{1}(t)), f_{2}(u_{2}(t)),\allowbreak\ldots,f_{n}(u_{n}(t)))^{T}\in \mathbb{R}^{n}$, $f(u(qt))=(f_{1}(u_{1}(qt)), f_{2}(u_{2}(qt)),\ldots, f_{n}(u_{n}(qt)))^{T}\in \mathbb{R}^{n}$, in which u _i (t) and u _i (qt) correspond to the state of the ith neuron at time t and qt, respectively, f _i (u _i (t)) and f _i (u _i (qt)) denote the activation functions of the jth neuron at time t and qt; respectively. qt=t−(1−q)t, in which (1−q)t=τ(t) denotes delay function, and (1−q)t→+∞ as t→+∞; I=(I ₁,I ₂,…,I _n )^T, in which I _i denotes the constant input. u ₀=(u ₁₀,u ₂₀,…,u _n0)^T, in which u _i0, i=1,2,…,n are constants which denote initial value of u _i (t), i=1,2,…,n at t∈[q,1]. Assume the activation function f _j (⋅) satisfies

(2.6)

where l _j is a nonnegative constant, and let l=max_1≤j≤n {l _j }.

3 Main results

Theorem 3.1

If there exist positive constants σ ₁,σ ₂, and σ ₃, such that

then system (2.5) satisfies

$$ \bigl\langle u(t),\dot{u}(t)\bigr\rangle \leq\gamma+\alpha \bigl\Vert u(t)\bigr\Vert_{2}^2+\beta\bigl\Vert u(qt)\bigr\Vert_{2}^2. $$

(3.1)

Proof

According to the inner product properties, we have

(3.2)

By 〈x,y〉=y ^T x, (2.6) and Lemma 2.3, we obtain

(3.3)

(3.4)

(3.5)

and

(3.6)

By using (3.3), (3.4), (3.5), and (3.6) in (3.2), we obtain

The proof is completed. □

Obviously, γ≥0, β≥0.

By the change of the independent variable

$$ v(t)=u\bigl(\mathrm{e}^t\bigr), $$

(3.7)

system (2.5) can be transformed into cellular neural networks with constant delays and varying coefficients

$$ \left\{ \begin{aligned} &\dot{v}(t)=\mathrm{e}^t\bigl \{-Dv(t)+Af\bigl(v(t)\bigr) \\ &\phantom{\dot{v}(t)=\,}+Bf\bigl(v(t-\tau)\bigr)+I\bigr\},\quad t\geq0, \\ &v(t)=\varphi(t),\quad -\tau\leq t\leq0, \end{aligned} \right. $$

(3.8)

where τ=−logq>0, φ(t)=u ₀.

From (3.1), we have

(3.9)

where $\alpha=-\lambda_{\min}(D)+\frac{1}{2}(\sigma_{1}\|A\|_{2}^{2}l^{2}+\sigma_{1}^{-1}+ \sigma_{2}^{-1}+\sigma_{3}^{-1})$, $\beta=\frac{1}{2}\sigma_{2}\|B\|_{2}^{2}l^{2}$, $\gamma=\frac{1}{2}\sigma_{3}\Vert I\Vert_{2}^{2}$.

Remark 3.2

System (2.5) is equivalent to system (3.8).

In fact, when e^t≥1, then t≥0 and $\dot{v}(t)=\dot{u}(\mathrm{e}^{t})\mathrm{e}^{t}$, i.e.,

$$ \dot{u}\bigl(\mathrm{e}^{t}\bigr)=\dot{v}(t) \mathrm{e}^{-t}. $$

(3.10)

Let

$$ \mathrm{e}^{t}=z,\quad z\geq1, $$

(3.11)

then (3.10) is written as

$$ \dot{u}(z)=z^{-1}\dot{v}(t). $$

(3.12)

From (2.5) and (3.12), one gets

$$\dot{v}(t)z^{-1}=-Du(z)+Af\bigl(u(z)\bigr)+Bf\bigl(u(qz)\bigr)+I. $$

Namely,

$$ \dot{v}(t)=\mathrm{e}^{t}\bigl\{-Du\bigl( \mathrm{e}^{t}\bigr)+Af\bigl(u\bigl(\mathrm{e}^{t}\bigr) \bigr)+Bf\bigl(u\bigl(q\mathrm{e}^{t}\bigr)\bigr)+I\bigr\}. $$

(3.13)

By (3.7), we have

(3.14)

where τ=−logq>0. Using (3.7), (3.14) in (3.13), we obtain

(3.15)

(2) When e^t∈[q,1], then t∈[−τ,0]. From (2.5), we have

$$ u\bigl(\mathrm{e}^{t}\bigr)=u_{0},\quad t\in[- \tau,0], $$

(3.16)

where τ=−logq>0. Thus, the initial function associated with system (3.13) is given by

$$ v(t)=\varphi(t),\quad -\tau\leq t \leq 0, $$

(3.17)

where φ(t)=u ₀.

Conversely, let τ=−logq in (3.15), by (3.7), then (3.15) can be written as (2.5) for t≥1, and for t∈[q,1], by (3.16) and (3.17), the initial function associated with system (2.5) is given by u(t)=u ₀, t∈[q,1].

Thus, system (2.5) is equivalent to system (3.8).

Theorem 3.3

Under condition (2.6), suppose v(t) is a solution of (3.8) and satisfies (3.9), and α+β<0, then for any given ε>0, there exist t=T(Φ,ε), $\varPhi=\sup_{-\tau\leq t\leq0}\Vert\varphi(t)\Vert_{2}^{2}$, such that for all t>T

$$ \bigl\Vert v(t)\bigr\Vert_{2}^2<-\frac{\gamma}{\alpha+\beta}+ \varepsilon. $$

(3.18)

Hence system (3.8) is dissipative, and the open ball $B=B(0,\sqrt{-\frac{\gamma}{\alpha+\beta}+\varepsilon})$ is an absorbing set for any ε>0. where $\alpha=-\lambda_{\min}(D)+\frac{1}{2}(\sigma_{1}\|A\|_{2}^{2}l^{2}+\sigma_{1}^{-1}+\sigma_{2}^{-1}+\sigma_{3}^{-1})$, $\beta=\frac{1}{2}\sigma_{2}\|B\|_{2}^{2}l^{2}$, $\gamma=\frac{1}{2}\sigma_{3}\Vert I\Vert_{2}^{2}$.

Proof

Define

$$ V(t)=\bigl\Vert v(t)\bigr\Vert_{2}^2=\bigl\langle v(t),v(t)\bigr\rangle, $$

(3.19)

then

(3.20)

If β > 0, the conclusion follows directly from (3.20) and Lemma 2.2.

If β=0, (3.20) yields

(3.21)

Integrating (3.21) from 0 to t gives

$$V(t)\leq \mathrm{e}^{2\alpha\int_{0}^{t}\mathrm{e}^{s}\,ds}V(0)+\bigl(1-\mathrm{e}^{2\alpha\int_{0}^{t}\mathrm{e}^{s}\,ds}\bigr) \frac{\gamma}{-\alpha},\quad t>0, $$

which shows that (3.18) holds for any t>T. The proof is completed. □

Corollary 3.4

Suppose under condition (2.6) there exist positive constants σ ₁,σ ₂,σ ₃, such that

(3.22)

holds, then system (2.5) is dissipative and the open ball $B=B(0,\sqrt{-\frac{\gamma}{\alpha+\beta}+\varepsilon})$ is an absorbing set for any ε>0, where $\alpha=-\lambda_{\min}(D)+\frac{1}{2}(\sigma_{1}\|A\|_{2}^{2}l^{2}+\sigma_{1}^{-1}+\sigma_{2}^{-1}+\sigma_{3}^{-1})$, $\beta=\frac{1}{2}\sigma_{2}\|B\|_{2}^{2}l^{2}$, $\gamma=\frac{1}{2}\sigma_{3}\Vert I\Vert_{2}^{2}$.

If taking ε=1 in Lemma 2.3, we have

$$ 2a^{T}b\leq a^{T}Xa+b^{T}X^{-1}b, $$

(3.23)

using (3.23) in the proof of Theorem 3.1, we obtain the following result.

Corollary 3.5

Suppose under condition (2.6),

$$ -\lambda_{\min}(D)+\frac{1}{2}\bigl\{\bigl(\|A \|_{2}^{2}+\|B\|_{2}^{2} \bigr)l^2+3\bigr\}<0 $$

(3.24)

holds, then system (2.5) is dissipative and the open ball $B=B(0,\sqrt{-\frac{\gamma}{\alpha+\beta}+\varepsilon})$ is an absorbing set for any ε>0, where $\alpha=-\lambda_{\min}(D)+\frac{1}{2}(\|A\|_{2}^{2}l^{2}+3)$, $\beta=\frac{1}{2}\|B\|_{2}^{2}l^{2}$, $\gamma=\frac{1}{2}\Vert I\Vert_{2}^{2}$.

Remark 3.6

From the viewpoint of time delay, delay function τ(t)=(1−q)t with (1−q)t→+∞ as t→+∞ in the paper, is different from others, such as constant delay, varying-delay and distributed delay and so on. Thus, obtained results in [2, 7–19] cannot be applied to models (2.5) and (3.8).

Remark 3.7

In [2, 7–19], some delay-independent or delay-dependent sufficient conditions of dissipativity of dynamical neural networks with time delays were obtained by constructing Lyapunov functional, or Lyapunov–Krasovskii functionals and LMI etc. However, in this paper, two new delay-independent sufficient conditions of dissipativity of cellular neural networks with proportional delays are obtained by using the property of inner product and matrix theory only.

Remark 3.8

In the paper, activation function is Lipschitz continuous, and it may be unbounded, nondifferentiable, nonmonotone increasing; etc.

Remark 3.9

In the paper, model (3.8) is different from the model in [30]. Model (3.8) is cellular neural networks with constant delays and varying coefficients, where varying coefficients contain e^t, therefore, it is unbounded time-varying. But time-varying coefficients of the model in [30] are bounded.

4 Example

Example 4.1

In (2.5), taking

where q=0.5, $f(u)=\sin(\frac{1}{4}u)+\frac{1}{4}u$, hence $l=\frac{1}{2}$, where f(u) is an unbounded function. Taking σ ₁=σ ₂=σ ₃=1, thus, we have

hence

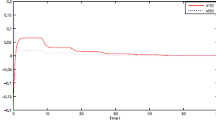
it satisfies the condition of Corollary 3.4, then the system is dissipative, and $\alpha=-\lambda_{\min}(D)+ \frac{1}{2}(\|A\|_{2}^{2}l^{2}+3)=-0.8750$, $\beta=\frac{1}{2}\|B\|_{2}^{2}l^{2}=0.6545$, $\gamma=\frac{1}{2}\Vert I\Vert_{2}^{2}=4$, then the open circle $B= B(0,\sqrt{-\frac{\gamma}{\alpha+\beta}+\varepsilon})=B(0,\sqrt{18.1406+\varepsilon})$ is an absorbing set for any ε>0. Take ε=0.01, the simulation results by using Matlab is shown in Fig. 1.

Fig. 1

Phase trajectories and an absorbing set of Example 4.1

On the other hand, it can be easily checked that

$$A+A^{T}+BB^{T}+\frac{1}{q}E= \left ( \begin{array}{c@{\quad}c} 11&-1\\ -1&7 \end{array} \right ) >0. $$

Theorems 5 and 6 in [19] are not satisfied, so those in [19] are not applicable to this example. Here E denotes the identity matrix.

Example 4.2

In (2.5), taking

where q=0.5, $f(u)=\frac{1}{4}(|u+1|-|u-1|)$, hence $l=\frac{1}{2}$, where f(u) is not a differentiable and monotonically increasing function. We have

Hence

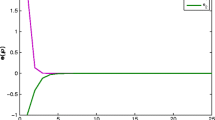
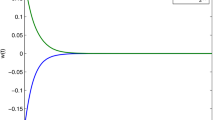
it satisfies the condition of Corollary 3.5, then the system is dissipative, and $\alpha=-\lambda_{\min}(D) +\frac{1}{2}(\|A\|_{2}^{2}l^{2}+3)=-2.1291$, $\beta=\frac{1}{2}\|B\|_{2}^{2}l^{2}=1.9105$, $\gamma=\frac{1}{2}\Vert I\Vert_{2}^{2}=7$, then the open ball $B= B(0,\sqrt{-\frac{\gamma}{\alpha+\beta}+\varepsilon})=B(0,\sqrt{32.0220+\varepsilon})$ is an absorbing set for any ε>0. Take ε=0.01. The simulation results by using Matlab are shown in Figs. 2 and 3, where the profile of open ball was drawn off in Fig. 3 so that these trajectories in attracting set inside can been observed.

Fig. 2

Phase trajectories and an absorbing set of Example 4.2

Fig. 3

Phase trajectories and profile of an absorbing set of Example 4.2

On the other hand, it can be easily checked that

By using Matlab, we find that the eigenvalue of the above matrix are λ ₁=2.4516, λ ₂=11.3350, and λ ₃=21.2134, respectively. Therefore, the matrix is positive definite. Theorems 5 and 6 in [19] are not satisfied, so those in [19] are not applicable to this example.

5 Conclusions

In this paper, the dissipativity of a class of cellular neural networks with proportional delays is considered. By using inner product properties and matrix theory, two new delay-independent sufficient conditions are derived for the dissipativity of the system, which might have an impact in the studying the stability, instability, and the existence of periodic solutions. It can be shown that the derived criteria are less conservative than previously existing results through the numerical examples and their simulation results. The dissipativity criterion is also suitable for Hopfield neural networks with proportional delays in the paper.