1 Introduction

In the past decades, neural networks have received considerable attention due to their wide applications in various areas such as image processing, signal processing, associative memory, pattern classification, optimization, and moving object speed detection [1]. It has been shown that time delays may be an important source of oscillation, divergence, and instability in systems [2–6], and thus neural networks with time delay have been widely studied in recent years. For example, the stability analysis problem has been addressed in [7–13]. The state estimation problem has been investigated in [14–16]. The passivity problem have been studied in [17–21].

In recent years, there has been a growing interest in stochastic models since stochastic modeling has come to play an important role in many branches of science and engineering [22]. It has also been shown that a neural network could be stabilized or destabilized by certain stochastic inputs [23]. Hence, there has been an increasing interest in neural networks in the presence of stochastic perturbation, and some related results have been published. The problem of stochastic effects to neural networks has been first investigated in [24]. When time delay appears in the stochastic neural networks, the problem of stability has been investigated in [25, 26] based on the delay partitioning approach [27, 28]. The stability analysis problem has been considered for stochastic neural networks with both the discrete and distributed time delays in [29, 30]. It is noted that the results in [25, 26, 29, 30] are concerned with the constant time delay. The stability problem of stochastic neural networks with time-varying delay has been discussed in [31, 32]. The passivity analysis of stochastic neural networks with time-varying delays and parametric uncertainties has been investigated in [33], where both delay-independent and delay-dependent stochastic passivity conditions have been presented in terms of LMIs.

On the other hand, it has been shown that the theory of dissipative systems plays an important role in system and control areas, and the dissipative theory gives a framework for the design and analysis of control systems using an input–output description based on energy-related considerations [34]. Thus, dissipativity has been attracting a great deal of attention [35]. Very recently, the problem of delay-dependent dissipativity analysis has been investigated for deterministic neural networks with distributed delay in [36], where a sufficient condition has been given to guarantee the considered neural network dissipative. In [37], some delay-dependent dissipativity criteria have been established for static neural networks with time-varying or time-invariant delay. Although the importance of dissipativity has been widely recognized, few results have been proposed for the dissipativity of stochastic neural networks with time-varying delay or constant time delay, which motivates the work of this paper.

In this paper, we are concerned with the problem of dissipativity for stochastic neural networks with time delay. By use of the delay partitioning technique and the stochastic integral inequalities, some criteria are derived to ensure the exponential stability and dissipativity of the considered neural networks. Some special cases are also considered. The obtained delay-dependent results also rely upon the partitioning size. Finally, several numerical examples are given to demonstrate the reduced conservatism of the proposed methods.

Notation: The notations used throughout this paper are fairly standard. ℝn and ℝm×n denote the n-dimensional Euclidean space and the set of all m×n real matrices, respectively. The notation X>Y (X≥Y), where X and Y are symmetric matrices, means that X−Y is positive definite (positive semidefinite). I and 0 represent the identity matrix and a zero matrix, respectively. The superscript “T” represents the transpose, and diag{⋯} stands for a block-diagonal matrix. ∥⋅∥ denotes the Euclidean norm of a vector and its induced norm of a matrix. \(\mathcal{L}_{2}[0,+\infty)\) represents the space of square-integrable vector functions over [0,+∞). \(\mathbb{E}\{x\}\) means the expectation of the stochastic variable x. For an arbitrary matrix B and two symmetric matrices A and C, denotes a symmetric matrix, where “∗” denotes the term that is induced by symmetry. Matrices, if their dimensions are not explicitly stated, are assumed to have compatible dimensions for algebraic operations.

2 Preliminaries

Consider the following stochastic neural network with time-delay:

$$ \begin{cases} \mathrm{d} {x}(t)=\bigl[-Cx(t)+Af \bigl(x(t)\bigr)\\ \qquad\quad {}+Bf\bigl(x\bigl(t-\tau(t)\bigr)\bigr) +u(t)\bigr]\,\mathrm{d}t\\ \qquad\quad {}+ \bigl[M_1x(t)+M_2x\bigl(t-\tau(t)\bigr)\bigr] \,\mathrm{d}\omega(t)\\ y(t)=f\bigl(x(t)\bigr) \end{cases} $$
(1)

where x(t)=[x 1(t) x 2(t) ⋯ x n (t)T, f(x(k))=f 1(x 1(t)) f 2(x 2(t)) ⋯ f n (x n (t))]T, x i (t) is the state of the ith neuron at time t, and f i (x i (t)) denotes the neuron activation function; y(t) is the output of the neural network, \(u(t) \in\mathcal{L}_{2}[0,+\infty)\) is the input, and ω(t) is a one-dimensional Brownian motion satisfying \(\mathbb{E}\{\mathrm{d}\omega (t)\}=0\) and \(\mathbb{E}\{\mathrm{d}\omega^{2}(t)\}=\mathrm{d}t\); C=diag{c 1,c 2,…,c n } is a diagonal matrix with positive entries; A=(a ij ) n×n and B=(b ij ) n×n are, respectively, the connection weight matrix and the delayed connection weight matrix; M 1 and M 2 are known real constant matrices; τ(t) is the time-delay and in this paper, two cases of τ(t), namely, time-varying and constant, will be discussed, respectively.

Throughout this paper, we shall use the following assumption and definitions.

Assumption 1

([12]) Each activation function f i (⋅) in (1) is continuous and bounded, and satisfies

$$ l_i^{-}\leq \frac{f_i(\alpha_1)-f_i(\alpha_2)}{\alpha_1-\alpha_2}\leq l_i^{+},\quad i=1,2,\ldots,n $$
(2)

where f i (0)=0, α 1, α 2∈ℝ, α 1≠α 2, and \(l_{i}^{-}\) and \(l_{i}^{+}\) are known real scalars and they may be positive, negative, or zero, which means that the resulting activation functions may be nonmonotonic and more general than the usual sigmoid functions and Lipschitz-type conditions.

Definition 1

[22] Stochastic time-delay neural network (1) with u(t)=0 is said to be mean-square exponentially stable if there is a positive constant λ such that

$$ \lim _{t\rightarrow+\infty}\sup\frac{1}{t}\log\mathbb{E} \bigl\{ \bigl\Vert x(t)\bigr\Vert ^2\bigr\} \leq - \lambda. $$
(3)

We are now in a position to introduce the definition on dissipativity. Let the energy supply function of neural network (1) be defined by

(4)

where \(\mathcal{Q}\), \(\mathcal{S,}\) and \(\mathcal{R}\) are real matrices with \(\mathcal{Q}\), \(\mathcal{R}\) symmetric, and \(\langle{a},b\rangle_{T}=\int_{0}^{T}a^{\mathrm{T}}b\,\mathrm{d}t\). Without loss of generality, it is assumed that \(\mathcal{Q}\leq 0\) and denoted that \(-\mathcal{Q}=\mathcal{Q}_{-}^{\mathrm{T}}\mathcal{Q}_{-}\) for some \(\mathcal{Q}_{-}\).

Definition 2

Neural network (1) is said to be strictly \((\mathcal{Q},\mathcal {S},\mathcal{R})\)-γ-dissipative if, for some scalar γ>0, the following inequality:

$$ \mathbb{E}\bigl\{G(u,y,T)\bigr\}\geq \gamma\mathbb{E}\bigl\{ \langle u,u\rangle_T\bigr\},\quad \forall T\geq 0 $$
(5)

holds under zero initial condition for any nonzero disturbance \(u \in \mathcal{L}_{2}[0,\infty)\).

The main purpose of this paper is to establish some delay-dependent conditions, which ensures neural network (1) is mean-square exponentially stable and strictly \((\mathcal{Q},\mathcal{S},\mathcal {R})\)-γ-dissipative.

To end this section, we introduce the following integral inequalities, which will play important roles in deriving main results.

Lemma 1

(Jensen inequality) [38]

For any matrix W>0, scalars γ 1 and γ 2 satisfying γ 2>γ 1, a vector function ω:[γ 1,γ 2]→ℝn, if the following integrations concerned are well defined, then

(6)

Lemma 2

Let n-dimensional vector functions x(t), φ(t), and g(t) satisfy the stochastic differential equation

$$ \mathrm{d} {x}(t)=\varphi(t)\,\mathrm{d}t+g(t) \,\mathrm{d}\omega(t) $$
(7)

where ω(t) follows the same definition as that in (1). For any matrix , scalars γ 1, γ 2, γ(t) satisfying γ 1≤γ(t)≤γ 2, if the following integrations concerned are well defined, then

(8)

where

Proof

Denote \(\delta_{1}(t)=\int_{t-\gamma(t)}^{t-\gamma_{1}}\varphi(\alpha )\,\mathrm{d}\alpha\) and \(\delta_{2}(t)=\int_{t-\gamma_{2}}^{t-\gamma(t)}\varphi(\alpha)\, \mathrm{d}\alpha\). When γ 1<γ(t)<γ 2, according to Lemma 1, we have that

(9)

Based on the lower bounds lemma of [39], we get

(10)

which implies

(11)

Then, we can get from (9) and (11) that

(12)

It is noted that when γ(t)=γ 1 or γ(t)=γ 2, we have δ 1(t)=0 or δ 2(t)=0, respectively, and thus (12) still holds based on Lemma 1. On the other hand, it is clear from (7) that

(13)

and

(14)

Substituting (13) and (14) into (12) and considering

we can get (8) immediately. This completes the proof. □

Remark 1

It is noted that a stochastic integral inequality is proposed in Lemma 2 based on the lower bounds lemma of [39]. It can be found that when γ(t)=γ 1 or γ(t)=γ 2, the stochastic integral inequality (8) reduces to the following stochastic integral inequality:

(15)

3 Main results

In this section, we make use of the delay partitioning technique to derive some new delay-dependent dissipativity criteria for neural network (1). Both time-varying and constant time delays are treated, respectively. For presentation convenience, we denote e i =[02n×2(i−1)n I 2n 02n×2(m+1−i)n ] (i=1,2,…,m+1) and

3.1 The case of a time-varying delay

In this subsection, the delay τ(t) is time-varying and satisfies 0≤τ(t)≤τ and \(\dot{\tau}(t)\leq \mu\). It is noted that the neural network (1) can be rewritten as

$$ \begin{cases} \mathrm{d} {x}(t)=\varphi(t) \,\mathrm{d}t+g(t)\,\mathrm{d}\omega(t)\\ z(t)=\varPi_2\eta(t) \end{cases} $$
(16)

where \(\varphi(t)=\mathcal{C}_{1}e_{1}\theta(t)+\mathcal{C}_{2}\eta(t-\tau (t))+u(t)\) and g(t)=M 1 Π 1 e 1 θ(t)+M 2 Π 1 η(t−τ(t)).

Theorem 1

Given an integer m>0, neural network (1) is mean-square exponentially stable and strictly \((\mathcal{Q},\mathcal{S},\mathcal {R})\)-γ-dissipative, if there exist matrices P>0, (i=1,2,…,m), Y>0, Q>0, diagonal matrices F l (l=1,2,…,m+2), G 1=diag{λ 1,λ 2,…,λ n }>0, G 2=diag{δ 1,δ 2,…,δ n }>0, and a scalar γ>0, such that for any \(j\in\mathcal{J}=\{ 1,2,\ldots,m\}\)

(17)

where \(\hat{Z}= (\frac{\tau}{m} )^{2}\sum_{i=1}^{m}Z_{i}\), \(\hat{P}=P+(G_{1}+G_{2})(L^{+}-L^{-})\), and

Proof

First, let us consider stability of neural network (1) with u(t)=0. By Schur complement, we obtain from (17) that

(18)

It is clear from (18) that we can always find two small enough scalars ε 1>0 and ε 2>0 such that

(19)

where \(\hat{\varXi}_{11}^{j}= \varXi_{11}^{j}+\tau^{2}\varepsilon_{1}e_{1}^{\mathrm{T}}\varPi_{1}^{\mathrm{T}}\varPi_{1}e_{1}\) and \(\bar{Z}= (\frac{\tau}{m} )^{2}\sum_{i=1}^{m}Z_{i}+\tau^{2}\varepsilon_{2}\). Choose the following Lyapunov–Krasovskii functional for neural network (1) with u(t)=0:

$$ V(t)=V_1(t)+V_2(t)+V_3(t)+V_4(t) $$
(20)

where

where \(\hat{\varphi}(t)=\mathcal{C}_{1}e_{1}\theta(t)+\mathcal{C}_{2}\eta (t-\tau(t))\). By Itô’s formula, we have

$$ \mathrm{d} {V}(t)=\mathbb{L} {V}(t)\,\mathrm{d}t+\sigma(t)\,\mathrm{d} \omega(t) $$
(21)

where σ(t)=2x(t)T(P−L − G 1+L + G 2)g(t)+2f(x(t))T(G 1−G 2)g(t). It can be calculated that

(22)
(23)
(24)
(25)

It is noted that, for any t≥0, there should exist an integer \(j\in\mathcal{J}\) such that \(\tau(t)\in [\frac{(j-1)\tau}{m},\,\frac {j\tau}{m} ]\). Then based on Lemma 2, we can get that

(26)

where

Meanwhile, we can also get from (15) that

(27)

On the other hand, by (2), we have that for any i∈{1,2,…,m+1}

(28)

which implies

$$ 0\leq 2\sum _{i=1}^{m+1}\theta(t)^\mathrm{T}e_i^\mathrm{T} \mathcal {D}_1^\mathrm{T}F_{i}\mathcal{D}_2e_i \theta(t). $$
(29)

We can also get from (2) that

$$ 0\leq 2\eta\bigl(t-\tau(t) \bigr)^\mathrm{T}\mathcal{D}_1^\mathrm {T}F_{m+2}\mathcal{D}_2\eta\bigl(t-\tau(t)\bigr). $$
(30)

On the other hand, it can be easily obtained from (20) that there exists a scalar ε 3>0 such that

(31)

Thus, we have from (22)–(27) and (29)–(31) that for \(\tau(t)\in [\frac{(j-1)\tau}{m},\,\frac{j\tau }{m} ]\),

(32)

Let λ>0 be sufficiently small such that

$$ \lambda\varepsilon_3- \varepsilon_1{\tau}<0,\qquad \lambda\varepsilon_3- \varepsilon_2{\tau} < 0 $$
(33)

and for any \(j\in\mathcal{J}\),

$$ \lambda\varepsilon_3+ \lambda_{\max}\bigl(\hat{\varXi}^j\bigr)<0. $$
(34)

Then we can get from (32), (33), and (34) that

$$ \mathbb{E}\bigl\{\mathbb{L} {V}(t)+ \lambda{V}(t)\bigr\}<0. $$
(35)

By Itô’s formula, we have

(36)

Integrating from 0 to t and taking expectation on both sides of (36) yields

(37)

Combining (20), (35), and (37), we have

(38)

which implies (3) holds. Thus, the mean-square exponential stability of neural network (1) is proved.

Now let us proceed to discuss the strictly \((\mathcal{Q},\mathcal {S},\mathcal{R})\)-γ-dissipativity of neural network (1). To this end, choose the following Lyapunov–Krasovskii functional for neural network (1):

$$ V(t)=V_1(t)+V_2(t)+V_3(t) $$
(39)

where V 1(t) and V 2(t) follow the same definitions as those in (20), and

$$ V_3(t)=\frac{\tau}{m}\sum _{i=1}^{m}\int _{-\frac {i}{m}\tau}^{-\frac{i-1}{m}\tau} \int _{t+\alpha}^{t}{\varphi }(s)^\mathrm{T}Z_i{ \varphi}(s)\,\mathrm{d}s\,\mathrm{d}\alpha. $$

Applying a similar analysis method employed in the proof of stability, we have that for \(\tau(t)\in [\frac{(j-1)\tau}{m},\,\frac{j\tau }{m} ]\),

(40)

where

We can get from (18) that for any nonzero disturbance u(t)∈L 2[0,∞),

$$ \mathbb{E} \biggl\{\int _{0}^{T}\mathbb{L} {V}\bigl(x(t)\bigr)\,\mathrm {d}t-G(u,y,T)+\gamma\langle u,u\rangle_T \biggr\}<0 $$
(41)

which, by Dynkin’s formula, implies under zero initial condition

(42)

Thus, we find (5) holds. Therefore, neural network (1) is strictly \((\mathcal{Q},\mathcal{S},\mathcal{R})\)-γ-dissipative. This completes the proof. □

Remark 2

A dissipativity condition is proposed in Theorem 1 for neural network (1) based on the delay partitioning technique and stochastic integral inequality (8) and (15). It is noted that the Lyapunov–Krasovskii functional (20) makes full use of the information on neuron activation functions and the involved time delay, and thus our result has less conservatism. Moreover, the conservatism reduction of the proposed condition becomes more obvious with the partitioning getting thinner (i.e., m becoming larger), which will be demonstrated in Sect. 4. It should be pointed out that the LMIs in (17) are not only over the matrix variables, but also over the scalar γ, and thus by setting δ=−γ and minimizing δ subject to (17), we can obtain the optimal dissipativity performance γ (by γ=−δ).

Remark 3

If we make use of the free-weighting matrix method together with the delay partitioning technique to deal with the same problem, then in order to get a less conservative result, for any subinterval \([\frac{(j-1)\tau}{m},\,\frac{j\tau}{m} ]\), we need to introduce the following two equalities:

and

Therefore, 4mn 2 decision variables should be introduced. But in this paper, we utilize the stochastic integral inequality (8) to deal with the term \(\int_{t-\frac{j\tau}{m}}^{t-\frac{j-1}{m}\tau}\hat {\varphi}(s)\,\mathrm{d}s\) instead of the free-weighting matrix method, and only mn 2 decision variables are required. Thus, our condition has computational advantage over the condition based on the free-weighting matrix method.

From Theorem 1, it is easily get the following stability condition for neural network (1) with u(t)=0.

Corollary 1

Given an integer m>0, neural network (1) with u(t)=0 is mean-square exponentially stable, if there exist matrices P>0, (i=1,2,…,m), Y>0, Q>0, diagonal matrices F l (l=1,2,…,m+2), G 1=diag{λ 1,λ 2,…,λ n }>0, and G 2=diag{δ 1,δ 2,…,δ n }>0, such that for any \(j\in\mathcal{J}\),

(43)

where \(\varXi_{12}^{j}\), \(\varXi_{22}^{j}\), \(\hat{Z}\), and \(\hat{P}\) follow the same definitions as those in Theorem 1, and

Remark 4

It is noted that the stability condition of [32] is only valid for the case of \(l_{i}^{-}=0\). Moreover, if setting m=1, λ i =0, δ i =0, , and , the Lyapunov–Krasovskii functional (20) coincides with that of [32]. Thus, our Lyapunov–Krasovskii functional is much more general than that of [32] even for the case of m=1, that is, our result has less conservatism than the condition of [32] even when m=1.

Next, we specialize Theorem 1 to the problem of passivity analysis of neural network (1). Choosing \(\mathcal{Q}=0\), \(\mathcal{S}=I\), and \(\mathcal{R}=2\gamma I\), we can get the following corollary based on Theorem 1.

Corollary 2

Given an integer m>0, neural network (1) is passive, if there exist matrices P>0, (i=1,2,…,m), Y>0, Q>0, diagonal matrices F l (l=1,2,…,m+2), G 1=diag{λ 1,λ 2,…,λ n }>0, G 2=diag{δ 1,δ 2,…,δ n }>0, and a scalar γ>0, such that for any j∈{1,2,…,m}

(44)

where \(\bar{{\varXi}}_{11}^{j}\) follows the same definition as that in Corollary 1, \(\varXi_{12}^{j}\), \(\varXi_{22}^{j}\), \(\hat{Z}\), and \(\hat{P}\) follow the same definitions as those in Theorem 1, and \(\bar{\varXi}_{13}=-e_{1}^{\mathrm{T}}\varPi_{2}^{\mathrm{T}}+e_{1}^{\mathrm{T}}\varPi_{1}^{\mathrm{T}}(P-L^{-}G_{1}+L^{+}G_{2})+e_{1}^{\mathrm{T}}\varPi_{2}^{\mathrm{T}}(G_{1}-G_{2})\).

Remark 5

It should be pointed out that when λ i =0, δ i =0, Q=0, , and Z i =mZ, the Lyapunov–Krasovskii functional (20) coincides with that of [33]. Thus, our Lyapunov–Krasovskii functional is much more general than that of [33]. Moreover, the passivity condition of [33] is only valid for the case of \(l_{i}^{-}=0\). Thus, our result is more effective that of [33].

3.2 The case of a constant time delay

For simplicity, we rewrite neural network (1) as

$$ \begin{cases} \mathrm{d} {x}(t)=\check{\varphi}(t) \,\mathrm{d}t+\hat{g}(t)\,\mathrm{d}\omega(t) \\ z(t)=\varPi_2\eta(t) \end{cases} $$
(45)

where \(\check{\varphi}(t)=(\mathcal{C}_{1}e_{1}+\mathcal{C}_{2}e_{m+1})\theta (t)+u(t)\) and \(\hat{g}(t)=(M_{1}\varPi_{1}e_{1}+M_{2}\varPi_{1}e_{m+1})\theta(t)\).

Theorem 2

Given an integer m>0, neural network (1) is mean-square exponentially stable and strictly \((\mathcal{Q},\mathcal{S},\mathcal {R})\)-γ-dissipative, if there exist matrices P>0, Z i >0 (i=1,2,…,m), Q>0, diagonal matrices F l (l=1,2,…,m+1), G 1=diag{λ 1,λ 2,…,λ n }>0, G 2=diag{δ 1,δ 2,…,δ n }>0, and a scalar γ>0, such that

(46)

where Ξ 13, \(\hat{Z}\), and \(\hat{P}\) follow the same definitions as those in Theorem 1, and

Proof

First, let us consider stability of neural network (1) with u(t)=0. By Schur complement, we obtain from (46) that

(47)

It is clear from (47) that we can always find two small enough scalars ε 1>0 and ε 2>0 such that

(48)

where \(\hat{\varOmega}_{11}=\varOmega_{11}+\tau^{2}\varepsilon_{1}e_{1}^{\mathrm{T}}\varPi_{1}^{\mathrm{T}}\varPi_{1}e_{1}\). Choose the following Lyapunov–Krasovskii functional for neural network (1) with u(t)=0:

$$ V(t)=V_1(t)+{V}_2(t)+V_3(t)+V_4(t) $$
(49)

where V 1(t) follows the same definition as that in (20), and

where \(\bar{\varphi}(t)=(\mathcal{C}_{1}e_{1}+\mathcal{C}_{2}e_{m+1})\theta (t)\). By Itô’s formula, we have

$$ \mathrm{d} {V}(t)=\mathbb{L} {V}(t)\,\mathrm{d}t+\sigma(t)\,\mathrm{d} \omega(t) $$
(50)

where \(\sigma(t)=2x(t)^{\mathrm{T}}(P-L^{-}G_{1}+L^{+}G_{2})\hat {g}(t)+2f(x(t))^{\mathrm{T}}(G_{1}-G_{2})\hat{g}(t)\). It can be calculated that

(51)
(52)
(53)
(54)

We can get from (15) that

(55)

On the other hand, it can be easily obtained from (49) that there exists a scalar ε 3>0 such that

(56)

Thus, we have from (51)–(56) and (29) that

(57)

Let λ>0 be sufficiently small such that

(58)

which combining with (57) implies

$$ \mathbb{E}\bigl\{\mathbb{L} {V}(t)+ \lambda{V}(t)\bigr\}<0. $$
(59)

Then, by using a similar method as employed in Theorem 1, we can get prove the mean-square exponential stability of neural network (1).

Now let us proceed to discuss the strictly \((\mathcal{Q},\mathcal {S},\mathcal{R})\)-γ-dissipativity of neural network (1). To this end, choose the following Lyapunov–Krasovskii functional for neural network (1):

$$ V(t)=V_1(t)+V_2(t)+V_3(t) $$
(60)

where V 1(t) follows the same definition as that in (20), V 2(t) follows the same definition as that in (49), and

$$ V_3(t)=\frac{\tau}{m}\sum _{i=1}^{m}\int _{-\frac {i}{m}\tau}^{-\frac{i-1}{m}\tau} \int _{t+\alpha}^{t}\check {{\varphi}}(s)^\mathrm{T}Z_i \check{{\varphi}}(s)\,\mathrm{d}s\,\mathrm {d}\alpha. \\ $$

Then, by using a similar method as employed in Theorem 1, we can easily get that neural network (1) is strictly \((\mathcal {Q},\mathcal{S},\mathcal{R})\)-γ-dissipative. This completes the proof. □

Similarly, it is easy to get the following stability and passibility conditions for neural network (1) with constant time delay.

Corollary 3

Given an integer m>0, neural network (1) with u(t)=0 is mean-square exponentially stable, if there exist matrices P>0, Z i >0 (i=1,2,…,m), Q>0, diagonal matrices F l (l=1,2,…,m+1), G 1=diag{λ 1,λ 2,…,λ n }>0, and G 2=diag{δ 1,δ 2,…,δ n }>0, such that

(61)

where \(\hat{Z}\), and \(\hat{P}\) follow the same definitions as those in Theorem 1, Ω 13 and Ω 14 follow the same definitions as those in Theorem 2, and

Remark 6

It is noted that compared with the Lyapunov–Krasovskii functionals applied in [25, 26], the Lyapunov–Krasovskii functional (49) includes more information on neuron activation functions and the involved constant delay. Thus, our Lyapunov–Krasovskii functional is more general and leads to an improved stability criterion.

Corollary 4

Given an integer m>0, neural network (1) is passive, if there exist matrices P>0, Z i >0 (i=1,2,…,m), Q>0, diagonal matrices F l (l=1,2,…,m+1), G 1=diag{λ 1,λ 2,…,λ n }>0, G 2=diag{δ 1,δ 2,…,δ n }>0, and a scalar γ>0, such that

(62)

where \(\bar{\varOmega}_{11}\) follows the same definition as that in Corollary 3, \(\bar{\varXi}_{13}\) follows the same definitions as those in Corollary 2, \(\hat{Z}\), and \(\hat{P}\) follow the same definitions as those in Theorem 1, Ω 13 and Ω 14 follow the same definitions as those in Theorem 2.

4 Numerical examples

In this section, we shall give several numerical examples to show the validity and potential of our developed theoretical results.

Example 1

Consider neural network (1) with u(t)=0 and the following parameters:

and A=0, \(l_{1}^{-}=l_{2}^{-}=l_{3}^{-}=0\), \(l_{1}^{+}=0.4129\), \(l_{2}^{+}=3.8993\), \(l_{3}^{+}=1.0160\).

In this example, we suppose the time delay is a constant time delay. Applying the stability criteria in [25, 26], and Corollary 3 in this paper, the maximum admissible upper bounds of τ are listed in Table 1, from which it can be found that Corollary 3 in this paper has less conservative than the those criteria in [25, 26].

Table 1 Maximum admissible upper bounds of τ
Full size table

Example 2

Consider neural network (1) with u(t)=0 and the following parameters:

and take the activation functions f 1(s)=f 2(s)=tanh(0.5s). It is clear that the activation functions satisfy Assumption 1 with \(l_{1}^{-}=l_{2}^{-}=0\) and \(l_{1}^{+}=0.5\), \(l_{2}^{+}=0.5\).

In this example, we suppose the time delay is a time-varying delay. By using the stability criteria in [32] and Corollary 1 in this paper, the maximum admissible upper bounds of τ for various μ are listed in Table 2, from which it can be found that Corollary 1 in this paper gives better results than the condition in [32] even for m=1.

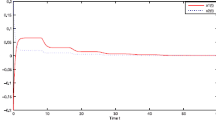
Table 2 Maximum admissible upper bounds of τ
Full size table

It is assumed that τ(t)=3.97+sin(0.8t). A straightforward calculation gives τ=4.97 and μ=0.8. The corresponding state responses of the considered neural network are shown at Fig. 1, where the initial condition x(t)=[3 2]T t∈[−4.97, 0]. We can find from Fig. 1 that the corresponding state responses converge to zero.

Fig. 1
figure 1

State responses of the considered neural network

Full size image

Example 3

Consider neural network (1) with the following parameters:

In this example, we suppose the time delay is a time-varying delay. We first compare the passivity condition in Corollary 2 of this paper with that of [33]. To this end, we let τ=1.5, \(l_{1}^{-}=l_{2}^{-}=0\), and \(l_{1}^{+}=l_{2}^{+}=1\). Table 3 provides the minimum passivity performance γ for different methods. It is clear that Corollary 1 in this paper greatly improves the criterion in [33]. In particular, when μ=0.8, the method of [33] fails, but Corollary 2 of this paper is still valid.

Table 3 Minimum passivity performance γ
Full size table

Next, let us pay attention to the dissipativity of the considered neural network and choose

τ=1, \(l_{1}^{-}=-0.1\), \(l_{2}^{-}=0.1\), and \(l_{1}^{+}=l_{2}^{+}=0.9\). The optimal dissipativity performance γ for different m and μ can be found in Table 4, from which we can find that the optimal dissipativity performance γ depends on m and μ. Specifically, when m is fixed, the larger μ(≤1) corresponds to the smaller γ, and when μ is fixed, the larger m corresponds to the larger γ. Furthermore, when μ(≥1), the conservatism of Theorem 1 is dependent on m and independent of μ.

Table 4 Optimal dissipativity performance γ
Full size table

5 Conclusion

In this paper, the problem of dissipativity analysis has been investigated for stochastic neural networks with time delay using the delay partitioning technique. A stochastic integral inequality has been given. Several delay-dependent sufficient conditions have been proposed to guarantee the exponential stability and dissipativity of the considered neural networks. Some other cases have also been considered. All the results given in this paper are delay-dependent as well as partition-dependent. The effectiveness as well as the reduced conservatism of the derived results has been shown by several numerical examples. We would like to point out that it is possible to extend our main results to more general neural networks with mixed time-delays, uncertainties, and Markov jump parameters, and the corresponding results will appear in the near future.