1 Introduction

Switched dynamical systems are useful in many engineering applications such as mechanical systems [1], electrical circuits [2], communication networks [3], etc., which operate among a set of two or more dynamical systems according to certain switching rules. Generally, switching from one dynamical subsystem to another often occurs on a set of borders, which are defined on certain critical conditions of the state variables or related to the fixed time for the occurrence of the alteration [4, 5]. When the switched system crosses the borders, the vector fields of the switched system may alternate between two types of flows, described by the subsystems, leading to nonsmooth phenomena occurring at the switching points such as grazing bifurcation, border collision bifurcation, and multiple-crossing bifurcation [6]. Being the wide existence of switches and many interesting characteristic phenomenon in the switched system, it has attracted a lot of attention in recent years and many results have been reported [7, 8]. Bhattacharyya and Mukhopadhyay presented the condition of global stability of an eco-epidemiological model with switch [9]. Li et al. dealt with the problem of liable stabilization and control scheme of a class of switched Lipschitz systems [10]. Xiang et al. investigated the robust reliable control of switched neutral systems [11]. Sharan and Banerjee derived the nature of the switching map for the case of grazing orbits of power electrical circuits [12].

Up to now, much attention has been paid to the stability, chaos, and the control schemes of the switched systems [13–15]. In [13], a class of switching laws to stabilize the switched system was established if there is a stable convex combination of the unstable descriptor systems. In [14], some sufficient conditions were established to ensure the asymptotically stability of the switched linear system under some periodically switching signal. In [15], the stability properties of a general class of nonautonomous switched nonlinear systems were studied via multiple Lyapunov functions. However, many problems for the switched systems such as the dynamical evolution with the variation of the parameters and the bifurcations associated with the switches as well as the mechanism of complexity still need further research.

For the switched system, some critical changes may occur at the borders, that is, the solution function of this system is no longer differentiable at the switching points, though it remains continuous. The conventional method cannot be used to investigate the dynamics near the neighborhood of the nonsmooth regions, since there is little knowledge about bifurcations in nonsmooth systems, which leads to the difficulties in investigating the bifurcation behaviors of the switched system. To overcome above difficulties, here we investigate the associated bifurcations of the fixed points of piecewise smooth maps, which is corresponding to the bifurcations of the periodic solutions of the switched system.

To explore the dynamical behaviors and the mechanisms of the switched systems, here we consider a periodic parameter-switching system between two Lorenz oscillators. We establish a switched system, and define its solutions, local sections, and local mappings. Upon these definitions, the Poincaré mapping is constructed as a composite of local mappings. Then the location of the fixed point corresponding to the periodic orbit of the switched system and the parameter values of local bifurcations covering the standard period-doubling and saddle-node bifurcation are calculated by Newton–Raphson and the QR methods, respectively. Meanwhile, upon the analysis of the equilibrium points of the two subsystems as well as the critical behaviors at the switches, the mechanisms related to the special phenomena observed in the switched systems are presented to account for the evolutions of the trajectories.

2 The model of switched system

2.1 Model description

We begin our analysis by considering two dynamical systems

$$ d\mathbf{X}/dt = f_{k}(t,\mathbf{X},\lambda, \lambda_{k}),\quad k \in\{1,2 \} $$
(1)

where t∈R, X=(x,y,z)T. λ∈R r is an invariant parameter of f 1, f 2, while λ k ∈R s is a parameter depending on f k . r and s are integers. f k is the vector fields with f k (X)=(α(y−x),x(δ k −z)−y,xy−β k z)T.

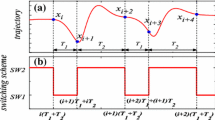
Then we define the switching condition: suppose that the system starts from the vector of f 1(X) with the initial point X 0. After the time T 1, the trajectory turns to the flow f 2(X). When the subsystem 2 runs with time T 2, the trajectory changes back to the vector field f 1(X).

Obviously, the two subsystems correspond to the typical form of Lorenz oscillator with different parameters, implying that the solution of the switched system (1) is governed by the two famous state equations. Suppose that the solutions for the two subsystems are respectively given by

$$ \begin{array}{@{}l} X(t) = \varPhi( t,X_{0},\alpha,\beta_{1},\delta_{1} ), \\\noalign{\vspace{4pt}} X(t) = \varPsi( t,X_{1},\alpha,\beta_{2},\delta_{2} ), \end{array} $$
(2)

where X 1(t)=Φ(T 1,X 0,α,β 1,δ 1) is the initial point of the subsystem 2.

2.2 Poincaré map and periodic orbit

In this section, we investigate the generation of the period solutions of the whole system (1). The shooting method [16] will be applied, since it is a classical method to find the limit cycle and the associated bifurcations of the system.

Since the system (1) is the time switched system, we begin the shooting method program by giving the following two local sections

$$ \begin{array} {@{}l} \varSigma_{1} = \bigl\{ (X,t) \in R^{3} \times R^{ + }| t = T_{1} \bigr\}, \\\noalign{\vspace{4pt}} \varSigma_{2} = \bigl\{ (X,t) \in R^{3} \times R^{ + }| t = T_{1} + T_{2} \bigr\}. \end{array} $$
(3)

Then the local mappings can be defined as (see Fig. 1)

$$ \begin{array}{@{}l@{\quad}l} P_{1}{:} & \varSigma_{1} \to\varSigma_{2} \\\noalign{\vspace{2pt}} & X_{0} \mapsto X_{1} = \varPhi( T_{1},X_{0},\alpha,\beta_{1},\delta_{1} ), \\\noalign{\vspace{4pt}} P_{2}{:} & \varSigma_{2} \to\varSigma_{1} \\\noalign{\vspace{2pt}} & X_{1} \mapsto X_{2} = \varPsi( T_{2},X_{1},\alpha,\beta_{2},\delta_{2} ). \end{array} $$
(4)

Assume that the switching surface Σ 1 is the Poincaré section. We define the Poincaré map P from Σ 1 to Σ 1 as follows:

$$ P = P_{2} \circ P_{1}, $$
(5)

namely,

$$ \begin{array} {@{}l@{\quad}l} P{:} & \varSigma_{1} \to \varSigma_{1} \\ \noalign{\vspace{2pt}} & \begin{aligned} X_{0} \mapsto X_{2} = \varPsi\bigl( & T_{2},\varPhi(T_{1},X_{0},\alpha, \beta_{1},\delta_{1} ), \\ & \alpha,\beta_{2}, \delta_{2} \bigr). \end{aligned} \end{array} $$
(6)

The fixed point of this map can be obtained by solving the following equation:

$$ P( X ) - X = 0. $$
(7)

Since the analytic expression of the Poincaré mapping is unknown, in order to compute the fixed point, we need to compute the Jacobian matrix

$$ DP = \frac{dX_{2}}{dX_{0}} = \frac{dX_{2}}{dX_{1}}\frac{dX_{1}}{dX_{0}} = DP_{2} \times DP_{1}, $$
(8)

where dX 1/dX 0 is the solution of the following variational equations from t=0 to t=T 1,

$$ \everymath{\displaystyle} \left\{\begin{array}{l} \frac{d}{dt}\biggl( \frac{\partial \varPhi}{\partial X}\biggr) = \frac{\partial f_{1}}{\partial X}\biggl( \frac{\partial \varPhi}{ \partial X} \biggr), \\\noalign{\vspace{6pt}} \frac{\partial \varPhi}{\partial X} \bigg|_{t = 0} = I, \end{array} \right. $$
(9)

where I is an identity matrix. Putting (9) and subsystem 1 together and calculating it by Runge–Kutta method, out comes the numerical solution of (9). At t=T 1, X 1 is regarded as the initial point of subsystem 2. dX 2/dX 1 is the solution of the following different equations from t=T 1 to t=T 1+T 2:

$$ \everymath{\displaystyle} \left\{\begin{array}{l} \frac{d}{dt}\biggl( \frac{\partial \varPsi}{\partial X} \biggr) = \frac{\partial f_{2}}{\partial X}\biggl( \frac{\partial \varPsi}{\partial X} \biggr), \\\noalign{\vspace{6pt}} \frac{\partial \varPsi}{\partial X} \bigg|_{t = T_{1}} = I. \end{array}\right. $$
(10)

Similarly, by resolving the simultaneous equations of (10) and subsystem 2, we can obtain the numerical solution of Eqs. (10).

Fig. 1
figure 1

Switching surfaces and local mappings

Full size image

We now use the Newton–Raphson method to compute the correction to be applied

$$ X_{0}' = X_{0} - \frac{X_{2} - X_{0}}{dX_{2} / dX_{0} - I}. $$
(11)

Then the location of fixed point and Jacobian matrix of the Poincaré map can be obtained. Hence, the period of periodic switching oscillation T has the following form:

$$ T = T_{1} + T_{2}. $$
(12)

Meanwhile, according to the roots {μ 1,μ 2,μ 3} of the characteristic equation

$$ \det( DP - \mu I ) = 0. $$
(13)

We can determine the stability of the periodic switching oscillation and analyze the bifurcation behavior based on the Floquet theory.

For example, we fix the parameters at α=5.0, β 1=1.0, δ 1=10.0, β 2=2.3, δ 2=16.0, T 1=T 2=10.0, X 0=(−3.7,−3.7,10.0). By using the Newton–Raphson method to (11) and (13), the fixed point A=(−2.888,−3.279,10.208) and the Floquet multipliers μ=(−0.72211+0.20994i,−0.72211−0.20994i,4.0×10−7) can be obtained. Thus, a stable periodic switching oscillation is obtained and shown in Fig. 2.

Fig. 2
figure 2

Phase portrait of a single periodic switching oscillation on (x,y) plane, where A′ is the projection of the fixed point A, the black and gray trajectories are governed by the subsystem 1 and 2, respectively

Full size image

3 Switching behaviors and associated bifurcation mechanisms

In this section, using the analysis methods developed in the foregoing section, we will investigate the complicated bifurcation behavior of the switched system (1). We fix some of the parameters at α=5.0, β 1=1.0, δ 1=10.0, δ 2=16.0, T 1=T 2=10.0, and take β 2 as the bifurcation parameter to investigate the dynamical evolutions of the oscillator.

3.1 Equilibrium points and bifurcation of the subsystems

Because the switched system (1) may involve in the two vector fields, the stability analysis of equilibrium point related to the two subsystems is very important.

Note that the subsystem 1 has two stable focuses \(E_{ \pm }^{1} = ( \pm 3, \pm 3,9 )\) and a saddle \(E_{0}^{1} = ( 0,0,0 )\) for the above fixed parameters (see Fig. 3(a)). By varying the parameter β 2, the equilibrium points of subsystem 2 are presented in Fig. 3(b). It can be seen that when β 2>0 there are three equilibria in subsystem 2, denoted by

$$E_{0}^{2} = ( 0,0,0 ),\qquad E_{ \pm }^{2} = (\pm\sqrt{15\beta_{2}} , \pm\sqrt{15\beta_{2}} ,15 ). $$

As shown in Fig. 3(b), the solid branches of SF ± represent stable focuses and the dashed branches UF ± and Sa represent unstable focuses and saddles, respectively, the points H ± are Hopf bifurcation points of equilibria \(E_{ \pm }^{2}\) with β 2=1.143 and the point BP is fold bifurcation of the equilibria with β 2=0.

Fig. 3
figure 3

(a) The equilibrium points of subsystem 1: two stable focuses \(E_{ \pm }^{1}\) separated by the saddle \(E_{0}^{1}\); (b) The equilibrium points of subsystem 2 for different parameter β 2

Full size image

3.2 Periodic oscillations and bifurcation mechanisms

Once the switches described above are introduced, not only periodic movements but also chaotic oscillations can be found. The bifurcation diagram and associated maximal Lyapunov exponent σ by changing the parameter β 2 from β 2=2.3 (single periodic switching oscillation) is plotted in Fig. 4(a). To reveal the details of dynamical evolution of the switched system (1), here we focus on several typical regions of the parameter β 2, i.e., 2.3<β 2<3.0, 5.25<β 2<11.0, 16.75<β 2<20.5 (see Fig. 4(b–d)).

Fig. 4
figure 4

(a 1 ) Bifurcation diagram of the switched system with respected to the parameter β 2. (a 2 ) Associated maximal Lyapunov exponent σ. (b–d) are the enlargement of (a 1 )

Full size image

3.2.1 Case 1: 2.3<β 2<3.0

Note that when 2.300<β 2<2.457, a periodic oscillation of 1T can be observed. When β 2=2.4, the typical phase portrait of such oscillation is plotted in Fig. 5(a). According to (11), the associated fixed point A of the Poincaré map of this periodic oscillation is computed as A=(−3.024,−3.446,10.142). Meanwhile, the overlap of the phase portrait related to the oscillation of 1T with the equilibrium attractors of the two subsystems in (x,y) plane is presented in Fig. 5(b). One may find that a clear understanding that the vector field of switched system may alternate between the two stable focuses \(E_{ - }^{1}\) and \(E_{-}^{2}\).

Fig. 5
figure 5

Periodic oscillation of 1T (a) and its overlay with the equilibrium attractors of the subsystems (b), where the subfigure gives a clear understanding of the rectangular region

Full size image

Next, we will give a detailed analysis of the evolution of such oscillation. Assume the fixed point A is the initial point. During the time (0,T 1), the subsystem 1 is activated, causing the trajectory moves asymptotically to the stable focus \(E_{ - }^{1}\) along with ABC to the point C, while with in (T 1,T 1+T 2) the subsystem 2 is activated, leading the trajectory scrolls down to the stable focus \(E_{ - }^{2}\) along with CDA back to the fixed point A. Thus, the periodic oscillation of 1T with two switching points A and B is created.

With the increase of the parameter β 2, as presented in Fig. 6, the number of switching points in the periodic attractor changes from two to four and continue to be doubled.

Fig. 6
figure 6

Periodic switching attractors to chaos. (a) β 2=2.60; (b) β 2=2.88; (c) β 2=2.91

Full size image

The phenomenon can be understood by the analysis of the Floquet multipliers computed by (13) with appropriate numerical calculations. For β 2 increased from 2.300 to 2.457, the switched system (1) behaves as periodic switching oscillation of 1T and all the Floquet multipliers lie inside the unit circle {μ∈C 1∣|μ|=1}. However, when β 2 increases through 2.457, one of the Floquet multiplier goes through the unit circle from the direction of −1 (see Table 1(a)). According to the Floquent theory, the stable periodic oscillation of 1T becomes stable periodic oscillation of 2T via period-doubling bifurcation. While the parameter β 2=2.837, the Floquet multipliers of periodic oscillation of 2T goes through the unit circle from the direction of −1 again (see Table 1(b)), causing the stable periodic switching oscillation of 2T becomes stable periodic switching oscillation of 4T. Further increase of the parameter β 2 may lead to complicated switching behaviors, evolving to chaos via period-doubling bifurcations. These results agree well with the bifurcation diagram in Fig. 4(b).

Table 1 The Floquet multipliers of periodic oscillation
Full size table

3.2.2 Case 2: 5.25<β 2<11.0

As shown in Table 2(a), when β 2=5.407, the Floquet multiplier μ 1 goes through the unit circle from the direction of 1, while β 2=10.23, it goes through the unit circle from the direction of −1 (see Table 2(b)). Based similarly on the Floquet theory, the chaotic oscillation suddenly changes to periodic switching oscillation of 2T via saddle-node bifurcation at β 2=5.407. Numerical simulations (for example, see Table 2(b)) further show that such stable periodic oscillation of 2T becomes stable periodic oscillation of 4T via period-doubling bifurcation, and finally evolves to chaos. The typical phase portraits are presented in Fig. 7. These results are consistent with the bifurcation diagram in Fig. 4(c).

Fig. 7
figure 7

Periodic switching attractors to chaos. (a) β 2=5.35; (b) β 2=6.0; (c) β 2=10.35; (d) β 2=10.70

Full size image
Table 2 The Floquet multipliers of periodic oscillation
Full size table

We now focus on the periodic oscillation of 2T for the parameter β 2∈(5.407,10.230). Take the case when β 2=5.45 as an example, the fixed point A is computed as A=(7.418,9.549,10.886) by (11) and the corresponding phase portrait on (x,y) plane is presented in Fig. 8(a). It can be seen that the vector field of switched system may alternate among four stable focuses \(E_{ \pm }^{1}\) and \(E_{ \pm }^{2}\), which is different from the case 1 β 2=2.4.

Fig. 8
figure 8

Periodic oscillation of 2T for β 2=5.45. (a) Phase portrait; (b) Overlap of the phase portrait and the attractors of the subsystems

Full size image

To explore the mechanism of the movement, we assume that the trajectory of the solution is starting from the fixed point A in subsystem 1, presented in Fig. 8(b). Because of the attraction of the stable focus \(E_{ - }^{1}\), the trajectory may move asymptotically to \(E_{ - }^{1}\) along with AB. However, at time T 1 the subsystem 2, with the switching point B as the initial point, is activated. Then the trajectory may settle down to the stable focus \(E_{ - }^{2}\) along with BC until another switching happen at the point C after time T 2. Note that the switching point C is attracted by the other stable focus \(E_{ + }^{1}\) of the subsystem 1, then the trajectory tends asymptotically to the stable focus \(E_{ + }^{1}\) with the path CD. A new switching point D occurs when the system is governed by the subsystem 1 after time T 1 once more, at which the trajectory turns to be governed by the subsystem 2 and is along with DA to the stable focus \(E_{ + }^{2}\). The trajectory may return back to the fixed point A after time T 2, forming the periodic switching oscillation of 2T.

3.2.3 Case 3: 16.75<β 2<20.5

As shown in Table 3, when β 2=17.811 and β 2=17.90, one of the Floquet multipliers goes through the unit circle from the direction of −1, causing the stable periodic switching oscillation of 4T becomes the stable periodic switching oscillation of 2T at β 2=17.811, and at β 2=17.90 the stable periodic switching oscillation of 2T changes to the stable periodic switching oscillation of 1T via a cascading of period-doubling bifurcation. The typical phase portraits are presented in Fig. 9. These results are equal to the bifurcation diagram in Fig. 5(d).

Fig. 9
figure 9

Periodic switching attractors to chaos. (a) β 2=17.5; (b) β 2=17.815; (c) β 2=18.0

Full size image
Table 3 The Floquet multipliers of periodic switching oscillation
Full size table

Next, we still explore the mechanism of the periodic oscillation. When β 2=17.9, the fixed point A is computed as A=(−16.128,−16.474,14.432) and the corresponding periodic orbit on (x,y) plane is shown in Fig. 10(a). By overlapping the phase portrait with the attractors of the two subsystems (Fig. 10(b)), it can be seen that the trajectory of periodic solution may alternate between the transient process of the stable focuses \(E_{ - }^{1}\) and \(E_{ - }^{2}\), which is the same as the behavior of the periodic oscillation of the parameter β 2=2.4 discussed above.

Fig. 10
figure 10

Periodic oscillation of 2T (a) and its overlay with the equilibrium attractors of the subsystems (b), where the subfigure gives a clear understanding of the rectangular region

Full size image

4 Conclusions

The periodic parameter-switching system may exhibit very complex behaviors such as periodic switching oscillation of 1T and periodic switching oscillation of 2T, etc. The existence of these solutions can be demonstrated by computing the fixed point of the Poincaré mapping of the whole system, while the mechanisms of these solutions can be understood by the overlap of the phase portrait related to the periodic solution with the equilibrium attractors of the two subsystems. It is found that the trajectory of the periodic solution can be divided into parts determined by the transient processes of different attractors of the subsystems, which forms periodic solutions with different forms of switchings. Furthermore, based on the Floquent theory, the evolution processes, and the associated mechanisms of these periodic solutions are investigated. Study shows that, with the increase of the parameter, the switched system can evolve to chaos by cascading of period-doubling bifurcations or immediately via saddle-node bifurcation from the periodic solutions.