1 Introduction

Induction motors (IMs) are widely used in electrical drives and servo systems. From the control point of view, IMs represent complex multivariable nonlinear problems and constitute one of the important areas of application for control theory. The control problems are further complicated by the fact that IM drive systems are subject to unknown load torque disturbances and the motor parameters are of great uncertainty. Existing solutions to these problems have been given, for instance, field orientation control (FOC), direct torque control (DTC) and sensorless control [1]. With the development of computer control technology [2] and control theory, IM dirves control strategies such as L2 gain disturbance attenuation [3], passivity-based control [4], back-stepping principle [5], sliding mode control [6], adaptive control [7], feedback linearization [8], and intelligent control [9] have made important progress. However, these nonlinear control methods are too complicated to be implemented easily. Recently, the Energy-Shaping (ES) and Port-Controlled Hamiltonian (PCH) theory have attracted a lot of attention [10–15]. The PCH systems with dissipation has become an important design tool for nonlinear control systems.

The ES consists in shaping the energy function of the system in order to obtain a new closed-loop energy function that has a minimum point at the desired equilibrium point, preserving the original interconnection structure and dissipative function. Thus, the closed-loop system preserves the PCH form with a stable equilibrium point at the state of minimum energy. IMs can be viewed as two-port (electrical port and mechanical port) energy-transformation device. The action of a controller may also be understood in energy terms as another dynamical system-interconnected with the electromechanical system to modify its behavior. The control problem can then be described as finding a dynamical system and an interconnection pattern such that the overall energy function takes the desired form. The energy-shaping approach is applied to IMs control systems. Attention of the control method is now focused on the interconnection and damping structures of the system. Energy is injected into the electrical port for determining the full system’s behavior. Many theoretical extensions and practical applications have been reported in the literature [15–18], for instance, permanent magnet synchronous motor systems [15, 16], stepper motor systems [17], and induction motor systems [18].

In this paper, based on a novel state error PCH and energy-shaping control principle, the modeling and pulse width modulation (PWM) control of IM drive system, which consists of IM and power converter are studied. The main characteristic of the method is that the system has PCH structure. The closed-loop energy function can be used as Lyapunov (or storage) function rendering the stability analysis more transparent. Based on the interconnection assignment and damping injection and energy-shaping principle, the PCH controller is designed when the load torque is known. The proportional integral (PI) control action of speed error is added into the system which is used to estimate the load torque disturbance. The load torque observer is also developed to estimate the unknown load torque. Using space vector pulse-width modulation (SVPWM) signal transformation technology, speed regulation of IM drive system is implemented by controlling the state of each switch in the inverter.

2 Control principle of the state error PCH systems

2.1 PCH systems

Consider an affine nonlinear system

(1)

The system (1) is passive if it is possible to find a nonnegative function V(x) such that V(0)=0 and

$$ V\bigl(x(t)\bigr)-V\bigl(x(0)\bigr)\leq \int_{0}^{t}y^{T}( \tau )u(\tau )\,d\tau. $$
(2)

The PCH systems with dissipation can be expressed as [8]

(3)

where x∈ℜn is the state vector, u,y∈ℜm are the input and output vector, respectively, inputs and outputs are conjugated variables whose product has units of power, R(x)=R T(x)≥0 represents the dissipation, the interconnection structure is captured in matrix g(x) and the skew-symmetric matrix J(x)=−J T(x), and H(x) is the total stored energy function of the system.

The most important feature of PCH systems is its input-output passivity and stability properties. Given a dynamical system (3), the variation of internal energy equals the dissipated power plus the power provided to the system by the environment. The energy balance equation for system (3) is given by

(4)

then, integrating (4) over an time-interval [0,t] results in the following well-known dissipative inequality,which ascertains the passivity properties of PCH systems

$$H\bigl(x(t)\bigr)-H\bigl(x(0)\bigr)\leq \int_{0}^{t}y^{T}( \tau )u(\tau )\,d\tau, $$

which is the same as (2).

2.2 Control principle of the state error PCH systems

The final design objective of the PCH system (3) is to find a feedback u=β(x) such as the closed-loop dynamics is a state error PCH system with dissipation. The following theorem presents a general formulation of the controller design technique.

Theorem 1

Consider the PCH system (3), given H(x), J(x), R(x) and g(x), let x 0 be a desired equilibrium and \(\tilde{x}=x-x_{0}\) be the state error. Assign a closed-loop system desired energy function \(H_{d}(\tilde{x})>0\) and H d (0)=0. Assume we can find β(x), J a and R a , satisfying

(5)
(6)

and the closed-loop PCH system (3) with u=β(x) takes a the state error PCH form

$$ \dot {\tilde{x}}=\bigl[J_{d}( \tilde{x})-R_{d}(\tilde{x})\bigr]\frac{\partial H_{d}(\tilde{x})}{\partial \tilde{x}} . $$
(7)

Then \(\tilde{x}=0\) is stable equilibrium of the closed-loop system (7). Furthermore, it is asymptotically stable if, in addition, the largest invariant set under the closed-loop dynamics contained in \(\{\tilde{x}\in R^{n}\mid [ \frac{\partial H_{d}(\tilde{x})}{\partial \tilde{x}} ]^{T}R_{d}(\tilde{x})\frac{\partial H_{d}(\tilde{x})}{\partial \tilde{x}}=0 \}\) equals {0}.

Proof

Since \(J_{d}(\tilde{x})\) is skew-symmetric matrix, thus

$$ \bigg[ \frac{\partial H_{d}(\tilde{x})}{\partial \tilde{x}}\bigg]^{T}J_{d}(\tilde{x}) \frac{\partial H_{d}(\tilde{x})}{\partial \tilde{x}}=0. $$
(8)

As \(R_{d}(\tilde{x})\geq0\), therefore, along the trajectories of the system (7), the time derivative of \(H_{d}(\tilde{x})\) is

(9)

Applying Lyapunov’s stability theorem, \(\tilde{x}=0\) is stable equilibrium of the closed-loop system (7). The asymptotic stability follows immediately invoking La Salle’s invariance principle.

Theorem 1 shows that the system (3) can be expressed as the form of system (7) by u=β(x). Moreover, applying Theorem 2 below, the feedback control law u=β(x) can be solved. □

Theorem 2

Consider the system of Theorem 1 in closed-loop with u=β(x), if

(10)
(11)
(12)

then the closed-loop state error PCH system can be rewritten in the form (7).

Proof

Define \(\tilde{x}=x-x_{0}\). Then \(x=\tilde{x}+x_{0}\), substituting into (3), we get

(13)

where

$$\frac{\partial H(x)}{\partial x}=D^{-1}x $$

and

$$\frac{\partial H_{d}(\tilde{x})}{\partial \tilde{x}}=D^{-1}\tilde{x}. $$

From (3), we have

$$\dot{x}_{0}=\bigl[J(x_{0})-R\bigr]D^{-1}x_{0}+g(x_{0})u_{0}. $$

Substitution of above formula and (10) into (13) gives that the state error system model is

(14)

Let

(15)

Then, according to (5) and (15), Eq. (14) can be written as

$$ \dot {\tilde{x}}=\bigl[J_{d}( \tilde{x})-R_{d}\bigr]\frac{\partial H_{d}(\tilde{x})}{\partial \tilde{x}}+\xi. $$
(16)

The above equation can be expressed as the system (7), provided that ξ=0. Obviously, Eq. (12) ensures that ξ=0.

Theorem 2 provides the solution of the controller, feedback control u=β(x) can be obtained from (12). □

3 Controller design of induction motor drives

3.1 PCH model of the induction motor

The model of the induction motor can be described in a synchronously rotating d−q reference frame, and then we get the electrical subsystem

(17)

and the mechanical subsystem

$$ J_{m}\dot{\omega}=\tau -\tau_{L}-R_{m}\omega =n_{p}\lambda_{r}^{T}J_{2}i_{r}- \tau_{L}-R_{m}\omega , $$
(18)

where

(19)
(20)

, , , and \(\lambda =[ { \lambda_{s}^{T} \ \ \lambda_{r}^{T} } ]^{T}= [ { \lambda_{sd} \ \ \lambda_{sq}\ \ \lambda_{rd} \ \ \lambda_{rq} } ]^{T}\), \(i=[ { i_{s}^{T} \ \ i_{r}^{T} } ]^{T}= [ { i_{sd} \ \ i_{sq} \ \ i_{rd} \ \ i_{rq} } ]^{T}\), u s =[u sd u sq ]T, τ and τ L are electromagnetic torque and load torque, respectively, the subscripts s and r indicate the variables for the stator and the rotor, respectively, J m is the moment of inertia, L s , L r , L m are the stator, rotor, mutual inductances, respectively, R s and R r are the resistances for the stator and the rotor, respectively, n p is the number of pole pairs, ω s is electrical angular speed of the stator (the rotating speed of the synchronously d−q reference frame), ω is mechanical angular speed of the rotor, ω r  is electrical angular speed of the rotor, R m is the friction coefficient of the rotor, and

$$ \omega_{r}=n_{p}\omega. $$
(21)

We define the mechanical momentum, state vector and input vector as follows:

(22)

Using (18) and (22), we can get

$$ \dot{p}=J_{m}\dot{\omega}=n_{p}\lambda_{r}^{T}J_{2}i_{r}-R_{m} \omega -\tau_{L}. $$
(23)

The Hamiltonian (storage) function of the IM system is given by

(24)
(25)

Equations (17) and (23) can be rewritten in (3), and then the PCH model of IM can be written as

(26)

where

(27)
(28)

3.2 The case of known load torque

Assuming that rotor flux vector has been aligned with the d-axis of the d−q reference frame. Following the idea of field orientation, given λ r0, then the desired equilibrium is

(29)

We can get x 0 from λ s0. Using (17) and (18) yield

(30)
(31)

From (30), we obtain

(32)
(33)
(34)

then

$$ i_{sd0}=\frac{\lambda_{rd0}}{L_{m}}. $$
(35)

Using (19) and (31), we can get

$$ i_{sq0}=\frac{L_{r}\tau_{0}}{L_{m}n_{p}\lambda_{rd0}} $$
(36)

since

$$\lambda_{rq0}=L_{m}i_{sq0}+L_{r}i_{rq0}=0, $$

thus

$$ i_{rq0}=-\frac{L_{m}}{L_{r}}i_{sq0}=-\frac{\tau_{0}}{n_{p}\lambda_{rd0}}. $$
(37)

Substituting (37) into (33), we have

(38)
(39)

Since Eq. (27) satisfying (10), thus from (12) we get

(40)

Supposing

(41)

and substituting into (40), we have

(42)
(43)
(44)

To ensure that Eq. (42) holds, we choose

$$ J_{13}=-n_{p}L_{m}J_{2}i_{r0}, \quad\quad J_{23}=n_{p}L_{m}J_{2}i_{s0}. $$
(45)

Substituting (43) into (41), we can obtain

(46)

Substituting (43) into (40), we get the controller

(47)

From (20), we have

(48)
(49)

Substituting (29) and (38) into (46), and substituting (30) and (49) into (47), the controller can be written as

(50)
(51)

λ r in (50) and (51) is not directly measurable, so an observer is needed to estimate it. In order to get rid of rotor resistance changes, we use an open-loop rotor flux observer. From (17) and (20), we get the observer as follows:

(52)
(53)

3.3 Load torque disturbance attenuation

The proportional integral (PI) control action of speed error is lead into the system in the presence of load torque disturbance. The integral separation principle is used to avoid being integral saturation aiming at the load torque estimating problem. So, we design the load torque estimator as follows:

(54)

where ρ is integral action separation threshold value. Then (31) can be replaced by \(\tau_{0}=\hat{\tau}_{L}+R_{m}\omega_{0}\), and new equilibrium can be obtained. With the controller in (50) and (51), speed control of induction motor is implemented when load torque is unknown.

3.4 The case of unknown load torque

In practical applications, the load torque is unknown, thus we need to design load torque observer. When the load torque is known and constant, from (18) and (19), we get

(55)

In a practical motor running system, the load torque is unknown. Because ω and i s are measurable, and λ r can be obtained using rotor flux observer,the load torque observer equations are given by

(56)

where k 1 and k 2 are the parameters to be designed. Let \(\tilde{\omega}=\omega -\hat{\omega}\) and \(\tilde{\tau}_{L}=\tau_{L}-\hat{\tau}_{L}\), the observation error equation has the form

$$ \left [ \begin{array}{c} \dot{\tilde{\omega}} \\[4pt] \dot{\tilde{\tau}}_{L} \end{array} \right ] =\left [ \begin{array}{c@{\quad}c} -(k_{1}+\frac{R_{m}}{J_{m}}) & -\frac{1}{J_{m}} \\[4pt] -k_{2} & 0 \end{array} \right ] \left [ \begin{array}{c} \tilde{\omega} \\[4pt] \tilde{\tau}_{L} \end{array} \right ]. $$
(57)

This is a linear and homogeneous system, which is asymptotically stable for all positive k 1 and negative k 2. The poles of the observer can be obtained from (57)

$$s_{1,2}\hspace{-0.5pt}=\hspace{-0.5pt} -\frac{k_{1}J_{m}+R_{m}}{2J_{m}}\hspace{-0.5pt}\pm\hspace{-0.5pt} \frac{1}{2J_{m}}\sqrt{(J_{m}k_{1}+R_{m})^{2}+4J_{m}k_{2}}. $$

All the poles of the observer are set to be s 1=s 2=−s p by selection of parameters as

$$ k_{1}=2s_{p}-\frac{R_{m}}{J_{m}},\quad\quad k_{2}=-J_{m}s_{p}^{2}. $$
(58)

Thus, the load torque estimation errors decay rapidly to zero by the pole placement. We can replace τ L with \(\hat{\tau}_{L}\) in (31), \(\tau_{0}=\hat{\tau}_{L}+R_{m}\omega_{0}\), and then we get new equilibrium. With the controller in (50) and (51), speed regulation of induction motor is implemented when load torque is unknown.

When load torque is unknown, the condition of (5) still holds, and PCH structure of closed-loop system is preserved. So, equilibrium of the closed-loop system is asymptotically stable when load torque is unknown.

4 Controller implementation and simulation results

4.1 Controller implementation

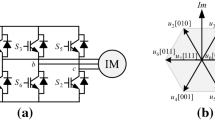
The main circuit diagram of IM control system is shown in Fig. 1. The IM is connected to the converter including a three-phase AC/DC diode-rectifier and a three-phase DC/AC voltage-source inverter. The outputs of the inverter are connected to the three-phase stator windings of IM which are Wye-connected, U DC is the output DC voltage of the rectifier which is essentially constant. Moreover, using the SVPWM signal transformation technology, speed regulation of IM drive systems is implemented, and the speed control of IM can be implemented by controlling the state of each switch in the inverter to provide the desired three-phase voltages. Transforming u s =[u sd u sq ]T in (51) to u αβ =[u α u β ]T through the dq−αβ transformation matrix,we get

$$ \left [ \begin{array}{c} u_{\alpha } \\[4pt] u_{\beta } \end{array} \right ] =\left [ \begin{array}{c@{\quad}c} \cos \omega_{s}t & -\sin \omega_{s}t \\[4pt] \sin \omega_{s}t & \cos \omega_{s}t \end{array} \right ] \left [ \begin{array}{c} u_{sd} \\[4pt] u_{sq} \end{array} \right ]. $$
(59)

Then, applying SVPWM signal transformation principle, we can get six pulses which are used to control the power converter to provide the desired three-phase voltages u sabc =[u a u b u c ]T. The motor is just controlled by u sabc . Therefore, the speed regulation of IM can be implemented by controlling u αβ .

Fig. 1
figure 1

Main circuit diagram of IM control system

Full size image

4.1.1 Sector of composed voltage vector

Composed voltage vector of the three-phase voltages provided to the motor is u N (N=1,2,3,4,5,6), which is shown in different sectors in Fig. 2. u sα and u sβ are the voltages of u s in α−β reference frame, respectively.

Fig. 2
figure 2

Sector of composed voltage vector

Full size image

We choose

We can decide the sector of composed voltage by the value of N. The relationship of the sector and N is shown in Table 1.

Table 1 The relationship between operation time and the sector
Full size table

4.1.2 Operation time of two neighbor composed voltages

We choose

The relationship between operation time of two neighbor composed voltages and the sector is shown in Table 2, where, T s is the switching frequency of IGBT inverter switches. When t 1+t 2>T s , we choose

$$t'_{1}=t_{1}\frac{T_{s}}{t_{1}+t_{2}},\quad\quad t'_{2}=t_{2}\frac{T_{s}}{t_{1}+t_{2}}. $$
Table 2 The relationship of the sector and N
Full size table

4.1.3 Switching time of composed voltage vector

Given \(t_{a}=\frac{(T_{s}-t'_{1}-t'_{2})}{4}\), \(t_{b}=\frac{t_{a}+t'_{1}}{2}\) and \(t_{c}=\frac{t_{b}+t'_{2}}{2}\), the switching time of V 1, V 2, and V 3 is t cm1, t cm2, and t cm3, respectively, and the relationship between the switching time and the sector is shown in Table 3.

Table 3 The relationship between the switching time and the sector
Full size table

4.1.4 Implementation of SVPWM

Comparing t cm1, t cm2, and t cm3 with an isosceles triangle which frequency is T s , and the amplitude is \(\frac{T_{s}}{2}\), we get three PWM waves to control V 1, V 3, and V 5. The two switches of the same bridge are on alternatively, then we can get the other three PWM waves to control V 4, V 6, and V 2. Then the SVPWM control can be implemented.

4.2 Simulation results

In order to evaluate the performance of proposed control method, the simulation is performed for the IM drives. The parameters of the IM are: R s =0.687 Ω, R r =0.642 Ω, n p =2, L s =0.084 H, L r =0.0852 H, L m =0.0813 H, J m =0.3 kg m2, n p =2, R m =0.001 kg m2/s.

The IM is initially at standstill with zero load torque. At startup, the load torque τ L is set to 3 Nm, bus voltage U DC =220 V, and the desired speed ω 0 is set to 60 rad/s, λ rd0=1 Wb. From Eqs. (32), (35), (36), and (37) , we get the equilibriums as follows: i sd0=12.3001 A, i sq0=1.572 A, i rd0=0 A, i rq0=−1.5 A. Figure 3 gives the speed responses of different damping parameters (r s =−0.2, r s =0 and r s =0.5). From Fig. 3, we can know that speed response is faster when r s =−0.2. Thus, we select r s =−0.2 as the simulating condition below. At t=1 s, the desired speed ω 0 is set to 80 rad/s. Figure 4 shows that the system has good speed tracking performance.

Fig. 3
figure 3

Speed curve with known load torque

Full size image
Fig. 4
figure 4

Speed tracking curve

Full size image

At t=1 s, different load disturbances are added to the system, and the magnitudes of the disturbances are 3 Nm and 6 Nm. Figure 5 shows that the rotor speed ω decreases and the steady-state error exists when the load torque disturbance increases. The PI parameters of load torque estimator are k p =0.1 and k i =150. Figure 6 shows that the estimator has good load torque tracking performance, and Fig. 7 exhibits that the controller has good speed tracking performance. Figure 8 shows the phase current response when the load torque disturbance is added to the system at t=1 s. From Fig. 8, we can see that the frequency and the amplitude of current turns to be larger.

Fig. 5
figure 5

Speed curve without an estimator

Full size image
Fig. 6
figure 6

Estimated load torque curve

Full size image
Fig. 7
figure 7

Speed curve with an estimator

Full size image
Fig. 8
figure 8

A-phase current curve with an estimator

Full size image

When the load torque is initially unknown (3 Nm), at t=1 s, we add an unknown load torque disturbance (3 Nm) again. Figure 9 shows that rotor speed response exists steady-state error when the load torque is unknown. In order to track the changes of the load torque better, we add a load torque observer to the system. At t=1 s, unknown load torque is added to the system, the magnitude of the unknown load torque is 3 Nm. Figure 10 gives the responses of the load torque observer for various values of s p (s p =−500,−200,−100). Figure 10 also shows that the observer has better unknown load torque tracking performance when s p =−500. Moreover, Fig. 11 shows that rotor speed steady-state error is eliminated when the load torque observer is used. From Fig. 12, we can see that the amplitude of current turns to be larger.

Fig. 9
figure 9

Speed curve with unknown load torque

Full size image
Fig. 10
figure 10

Responses of the load observer

Full size image
Fig. 11
figure 11

Speed curve with an observer

Full size image
Fig. 12
figure 12

A-phase current curve with an observer

Full size image

5 Conclusion

Based on energy-shaping and state error Port-Control Hamiltonian systems theory, nonlinear control of IM drives is presented. The clear-cut definition of the interconnection structure and the damping is given in the PCH model. It has very clear physical meanings. Based on the interconnection assignment and damping injection method, the desired state error PCH structure is assigned to the closed-loop IM drive systems by energy-shaping control. Following the idea of field orientation, the desired equilibrium of the system is obtained. The equilibrium stability of the closed-loop system is also verified according to Lyapunov’s stability theorem. Feedback stabilization controller is designed when the load torque is known. An estimator is designed in the presence of the load torque disturbance. The load torque observer is developed when the load torque is unknown. Applying SVPWM signal transformation technology, speed regulation of IM drive system is implemented by controlling the state of each switch in the inverter. Theoretical analysis and simulation results show that the system has good load disturbances attenuation and speed tracking performance. The designed controller is simple and can be implemented easily.