1 Introduction

Stability analysis is of crucial importance for most control systems, especially in real-world industries. As a powerful tool, the concept of Lyapunov exponents, which are numbers reflecting the averaged exponential rate of divergence or convergence of nearby orbits in the state space, has been the subject of intensive research for diagnosing chaotic systems and revealing stability of complex nonlinear systems [1–6].

The general approach of calculating Lyapunov exponents is very constructive. Basically, the model-based method [2, 7] can estimate the spectrum of Lyapunov exponents accurately for systems of which the mathematical models are well developed, provided that the numerical artifact is under control. For the cases that rather than knowing system models, only experimental data are at hand, the time-series-based method using linear mapping was developed [2, 8]. The major shortcoming of this method comes from the fact that it is not reliable for estimating negative exponents, due to the inaccuracy induced by the local linear mapping [2, 9]. Brown et al. did an excellent research by introducing the higher-order Taylor expansion for the local neighborhood-to-neighborhood mapping [9], which separated the problem of finding the analogue Jacobian matrices from the determination of mapping neighborhoods to neighborhoods, and improved the accuracy of the full set of Lyapunov exponents significantly. Later, Yang and Wu [10] successfully applied this method to a biped control system, of which the both negative Lyapunov exponents can be estimated accurately using a quadratic polynomial mapping. However, compared with linear mapping, nonlinear mapping involves the heavy load of mathematical derivations. Both the size of the neighborhood-to-neighborhood matrices associated with nonlinear mapping and the number of unknown parameters associated with such matrices grow rapidly with the increment of the embedding dimension and the order used in the Taylor expansion. In addition, the numerical precision of the estimated Lyapunov exponents reported in Brown’s work showed that it does not always get improved along with increasing the order of the Taylor expansion, which should be determined properly in what manner remains problematic. Recently, although a more general form developed for deriving the neighborhood-to-neighborhood matrix of arbitrary dimensionality has been reported by Yang and Wu [11], the order of the Taylor expansion in their derivation was restricted only to be 2.

On the other hand, Gencay and Dechert proposed an advanced method based on the neural model [12], where multiple layer feedforward (MLF) networks were employed to discover the embedded mapping, providing the Jacobian matrices of the reconstructed dynamics. However, the details of the networks employed for the corresponding systems were not provided in their paper. More recently, under the assumption that all the system states are available, a similar method based on the radial-basis-function (RBF) network was developed [13], where a multiple-input-multiple-output (MIMO) RBF network was constructed to approximate the original nonlinear system. This method features advantages in three folds. First of all, no mathematical models are required, which inherits the attractiveness of the time-series-based methods; Secondly, the derivation of Jacobian matrices based on the RBF network is quite straightforward even to systems of large dimension; last but not least, Lyapunov exponents can be estimated reliably regardless of the signs, that is the very merit of the model-based method. However, for developing the MIMO neural model, the precondition that all states are at hand can rarely be satisfied in the real world, which stimulated the research presented in this paper.

Apart from the derivation of Jacobian matrices, developing a noise resistant method for reliably estimating Lyapunov exponents using a time series is another challenge. In practice, it is inevitable to have measurement noise in the observations. Several methods for estimating Lyapunov exponents using a noisy time series for chaotic systems have been developed [2, 9, 12, 14, 15]. Regarding to the nonlinear mapping method, it was documented that the values of negative exponents in “thin” directions of the data set start to become affected when the measurement noise level grows above about 10 % of the thickness of the data set in the associated Lyapunov direction [9]. However, in Yang and Wu’s work, it can be observed that the negative exponent of the certain system under study was apparently underestimated using nonlinear mapping even the measurement noise was maintained at a relatively low level as 5 % [15]. Regarding the methods based on the neural models, due to the existence of noise, the extent to which the deterministic map can be uncovered is reduced, and the performance of successive rescaling and reorthogonalization may also be deteriorated when calculating the exponents [12]. Although in [12] the method was successfully applied to the observed chaotic data with measurement noise as well as system noise, of which the largest exponents are all positive, the validity of the method has not been tested on exponentially stable systems featuring only negative exponents, leaving the power of the method less convincing.

Motivated by the above analysis, estimating Lyapunov exponents reliably from a scalar time series with additive measurement noise becomes the exact object of this paper. Consider that one can always find an existing RBF network capable of accurately mimicking a specified MLF network, or vice versa [16], in this paper, the previously proposed method based on the RBF network is combined with Gencay and Dechert’s work in the way that the system attractor is reconstructed in an embedding space first using a scalar time series, then instead of carrying out system approximation directly, the RBF model is tuned properly to reveal the embedded mapping. In fact, owing to the reconstruction of the system attractor, a time series along only one state is required, and approximation using the RBF network makes the derivation of Jacobian matrices constructive and reliable. Here, not restricted to the chaotic systems, a standing biped balance system is taken as an additional case study to demonstrate the effectiveness of the proposed method besides the classical Hénon map and the Lorenz system. The biped is simplified by a two-link inverted pendulum representing the leg and the torso, respectively, with an additional one rigid foot-link. The control torques are applied at the ankle and the hip joints to maintain the biped at the upright posture with the minimal energy consumption. Rather than being pinned to the ground, the foot-link is required to be stationary on the ground, indicating that there is no lifting, no slipping, and no rolling over during standing. As documented in some early works [17, 18], these three constraints jointly determine that the control bounds change with the biped states, and for such a case analyzing the system stability via the classical Lyapunov’s second method is extremely difficult. Thus, the concept of Lyapunov exponents is employed in this work. To investigate the sensitivity of our method to the measurement noise, numerical results of the estimated Lyapunov exponents for three different systems are also provided, respectively. For the Lorenz and the biped balance system, analysis and discussion are carried out in order of two different circumstances: in the first circumstance, the noisy data series are used only for calculating the exponents; while in the second one, the noisy data series are employed for tuning the network first, then estimating the exponents.

2 Mathematical preliminary

2.1 The concept of Lyapunov exponents

A Lyapunov exponent of a dynamic system is a quantity that characterizes the averaged rate of separation of infinitesimally close trajectories in the state space. Consider a smooth dynamic system in an n-dimensional state space expressed in the following form:

(1)

where x∈ℝn is the state vector, x(0)=x 0, and f(x,t) is a continuously differentiable vector function. Monitoring the long-term evolution of an infinitesimal n-sphere of initial conditions, the sphere becomes an n-ellipsoid due to the local deforming nature of the flow. Figure 1 shows the evolution of a 2-dimensional sphere which is initially infinitesimal. The ith dimensional Lyapunov exponent is then defined in terms of the length of the ellipsoidal principal axis ∥δx i (t)∥:

(2)

where ∥δx i (t 0)∥ and ∥δx i (t)∥ represent the lengths of the ith principal axis of the infinitesimal n-dimensional hyperellipsoid at initial and current time instances, t 0 and t, respectively. This definition indicates that Lyapunov exponents are related to the expanding or contracting nature of different directions in the state space, and the spectrum of Lyapunov exponents is equal in number to the dimensionality of the state space. In addition, the concept of Lyapunov exponents provides a generalization of the linear stability analysis for nonlinear dynamic systems. They are global properties and independent of the fiducial trajectory selected to estimate them. This feature was presented in Oseledec’s work [1], which has been applied in the limit of infinite time. While in practical applications, finite-time Lyapunov exponents are frequently used in the following form:

(3)

In the limit as t→∞, the finite-time Lyapunov exponents converge to the true Lyapunov exponents [14].

Fig. 1
figure 1

Evolution of an initially infinitesimal 2-dimensional sphere

Full size image

Wolf et al. [2] developed the algorithm for calculating the spectrum of Lyapunov exponents from explicit mathematical models of the systems. In Wolf’s algorithm, a fiducial trajectory (the center of the sphere) is defined by the action of the nonlinear motion equations on some initial conditions. The principal axes are determined by the evolution via the linearized equations of an initially orthonormal vector frame anchored to the fiducial trajectory. This leads to the following set of equations [2]:

(4a)
(4b)

where Ψ t is the state transition matrix of the linearized system δ x(t)=Ψ t δ x(0). The initial conditions for numerical integrations are , where I is the identity matrix of a proper dimension. The Jacobian matrix J(x(t)) is defined as

(5)

of which the significance lies in the fact that it is related to a linear approximation to a nonlinear function near a given point. In this sense, the Jacobian matrix of a dynamic system describes the amount of flow distortion induced by a transformation in the neighborhood of a given point.

To avoid misalignment of all the vectors δx i along the direction of maximal expansion, they are reorthonormalized at each integration step by involving the Gram–Schmidt Reorthonormalization (GSR) scheme, which generates an orthonormal set {u 1,…,u n } of n vectors with the property that {u 1,…,u n } spans the same subspace as {δx 1,…,δx n }. This orientation-preserving property of GSR suggests that the initial labeling of the vectors may be done arbitrarily. Figure 2 shows the geometrical interpretation of the orthonormalization for two principle axes at the jth step. Once the orthonormal vector frame {u 1,…,u n } is produced by GSR, for a large enough integer k, one can obtain Lyapunov exponents as follows with the time-step h properly chosen:

(6)

where j is the number of integration steps.

Fig. 2
figure 2

The geometrical interpretation of GSR for \(\delta x_{1}^{(j)}\) and \(\delta x_{2}^{(j)}\) (j=1,…,k and j is the number of integration step). \(\delta x_{1}^{(j)}\) and \(\delta x_{2}^{(j)}\) are orthogonalized into \(v_{1}^{(j)}\) and \(v_{2}^{(j)}\), and then normalized into \(u_{1}^{(j)}\) and \(u_{2}^{(j)}\). Here, \(\mathrm{proj}_{v_{1}^{(j)}}(\delta x_{2}^{(j)})\) denotes the projector of the vector \(\delta x_{2}^{(j)}\) on the vector \(v_{1}^{(j)}\). And \(v_{2}^{(j)}\) is exactly equal to \(\delta x_{2}^{(j)}-\mathrm{proj}_{v_{1}^{(j)}}(\delta x_{2}^{(j)})\)

Full size image

2.2 Noise levels

One important issue of estimating Lyapunov exponents using experimental data is the robustness of the estimates to the measurement noise. In this work, only additive Gaussian white noise is considered. Gaussian white noise is of special interest here since it is the type of measurement noise commonly encountered in experimental situations, especially for mechanical systems [15]. The noise level has been frequently represented by the signal-to-noise ratio (SNR), which is defined as the power ratio between a signal and the background noise. It is usually expressed using the logarithmic decibel scale as follows:

(7)

where P is the average power. Consequently, as an alternative measure of the noise level, the percentage of noise can be obtained as

(8)

The percentage of noise varies upon the measured signals; it can be easily controlled below 2 % for robots consisting of close-to-rigid links. When the percentage of noise is greater than 5 %, the measured values would be considered unreliable. Correspondingly, a time series with an SNR greater than 35 dB is believed to be contaminated with low noise, and those with an SNR less than 25 dB are regarded as having high noise.

3 Methodology

3.1 Main idea

Two important components constitute the main idea of this paper for estimating Lyapunov exponents, which are introduced in the following two subsections, respectively. One is reconstruction of the system attractor in an embedding phase space using a scalar time series, and another one is approximation of the reconstructed attractor through tuning an RBF network, which actually provides structure information for deriving Jacobian matrices of the reconstructed mapping. Once the approximated sequence of Jacobian matrices are at hand, Lyapunov exponents can be estimated following the model-based algorithm with ease.

3.2 The reconstruction of system attractors

Associated with the dynamic system in Eq. (1), there is a collected scalar time series x i =x(iΔt), where i=1,2,…,N. N is the number of observations and Δt is the time interval between measurements. According to the conventional time delay embedding technique [19], an orbit representing the time evolution of the system can be reconstructed using the vectors formed by the delay coordinates:

(9)

where d E is the embedding dimension, T lag denotes the time lag, k labels the iteration step such that after one step iteration, \(\boldsymbol {y}_{k}^{d_{E}}\) becomes \(\boldsymbol{y}_{k+1}^{d_{E}}\). The whole iteration steps can be inferred as K−1 since K is the total number of the reconstructed vectors \(\boldsymbol{y}^{d_{E}}\). i may arbitrarily selected from [1,N−(K+d E −2)×T lag] and it unnecessarily equals k. The superscript ‘T’ stands for matrix transposition. It is different from the notation used in [12], where T lag was defaulted to be 1 for all systems. This default value, in some cases where sampling rate Δt is very small, will cause that the delayed coordinates at successive points in the state space represent almost the same information. To avoid this shortcoming, no fixed values are assigned to T lag in this paper, making our method more general.

Rather than a single point in the reconstructed space, Eq. (9) depicts a fiducial trajectory for the estimation of Lyapunov exponents. Generically, for d E ≥2n+1 there exists a mapping \(\boldsymbol{L}: \mathbb{R}^{d_{E}}\rightarrow\mathbb{R}^{d_{E}}\) such that:

(10)

where \(\boldsymbol{y}_{k+1}^{d_{E}}=(x_{i+T_{\mathrm{lag}}}, x_{i+2T_{\mathrm{lag}}}, \ldots, x_{i+d_{E}T_{\mathrm{lag}}})^{\mathrm{T}}\). The mapping L is to be estimated by an RBF network. Considering that L may be taken as

(11)

estimating L can be reduced to estimating the regression equation

(12)

Consequently, the derivatives of L can be expressed as

(13)

which provides the general form of the Jacobian matrix of the reconstructed map, making the model-based algorithm applicable.

3.3 The Radial-Basis-Function (RBF) network

To estimate the reconstructed mapping g, the off-line identification, say, system approximation via an RBF network is adopted in this paper. Modeling through RBF networks is a widely-used method for nonlinear mapping approximation. It has been reported that any Borel-measurable function (a function for which all subsets of the type E(x:f(x)≥α) in its domain of definition are Borel sets, such functions are known as Borel-measurable functions [20]) with respect to an appropriate norm can be approximated to any desired degree of accuracy by carefully choosing parameters of the network, provided the network structure is sufficiently large [21, 22].

The classical architecture of the RBF network is a three-layer feedforward network which contains the input layer, the hidden layer, and the output layer. A typical RBF network configuration with l hidden nodes is depicted in Fig. 3. Such a network implements a mapping f:ℝn→ℝ according to the overall outputs:

$$ \hat{y}=w_{0}\times \operatorname{bias}+\sum _{j=1}^lw_{j}\phi_j\bigl(\| \boldsymbol{x}-\boldsymbol{c}_j\|\bigr), $$
(14)

where x∈ℝn is the input vector, w j are the output weights. The bias neuron always emits 1, and its connection weight w 0 has an effect of increasing or lowering the net input of the summation junction in the next layer, which facilitates training. ϕ j (⋅) is a given radial basis function with its center vector defined as c j =[c j1,c j2,…,c jn ]T, where 1≤j≤l. In our study, we select the Gaussian function for ϕ j , which has the following expression:

$$ \phi_j=\exp\biggl(-\frac{\|\boldsymbol{x}-\boldsymbol{c}_j\|^2}{2\sigma_j^2}\biggr), $$
(15)

where σ j is the width of the jth Gaussian function.

Fig. 3
figure 3

A typical schematic of the RBF network

Full size image

It is worthy to point out that the transfer function for the radial basis neurons are unnecessarily of Gaussian type as expressed in Eq. (15). Functions of other types whose values depend only on the distance r j =∥x−c j ∥ from certain centers c j , e.g., Multiquadratics (\(\phi_{j}=\sqrt{\epsilon^{2}+r_{j}^{2}}\) for some ϵ>0), Inverse multiquadratics (\(\phi_{j}=(\epsilon^{2}+r_{j}^{2})^{-\frac {1}{2}}\) for some ϵ>0), Inverse quadratics (\(\phi_{j}=(\epsilon^{2}+r_{j}^{2})^{-1}\) for some ϵ>0), etc., can also be implemented in principle for the approximation of any continuous function on a compact interval [16]. Among them, the inverse multiquadratic function, the inverse quadratic function, and the Gaussian function share a common property: the nonlinearity ϕ j →0 as r j →∞. By contrast, the multiquadratic function becomes unbounded along with r j →∞. Theoretical investigation and practical results suggest that the choice of the radial basis function ϕ j is not crucial to the performance of the RBF network [21].

To appropriately choose the parameters of the network, the centers of the RBF network c j can be determined using the K-means clustering method, while the width σ j can be fixed by employing the K-nearest neighbors heuristic typically. Briefly speaking, the aim of the K-means algorithm is to partition a collection of n-dimensional vectors x j ,j=1,…,n, into l groups G i ,i=1,…,l, and find a cluster center in each group such that a cost function of dissimilarity measure is minimized [23, 24]. The K-nearest neighbors algorithm is used to vary the widths in order to achieve a certain amount of response overlap between the hidden nodes [23]. For the output layer, the linear weights w j can be found by following the steps of gradient descent with momentum algorithm as addressed below:

Step 1: Find the error \(E(k)=\frac{1}{2} (y(k)-\hat{y}(k) )^{\mathrm{T}} (y(k)-\hat{y}(k) )\) at step k, where \(\hat{y}(k)\) denotes the RBF output at step k and y(k) represents the output of the actual system associated with the input data x(k) at step k known as the clustering sample.

Step 2: Change the connection weights in the following way:

(16)

Step 3: If the error becomes lower than a predetermined value, stop training. Otherwise, replace k by k+1 and go back to step 1.

Here, μ is the learning rate and η is the momentum constant introduced to prevent the network from being trapped in a local minimum. These two parameters are both positive constants suggested being limited to the range (0,1) [16].

Once the RBF network is developed for an unknown multiple-input single-output (MISO) system, the system Jacobian matrices can be obtained from the structure information of the network. Specifically, at step k, one entry of the Jacobian matrix, located at the nth column can be written in the following form:

(17)

Given the series of neural model Jacobian matrices at different time instances, computing Lyapunov exponents based on a time series, reduces to the problem of calculating exponents from an explicit mathematical expression, which is a substitute for the reconstructed mapping featuring the same dynamics as the system under study.

4 Case studies

To demonstrate the validity of the presented method, three distinguished examples were investigated in this section. All the data were generated by the computer simulations under the MATLAB environment, and the actual system Lyapunov exponents were calculated from mathematical models of the dynamic systems, provided that the numerical artifact was under control. Notice that the best number of the hidden units depends in a complex way on the numbers of input and output data, the noise level of the data points, the complexity of the function to be approximated, the type of hidden unit transfer function, the training algorithm, etc. [25]; in our paper, the numbers of hidden nodes when training the RBF models for all three cases were selected based on the trial-and-error following no specific rules. Furthermore, the numbers of clustering samples for tuning the neural models of three cases were selected respectively according to the length of the collected useful observations, which to be specific, were proportional to the total number of the corresponding data series in this work. Some remarks are provided as well at the end of this section.

4.1 Case study I: the Hénon map

The Hénon map:

(18)

is a widely used example for studying strange attractors, which is selected in this paper as one of our case studies since of which the full set of Lyapunov exponents has been well investigated. Here, a time series including 400 data along the x direction was generated first with the initial condition setting to (0.0,0.0). To avoid transients, the first 200 observations were discarded, thus the number of observations used in estimating the exponents was only 200 along with setting T lag=1, d E =2. Figure 4(A) displays the dynamics of the Hénon map in the original phase space and Fig. 4(B) shows the one in a 2-dimensional embedding space, where x new denotes the first component of the reconstructed vector and y new is corresponding to the second component analogously. It can be seen from Fig. 4(B) that the chaotic geometric structure of the Hénon map in Fig. 4(A) is retrieved in the embedding space.

Fig. 4
figure 4

The trajectory of the Hénon map in (A) the original phase space; (B) a 2-dimensional embedding space

Full size image

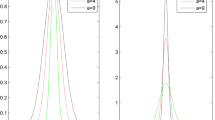
To derive the sequence of Jacobian matrices of the reconstructed attractor shown in Fig. 4(B), an RBF network summarized in Table 1, was tuned for approximating the nonlinear regression mapping g in Eq. (12) first. Lyapunov exponents were then estimated based upon the structure information of the tuned network. Figure 5 shows the evolution of the estimated Lyapunov exponents of the Hénon map, of which the converged constants are 0.409 and −1.612, respectively, as listed in Table 2, with respect to the standards 0.408 and −1.620 derived from the mathematical model. To make a comparison, the numerical results estimated from the linear and nonlinear mapping methods, the Gencay and Dechert’s method proposed in [12] are also provided in Table 2. It can be seen from the percentage errors shown in the table that, for the positive exponent, the newly proposed method in this paper can generate the most accurate estimate compared with the other three methods that is 0.24 % vs. 116.18 %, 9.58 %, and 0.74 %. Regarding to the negative exponent, although the accuracy in terms of percentage error using our method is at the weak position compared with the Gencay and Dechert’s method (0.49 % vs. 0.31 %), it is still within the acceptable level (far below 15 %), let alone winning in the competition with the linear (46.60 %) and the nonlinear mapping (6.81 % ) methods. Moreover, the newly proposed method overwhelms the linear and nonlinear mapping methods not only in terms of accuracy, but also in the way of the length of observations used for estimating (200 vs. 50,000 and 11,000).

Fig. 5
figure 5

Evolution of Lyapunov exponents in the 2-dimensional embedding phase space

Full size image
Table 1 Structure of the RBF network for estimating the regression Eq. (12) for the Hénon map
Full size table
Table 2 Lyapunov exponents (LEs) and their percentage errors for the Hénon map in 2-dimensional embedding space
Full size table

To investigate the robustness of our method to the measurement noise, Gaussian white noise was added to the data set and the noise level was increased gradually. Table 3 presents the estimated Lyapunov exponents under different noise levels using the newly proposed method, along with the corresponding results derived from Gencay and Dechert’s method for comparison. Parameters used for estimating are the same as those in Table 2, i.e., N=200,T lag=1,d E =2. Each entry in Table 3 is an average of 100 simulations and \(\sigma_{\lambda_{i}}\) denotes the standard deviation of the corresponding λ i . Compared with the results reported in [12], the estimated Lyapunov exponents using the newly proposed method achieve much higher accuracy. The smallest gap occurs when the noise level is set to 0.01 %, where the algorithm performance in terms of percentage error is 6.49 % vs. 0.51 % for the negative exponent; when the noise level is increased to 0.1 %, the gap is enlarged to 38.98 % vs. 0.32 %. Since no details of the network approximating the Hénon map was provided in [12], we infer that the disadvantage of Gencay and Dechert’s method shown in Table 3 may probably come from the overfitting of the trained network in the noisy environment.

Table 3 Lyapunov exponents (LEs) and their percentage errors for the Hénon map in a 2-dimensional embedding space with different measurement noise levels
Full size table

4.2 Case study II: Lorenz system

The Lorenz system

(19)

is selected as another case study to demonstrate the efficacy of the newly proposed method applied to chaotic systems. The system parameters are taken from [15] as σ=16,r=45.92, and b=4.0. Employing the fourth-order Runge–Kutta method, a time series including 1000 data along the x direction was generated first with a sampling rate Δt=0.01 s, and the initial condition was (10.0,1.0,0.0). Again the first 200 observations were discarded to avoid transients. Thus, with setting T lag=6Δt=0.06 s, d E =3, the number of observations used in estimating the exponents is only 132, indicating that the total useful length of the observations in terms of time is 131×T lag=7.86 s. The original chaotic attractor of the Lorenz system is displayed in Fig. 6(A), while Fig. 6(B) shows the reconstructed one in a 3-dimensional embedding space. Similar as the legend labeled in the reconstructed Hénon map, x new in Fig. 6(B) denotes the first component of the reconstructed vector, y new and z new are corresponding to the second and third components of the reconstructed vector in the delay coordinates, respectively. The chaotic geometric structure of the Lorenz attractor in Fig. 6(A) is restored in the embedding space as shown in Fig. 6(B)

Fig. 6
figure 6

The trajectory of the Lorenz system in (A) the original phase space; (B) a 3-dimensional embedding space

Full size image

Table 4 lists the summary of the RBF network tuned for approximating the nonlinear regression mapping g in Eq. (12). As an approximation of the reconstructed attractor in the 3-dimensional embedding space, the structure information of the network was extracted for deriving the sequence of Jacobian matrices. The estimated Lyapunov exponents of the Lorenz system evolved to constant numbers as shown in Fig. 7, of which the numerical values and their percentage errors with respect to those exponents estimated from the mathematical model are listed in Table 5, where the results of the traditional time-series-based method using linear mapping and the nonlinear mapping method proposed by Brown et al. [9] are also provided for comparison.

Fig. 7
figure 7

Evolution of Lyapunov exponents in the 3-dimensional embedding phase space

Full size image
Table 4 Structure of the RBF network for estimating the regression Eq. (12) for the Lorenz system
Full size table
Table 5 Lyapunov exponents (LEs) and their percentage errors for the Lorenz system in 3-dimensional embedding space
Full size table

It can be seen from Table 5 that, for the positive exponent, although the nonlinear mapping method can achieve the highest level of accuracy in terms of percentage error (1.87 %) among the listed three methods, the numerical accuracy of the newly proposed method in this paper is still preferable in terms of percentage error (4.57 %) compared with the one of the linear mapping method (5.67 %). For the negative exponent, the numerical accuracy using the new method hits the highest level as the percentage errors of three methods turn out to be 7.69 % (new method) vs. 63.54 % (linear mapping) and 41.35 % (nonlinear mapping), and the sum of the exponents spectrum using three different methods are correspondingly −19.77 (new method) vs. −6.91 (linear mapping), −12.23 (nonlinear mapping), showing that the newly proposed method can approximate the averaged convergence rate for the hypervolume in the state space best associated with the standard rate −21.00.

For counteracting the effect of the measurement noise on the numerical accuracy of estimated Lyapunov exponents, Table 6 provides the average values of the estimated Lyapunov exponents of 100 estimations, along with the percentage errors using the newly proposed method for the Lorenz system undergoing different noise levels. Same as Table 4, \(\sigma_{\lambda_{i}}\) denotes the standard deviation of the corresponding λ i . The numerical results were carried out under two circumstances as shown in Table 6: The noisy data only got involved for computing Lyapunov exponents in the first circumstance, provided that the RBF model was derived from noise-free data; while in the second circumstance both the neural model and Lyapunov exponents were estimated using the noisy observations. As shown in circumstance I, since the structure information of the embedded map estimated from the noise-free data is at hand, the percentage errors of all nonzero exponents are below 9 % even the noise level is increased to 10 % (i.e., 8.20 % for the positive exponent and 8.79 % for the negative one). However, once the available structure information is also estimated from the contaminated observations, as shown in circumstance II, the numerical accuracy of the estimated Lyapunov exponents can only be maintained at a high level in terms of the percentage error lower than 10 % within a very limited range of noise level (less than 0.1 %). When the noise level is increased to 1 %, the percentage error of the negative exponent exceeds 15 %, achieving 17.13 %. Thus, a conclusion can be driven from Table 6 that the RBF model approximating the embedded attractors plays a dominant role for estimating Lyapunov exponents reliably.

Table 6 Lyapunov exponents (LEs) and their percentage errors for the Lorenz system in a 3-dimensional embedding space with different measurement noise levels
Full size table

4.3 Case study III: the biped balance system

Figure 8(A) shows a standing biped robot, which is simplified as a two-link inverted pendulum system representing the leg and the torso, respectively, with an additional rigid foot-link. The joints 1 and 2 can be considered as the ankle and hip joints, and the foot-link provides a base of support (BOS) on the ground. The free body diagrams of the two-link inverted pendulum and the foot-link are respectively shown in Fig. 8(B) and (C). The biped is assumed to move in the sagittal plane and the foot-link is required to be stationary but not fixed on the ground, which imposes constraints between the foot-link and the ground. The control torques are applied at both joints to maintain the biped at the upright posture, minimize an energy consumption related index, and to satisfy the constraints during standing. All the model parameters were taken from [13] and their values are shown in Table 7.

Fig. 8
figure 8

(A) the simplified biped model, (B) the free body diagram of the two-link inverted pendulum, and (C) the free body diagram of the foot-link

Full size image
Table 7 Biped model parameters
Full size table

According to the Euler–Lagrangian equation, the dynamics of the controlled biped can be formulated in the following forms:

(20)
(21)
(22)

where τ=[τ 1,τ 2]T are control torques applied at the corresponding joints, respectively, θ=[θ 1,θ 2]T are the two joint angles (clockwise as “+”), \(\dot {\boldsymbol{\theta}}=[\dot{\theta}_{1}, \dot{\theta}_{2}]^{\mathrm{T}}\) and \(\ddot{\boldsymbol {\theta}}=[\ddot{\theta}_{1}, \ddot{\theta}_{2}]^{\mathrm{T}}\). F gx and F gy are the horizontal and vertical ground reaction forces. The matrices D(θ), \(\boldsymbol{C}(\boldsymbol{\theta}, \dot{\boldsymbol{\theta }})\), G(θ) and parameters a x1, a x2, a y1, a y2 can be expressed as follows:

Since the foot link is assumed to be still, but not fixed on the ground, there is a set of constraints imposed on the system. The gravity constraint F gy >0 guarantees the biped’s foot will not lift from the ground; the friction constraint |F gx |≤μF gy ensures the biped’s foot will not slide on the ground; and the center of pressure (COP) constraint 0≤x COP≤L f along with \(x_{\mathrm{COP}}=L_{a}-\frac{L_{b}F_{gx}+\tau_{1}-L_{c}m_{f}g}{F_{gy}}\) ensures the COP will always reside within the BOS, i.e., there is no rolling of the foot-link about either the toe or the heel. These constraints jointly determine the bounds on the control torques, which change with the states of the system [18]. However, owing to the high nonlinearity of this three-link biped model, the analytical expression of the control bounds cannot be obtained in terms of θ, \(\dot{\boldsymbol{\theta}}\) and \(\ddot{\boldsymbol{\theta}}\). Thus, here we only monitor the evolutions of F gx , F gy and the location of pressure center x COP. The control torques and the simulation will be terminated if any of these three constraints is violated.

Defining \(\boldsymbol{q}=[q_{1}, q_{2}, q_{3}, q_{4}]^{\mathrm{T}}=[\theta_{1}, \theta_{2},\dot {\theta}_{1},\dot{\theta}_{2}]^{\mathrm{T}}\) and D as the determinant of the matrix D(θ), the motion equation of the biped balance system then becomes:

$$ \left \{ \everymath{\displaystyle} \begin{array}{rcl} \dot{q}_1&=&q_3,\\[2pt] \dot{q}_2&=&q_4,\\[2pt] \dot{q}_3&=& \biggl(\delta\tau_1-\biggl(\delta+\frac{\beta}{2}\cos q_2\biggr)\tau_2\\[10pt] &&{}+\frac{\beta}{2}\sin q_2 \biggl(\delta q_4(q_3+q_4) -\frac{\beta}{2}q_3q_4\cos q_2 \biggr)\\[10pt] &&{}+ \biggl(\delta(m_1l_{c1}+m_2l_1)\sin q_1\\[10pt] &&{}-\frac{\beta}{2}m_2l_{c2}\cos q_2\sin(q_1+q_2) \biggr)g \biggr)/D,\\[10pt] \dot{q}_4&=& \biggl(-\biggl(\delta+\frac{\beta}{2}\cos q_2\biggr)\tau_1+(\alpha+\beta\cos q_2)\tau_2\\[10pt] &&{}+\frac{\beta}{2}(\sin q_2)q_4 \\[10pt] &&{}\times\biggl(q_3(\alpha-2\delta)-q_4\biggl(\delta+\frac{\beta}{2}\cos q_2\biggr) \biggr)\\[10pt] &&{}+ \biggl(\biggl(\alpha-\delta+\frac{\beta}{2}\cos q_2\biggr)m_2l_{c2}\sin(q_1+q_2)\\[10pt] &&{}-\biggl(\delta+\frac{\beta}{2}\cos q_2\biggr)\\[10pt] &&{}\times (m_1l_{c1}+m_2l_1)\sin q_1\biggr)g \biggr)/D. \end{array} \right . $$
(23)

To stabilize the standing biped at the minimum energy cost, a classical state feedback control law via linear-quadratic regulator (LQR) algorithm is adopted. It has been established that for a controllable linear time-invariant system, described by \(\dot{\boldsymbol{x}}=\boldsymbol{A}\boldsymbol {x}+\boldsymbol{B}\boldsymbol{u}\) with a quadratic cost function defined as \(J=\frac {1}{2}\int_{0}^{\infty}(\boldsymbol{x}^{\mathrm{T}}\boldsymbol{Q}\boldsymbol{x}+\boldsymbol{u}^{\mathrm{T}}\boldsymbol{R}\boldsymbol {u})\,dt\), a feedback control law u=−Fx may force the closed-loop system to be stable at minimum cost, where the gain matrix F can be calculated by solving the algebraic Riccati equation [26]. For obtaining the LQR parameters, system (23) was linearized first via Taylor’s first-order expansion about the equilibrium point, which is specified as the upright position of the link 1 and 2 (q=[0,0,0,0]T). The system initial condition was given by \(\boldsymbol{q}=[-0.05~\mathrm{rad}, 0.03~\mathrm{rad}, 0.05~\mathrm{rad/s}, -0.03~\mathrm{rad/s}]^{\mathrm{T}}\). Figure 9(A) and (B) show the evolution of the system states and control torques, respectively, indicating that the biped can be successfully driven close to the upright posture within 2.5 seconds subject to the proposed controller. Yet a close-up view of the states trajectories is provided in Fig. 9(A), from which one can see that rather than exactly reached to the equilibrium, the biped evolved to the upright position asymptotically. Meanwhile, time history versus F gy , F gx are displayed in Fig. 10(A) and (B), respectively. The positive vertical ground reaction force F gy implies the support foot was always in contact with the ground. And the horizontal ground reaction force F gx can be observed residing within the bounds of the static friction ([−μF gy ,μF gy ]) represented by two straight dashed lines, which suggests the foot-link did not slip. Additionally, the location of the COP staying within the contact surface between the foot-link and the ground is displayed in Fig. 10(C).

Fig. 9
figure 9

Evolution of (A) the system states, and (B) the control torques

Full size image
Fig. 10
figure 10

Evolution of (A) F gy , (B) F gx , and (C) x COP

Full size image

Due to the complexity of the forced biped system, the concept of Lyapunov exponents was employed to carry out the stability analysis. The estimated Lyapunov exponents from the mathematical model were used as a reference for comparison. With setting the numerical integration time step h=0.001 s, a time series including 100,000 data points along the coordinate of q 1 was generated first from the mathematical model, among which 1,426 observations were used to reconstruct the attractor in a 4-dimensional embedding phase space with setting T lag=70, equivalently in terms of time, T lag=70×0.001=0.07 s.

To derive the Jacobian matrices described by Eq. (13) at different time instances, an RBF network summarized in Table 8 was then constructed for the estimation of the regression mapping g presented in Eq. (12), based on which the Lyapunov exponents of the reconstructed attractor can be easily estimated following the model-based algorithm. Figure 11 shows the evolution of Lyapunov exponents of the reconstructed attractor. It can be seen that all Lyapunov exponents remain negative and converge to constants after around 30 s, indicating that the biped balance system is exponentially stable about its equilibrium (i.e., the upright posture). The property of the exponents remaining negative suggests that the nearby trajectories converge monotonically, which is an important condition for system stability. Otherwise, the stability of the systems cannot be guaranteed even though the averaged exponents are negative [27].

Fig. 11
figure 11

Evolution of Lyapunov exponents (LEs) in the 4-dimensional embedding phase space of the biped balance system

Full size image
Table 8 Structure of the RBF network for estimating the regression Eq. (12) for the biped balance system
Full size table

Table 9 lists the numerical values of all four negative estimates and their relative errors with respect to the ones computed from the mathematical model, where the low relative errors demonstrate that the proposed method is effective for the estimation of Lyapunov exponents. Moreover, a comparison between the results derived from the same time series but different methods, i.e., the traditional time-series-based method using linear mapping and the newly proposed method in this paper, can be observed in Table 9, where the estimated Lyapunov exponents after 99.75 s (1425×T lag) and the corresponding relative errors with different T lag are provided. We did not estimate the exponents using nonlinear mapping method since our biped system is a 4-dimensional system, for which using the higher-order Taylor expansion would introduce complicated mathematical derivation. It can be found that using the proposed method, the numerical values of Lyapunov exponents estimated from an approximated 4-dimensional embedding space are much more accurate, compared with those derived directly from a reconstructed space with even a higher embedding dimension (d E =2×4+1). To be specific, the smallest percentage error regarding to the largest Lyapunov exponent using the traditional linear mapping method turns out to be 56.33 % when T lag is set to 70, which is nearly 25 times the number as compared with the corresponding result derived from the new method (2.30 %). Even the difference between the percentage errors following two methods reaches the lowest level when T lag is equal to 50, the result based on the linear mapping method, 60.46 %, is still more than 5 times the one derived from the new method, which is 11.55 % only. This difference becomes smaller although with respect to the remaining three exponents (e.g., for the fourth exponent with T lag is 50, the competition between the percentage errors from two methods is 53.25 % vs. 19.66 %), the gap is still striking. In addition, within the range of T lag from 60 to 90, the accuracy of the estimated Lyapunov exponents are not sensitive to T lag as the percentage errors of four different sets are below 15 %. All these findings demonstrate that the newly proposed method can estimate Lyapunov exponents much more reliably compared with the traditional time-series-based method using linear mapping.

Table 9 Lyapunov exponents (LEs) and their relative errors for the biped balance system
Full size table

It has been documented that in estimating Lyapunov exponents based on a time series, some parameters for the phase space reconstruction have significant effects on the accuracy of the estimated Lyapunov exponents. In our method, such parameters include the value of the time lag (T lag), and the embedding dimension (d E ). These two parameters determine the number of the data points to be used in the analysis. Regarding the time lag (T lag), Taken’s results [19] indicate that the choice of T lag is arbitrary. However, in practice, if T lag is quite small, the components of the successive vectors to be plotted are almost identical; while if T lag is very large, then there is only very little correlation between the components of the vectors, and the trajectories on the attractor appear to wander all around the phase space, leaving the structure hard to be detected [28]. Methods have been developed for determining T lag [15, 29, 30]. In this case, it is found that T lag=70 is a good approximation of the reconstruction delay where the autocorrelation function drops to \(1-\frac{1}{3e}\) of its initial value.

On the other hand, Taken’s theorem stated that in order to preserve the dynamical properties of the original attractor, theoretically the embedding dimension should satisfy d E ≥2n+1, where n is the dimensionality of the system to be investigated. In Yang and Wu’s works [10], it has been demonstrated that for the biped system, the embedding dimension of n is large enough to guarantee the accuracy of the estimated Lyapunov exponents when the nonlinear mapping is introduced. For the cases of unknown system dimensions, various d E have to be used, which leads to spurious exponents. Identifying true Lyapunov exponents from spurious ones is not within the scope of this paper, which actually can be referred to in[12].

To validate the findings about the noise robustness of our new method derived from the test on the Lorenz system, Table 10 shows the estimated Lyapunov exponents and their percentage errors for the biped balance system with different measurement noise levels using the proposed method. T lag is set to 70 and the embedding dimension is 4. Each entry in Table 10 is an average of 100 simulations and \(\sigma_{\lambda_{i}}\) denotes the standard deviation of the corresponding λ i . The results listed in this table are also obtained under two different circumstances. In circumstance I, the noisy data are used only for calculating the exponents, based upon the approximated Jacobian matrices, which are derived from an RBF model trained with a noisy-free data sequence. In circumstance II, even the Jacobian matrices are derived from the RBF network tuned by noisy data. It can be observed that the results are very robust to the noise in circumstance I as the percentage errors of all exponents are below 10 % (specifically, 9.34 % is the biggest error) even the noise level is increased to 10 % with the standard deviation of all exponents being very small (\(\sigma_{\lambda_{4}}=0.9517\) is the largest value). From circumstance II, one can find that the percentage errors of the estimated Lyapunov exponents, especially those of the last two exponents, grow up obviously along with the increment of noise levels, which are limited within 1 %. To be specific, when the SNR is set to 60 dB (0.1 % noise level), both the percentage errors for the third and fourth exponents exceed 20 %, turning to be 21.49 % and 25.35 %, respectively. The cause of this degraded accuracy may be inferred as the noisy data are employed for approximating the embedded attractor, leading to the sequence of the approximated Jacobian matrices being contaminated. In one word, the findings from Table 10 indicate again that the RBF model plays a crucial role for estimating Lyapunov exponents. If the structure information of the RBF model can be derived accurately, the sensitivity of our method is very low to a noisy time series. To put it another way, noise control is critical to the numerical accuracy of the estimated Lyapunov exponents even for our newly proposed method, especially in the procedure of approximating the reconstructed dynamics based on the RBF model.

Table 10 Lyapunov exponents (LEs) and their percentage errors for the biped balance system in a 4-dimensional embedding space with different measurement noise levels
Full size table

Remark 1

The three dynamic systems studied in this paper are quite different. Both the Hénon map and the Lorenz system have strange attractors, while the actuated biped model features an exponentially stable equilibrium point. It has been demonstrated that in spite of the noise involved in the time series, for all the above dynamic systems, the proposed method works well in terms of achieving highly accurate estimates of the entire spectra of the system Lyapunov exponents. Notice that the forced biped was regulated by a state feedback controller; all three dynamic systems are autonomous systems. However, the proposed method can also be applied to those nonautonomous systems which can be represented by a set of ordinary differential equations with finite dimensions. For such a system in the form of Eq. (1), by treating t as an additional state with \(\dot{t}=1\), calculating Lyapunov exponents can be reduced to the problem of computing exponents for an autonomous system at the expense of increasing the dimension by only one [31].

Remark 2

It should be clarified here that the data segment representing the system transient section discarded in the Hénon and the Lorenz examples were counted in the biped case. However, if one estimates the Lyapunov exponents for the controlled biped following the same procedure, i.e., discard the data collected from the transient period, the same convergent exponents would be obtained. Indeed, the invariance property of Lyapunov exponents to the initial conditions warrants that within the same basin of attraction, the numerical values of the exponents estimated from different initial conditions should be identical. This characteristic of Lyapunov exponents can be perceived from the computational viewpoint: The effects of the data points selected from the transient period are removed due to the averaging process.

Remark 3

From Figs. 9 and 11, one may notice that while the actuated biped moved to the position close to the upright one after around 2.5 seconds, the Lyapunov exponents did not converge to their final values until about 20 seconds. Thus, it is important to distinguish these two time scales. Basically, the transient period in terms of settling time of the system states, and the convergent period of the Lyapunov exponents are different in concept, and both can be selected by the researchers based on different design principles. In our work, an exponent is considered to achieve the converged constant if the change in the numerical values of the exponent between two subsequent steps is within 10−4. To the best of our knowledge, there is no quantitative relationship between the transient period for the system states and the convergent period for the exponents, since the former is determined by the system dynamics and the initial conditions, while the latter is determined by the system dynamics in terms of the right-hand side of the state space model, and its derivatives with respect to the states in the tangent space of the states. On the other hand, the Lyapunov exponents quantify the time-averaged behaviors of nearby orbits in the state space; they are not local quantities in either the spatial or the temporal sense [2]. Thus, one cannot determine the adequate data length required for estimating Lyapunov exponents merely from the transient period of the system states; and although important, finding the determination rule for the data length is beyond the scope of this paper.

5 Conclusion

A method of reliably estimating Lyapunov exponents using a scalar time series has been developed in this work, which is composed of two key components: reconstruction of the system attractor in an embedding phase space, and approximation of the reconstructed attractor through tuning an RBF network. The proposed method not only inherits the advantages of the earlier RBF-based method in that (1) no mathematical models are required, (2) derivation of Jacobian matrices based on the RBF network is quite straightforward, and (3) all Lyapunov exponents can be estimated reliably, but also features other two attractive points. First, instead of recording the time history for all system states in advance, only a scalar time series is required. Second, as compared with the existing methods, our proposed method is more robust to the noise, and is particularly effective when the RBF network is trained with noisy-free or slightly contaminated data. The validity of this new proposed method has been demonstrated via three case studies: the Hénon mapping, the classical Lorenz system, and a standing biped balance system. For Cases I and II, not only the positive exponent, but also nonpositive exponents are exhibited in the spectrum; for Case III, all the Lyapunov exponents are negative. The high numerical accuracy of the estimated Lyapunov exponents from the noisy observations using the newly proposed method can be guaranteed for both the chaotic and the exponentially stable systems in most cases except that when the structure information of the reconstructed attractor are corrupted seriously. For this circumstance, even reconstructing the attractors in the embedding space and revealing the original dynamics becomes challenging. From this viewpoint, exploring the effects of the time series with additive noise on training the RBF network and approximating the embedded attractor, is highly desirable.

Moreover, the method presented in this work only dealt with additive measurement noise of Gaussian white type, apart from which, however, various noise models with different spectral characteristics, and the dynamical noise generated within a system itself, are common in many dynamic systems. Investigating the effects of these noise types is another one of our future works, as well as the determination rule of how much data one needs for obtaining the accurate estimates subject to different noise levels.