1 Introduction

Complex networks are universal, with many examples ranging from the Internet to epidemiology, metabolic networks, biological neural works, scientific citation webs, social interactions [1–3], etc. Since the small-world property [4] and the scale-free property [5] of complex networks were proposed, many scientists and engineers from various disciplines, such as mathematics, physics, biology, engineering, and so on, have paid increasing attention to the studies of complex networks.

The complexity of complex networks leads to a series of important research topics. Synchronization of all dynamical nodes is an interesting phenomenon and has received rapidly increasing attention from various fields of science and society in recent years [6–10]. There are different types of definition for synchronization, such as complete synchronization, phase synchronization, lag synchronization, generalized synchronization, cluster synchronization, projective synchronization, etc. It is well known that many effective control methods including adaptive control [11–14], pinning control [15–19], impulsive control [20–23], hybrid control [24–27], and so on, have been proposed to realize the synchronized dynamics for complex networks. Amongst various types of synchronization, projective synchronization is an interesting chaos synchronization phenomenon, because of its proportionality between the synchronized state vectors with a scaling factor, which can be used for digital communication in secure communication. Mainieri and Rehacek [28] were the first to study it and they declared that two identical systems could be synchronized up to a scaling factor, which is a constant transformation between the synchronized variables of the drive and response systems. Recently, the projective synchronization of driven-response complex dynamical networks has obtained much more attention [29–37]. Hu et al. [33] introduced a driven-response dynamical network model whose nodes are partially linear systems and further investigated its projective synchronization properties by using pinning control method. A short time later, they investigated projective cluster synchronization in a driven-response dynamical network with coupled partially linear chaotic systems [34]. In [35], Zhao et al. discussed the impulsive projective synchronization of driven-response dynamical networks model without time delays. Actually, the characteristic of time-delayed coupling commonly exists in nature, and the effects of time delay on the dynamics of various coupled dynamical systems are very significant in science. Consequently, the time delay case should be considered. Sun et al. [36] investigated the projective synchronization in driven-response dynamical networks of partially linear systems with coupling time-varying delay. Xu et al. [37] studied the projective synchronization of a class of the driven-response dynamical networks with coupling delays. However, the time-varying coupling was not considered in the above works. In many practical situations, some real-world networks are not static but more likely to be time-varying evolving [38–41]. This kind of network can be found in many evolutionary processes, such as optimal control model in economics, bursting rhythm model in pathology, communication networks, social networks, and so on. It is therefore necessary that time-varying couplings and time delays should be taken into account when simulating more realistic driven-response dynamical networks.

Motivated by the above discussions, in this paper, we introduce a driven-response dynamical network with time-varying coupling delay, in which the weights of links are time varying, and investigate the projective synchronization properties of this model via impulsive control, where the state vectors of the drive system and response networks could be synchronized onto a desired scaling factor. Based on the stability theory of the impulsive differential equations, we derive projective synchronization conditions for the time-varying network model. Furthermore, numerical simulations show that the driven-response network can realize the projective synchronization with the desired scaling factor.

Notations

Throughout this paper, R and R n denote the real number set and n-dimensional Euclidean space, respectively. ∥⋅∥ stands for either the Euclidean vector norm or its induced matrix 2-norm. λ max(A)(λ min(A)) represents the largest (smallest) eigenvalue of the symmetric matrix A. μ(A)=λ max(A T+A), \(\| A \| = \sqrt{\lambda_{\max} (A^{T}A)}\). sup denotes the upper bound. ⊗ is the Kronecker product of two matrices. I n is the identity matrix with order n. Matrices, if not explicitly stated, are assumed to have compatible dimensions.

The organization of the remaining parts is as follows: In Sect. 2, description of the driven-response dynamical networks model and some preliminaries are given. In Sect. 3, some criteria for the projective synchronization are derived. Numerical simulations for verifying the theoretical result are presented in Sect. 4. Finally, conclusions are drawn in the last section.

2 Model description and preliminaries

The driven-response dynamical networks with coupling time-varying delay, in which the coupling matrix is time varying, are described by the following equations:

$$ \left \{ \begin{array}{@{}l} \dot{u}_{d}(t) = M(z)u_{d}(t), \\[3pt]\dot{z}(t) =f (u_{d}(t),z(t) ), \\[3pt]\dot{u}_{ri}(t) = M(z)u_{ri}(t)\\[3pt]\hphantom{\dot{u}_{ri}(t) =} + c\sum_{j = 1}^{N}c_{ij}(t)u_{rj} (t - \tau(t) ) ,\\[3pt]\quad i = 1,2, \ldots,N, \end{array} \right .$$
(1)

where the constant c>0 is the coupling strength, the drive system and the response network systems are linked through the variable z(t)∈R 1. \(u_{d}(t) = (u_{d}^{1}(t),u_{d}^{2}(t), \ldots,u_{d}^{n}(t))^{T} \in R^{n}\) and \(u_{ri}(t) =(u_{ri}^{1}(t),\allowbreak u_{ri}^{2}(t), \ldots,u_{ri}^{n}(t))^{T} \in R^{n}\) are the state vectors of the drive and response network systems, respectively. The subscript of d denotes the drive system and r represents the response systems. M(z)∈R n×n is a matrix which depends on the variable z(t). τ(t) is the bounded time-varying delay satisfying 0≤τ(t)≤τ (τ>0 is a positive constant). C(t)=(c ij (t)) N×N ∈R N×N is the coupling configuration matrix and reflects the topological structures of the whole network, in which c ij (t)≠0 if there is a link from node i to node j (i≠j), and c ij (t)=0 otherwise, the diagonal elements of matrix C(t) are defined by \(c_{ii}(t) = - \sum_{j = 1,j \ne i}^{N} c_{ij}(t) \), i=1,2,…,N. It is assumed that the coupling configuration matrix C(t) is bounded and continuous.

Before stating our main results, we give some necessary definitions and lemmas, which are useful in deriving projective synchronization criteria.

Definition 1

If there exists a constant α (α≠0) such that lim t→∞=∥u ri (t)−αu d (t)∥=0 for all i=1,2,…,N, then the projective synchronization of the drive-response network (1) is obtained, where α is a desired scaling factor.

Lemma 1

(See [25]) Given a positive constant ζ>0, then \(2x^{T}y \leq \frac{1}{\zeta} x^{T}x + \zeta y^{T}y\), for all x∈R n and y∈R n.

Lemma 2

(See [42]) Let 0≤τ(t)≤τ. u(t) and υ(t) belong to the set PC(1), PC(l)={φ:[−τ,∞]→R l, φ(t) is continuous everywhere except for the finite number of points t k at which \(\varphi(t_{k}^{ +} ) =\varphi(t_{k})\) and \(\varphi(t_{k}^{ -} )\}\). If there exist constants ϑ, \(\tilde{\vartheta} \), \(\bar{\omega} > 0\) such that

$$\left \{ \begin{array}{@{}l@{\quad }l}D^{ +} u(t) \leq \vartheta u(t) +\tilde{\vartheta} u (t - \tau(t) ),& t \ne t_{k}, \\[3pt]u(t_{k}) \leq \bar{\omega} u (t_{k}^{ -} ),&k \in N, \end{array} \right .$$
$$\left \{ \begin{array}{@{}l@{\quad }l}D^{ +} \upsilon(t) > \vartheta\upsilon(t) +\tilde{\vartheta} \upsilon (t - \tau(t) ), & t\ne t_{k}, \\[3pt]\upsilon(t_{k}) = \bar{\omega} \upsilon (t_{k}^{ -}\bigr),&k \in N, \end{array} \right .$$

then u(t)≤υ(t) for −τ≤t≤0 implies that u(t)≤υ(t) for t>0, where the right and upper Dini’s derivative D + u(t) is defined as \(D^{ +} u(t) = \overline{\lim}_{h \to 0^{+}} \frac{u(t + h) - u(t)}{h}\).

In [36], the authors investigated the projective synchronization in the driven-response dynamical networks of partially linear systems with time-varying coupling delay. By adaptive control technique, the scaling factor can be directed onto the desired value. However, the main objective of this paper is to choose a suitable impulsive controller such that the states of drive system and response time-varying coupling network in (1) can be synchronized to a definite proportional scaling factor α.

By selecting proper control gain matrix B k which is a n×n constant matrix, the driven-response time-varying coupling network (1) can be rewritten as the following impulsive differential equations:

$$ \left \{ \begin{array}{@{}l}\dot{u}_{d}(t) = M(z)u_{d}(t), \\[3pt]\dot{z}(t) =f (u_{d}(t),z(t) ), \\[3pt]\dot{u}_{ri}(t) = M(z)u_{ri}(t)\\[3pt]\hphantom{\dot{u}_{ri}(t) =}+ c\sum_{j = 1}^{N}c_{ij}(t)u_{rj} (t - \tau(t) ) ,\quad t \ne t_{k},\\[3pt]\Delta u_{ri} = B_{k}[u_{ri} - \alpha u_{d}],\quad t = t_{k}, \end{array} \right .$$
(2)

where the impulsive time instants t k satisfy 0=t 0<t 1<t 2<⋯<t k <⋯ and lim k→∞ t k =+∞, \(\Delta u_{ri} = u_{ri}(t_{k}^{ +} ) - u_{ri}(t_{k}^{ -} )\) is the control law in which \(u_{ri}(t_{k}^{ +} ) = \lim_{t \to t_{k}^{ +}}\!u_{ri}(t)\) and \(u_{ri}(t_{k}^{ -} ) = \lim_{t \to t_{k}^{ -}}\!u_{ri}(t)\). Without loss of generality, we assume that \(\lim_{t \to t_{k}^{ -}} u_{ri}(t) = u_{ri}(t_{k})\), which means that the solution of (2) is left continuous at time t k .

Defining the projective synchronization error as e i (t)=u ri (t)−αu d (t), the error dynamical network is characterized by

(3)

Let \(e(t) = (e_{1}^{T}(t),e_{2}^{T}(t), \ldots,e_{N}^{T}(t))^{T}\), rewriting (3) in its compact form

$$ \left \{ \begin{array}{@{}l}\dot{e}(t) = (I_{N} \otimes M(z) )e(t)\\[3pt]\hphantom{\dot{e}(t) =}+ c (C(t)\otimes I_{n} )e (t - \tau(t) ),\quad t \ne t_{k},\\[3pt]\dot{z}(t) = f (u_{d}(t),z(t) ), \\[3pt]e (t_{k}^{ +} ) = (I_{Nn} + (I_{N}\otimes B_{k}) )e(t_{k}),\\[3pt]\quad t =t_{k},\ k = 1,2, \ldots. \end{array} \right .$$
(4)

Let C([−τ,0],R n) be the Banach space of continuous vector-valued functions mapping the interval [−τ,0] into R n with a topology of uniform convergence. ∥ϕ∥=sup−τ≤s≤0∥ϕ(s)∥ is used to denote the norm of a function ϕ∈C([−τ,0],R n). For the functional differential in (4), its initial condition is given by e(s)=ϕ(s)∈C([−τ,0],R n). And we always assume that (4) has an unique solution with respect to initial condition [43].

3 Main results

In this section, some sufficient conditions for the projective synchronization in the driven-response delayed dynamical network with time-varying coupling are derived by the stability analysis of the impulsive functional different equations. Moreover, the error system (4) can converge globally exponentially to a given decay rate.

Denote 0<ρ=sup{t k −t k−1}<∞, k∈N, based on the theory of impulsive functional differential equations and comparison method, we can establish the following results.

Theorem 1

For given synchronization scaling factor α, projective synchronization in the driven-response time-varying coupled dynamical network with time delays model will occur if there exists a positive constant ζ>0 such that

(5)

and

$$ \frac{\ln \eta}{\rho} + \frac{c\zeta}{\eta} + \theta < 0$$
(6)

where

then the error system (4) converges globally exponentially to a decay rate λ/2, where λ>0 is the solution of λ−a+be λτ=0 with \(a = - \theta - \frac{\ln \eta}{\rho}\) and \(b = \frac{c\zeta}{\eta}\). That is to say, the coupled delayed dynamical driven-response time-varying network (1) can realize the projective synchronization under the impulsive control.

Proof

Choose the Lyapunov function candidate as follows:

$$V(t) = e^{T}(t)e(t).$$

For t≠t k , the derivative of V(t) along the trajectories of the error system (4) is given by

From Lemma 1, it is clear that

Then, we have

Let P(t)=C(t)⊗I n , we get

(7)

From the definition of θ, we have

$$ \dot{V}(t) \leq \theta V(t) + c\zeta V\bigl(t - \tau(t)\bigr).$$
(8)

On the other hand, when t=t k ,

(9)

For any ε>0, let υ(t) be an unique solution of the following impulsive delayed system:

$$ \left \{ \begin{array}{@{}l}\dot{\upsilon} (t) = \theta\upsilon(t) +c\zeta\upsilon (t - \tau(t) ) + \varepsilon,\quad t \ne t_{k},\\[3pt]\upsilon (t_{k}^{ +} ) = \eta\upsilon(t_{k}),\quad k \in N, \\[3pt]\upsilon(s) = \Vert \phi(s) \Vert ^{2},\quad -\tau \leq s \leq 0.\end{array} \right .$$
(10)

From Lemma 2, and V(t)≤∥ϕ(t)∥2 for −τ≤t≤0, we can conclude that V(t)≤υ(t), for t>0. By the formula for the variation of parameters [43], one obtains from (10) that

(11)

where ω(t,s), 0≤s≤t, is Cauchy matrix of the linear impulsive system, which has the following form:

$$ \left \{ \begin{array}{@{}l} \dot{\varsigma} (t) =\theta\varsigma(t),\quad t \ne t_{k},\\[3pt]\varsigma (t_{k}^{ +} ) = \eta\varsigma(t_{k}),\quad k \in N.\end{array} \right .$$
(12)

According to the representation of the Cauchy matrix [43], we get the estimation of ω(t,s) since 0<η<1 and t k −t k−1≤ρ,

(13)

Let \(\gamma = \frac{1}{\eta} \sup_{ - \tau \leq s \leq 0}\| \phi(s)\|^{2}\), from (11) and (13), we obtain

(14)

Denote φ(λ)=λ−a+be λτ, from (6), we have a>0, b>0 and a−b>0, and also φ(0)<0, φ(+∞)>0, φ′(λ)=1+bτe λτ>0, then φ(λ)=0 has an unique solution λ>0.

Since \(\frac{\varepsilon}{\eta} > 0\), λ>0, a−b>0 and \(\frac{1}{\eta} > 1\), we have

(15)

In the following, we will prove that the following inequality holds:

(16)

If it is not true, that is, it is assumed that there exists a t′>0 such that

(17)

and

(18)

According to (14) and (18), we get

(19)

which contradicts (17). Consequently, the assumption is not true and (16) holds.

Let ε→0, then

$$ V(t) = \bigl \Vert e(t) \bigr \Vert ^{2} \leq \upsilon(t)\leq \gamma e^{ - \lambda t}.$$
(20)

Thus, we have

(21)

When t→∞, the error system (4) is global exponential asymptotically stable with a convergence rate λ/2, which implies the drive system and the response networks (1) achieve the projective synchronization with the desired scaling factor α via the impulsive control method. The proof of Theorem 1 is completed. □

If the constant η≥1, we can replace 0<ρ=sup{t k −t k−1}<∞ with 0<ρ=inf{t k −t k−1}<∞, then, the following Corollary 1 is easily obtained.

Corollary 1

If there exists a positive constant ζ>0 such that

(22)
(23)

where \(\theta = \sup[ \mu(I_{N} \otimes M(z)) + \frac{c\| P(t)\|^{2}}{\zeta} ]\), P(t)=C(t)⊗I n , then the error system (4) converges globally exponentially to a decay rate λ/2, where λ>0 is the solution of λ−a+be λτ=0 with \(a = - \theta - \frac{\ln \eta}{\rho}\) and b=cζη.

The proof of Corollary 1 is more or less similar with the proof of Theorem 1, so we omit it to avoid repetition.

Remark 1

The conditions given by Theorem 1 and Corollary 1 do not require the time-varying coupling matrix to be symmetric and irreducible, which can be applied to many real-world dynamical networks, including those coupling schemes used in the above previous works. Moreover, when C(t)=C is a constant matrix, the time-varying network (1) becomes a time-invariant network, the other conditions are chosen as Theorem 1 and Corollary 1, the error system (4) can also converge globally exponentially to a decay rate λ/2, where

Remark 2

In [36], Sun et al. studied the projective synchronization in driven-response dynamical networks with time-varying coupling delay, but the time-varying delay in the paper is differential and its derivative is simultaneously required to be not greater than 1, which is a very strict condition. Obviously, we do not need these limit conditions in Theorem 1 and Corollary 1.

4 Numerical simulation

In this section, to verify and demonstrate the effectiveness of the proposed methods, we consider the unified chaotic system as the drive system. It is well known that the unified chaotic system is described by

(24)

where

The system (24) especially is always chaotic in the whole interval δ∈[0,1].

Firstly, a driven-response time-varying coupling dynamical network (1) with coupling delays is given by

(25)

where the coupling strength c=0.1 and the time-varying delay τ(t)=2−2cost.

The time-varying coupling configuration matrix C(t) is chosen as

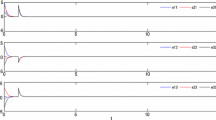
$$C(t) = \scriptsize{ \left ( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c}- 2\sin t & - 1 & 0 & 2\sin t & 1 \\ \sin t & - \sin t - \cos t & 0 & 0 & \cos t \\ 0 & \cos t & 0 & - \cos t & 0\\ 0 & \sin t\cos t & 1 & - \sin t\cos t & - 1 \\ - 1 & - 2\sin t & 0 &- 1 & 2 + 2\sin t \end{array} \right )}.$$

In the numerical simulations, the initial values of the drive system and the response systems are chosen as (1,1,−1) and (1,2,2,−2,−1,1,−2,3,−1,−1), respectively. The time-varying delay is τ(t)=2−2cost, which is bounded by τ=4. Choose the impulsive control gain matrix B k ={−0.79,−0.79} and system parameter δ=0.5. Let the positive constant \(\zeta = \sup( \sqrt{\eta} \| P(t) \| )\). According to the definition of Kronecker product, it is easy to obtain \(\lambda_{\max} [(I_{Nn} +(I_{N} \otimes B_{k}))^{T}(I_{Nn} + (I_{N} \otimes B_{k}))] =\lambda_{\max} [(I_{n} + B_{k})^{T}\*(I_{n} + B_{k})]\), μ(I N ⊗M(z))=μ(M(z)). After a simple computation, one has η=0.0441<1, ζ=1.0612>0, sup(μ(M(z)))=36.6070, θ=36.8476. According to Ref. [44], let the decay rate λ 0=0.8, then \(\varTheta : = \theta + b(1 + e^{\lambda _{0}\tau} ) = 100.8885\), the upper bound of the impulsive interval \(\rho = \sup\{ t_{k} - t_{k - 1}\} = -\ln\sqrt{\eta} /\varTheta = 0.0155\). Taking the impulsive interval t k −t k−1=0.01, then all the conditions of Theorem 1 are satisfied for the desired scaling factor α, which means the controlled dynamical network (2) can be asymptotically exponentially synchronized onto the desired value α. Figure 1 displays the trajectories of state variables in the driven-response dynamical networks with desired scaling factor α=0.5. Figure 2 shows the trajectories of projective synchronization in the x–y plane. The synchronization errors e i1=x i1−0.5x 1 and e i2=x i2−0.5x 2 (i=1,…,5) are shown in Fig. 3, respectively. The numerical results show that the impulsive controlling scheme for the driven-response complex network (1) is effective in Theorem 1.

Fig. 1
figure 1

State trajectories of drive system (the red dash line) and response network (the blue solid line) with α=0.5

Full size image
Fig. 2
figure 2

The phase plot of x–y with α=0.5. The red dash line and the blue solid line represent phase graph of drive system and response network, respectively

Full size image
Fig. 3
figure 3

The projective synchronization errors with α=0.5

Full size image

Then, a small-world driven-response dynamical network with time-varying delay is described by the following equations:

(26)

Take the parameters N=100, K=2 and p=0.1, and the coupling matrix C(t)=C of the network (26) can be randomly generated according to the rule [45]. The time-varying delay τ(t)=0.01sint≤0.01. Let the decay rate λ 0=20, after calculations, θ=84.2251, \(\varTheta : = \theta + b(1 + e^{\lambda _{0}\tau} ) =190.0041\), the upper bound of the impulsive interval ρ=0.0082. Selecting the impulsive interval t k −t k−1=0.005, the projective synchronization can be obtained with the desired scaling factor α=−0.5 (see Figs. 4, 5 and 6).

Fig. 4
figure 4

State trajectories of drive system (the red dash line) and response network (the blue solid line) with α=−0.5

Full size image
Fig. 5
figure 5

The phase plot of x–y with α=−0.5. The red dash line and the blue solid line represent phase graph of drive system and response network, respectively

Full size image
Fig. 6
figure 6

The projective synchronization errors with α=−0.5

Full size image

Remark 3

In [36], the authors proposed an adaptive feedback controller and an updated law to realize the projective synchronization in driven-response dynamical network. In this paper, the projective synchronization of driven-response time-varying network is studied by employing the impulsive control. To our best of knowledge, compare with the controller used in adaptive control method, the controller used in impulsive method usually is relatively simple and is easy to implement. In the impulsive synchronization scheme, the response networks receive the information from the drive system only in discrete times, which can reduce the information redundancy in the transmitted signal, increase the robustness and reduce the control cost. Furthermore, from the simulation results, it is clear that the proposed impulsive control scheme is more effective than the adaptive control scheme in [36], and the driven-response time varying coupling network (1) is global exponential asymptotically stable with a convergence rate λ/2, as t→∞.

5 Conclusion

In this paper, the projective synchronization of the driven-response time-varying dynamical network with coupling delay has been investigated by employing the impulsive control, where the weight coupling matrix is time varying. Some sufficient conditions for realizing the projective synchronization are established based on the stability analysis of impulsive functional differential equations and comparison method. Moreover, it should be pointed out that we do not require that τ(t) is a differential function with a bound of its derivative, which means that the time-varying delay including a wide range of functions. Finally, the effectiveness and feasibility of the proposed method have been verified by two typical numerical simulations.