1 Introduction

A hyperchaotic system is characterized as a chaotic system with at least two positive Lyapunov exponents, indicating that its dynamics are expand in more than one direction and give rise to a more complex attractor. Historically, the two most well-known hyperchaotic systems are the hyperchaos Rössler [1] and hyperchaos Chua’s circuit [2]. Due to the great potential in technological application, the hyperchaos generation has become a focal research topic [3–8]. Very recently, hyperchaos has been generated numerically and experimentally by adding a controller [9–13] in the generalized Lorenz system [14], Chen system [15], Lü system [16] or a unified chaotic system [17].

Since Ott et al. [18] introduced the OGY control method, researchers have increasingly interested in controlling chaos of the nonlinear systems. Chaos control, in a broader sense, is now understood for two different purposes: one is to suppress the chaotic dynamical behaviors when chaos effect is undesirable in practice, and the other is to generate or enhance chaos when it is useful under some circumstances, for example, in heartbeat regulation [19], encryption [20], digital communications [21], etc. The process of generating or enhancing chaos is called chaotification or anti-control of chaos. At present, generating and controlling hyperchaos are usually achieved by state feedback methods [22–24] or parameter perturbations [25–28], which are identified as non-feedback control. However, parameter perturbation can be more easily realized in practical systems and it is also more robust to noise, because it does not require determining the system state variables and continuous tracking of the system state.

In this paper, we focus on hyperchaos and hyperchaos control based on the newly presented simplified Lorenz system [29] with a sinusoidal parameter forcing. Compared with previous references, dynamics of the forced system are analyzed with both frequency variation and amplitude variation, and the generated hyperchaos is not only demonstrated by Lyapunov exponent spectrum and bifurcation diagrams, but also verified by Poincaré sections. In addition, a simple feedback controller is designed to stabilize the nonautonomous hyperchaotic system to different periodic orbits. It is organized as follows: The mode of sinusoidally forced simplified Lorenz system is presented in Sect. 2. In Sect. 3, the dynamical behaviors, including hyperchaotic behaviors, are analyzed by calculating the Lyapunov exponents, bifurcation diagrams, and Poincaré sections. In Sect. 4, a feedback controller is applied to the forced system, and some periodic orbits are obtained from the controlled hyperchaotic simplified Lorenz system. Finally, we summarize the results and indicate the future directions.

2 The sinusoidally forced simplified Lorenz system

The simplified Lorenz system with a single adjustable parameter c is described by

$$ \left\{ \begin{array}{l}\dot{x} = 10(y - x) \\ \noalign {\vspace {4pt}}\dot{y} = (24 - 4c)x - xz + cy \\ \noalign {\vspace {4pt}}\dot{z} = xy - 8z/3 \\\end{array} \right.$$
(1)

where x,y and z are state variables. When the parameter c∈(−1.59,7.75), the system is typically chaotic. The system is ‘simplified’ in these senses that: (1) There is only one parameter c; (2) for c=0 or c=6, the term y or x is removed from the second equation; (3) for c=−1, it is the conventional Lorenz system with the standard parameters. This system can be reformulated in the following canonical form [14, 30]:

(2)

According to the canonical-form criterion formulated in Ref. [19], the sign of a 12 a 21 distinguishes nonequivalent topologies. For the simplified Lorenz system, a 12 a 21>0 when c<6; a 12 a 21=0 when c=6; and a 12 a 21<0 when c>6. So the system includes three different topological structures and has abundant dynamic properties.

Consider a simple sinusoidal control function c=c 0sin(ωt), then c∈[−c 0,c 0]. Noticing that the function c=c 0sin(ωt) is a time-varying forcing term, the three-dimensional autonomous system (1) is changed to a three-dimensional nonautonomous system, which is equivalent to a four-dimensional autonomous system

$$ \left\{ \begin{array}{l}\dot{x} = 10(y - x) \\ \noalign {\vspace {4pt}}\dot{y} = (24 - 4c_{0}\sin(u))x - xz + c_{0}\sin(u)y \\ \noalign {\vspace {4pt}}\dot{z} = xy - 8z/3 \\ \noalign {\vspace {4pt}}\dot{u} = \omega\\\end{array} \right.$$
(3)

where c 0 is the amplitude and ω is the angular frequency of the forcing function. Since the forced system is a four-dimensional autonomous system, limit cycles, tori, chaotic or hyperchaotic attractors may appear. The attractor of system (1) with c=1 and the attractor of system (3) with c 0=1, ω=4.5 are shown in Fig. 1. The structure of the sinusoidally forced system (3) is apparently more complex than that of the original system (1).

Fig. 1
figure 1

Attractors of system (1) and system (3) with different parameter. (a) System (1) with c=1. (b) System (3) with c 0=1,ω=4.5

Full size image

3 Hyperchaotic behaviors of the sinusoidally forced system

3.1 Dynamics of the forced system with frequency variation

When the perturbation amplitude c 0 is a constant, the dynamics are only dependent on the forcing frequency ω. As is well known, the Lyapunov exponents measure the exponential rates of divergence and convergence of nearby trajectories in state space, and the bifurcation diagram is another important indicator for different dynamical states. When c 0=1, the Lyapunov exponents versus ω and the corresponding bifurcation diagram of the local maximum of x are shown in Fig. 2, where the frequency variation ω∈[0,20] with an increment of Δω=0.01.

Fig. 2
figure 2

Lyapunov exponents and bifurcation diagram of system (3) with c 0=1. (a) Lyapunov exponents versus ω. (b) Bifurcation diagram

Full size image

From Fig. 2, it is shown that system (3) is chaotic in most of the range ω∈[0,20] with at least three windows of periodicity when ω∈(7.8,10), and the system (3) is chaotic even when ω exceeds 20. The observed dynamical states over the range ω∈[0,20] are listed in Table 1, which are determined by the sign of the four Lyapunov exponents and the fractal dimension. So this sinusoidal forcing not only can suppress the original chaotic behavior to periodic orbits in ω∈(7.80,8.10]∪(8.30,8.50]∪(8.85,10.00], but also can generate hyperchaos in the range of ω∈(0,5.85]. The results are consistent with those in Ref. [25], where it was found that the optimum frequency for suppressing chaos with the smallest amplitude forcing in the Lorenz system is twice the frequency of the lowest unstable periodic orbit whose period is about 1.55 when c=0, corresponding to a frequency of ω≅4π/1.55≅8.1 for the system (3) when c 0=1.

Table 1 The dynamics of system (3) for the different ranges of ω with c 0=1
Full size table

To observe the periodic behaviors, the periodic window is expanded with steps of 0.002 in Fig. 3. Two sets of symmetrical initial conditions are selected for visualizing the pitchfork bifurcation, and the corresponding bifurcation diagram is drawn in blue and red in Fig. 3(b). Obviously, four kinds of bifurcation exist in the periodic window, including a period-doubling bifurcation when ω≅7.87, an interior crisis when ω≅9.05, a pitchfork bifurcation when ω≅9.83, and a tangent bifurcation when ω≅10.

Fig. 3
figure 3

Lyapunov exponent and bifurcation diagram of system (3) with c 0=1. (a) Lyapunov exponents versus ω. (b) Bifurcation diagram (blue and red correspond to two symmetrical initial conditions)

Full size image

The hyperchaotic state of a system can often be revealed in its Poincaré section. This method amounts to taking a plane slice through the strange attractor at a fixed value of the phase z, which reduces the dimension of the attractor by 1.0, and it can provide much convincing evidence for hyperchaos. The Poincaré sections generate in the hyperplane z=24 (which passes through the equilibrium points) of system (3) with c 0=1, ω=0 (which is chaotic) and with c 0=1, ω=4.5 (which is hyperchaotic) are shown in Fig. 4. Apparently the sinusoidally forced system is hyperchaotic as evidenced by the two-dimensional Poincaré section.

Fig. 4
figure 4

Poincaré sections of system (3) for different ω. (a) c 0=1, ω=0 (chaotic). (b) c 0=1, ω=4.5 (hyperchaotic)

Full size image

3.2 Dynamics of the forced system with amplitude variation

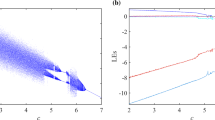
Now we analyze the dynamical behaviors of the sinusoidally forced system with different forcing amplitudes. In this case, ω is fixed at 4.5 while the system is hyperchaotic. The Lyapunov exponents versus c 0 and the corresponding bifurcation diagram of x are shown in Fig. 5 where the range of amplitude variation is c 0∈[0,12] and the step size of c 0 is 0.005. To observe the periodic behaviors, the periodic window is expanded with steps of 0.002 in Fig. 6. Figures 5 and 6 show that system (3) is chaotic in most of the range c 0∈[0,12].

Fig. 5
figure 5

Lyapunov exponents and bifurcation diagram of system (3) with ω=4.5. (a) Lyapunov exponents versus c 0. (b) Bifurcation diagram (blue and red correspond to two symmetrical initial conditions)

Full size image
Fig. 6
figure 6

Lyapunov exponent and bifurcation diagram of system (3) with ω=4.5. (a) Lyapunov exponents versus c 0∈[8.88,12]. (b) Bifurcation diagram (blue and red correspond to two symmetrical initial conditions)

Full size image

The different dynamical states over the range c 0∈[0,12] are listed in Table 2. We find the amplitude variation not only can suppress the original hyperchaotic behavior to chaotic behavior, or to a periodic orbit, but also can preserve the hyperchaos in the range of c 0∈[0.53,1.30).

Table 2 The dynamics of system (3) for the different ranges of c 0 with ω=4.5
Full size table

The Poincaré sections are shown in Fig. 7 for demonstrating the existence of hyperchaos in the forced system. These sections generate in the hyperplane z=24 of system (3) with c 0=0, ω=4.5 (which is chaotic) and with c 0=1.2,ω=4.5 (which is hyperchaotic). Obviously the sinusoidally forced system is hyperchaotic on the evidence of its two-dimensional Poincaré section.

Fig. 7
figure 7

Poincaré sections of system (3) for the different c 0. (a) c 0=0, ω=4.5 (chaotic). (b) c 0=1.2, ω=4.5 (hyperchaotic)

Full size image

Interestingly, the three-attractor coexisting phenomenon occurs in this forced system. There exist three attractors when c 0=8.6,ω=4.5 and c 0=10.6, ω=4.5, respectively. The coexisting attractors are shown in Fig. 8, denoted in green, blue and red corresponding to different initial conditions. The initial conditions of this first case are chosen as [x 0,y 0,z 0,u 0]=[−15.0794,−4.1277,60.8300,2.8345], [x 0,y 0,z 0,u 0]=[−1.1578,−0.5678,18.7900,5.2480] and [x 0,y 0,z 0,u 0]=[6.5245,7.4527,39.1987,3.8621], respectively. The initial conditions of the second case are set to [x 0,y 0,z 0,u 0]=[5.0546,5.5616,40.7255,4.0424], [x 0,y 0,z 0,u 0]=[−22.3068,−35.0684,49.7511,2.5573] and [x 0,y 0,z 0,u 0]=[0.7080,0.8707,6.0358,1.2553], respectively.

Fig. 8
figure 8

Coexisting attractors of system (3) for the different c 0. (a) c 0=8.6, ω=4.5. (b) c 0=10.6, ω=4.5.

Full size image

4 Hyperchaos control for the sinusoidally forced system

Since chaos (or hyperchaos) may cause irregular behaviors which is undesirable, in this section, a feedback controller is designed to stabilize the nonautonomous hyperchaotic system to periodic orbits.

Assume that the controlled hyperchaotic system is given by

$$ \left\{ \begin{array}{l}\dot{x} = 10(y - x) + v_{1} \\ \noalign {\vspace {4pt}}\dot{y} = (24 -4c_{0}\sin(u))x - xz + c_{0}\sin(u)y + v_{2} \\ \noalign {\vspace {4pt}}\dot{z} = xy - 8z/3 + v_{3} \\ \noalign {\vspace {4pt}}\dot{u} = \omega + v_{4} \\\end{array} \right.$$
(4)

where v 1,v 2,v 3 and v 4 are feedback control input. To keep it simple, we set v 1=kx,v 2=v 3=v 4=0, so that the controlled hyperchaotic system becomes

$$ \left\{ \begin{array}{l}\dot{x} = 10(y - x) + kx \\ \noalign {\vspace {4pt}}\dot{y} = (24 - 4c_{0}\sin(u))x - xz + c_{0}\sin(u)y \\ \noalign {\vspace {4pt}}\dot{z} = xy - 8z/3 \\ \noalign {\vspace {4pt}}\dot{u} = \omega\\\end{array} \right.$$
(5)

where k is the feedback coefficient, and the system parameters are chosen as ω=4.5 and c 0=1 to ensure that the original perturbed system is hyperchaotic.

For the hyperchaos control, one problem is how to choose the feedback coefficient k. Firstly, find the range of k by analyzing the equilibrium and stability of system (5) at ω=0. Secondly, calculate the Lyapunov exponents and plot the bifurcation diagram of system (5) in the nearby range. Then we can easily determine the feedback coefficient k required to control the hyperchaos to stable periodic orbits. The Lyapunov exponents versus k and the corresponding bifurcation diagram of system (5) are shown in Fig. 9 where the range of feedback coefficient is k∈[−6,9] and the step size of k is 0.005.

Fig. 9
figure 9

Lyapunov exponents and bifurcation diagram of system (5) with ω=4.5, c 0=1. (a) Lyapunov exponents versus k∈[−6,9]. (b) Bifurcation diagram

Full size image

Table 3 lists the different k values and the corresponding Lyapunov exponents for different periodic orbits. The phase diagrams are shown in Fig. 10. Evidently, hyperchaotic behavior is successfully controlled to different periodic orbits.

Fig. 10
figure 10

State space plots of system (5) with different feedback coefficients (a) k=−6.00, (b) k=−3.05, (c) k=5.25, (d) k=7.02

Full size image
Table 3 Control of hyperchaos to periodic orbits with different k
Full size table

5 Conclusions

This paper investigates a simple control method of using a sinusoidal parameter forcing to drive the simplified Lorenz system to hyperchaos. It is found that the sinusoidal forcing not only suppresses the original chaotic behavior to a periodic orbit, but also generates hyperchaos in some parameter ranges. The basic properties of the dynamics are analyzed by using the Lyapunov exponents, bifurcation diagrams, and Poincaré sections. With both the change of frequency variation ω and amplitude variation c 0, the sinusoidal forced system exhibits limit cycles, pitchfork bifurcations, period-doubling bifurcations, chaos, and hyperchaos. It has more complex dynamical behaviors than that of the original system. Furthermore, hyperchaotic states also can be controlled to chaos or a periodic orbit by a simple feedback control, which is desirable for engineering applications. Future works on this topic could include its circuit implementation, as well as a theoretical analysis of the counterpart fractional-order system.