1 Introduction

Nowadays, it is well known that the rheological properties of rock materials contribute to the safety of buildings and slopes (Zhao et al. 2017; Xu et al. 2019; Cao et al. 2020). The essential purpose of rock rheology research is to analyze the actual mechanical properties of rock mass and the relationship between mechanical properties and rock structure, i.e., to establish the constitutive equation of rock. The creep fracture or creep failure of rock has time effects. Many scholars have made in-depth studies on the creep properties of stones, and a series of valuable results have been obtained (Chaboche 1982; Zhong and Ma 1987; Kachanov 1993; Wong et al. 2006; Jiang et al. 2013; Wu et al. 2020; Li et al. 2021).

As we know, the creep model of rock mainly includes two categories of mechanical models and physical models (Cao et al. 2020; Li et al. 2021). Mechanical models are widely used due to their easy understanding and clear physical mechanics concepts. However, it has difficulty to characterize nonlinear deformation properties (Liu et al. 2020). Physical models establish the rheological constitutive relations from the perspective of solid-state physics. They can consider the effects of physical and chemical properties inside materials, crystal and crystal boundary defects on the rheological properties. Unluckily, the development of the two kinds of models is relatively independent, there is lack of effective bridging and transition methods between them because the question of an organic combination between them has not yet been substantively resolved (Xue and Zhang 2015) in recent years, the introduction of damage mechanics provides a way to solve this problem.

Previous studies have shown that correctly defining the damage variable is essential for constructing the damage creep models. Since the concept of continuous damage was proposed (Kachanov 1958), the damage variable has been defined from various perspectives and approaches. The familiar theoretical bases of the definition can be divided into three categories. One is the effective bearing area, earlier, Chaboche (1982) pointed out that material damage mainly represents a reduction in the effective bearing area at a macro level. Then, based on the concept, Kachanov (1993) obtained the time-dependent damage variable by considering the stress and material properties. Another is the so-called geometric damage theory, which focuses on the quantitative relation between the mesoscopic cracks and the damage, such representative damage variables can be found in Grady (1980), Chen and Taylor(1985), and Yang (1996). The last is the statistical damage theory. Tang and Kaiser (1998) proposed that the cumulative seismic damage calculated by the simulated event rate can be used as the damage parameter to describe the damage evolution mechanism. Wong et al. (2006) postulated that the statistics of damage properties follow the Weibull distribution with time parameters at the grain scale. To accurately study some dynamic mechanical behaviors of rock, such as accelerated creep behavior, time as an essential parameter is further coupled into the damage variable (Jiang et al. 2013; Wang et al. 2014, 2017; Liu et al. 2017; Wu et al. 2020; Yan et al. 2020).

It is observed that these researches introduce a single damage variable into the damage evolution equation for changing physical constants into nonlinear variables. In light of the above discussion, there are two main ideas for dealing with the coupling behavior of time and damage in mechanical models. One is to convert some physical constants into equivalent variables based on the concept of effective bearing area, and the other is to directly reduce the values of physical constants based on the damage deterioration characteristics of materials. However, in these damage creep models mentioned above, only one of the two is adopted. That is, only a single time-dependent damage variable is used to capture the nonlinear characteristics for accelerated damage creep behavior of rock under different mechanical and physical mechanisms. As a result, these models have some shortcomings in theory and need further research.

In addition, according to the experiments on the total stress–strain relationship of the rock, there is still a particular residual strength after the failure of the rock (Xu et al. 2018; Zhu et al. 2019). The residual strength should be incorporated into the time-dependent damage variable, which can improve the rigor of the damage creep model. Still, there are few studies on the residual strength in creep constitutive models of rock.

Another problem, the current consensus is that the accelerated creep characteristics of rock are mainly related to the deterioration of the properties of elastic modulus and viscosity coefficient. Previous studies of the static damage model of rock also show that it is not adequate to describe three-dimensional isotropic damage only by a single damage scalar. Two independent damage scalars are needed (Fares 1993; Kachanov 1993; Gao et al. 1996). Although many damage creep models exist, the damaging effect on elastic modulus and viscosity coefficient is rarely considered simultaneously.

This paper aims to introduce a new viscoelasto-plastic damage element considering double time-dependent damage variables. The damage correction coefficient is firstly utilized to improve the time-dependent damage variable. Then, a one-dimensional damage creep model is obtained using a constitutive differential equation with double damage scalars. To better accord with the engineering practice, considering the failure criterion and the flow law, the three-dimensional creep damage constitutive equation of rock is further derived. Finally, experimental data and the Burgers model are used to verify and analyze the proposed constitutive model. For the safe design and construction of slopes and underground structures, this study can provide a theoretical reference and can better guarantee the stability and safety of the projects.

2 Establishment of the damage viscoelastic-plastic creep model

2.1 Definition of double time-dependent damage variables

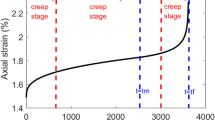
The typical creep curve of rocks consists of three stages, transient creep, steady creep, and accelerated creep, as shown in Fig. 1. When the loading stress level is lower than the long-term strength of the rock, the internal damage of rock material has little influence on creep, and the creep curve of the stone only includes the transient and steady stages. On the contrary, the damage will occur to the rock and result in a faster rate of rock deformation, and then rock creep will enter the accelerated stage.

Fig. 1
figure 1

Typical creep curve of rock

Full size image

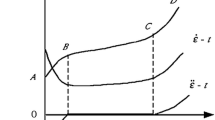
In general, the initial two stages can be accurately described by the traditional Burgers model, as shown in Fig. 2, and the corresponding constitutive differential equation can be written as Eq. (1) (Chen et al. 2017)

$$\ddot{\sigma } + \left( {\frac{{E_{1} }}{{\eta_{3} }} + \frac{{E_{1} }}{{\eta_{2} }} + \frac{{E_{2} }}{{\eta_{2} }}} \right)\dot{\sigma } + \frac{{E_{1} E_{2} }}{{\eta_{2} \eta_{3} }}\sigma = E_{1} \ddot{\varepsilon } + \frac{{E_{1} E_{2} }}{{\eta_{2} }}\dot{\varepsilon }$$
(1)

where \(\dot{\sigma }\) and \(\ddot{\sigma }\) represent the first and second derivatives of stress to time, respectively. \(\dot{\varepsilon }\) and \(\ddot{\varepsilon }\) represent the first and second derivatives of strain versus time, respectively. E1 is the elastic modulus of the elastic body. η3 is the viscosity coefficient of the viscous body. E2 and η2 are the elastic modulus and viscosity coefficient of the viscous body, respectively. By solving Eq. (1), the one-dimensional creep equation of the Burgers model can be obtained as

$$\varepsilon = \frac{\sigma }{{E_{1} }} + \frac{\sigma }{{E_{2} }}\left( {1 - e^{{ - \frac{{E_{2} }}{{\eta_{2} }}t}} } \right) + \frac{\sigma }{{\eta_{3} }}t$$
(2)

where ε is the total strain of the Burgers model. σ is the stress inside the rock. t is the cumulative loading time, and the meanings of other parameter symbols are the same as above.

Fig. 2
figure 2

Burgers model

Full size image

Compared to the initial two stages of rock creep, the third stage, i.e. the acceleration stage of creep, has nonlinear characteristics. Existing studies (Kachanov 1958, 1993; Chaboche 1982; Fares 1993) have shown that the evolution and development of internal mseo-cracks under external load will be produced along with the stress–strain change process of rock. These mesoscopic defects will slowly evolve to macro performance deterioration, eventually leading to rock destruction. So the damage variables are defined here from two aspects of macroscopic and mesoscopic.

Firstly, from the macroscopic point of view, under the external force, dislocation creep and diffusion creep both lead to the generation of mesoscopic cracks and holes, as time goes on, these accumulated defects will lead to a reduction in effective bearing area, which in turn leads to an increase in effective stress. Herein, concerning the concept of effective stress proposed by Kachanov (1992, 2007), the expression of time-dependent damage variable D1 relating to effective stress is given as

$$\dot{D}_{1} = C\left( {\frac{\sigma }{{1 - D_{1} }}} \right)^{n}$$
(3)

where \(\dot{D}_{1}\) represents the first derivative of the damage variable with respect to time. C and n are material parameters.

According to the principle of strain equivalence (Lemaitre 1990), the stress–strain relation with damage is given as

$$\left\{ \begin{gathered} \sigma = \sigma^{ * } \left( {1 - D_{1} } \right) \hfill \\ \sigma^{ * } = E\varepsilon \hfill \\ \end{gathered} \right.$$
(4)

where σ represents the effective stress; σ* denotes the apparent stress; E is the elastic modulus, and ε is the strain. Equation (4) can be combined and rewritten into the following formula

$$\sigma = E\varepsilon \left( {1 - D_{1} } \right)$$
(5)

It should be noted that D1 only reflects the impact of damage on the stress of rock, but does not involve the impact on elastic modulus. Then, by observing Eq. (5), it can be found that when the damage approaches the maximum value, D1= 1, the effective stress approaches infinity. As seen in the introduction, existing experiments have shown that residual strength remains after rock failure. Therefore, the residual strength correction factor δ is introduced here to resolve this conflict (Yuan et al. 2019), and the corresponding model is

$$\delta = \sqrt {\frac{{\sigma_\text{r} }}{{\sigma_{{\text{c} }} }}}$$
(6)

where σr represents the residual strength; σc is the long-term strength.

Substitute Eq. (6) into Eq. (3), then Eq. (3) can be written as

$$\dot{D}_{1} = C\left( {\frac{\sigma }{{1 - \delta D_{1} }}} \right)^{n}$$
(7)

Through integrating Eq. (7), the following expression can be obtained as

$$\frac{{\left( {1 - \delta D_{1} } \right)^{1 + n} }}{1 + n} + A = C\sigma^{n} t$$
(8)

where A is the integration constant, to solve Eq. (8), the boundary conditions are introduced as follows:

$$\left\{ \begin{gathered} D_{1} = 0 \, for \, t = 0 \hfill \\ D_{1} = \delta \, for \, t = t_{f} \hfill \\ \end{gathered} \right.$$
(9)

Substitute Eq. (9) into Eq. (8), the functional expression of initial time tf  when creep failure occurs can be given as:

$$t_\text{f} = \frac{{1 - (1 - \delta )^{1 + n} }}{{C(1 + n)\sigma^{n} }}$$
(10)

By combining Eqs. (7) and (10) with suitable integration and arrangements, the time-dependent damage variable D1 considering residual strength can be obtained as

$$D_{1} = 1 - \left( {1 - \frac{t}{{t_{f} }}\left( {1 - \left( {1 - \delta } \right)^{1 + n} } \right)} \right)^{{\frac{1}{n + 1}}}$$
(11)

Crystal is a kind of polycrystalline structured material. Its defect is the root of the weakness of the mechanical properties from the mesoscopic point of view. In the mechanical model of rock creep, the elastic modulus and the viscosity coefficient are critical physical parameters that reflect a rock's ability to resist deformation under the action of external forces. As far as stones are concerned, the dislocation slip of crystals is an essential factor affecting these two physical parameters. Previous studies have shown that the existence of dislocations causes the surrounding atoms to be disturbed and disarranged, thus causing lattice distortion or local strain. Considering macroscopic continuity, such strain will lead to distortion of the stress field and accumulation of strain energy (Liu 1994).

Based on the above analysis, it is assumed that the constant accumulation of stress field energy will accelerate the lattice distortion or local strain over time. This physical assumption is reflected in phenomenology as the elastic modulus and viscosity coefficient deterioration with time. In general, the damage properties inside the rock are close to the power function of time (Yang et al. 1999), so the suggestion of Hou et al. (2019) is adopted, a time-dependent damage variable relating to elastic modulus and viscosity coefficient can be given as

$$D_{2} = 1 - \exp \left( { - at} \right)$$
(12)

where D2 is the time-dependent damage variable relating to elastic modulus and viscosity coefficient, 0 < D2 < 1; a is an unstable constant related to the internal properties of the material.

2.2 A new element of time-dependent damage

Continuum damage mechanics is introduced here to more appropriately describe the nonlinear characteristic of the accelerated creep from the perspectives of effective area and internal structure damage, and put forward a new element of viscoelastic-plastic damage. Elastic modulus and viscosity coefficient in this new element are both transformed into unstable constants by time-dependent damage variables. The concrete form of the damaged mechanical element is depicted in Fig. 3. The physical meanings of D1 and D2 are the same as above.

Fig. 3
figure 3

The element of viscoelastic-plastic damage

Full size image

Through the principle of effective stress (Kachanov 1992, 2007), the constitutive relation of the damaged viscous body in Fig. 3 can be expressed in Eq. (13).

$$\varepsilon_{{\text{v} }} = \frac{\sigma }{{\eta_{4} }}t = \frac{\sigma }{{\eta_{4} \left( {1 - D_{1} } \right)}}t$$
(13)

where εv and η4 represent the strain and viscosity coefficient of the damaged viscous body in Fig. 3.

Substitute Eq. (11) into Eq. (13), and by integration, the one-dimensional creep equation of the damaged viscous body is obtained as

$$\varepsilon_{\text{v}} = \frac{\sigma }{{\eta_{4} }}\frac{(1 + n)}{n}\frac{{t_\text{f} }}{{(1 - \delta )^{1 + n} - 1}}\left( {\left( {1 - D_{1} } \right)^{n} - 1} \right)$$
(14)

For the deterioration of rock physical properties in the stress field, for the simplicity of computation and applicability of the formula, take the traditional approach here. The time-dependent damage variable D2 is directly introduced into the viscosity coefficient, then the final one-dimensional creep equation of the damaged viscous body can be written as

$$\varepsilon_{\text{v}} = \frac{\sigma }{{\eta_{4} (1 - D_{2} )}}\frac{(1 + n)}{n}\frac{{t_\text{f} }}{{(1 - \delta )^{1 + n} - 1}}\left( {\left( {1 - D_{1} } \right)^{n} - 1} \right)$$
(15)

Duo to the damage elastic body and damage viscous body are in series in Fig. 3. According to the superposition principle, the creep equation of the damaged viscoelastic body in Fig. 3 in a one-dimensional stress state is given as

$$\varepsilon_{\text{ve}} = \frac{\sigma }{{E_{4} \left( {1 - D_{1} } \right)(1 - D_{2} )}} + \frac{\sigma }{{\eta_{4} (1 - D_{2} )}}\frac{(1 + n)}{n}\frac{{t_\text{f} }}{{(1 - \delta )^{1 + n} - 1}}\left( {\left( {1 - D_{1} } \right)^{n} - 1} \right)$$
(16)

where εve represents the strain of the damaged viscoelasto body, and E4 is the elastic modulus of the damaged elastic body.

As is known to all, plastic deformation occurs only when the stress level of rock exceeds the long-term strength σs, so σ should be replaced by σ–σs. Then, the final creep equation of the damaged viscoelasto-plastic body is as

$$\varepsilon_{\text{vep}} = \frac{{\sigma - \sigma_\text{s} }}{{E_{4} \left( {1 - D_{1} } \right)(1 - D_{2} )}} + \frac{{\sigma - \sigma_\text{s} }}{{\eta_{4} (1 - D_{2} )}}\frac{(1 + n)}{n}\frac{{t_\text{f} }}{{(1 - \delta )^{1 + n} - 1}}\left[ {(1 - D_{1} )^{n} - 1} \right]$$
(17)

where εvep represents the whole strain of the damaged viscoelasto-plastic body.

2.3 The one-dimensional creep equation of the creep model presented

Since the Burgers model can well capture the characteristics of the initial two stages of rock creep, which can be connected in series with the proposed element of viscoelastic-plastic damage to establish a new damage creep model as shown in Fig. 4.

Fig. 4
figure 4

The creep damage model

Full size image

The proposed creep damage model in Fig. 4 is subdivided into four parts: elastic body, viscous body, viscoelastic body, and damaged viscoelasto-plastic body. Thus, the one-dimensional creep equation obtained according to the superposition principle is written as

$$\varepsilon (t) = \left\{ \begin{gathered} \frac{{\sigma_{0} }}{{E_{1} }} + \frac{{\sigma_{0} }}{{E_{2} }}\left[ {1 - \exp \left( { - \frac{{E_{2} }}{{\eta_{2} }}t} \right)} \right] + \frac{{\sigma_{0} }}{{\eta_{3} }}t\,{\text{ For }}\sigma_{0} < \sigma_\text{s} \, \hfill \\ \frac{{\sigma_{0} }}{{E_{1} }} + \frac{{\sigma_{0} }}{{E_{2} }}\left[ {1 - \exp \left( { - \frac{{E_{2} }}{{\eta_{2} }}t} \right)} \right] + \frac{{\sigma_{0} }}{{\eta_{3} }}t + \frac{{\sigma_{0} - \sigma_\text{s} }}{{E_{4} (1 - D_{1} )(1 - D_{2} )}} + \frac{{\sigma_{0} - \sigma_\text{s} }}{{\eta_{4} (1 - D_{2} )}}\frac{(1 + n)}{n}\frac{{t_\text{f} }}{{(1 - \delta )^{1 + n} - 1}}\left[ {\left( {1 - D_{1} } \right)^{n} - 1} \right]\,{\text{ For }}\sigma_{0} \ge \sigma_\text{s} \hfill \\ \end{gathered} \right.$$
(18)

2.4 The three-dimensional creep equation of the creep model presented

The actual rock mass is in a complex stress environment, so it is necessary to establish the three-dimensional creep equation further. Before derivation, some assumptions should be made as follows:

  1. (1)

    The rock is isotropic material, and the damage law in all directions is consistent.

  2. (2)

    Damage occurs only during the accelerated creep phase.

  3. (3)

    The damage time and creep time are consistent in the accelerated creep stage.

Suppose that the total strain of the proposed creep model is \(\varepsilon_{ij}^{t}\), the strain of the elastic body is \(\varepsilon_{ij}^\text{e}\), the strain of the viscous body is \(\varepsilon_{ij}^{{\text{v}}}\), the strain of the viscoelastic body is \(\varepsilon_{ij}^{{{\text{ve}}}}\), and the strain of the damaged viscoelasto-plastic body is \(\varepsilon_{ij}^{{{\text{vep}}}}\). According to the superposition principle, the total strain \(\varepsilon_{ij}^{t}\) can be expressed as

$$\varepsilon_{ij}^{t} = \varepsilon_{ij}^\text{e} + \varepsilon_{ij}^\text{v} + \varepsilon_{ij}^\text{ve} + \varepsilon_{ij}^\text{vep}$$
(19)

For elastic materials, the total stress tensor \(\sigma_{ij}\) and the total strain tensor \(\varepsilon_{ij}\) at any point in the interior are composed of two parts; the specific relationship is as follows

$$\left\{ \begin{gathered} \sigma_{ij} = S_{ij} + \delta_{ij} \sigma_{m} \hfill \\ \varepsilon_{ij} = e_{ij} + \delta_{ij} \varepsilon_{m} \hfill \\ \end{gathered} \right.$$
(20)

where δijσm denotes the spherical tensor of stress. Sij is the deviatoric tensor of stress. δijεm is the spherical tensor of strain. eij is the deviatoric tensor of strain, and δij is Kronecker delta.

According to the generalized Hooke's law, the three-dimensional constitutive relation of elastic materials is

$$\left\{ \begin{gathered} \sigma_{m} = 3K\varepsilon_{m} \hfill \\ S_{ij} = 2Ge_{ij} \hfill \\ \end{gathered} \right.$$
(21)

where K is the bulk modulus; G is the shear modulus.

Combined with Eqs. (20) and (21), the three-dimensional creep equations of the elastic body, viscous body, and viscoelastic body can be derived. We have

$$\left\{ \begin{gathered} \varepsilon_{ij}^\text{e} = \frac{1}{{2G_{1} }}S_{ij} + \frac{1}{{3k_{1} }}\delta_{ij} \sigma_{m} \hfill \\ \varepsilon_{ij}^\text{v} = \frac{{S_{ij} }}{{2\eta_{3} }}t \hfill \\ \varepsilon_{ij}^\text{ve} = \frac{{S_{ij} }}{{2G_{2} }}\left[ {1 - \exp \left( { - \frac{{G_{2} }}{{\eta_{2} }}t} \right)} \right] \hfill \\ \end{gathered} \right.$$
(22)

where K1 and G1 are the bulk and shear modulus of the elastic body, respectively; G2 is the shear modulus of the viscoelastic body.

The three-dimensional creep constitutive relation of rock caused by friction sheet in the damaged viscoelasto-plastic body is related to the yield criterion and plastic potential function and the flow law. To sum up, the three-dimensional creep equation of the damaged viscoelasto-plastic body can be written as

$$\varepsilon_{ij}^\text{vep} = \left\{ {\frac{1}{{2G_{4} \left( {1 - D_{1} } \right)(1 - D_{2} )}} + \frac{(1 + n)}{{\eta_{4} (1 - D_{2} )n}}\frac{{t_\text{f} }}{{(1 - \delta )^{1 + n} - 1}}\left[ {(1 - D_{1} )^{n} - 1} \right]} \right\}\left\langle {\Phi (\frac{F}{{F_{0} }})} \right\rangle \frac{\partial Q}{{\partial \sigma_{ij} }}$$
(23)

with

$$\left\langle {\Phi (\frac{F}{{F_{0} }})} \right\rangle \frac{\partial Q}{{\partial \sigma_{ij} }} = \left\{ \begin{gathered} \Phi \left( {\frac{F}{{F_{0} }}} \right) \, \left( {{\text{F}} \ge {0}} \right) \hfill \\ 0 \, \left( {{\text{F}} < {0}} \right) \hfill \\ \end{gathered} \right.$$
(24)

where G4 is the shear modulus of viscoelasto-plastic body. F is the yield function. F0 is the initial value of the yield function, which is generally 1 for simplification of calculation; Q is the plastic potential function. \(\Phi \left( {\frac{F}{{F_{0} }}} \right)\) is the form of power function. In general, the value of the power exponential is 1. In addition, the correlative flow rule is used, which is F = Q.

At room temperature or below, the deviatoric strain is the main effect on rock creep, while the spherical strain plays a secondary role. Herein, Mises yield function is adopted, and its form is as

$$F = \sqrt {J_{2} } - {{\sigma_{s} } \mathord{\left/ {\vphantom {{\sigma_{s} } {\sqrt 3 }}} \right. \kern-\nulldelimiterspace} {\sqrt 3 }}$$
(25)

where J2 is the second invariant of deviatoric stress.

In the conventional triaxial creep experiment of rock (σ1 ≥ σ2 = σ3), when the accelerated creep of rock begins, the stress should satisfy the following conditions:

$$\left\{ \begin{gathered} \sigma_{m} = \frac{1}{3}(\sigma_{1} + 2\sigma_{3} ) \hfill \\ S_{11} = \sigma_{1} - \sigma_{m} = \frac{{2(\sigma_{1} - \sigma_{3} )}}{3} \hfill \\ \sqrt {J_{2} } = \frac{{\sigma_{1} - \sigma_{3} }}{\sqrt 3 } \hfill \\ \end{gathered} \right.$$
(26)

where σm is the mean spherical stress; S11 is the axial deviatoric stress.

By combining Eqs. (21)–(26), the three-dimensional creep equation of rock can be obtained as

$$\varepsilon_{11}^{t} = \left\{ \begin{gathered} \frac{{\sigma_{1} + 2\sigma_{3} }}{{9K_{1} }} + \frac{{\sigma_{1} - \sigma_{3} }}{{3G_{1} }} + \frac{{\sigma_{1} - \sigma_{3} }}{{3G_{2} }}\left[ {1 - \exp \left( { - \frac{{G_{2} }}{{\eta_{2} }}t} \right)} \right] + \frac{{\sigma_{1} - \sigma_{3} }}{{3\eta_{3} }}t \hfill \\ \, \sigma_{0} < \sigma_\text{s} \hfill \\ \frac{{\sigma_{1} + 2\sigma_{3} }}{{9K_{1} }} + \frac{{\sigma_{1} - \sigma_{3} }}{{3G_{1} }} + \frac{{\sigma_{1} - \sigma_{3} }}{{3G_{2} }}\left[ {1 - \exp \left( { - \frac{{G_{2} }}{{\eta_{2} }}t} \right))} \right] + \frac{{\sigma_{1} - \sigma_{3} }}{{3\eta_{3} }}t + \frac{{\sigma_{1} - \sigma_{3} { - }\sigma_\text{s} }}{{6G_{4} (1 - D_{1} )(1 - D_{2} )}} + \hfill \\ \frac{{\sigma_{1} - \sigma_{3} - \sigma_\text{s} }}{{3\eta_{4} (1 - D_{2} )}}\frac{(1 + n)}{n}\frac{{t_\text{f} }}{{(1 - \delta )^{1 + n} - 1}}\left[ {\left( {1 - D_{1} } \right)^{n} - 1} \right] \hfill \\ \, \sigma_{0} \ge \sigma_\text{s} \hfill \\ \end{gathered} \right.$$
(27)

3 Validations of model

3.1 Parameter identification

Parameter identification is mainly divided into one-dimensional state and three-dimensional state. Before the nonlinear fitting of parameters, it is necessary to determine some parameters that do not need fitting and can be easily obtained through experimental curves.

In Eq. (18), the instantaneous elasticity modulus E1 can be determined by the stress–strain relationship curve, i.e.

$$E_{1} = \frac{\sigma }{{\varepsilon_{1} }}$$
(28)

where ε1 is the instantaneous elasticity strain when t = 0, which can be obtained from the creep curve. In addition, according to the characteristics of transition creep, we have

$$\varepsilon^{\prime} = \frac{\sigma }{{E_{1} }} + \frac{\sigma }{{E_{2} }}$$
(29)

where ε' is the strain value at the intersection of the extension line of the stable creep curve and the longitudinal axis, E2 can be determined. And finally, \(\eta_{3}\) can be determined by the slope of the steady creep curve.

In Eq. (27), G1 and K1 are shear modulus and bulk modulus, respectively, which the following formulas can determine

$$\left\{ \begin{gathered} K_{1} = \frac{E}{3(1 - 2\mu )} \hfill \\ G_{1} = \frac{E}{2(1 + \mu )} \hfill \\ \end{gathered} \right.$$
(30)

where E is the instantaneous elasticity modulus.

After completing the above work, other undetermined parameters must be determined by nonlinear fitting algorithm. As is known to all, statistical fitting of nonlinear creep models and experimental data is a challenging task, and the scientific selection of initial parameters is significant. To avoid improper initial values of parameters resulting in complex convergence of calculation, the Levenberg–Marquardt method and the Universal-Global-Optimization method are combined to determine the other parameters in Eqs. (18) and (27).

3.2 Verification of one-dimensional creep equation

The experimental data used for parameter identification in the one-dimensional creep equation is chosen from Okubo et al. (1991), the parameters of the creep model listed in Table 1 are determined by the above method, and the contrastive analysis of the creep calculation curve and experimental data are illustrated in Fig. 5.

Table 1 Parameters of the one-dimensional creep model for Kawazu tuff rock
Full size table
Fig. 5
figure 5

Comparison between the Burgers model and the proposed model for Kawazu tuff rock from Okubo et al. (1991)

Full size image

It can be seen in Fig. 5 that in a one-dimensional stress state, the model proposed here can fully capture the creep mechanical behavior of rock. In addition, since the experimental curve of Kawazu tuff rock under static load is relatively smooth, the error between the theoretical curve and the experimental point is tiny, in contrast, the traditional Burgers model has some shortcomings in describing the accelerated creep stage, and the fitting effect is poor. On the whole, the proposed damage creep model can accurately describe the characteristics of three phases of rock creep, which verifies the rationality of the proposed model.

3.3 Verification of three-dimensional creep equation

To further demonstrate the applicability of the presented creep model, other three kinds of rock (Jiang et al. 2013; Qui et al. 2003; Zhong and Ma 1987) are utilized to verify the proposed model. Otherwise, the comparison between the proposed model and Burgers model in three-dimensional stress state is continued as with a one-dimensional stress state. However, it can be observed from Eq. (2), and Fig. 5 that the Burgers model can only describe the linear growth of creep. To illustrate it more intuitively, the Burgers model of Wanzhou sandstone from Jiang et al. (2013) and Changshan salt rock from Qui et al. (2003) is established, respectively. The corresponding parameters of the three kinds of rock are determined as above. The physical parameters are listed in Tables 2 and 3, and the contrastive analyses of creep calculation curves and experimental data are depicted in Figs. 6, 7, and 8.

Table 2 Parameters of the proposed three-dimensional creep model
Full size table
Table 3 Parameters of the Burgers model
Full size table
Fig. 6
figure 6

Comparison between the Burgers model and the proposed model for Wanzhou sandstone from Jiang et al. (2013)

Full size image
Fig. 7
figure 7

Comparison between the Burgers model and the proposed model for Changshan salt rock from Qui et al. (2003)

Full size image
Fig. 8
figure 8

Comparison between experimental date and computational solution of sandy shale rock from Zhong and Ma (1987)

Full size image

It is worth discussing that, as seen in Table 2, the same physical parameter of different rocks differs significantly. For example, although Wanzhou sandstone and Sandy shale rock are both sandstone in nature, most of the physical parameter values of sandy shale rock are greater than Wanzhou sandstone. There are two possible reasons for this phenomenon. One is that the inner structure of sandstone may be various microscopic compositions due to different times of formation and environments. Another possibility is the problem of stability of the optimization algorithm.

From Figs. 6, 7, 8, it can be seen that the proposed damage creep model with double time-dependent damage variables could accurately simulate the three creep stages of rock in a three-dimensional stress state. Besides, no matter which stress state of confining pressure is low, medium, or high, the creep failure behaviors of rock can be well described by the model. Figures 6 and 7 show that the ability of the Burgers model to describe the accelerated creep behavior of rock in the three-dimensional stress state is still rather rough and weaker than the creep model with two damage factors proposed here.

The damage viscoelastic-plastic element is the crucial part of the presented model, and the variation rules of η4 and G4 under different confining pressures are studied, as shown in Figs. 7 and 8, given the experimental data of sandy shale rock, is relatively sufficient, which can better illustrate the problem, so take it for example. According to Figs. 9, 10 for sandy shale rock, it is observed that η4 decreases with the increment of confining pressure, while G4 declines with the increase of confining pressure.

Fig. 9
figure 9

The variation rule of G4 under different confining pressures for sandy shale rock

Full size image
Fig. 10
figure 10

The variation rule of η4 under different confining pressures for sandy shale rock

Full size image

4 Conclusions

Double time-dependent damage variables are discussed here based on the rock's effective stress and mesoscopic physical damage mechanism. A new element of viscoelastic-plastic damage was further constructed with the combination of residual strength. The final damage creep model and three-dimensional creep equations are derived and verified by experimental data and the Burgers model, and sound fitting effects are obtained.

  1. (1)

    Combined with the damage mechanism of the rock's internal structure, double time-dependent damage variables are defined to set up a nonlinear creep model with residual strength. The case study indicates that the model proposed here is more comprehensive and rigorous relative to conventional Burgers model.

  2. (2)

    The proposed model's and three-dimensional damage creep equations are derived, and related model parameters identification methods are also given. Furthermore, four groups of experimental data are used for verification. The results show that the proposed creep model with better description can reflect the creep characteristics in the whole stage well compared with the traditional Burgers model.

  3. (3)

    According to the fitting data analysis of sandy shale rock, when the presented model identifies the parameters, the viscosity coefficient increases in the element of viscoelasto-plastic damage, and the elastic modulus decreases with the rise in deviator stress.

Although the presented model provides a helpful way to accurately capture the creep characteristics of the given rocks with limited experimental data, more experimental data are needed to verify the applicability. And to facilitate the engineering application of practical problems, how to incorporate the model presented here into the existing commercial software is still required to be studied in future.