1 Introduction

As the most common problem in engineering, landslides have seriously affected traffic safety and people’s lives (Hassiotis et al. 1997; Guo and Qin 2010; Yazdanpanah et al. 2016). Therefore, experienced geotechnical engineers try to provide a reasonable design and reinforcement to overcome stability problems (Ito et al. 1981; Poulos 1995). Many measures have been put forward in the study of landslide prevention and control. Anti-slide piles are widely applied as an important structure to prevent landslides and in slope engineering generally (Popov and Okatov 1980; Poulos 1995; Yazdanpanah et al. 2016). However, the calculation method for anti-slide piles still has some limitations. According to actual engineering practice in a large number of anti-slide pile design cases, the distribution of soil resistance acting on the piles is often ignored (considering only the landslide thrust), so that the calculation results are inconsistent with the actual condition, increasing the construction cost significantly (Poulos 1995; Tang et al. 2014).

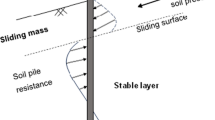
The landslide body transfers the landslide thrust from the anti-slide pile to the underlying stable layers, enabling the stabilization of the landslide (Ausilio et al. 2001; Tang et al. 2014). Reasonable and effective designs of anti-slide piles should be based on the distribution of soil resistance acting on the piles. Traditional calculation methods revealed that the distribution of landslide thrust acting on the anti-slide pile may be triangular, rectangular and trapezoid in shape, while the distribution of soil resistance assumes a triangular shape (Hassiotis et al. 1997; Ito et al. 1981; Dai 2002; Li et al. 2013). Additionally, model tests on landslides constituted of clay, loess or sand have also demonstrated that the distribution of soil resistance assumes triangular shapes (Ito and Matsui 1975; Xu et al. 1988; Tang et al. 2014). Xiong (2000) indicated that in a sliding mass, the landslide thrust acting on deeply buried anti-slide piles basically presented a rectangular distribution in a loess landslide. Dai (2002) summarized the different distribution shapes of landslide thrust and soil resistance acting on the piles, but no further validation or calculation equations were given.

In fact, the actual distribution of soil resistance is still considered to be triangular in shape in practical engineering. In addition, there is limited validation in the literature for the influence of soil resistance on the internal force of anti-slide piles (including laboratory model experiments, field experiments and numerical simulation), and the main focus has been on the study of the landslide thrust and internal forces of the piles (Griffiths and Lane 1999; Won et al. 2005; Wen et al. 2007; Alonso and Pinyol 2010; Cojean and Caï 2011; Ashour and Ardalan 2012; Zhou et al. 2014). As for the actual distribution of soil resistance, such as inverted trapezoidal shapes (in a landslide body composed of rock or clay) and parabolic shapes (in a landslide body composed of sand or bulk material), less consideration was given to this in previous calculation equations and few designs considered the soil resistance acting on the pile in practical engineering (Dai 2002; Tang et al. 2014). For example, Ito et al. (1979) proposed a new analytical method of slope retention by analyzing the mechanical properties of anti-slide piles under different pile spacings, materials and section properties. Stewart et al. (1994) divided the calculation of the internal force of anti-slide piles into three methods: pressure method, displacement method and finite element method. Lin and Huang (2000) improved the calculation method of landslide thrust and validated the accuracy of this new function by using field data. However, for the transfer coefficient method assumes the direction of the resultant force, the strip generally cannot meet the torque balance conditions, which may make the thrust calculation results smaller. This is a potential danger that cannot be ignored for the governance project. Therefore, in order to ensure the safety, reliability and economy of the treatment project, it is necessary to use other methods to carry out parallel evaluation and determine the final scheme by synthesizing various evaluation results. Dai (2002) and Yang et al. (2006) deduced an analytic expression and computational method to determine the form of the internal force on the anti-slide piles due to landslide soil pressure distributions of triangular, rectangular and parabola shapes. However, its rationality has not been verified by more tests and a large number of engineering examples. In addition, Dai (2002) failed to combine the proposed distribution function of landslide thrust and soil resistance with the foundation coefficient method to derive the calculation formula of internal force and displacement of anti-slide pile with the soil resistance in front of the pile. Moreover, after considering the soil resistance acting on the pile, the mechanical characteristics and change rules of the anti-slide pile are not very clear, and the design calculation formula and theory of the anti-slide pile after considering the soil resistance acting on the pile are not perfect, which needs further discussion and solution. Cai and Ugai (2003) obtained the function of internal force and displacement of the anti-slide pile by using the foundation coefficient method, this being close to the field monitoring results. However, Cai and Ugai (2003) did not choose the appropriate distribution function of landslide thrust and soil resistance according to the different properties of landslide. Bouafia (2007) investigated the lateral reaction modulus and the lateral soil resistance by full-scale lateral loading tests of single instrumented piles.

In the design of anti-slide piles, many technicians ignore the soil resistance acting on the piles, only analyzing the landslide thrust. Although this consideration can achieve a relatively satisfactory landslide control effect, the cost of the whole project will be too high due to the excessive use of materials. In this paper, ABAQUS software was used to establish a three-dimensional numerical model to verify the quantitative effect of the internal force of anti-slide piles both considering and ignoring the soil resistance acting on the piles. Based on the actual distribution functions of soil resistance acting on the anti-slide piles, the formula for calculating the internal force of the piles was derived. With reference to field slope engineering in Yunnan, China, the optimum quantity of steel reinforcement and the safety factor were compared using the proposed formula.

2 Numerical validation of internal force considering soil resistance acting on anti-slide piles

2.1 Establishment of numerical model

  1. 1.

    Model overview

In the ABAQUS modeling analysis, Mohr–Coulomb model was selected as the soil constitutive model, which required fewer parameters and could be obtained through conventional tests. In order to speed up the calculation, a simplified pile–soil model is established for numerical calculation. Five square piles with the same specifications were selected to establish the full-pile model, and the influence of soil resistance acting on the pile on the internal force of the anti-slide pile was analyzed by means of loading and control analysis step. In addition, the mechanical model of contact surface in ABAQUS is mainly composed of normal action and tangential action. When analyzing the pile–soil contact problem, the contact pressure limit in the normal direction of the contact interface need not be specially defined, only the contact property is defined as “hard contact” and the contact surface is allowed to separate. It determines that the contact constraint occurs when the clearance between the contact surfaces is zero, and the contact pressure is less than or equal to zero when the contact surface is separated, so that the contact pair can be re-established to make the simulation results more accurate whenever the relative slip occurs. The tangential contact behavior is defined by coulomb friction model. It is considered that when the equivalent friction stress is less than the ultimate shear stress, the contact surface is in the bond state and no relative sliding occurs. When the friction force exceeds the ultimate shear stress, the relative sliding occurs between the contact surfaces (Fei and Zhang 2010).

Taking a project slope in Yunnan, China, as an example, the model size, slope height, slope gradient and section size of the anti-slide pile were 40 m × 28 m × 20 m, 10 m, 1:1.5 and 2.5 m × 2 m, respectively. The distance between pile center was L = 6 m. The side perpendicular to the direction of the landslide was defined as the short side, and the length of the anti-slide pile was 14 m. According to the experimental geological prospecting data, it can be roughly divided into two layers of soil. The geotechnical parameters selected for the calculation model are shown in Table 1.

Table 1 Geotechnical parameters
Full size table
  1. 2.

    Contact interface between pile and soil

“Master–Slave” contact was used to define the contact interface in this model, and the contact surfaces of the model were defined as the main control surface and the subordinate surface, respectively. According to the contact behavior between the slope and anti-slide pile, each contact surface of the pile was defined as the “Master Surface” and each contact surface of the slope was defined as the “Slave Surface” (Li et al. 2013; Liu et al. 2018).

  1. 3.

    Mesh and boundary conditions

The anti-slide pile and slope soil were considered as entities after establishing this model. To make the mesh unified, C3D4 (three-dimensional four-node entity element) was selected (Li et al. 2013; Liu et al. 2018; Liu et al. 2018). Because the slope and anti-slide pile were two independent individuals, the grid of the anti-slide pile and landslide should be divided separately (see Fig. 1).

Fig. 1
figure 1

Mesh of model

Full size image
  1. 4.

    Load

The soil layer at the bottom of the slope was fully consolidated, limiting the displacement \(U_{1} , U_{2}\) and \(U_{3}\) of the slope bottom in three directions. The front and rear sides of the slope were constrained by the x-axis direction, limiting horizontal displacement \(U_{1}\), and the top and bottom of sides of the slope were constrained by the y-axis direction, limiting horizontal displacement \(U_{2}\), while the left and right sides of the slope were constrained by the z-axis direction, limiting displacement \(U_{3}\) in the z-axis direction. Gravity was defined under the condition of in situ stress balance, and the influence of other factors on the applied load was neglected (Gu et al. 2014).

In the loading analysis of ABAQUS, the load analysis step is mainly determined according to the loading conditions of slope and anti-slide pile. The first step is defined as “Load Step” (i.e., Geostatic stress). In this step, anti-slide pile element is not considered, and only initial in situ stress analysis of slope soil is carried out (this step is used for stress balance of slope land). In the second step, it is defined as “Reduce Step” (i.e., strength reduction analysis step). In this analysis step, the anti-slide pile element is still not considered, and only the strength reduction is carried out on the sliding body part of the slope. The third step is defined as “Remove Step,” in which the anti-slide pile element is still not considered. The purpose of this analysis step is to remove (excavate) the soil before the pile above the sliding surface, activate the pile–soil interaction, and establish the initial contact relationship between the anti-slide pile and the soil under the “Gravity Load,” so that the model calculation can be more easily convergent. In the post-processing of the model, the shear force and bending moment on each side of the anti-slide pile are extracted, respectively, after considering the soil resistance acting on the pile (i.e., under the “Load step”) and without considering the soil resistance acting on the pile (i.e., under the “Remove Step”).

2.2 Analysis of internal force of anti-slide pile

Figure 2 presents the shear force versus the depth of the anti-slide pile. Both when considering and ignoring the soil resistance (refers to the displacement of pile to soil under the action of external force (such as horizontal load). Excessive displacement will make the soil slide at a certain depth. The state of soil acting on the pile is called passive limit parallel state. At this time, the horizontal force of the soil around the pile is essentially the soil resistance provided by the soil.) acting on the anti-slide piles, the distribution of shear force was basically the same. Above the sliding surface, the longer the anti-slide pile, the larger the shear force was. However, below the sliding surface, the direction of shear force had changed significantly. At the pile bottom, the shear force tended to be zero, and the maximum shear force was obtained at 11.65 m. When ignoring the factor of soil resistance, the shear force of the anti-slide piles far exceeded the shear force considering the soil resistance. Under this condition, the peak shear force reached 5393.62 kN, but when the soil resistance was included in the analysis mechanism, the peak shear force was 4298.73 kN.

Fig. 2
figure 2

Shear force versus depth of pile of anti-slide pile

Full size image

From Fig. 3, the distribution of bending moment is basically the same under the two different conditions (considering and ignoring the soil resistance acting on the anti-slide piles). With the increase in the depth of the anti-slide pile, the bending moment first increased to a maximum value at approximately 9 m and then decreased to 0 at the pile bottom. However, the direction of bending moment did not change. That is to say, the whole pile kept the tension state on the left side all the time. When ignoring and considering the soil resistance acting on the piles, the peak bending moments reached 24,364.47 kN m and 21,096.99 kN m, respectively.

Fig. 3
figure 3

Bending moment versus depth of pile of anti-slide pile

Full size image

The soil resistance acting on the anti-slide piles can resist some of the landslide thrust (refers to the load acting on the retaining structure when the slope with potential sliding surface loses stability and the sliding body slides downward along the potential sliding surface.). Considering the soil resistance, the shear force decreased by 1094.89 kN and the bending moment reduced by 3267.48 kN m. Therefore, during the design of anti-slide piles, the soil resistance acting on the piles should be considered and analyzed comprehensively.

2.3 Analysis of lateral displacement of anti-slide pile

From Fig. 4, it was noted that the lateral displacement of the anti-slide piles was more significant after the soil before the piles was excavated, especially the displacement of the pile top. Compared with the lateral displacement of the anti-slide pile without excavation, the landslide was stable under the support of the anti-slide pile, and the magnitude of the maximum lateral displacement of the slope reached 10−5 (0.1 mm). When the pile depth increased gradually, the lateral displacement of the piles showed the same tendency under the two different conditions (considering and ignoring the soil resistance). The lateral displacement of the piles decreased at the beginning, then increased gradually and lasted until the magnitude of lateral displacement of the pile bottom was 10−6 (0.01 mm). The lateral displacement at the bottom of the anti-slide pile was negligible and can be regarded as 0. Therefore, the soil resistance acting on the anti-slide piles has a significant influence on their lateral displacement.

Fig. 4
figure 4

Lateral displacement versus depth of pile of anti-slide pile

Full size image

2.4 Effect of gradient of soil before pile (GSBP) on internal force of anti-slide pile

He et al. (2015a, b) indicated that the slope angle can have a significant effect on the distribution of the soil-pile pressure acting on the stabilizing piles in sandy slopes. From the analysis of the numerical simulation results in Sects. 2.2 and 2.3, it is noted that the soil resistance acting on anti-slide piles has a significant influence on the internal force of the piles and plays an important role in balancing the landslide thrust when piles are supporting slopes. However, in practical engineering, to ensure the safety of anti-slide piles, not all slopes in the design and calculation of the piles consider the soil resistance acting on them. Therefore, it is necessary to further verify which slope conditions really need to consider the influence of the soil resistance. The soil resistance acting on anti-slide piles comes from the smaller values of the passive earth pressure, residual anti-sliding force and elastic resistance (Terzaghi et al. 1996; Zheng et al. 2010; Zhang et al. 2011). Therefore, the factors affecting the soil resistance acting on anti-slide piles can be determined whether the factors affecting the passive earth pressure, residual sliding resistance and elastic resistance are determined.

According to Rankine’s earth pressure theory (Zheng et al. 2010), the passive earth pressure can be obtained. From the equation of passive earth pressure, with increase in the internal friction angle and cohesion of the soil before the pile, the resistance provided by the soil in the limit state before the pile will also be increased. The expressions of the residual sliding force and residual anti-sliding force show that with increase in the grade of the side slope, the residual sliding force increases and the safety factor of the soil before the pile decreases, further reducing the stability (Terzaghi et al. 1996). Therefore, under the condition of ensuring the stability of the soil before the pile, the residual anti-sliding force provided by the soil before the pile can be controlled by changing the gradient of soil before pile (GSBP).

Therefore, in this paper, seven gradients of soil before the pile (0°, 10°, 20°, 30°, 40°, 50°, and 60°) and five parameters including different cohesion and internal friction angles were selected to investigate the effect of the gradient of the soil before the pile and the shear strength parameters on the soil resistance acting on anti-slide piles (see Fig. 5 and Table 2 (Sun et al. 2001)).

Fig. 5
figure 5

Sketch map of seven gradients of soil before pile

Full size image
Table 2 Shear strength parameters (Sun et al. 2001; Liu 2017)
Full size table

In the analysis of the anti-slide pile-slope model, five anti-slide piles were assumed to share the landslide thrust equally. To simplify the analysis, the same anti-slide pile was selected for comparison. Figures 6, 7, 8, 9, 10, 11, 12 and 13 present the displacement diagram of the anti-slide pile and slope with the different GSBP. From the cloud images, it was obvious that different GSBPs can have different influences on the displacement of the anti-slide pile and slope.

Fig. 6
figure 6

Displacement diagram of anti-slide pile and slope with the GSBP = 0°

Full size image
Fig. 7
figure 7

Displacement diagram of anti-slide pile and slope with the GSBP = 10°

Full size image
Fig. 8
figure 8

Displacement diagram of anti-slide pile and slope with the GSBP = 20°

Full size image
Fig. 9
figure 9

Displacement diagram of anti-slide pile and slope with the GSBP = 30°

Full size image
Fig. 10
figure 10

Displacement diagram of anti-slide pile and slope with the GSBP = 40°

Full size image
Fig. 11
figure 11

Displacement diagram of anti-slide pile and slope with the GSBP = 50°

Full size image
Fig. 12
figure 12

Displacement diagram of anti-slide pile and slope with the GSBP = 60°

Full size image
Fig. 13
figure 13

Displacement diagram of anti-slide pile and slope with the GSBP = 90°

Full size image

The displacement data from Figs. 67, 8, 9, 10, 11, 12 and 13 are plotted in Figs. 14 and 15. The resistance provided by the pile and soil can resist the landslide thrust. From Fig. 14, with increase in the pile depth, the resistance provided by the pile increases gradually. Additionally, with the same pile depth, the larger the GSBP, the larger the resistance provided by the pile is. At pile depths less than 4 m, the resistance provided by the pile increases parabolically with increase in the pile depth. When the pile depth exceeds 4 m, the resistance provided by the pile increases linearly with increase in the pile depth. Similarly, the resistance provided by the soil increases parabolically with increase in the pile depth (see Fig. 15). Comparing the two resistances, when the pile depth was large, the increase in resistance provided by the soil with pile depth was smaller than the resistance provided by the piles.

Fig. 14
figure 14

Resistance provided by pile versus the depth of pile

Full size image
Fig. 15
figure 15

Resistance provided soil versus the depth of pile

Full size image

Figures 16 and 17 present the average value and loss percentage of the soil resistance (the ratio of soil resistance acting on the anti-slide piles to that with the GSBP of 0° under different GSBP (10°, 20°, 30°, 40°, 50° and 60°), which is used to express the exertion of soil resistance acting on the anti-slide piles) acting on the anti-slide piles. Figures 18 and 19 present the maximum value and loss percentage of the soil resistance acting on the anti-slide piles. When the strength parameters of the soil remain unchanged, the gradient of the soil before the pile increased gradually, and the soil resistance acting on the anti-slide piles decreased obviously. At a given GSBP value, if the shear strength parameters gradually increased, the maximum value of soil resistance acting on the anti-slide piles presented an obvious increment. At GSBP of 50° or 60°, the loss percentage of the soil resistance acting on the anti-slide piles played a relatively small role, and there was a big gap with the GSBP of 40°. The difference of the average value and loss percentage of the soil resistance acting on the anti-slide piles reached approximately 220 kN and 18%, while the difference was 350 kN and 20% for the maximum value and loss percentage of the soil resistance acting on the piles, respectively. Therefore, when the GSBP exceeded 40°, the influence of the soil resistance acting on the anti-slide piles can be neglected. Contrarily, when the GSBP was less than 40°, analysis of the soil resistance acting on the piles should be emphasized and strengthened and can be regarded as a safety reserve without excessive waste of engineering cost and materials.

Fig. 16
figure 16

Average value of soil resistance acting on anti-slide pile under different GSBP

Full size image
Fig. 17
figure 17

Loss percentage in average value of soil resistance acting on anti-slide pile under different GSBP

Full size image
Fig. 18
figure 18

Maximum value of soil resistance acting on anti-slide pile under different GSBP

Full size image
Fig. 19
figure 19

Loss percentage in maximum value of soil resistance acting on anti-slide pile under different GSBP

Full size image

3 Calculation equations of internal force of anti-slide pile

3.1 Distribution function of soil resistance acting on anti-slide pile

According to different soil types, Dai (2002) summarized the actual distribution functions of the landslide thrust and soil resistance acting on piles as shown in Table 3. It was assumed that the action point of the soil resistance was located below the pile top, i.e., \(z_{0}^{'} = k^{'} h_{1}\), and the action point of the landslide thrust was located below the pile top, i.e., \(z_{0} = kh_{1}\). The distribution function of landslide thrust and soil resistance is expressed by \(q\left( z \right) = \xi z^{2} + \eta z + \psi\), and \(p\left( z \right) = \xi^{\prime}z^{2} + \eta^{\prime}z + \psi^{\prime}\), respectively (Zheng et al. 2010; Zhang et al. 2011).

Table 3 Actual distribution functions of landslide thrust and soil resistance acting on piles (Dai 2002)
Full size table

Here, \(q\left( z \right)\) and \(p\left( z \right)\) represent the distributed load of the landslide thrust and soil resistance along the depth of the pile, respectively. \(h_{1}\) stands for the pile length above the sliding surface. E represents the landslide thrust at the position of the pile. \(E^{\prime }\) is the soil resistance at the position of the pile. \(\xi\), \(\eta\), \(\psi\) represent the coefficients of the distribution function under different distribution forms of landslide thrust based on different types of rock and soil. \(\xi^{'}\), \(\eta^{\prime }\), \(\psi^{\prime }\) represent the coefficients of the distribution function under different distribution forms of soil resistance based on different types of rock and soil.

3.2 Calculation of internal force considering soil resistance acting on anti-slide pile

The landslide thrust and soil resistance acting on piles are necessary conditions for the calculation of anti-slide piles. Currently, in the process of design calculation of anti-slide piles, the methods for calculating the soil resistance of the piles in the loading section are divided (Dai 2002). Moreover, in the existing code or part of the engineering design, the elastic resistance (p) generated by the interaction of the anti-slide pile and the slope soil is regarded as the soil resistance acting on the piles. Combined with Table 3, the equation of the internal force of the elastic anti-slide pile was deduced.

A diagrammatic sketch of the anti-slide pile–soil interaction is shown in Fig. 20 (Xiao 2017). The landslide thrust was expressed as \(q(z) = \xi z^{2} + \eta z + \psi\). The soil resistance acting on the piles is given as \(p(z) = \xi^{\prime } z^{2} + \eta^{\prime } z + \psi^{\prime }\). Moreover, flexural deformation appeared along the whole length of the pile.

Fig. 20
figure 20

A diagrammatic sketch of anti-slide pile–soil interaction (Xiao 2017)

Full size image

3.2.1 Derivation of formula of foundation coefficient method

The internal force of the anti-slide pile in OA was deduced as (Zheng et al. 2010):

$${\text{EI}}\frac{{{\text{d}}^{4} x_{z} }}{{{\text{d}}z^{4} }} = \xi z^{2} + \eta z + \psi - {\text{CB}}_{P} x_{z}$$
(1)
$$\frac{{{\text{d}}^{4} x_{z} }}{{{\text{d}}z^{4} }} = \frac{\xi }{\text{EI}}z^{2} + \frac{\eta }{\text{EI}}z + \frac{\psi }{\text{EI}} - \alpha^{5} z \cdot x_{z}$$
(2)

where C is the foundation coefficient, \(C = mz\); \(m\) denotes the ratio coefficient of the foundation coefficient \(\alpha = \sqrt[5]{{\frac{{mB_{P} }}{\text{EI}}}}\); \(B_{\text{P}}\) is the calculation width of the pile; and \(x_{z}\) represents the lateral displacement of the pile at the depth \(z\).

Based on the initial condition, i.e., \(z = 0\), we can obtain

$$\left\{ {\begin{array}{*{20}l} {x_{(z = 0)} = x_{0} } \hfill \\ {\frac{{{\text{d}}x_{z} }}{{{\text{d}}z_{(z = 0)} }} = \varphi_{0} } \hfill \\ {{\text{EI}}\frac{{{\text{d}}^{2} x_{z} }}{{{\text{d}}z_{(z = 0)}^{2} }} = M_{0} } \hfill \\ {{\text{EI}}\frac{{{\text{d}}^{3} x_{z} }}{{{\text{d}}z_{(z = 0)}^{3} }} = Q_{0} } \hfill \\ \end{array} } \right.$$
(3)

It was assumed that

$$x_{z} = \mathop \sum \limits_{i = 0}^{\infty } a_{i} z^{i} = a_{0} + a_{1} z + \cdots + a_{i} z^{i}$$
(4)

where \(a_{i}\) is the i-th undetermined coefficient and \(i\) values vary from 0 to infinity; \(z\) represents the calculation depth of the piles.

For Eq. (4), the four derivatives were obtained as follows:

$$\frac{{{\text{d}}^{4} x_{z} }}{{{\text{d}}z^{4} }} = \mathop \sum \limits_{i = 4}^{\infty } a_{i} \cdot i \cdot \left( {i - 1} \right) \cdot \left( {i - 2} \right) \cdot \left( {i - 3} \right)z^{i - 4}$$
(5)

In addition, the following identities can be obtained from simultaneous Eq. (5), Eq. (2) and Eq. (3):

$$\sum\limits_{i = 4}^{\infty } {\left( {i - 3} \right)} \left( {i - 2} \right)\left( {i - 1} \right)i \cdot a_{i} z^{i - 4} = \frac{\xi }{\text{EI}}z^{2} + \frac{\eta }{\text{EI}}z + \frac{\psi }{\text{EI}} - \alpha^{5} z\sum\limits_{i = 0}^{\infty } {a_{i} } z^{i}$$
(6)

Equation (6) can be used to get all the coefficients of the equation, so Eq. (4) can be expressed as (Zheng et al. 2010):

$$\begin{aligned} x_{z} & = \sum\limits_{i = 0}^{\infty } {a_{i} } z^{i} = a_{0} + a_{1} z + a_{2} z^{2} + \cdots + a_{n} z^{n} + \cdots + a_{i} z_{i} = a_{0} + a_{1} z + a_{2} z^{2} + a_{3} z^{3} \\ & \quad + \left( { - 1} \right)^{k - 1} \left( {\alpha^{5} } \right)^{k - 1} \left( {\frac{\psi }{\text{EI}}} \right)\frac{{\left( {5k - 5} \right)!!}}{{\left( {5k - 1} \right)!}}z^{5k - 1} + \left( { - 1} \right)^{k - 1} \left( {\alpha^{5} } \right)^{k - 1} \left( {\frac{\eta }{EI} - \alpha^{5} a_{0} } \right)\left( {\frac{{\left( {5k - 4} \right)!!}}{{\left( {5k} \right)!}}} \right)z^{5k} \\ & \quad + \left( { - 1} \right)^{k - 1} \left( {\alpha^{5} } \right)^{k - 1} \left( {\frac{\xi }{\text{EI}} - \alpha^{5} a_{1} } \right)\left( {\frac{{\left( {5k - 3} \right)!!}}{{\left( {5k + 1} \right)!}}} \right)z^{5k + 1} + \left( { - 1} \right)^{k - 1} \left( {\alpha^{5} } \right)^{k - 1} \frac{{2\left( {5k - 2} \right)!!}}{{\left( {5k + 2} \right)!}}a_{2} z^{5k + 2} \\ & \quad + \left( { - 1} \right)^{k} \left( {\alpha^{5} } \right)^{k} \frac{{\left( {3!} \right)\left( {5k - 1} \right)!!}}{{\left( {5k + 3} \right)!}}a_{3} z^{5k + 3} \\ \end{aligned}$$
(7)

where \(k = 1, 2 ,3, 4 \ldots\).

$$\begin{aligned} x_{z} & = a_{0} + a_{1} z + a_{2} \left[ {z^{2} + \left( { - 1} \right)^{k - 1} \left( {\alpha^{5} } \right)^{k - 1} \frac{{2\left( {5k - 2} \right)!!}}{{\left( {5k + 2} \right)!}}z^{5k + 2} } \right] + a_{3} z^{3} \\ & \quad + a_{3} \left[ {\left( { - 1} \right)^{k} \left( {\alpha^{5} } \right)^{k} \frac{{\left( {3!} \right)\left( {5k - 1} \right)!!}}{{\left( {5k + 3} \right)!}}z^{5k + 3} } \right] + \left( { - 1} \right)^{k - 1} \left( {\alpha^{5} } \right)^{k - 1} \left( {\frac{\psi }{\text{EI}}} \right)\frac{{\left( {5k - 5} \right)!!}}{{\left( {5k - 1} \right)!}}z^{5k - 1} \\ & \quad + \left( { - 1} \right)^{k - 1} \left( {\alpha^{5} } \right)^{k - 1} \left( {\frac{\eta }{\text{EI}} - \alpha^{5} a_{0} } \right)\left( {\frac{{\left( {5k - 4} \right)!!}}{{\left( {5k} \right)!}}} \right)z^{5k} \\ & \quad + \left( { - 1} \right)^{k - 1} \left( {\alpha^{5} } \right)^{k - 1} \left( {\frac{\xi }{\text{EI}} - \alpha^{5} a_{1} } \right)\left( {\frac{{\left( {5k - 3} \right)!!}}{{\left( {5k + 1} \right)!}}} \right)z^{5k + 1} \\ \end{aligned}$$
(8)

where (5 k − 1)!!, (5 k − 2)!!, (5 k − 3)!!, (5 k − 4)!! and (5 k − 5)!! represent a symbol, which is

$$\begin{aligned} \left( {5k - 1} \right)!! & = \left( {5k - 1} \right) \times \left[ {5\left( {k - 1} \right) - 1} \right] \times \left[ {5\left( {k - 2} \right) - 1} \right] \times \cdot \cdot \cdot \times \left( {5 \times 3 - 1} \right) \times \left( {5 \times 2 - 1} \right) \times \left( {5 \times 1 - 1} \right) \\ x_{z} & = a_{0} X_{0} \left( z \right) + a_{1} X_{1} \left( z \right) + a_{2} X_{2} \left( z \right) + a_{3} X_{3} \left( z \right) + X_{4} \left( z \right) + X_{5} \left( z \right) + X_{6} \left( z \right) \\ \end{aligned}$$
(9)

By obtaining the first, second and third derivatives of Eq. (9) separately and the initial conditions, Eq. (3) was substituted (Zheng et al. 2010):

$$x_{0} = a_{0} ,\; \, \varphi_{0} = a_{1} ,\; \, a_{2} = \frac{{M_{0} }}{{2{\text{EI}}}},\; \, a_{3} = \frac{{Q_{0} }}{{6{\text{EI}}}}$$
(10)
$$x_{z} = x_{0} X_{0} (z) + \varphi_{0} X_{1} (z) + \frac{{M_{0} }}{2EI}X_{2} (z) + \frac{{Q_{0} }}{6EI}X_{3} (z) + X_{4} (z) + X_{5} (z){ + }X_{6} (z)$$
(11)

The flexure differential equation of the pile was derived as:

$$x_{z} = x_{0} A_{1} + \frac{{\varphi_{0} }}{\alpha }B_{1} + \frac{{M_{0} }}{{\alpha^{2} {\text{EI}}}}C_{1} + \frac{{Q_{0} }}{{\alpha^{3} {\text{EI}}}}D_{1} + \frac{\psi }{{\alpha^{4} {\text{EI}}}}E_{1} + \frac{\eta }{{\alpha^{5} {\text{EI}}}}F_{1} + \frac{\xi }{{\alpha^{6} {\text{EI}}}}G_{1}$$
(12)

The first derivative of Eq. (12) was calculated as:

$$\frac{{{\text{d}}x_{z} }}{{{\text{d}}z}} = \varphi_{z} = x_{0} \alpha A_{2} + \frac{{\varphi_{0} \alpha }}{\alpha }B_{2} + \frac{{M_{0} }}{{\alpha^{2} {\text{EI}}}}C_{2} + \frac{{Q_{0} }}{{\alpha^{3} {\text{EI}}}}D_{2} + \frac{\psi }{{\alpha^{4} {\text{EI}}}}E_{2} + \frac{\eta }{{\alpha^{5} {\text{EI}}}}F_{2} + \frac{\xi }{{\alpha^{6} {\text{EI}}}}G_{2}$$
(13)

The first derivative of Eq. (13) was calculated as:

$$\frac{{{\text{d}}^{2} x_{z} }}{{{\text{d}}z^{2} }} = \frac{{M_{z} }}{\text{EI}} = x_{0} \alpha^{2} A_{3} + \frac{{\varphi_{0} }}{\alpha }\alpha^{2} B_{3} + \frac{{M_{0} }}{{\alpha^{2} {\text{EI}}}}\alpha^{2} C_{3} + \frac{{Q_{0} }}{{\alpha^{3} {\text{EI}}}}\alpha^{2} D_{3} + \frac{\psi }{{\alpha^{4} {\text{EI}}}}\alpha^{2} E_{3} + \frac{\eta }{{\alpha^{5} {\text{EI}}}}\alpha^{2} F_{3} + \frac{\xi }{{\alpha^{6} {\text{EI}}}}\alpha^{2} G_{3}$$
(14)

The first derivative of Eq. (14) was calculated as:

$$\frac{{{\text{d}}^{3} x_{z} }}{{{\text{d}}z^{3} }} = \frac{{Q_{z} }}{\text{EI}} = x_{0} \alpha^{3} A_{4} + \frac{{\varphi_{0} }}{\alpha }\alpha^{3} B_{4} + \frac{{M_{0} }}{{\alpha^{2} {\text{EI}}}}\alpha^{3} C_{4} + \frac{{Q_{0} }}{{\alpha^{3} {\text{EI}}}}\alpha^{3} D_{4} + \frac{\psi }{{\alpha^{4} {\text{EI}}}}\alpha^{3} E_{4} + \frac{\eta }{{\alpha^{5} {\text{EI}}}}\alpha^{3} F_{4} + \frac{\xi }{{\alpha^{6} {\text{EI}}}}\alpha^{3} G_{4}$$
(15)

Finally, we can obtain:

$$\left\{ {\begin{array}{*{20}l} {x_{z} = x_{0} A_{1} + \frac{{\varphi_{0} }}{\alpha }B_{1} + \frac{{M_{0} }}{{\alpha^{2} {\text{EI}}}}C_{1} + \frac{{Q_{0} }}{{\alpha^{3} {\text{EI}}}}D_{1} + \frac{\psi }{{\alpha^{4} {\text{EI}}}}E_{1} + \frac{\eta }{{\alpha^{5} {\text{EI}}}}F_{1} + \frac{\xi }{{\alpha^{6} {\text{EI}}}}G_{1} } \hfill \\ {\frac{{\varphi_{z} }}{\alpha } = x_{0} A_{2} + \frac{{\varphi_{0} }}{\alpha }B_{2} + \frac{{M_{0} }}{{\alpha^{2} {\text{EI}}}}C_{2} + \frac{{Q_{0} }}{{\alpha^{3} {\text{EI}}}}D_{2} + \frac{\psi }{{\alpha^{4} {\text{EI}}}}E_{2} + \frac{\eta }{{\alpha^{5} {\text{EI}}}}F_{2} + \frac{\xi }{{\alpha^{6} {\text{EI}}}}G_{2} } \hfill \\ {\frac{{M_{z} }}{{\alpha^{2} EI}} = x_{0} A_{3} + \frac{{\varphi_{0} }}{\alpha }B_{3} + \frac{{M_{0} }}{{\alpha^{2} {\text{EI}}}}C_{3} + \frac{{Q_{0} }}{{\alpha^{3} {\text{EI}}}}D_{3} + \frac{\psi }{{\alpha^{4} {\text{EI}}}}E_{3} + \frac{\eta }{{\alpha^{5} {\text{EI}}}}F_{3} + \frac{\xi }{{\alpha^{6} {\text{EI}}}}G_{3} } \hfill \\ {\frac{{Q_{z} }}{{\alpha^{3} EI}} = x_{0} A_{4} + \frac{{\varphi_{0} }}{\alpha }B_{4} + \frac{{M_{0} }}{{\alpha^{2} {\text{EI}}}}C_{4} + \frac{{Q_{0} }}{{\alpha^{3} {\text{EI}}}}D_{4} + \frac{\psi }{{\alpha^{4} {\text{EI}}}}E_{4} + \frac{\eta }{{\alpha^{5} {\text{EI}}}}F_{4} + \frac{\xi }{{\alpha^{6} {\text{EI}}}}G_{4} } \hfill \\ \end{array} } \right.$$
(16)

The calculation equations of the internal force of the anti-slide pile in AB were:

$$\left\{ {\begin{array}{*{20}l} {x_{B} = x_{A} \varphi_{1} + \frac{{\varphi_{A} }}{\beta }\varphi_{2} + \frac{{M_{A} }}{{\beta^{2} {\text{EI}}}}\varphi_{3} + \frac{{Q_{A} }}{{\beta^{3} {\text{EI}}}}\varphi_{4} } \hfill \\ {\frac{{\varphi_{B} }}{\beta } = - x_{A} \cdot 4\varphi_{4} + \frac{{\varphi_{A} }}{\beta }\varphi_{1} + \frac{{M_{A} }}{{\beta^{2} {\text{EI}}}}\varphi_{2} + \frac{{Q_{A} }}{{\beta^{3} {\text{EI}}}}\varphi_{3} } \hfill \\ {\frac{{M_{B} }}{{\beta^{2} EI}} = - x_{A} \cdot 4\varphi_{3} - \frac{{\varphi_{A} }}{\beta } \cdot 4\varphi_{4} + \frac{{M_{A} }}{{\beta^{2} {\text{EI}}}}\varphi_{1} + \frac{{Q_{A} }}{{\beta^{3} {\text{EI}}}}\varphi_{2} } \hfill \\ {\frac{{Q_{B} }}{{\beta^{3} EI}} = - x_{A} .4\varphi_{2} - \frac{{\varphi_{A} }}{\beta } \cdot 4\varphi_{3} + \frac{{M_{A} }}{{\beta^{2} {\text{EI}}}} \cdot 4\varphi_{4} + \frac{{Q_{A} }}{{\beta^{3} {\text{EI}}}}\varphi_{1} } \hfill \\ \end{array} } \right.$$
(17)

where \(\alpha\) and \(\beta\) are the deformation coefficient of the pile, \(\alpha = \sqrt[5]{{(mB_{p} )/({\text{EI}})}}\); \(A_{i}\), \(B_{i}\), \(C_{i}\), \(D_{i}\), \(E_{i}\), \(F_{i}\), \(G_{i}\) stand for the influence value with the change of conversion depth \(\alpha h_{1}\) of the pile, for different values of \(i\) = 1, 2, 3, 4; \(\varphi_{i} ( {\text{i = 1,2,3,4)}}\) is the value with the change of conversion depth \(\beta h_{2}\) of the pile, \(\beta = \sqrt[4]{{\left( {{\text{CB}}_{P} } \right)/\left( {4{\text{EI}}} \right)}}\).

3.2.2 Derivation of formula of cantilever pile method

The internal force of the anti-slide pile in OA was deduced as:

  1. 1.

    Shear force calculation

Landslide thrust (T) at any height z above the sliding surface:

$$\begin{aligned} T & = \int\limits_{0}^{{z_{1} }} {q\left( z \right)} {\text{d}}z = \int\limits_{0}^{{z_{1} }} {\left( {\xi z^{2} + \eta z + \psi } \right)} {\text{d}}z \\ T & = \frac{1}{3}\xi z_{1}^{3} + \frac{1}{2}\eta z_{1}^{2} + \psi z_{1} ,\quad 0 \le z_{1} \le h_{1} \\ \end{aligned}$$
(18)

Similarly, the soil resistance R at any height z above the sliding surface can be obtained:

$$R = \frac{1}{3}\xi^{'} z_{2}^{3} + \frac{1}{2}\eta^{'} z_{2}^{2} + \psi^{'} z_{2} ,\quad 0 \le z_{ 2} \le h_{1}$$
(19)

Finally, the shear force calculation formula of the load section of the anti-slide pile can be obtained as follows:

$$Q\left( z \right) = T - R = \left( {\frac{1}{3}\xi z_{1}^{3} + \frac{1}{2}\eta z_{1}^{2} + \psi z_{1} } \right) - \left( {\frac{1}{3}\xi^{\prime } z_{2}^{3} + \frac{1}{2}\eta^{\prime } z_{2}^{2} + \psi^{\prime } z_{2} } \right)$$
(20)
  1. 2.

    Bending moment calculation

Bending moment (\({\text{M}}_{ 1}\)) caused by landslide thrust (T):

$$M_{1} = T\left( {z - z_{0} } \right)$$
$$M_{1} = \left( {\frac{1}{3}\xi z_{1}^{3} + \frac{1}{2}\eta z_{1}^{2} + \psi z_{1} } \right)\left( {z_{1} - z_{0} } \right)$$
(21)

Bending moment (\({\text{M}}_{ 2}\)) caused by soil resistance (R) in front of pile:

$$M_{2} = \left( {\frac{1}{3}\xi^{\prime } z_{2}^{3} + \frac{1}{2}\eta^{\prime } z_{2}^{2} + \psi^{\prime } z_{2} } \right)\left( {z_{2} - z_{0}^{\prime } } \right)$$
(22)

The internal force at any height z above the sliding surface of the anti-slide pile is calculated as:

$$\left\{ {\begin{array}{*{20}l} {Q = \left( {\frac{1}{3}\xi z_{1}^{3} + \frac{1}{2}\eta z_{1}^{2} + \psi z_{1} } \right) - \left( {\frac{1}{3}\xi^{\prime } z_{2}^{3} + \frac{1}{2}\eta^{\prime } z_{2}^{2} + \psi^{\prime } z_{2} } \right)} \hfill \\ {M = \left( {\frac{1}{3}\xi z_{1}^{3} + \frac{1}{2}\eta z_{1}^{2} + \psi z_{1} } \right)\left( {z_{1} - z_{0} } \right) - \left( {\frac{1}{3}\xi^{'} z_{2}^{3} + \frac{1}{2}\eta^{\prime } z_{2}^{2} + \psi^{\prime } z_{2} } \right)\left( {z_{2} - z_{0}^{\prime } } \right)} \hfill \\ \end{array} } \right.$$
(23)

Finally, we can obtain:

$$\left\{ \begin{aligned} Q_{A} & = \left( {\frac{1}{3}\xi h_{1}^{3} + \frac{1}{2}\eta h_{1}^{2} + \psi h_{1} } \right) - \left( {\frac{1}{3}\xi^{\prime } h_{1}^{3} + \frac{1}{2}\eta^{\prime } h_{1}^{2} + \psi^{\prime } h_{1} } \right) \\ M_{A} & = \left( {\frac{1}{3}\xi h_{1}^{3} + \frac{1}{2}\eta h_{1}^{2} + \psi h_{1} } \right)\left( {h_{1} - z_{0} } \right) - \left( {\frac{1}{3}\xi^{\prime } h_{1}^{3} + \frac{1}{2}\eta^{\prime } h_{1}^{2} + \psi^{\prime } h_{1} } \right)\left( {h_{1} - z_{0}^{\prime } } \right) \\ x_{A} & = \frac{{M_{A} }}{{\beta^{2} {\text{EI}}}} \times \frac{{4\varphi_{4}^{2} + \varphi_{1} \varphi_{3} }}{{4\varphi_{3}^{2} - 4\varphi_{2} \varphi_{4} }} + \frac{{Q_{A} }}{{\beta^{3} {\text{EI}}}} \times \frac{{4\varphi_{4}^{2} + \varphi_{1} \varphi_{3} }}{{4\varphi_{3}^{2} - 4\varphi_{2} \varphi_{4} }} \\ \varphi_{A} & = - \frac{{M_{A} }}{{\beta^{2} {\text{EI}}}} \times \frac{{4\varphi_{3} \varphi_{4} + \varphi_{1} \varphi_{2} }}{{4\varphi_{3}^{2} - 4\varphi_{2} \varphi_{4} }} + \frac{{Q_{A} }}{{\beta^{3} {\text{EI}}}} \times \frac{{4\varphi_{2}^{2} + \varphi_{1} \varphi_{3} }}{{4\varphi_{3}^{2} - 4\varphi_{2} \varphi_{4} }} \\ \end{aligned} \right.$$
(24)

The calculation equations of the internal force of the anti-slide pile in AB were:

The soil resistance around the pile in the anchorage section (AB) of anti-slide pile is still \(\sigma_{z} = P = {\text{CB}}_{P} x_{z}\), so the expressions of internal force and displacement in the anchorage section of anti-slide pile are still the same as those in the anchorage section of Sect. 3.2.1.

$$\left\{ \begin{aligned} x_{z} & = x_{A} \varphi_{1} + \frac{{\varphi_{A} }}{\beta }\varphi_{2} + \frac{{M_{A} }}{{\beta^{2} EI}}\varphi_{3} + \frac{{Q_{A} }}{{\beta^{3} EI}}\varphi_{4} \\ \varphi_{A} & = \beta \left( { - 4x_{A} \varphi_{4} + \frac{{\varphi_{A} }}{\beta }\varphi_{1} + \frac{{M_{A} }}{{\beta^{2} {\text{EI}}}}\varphi_{2} + \frac{{Q_{A} }}{{\beta^{3} {\text{EI}}}}\varphi_{3} } \right) \\ Q_{z} & = \beta^{3} {\text{EI}}\left( { - 4x_{A} \varphi_{2} - \frac{{\varphi_{A} }}{\beta } \cdot 4\varphi_{3} - \frac{{M_{A} }}{{\beta^{2} {\text{EI}}}} \cdot 4\varphi_{4} + \frac{{Q_{A} }}{{\beta^{3} {\text{EI}}}}\varphi_{1} } \right) \\ \, & = - 4\beta^{3} {\text{EI}}x_{A} \varphi_{2} - 4\beta^{2} {\text{EI}}\varphi_{A} \varphi_{3} - 4\beta M_{A} \varphi_{4} + Q_{A} \varphi_{1} \\ M_{z} & = \beta^{2} {\text{EI}}\left( { - 4x_{A} \varphi_{3} - \frac{{\varphi_{A} }}{\beta } \cdot 4\varphi_{4} - \frac{{M_{A} }}{{\beta^{2} {\text{EI}}}}\varphi_{1} + \frac{{Q_{A} }}{{\beta^{3} {\text{EI}}}}\varphi_{2} } \right) \\ \, & = - 4\beta^{3} {\text{EI}}x_{A} \varphi_{3} - 4\beta {\text{EI}}\varphi_{A} \varphi_{4} + M_{A} \varphi_{1} + \frac{{Q_{A} }}{\beta }\varphi_{2} \\ \end{aligned} \right.$$
(25)

The meanings and values of the symbols in the above expressions are the same as in Sect. 3.2.1.

3.3 Comparison of internal force with different methods

A slope with the gradient ratio of 1:1.5 and the height of 22 m was selected to compare the internal force with the different methods (see Fig. 21). Gravel and mudstone exist above the sliding surface of the slope. It was assumed that the deformation was uniform from top to bottom (\(\gamma_{1}\) = 19 kN/m3, \(\varphi\) = 26°). Below the sliding surface of the slope, there were mudstone and shale with a low degree of weathering, which can be calculated as a rock layer. The design length of the anti-slide pile was H = 15 m. The length of the anti-slide pile under load was h1 = 10 m. The length of the anchor section was h2 = 5 m, and the distance of the pile center was L = 6 m. The anti-slide pile had a rectangular cross-section form, and its cross-sectional area was A = a×b = 3 m × 2 m. In addition, the elastic modulus of the pile, the landslide thrust and the residual anti-slide force before the pile were E = 26 × 106 N/m2, En = 1000 N/m and \(E_{n}^{\prime }\) = 600 kN/m. The coefficient of foundation under the sliding surface was C = 2.5 × 105 kN/m3. The landslide body was selected as rock in the distribution functions of landslide thrust and soil resistance acting on the anti-slide pile.

Fig. 21
figure 21

A slope sketch

Full size image

From Fig. 22, above the sliding surface, the shear force increased with increase in the pile depth, but first increased and then decreased below the sliding surface. The shear force values at the bottom of the pile were all zero, and the maximum shear force was located at the anchorage area of the anti-slide pile, about 12.5 m away from the pile top. The difference between the traditional method (Zheng et al. 2010), ignoring the soil resistance method, and the numerical method became gradually larger with the increasing pile depth above the sliding surface. In addition, below the sliding surface, the difference first increased and then decreased. As for the bending moment of the anti-slide piles under the four methods, it also first increased and then decreased, and the maximum bending moment of the anti-slide piles was obtained when not considering the soil resistance. The maximum bending moment appeared at 10.5 m from the anchorage section of the anti-slide pile toward the top of the pile. The displacement of the anti-slide pile in the anchorage area was related linearly to the depth of pile. The displacement of the anti-slide pile in the method ignoring the soil resistance was the largest, and it was smallest in the numerical method. Comparing these four methods, the moment, shear force and displacement of the anti-slide piles using the proposed method in this paper are the closest to the numerical results considering the soil resistance acting on the piles.

Fig. 22
figure 22

Comparison of internal force of anti-slide pile with different methods

Full size image

4 Conclusion

The internal force of anti-slide piles considering the actual distribution of soil resistance acting on the piles was investigated based on numerical and theoretical methods. The main conclusions are as follows:

  1. (1)

    According to the numerical simulation results, when considering the soil resistance acting on anti-slide piles, the magnitude of lateral displacement of the piles decreased by about 100 times. In addition, the bending moment and shear force of the piles decreased significantly, reducing by 3267.48 kN m and 1094.89 kN, respectively. Especially, when the GSBP was less than 40°, the effect of soil resistance was remarkable, so it should be considered in the design of anti-slide piles.

  2. (2)

    Based on the actual distribution functions of soil resistance acting on anti-slide piles, the formula for calculating the internal force of the piles was derived. Further, the stability of the slope was calculated to verify the rationality of the formula proposed in this paper.

  3. (3)

    Relying on practical engineering, the internal force of the anti-slide pile was calculated utilizing the proposed method that considers the actual distribution of soil resistance acting on the piles. The amount of steel reinforcement needed for the pile reduced compared with the traditional calculation method, which potentially reduces the construction cost, especially in large and neutral landslide engineering.