1 Introduction

Earthquakes, as many other natural hazards (such as tsunamis, tornados, floods, etc.), can cause both immediate and long-term considerable economic and social losses (i.e. number of deaths and injuries, repair cost of the impacted civil infrastructures such as buildings, utility lines and transportation structures, indirect losses such as interruption of business activities and services, etc). The devastating effects of the 1995 Kobe earthquake in Japan provide a vivid reminder that seismic events are a global issue in both developed and developing countries (e.g. Beer 2007). Estimating likely losses from future seismic events and trading off potential investments in infrastructure risk reduction are key elements to support decision-making processes in planning earthquake protection and mitigation strategies (e.g. Ellingwood and Kinali 2009). Among the available approaches (see for instance Klügel 2008 for a review), the scenario-based earthquake risk assessment constitutes a powerful tool to meet such objectives and to identify the areas of needed intervention and specific action measures for risk reduction considering the definition of a given earthquake scenario (for instance considering a single earthquake of given ground-motion characteristics).

The presence of sources of uncertainty is an unavoidable aspect of any risk analysis methodologies (see for instance Paté-Cornell 1996 for a general discussion in the field of risk analysis). These uncertainties can exert a strong influence on the loss estimates and the key issue for an efficient risk management is a proper assessment of uncertainties so that decision makers are provided with the information on the uncertainties involved (in terms of error bounds on the final risk analysis output for instance) as outlined by numerous authors in the field of earthquake risk assessment (e.g. Grossi et al. 1999; Steimen 2004; Bommer et al. 2006; Der Kiureghian and Ditlevsen 2007; Ellingwood and Kinali 2009).

When dealing with uncertainties, two facets should be considered (e.g. Abrahamson 2000). The first facet corresponds to “aleatoric uncertainty” (also named “random variability”) and arises from the natural variability owing to either heterogeneity or the random character of natural processes (i.e. stochasticity). A common example of aleatoric uncertainty is the variability in weather. The second facet corresponds to “epistemic uncertainty” and arises when dealing with “partial ignorance” i.e. when facing “vague, incomplete or imprecise information” such as limited databases and observations or “imperfect” modelling. The large impact of epistemic uncertainty has been underlined at each stage of the earthquake risk assessment in various studies, in particular (Spence et al. 2003; Steimen 2004; Crowley et al. 2005). Epistemic uncertainties are knowledge-based, and the advantage of categorizing the uncertainties into “aleatoric” and “epistemic” can guide the decision maker in allocating the resources for risk reduction through additional data acquisition and analysis and in developing engineering models (Der Kiureghian and Ditlevsen 2007; Ellingwood and Kinali 2009).

Whereas randomness can rigorously be represented in a probabilistic framework, representing epistemic uncertainties by means of a single probability distribution in a context of “partial ignorance” (in particular when facing limited databases and observations) may seriously bias the outcome of a risk analysis in a non-conservative manner (Ferson 1996). Therefore, adequate formal tools for their assessment and incorporation are required (Ferson and Ginzburg 1996).

In the field of seismic risk assessment, a commonly used tool to take into account epistemic uncertainties is the logic tree approach as described by Wen et al. (2003). To illustrate the application of such a tool, one can refer to the probabilistic seismic hazard assessment of the Pyrenean region carried out by Secanell et al. (2008). The idea is to take advantage of expert judgement to compensate for the incompleteness of existing information. For each input parameter, alternative parameters or models occupy different branches. The branches at each node are assigned weights. Once a logic tree has been set up, the hazard calculation is performed following each of the possible routes. The final output is a range of risk curves associated with weights. However, this tool presents two main drawbacks. First, all types of epistemic uncertainties are merely represented by a single weight, whose interpretation in terms of probabilities or statements of belief remains a cause of debate (Abrahamson and Bommer 2005). In practice, the existing information is often richer than a single weight and the expert may feel more comfortable in expressing his judgement in terms of a range of possible values.

In this context, we propose alternative tools from the formal framework of possibility theory developed on the basis of fuzzy set (Zadeh 1965, 1978; Zimmermann 1991; Dubois and Prade 1988) for the representation of three types of epistemic uncertainties, namely imprecision, model uncertainty and vagueness due to qualitative information.

The second drawback of the logic tree approach deals with the choice of the correct risk curve for a proper use for risk management (Abrahamson and Bommer 2005). The question is to know whether the most approximate decision curve is the mean or a fractile, or the minimal or the maximal of all possible risk curves resulting from the combination of the tree branches. To tackle this issue, we propose to use methodological tools about uncertainty processing initially elaborated by Guyonnet et al. (2003) and further developed by Baudrit et al. (2005); Baudrit and Dubois (2006); Baudrit et al. (2007). These tools have already been successfully used in the field of environmental risk assessment (Guyonnet et al. 2003; Baudrit et al. 2005) and CO2 risk assessment (Bellenfant and Guyonnet 2008).

The first section of the paper presents the scenario-based earthquake risk model. Sections 3 and 4, respectively, deal with the representation and the propagation of the epistemic uncertainties within the model. All the presented methodologies are illustrated using the example of the earthquake scenario model, applied to Lourdes in Southern France (Bernardie et al. 2006). Uncertainties on the earthquake scenario itself have not been considered. Note that the scenario of Lourdes has been chosen for demonstration purpose only. All the presented results should not be interpreted as a definitive uncertainty assessment.

2 Earthquake risk model

In this section, we describe the main steps of the model used for the assessment of the earthquake risk in the case of the city of Lourdes. The earthquake risk model is based on the scenario-based model (Sedan and Mirgon 2003) developed by BRGM (the French Geological Survey). It is adapted from the Risk-UE methodology (Lagomarsino and Giovinazzi 2006), which was initially developed during the European Commission funded project of the same name (Mouroux et al. 2004).

2.1 Context of Lourdes

The city of Lourdes is situated in southern France in a seismically active region, the Pyrenees mountain chain (see Fig. 1). Over the past millennium, the city has already been affected by moderate earthquakes associated with macroseismic intensities up to VIII. Thus, mitigating seismic risk is crucial for the management of the city. In this view, an earthquake scenario has been developed by BRGM during 2005 and 2006 (Bernardie et al. 2006).

Fig. 1
figure 1

Situation of the French city of Lourdes: vulnerability analysis with the defined sets of buildings (on the left) and the defined geotechnical zones (on the right)

Full size image

The information used to support decision-making for risk management is the damage assessment in each city district. It is the output of the earthquake risk assessment methodology, which can be basically decomposed into two main steps:

  • Step 1: The seismic hazard assessment, which consists in evaluating the likelihood and the intensity of the seismic ground motion in the city.

  • Step 2: The vulnerability assessment, which consists in analysing the behaviour of each structure and their repartition in the city under seismic loading. In the case of Lourdes, only current buildings have been considered.

2.2 Step 1: seismic hazard assessment

2.2.1 Seismic hazard at regional scale

The first step is the definition of the earthquake risk scenario on the basis of which the seismic hazard is evaluated. This can be performed using the definition of an individual earthquake (epicentre, source depth, magnitude, faulting mechanism and source geometry). The alternative, which is chosen in the case of Lourdes, is the definition of a scenario hypothesis on the basis of a regional probabilistic seismic hazard assessment. A single ground-motion parameter (peak ground acceleration, denoted PGA) is chosen for this hazard assessment. In order to allow seismic risk comparison between various French cities, the earthquake scenario is defined based on the national probabilistic regional seismic hazard maps (Martin and Combes 2002; Secanell et al. 2008). The reference PGA on bedrock (of 0.2 g) is considered deterministic in the case of Lourdes.

2.2.2 Seismic hazard at local scale

At the local scale, site effects phenomena exist, which might amplify the ground motion. Such effects are taken into account by an amplification factor A LITHO, which depends on the geotechnical and geological properties of the soil. The amplification is assumed to be homogeneous in the so-called geotechnical zones (see illustration in the case of Lourdes, Fig. 1 on the right). The amplified PGA in the geotechnical zone is modelled as follows:

$$ {\text{PGA}}\, = A_{\text{LITHO}} \times {\text{PGA}}_{\text{BEDROCK}} $$
(1)

2.2.3 Macroseismic intensity assessment

The final output of the seismic hazard assessment is the macroseismic intensity I. It is defined according to the European macroseismic scale EMS-98 (Grunthal 1998) and is considered a continuous parameter in the framework of the macroseismic approach. It is derived from the PGA using empirical laws f of conversion. The seismic hazard assessment can be summarized as follows:

$$ I = f(A_{\text{LITHO}} \times {\text{PGA}}_{\text{BEDROCK}} ) $$
(2)

2.3 Step 2: vulnerability assessment

2.3.1 Vulnerability classification

In the RISK-UE methodology, the seismic behaviour of buildings is subdivided into vulnerability classes (referred to as vulnerability typologies), showing that different types of buildings may perform in a similar way during earthquakes. The vulnerability is evaluated by means of the vulnerability index (denoted ViTYP) ranging from 0 to 1 (i.e. least to most vulnerable).

2.3.2 Building stock inventory

For understandable financial, time and spatial scale reasons, the studied urbanized area is subdivided into districts, which define sets of buildings (see Fig. 1 for illustration). The inventory consists in evaluating the ratio of vulnerability classes within each defined district. The ratio (also called the “proportion”) is denoted p j . The output is the vulnerability index of the set of building in a given district Vi such that:

$$ {\text{Vi}} = \sum\limits_{j = 1}^{{N_{\text{TYP}} }} {p_{j} \times {\text{Vi}}_{{{\text{TYP}}_{j} }} } $$
(3)

where N TYP is the number of vulnerability classes in the considered district and ViTYPj is the vulnerability index associated with the jth vulnerability classes.

2.4 Probabilistic damage assessment

To model the physical damage to the building, the EMS-98 damage grades (Grunthal 1998) are used. Six damage grades D k (with k from 0 to 5) are considered: D 0 = 0 corresponds to “no damage”, D 1 = 1 to “slight damage”, D 2 = 2 to “moderate damage”, D 3 to “heavy damage”, D 4 = 4 to “very heavy damage” and D 5 = 5 to “maximal damage”. The Risk-UE methodology (Lagomarsino and Giovinazzi 2006) proposes a probabilistic approach for damage assessment. The probabilistic damage curve is defined as the cumulative probability distribution F of the event “d ≤ D k ”.

$$ F(d \le D_{k} ) = \int\limits_{0}^{{D_{k} }} {p(\theta )d\theta } $$
(4)

where p is the density probability of the Beta law, such that:

$$ p(d) = {\frac{\Upgamma (8)}{\Upgamma (q)\Upgamma (8 - q)}}{\frac{{d^{q - 1} (6 - d)^{7 - q} }}{{6^{7} }}} $$
(5)

where Γ is the gamma function.

The curve determined by Eq. 5 corresponds to the decision curve to support risk management. The form of the Beta law is determined by q, which depends on the mean damage value r D such that (Lagomarsino and Giovinazzi 2006):

$$ \frac{q}{8} = 0.007r_{\text{D}}^{3} - 0.0525r_{\text{D}}^{2} + 0.2875r_{\text{D}} $$
(6)

The mean damage value r D is the key parameter of the earthquake risk model. For a set of buildings in a given city district, r D directly correlates the seismic ground-motion parameter, namely the macroseismic intensity I and the vulnerability index of the set of buildings Vi. Both parameters are respectively defined in the step 1 (“seismic hazard assessment”) and in the step 2 (“vulnerability analysis”) of the model. The correlation is defined as follows (Lagomarsino and Giovinazzi 2006):

$$ r_{\text{D}} = 2.5\left( {1 + \tanh \left( {{\frac{{I + 6.25{\text{Vi}} - 13.1}}{2.3}}} \right)} \right) $$
(7)

As an example, let us consider the district No. 81 in Lourdes, in which 10% of buildings are of vulnerability class no. 1 (associated with ViTYP1 = 0.807) and 90% of buildings are of vulnerability class no. 2 (associated with ViTYP2 = 0.776) are inventoried. The resulting vulnerability index for the district (Eq. 3) is Vi = 0.10 × ViTYP1 + 0.90 × ViTYP2 = 0.7791. The macroseismic I reaches VIII for the given earthquake scenario. The resulting mean damage reaches r D = 2.25 (Eq. 7) corresponding to a Beta law parameter q = 3.687 (Eq. 6). Using Eqs. 4 and 5, the probability of being inferior to the damage grades D k (with k ranging from 1 to 5), respectively, reaches 3.15, 24, 59.2, 88 and 99%.

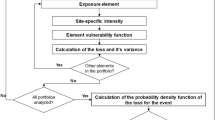
In summary, Fig. 2 illustrates the main steps of the earthquake risk assessment described earlier. Four sources of epistemic uncertainties are identified, namely the amplification factor A LITHO, the macroseismic intensity I, the vulnerability index Vi and the typology proportion pr j (with j from 1 to N TYP ).

Fig. 2
figure 2

Earthquake risk assessment used in this study

Full size image

3 Representation of epistemic uncertainties

This section presents the methodology to represent the epistemic uncertainties in the described earthquake risk model. Three types of epistemic uncertainties are dealt with: imprecision (Sect. 3.1), model uncertainty (Sect. 3.2) and vagueness due to qualitative information (Sect. 3.3).

3.1 Imprecision representation

Let us consider a model parameter, which cannot be precisely estimated owing to sparse data sets. The simplest approach to represent such an uncertainty is the interval, which is defined by a lower and an upper bound. But in most cases, experts may provide more information by expressing preferences inside this interval. For example, “expert is certain that the value for the model parameter is located within the interval [a, b]”. However, according to a few measurements and its own experience, expert may be able to judge that “the value for the model parameter is most likely to be within a narrower interval [c, d]”. To represent such information, an appropriate tool is the possibility distribution, denoted π, which describes the more or less plausible values of some uncertain quantity (Zadeh 1978; Zimmermann 1991; Dubois and Prade 1988). The preference of the expert is modelled by a degree of possibility (i.e. likelihood) ranging from 0 to 1. In practice, the most likely interval [c, d] (referred to as the “core” of π) is assigned a degree of possibility equal to one, whereas the “certain” interval [a, b] (referred to as the “support” of π) is assigned a degree of possibility zero, such that values located outside this interval are considered impossible. The intervals defined as \( \pi_{\alpha } = \left\{ {e,\pi (e) \ge \alpha } \right\} \) are called α-cuts. They contain all the values that have a degree of possibility of at least α (lying between 0 and 1) (see Fig. 3). They formally correspond to the confidence intervals 1-α as defined in the probability theory, i.e. \( P(e \in \pi_{\alpha } ) \ge 1 - \alpha . \) Figure 3a depicts a trapezoidal possibility distribution associated with the core [c; d] and the support [a, b].

Fig. 3
figure 3

Illustration of a possibility distribution associated with an imprecise parameter (a) and definition of the measure of possibility and necessity (b)

Full size image

Possibility distribution encodes a probability family (De Cooman and Aeyels 1999; Dubois and Prade 1992c) limited by an upper probability bound called the possibility measure \( \prod (e \in E) = \mathop {\sup }_{e \in E} \pi (e) \) (see for instance the upper cumulative probability bound on Fig. 3b) and a lower probability bound called the necessity measure \( N(e \in E) = \mathop {\inf }_{e \notin E} (1 - \pi (e)) \) where E represents a specific interval.

This approach is carried out to represent the imprecision on two parameters, namely the amplification factor A LITHO and the typology class vulnerability index ViTYP.

3.1.1 Representing imprecision on the site effects

As described in the previous section, the geotechnical zones in which amplification is homogeneous are defined from the processing of geological, geophysical (spectral analysis of surface waves and analysis of ambient vibrations) and geotechnical information. In the Lourdes case, 13 so-called geotechnical zones were defined (Fig. 1 on the right) and each of which are associated with response spectra based on 1D site response analyses (Modaressi et al. 1997). The amplification factor A LITHO is derived from the comparison between the four response spectra (two from synthetic time-histories and two from natural accelerograms) computed for the zones located on bedrock outcrops and the numerically calculated spectra for the various zones.

A sensitivity analysis is carried out for each bedrock spectrum by Bernardie and co-authors (Bernardie et al. 2006). It results in the definition of the interval within which the Bernardie and co-authors (i.e. the panel of experts, who are in charge of the site effect analysis) are certain to find the real value. The latter defines the support of the possibility distribution associated with A LITHO. Besides, the mean value between all the possible outcomes given by each bedrock spectrum plus one standard deviation is considered by Bernardie and co-authors the most likely value for A LITHO. The latter gives the core of the possibility distribution.

3.1.2 Representing imprecision on the vulnerability index

The Risk-UE methodology gives the most likely Vi0 for each type of current buildings (Lagomarsino and Giovinazzi 2006). The range of probable values V−/V+ for the index is provided as well. As a first approximation, the expert chooses to define a simple triangular possibility distribution such that Core = {Vi0} and Support = [V−, V+]. More sophisticated representation may also be used based on the definition of the less probable values V–/V ++, but considering the structural and the non-structural components of the current buildings in the context of Lourdes city, the expert has judged these values not reliable.

3.2 Model uncertainty representation

3.2.1 Definition

Model uncertainty is of epistemic nature (e.g. Der Kiureghian and Ditlevsen 2007) and arises from imperfect scientific and engineering modelling so that different models may be a priori adequate to describe the studied physical process and the selection among alternative models may not be straightforward. This uncertainty is encountered in the seismic risk model in the step of conversion between the ground-motion parameter PGA and the macroseismic intensity I. For the scenario of Lourdes, two distinct models of conversion are selected as adequate by the expert, namely: model no. 1 (Atkinson and Sonley 2000) and model no. 2 (Ambraseys 1974).

A classical approach would consist in calculating the pair of macroseismic intensity resulting from both models and then in aggregating the results by means of the MAX or of the MEAN operator. If the MEAN operator is chosen, the information on the upper and the lower bounds would be lost. If the MAX operator is chosen, the most risky value for the seismic hazard estimation is chosen, but the resulting value might be too conservative, leading to a possible over estimation of the final output of the damage. The possibility distribution provides a good compromise of both described alternatives, as the support interval represents the range of all possible values between the minimum and the maximum of the calculated macroseismic intensities, whereas the core represents the most likely intensity.

3.2.2 Dealing with sources of information in conflict

Besides, the possibility theory offers tools to aggregate (i.e. combine) sources of information, which might be in conflict (i.e. in disagreement). The notion of conflict between sources of information (represented by the possibility distribution π1 and π2) is illustrated on the Fig. 4a. It appears when π1 and π2 do not share the same range of possible values i.e. the same support. The greater the intersection between sources, the smaller the value of the conflict, and conversely when the sources are completely disjoint, the conflict reaches a maximal value.

Fig. 4
figure 4

Combination of two possibility distributions in conflict (a); the final result (b)

Full size image

Let us define the consensus zone as the area under the function defined as the conjunction of π1 and π2 (corresponding to the light grey coloured area in Fig. 4a). We assign to this consensus zone an indicator h defined as the degree of possibility of the intersection point between π1 and π2 (Fig. 4a) and formally reads as h = sup s (min(π1(s); π2(s)). This indicator represents the degree of concordance (also named “consensus level”) between the information sources so that the quantity 1 − h represents the “degree of conflict”. To deal with sources of information in conflict, we propose to use the adaptive combination rule developed by (Dubois and Prade 1992a), which reads as follows:

$$ \pi (s) = \max \left( {{\frac{{\min (\pi_{1} (s);\pi_{2} (s))}}{h}};\min (\max (\pi_{1} (s);\pi_{2} (s));1 - h)} \right) $$
(8)

Figure 4b depicts the final possibility distribution resulting from the combination of the sources of information in conflict π1 and π2. The first term min((π1(s); π2(s))/h in Eq.  8 represents the consensus zone between the information sources (normalized by the degree of concordance), hence corresponding to the “most likely” values for the imprecise parameter s. In Fig. 4b, this zone is depicted by a light grey coloured area. The second term min(max(π1(s); π2(s)); 1 − h) in Eq.  8 allows taking into account the possible values for s, which are not within the consensus zone. The influence of both sources of information are restricted outside the consensus zone regarding the degree of conflict 1 − h so that the degree of possibility of π is equally supported by both distributions π1 and π2 and cannot be greater than 1 − h. In Fig. 4b, the zone outside the consensus zone is depicted by a dark grey coloured area.

3.3 Qualitative information representation

This type of epistemic uncertainty results from the vagueness of the qualitative information. An approach based on the fuzzy logic methodology (Zadeh 1975; Dubois and Prade 1992b) is presented in this section and illustrated with the inventory of the vulnerability classes in each city district.

3.3.1 Context

In a classical statistical approach, this inventory should be developed from a representative sample i.e. a random sampling of the considered building set. In such a context, the uncertainties would depend on the size of the sample. However, such an approach faces in practice the following constraints, which prevents the building sample from being fully representative: a) financial/time constraint prevents the inspection of each building in detail since it is often carried out from the roadside; b) due to the spatial extension of the district, the expert is only able to inspect a few districts, where it is possible to do so; and c) the heterogeneity of the typologies within a given district affects the representative property of the sample as well. In such a context, the resulting sample cannot be a purely random sampling, and the probabilistic approach shows limitations.

We propose to treat the uncertainty on the typology proportion p i using a triangular possibility distribution. The core of such a distribution is defined by the observed value and the support is defined by [p i − ε, p i  + ε]. Nevertheless, quantifying the error, ε, is rarely an easy task, and the available information is often vague and qualitative. For instance, the experts may only be able to state whether the imprecision is “low” or “medium” or “high”. At this level, two sources of uncertainty should be dealt with: i) how to represent the vagueness linked with the qualified statement of imprecision and ii) how to decide which class of imprecision to choose (i.e. decision under vagueness).

3.3.2 Vagueness representation

Experts may feel more comfortable asserting a range of values from their specific or general knowledge about each qualified imprecision statement than a single crisp value. Thus, we propose to tackle the vagueness linked with each imprecision statement by means of fuzzy sets (Zadeh 1965, 1975). A fuzzy set F is identified with a membership function μ F from a finite set S to the unit interval. The value μ F(s) is the membership grade of element s in the fuzzy set. A possibility distribution π is seen as the membership function μ F of a normalized fuzzy set F.

The imprecision of the inventory (in percentage) is qualified using the following statements “low”, “medium” and “high”. To illustrate, the representation of the vagueness linked with the statement “low imprecision”, a trapezoidal fuzzy set is constructed as follows. The imprecision is judged preferentially “low” for a percentage ranging from 0 to 1%, but the value 5% is judged “still relevant” to be taken into account. In case of Lourdes, we use two decision criteria namely the district density (in numbers of buildings per km²) and the heterogeneity of the typologies (in numbers of vulnerability classes) in order to assess the imprecision of the inventory (see hereafter Sect. 3.3.3). Each decision criterion is also qualified using the following statement “low”, “medium” and “high” and to each qualified statement, a fuzzy set is assigned (as described in Sect. 3.3.2). The assumptions for the fuzzy set definition are given in Table 1.

Table 1 Numerical choices for Lourdes inventory imprecision assessment
Full size table

3.3.3 Decision under vagueness

In case of Lourdes, logical rules (see Table 2) exist between two decision criteria, namely the district density, the heterogeneity of the typologies, and the resulting imprecision of the inventory.

We propose to tackle the arbitrary choice of the proper class of imprecision, by means of an approach adapted from fuzzy logic (Zadeh 1975; Dubois and Prade 1992b).

Table 2 Logical rules for imprecision assessment
Full size table

Table 2 should be read as follows: IF “Low density” AND “Low heterogeneity” THEN “Low imprecision”. Such statements are named “Fuzzy rules”.

Figure 5 illustrates the methodology, which is divided into three main steps.

Fig. 5
figure 5

Methodology for inventory imprecision assessment, adapted from the approximate reasoning adapted from (Zadeh 1975)

Full size image

  • Step A: “Characterization”. A fuzzy set is assigned to each qualified decision criterion. The membership values in each decision criterion class of the considered district are then estimated.

  • Step B: “Combination”. A district may be a member of a fuzzy imprecision class “to some degree”, depending on its density value and on its heterogeneity in terms of number of vulnerability classes. Given step A, the membership values, μ, of the corresponding district in each imprecision class are determined from the min/max combination approach (e.g. Cox 1994). The membership function associated with the uncertainty on the imprecision evaluation is then constructed based on the combination of the fuzzy sets associated with each qualified statement (“low imprecision”, “medium imprecision” and “high imprecision”) and weighed by the corresponding membership values μ.

  • Step C: “Defuzzyfication”. The membership function associated with the uncertainty on the imprecision evaluation is then converted to a crisp value synthesizing the vagueness of the qualified imprecision. The chosen “defuzzyfication” method is the “centroid” method (e.g. Cox 1994). Graphically, this method consists in calculating the centre of gravity of the area under the curve of the membership function (i.e. “centroid”). The x-coordinate of this “centroid” represents the “defuzzified” value, which provides an indicator for the vagueness of the qualified statement (of the imprecision related to the inventory of the vulnerability classes in each city district in this case).

To illustrate, the Lourdes district no. 18 is characterized by two vulnerability classes and 2 542 buildings per km². The corresponding membership (following step A) values are μ(low heterogeneity) = 0.5; μ(medium heterogeneity) = 0.5; μ(high heterogeneity) = 0; μ(low density) = 0; μ(medium density) = 0.64 and μ(high density) = 0.36. The combination under the min/max approach (step B) gives the results in Table 3.

Table 3 Imprecision assessment in the district no. 18 (2 vulnerability classes; 2 542 buildings/km²)
Full size table

The resulting membership values in the imprecision classes are

μ(low imprecision) = Max(0.5, 0, 0) = 0.5; μ(medium imprecision) = Max(0.36, 0.5, 0) = 0.5 and μ(high imprecision) = Max(0.36, 0, 0.36) = 0.36. For the Lourdes district no. 18, the “defuzzyfication” process (step C) gives a value of 15.5%. This means that the imprecision of the proportion evaluation of each vulnerability classes reaches 15.5% in this district. This value synthesizes the whole vagueness associated with each qualified statement (“low imprecision”, “medium imprecision” and “high imprecision”), each of them being weighed by the membership values estimated from the qualified statements for the district heterogeneity and density.

4 Propagation of epistemic uncertainties

This section describes the methodology used to propagate and to summarize the epistemic uncertainties within the scenario-based earthquake risk model.

4.1 Fuzzy interval analysis

As the uncertainty on each model parameters is represented in the possibility framework, the propagation approach is based on fuzzy interval analysis (Dubois et al. 2000). This approach basically consists in an interval analysis for each α-cut, with α ranging from 0 to 1. Fig. 6 illustrates the Fuzzy interval analysis for the addition of two imprecise parameters A and B.

Fig. 6
figure 6

Fuzzy interval analysis for A + B with illustration of the interval analysis for α = 0.8

Full size image

4.1.1 Seismic hazard assessment

The described approach is carried out to calculate the possibility distribution of PGA in the studied zone from the definition of the scenario (i.e. the definition of the reference PGA on bedrock) and from the definition of the possibility distribution assigned to the amplification factor in each geotechnical zone using Eq. 1. The pair of possibility distributions assigned to the macroseismic intensity is then calculated for both conversion models (Sect. 3.2), and a unique possibility distribution is derived using the methodology to combine several sources of information (Eq.  8 in Sect. 3.2.2). For illustration of this procedure, see Fig. 4.

4.1.2 Vulnerability assessment

The vulnerability analysis results in a possibility distribution assigned to the vulnerability index in each city district. The latter is calculated based on the fuzzy interval analysis using Eq. 3 for the possibility distributions assigned to each vulnerability index and for the triangular possibility distributions assigned to the typology proportion derived from the fuzzy logic approach described in Sect. 3.3.

4.1.3 Damage assessment

The outputs of the hazard and of the vulnerability assessment are used as inputs for the damage assessment using Eq. 7 to calculate the mean damage grade r D. The latter is used for the definition (Eqs. 4, 5 and 6) of the probabilistic damage curve i.e. the decision curve.

In a seismic analysis with no uncertainty (i.e. a deterministic assessment), the result of the hazard and of the vulnerability assessment are crisp values. In this case, the output is a unique decision curve. If the epistemic uncertainties on the model parameters were simply represented by intervals, the risk model output would be a set of damage curves, which would be determined by its pair of lower and upper curves.

The proposed methodology uses possibility distributions, which are seen as a set of intervals associated with a degree of possibility corresponding to the α-cuts and formally, correspond to the confidence intervals 1 − α (as defined in the probability theory, see Sect. 3.1). For each degree α, a pair of damage lower and upper bounds can be constructed, thus defining a family of damage curves associated with each degree α (with α ranging from 0 to 1). Fig. 7 illustrates the methodology to be used for the construction of the family of probabilistic damage curves on the basis of the α-cuts of the imprecise mean damage value r D depicted in Fig. 7a).

Fig. 7
figure 7

Illustration of the family of probabilistic damage curves (right) associated with the α-cuts of the imprecise parameter r D (left)

Full size image

4.2 Synthesis of uncertainty information

The output of the propagation procedure gives the decision maker all the possible alternatives for the probabilistic damage curves. This set of decision curves should be summarized for an efficient use in risk management. The objective is to provide a simple measure of the whole epistemic uncertainty. In this view, we use methodological tools (Baudrit et al. 2005; Baudrit and Dubois 2006; Baudrit et al. 2007) about uncertainty processing in the framework of fuzzy random variables.

In the literature, fuzzy random variables can be interpreted in different ways depending on the context of the study (see Gil 2001 for an overview).

In this paper, a fuzzy random variable is interpreted as a possibility distribution over classical random variables (named the second-order model, see Couso et al. 2002; Couso and Sánchez 2008). In the following, we briefly introduce the basic notion of fuzzy random variable inducing a second-order possibility measure in order to have a better understanding of the fuzzy random variable post-processing.

Let us consider the random variable T = f(X, Y) and P T its associated probability measure, where f: ℜ2 → ℜ is a known mapping, X a random variable and Y is another imprecisely known random variable described by a fuzzy set \( \tilde{Y} \) associated with the possibility distribution \( \pi_{{\tilde{Y}}} \): ℜ → [0, 1]. The value \( \pi_{{\tilde{Y}}} (y) \) represents the possibility grade that Y coincide with y. Then, \( \tilde{T} = f(X,\tilde{Y}) \) is a fuzzy random variable defined by the extension principle:

$$ \pi_{{\tilde{T}}} (t) = \mathop {\sup }\limits_{t = f(x,y)} \pi_{{\tilde{Y}}} (y) $$
(9)

The Fig. 8a displays a 20 samples \( \left( {\tilde{T}_{i} } \right)_{i = 1 \ldots 20} \) of \( \tilde{T} \) using a Monte Carlo sampling combined with fuzzy interval analysis where f corresponds to the addition, X has a uniform probability distribution on [0, 1] while Y is represented by a triangular possibility distribution of core {3} and support [2, 4].

Fig. 8
figure 8

a A twenty sampling of the fuzzy random variable T = X + Y, where X is uniformly distributed on [0, 1] and Y is represented by a possibility distribution of core {3} and support [2,4]. b First-order versus second-order model induced from a fuzzy random variable sampling

Full size image

The fuzzy random variable \( \tilde{T} \) represents the imprecise information about T. Let us define the α-cuts of \( \tilde{T} \) such that \( [\tilde{T}]_{\alpha } = \{ f(x,y)/y \in [\tilde{Y}]_{\alpha } \} . \) On this basis, \( T \in [\tilde{T}]_{\alpha } \) with a confidence level 1 − α. For the sake of clarity, let us assume that X takes a finite number of different values \( x_{1} , \ldots ,x_{m} \) with respective probabilities \( p_{1} , \ldots ,p_{m} . \) In the discrete case, we can define a lower and upper probability bound \( \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{P}_{\alpha }^{T} ,\bar{P}_{\alpha }^{T} } \right] \) of P T with a confidence level \( D_{0} = 0, \ldots ,D_{ 5} = 5 \) such that

$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{P}_{\alpha }^{T} (A) = \sum\limits_{{i,[\tilde{T}_{i} ]_{\alpha } \subseteq A}} {p_{i} \le P(T \in A) \le \sum\limits_{{i,[\tilde{T}_{i} ]_{\alpha } \cap A \ne \emptyset }} {p_{i} } } = \bar{P}_{\alpha }^{T} (A) $$
(10)

where \( p_{i} = 1/20 \) in the given example. For each α, \( \underline{P}_{\alpha }^{T} \) gathers the imprecise evidence that asserts the statement “\( T \in A \)”, whereas \( \overline{P}_{\alpha }^{T} \) gathers the imprecise evidence that does not contradict the statement “\( T \in A \)”. For instance, Fig. 8b depicts the lower and upper cumulative probability bounds \( \left[ {\underline{F}_{\alpha } ,\overline{F}_{\alpha } } \right] \) for α = 1 and α = 0 resulting from the 20 samples by means of the following expression:

$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{F}_{\alpha} (x) = \frac{1}{20}{\text{card}}\left\{ i/\left[ {\tilde{T}_{i}}\right]_{\alpha } \subseteq ( -\infty,x]\right\}\;{\text{and}}\;\overline{F}_{\alpha } (x)=\frac{1}{20}{\text{card}}\left\{ {i/\left[ {\tilde{T}_{i}}\right]_{\alpha } \cap ( - \infty ,x] \ne {\O} } \right\} $$
(11)

where “card” corresponds to the cardinality operator (i.e. size) of the considered set, ∞ is the infinite bound and \( {\O} \) is the null set.

In the continuous case, the same principle can be followed (Smets 2005). A second-order possibility distribution is then defined, over a set of probability measures by means of α-cuts \( \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{P}_{\alpha }^{T} ,\bar{P}_{\alpha }^{T} } \right]. \) In this framework, the probability of a given event A is “not precise” meaning that it cannot be represented by a crisp value, but rather by a range of possible values. The described formal concepts let us state for instance that “the probability that the true probability of the event A is 0.5 ranges between 0.4 and 0.7”. Couso et al. (2002) showed that the interval defined by Eq. 12 provides the smallest envelope of the “true” probability of A given the available information.

$$ \left[ {\underline{P}^{T} (A),\overline{P}^{T} (A)} \right]: = \left[ {\int\limits_{0}^{1} {\underline{P}_{\alpha }^{T} (A){\text{d}}\alpha } ,\int\limits_{0}^{1} {\overline{P}_{\alpha }^{T} (A){\text{d}}\alpha } } \right] $$
(12)

This means that the measure \( \underline{P}^{T} (A) \) (resp. \( \overline{P}^{T} (A) \)) corresponds to the greatest lower bound (resp. smallest upper bound) that we give to the probability of A.

4.3 Use for an informed decision

In a classical probabilistic approach, uncertainty propagation within the earthquake risk model would have resulted in a single probability value for the damage level to exceed a given damage grade D k (k = 0–5). Yet, the model is tainted with imprecision, vague qualified information and unambiguous choice of the appropriate model. Under such a situation of “partial ignorance”, we can see \( D_{k} \) as a fuzzy random variable and the results depicted in Fig. 7b) as the second-order possibility induced by its α-cuts \( \left[ {\underline{F}_{\alpha } ,\overline{F}_{\alpha } } \right] \) according to the Sect. 4.1.3 “damage assessment”. The strong relationship with the fuzzy random variables allows us to summarize, using Eq. 12, the uncertainty on the damage grade D k in a pair of indicators \( \underline{[P} ,\overline{P} ] \) associated with the event: “d ≤ D k ; for \( D_{0} = 0, \ldots ,D_{ 5} = 5. \)”, which bound the “true” probability. Figure 9 gives the output of the synthesis methodology for the family of probabilistic damages of curves described in Fig. 7.

Fig. 9
figure 9

Synthesis in a pair of probabilistic indicators of all the possible alternatives for the probabilistic damage curves associated with the α-cuts of the imprecise parameter r D

Full size image

The gap between the two indicators exactly reflects the incomplete nature of our knowledge, thus explicitly displaying “what is unknown”. Besides, this pair of indicators underlines the zones where the epistemic uncertainty is the highest i.e. where efforts should be made in terms of additional campaigns (e.g. vulnerability assessment).

Figure 10 gives the final output of the Lourdes scenario. It consists of a pair of maps, representing the lower and upper probability bounds of the event: “d ≥ D 4”. Prioritization of the districts for seismic risk management should then be based on the two indicators as shown by the following examples.

Fig. 10
figure 10

Mapping of lower (on the left) and upper (on the right) probabilistic indicator of the event: “exceeding damage grade D 4”, location of district no. 10, no. 81 and no. 40

Full size image

  • The probability of exceeding the grade of damage D 4 is between 1.7 and 11% in the district no. 10. When considering the district no. 81, the lower indicator is 2.63% and the upper one is 13.5%. The comparison is straightforward, as both indicators show that the probability of the event “d ≥ D 4” is the higher in the district no. 81.

  • When considering the lower and upper indicators in the district no. 40 of respectively 0.9 and 18%, no conclusion can be drawn from the comparison of the indicators for districts no. 81 and no. 10. In the district no. 40, the epistemic uncertainties are very large (around 17.9%), whereas it reaches around 10% in the other districts. Such an analysis points out that additional investigations should be undertaken in the district no. 40.

5 Conclusion and further works

A methodology is developed to represent and propagate the epistemic uncertainties in a scenario-based earthquake risk assessment procedure adapted by the BRGM (French geological survey) from the Risk-UE methodology. Tools are developed under the possibility framework (Zadeh 1978; Zimmermann 1991; Dubois and Prade 1988). The earthquake scenario of the city of Lourdes (South France) is used for illustration. Three types of epistemic uncertainties are dealt with. (1) Instead of synthesizing the imprecision on the site effect and on the vulnerability measurement by a single weight (logic tree approach), we propose to construct a possibility distribution based on expert opinion. The latter is interpreted in terms of a set of confidence intervals. (2) The ambiguous choice of the correct conversion law from peak ground acceleration to macroseismic intensity (“model uncertainty”) is assessed using the combination rule of (Dubois and Prade 1992a). (3) An approximate reasoning approach (Zadeh 1975; Dubois and Prade 1992b) is constructed to assess the vague information associated with the exposed building inventory.

The propagation of these epistemic uncertainties under the fuzzy α-cut analysis results in a family of probabilistic risk curves. Instead of arbitrarily choosing a single decision curve, this rich information source is synthesized using the framework of fuzzy random variables (Baudrit et al. 2005; Baudrit and Dubois 2006; Baudrit et al. 2007). The output of the uncertainty propagation is a pair of indicators bracketing the probability to exceed a given grade of damage. The gap between the two indicators reflects the imprecise character of uncertainty related to the earthquake scenario model, thus picturing the extent of what is ignored. This gap can be used for risk management as a guidance to outline the zones, where further investigations should be carried out.

Further studies should be undertaken to refine the epistemic uncertainty representation. In particular, the uncertainties in ground motion (the so-called “attenuation equations”) models (Cotton et al. 2006) should be further investigated, in particular the choice of an appropriate model (Douglas 2003).