Abstract
“Market Coupling” is currently seen as the most advanced market design in the restructuring of the European electricity market. Market Coupling, by construction, introduces what is generally referred to as an incomplete market: it leaves several constraints out of the market and hence avoids pricing them. This may or may not have important consequences in practice depending on the case on hand. Quasi-Variational Inequality problems and the associated Generalized Nash Equilibrium can be used for representing incomplete markets. Recent papers propose methods for finding a set of solutions of Quasi-Variational Inequality problems. We apply one of these methods to a subproblem of market coupling namely the coordination of counter-trading. This problem is an illustration of a more general question encountered, for instance, in hierarchical planning in production management. We first discuss the economic interpretation of the Quasi-Variational Inequality problem. We then apply the algorithmic approach to a set of stylized case studies in order to illustrate the impact of different organizations of counter-trading. The paper emphasizes the structuring of the problem. A companion paper considers the full problem of Market Coupling and counter-trading and presents a more extensive numerical analysis.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The restructuring of the European electricity market is a long process. The integration of various national markets through the so called “Market Coupling” (MC) is today the most advanced market design in continental Europe. MC currently links the electricity markets of France, Germany, Belgium and the Netherlands. It is based on the separation of the energy and transmission markets. The energy market is subdivided into zones, each controlled by a Power Exchange (PXFootnote 1). These are interconnected by capacitated interconnections, which, together with the zones, provide a simplified representation of the grid. PXs clear the intra and inter zonal energy market taking these limited capacities into account and assuming no limitation in the domestic grid. Because the resulting flows may be not feasible for the real network TSOs may have to intervene in order to eliminate overflows and restore network feasibility. This is done by buying power injections and withdrawals at the different nodes of the grid. This set of operations is known as counter-trading or re-dispatching. They are the object of this paper. In contrast with the now standard nodal US approach to restructuring that integrates the network constraints in the energy market, MC concentrates on the energy market and leaves it to the Transmission System Operators (TSOsFootnote 2) to take care of these network constraints by a mix of market and quantitative constructs. The result is what economists call an incomplete market where several resources (here network services) are not priced by the market. We concentrate on the removal of congestion through counter-trading and look at its organization by different TSOs through the glasses of a Generalized Nash Equilibrium (GNE), which we show provides a natural context for modeling incomplete markets as also explained by Smeers (2003a, b).
A Nash Equilibrium describes an equilibrium between agents interacting through their payoffs: the action of one agent influences the payoff of another agent. A Generalized Nash Equilibrium involves agents that interact both at the level of their payoffs, but also through their strategy sets: the action of an agent can influence the payoff of another agent, but it can also change the set of actions that this agent can undertake. The idea of using Generalized Nash Equilibrium for modeling electricity transmission controlled by several TSOs arises in a natural way: because of Kirchhoff’s laws, the actions of one operator influence the set of possible actions of another operator. The concept of GNE was first introduced by Arrow and Debreu (1954) and Debreu (1952) where they refer to these problems as an abstract economy. The fundamental paper of Rosen (1965), which introduces the notion of shared constraints and normalized Nash Equilibrium (where the multipliers of the shared constraints are equal among all players up to a constant factor), is also of particular interest for this work. Apart from these pioneering contributions, only in the nineties were GNEs recognized for their numerous applications in economics, mathematics and engineering. In the context of electricity applications, Smeers and Wei (1999), solve a GNE problem for an oligopolistic electricity market where generators behave à la Cournot and transmission prices are regulated. Pang and Fukushima (2005) show how a non-cooperative multi-leader-follower game applied to the electricity market can be expressed as a GNE problem. This latter model is an example of an Equilibrium Problem subject to Equilibrium Constraints (EPEC) (see Ralph and Smeers 2006, for a related example of such a problem in electricity). EPECs are more complex than the GNE problems discussed here where we concentrate on shared constraints problems (Rosen 1965) that arise when players share a common good (like power, transport and telecommunication networks), but are not valued by the market at a single price.
Generalized Nash Equilibria are related to Quasi-Variational Inequality (QVI) models for which computational advances have recently been proposed. QVIs are extensions of Variational Inequality (VI) problems (see Facchinei and Pang 2003, 2010) They differ by both their mathematical properties and economic interpretations. A QVI problem generally has a plurality of solutions that include those of the underlying VI problem. This paper uses the QVI problem and its associated VI by respectively referring to the Generalized Nash Equilibrium (GNE) problem and one of its solutions. The multiplicity of dual variables of the common constraints in a QVI reflects the lack of a unique price for shared constraints and hence point to a market incompleteness; the particular solution given by the VI gives a unique price for each constraint and hence represents the complete market. From a mathematical point of view, we are interested in characterizing the market incompleteness by exploring solutions of the QVI where the dual variables of the shared constraints differ. In his seminal paper (see Theorem 6 of Harker 1991), Harker proves that the VI solutions are the only points in the solution set of the QVI when the dual variables associated to shared constraints are identical for all players. This has an important implication: solving the VI gives a solution to the QVI. Facchinei et al. (2007) and Kulkarni and Shanbhag (2010) have pointed out the restrictive nature of Harker’s assumptions and proposed alternative ways to derive these results under more general conditions. We follow Facchinei et al. (2007) presentation, which directly applies to Rosen (1965) initial formulation of shared constraints and hence perfectly fits our problem.
Solving the VI associated to a QVI does not say anything about the other solutions of the QVI. Differently from VI, only few methods are available for solving GNE problems (see Fukushima 2008 and Facchinei and Kanzow 2007 for a complete overview). This raises an interesting problem: because the multiplicity of solutions is linked to market incompleteness, completing the market by adding traded products should reduce the space of dual variables and eventually lead to a single vector of dual variables, that is to a QVI for which the solution set coincides with the one of the associated VI. This type of problem has been studied in a different context by Kulkarni and Shanbhag (2009). Besides their mathematical interest, we shall argue that these GNE problems with unique solutions are of economic and policy relevance.
But, in this paper, our aim is to explore the set of solutions of the GNE problem in order to assess possibly extreme welfare consequences of market incompleteness. A recent paper by Fukushima in collaboration with Nabetani and Tseng (see Nabetani et al. 2009) presents two parametrized VI approaches respectively called “price-directed” and “resource-directed”, to capture all GNEs. Both methods resort to a sampling of candidate VI problems to identify those that are true GNE problems. Experience shows that the sampling can be rather inefficient in the sense that a large number of candidate problems need to be tested in order to identify true GNE. More recently, Facchinei and Sagratella (2010) provide an alternative “resource-directed” method that does not suffer from the sampling problems of Nabetani et al.’s approach. Kubota and Fukushima (2010), instead, use a regularized gap function to formulate minimization problems equivalent to GNE problems. They prove that under suitable assumptions any stationary point of the minimization problems solves the given GNE problem. Solutions are computed using an algorithm based on a barrier technique. For reason of economic intuition, we resort to the price-directed approach, which can easily be interpreted in terms of market incompleteness (difference of prices seen by different economic agents). We thus explore the set of GNEs on the basis of economic intuition without resorting to sampling.
The contribution of this paper can be summarized as follows. We formalize a problem arising in the restructured European electricity system, namely the organization of counter-trading by several TSOs as a GNE problem and explore the space of GNE solutions through the price-directed parametrization algorithm proposed by Nabetani et al. (2009). This technique offers a natural economic interpretation in terms of market incompleteness and price multiplicity. We first discuss the economic interpretation of the variational and quasi-variational inequality problems and some of its implications for algorithmic purposes. We then apply the analysis to a set of counter-trading case studies and report the results. Because the set of the transmission constraints is not compact (flows and counter flows on a line can go to infinity while not constraining the lines or inducing losses) the question of existence of QVI solutions is of particular relevance. A result of the paper is to give an economic interpretation to the existence of the solution in terms of market completeness. Specifically the solution set of the QVI boils down to the solution set of the associated VI (that is a single solution in this case) when the market is complete (and in that case efficient in the sense of welfare maximizing). We also assess welfare losses in an incomplete market. The analysis is conducted on a six node network that we assume to be subdivided into two zones (North and South) linked by a capacitated inter-connector. Each zone is controlled by a PX and a TSO. PXs are coordinated and operate as if they were a sole entity; in contrast TSOs can operate with different degrees of coordination leading to different GNE problems.
This paper concentrates on the models and their mathematical properties. Two companion papers go in more details into the economics of the problem (see Oggioni and Smeers 2010a, b). More specifically, we apply these models to conduct more in depth numerical tests and illustrate the extreme cases (loss of efficiency, loss of equilibrium, loss of counter-trading possibilities) that these organizations can lead to. In fact, the separation of the energy and the transmission markets typical of Market Coupling creates inefficiencies that can be enhanced by the difficult cooperation among TSOs in managing transmission services. In Oggioni and Smeers (2010b), we study these economic inefficiencies by comparing two different zonal organizations of the six node market here studied. We show that Market Coupling can be quite vulnerable to the particular situation on hand and counter-trading can work well or completely fail depending on the degree of TSOs’ integration and the market zonal subdivision. The problem is that it is not clear beforehand what will happen. These results are confirmed in Oggioni and Smeers (2010a), where we enlarge the study to a prototype of the North-Western European electricity market to take into account the recent evolution of this market organization.
The remainder of the paper is organized as follows. In Section 2, we recall the mathematical background; Section 3 introduces the economic interpretation, the data and the network used for the empirical analysis. Section 4 is devoted to the explanation of the models and some theoretical results, while the results of the simulations are reported in Section 5. Finally, Section 6 concludes with the last observations.
2 Mathematical background
This section reviews the mathematical instruments used in the paper. The QVI problem defined by the pair (K,F) is to find a vector x∗ ∈ K(x∗) such that:
where K(x) is a point-to-set mapping from \(\Re^{n}\) into a subset of \(\Re^{n}\) and F is a point-to-point mapping from \(\Re^{n}\) into itself.
Suppose an economy where each player \(i \in I=\left\{1, 2, \dots, N\right\}\) solves a utility maximization problem. Each player i controls the variables \(x^i \in \Re^{n_{i}}\). Denote by x the vector of the decision variables x ≡ ((x 1)T,(x 2)T, ..., (x N)T)T and let x − i be the vector of the decision variables of all players − i with − i ∈ I and i ≠ − i. We write the vector x as x = (x i, x − i) to emphasize decisions of player i. A shared constraint imposes that x belongs to a set \(C \subseteq \Re^n\) such that n = n 1 + n 2 + ... + n N . In a Generalized Nash Equilibrium with shared constrained C, each player i sees the following optimization problem:
where for each i ∈ I, the set valued maps \(K^i: \prod_{j\neq i} \Re^{n_{j}}\rightarrow 2^{\Re^{n_i}}\) and the map \(K: \Re^{n}\rightarrow 2^{R^{n}}\) are defined as:
For any x − i, we denote the solution set of this problem as SOL GNE (x − i) and thus solve a GNE problem that consists in finding a vector x∗ such that \(x^{\ast i} \in SOL_{GNE}(x^{\ast -i})\) ∀ i.
The QVI formulation of this GNE problem is then defined as follows: each agent i solves
which can be restated for all agents in more compact form as:
where \(F(x^{\ast })^{T}\equiv (-\nabla _{x^{1}}^{T}u^{1}(x^{\ast }),...,-\nabla _{x^{N}}^{T}u^{N}(x^{\ast }))\) and K(x∗) ≡ \( \prod_{i}^{N}K^{i}(x^{\ast -i})\).
Note that the variational inequality VI(K,F) associated to the given QVI(K,F) problem is as follows:
where \(F(x^{\ast })^{T}\equiv (-\nabla _{x^{1}}^{T}u^{1}(x^{\ast }),...,-\nabla _{x^{N}}^{T}u^{N}(x^{\ast }))\) and K is a given closed and convex set.
Different particularizations of the solution set of the QVI have been offered in the literature. They are presented in the following through an example that we complement with some economic interpretations that will be important in the rest of the paper.
2.1 Particular cases
Consider the following market with three players (i = 1,...,3) with respective cost functions θ 1, θ 2 and θ 3 where θ 1 = (x 1)2 + 0.5(x 2)2 + 0.5(x 3)2 and similar expressions apply to the other players. These functions are continuously differentiable and strictly convex in the actions of each player (there are globally strictly convex, but this will not be used in this section). The standard NE is obtained when each player minimizes its cost function taking the actions of the others players as given. Player i = 1 solves the following optimization problem:
with the other players i = 2,3 solving similar problems. Dual variables of their constraints are indicated at the right hand side in parenthesis.
The complementarity conditions associated to these three players’ problems are as follows:
The (unique) solution of this NE problem is \(x^{\ast}=\left[0,0,0\right]^{T}\).
Introduce the following convex constraint x 1 + x 2 + x 3 ≥ 1 that expresses a common objective for the actions of the players,Footnote 3 for instance delivering a certain quantity of a product. Each player i solves its optimization problem taking into account the objective expressed in the common constraint and the action of the other agents. This gives a GNE problem with a shared constraint. The modified first player’ s model is indicated below:
Player i = 1:
with similar models solved by the other players i = 2,3.
The QVI(K,F) associated to the GNE problem indicated above is:
where F(x)T ≡ [2x 1, 2x 2, 2x 3]T and \(K^1(x^2,x^3)=\{x^1 \in \Re_{+} | \ x^{1}+x^{2}+x^{3}\geq 1 \}\), \(K^2(x^1,x^3)=\{x^2 \in \Re_{+} | \ x^{1}+x^{2}+x^{3}\geq 1 \}\) and \(K^3(x^1,x^2)=\{x^3 \in \Re_{+} | \ x^{1}+x^{2}+x^{3}\geq 1 \}\).
Note that the variational inequality VI(K,F) associated to the given QVI(K,F) problem is as follows:
where F(x)T coincides with that of the corresponding QVI and \(K=\left\{x \in \Re_{+}^3 | \ x^{1}+x^{2}+x^{3}\geq 1 \right\}\).
Theorem 3.1 of Facchinei et al. (2007) states that a solution x = (x 1,x 2,x 3) of this GNE problem that satisfies the KKT conditions of the players’ problems (Eqs. (11)–(13) and similar relations for the other players) with α 1 = α 2 = α 3, then x = (x 1,x 2, x 3) is also a solution of the VI(K,F) problem. We interpret this model as one where a market allocates the resources of the common constraint through a single price α (= α 1 = α 2 = α 3). This is interpreted as a complete market. It corresponds to a situation where the market players all have the same marginal cost and hence satisfy the common constraint in an efficient way.
The solution of the QVI for which the dual variables of all players’ common constraint are identical is obtained from the KKT conditions of the players’ problems as:
The solution is \(x^{\ast}=\left[0.33,0.33,0.33\right]^{T}\), the common constraint is binding and α amounts to 0.67.
Rosen (1965) considers another solution of the QVI problem where the dual variables of the shared constraints are equal among all players up to a constant exogenously given factor r i that depends on players, but not on constraints. This is mathematically expressed as:
Rosen refers to this solution as normalized equilibrium. The normalized equilibrium is based on the assumption that the set K, generated by the common constraints, is convex and compact. In our simple example, this set K is only convex. However, the players’ objective function are strictly convex and thus coercivity can replace the compactness assumption to guarantee the existence of a solution.
The complementarity conditions of the modified problem are as follows:
Rosen’s normalized equilibrium is obtained when the dual variables of the shared constraints are equal among all players up to a constant factor r i.
We interpret this situation as one where there is an incomplete market for driving the delivery of the good among the different players. Prices tend to equalize, but there remains a gap. This can easily be interpreted as the bid-ask spread found in insufficiently liquid markets. Assuming that r 1 = 1.05, r 2 = 1 and r 3 = 0.95, the solution of the normalized Nash equilibrium becomes \(x^{\ast}=\left[0.32, 0.33, 0.35\right]^{T}\) and the corresponding values of α i are as stated in Table 1.
Fukushima (2008) generalizes this notion and considers the more general case of a restricted QVI or GNE problem by allowing that the relative values of different resources differ among players. In order to illustrate this restricted GNE and prepare for the next case, we slightly modify our GNE problem by adding a new common constraint, let x 1 − 2x 2 − 4x 3 ≥ 0, to all players’ problem. The optimization problems solved by the three players becomes:
Player i = 1:
with similar problems for the other players i = 2,3.
Let m = 1,2 index the common constraints. Fukushima (2008) defines the tuple x = (x 1,x 2, x 3) to be a restricted GNE, if there exist Lagrange multipliers \(\lambda=(\lambda^i_m) \in \Re^{6}_{+}\) that satisfy \(\overline{KKT_i}, i=1,2,3\) together with the additional conditions:
where Λ is a nonempty cone \( \in \Re^{6}_{+}\). The class of restricted GNE extends the Rosen’s normalized equilibrium. In other words, one has a restricted GNE when the ratio of shadow prices associated with the common resources is neither too large nor too small for every pair of player Footnote 4. Considering the new formulation of three players’ example, this can be expressed by conditions:
where \(\overline{\delta}\), \(\underline{\delta}\), \(\overline{\epsilon}\) and \(\underline{\epsilon}\) are positive numbers such that \(\underline{\delta} \leq 1 \leq \overline{\delta}\) and \(\underline{\epsilon} \leq 1 \leq \overline{\epsilon}\).
One may be interested in other solutions of the QVI. Suppose for instance that we want to impose α 1 = α + 0.05, α 2 = α and α 3 = α − 0.05, β 1 = β + 0.1, β 2 = β and β 3 = β − 0.1.
The solution of this particular GNE is \(x^{\ast}=\left[0.72, 0.20, 0.08\right]^{T}\) and the corresponding values of α i are reported in Table 2.Footnote 5
A particular case of the above is to impose α 1 = α + 0.05, α 2 = α and α 3 = α − 0.05 while β i = β. The solution to this GNE thus becomes \(x^{\ast}=\left[0.68, 0.29, 0.02\right]^{T}\) with the corresponding α i and β i in Table 3. The interpretation of this situation is an economic system where some resources are effectively priced by the market (those that have identical dual variables), but others are not or only imperfectly priced. This is the kind of GNE that we want to tackle in this paper, when some but not all constraints have identical multipliers (are priced by the market) and the difference between dual variables can be interpreted as a lack of arbitrage in incomplete markets.
We motivate our interest in that problem in Section 3 where we discuss a real world example of that situation. We now explain that the parametrized VI approach proposed by Nabetani, Tseng, Fukushima (NTF hereafter), that we briefly present next, provides an attractive way to handle that problem, both numerically and in terms of its economic interpretation.
2.2 The NTF price directive algorithm
Consider again the GNE defined as follows. For each \(i \in I=\left\{1,...,N\right\}\), find x ∗ i such that for given x ∗ − i optimally solves the following convex optimization problem:
where g(x i,x − i) are the players’ common constraints (“shared constraints” such that \(g=(g_m)_{m=1}^M: \Re^n \rightarrow \Re^m\)) depending also on the other players’ decision variables (strategies) and \(x^i \in X^i \subseteq \Re^{n_i}\) are the individual constraints that only depend on player i’s decision variables (strategies). More specifically, we assume that the feasible strategy set K i(x − i) of player i is defined as follows:
and it holds that:
The parametrized VI approach proposed by Nabetani et al. solves that GNE problem through a family of VIs defined as follows. Consider a problem VI(X,F γ) where the (closed and convex) set X and the mapping \( F^{\gamma}: \Re^{n}\rightarrow \Re^{n}\) are as follows:
and γ i is a parameter assigned to each player i. These authors show that the solution set of a GNE problem is a subset of the union of solution sets of these parametrized VI(X,F γ). In Theorem 3.3 of Nabetani et al. (2009), they also give conditions for identifying when a solution of VI(X, F γ) is effectively a GNE. Consider the KKT conditions of the optimization programs that give VI(X, F γ):
Theorem 3.3 says that for any \(\gamma \in \Re^{Nm}_{+}\) and any \( (x^\ast, \pi^\ast) \in \Re^n\times \Re^m\) satisfying the KKT conditions indicated above, a sufficient condition for x∗ to be a GNE is that:
If in addition a constraint qualification condition holds at x∗, then Eq. (35) is also a necessary condition for x∗ to be a GNE . This algorithm can be easily adapted to the problem treated in this paper.
In the following, we develop models based on the assumption (verified in the counter-trading problem) that there exists a function θ(x) such that \(\nabla\theta(x)=\left[ [\nabla_{x^i} \theta^i(x)]_{i=1}^N \right]\) where \([\nabla_{x^i} \theta^i(x)]_{i=1}^N\) is the vector of the gradients of θ i(x) functions of players i computed with respect to x i. In addition, we assume (as is also the case in the counter-trading problem) that the common constraints g(x) are separable functions (see Section 3.2 for an example). This allows us to transform a VI problem into an equivalent optimization problem.
The following section provides the economic intuition that motivates this problem. We first present the problem in general terms and then adapt it to the particular situation that is treated in Section 3.3.
3 Economic interpretation
3.1 A general production context
Nash equilibria are commonly used in economics to describe markets affected by market power. In contrast, we concentrate in this paper on markets where all agents are price takers and hence there is no market power (see Metzler et al. 2003, for a fundamental paper dealing with the use of Nash equilibria in the more standard context of market power). This was the context adopted by Arrow and Debreu (1954) and Debreu (1952) for introducing social equilibrium. Specifically we consider the following social equilibrium problem that arises in production management. Consider the problem of decentralizing the activities of an organization into different Business Units (BU) that is each evaluated on its own performance. The interactions between the business units are of two types. First, actions of one BU can influence the payoff (performance index) of another BU. This is for instance the case of a marketing department, that depending on its efficiency generates a demand schedule for the production department that may force above or below normal utilization of capacities and hence of production costs. Second, all BUs share common constraints (resource availability or operations constraint) with the implication that the actions of one BU can change the remaining resources available to the other BUs. This is the case of a corporate department that conduct investment analysis for the different BUs. Its manpower is limited and cannot be modified instantaneously. More investment analysis for one BU limits the manpower available for the other departments. Note that both types of interactions are known by economists as externalities. Negative externalities create inefficiencies; positive externalities create benefits. While the organization can in principle achieve its best result by an overall optimization, it is believed that the centralization of operations required by this optimization decreases individual incentives to be efficient (moral hazard in economic parlance).
Decentralization consists in assembling activities in BUs and organizing internal markets for shared resources. We explained that integrating all operations would maximize efficiency. In a similar way, efficiency justifies creating an internal market for all common resources or restrictions in the decentralized organization (see the treatment of common constraints in Dantzig–Wolfe decomposition), except if, following Williamson’s theory (Williamson 1981), externalizing transactions through these markets would increase costs with respect to keeping them inside an integrated firm. There is thus a trade-off in decentralization between increasing individual incentives towards efficiency and incurring costs because of loss of coordination. We justify the introduction of our problem as an instrument to measure the economic cost resulting from the loss of coordination in decentralized operations.
The economic problem can be analyzed in two stages. A first question is to group activities into BUs, the other is to decide which resource or restriction to allocate through a market and which not. The first problem can be handled by testing different groupings of activities. Suppose, in order to treat the second question, that the decomposition of the overall organization in BUs is defined. The question then arises as to the creation of an internal market for common resources or restrictions. The resources or constraints allocated through an internal market have a common price charged by all BUs. The other resources can be valued differently by the different BUs without any market reconciling these different valuations into a single price or opportunity cost. Inefficiency arises from both improper grouping of activities and price differences that signal residual arbitrage possibilities. Assessing this inefficiency can then be done either by measuring the additional cost incurred by the decentralized organization or by valuing the remaining arbitrage possibilities. The NTF (price-directed) algorithm provides a particularly economically intuitive way to tackle that problem. We apply these general ideas to the particular problem of counter-trading in restructured electricity systems, that we describe after introducing a GNE formulation of the above discussion.
3.2 Formulation in terms of GNE
3.2.1 Problem statement
We formulate the above problem in the following abstract way. There are two BUs, each noted i = N,S (in order to use the same notation as in the rest of the paper), respectively representing players in the “North” and in the “South”. Each BU maximizes a utility function U i(x) where x is the sum of the x i, taking into account both common and individual constraints. We adopt this particular dependence of the payoff of a BU on the actions of other BUs because it is the dependence found in the rest of the paper (this allows us to avoid writing variational inequalities and conduct the whole discussion in terms of optimization. Some of the constraints are considered sufficiently important for organizing a common market. Others are seen as less important and hence left to informal arrangements.
Player N (North) solves the following problem:
s.t.
where the functions U N and X N are respectively the utility and the own constraint of player N; Y and Z are the common and separable constraints, Y denoting those for which a common market has been put in place.
The second player S (South) solves the following problem with the same characteristic:
s.t.
The two players compete in a GNE taking into account the shared constraints. Referring to the above interpretation we impose that the dual variables μ N and μ S are equal because they can be interpreted as a transfer price in the common market of constraints Y. In contrast, λ N and λ S can be different because no internal market has been created for these common constraints. ν N and ν S refer to BUs’ own constraints and hence can be expected to be different. This is a particular Generalized Nash Equilibrium in the sense that some of the constraints are priced by the market and hence their dual variables are equal for both players. But the market is incomplete in the sense that it does not cover all common constraints and the dual variables of the uncovered constraints can be different. The theory of GNE tells us that there may be several solutions to this problem, implying that the outcome of the organization is intrinsically ambiguous. It is thus relevant to inquire whether these different outcomes can be far apart, some of them being quite inefficient compared to an outcome where all constraints would be priced by a complete market. Conversely one may wonder whether there are cases where the GNE has a single outcome (the QVI and the associated VI having identical solution sets).
We explore this question by applying the parametrized variational inequality approach described by Nabetani et al. (2009) and construct the following parametrized model. Assume that one can find a function U(x N,x S) such that:
This is the situation encountered in the rest of the paper. We then state the problem:
s.t.
One can verify that the KKT conditions of this problem are:
which are those of the NTF parametrized VI problem (44)–(48).
Supposing that the NTF problem is feasible and adequate constraint qualification holds, changing the γ parameters leads to different Generalized Nash Equilibria provided that positive γ are associated to positive λ. There is only a single GNE if it is impossible to generate different GNE by modifying the γ. This can only happen if the NTF optimization problem is unbounded when setting γ at values different from zero. Unboundedness occurs when the NTS problem does not have any primal-dual solution and hence dual variables that price the constraints do not exist. We discuss some cases where the NTF problems do not have solution or do not lead to an equilibrium in Oggioni and Smeers (2010b).
3.2.2 Assessing inefficiencies
The above model can be used to test the inefficiency of a particular organization. These arise from two sources. One is in the delineation of the individual constraints of the BUs (the X constraints) when they result from an ex ante allocation of some common resources. The other source of inefficiency is the absence of a common market for the resources that remain common. This is is expressed by the difference of valuation of these resources by the BU (the dual variables). In all cases this implies a change of the utility function value of the BUs. It is this approach that we illustrate in the following application taken from the restructuring of the European electricity market.
3.3 Counter-trading in restructured electricity markets
The electricity system operating under the regulatory regime is the paradigm of a fully centralized organization where all machines constantly remain under the control of a single optimization problem. The underlying philosophy of the restructuring of the sector is that decentralizing operations improves the incentive of individual agents (generators, traders, consumers) to be efficient, possibly at the cost of some loss of coordination of operations. The question is to find a good trade-off by gaining sufficiently on incentives without losing too much on coordination. We here consider a particular illustration of that problem occurring in the so called “Market Coupling” organization of the European electricity restructuring. A full description of Market Coupling problems would lead us too far away from the numerical objective of this paper but a brief discussion of that organization is given in Appendix A. It suffices for the purpose of this paper to note that Market Coupling first clears the energy market on the basis of a simplified representation of the grid; this may require TSOs to restore the feasiblity of the grid in a second stage, in case market clearing has lead to overflows on some lines (see our companion paper Oggioni and Smeers 2010b, and some of the references therein for details). This paper focuses on this second stage, referred to as counter-trading, that we describe on the basis of a six node example initially presented by Chao and Peck (1998). We start from a given outcome of the clearing of the energy market, take the resulting grid flows and consider different organizations of counter-trading that we analyze in terms of the trade-off between decentralization and efficiency of operation.
3.3.1 The test problem
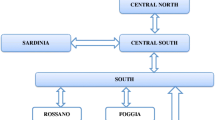
Consider the six nodes, eight lines network depicted in Fig. 1 (Chao and Peck 1998).Footnote 6 Lines (1–6) and (2–5) have limited capacity respectively of 200 and 250 MW. Kirchhoff’s laws are represented by a Power Transfer Distribution Factor (PTDF) matrix that indicates the portions of energy that, after being injected into a node or before being withdrawn from a hub node (node 6 in the example) flows through the lines. The PTDF matrix is only relevant for the capacitated lines (1–6) and (2–5) and its elements are reported in Table 4. Electricity is produced in nodes i = 1,2,4 and consumed in nodes j = 3,5,6. Marginal generation cost (c(q i )) and inverse demand (w(q j )) functions are given in Table 5.
Six node market (Chao and Peck 1998)
3.3.2 Counter-trading
Assume a zonal energy market decomposed in two Northern and Southern zones as depicted in Fig. 2 (see Oggioni and Smeers 2010b, for an alternative market organization). Zones are currently associated to countries in Europe and there is one PX and one TSO per country. We refer to the Northern and Southern TSOs as TSON and TSOS respectively.
Consider a set of energy trades resulting from the clearing of the energy market by the PXs in Market Coupling (see Appendix A). These trades have been obtained on the basis of a simplified representation of the grid (like in Fig. 2) and hence can sometimes lead to excessive flows on some lines of the real network. Counter-trading is the set of operations whereby TSOs buy incremental or decremental injections at different nodes of the grid so as to modify the flows on the lines and make them compatible with the real capability of the grid, namely the network in Fig. 1, in real time. Counter-trading does not change the energy transactions cleared in the energy market as these are settled at the prices arrived at by the PXs; counter-trading is effectively another market that is settled separately. It can be organized in different ways of which we discuss a few possibilities.
3.3.3 Counter-trading is fully optimized
We first consider an arrangement where both TSOs operate as a single entity. This corresponds to an overall optimization of all counter-trading operations by an entity that has access to all counter-trading resources (incremental and decremental injections and withdrawals). This implicitly assumes that the gains accruing from an overall optimization exceed the organizational costs incurred because of the full harmonization and integrated control of the TSOs. This situation is modeled in Section 4.1 and can be related to European and US energy markets. Joint optimization is quite clear in the USA where ISOs or RTOs are designed to fully integrate energy and transmission operations. One also observes some horizontal integration among European TSOs through mergers and acquisitions or the creation of coordinated groups.Footnote 7
3.3.4 Counter-trading is decentralised
The second arrangement takes place when the two TSOs retain separate operations. The interactions induced by Kirchhoff’s laws imply that the two TSOs physically share all the lines of the interconnected grid. Because of the numerical assumptions of this example, the capacities of the lines joining the Northern and Southern zones are the only relevant common constraints shared by both TSOs in this example. They can be priced or not depending on whether one introduces a market for transmission/line capacity at the counter-trading level or not. Pricing of interconnection lines can be found in systems such as the MISO-PJM market;Footnote 8 we are not aware of similar arrangement in Europe (see Cadwalader et al. 1998, for a technical treatment of that type of question). Pricing interconnection lines corresponds to (partially) completing the market and the goal is to check the impact of this pricing on the overall efficiency of counter-trading. Common economic sense indeed suggests (but theory does not prove) that the inception of a transmission/line capacity market increases efficiency.
Counter-trading resources at the generator or consumer levels constitute the other set of common resources. Because there are no bounds on generation and consumption data, these common resources are not common constraints in the sense of GNE problems. But different organizations of counter-trading can impose quantitative restrictions on access to counter-trading resources. We distinguish three scenarios. A first situation, modeled in Section 4.2, occurs when both TSOs have access to all incremental and decremental injections in both zones. In compliance with general non discrimination principles we assume that both TSOs access these resources at the same price. This corresponds to an internal market of counter-trading resources. A second case, presented in Section 4.3, supposes a limited cross-border access to counter-trading resources: a TSO can only access counter-trading resources in the other zone subject to quantitative limits that are often interpreted in terms of security requirements. The third situation occurs when there is no cross border market of counter-trading resources and each TSO can only access counter-trading resources in its own zone. This is described in Section 4.4; we also want to assess the impact of these different organizations on the overall efficiency of counter-trading. We here present the mathematical structure of all these counter-trading models and refer to our companion paper (Oggioni and Smeers 2010b) for a broader analysis of numerical results.
3.3.5 Note on counter-trading costs
Re-dispatching costs have to be paid and are normally included in grid charges in real systems. We report the average counter-trading cost α, which is easy to interpret and compare to the energy price. It is obtained by dividing the total counter-trading cost (TCC) that varies with the model considered by the total generation (∑ i = 1,2,4 q i ). This is defined as follows:
4 Modelling
The original Nabetani et al.’s paper is stated in terms of variational inequality problems; our example deals with variational inequality models that are integrable into optimization problems. We therefore describe the difference counter- trading counterfactuals in terms of the optimization version of Nabetani et al.’s variational inequality problems. We use the following nomenclature:
Sets
-
l = (1–6); (2–5) Lines with limited capacity;
-
n = 1,2,3,4,5,6 Nodes;
-
i(n) = 1,2,4 Subset of production nodes.
-
j(n) = 3,5,6 Subset of consumption nodes
Parameters
-
PTDF l,n Power Transfer Distribution Factor (PTDF) matrix of node n on line l;
-
\(\bar{F_{l}}\) Limit of flow through lines l = (1–6); (2–5);
-
q n Power traded (bought or sold) at node n (MWh); these quantities are determined in the Market Coupling problem and are taken as data in the counter-trading models.
Variables
-
Δq n Counter-trading variables: Incremental or decremental quantities of electricity with respect to q n (MWh).
Functions
-
c(ξ i ) Marginal cost function in €/MWh of generator located at node i = 1,2,4 (see Table 5);
-
w(ξ j ) Inverse demand function in €/MWh of consumer located at node j = 3,5,6 (see Table 5).
We assume that all agents are price takers. They bid in both the day-ahead and counter-trading markets. We do not separately model a balancing market taking care of deviations with respect to day-ahead.
4.1 Optimized counter-trading model
Assume that TSON and TSOS buy incremental and decremental quantities of electricity Δq n in their domestic market ( N = (1,2,3) and S = (4,5,6) respectively) and coordinate operations to remove congestion at the minimal counter-trading cost. This is stated in the optimization problem (53)–(59).
The global re-dispatching cost appears in the objective function (53). There are two classes of constraints. The first class involves both TSOs and includes the balance equations (54), (55) and the transmission capacity constraints (56) and (57). Conditions (54) and (55) impose that the sum of the incremental injections (Δq i = 1,2,4) and withdrawals (Δq j = 3,5,6) equals zero. This expresses that TSOs must globally remain in balance: the net result of counter-trading operations must be zero indicating that they cannot go to the energy market to counter-trade. This also defines the interpretation of the dual variable of constraint (55) as the price of the counter-trading services. As alluded to before, this rule separates the trading of energy (the q n that remain unchanged) and the counter-trading operations (Δthe q n variables that are counter-trading operations) in two different markets. It thus expresses a separation between the energy and congestion management services that is at complete variance with respect to the US integration of energy and congestion management services.
The dual variables \(\lambda _{l}^{\pm }\) associated with Eqs. (56) and (57) respectively define the marginal values of the capacited lines (1–6) and (2–5) in the two flow directions. Because there is a single optimization problem for both TSOs, they see the same value for the congested lines. In the second class, we group constraints (58) and (59) that are specific to the geographic zone covered by each TSO. The non-negativity constraints (58) state that the quantities of electricity demanded and produced in the Northern zone plus the incremental and decremental injections of the TSO N have to be non-negative. An identical constraint applies in condition (59) for the zone covered by TSOS.
s.t.
Constraints (54) and (55) could be restated as ∑ i = 1,2,4Δq i = 0 and ∑ j = 3,5,6Δq j = 0, possibly with a more direct interpretation. We justify our current formulation Eq. (55) (and the accompanying Eq. (54)), because it states the balance of the total energy exchanged in counter-trading and hence has a dual variable that is the price of the energy used in counter-trading services. The formulation therefore contains two key prices namely for line capacity (λ) and for counter-trading energy (μ). The following models involving two TSOs will keep these characteristics and contain the prices of line capacity and counter-trading energy seen by the two TSOs. Crucial for market completeness will be the capability to prove that these prices are equal among TSOs.
Problem (53)–(59) is strictly convex and admits a unique solution. This model provides the benchmark for evaluating other organizations of counter-trading. Finally, the average re-dispatching costs α is computed by dividing the objective function (53) by ∑ i = 1,2,4 q i .
4.2 Decentralized counter-trading Model 1: TSON and TSOS have full access to all re-dispatching resources
Suppose that TSON and TSOS no longer integrate for removing network congestion, but still have full access to all counter-trading resources of the system. This means that a TSO can buy and sell incremental and decremental injections and withdrawals in the control area of the other TSO (e.g. TSON can also counter-trade in the Southern zone and vice versa). This situation can be interpreted as the creation of an internal market of counter-trading resources. It is an implementation at the congestion management level of a general European philosophy that avoids forcing the integration of national institutions (here TSOs) while favoring the integration of the services that they provide. This idea is explicitly discussed for balancing services and we apply it here at the level of counter-trading resources. As part of this internal market of counter-trading resources, all TSOs adopt the same hub when counter-trading. A discussion of the realism of this assumption or of the distance that would remain between this assumption and a fully integrated counter-trading market is beyond the scope of this paper. We simply note here that this model requires an harmonization of market design that is well beyond what is currently institutionally feasible; it nevertheless constitutes a useful counterfactual somewhere on the path from full integration to full decentralization of counter-trading activities; it is also an illustration of the philosophy that aims at integrating services provided by TSOs without integrating the TSOs themselves.
Denoting the counter-trading variables of the Northern and Southern TSOs respectively as \(\Delta q_{n=1,...,6}^{N}\) and \(\Delta q_{n=1,...,6}^{S}\), the following presents the problem of TSON; TSOS’s problem is similar and is given in Appendix C.
4.2.1 Problem of TSON
TSON solves the optimization problem (60)–(65). It minimizes its re-dispatching costs Eq. (60) taking into account its balance constraints (61) and (62) and the counter-trading actions of the other TSO. Note that, in contrast with the preceding model, each TSO must now individually remain in balance in counter-trading. TSO’s counter-trading operations appear in the transmission constraints (63)–(64), and the overall non-negativity constraint (65) on generation and consumption. Note that constraints (61) and (62) are specific to the single Northen TSO while Eqs. (63)–(65) involve both TSOs. This also applies to their dual variables. Specifically the price of counter-trading services expressed by the dual variablle μ N,2 is now clearly assigned to the Northern TSO.
s.t.
where l = (1 − 6),(2 − 5)
In a similar vein, it is useful for the rest of the discussion to note that the \( \lambda_l^{\pm}\) of the coordinated problem (53)–(59) have now been split into Northern (\(\lambda _{l}^{N,\pm}\)) and Southern (\(\lambda _{l}^{S,\pm}\)) lambdas.Footnote 9 This reflects the different valuation of the lines (here the interconnections) by the two TSOs. The relation between the Northern \(\lambda _{l}^{N,\pm}\) and Southern \( \lambda _{l}^{S,\pm}\) of the two TSOs’ separate problems and the \( \lambda_l^{\pm}\) of the integrated TSO problem will become crucial when introducing the discussion on the line capacity market. We shall derive these relations in the next section using the Nabetani et al. (2009) (hereafter NTF) formalism.
4.2.2 An efficient Generalized Nash Equilibrium
The combination of both TSOs’ problems suggests analyzing the impact of markets for counter-trading resources and line capacity in terms of Generalized Nash Equilibrium model using the unifying NTF framework.
A first step towards the creation of an internal market of counter-trading resources is for both TSON and TSOS to access the same incremental and decremental injections and withdrawals. This is what we assume throughout this section and state in the constraints (61)–(62) of the TSON and Eqs. (108)–(109) of the TSOS’s problems (see Appendix C). The assumption implies that this access should be at the same price for both TSOs something that we infer from an application of general non discrimination principles. A second step would be to create a market of line capacity for counter-trading operations. We do not make that blanket assumption here but analyze the possible emergence of this market as a result of the integration of counter-trading resources. A market of line capacity is characterized by the equality of dual variables (\(\lambda _{l}^{N,-}\)) of constraints (63)–(64) for TSON and the dual variables (\(\lambda _{l}^{S,-}\)) of the analogous constraint for TSOS: both TSOs then see the same price for transmission resources. Imposing the equality of these dual variables amounts to introducing a market of line capacity among TSOs. In contrast, there is no market for line capacity in the counter-trading system if the dual variables of Eqs. (63)–(64) for TSON and Eqs. (110)–(111) for TSOS can be different.
The different assumptions about the existence of a line capacity market can easily be cast in the NTF parametrized optimization problem (66)–(74) (a parametrized VI problem in general in NTF). The objective function (66) combines the actions of both TSOs and also includes the parametersFootnote 10 γ N,S,± that perturb the dual variables \(\lambda _{l}^{+}\) and \(\lambda _{l}^{-}\) associated with the common transmission constraints (71) and (72). As the following proposition shows, setting the γ N,S,± to zero implies equal dual variables of the transmission constraints and hence a line capacity market. Setting them at different values represents the case where there is no line capacity market. While Eqs. (71) and (72) are common to TSON and TSOS, the balance conditions (67), (68), (69) and (70) apply to each individual TSO. Conditions (67)–(68) are identical to Eqs. (61)–(62) and refer to TSON, while Eqs. (69) and (70) regard TSOS (compare Eqs. (108) and (109) in Appendix C).
s.t.
where l = (1 − 6),(2 − 5)
The following proposition states these relations formally:
Proposition 1
Suppose that there is a solution to problem (66)–(74). Denote transmission constraints (71) and (72) respectively as \(g_{l}^{+}\) and \(g_{l}^{-}\) and suppose that \(\langle g_{l}^{+}(\Delta q),\gamma_{l}^{N/S,+}\rangle =0\) and \(\langle g_{l}^{-}(\Delta q),\gamma_{l}^{N/S,-}\rangle =0\) (Theorem 3.3 of Nabetani et al. 2009 ). Then the solution is a GNE and the following relations between the marginal values of transmission lines of the individual TSOs’ problems ( \(\lambda _{l}^{N,\pm}\) , \( \lambda _{l}^{S,\pm}\) ) and the \(\lambda _{l}^{\pm}\) of problem (66)–(74) hold:
Proof of Proposition 1
See Appendix E. □
While the above formulation accounts for the fact that both TSOs have access to the same counter-trading resources (balance conditions (67)–(70)), it does not impose explicitly a market of transmission resources as long as the \(\gamma _{l}^{N,+}\), \(\gamma _{l}^{N,-} \), \(\gamma _{l}^{S,+}\) and \(\gamma _{l}^{S,-}\) are different. The following proposition shows a somewhat surprising result: it states that this market is implicitly imposed in a GNE under the condition that the fully optimized counter-trading problem has a solution and that a sufficient number of counter-trading resources are involved to restore grid feasibility. There indeed exists a GNE where the market for counter-trading resources implies a market for transmission capacities and there exists no other GNE. Technically, the NTF problem only has an optimal solution if the γ of both TSOs are equal.
Proposition 2
Suppose the solution of problem (66)–(74) exists and satisfies \(q_{n}+\sum_{z=N,S}\Delta q_{n}^{z}> 0 \ \forall n\) . Denote transmission constraints (71) and (72) respectively as \(g_{l}^{+}\) and \(g_{l}^{-}\) and suppose that \(\langle g_{l}^{+}(\Delta q),\gamma_{l}^{N/S,+}\rangle =0\) and \(\langle g_{l}^{-}(\Delta q),\gamma_{l}^{N/S,-}\rangle =0\) (Theorem 3.3 of Nabetani et al. 2009 ). Then \(\gamma _{l}^{N,+}=\gamma _{l}^{S,+}\) and \(\gamma _{l}^{N,-}=\gamma _{l}^{S,-}\) and the optimal solution is a GNE.
Proof of Proposition 2
See Appendix F1. □
This proposition, as stated, is specific to the particular six node problem but some extension is presented in Appendix F2. An intriguing implication of the proposition is that the GNE is isolated in the sense that any attempt to find a GNE where the two TSOs see different prices leads to an unbounded problem, that is to a problem where there are no feasible dual variables. This isolated GNE also boils down to a full coordination model where there is a line capacity market. An economic reformulation of Proposition 2 is that the market for counter-trading resources completes the market for line capacity. This result is specific to the six node network but it can be extended in a weaker form to a general case. This is done in Appendix F2 where one shows that a market for counter-trading facilities together with a market where a sufficient number of line capacities are traded can complete the market in the sense that it also implies a market of the other line capacities. This proposition also has a mathematical interpretation: Generalized Nash Equilibrium has an infinite set of possible dual variables and the proof of Proposition 2 and its extension illustrates a construction of that subspace. Restricting the equilibrium on some variables (see Fukushima 2008) can make the QVI problem associated to the GNE a full VI problem. We can complete Proposition 2 by stating that the market of counter-trading resources also creates an internal market of energy exchanged in the counter-trading market. This is stated in the following proposition.
Proposition 3
Suppose the solution of problem (66)–(74) exists and satisfies \(q_{n}+\sum_{z=N,S}\Delta q_{n}^{z}> 0 \ \forall n\) . Denote transmission constraints (71) and (72) respectively as \(g_{l}^{+}\) and \(g_{l}^{-}\) and suppose that \(\langle g_{l}^{+}(\Delta q),\gamma_{l}^{N/S,+}\rangle =0\) and \(\langle g_{l}^{-}(\Delta q),\gamma_{l}^{N/S,-}\rangle =0\) (Theorem 3.3 of Nabetani et al. 2009 ). Then the following relations hold:
Proof of Proposition 3
See Appendix G1. □
The next implication is expected: a complete market is efficient and its outcome is identical to the one of the full optimization of counter-trading. This also proves that the solution of the GNE (66)–(74), if it exists, is unique. This is expressed in the following corollaries.
Corollary 1
Suppose the solution to coordinated counter-trading problem (53)–(59) exists. Then, the solution of the GNE problem (66)–(74) exists and coincides with that of the coordinated counter-trading problem (53)–(59).
Proof of Corollary 1
See Appendix H. □
Corollary 2
The solution of the GNE problem (66)–(74) is unique.
Proof of Corollary 2
Since the solution to problem (53)–(59) is unique (see Section 4.1), thanks to Corollary 1, we can immediately conclude that the solution to problem (66)–(74) is unique too. □
4.3 Decentralized counter-trading Model 2: TSON and TSOS have limited access to part of the counter-trading resources
4.3.1 A partial market of counter-trading resources
The model presented in Section 4.2 assumes that both TSOs have full access to all re-dispatching resources. We depart from this assumption here and model the case where both TSON and TSOS have a limited access to the counter-trading resources located outside of their control area. This means that the Northern TSO’s purchase of Southern counter-trading resources is limited and conversely. A more general situation where the following reasoning would apply is the case where one TSO has constraints (for instance on reliability and reserve) that the other does not have. Needless to say, the existence of local TSO requirements and hence the lack of full harmonization is the most likely situation to be observed in practice in Europe. While this analysis may look like invalidating the practical usefulness of the above result, it may alternatively be seen as a justification for more harmonization.
The TSO optimization problems are immediately derived from those in Section 4.2 by adding upper and lower constraints on the procurement of re-dispatching resources in the zone that they do not directly control. We do not report these individual optimization problems here, but directly present the model in the Nabetani, Tseng and Fukushima’s form. The additional constraints (80) and (81) impose the upper and lower bounds on the actions of TSOs in the other jurisdiction. Condition (80) limits the TSON’s purchase of Southern counter-trading resources and condition (81) does the same for TSOS in the Northern zone. This arrangement is likely to be more realistic than the above creation of an internal market: TSOs that are not integrated will probably insist on keeping resources under their sole control. We shall see that giving up the internal market of counter-trading resources can have dramatic consequences. We discuss these consequences in principle in this paper together with some numerical results. We further elaborate on these numerical results in Oggioni and Smeers (2010b).
4.3.2 Inefficient Generalized Nash Equilibrium
Let \(\overline{\Delta q_{n}^{N}}\) and \(\overline{\Delta q_{n}^{S}}\) be respectively the bounds (in absolute value) imposed on TSOs resorting to outside resources. The other conditions and constraints are as in Section 4.2. The NTS problem is stated as follows:
s.t.
where l = (1 − 6),(2 − 5)
The following proposition gives the condition for the existence of Generalized Nash Equilibrium and is a direct application of NTF results.
Proposition 4
Suppose that there is a solution to problem (75)–(85). Denote transmission constraints (82) and (82) respectively as \(g_{l}^{+}\) and \(g_{l}^{-}\) and suppose that \(\langle g_{l}^{+}(\Delta q),\gamma_{l}^{N/S,+}\rangle =0\) and \(\langle g_{l}^{-}(\Delta q),\gamma_{l}^{N/S,-}\rangle =0\) (Theorem 3.3 of Nabetani et al. 2009 ). Then this solution is a GNE.
Proof of Proposition 4
The proof is a direct application of NTF’s Theorem 3.3 (see Nabetani et al. 2009). □
In contrast with the case of the internal market of counter-trading resources, the outcome of the market is here ambiguous: there may be several GNEs and they may differ in terms of efficiency. We first state that we fall back on the case of the internal market of counter-trading resources (decentralized Model 1) if none of the quantitative restrictions of cross zonal resources is binding. This means that the resources remaining in the exclusive control of the zonal TSO are not too important. The extension of this proposition to the more general case considered in Appendix G2 is obvious.
Proposition 5
Suppose that there is a solution to problem (75)–(85). Denote transmission constraints (82) and (83) respectively as \(g_{l}^{+}\) and \(g_{l}^{-}\) and suppose that \(\langle g_{l}^{+}(\Delta q),\gamma_{l}^{N/S,+}\rangle =0\) and \(\langle g_{l}^{-}(\Delta q),\gamma_{l}^{N/S,-}\rangle =0\) (Theorem 3.3 of Nabetani et al. 2009 ). Suppose also \(q_{n}+\sum_{z=N,S}\Delta q_{n}^{z} > 0 \ \forall n\) . If no cross zonal counter-trading resource is binding, then \(\gamma _{l}^{N,+/-}=\gamma _{l}^{S,+/-}\) and the GNE is unique and identical to the solution of the optimized counter-trading (Eq. (53)–(59)).
Proof of Proposition 5
Apply the proof of Appendix F1 after noting that the KKT conditions of problem (66)–(74) are identical to those of problem (75)–(85) when cross zonal quantitative restrictions are not binding. □
As expected, things change when some of the cross zonal quantitative restrictions are binding. The following proposition states that the solution of the GNE (75)–(85), if it exists, is not unique when some of the quantitative limitations on counter-trading resources are binding. This is the normal GNE case and there is no longer any hope to implicitly complete the market; this immediately carries through to the more general case considered in Appendix F2.
Proposition 6
Suppose that there is a solution to problem (75)–(85) and some cross zonal restrictions are binding. Denote transmission constraints (82) and (83) respectively as \(g_{l}^{+}\) and \(g_{l}^{-}\) and suppose that \(\langle g_{l}^{+}(\Delta q),\gamma_{l}^{N/S,+}\rangle =0\) and \(\langle g_{l}^{}(\Delta q),\gamma_{l}^{N/S,-}\rangle\) (Theorem 3.3 of Nabetani et al. 2009 ). The valuation of the transmission capacity by both agents are identical when all \(\gamma _{l}^{N/S,/}\) are zero. The solution always satisfies \(\lambda _{l}^{N,-}-\) \(\lambda _{l}^{S,-}\) = \(\gamma _{l}^{N,-}-\) \(\gamma _{l}^{S,-}\) and \(\lambda _{l}^{N,+}-\) \(\lambda _{l}^{S,+}\) = \(\gamma _{l}^{N,+}-\) \(\gamma _{l}^{S,+}\).
Proofof Proposition 6
See Appendix I. □
This proposition separates the impact of the line capacity and counter-trading resource markets: it focuses on the case of a limited market of counter-trading resources and explicitly considers whether one introduces a market of line capacity at the TSO level. This market can be more or less extended depending on the set of those lines that are subject to congestion. Former discussions of the flowgate model in the US and its implementation in ERCOT show that it might be hazardous to ex ante claim that the number of lines subject to congestion is limited. We do not get into that subject here but note that the common wisdom today in discussions of the “flow-based” model in Europe is still that the number of “critical infrastructures” will be small. Our objective in this paper is simply to assess the impact of creating a more or less extended market for line capacities at the TSO level when counter-trading is decentralized and the market of counter-trading resources is limited. As for counter-trading resources, one can expect that a market of line capacities is a step in the right direction even if it fails to restore a fully efficient counter-trading. In contrast, the absence of a line capacity market, added to the lack or restriction of a market for counter-trading resources should further degrade efficiency. The NTS machinery allows one to assess these different situations in a particularly easy way. Specifically, setting the γ of a particular line to zero creates a market for that infrastructure. Introducing a wedge between these γ different from zero (while verifying that the conditions \(\langle g_{l}^{+}(x^{\ast }),\gamma _{l}^{N/S,+}\rangle =0\) and \(\langle g_{l}^{-}(x^{\ast }),\gamma _{l}^{N/S,-}\rangle =0\) for a GNE are maintained) parametrizes the extent to which the lack of a market for that infrastructure leads to a divergence in the valuation of the line capacity. This is briefly discussed in Section 5, but it is broader illustrated through further numerical examples in Oggioni and Smeers (2010b). Last it is also useful to recall that nothing proves that counter-trading is always feasible and it is interesting to verify whether one can easily obtain situations where this occurs.
Corollary 3
The solution of the GNE problem does not necessarily exist.
Proof of Corollary 3
It suffices to take a case where the NTF problem is infeasible. □
4.4 Decentralized counter-trading Model 3: TSON and TSOS only operate in their own control area
4.4.1 A segmented market of counter-trading resources
This section presents a more extreme situation. The following model, directly presented in the Nabetani, Tseng and Fukushima’s formulation, describes a market where each TSO manages the re-dispatching resources of its own area only, taking as given the action of the other TSO. There is no additional transaction from a TSO into the other TSO’s zone. Assumptions on the line capacity market can be made through the γ.
The problem is formulated through relations (86) to (94). The objective function (86) globalizes the counter-trading costs of the two TSOs. This problem is subject to the shared transmission constraints (91)–(92) and the balance constraints of TSON ((87) and (88)) and TSOS ((89) and (90)).
s.t.
where l = (1 − 6),(2 − 5)
Re-dispatching costs are then truly zonal: the average counter-trading cost in the Northern area is:
with a similar formula for the Southern area. A “global” average-dispatching cost can also be determined by dividing the the total re-dispatching costs \((\sum_{i=1,2}\int_{q_{i}^{t}}^{q_{i}+\Delta q_{i}^{N}}c_{i}(\xi )d\xi -\int_{q_{3}}^{q_{3}+\Delta q_{3}^{N}}w_{3}(\xi )d\xi +\int_{q_{4}}^{q_{4}+\Delta q_{4}^{S}}c_{4}(\xi )d\xi -\sum_{j=5,6}\int_{q_{j}}^{q_{j}+\Delta q_{j}^{S}}\) w j (ξ)dξ) by ∑ i = 1,2,4. q i
4.4.2 Further inefficient Generalized Nash Equilibrium
The following propositions are particular cases of those obtained in the preceding section. The first statement again directly obtains from NTF’s results: it simply states the conditions under which the solution of this problem is a GNE.
Proposition 7
Suppose that there is a solution to problem (86) to (94). Denote transmission constraints (91) and (92) respectively as \(g_{l}^{+}\) and \(g_{l}^{-}\) and suppose that \(\langle g_{l}^{+}(\Delta q),\gamma_{l}^{N/S,+}\rangle =0\) and \(\langle g_{l}^{-}(\Delta q),\gamma_{l}^{N/S,-}\rangle =0\) (Theorem 3.3 of Nabetani et al. 2009 ). Then the solution is a GNE.
Proof of Proposition 7
The proof is a direct application of NTF’s Theorem 3.3 (see Nabetani et al. 2009). □
There is no market of counter-trading resources in this case and there may thus be different GNEs. The following proposition states that the GNE solution of the (86) to (94), if it exists, is not unique.
Proposition 8
Suppose that there is a solution to problem (86) to (94). Denote transmission constraints (91) and (92) respectively as \(g_{l}^{+}\) and \(g_{l}^{-}\) and suppose that \(\langle g_{l}^{+}(\Delta q),\gamma_{l}^{N/S,+}\rangle =0\) and \(\langle g_{l}^{-}(\Delta q),\gamma_{l}^{N/S,-}\rangle =0\) (Theorem 3.3 of Nabetani et al. 2009 ). The valuation of the transmission capacity by both agents are identical when all \(\gamma _{l}^{N/S,+/-}\) are zero and the solution always satisfies \(\lambda _{l}^{N,-}-\) \(\lambda _{l}^{S,-}\) = \(\gamma _{l}^{N,-}-\) \(\gamma _{l}^{S,-}\) and \(\lambda _{l}^{N,+}-\) \(\lambda _{l}^{S,+}\) = \(\gamma _{l}^{N,+}-\) \(\gamma _{l}^{S,+}\).
Proof of Proposition 8
See Appendix J. □
These comments are parallel to those of Section 4.3.2. As already explained before setting all γ to zero creates a market for line capacity that can only improve efficiency even without an internal market of counter-trading resources. One can assess the range of possible inefficiencies by introducing a wedge between the valuations of the transmission constraints using the γ of the TSOs.
Last we again recall that there may not exist a GNE because counter-trading is not possible.
Corollary 4
The solution of the GNE problem does not necessarily exist.
Proof of Corollary 4
It suffices to take a case where the NTF problem is infeasible. □
5 Results
This section illustrates the different organizations of counter-trading. All computations start from the flows obtained from market clearing (as reported in Table 6) by solving the problem described in Appendix A with the original demand and marginal cost functions stated in Table 5. The reader is referred to Oggioni and Smeers (2010b) for the analysis of the interaction between the clearing of the energy market and the counter-trading process and the analysis of extreme cases where there is no equilibrium or even when counter-trading problems is not feasible (as has sometimes been observed in practice in the US and Europe). The following results are limited to illustrating the theoretical results and the mathematical insights of the developed model. The choice of parameters \(\gamma_l^{S,N, \pm}\) has been made bearing in mind Propositions 1 and 2.
We first present the results of the optimized counter-trading model presented in Section 4.1. We then discuss the efficiency levels of a selection of the possible results of the models presented in Sections 4.2, 4.3 and 4.4 where counter-trading operations are decentralized.
5.1 Optimized counter-trading model
The optimization of counter-trading implies that TSOs fully cooperate to relieve congestion. Applying this principle to the network depicted in Fig. 1, we find a counter-trading cost of 1,146 €, which in average amounts to 1.43 €/MWh. The re-dispatched quantities are indicated in Table 7; there is a net counter-trading flow from South to North equal to 50 MWh. Line (1–6) is congested in the North-South direction and its marginal value is 40 €/MWh. Because it is a cooperative solution, some regions may be better off by not participating. We do not deal with that question and assume that market operators are able to re-distribute resources among market players in such a way that no player or zone is worse off than by not participating.
5.2 Decentralized counter-trading Model 1: TSON and TSOS have full access to all counter-trading resources
Assume that TSON and TSOS can access all counter-trading resources. Setting all “\(\gamma _{l}^{N,S,\pm }\)” to zero (see discussion in Section 4.2), the problem describes a situation where both TSOs equally value line capacities. Numerically, we fall back on the solution of the optimized counter-trading problem. Applying different “\(\gamma_{l}^{N,S,\pm }\)” with the view of testing different valuations of transmission/line capacity, and hence the absence of a line capacity market, always leads to unbounded NTF problems. There is no primal dual solution to the NTF problem and hence no GNE. This complies with the theory stated in Section 4.2.2: an internal market of counter-trading resources implies a market of line capacity, at least in this example where the set of traded counter-trading resources is sufficient to complete the market.
The value of the dual variable of line (1–6) in the model where all “\( \gamma _{l}^{N,S,\pm }\)” are equal to zero is 40 €/MWh in the direction North-South. Re-dispatching quantities are given in Table 7. The sole important figure is the total (the sum over the two TSOs) re-dispatching; the allocation of this total between the two agents is arbitrary.
5.3 Decentralized counter-trading Model 2: TSON and TSOS have limited access to part of the counter-trading resources
The situation changes when constraining the access of a TSO to counter-trading resources in the other jurisdiction. Suppose limits of one TSO’s access to resources in the other zone as given in Table 8. These are selected by halving the counter-trading flows from South to North obtained for optimized counter-trading (compare Table 7). Taking into account these limits, we run five cases that differ by the values assigned to the parameters “\(\gamma _{l}^{N/S,\pm }\)” with the view of assessing the inefficiency that can result from different valuations of common resources by TSOs. Results are reported in Table 9. Recall that α defines the average counter-trading cost and can be used as a metric of this inefficiency. The bottom of Table 9 reports the total counter-trading costs (TCC) and the counter-trading costs of the two TSOs. The other row names are self explanatory.
These different cases are meant to produce different Generalized Nash Equilibria. Cases 1 and 2 are obtained with equal γ for the two TSOs and hence represent the impact of a market of line capacity.Footnote 11
The constraints on cross zonal access to resources are not binding and the solution is identical to the one of the optimized counter-trading. The policy implication of this finding is interesting: even though individual TSOs retain the exclusive control on some of their plants, which is a limitation to the internal market of counter-trading resources, the line capacity market overcomes the negative consequences of that limitation and restores efficiency. The other cases assume TSOs with different γ, therefore modeling the absence of a transmission/line capacity market. This leads to different phenomena.
Supposes first that the sole \(\gamma_{(1-6)}^{N,+}\) is positive and equal to 40 (case 3)Footnote 12. The absence of a line capacity market creates another GNE. Different valuations of the common line (1–6) capacity imply economic inefficiencies measured by an increase of 165 € of the re-dispatching costs compared to Case 1. The average re-dispatching cost becomes 1.64 €/MWh. The result of the counter-trading activity is a net flow of 36.36 MWh going from South to North. TSON’s re-dispatching costs amount to 1,454 €, while TSOS benefits from the operations as can be seen from its negative re-dispatching costs. Again, line (1–6) is congested and its marginal value becomes 42.42 €/MWh; this increase with respect to the 40 observed in the optimal counter-trading reflects the inefficiency created by the absence of the transmission/line capacity market.
Consider now the alternative arrangement where one imposes \( \gamma_{(1-6)}^{S,+}=40\) (case 4). The counter-trading flow from South to North is 43.28 MWh. This case is more efficient than Case 3, but counter-trading costs are still higher than in Case 1. In contrast with Case 3, TSON now gains from counter-trading, while TSOS incurs additional re-dispatching costs. Line (1–6) is still congested with a marginal value of 41.00 €/MWh (slightly higher than the 40 €/MWh of the optimal counter-trading).
Case 5 shows the worst degradation of all. The γ of the TSOs relative to line (1–6) are indicated in Table 9. Global re-dispatching costs amount to 1,489 €. TSON incurs most of this cost while TSOS still benefits. The net re-dispatch amounts to 30 MWh from South to North. The marginal value of line (1–6) is now 22.67 €/MWh.
5.4 Decentralized counter-trading Model 3: TSON and TSOS only operate in their own control area
Going one step further, suppose that TSOs remove congestion on the interconnection by only acquiring counter-trading resources in their jurisdiction. In other words, re-dispatching quantities sum to zero in each zone and there is no exchange of re-dispatching resources between the two zones.
This degrades efficiency as reported in Table 10. “\(\gamma_{l}^{N,S,\pm }\)” are all equal to zero in Case 1, which simulates a line capacity marketFootnote 13. Inefficiency is highlighted by significant re-dispatching costs of 2,521 € with average value of 3.15 €/MWh. Both TSOs counter-trade and TSON face the highest cost. Line (1–6) is congested in the North-South direction and has a marginal value of 146.67 €/MWh! Parallel to what we did for the decentralized counter-trading Models 1 and 2, we also consider the case where \(\gamma_{(1-6)}^{N,+}=\gamma _{(1-6)}^{S,+}=146.67\). This is Case 2 reported in Table 10. Attributing this particular value to the γ of both TSOs, we get again the results of Case 1, even though the dual variable of line (1–6) capacity falls to zero.
We further degrade the situation in Cases 3 and 4 that respectively assume \( \gamma _{(1-6)}^{N,+}\) and \(\gamma _{(1-6)}^{S,+}\) equal to 146.67. These cases have identical average and total re-dispatching costs that are also the worst among the scenarios considered. Parallel to what we observed with a restricted internal market of counter-trading resources (Model 2), TSOS significantly reduces its re-dispatch costs in Case 3, while TSON benefits in Case 4.
In Case 5, we assume that \(\gamma_{(1-6)}^{N,+}=102.67\) and \( \gamma_{(1-6)}^{S,+}=44.00\). These values are respectively the 70% and 30% of 146.67. Under this alternative assumption, system inefficiency increases, in comparison with Cases 1 and 2. Both TSOs face counter-trading costs whose global average is 3.26 €/MWh.
6 Conclusion
We apply the notion of Generalized Nash Equilibrium and its computation through the Nabetani, Tseng and Fukushima’s analysis of Quasi-Variational Inequality problem to study a situation of market design arising in the restructuring of the European electricity market. Specifically, we study different degrees of coordination in counter-trading activity in the context of the “Market Coupling” organization of the European electricity market. We also explain that the approach applies in general to problems of restructuring of an integrated organization into different Business Units.
The global optimization of counter-trading by a single integrated Transmission System Operator or by a set of Transmission System Operators acting in full coordination minimizes the cost of removing congestion. Even though efficient, this solution may require too much horizontal integration for being politically acceptable. Among different alternatives, we consider three organizations that all suppose that the grid remains operated by different TSOs.
The first case refers to a so called “internal market of counter-trading resources”. Following up on attempts in European circles to integrate services like balancing or reserve without necessarily integrating TSOs, we suppose that operators can freely resort to counter-trading resources in the whole market whether in their jurisdictions or outside. We show that this reproduces the result of the full optimization. This finding singles out an unusual situation where the solution set of a variational inequality problem (in our case the optimized counter-trading problem) coincides with that of the corresponding quasi-variational inequality problem (when all players have an un-discriminatory access at identical price to all market shared resources). The economic interpretation is also useful: the un-discriminatory access to the same set of counter-trading resources “completes the market” and hence makes it efficient. Last but not least the recourse to the NTF algorithm offers a neat explanation of why this happens: even though the organization appears to be of the imperfect coordination type, it may in fact be economically efficient because of the implications on valuation of line capacities of the arbitrage taking place in the procurement of counter-trading resources.
Restrictions on the internal market of counter-trading resources jeopardize this effect on the market of line capacities and hence degrade the situation. A first loss of efficiency happens when operators can only resort in a limited way to counter-trading resources outside of their jurisdiction. The situation can be remedied by creating a market of line capacity for TSOs, but full efficiency will only be restored in very particular cases. Here again, the resort to the NTF theory makes this analysis particularly easy.
The last case is the one where the market of counter-trading resources is fully segmented. Efficiency is further deteriorated even though the introduction of a common market of transmission resources can again help.
We conduct all the analysis on a simple six nodes region model and our results on market completeness are obtained in that particular case. Similar but weaker results can be obtained for the general case as we show in appendices. The numerical approach is general: specifically, the recourse to the NTF algorithm only requires solving an optimal power flow problem. This is now a standard model, which shows that the analysis can be conducted for any real world problem.
Notes
A Power Exchange (PX) is an operator with the mission of organizing and economically managing (clearing) the electricity market.
Transmission System Operator (TSO) is a company that is responsible for operating, maintaining and developing the transmission system for a control area and its interconnections. See ENTSO website.
Note that in Facchinei et al. (2007), the non-common constraints (Eq. (13) and the analogous variables for the other players) are assimilated to the common constraints. Those authors say: “Note that usually there are two groups of constraints, those which depend on x and those depending on a single player’s variables x i . For notational simplicity, and following the original paper by Rosen, we include these latter constraints in the former ones”.
Directly taken from Fukushima (2008).
This relation corresponds to what we state in Proposition 1 that is presented in Section 4.2.2.
For a global view of the European electricity market see, for instance, Leuthold et al. (2010).
For instance, TenneT (Dutch TSO) and Elia (Belgian TSO) respectively acquire E.ON and Vattenfall (German TSOs) grids and the Belgian and the French TSOs (respectively Elia and RTE) founded the company “Coreso” that has been recently joined by the Italian TSO Terna and the German TSO 50Herz Transmission (see all Press Releases available at http://www.coreso.eu/press-releases.php).
See Appendix C for the formulation of the problem.
The apeces N,S of the parameters γ N,S,± indicate “North” and “South”; while the signs “+” and “−” indicate the flow directions. The positive direction is from the Northern to the Southern zone; the negative direction is from the Southern to the Northern zone.
The choice of the value of \(\gamma_{l}^{N,S,\pm}\) has been conducted in the following way. In Case 1, we first run the problem by setting all \(\gamma_{l}^{N,S,\pm}\) equal to zero. Line (1–6) is congested and assumes a marginal value (\(\lambda_{(1-6)}^{+}\)) of 40 €/MWh. Taking into account the relations among \(\lambda_{l}^{\pm}\), \(\lambda_{l}^{N,S,\pm}\) and \(\gamma_{l}^{N,S,\pm}\) defined in Proposition 1, in Case 2 we set \(\gamma_{(1-6)}^{N,S,+}\) equal to 40 €/MWh. The marginal value of line (1–6) becomes zero, but both in Cases 1 and 2, \(\lambda_{(1-6)}^{N,S,+}\) are equal to 40, while \(\lambda_{(2-5)}^{N,S,+}\) are zero. Lines (1–6) and (2–5) are not congested in the opposite direction and then \(\lambda_{(l)}^{N,S,-}\) are equal to zero. Cases 1 and 2 are equivalent and leads to the same global counter-trading costs. In fact, the two TSOs attribute the same marginal value to the common congested transmission line. Counter-trading costs increase in Case 3, 4 and 5 where the two TSOs see different prices for the common congested lines.
Starting from the results of Cases 1 and 2, the values assigned to γ are chosen in such a way that GNEs are less efficient than in Cases 1 and 2. The economical interpretation of this, that also holds for Cases 4 and 5, is the absence of a capacity market that implies additional counter-trading costs.
The approaches used to select \(\gamma_{l}^{N,S,\pm }\) is identical to that adopted in the former Section.
References
Arrow KJ, Debreu G (1954) Existence of an equilibrium for a competitive economy. Econometrica 22:265–893
Cadwalader MD, Harvey SM, Hogan WW, Pope SL (1998) Market coordination of transmission loading relief across multiple regions. Available at http://www.hks.harvard.edu/fs/whogan/extr1298.pdf
Chao HP, Peck SC (1998) Reliability management in competitive electricity markets. J Regul Econ 14:198–200
Debreu G (1952) A social equilibrium existence theorem. Proc Natl Acad Sci 38:886–290
Facchinei F, Pang JS (2003) Finite-dimensional variational inequalities and complementarity problems, vols 1 and 2. Springer, New York
Facchinei F, Pang JS (2010) Nash equilibria: the variational approach. In: Palomar DP, Eldar YC (eds) Convex optimization in signal processing and communications. Cambridge University Press, Cambridge, pp 443–493
Facchinei F, Kanzow C (2007) Generalized Nash equilibrium problems. 4OR 5:173–210
Facchinei F, Sagratella S (2010) On the computation of all solutions of jointly convex generalized Nash equilibrium problems. Optim Lett. doi:10.1007/S11590-010-0218-6
Facchinei F, Fischer A, Piccialli V (2007) On generalized Nash games and variational inequalities. Oper Res Lett 35:159–164
Fukushima M (2008) Restricted generalized Nash equilibria and controlled penalty method. Comput Manag Sci. doi:10.1007/S10287-009-0097-4
Harker PT (1991) Generalized Nash games and quasi-variational inequalities. Eur J Oper Res 54:81–94
Kubota K, Fukushima M (2010) Gap function approach to the generalized Nash equilibrium problem. J Optim Theory Appl 144:511–513
Kulkarni AA, Shanbhag UV (2009) New insights on generalized Nash games with shared constraints: constrained and variational equilibria. In: Proceedings of the 48th joint IEEE conference on decision and control. Shanghai, PR China, 16–18 Dec 2009
Kulkarni AA, Shanbhag UV (2010) Revising generalized Nash games and variational inequalities. Available at https://netfiles.uiuc.edu/udaybag/www/Papers/comparison_final.pdf
Kurzidem MJ (2010) Analysis of flow-based market coupling in oligopolistic power markets. Dissertation ETH Zurich for the degree of Doctor of Sciences, No 19007. Available at http://www.eeh.ee.ethz.ch/uploads/tx_ethpublications/Kurzidem_diss.pdf
Leuthold FU, Weigt H, von Hirschhausen C (2010) A large-scale spatial optimization model of the European electricity market. Netw Spat Econ. doi:10.1007/s11067-010-9148-1
Metzler C, Hobbs BF, Pang JS (2003) Nash-Cournot equilibria in power markets on a linearized DC network with arbitrage: formulations and properties. Netw Spat Econ 3(2):123–150
Nabetani K, Tseng P, Fukushima M (2009) Parametrized variational inequality approaches to generalized Nash equilibrium problems with shared constraints. Comput Optim Appl. doi:10.1007/s10589-009-9256-3
Oggioni G, Smeers Y (2010a) Degree of coordination in market coupling and counter-trading. CORE discussion paper 01
Oggioni G, Smeers Y (2010b) Market coupling and the organization of counter-trading: separating energy and transmission again? CORE discussion paper, vol 53. Presented at the 17th power systems computation conference, Stockholm, Sweden, 22–26 Aug 2011
Pang JS, Fukushima M (2005) Quasi-variational inequalities, generalized Nash equilibria, and multi-leader-follower games. Comput Manag Sci. 2:21–56
Ralph D, Smeers Y (2006) EPECs as models for electricity markets. Invited paper, Power Systems Conference and Exposition (PSCE), pp 74–80. doi:10.1109/PSCE.2006.296252
Rosen JB (1965) Existence and uniqueness of equilibrium points for concave N-person games. Econometrica 33:520–534
Smeers Y (2003a) Market incompleteness in regional electricity transmission. Part I: the forward market. Netw Spat Econ 3(2):151–174
Smeers Y (2003b) Market incompleteness in regional electricity transmission. Part II: the forward and real time markets. Netw Spat Econ 3(2):175–196
Smeers Y, Wei JY (1999) Spatial oligopolistic electricity models with Cournot generators and regulated transmission prices. Oper Res 47:102–112
Williamson OE (1981) The economics of organization: the transaction cost approach. Am J Sociol 87(3):548–577
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Market Coupling model
Market Coupling (MC) organizes a partial integration of PXs and TSOs: PXs clear the energy markets on the basis of a simplified representation of the transmission grid given to them by TSOs. Market Coupling is the most advanced version of cross-border trade implemented in continental Europe. It currently links the electricity markets of France, Belgium, The Netherlands and since November 2010 Germany. Our problem formulation (realistically) assumes that PXs operate in a coordinated way to clear a two zone market organized as depicted in Fig. 2. The objective function (95) includes an average re-dispatching cost α that is here interpreted as part of the access change to the network. This levy is proportional to the quantity injected in the energy market. Because demand is equal to generation, this uniform access charge to the grid can equally be interpreted as paid by generators or consumers. Conditions (96) and (97) express the energy balance in the Northern and Southern zones respectively. The free variable I indicates the import/export between the two zones. The shadow variables ϕ N,S are the marginal energy prices of the Northern and Southern zones respectively. Constraints (98) and (99) impose that flow I does not exceed the transfer limit \(\overline{I}\) of the interconnecting line in the two possible directions. The dual variables δ 1 and δ 2 are the marginal costs of utilization of this zonal link. Finally, variables q n are non-negative.
s.t.
Appendix B: Complementarity conditions of the optimized counter-trading model
Consider the complementarity formulation of problem (53)–(59), as indicated below, where \(\lambda _{l}=(-\lambda _{l}^{+}+\lambda _{l}^{-})\)
where \(c_{i}(q_{i}+\Delta q_{i})=\frac{\partial \int_{q_{i}}^{q_{i}+\Delta q_{i}}c_{i}}{\partial \Delta q_{i}}\) for i = 1,2,4 and \(\omega _{j}(q_{j}+\Delta q_{j})=\frac{\partial \int_{q_{j}}^{q_{j}+\Delta q_{j}}w_{j}}{\partial \Delta q_{j}}\) for j = 3,5,6.
Appendix C: TSOS’ s problem in the decentralized counter-trading Model 1
The problem (107)–(112) solved by TSOS is similar to that of the TSON. Its formulation is as follows:
s.t.
where l = (1 − 6),(2 − 5)
Appendix D: Complementarity conditions of the decentralized counter-trading Model 1
We here present the mixed complementarity formulation of the decentralized counter-trading Model 1 (66)–(74). Setting \(\gamma _{l}^{N}=(-\gamma _{l}^{N,+}+\gamma _{l}^{N,-})\); \( \gamma _{l}^{S}=(-\gamma _{l}^{S,+}+\gamma _{l}^{S,-})\) and \(\lambda _{l}=(-\lambda _{l}^{+}+\lambda _{l}^{-})\) for l = ((1 − 6),(2 − 5)), the complementarity conditions are as follows:
where i = 1,2,4; j = 3,5,6 and the dual variables μ N,1, μ S,1, μ N,2 and μ S,2 associated with equality constraints are free variables. Note that:
Note that conditions (113), (114), (119) and (120) exclusively refer to TSON, while (115), (116), (121) and (122) are those of TSOS. Finally, (117) and (118) are the common transmission constraints.
Appendix E: Proof of Proposition 1
Consider the KKT conditions (113)–(116) of the decentralized counter-trading Model 1 (66)–(74) reported in Appendix D and compare them to the KKT conditions of the two TSOs’ problems (namely (60)–(65) for TSON and (107)–(112) for TSOS) computed with respect to \(\Delta q_{n}^{N}\) and \(\Delta q_{n}^{S}\) that we here report:
where \(\lambda_l^N=(-\lambda_l^{N,+}+ \lambda_l^{N,-})\) and \(\lambda_l^S=(-\lambda_l^{S,+}+ \lambda_l^{S,-})\).
The comparison between conditions (125)–(128) and (113)–(116) shows that
Following Theorem 3.3 of Nabetani et al. (2009) and thanks to the constraint qualification, the following relation (129)
is a necessary and sufficient condition for a solution x∗ to problem VI(F γ,K) to be a GNE. Note that g(x∗) refers to a transmission constraint shared by the two TSOs. Suppose this property holds for a solution of the parametrized problem (66)–(74) and bearing in mind that each transmission line can be congested in one direction only, we obtain:
□
Appendix F1: Proof of Proposition 2
Because all constraints are linear, constraint qualification holds. As already indicated,
is a necessary and sufficient condition for a solution x∗ to problem VI(F γ,K) to be a GNE.
Suppose this property holds for a solution of the parametrized problem (66)–(74). It is then a GNE and we can write the KKT conditions of that parametrized problem (see the complementarity conditions in Appendix D). Suppose that \(q_{n}+\Delta q_{n}^{N}+\Delta q_{n}^{S}>0\) for all n and note \(\lambda _{l}=(-\lambda _{l}^{+}+\lambda _{l}^{-})\), \(\gamma _{l}^{N}=(-\gamma _{l}^{N,+}+\gamma _{l}^{N,-})\) and \(\gamma _{l}^{S}=(-\gamma _{l}^{S,+}+\gamma _{l}^{S,-})\) in order to simplify the discussion. Then the optimality condition in (113)–(116) are binding and it follows that:
Subtracting (133) from (131) and (134) from (132) leads to the following conditions:
Because node 6 is the hub, we have PTDF 6,l = 0 and hence (μ N,1 + μ N,2) − (μ S,1 + μ S,2) = 0 in (136). This in turn implies \((\gamma _{(1-6)}^{N}-\gamma _{(1-6)}^{S})PTDF_{j,(1-6)}+(\gamma _{(2-5)}^{N}-\gamma _{(2-5)}^{S})PTDF_{j,(2-5)}=0\) for j = 3,5 and then:
This is verified only when \(\gamma _{l}^{N}=\gamma _{l}^{S}\) because the ratio \(\frac{PTDF_{j,(2-5)}}{PTDF_{j,(1-6)}}\) assumes a positive and a negative value. Taking stock of condition (130), we can deduce that:
□
Appendix F2: Generalizing Proposition 2
Assume now that the market is sub-dived in z = 1,...,Z zones each controlled by a TSO. The expressions \( q_{i}+\Delta q_{i}^{N}+\Delta q_{i}^{S} \) and \(q_{j}+\Delta q_{j}^{N}+\Delta q_{j}^{S}\) are respectively substituted by \(q_{i}+\sum_{z=1}^{Z}\Delta q_{i}^{z}\) and \(q_{j}+\sum_{z=1}^{Z}\Delta q_{j}^{z}\) where \(\Delta q_{i}^{z} \) and \(\Delta q_{j}^{z}\) are the variations operated by TSOz on power respectively produced and consumed in nodes i ∈ I and j ∈ J. Following former discussions in the now resolved flowgate/nodal pricing debate in the US and current discussions on the European “flow based” approach (see De Jong et al., Effects of flow-based market coupling for the CWE region. Available at http://www.nextgenerationinfrastructures.eu/download.php?field=document&itemID=449543 and Kurzidem 2010) we assume that the lines subject to congestion are few in the overall transmission infrastructure: we let L be this subset of potentially congested lines and adopt a European like terminology to refer to them as critical infrastructures (this terminology is used for the energy market in the European MC). We introduce the following NTF problem that generalizes the corresponding two zone problem (71)–(72).
s.t.
We can then state the following proposition that extends Proposition 2.
Proposition 9
Denote transmission constraints (141) and (142) respectively as \( g_{l}^{+}\) and \(g_{l}^{-}\) . Suppose that the optimization problem (138)–(143) has a solution that satisfies the conditions \(\left\langle g_{l}^{+}(x^{\ast}),\gamma _{l}^{z,+}\right\rangle =0\) and \(\left\langle g_{l}^{-}(x^{\ast }),\gamma _{l}^{z,-}\right\rangle =0\) defined by Theorem 3.3 of Nabetani et al. (2009). Suppose that the sum of the number of counter-trading resources and critical infrastructures traded among TSOs in the counter-trading market is greater or equal to the total number of critical infrastructures (cardinality of L .) Then, the solution of problem (138)–(143) exists if and only if \(\gamma _{l}^{z,+}=\gamma _{l}^{z^{\prime },+}\) and \(\gamma _{l}^{z,-}=\gamma _{l}^{z^{\prime },-}\) for all z . If so, then the optimal solution of that NTF problem is a GNE.
Proof of Proposition 9
Accounting for the above modifications and, in order to simplify the presentation, assuming that \(q_{i}+\sum_{z=1}^{Z}\Delta q_{i}^{z}>0\) and \( q_{j}+\sum_{z=1}^{Z}\Delta q_{j}^{z}>0\) and setting \(\lambda _{l}=(-\lambda _{l}^{+}+\lambda _{l}^{-})\), \(\gamma _{l}^{N}=(-\gamma _{l}^{N,+}+\gamma _{l}^{N,-})\) and \(\gamma _{l}^{S}=(-\gamma _{l}^{S,+}+\gamma _{l}^{S,-})\), one can deduce that conditions (131)–(134) can be generalized as follows:
Consider two different zones that we denote as z and z′. Subtracting (144) for zone z′ ≠ z from (144) for zone z and doing the same for (145), we obtain:
Assuming that n ∈ J is the hub node, we then have PTDF n,l = 0 and hence \((\mu ^{z,1}+\mu ^{z,2})-(\mu ^{z^{\prime },1}+\mu ^{z^{\prime },2})=0\) in Eq. (147). This in turn implies:
Note that now condition (148) denotes a homogeneous system. If the number of j ≠ n nodes is greater or equal to the number of the terms of the sum \(\sum_{l}(\gamma _{l}^{z}-\gamma _{l}^{z^{\prime }})PTDF_{j,l}\) for each of the Z − 1 independent couples \( \gamma _{l}^{z}-\gamma _{l}^{z^{\prime }}\) then \(\gamma _{l}^{z}=\gamma _{l}^{z^{\prime }}\) and thus \(\gamma _{l}^{z,+}=\gamma _{l}^{z^{\prime },+}\) , \(\gamma _{l}^{z,-}=\gamma _{l}^{z^{\prime },-}\). This particular solution corresponds to the case where a market for line capacity exists. In the opposite case, the system has infinite number of solutions. Suppose however that one creates a market of line capacities where the number of lines in that market is such that the number of j ≠ n nodes plus the line in the transmission market is equal to the number of the terms of the sum \( \sum_{l}(\gamma _{l}^{z}-\gamma _{l}^{z^{\prime }})PTDF_{j,l}\) for each of the Z − 1 independent couples , then \(\gamma _{l}^{z,-}=\gamma _{l}^{z^{\prime },-}\). □
Appendix G1: Proof of Proposition 3
In order to simplify the discussion, assume again that \(q_{n}+\Delta q_{n}^{N}+\Delta q_{n}^{S}>0\) ∀ n and define \(\lambda _{l}^{N}=(-\lambda _{l}^{N,+}+\lambda _{l}^{N,-})\) and \(\lambda _{l}^{S}=(-\lambda _{l}^{S,+}+\lambda _{l}^{S,-})\) for l = ((1 − 6),(2 − 5)). Replace \(q_{n}+\Delta q_{n}^{N}+\Delta q_{n}^{S}\) with \( q_{n}+\sum_{z=N,S}\Delta q_{n}^{z}\) ∀ n. The KKT conditions of the two TSOs’ problems (namely (60)–(65) for TSON and (107)–(112) for TSOS) obtained by deriving with respect to the variables \(\Delta q_{n}^{N}\) and \(\Delta q_{n}^{S}\) are as follows:
Summing (149) to (150), we have:
Since condition (151) holds for both TSOs, we can rewrite it in an explicit way:
Subtracting (153) from (152), we get:
We now subtract (150) from (149) and apply the above reasoning. We get:
that can be substituted by these two conditions:
Subtracting (157) from (156), one yields:
The combination of conditions (154) and (158) leads to the following equalities:
By setting, α = (μ N,1 + μ N,2) − (μ S,1 + μ S,2) and β = (μ N,1 − μ N,2) − (μ S,1 − μ S,2) conditions (159) and (160) become:
We observe that PTDF 6,l = 0. This implies that α = 0. If α = 0, then it holds that:
This corresponds to:
But \(\frac{PTDF_{j,(2-5)}}{PTDF_{j,(1-6)}}\) assumes a positive and a negative value respectively for j = 3,5 and then \(\mathbf{\lambda }_{l}^{N} \mathbf{=\lambda }_{l}^{S}\). This result means that the marginal values of transmission lines are identical for both TSOs. Consequently, the two TSOs are implicitly coordinated and there is no arbitrage. This also implies that α = β = 0 and then:
These can be rewritten as follows:
This implies that μ N,1 = μ S,1 and μ N,2 = μ S,2. □
Appendix G2: Generalizing Proof of Proposition 3
In this appendix, we generalize the results of Proposition 3. Assume again that the market is sub-dived in z = 1,...,Z zones each controlled by a TSO. The expressions \(q_{i}+\Delta q_{i}^{N}+\Delta q_{i}^{S}\) and \(q_{j}+\Delta q_{j}^{N}+\Delta q_{j}^{S}\) can be respectively substituted by \( q_{i}+\sum_{z=1}^{Z}\Delta q_{i}^{z}\) and \(q_{j}+\sum_{z=1}^{Z}\Delta q_{j}^{z}\) where \(\Delta q_{i}^{z}\) and \(\Delta q_{j}^{z}\) are the variations operated by TSOz on power respectively produced and consumed in nodes i ∈ I and j ∈ J.
Proposition 10
Suppose that the sum of the number of counter-trading resources and critical infrastructures that are explicitly traded among TSOs in counter-trading (for which there is an organized market) is greater or equal to the total number of critical infrastructures (cardinality of L .). If the solution of the GNE problem (138)–(143) exists, then it satisfies \(\gamma _{l}^{z,\pm }=\gamma _{l}^{z^{\prime },\pm }\) and \(\mu ^{z,1}=\mu ^{z^{\prime },1}\) and \(\mu ^{z,2}=\mu ^{z^{\prime },2}\).
Proof of Proposition 10
Assume again in order to simplify the discussion that \(q_{n}+\sum_{z=1}^{Z} \Delta q_{n}^{z}>0\) ∀ n and define \(\lambda _{l}=(-\lambda _{l}^{+}+\lambda _{l}^{-})\) for l ∈ L. We state the KKT conditions of the generalized parametrized problem (138)–(143). We get:
Summing (170) to (171), we have:
Since condition (172) holds for all TSOs, we can rewrite it as follows:
Subtracting (174) from (173), we get:
We now subtract (171) from (170) and apply the above reasoning. We get:
that can be substituted by these two conditions:
Again, subtracting (178) from (177), one yields:
The combination of conditions (175) and (179) leads to the following equalities:
By setting, \(\alpha =(\mu ^{z,1}+\mu ^{z,2})-(\mu ^{z^{\prime },1}+\mu ^{z^{\prime },2})\) and \(\beta =(\mu ^{z,1}-\mu ^{z,2})-(\mu ^{z^{\prime },1}-\) \(\mu ^{z^{\prime },2})\) conditions (180) and (181) become:
Assuming that n ∈ J is the hub node. This implies that α = 0. If α = 0, then it holds that:
Note that now condition (184) denotes a homogeneous system. If the number of j ≠ n nodes is greater or equal to the number of the terms of the sum \(\sum_{l}(\gamma _{l}^{z}-\gamma _{l}^{z^{\prime }})PTDF_{j,l}\) for each of the Z − 1 independent couples, then \( \lambda _{l}^{z}-\lambda _{l}^{z^{\prime }}\) then \(\lambda _{l}^{z}=\lambda _{l}^{z^{\prime }}\) and thus \(\lambda _{l}^{z,+}=\lambda _{l}^{z^{\prime },+} \), \(\lambda _{l}^{z,-}=\lambda _{l}^{z^{\prime },-}\). This particular solution corresponds to the case where a market for line capacity exists. In the opposite case, the system has infinite number of solutions. Suppose however that one creates a market of line capacities where the number of lines in that market is such that the number of j ≠ n nodes plus the line in the transmission market is equal to the number of the terms of the sum \(\sum_{l}(\gamma _{l}^{z}-\gamma _{l}^{z^{\prime }})PTDF_{j,l}\) for each of the Z − 1 independent couples , then \(\lambda _{l}^{z,-}=\lambda _{l}^{z^{\prime },-}\). Consequently, the TSOs are implicitly coordinated and there is no arbitrage. This also implies that α = β = 0 and then:
These can be rewritten as follows:
This implies that \(\mu ^{z,1}=\mu ^{z^{\prime },1}\) and \(\mu ^{z,2}=\mu ^{z^{\prime },2}\). □
Appendix H: Proof of Corollary 1
Corollary 3.2 of Nabetani, Tseng and Fukushima’s paper (see Nabetani et al. (2009)) proves that if the dual problem has solution then
We first consider the case where γ = 0. Under this assumption VI(F,K) = VI(F γ = 0,K) and the parametrized problem is identical to the optimized counter-trading problem. This can be easily done by imposing \(\Delta q_{n}^{N}+\) \(\Delta q_{n}^{S}\) = Δq n .
As already observed, the optimized counter-trading problem has a unique solution because of the convexity of the set K and the strict convexity of its objective function. This implies that the solution of the decentralized counter-trading problem (66)–(74) coincides with that of the optimized counter-trading model (53)–(59) when γ = 0.
We now show that the solution set of problem VI(F γ,K) when \( \gamma _{l}^{N,\pm }=\gamma _{l}^{S,\pm}\) and μ Z,1 = μ Z,2 reduces to a unique solution that is the solution of the optimized counter-trading problem (53)–(59).
Compare now the KKT conditions of the optimized counter-trading problem with those of the decentralized counter-trading problem. Denote \(\Delta q_{n}=\Delta q_{n}^{N}+\Delta q_{n}^{S}\) for all n and \(\lambda _{l}=(-\lambda _{l}^{+}+\lambda _{l}^{-})\), the optimality conditions of the optimized counter-trading model are as follows (compare complementarity conditions in Appendix B):
Denoting similarly \(\gamma _{l}^{N}=(-\gamma _{l}^{N,+}+\gamma _{l}^{N,-})\) \( \gamma _{l}^{S}=(-\gamma _{l}^{S,+}+\gamma _{l}^{S,-})\) and knowing that \( \gamma _{l}^{N,\pm }=\gamma _{l}^{S,\pm }\), the optimality conditions of the decentralized counter-trading Model 1 are as follows:
Setting \(\lambda_l=\lambda _{l}+\gamma_{l}^{N}\) one can easily see that the two groups of optimality conditions are identical and then the corresponding problems admit the same solution set.
Appendix I: Proof of Proposition 6
Let us denote the NTF’s formulation of problem (75)–( 85) as to \(VI(F^{\gamma },K_{2})\). The primal solution of problem \(VI(F^{\gamma =0},K_{2})\) is unique when all \(\gamma _{l}^{N/S}=0\). This is because both the objective function (75) and the set defined by the constraints are convex. Due to the lack of perfect arbitrage between the two TSOs, the equality \( \gamma _{l}^{N}=\gamma _{l}^{S}\) is no more ensured and then when \(\gamma _{l}^{N/S}\neq 0\) we have two different cases.
If \(\gamma _{l}^{N/S}\neq 0\) and \(\gamma _{l}^{N}=\gamma _{l}^{S}\), then the transformations applied to λ l in the complementarity version of problem (75)–(81) are simply translations (as we already seen in the Proof of Corollary 1 in Appendix H). This means that:
and implies that under this assumption the solution set of problem \( VI(F^{\gamma },K_{2})\) coincides with that of problem \(VI(F^{\gamma =0},K_{2})\). Since the solution set of the primal problem of \(VI(F^{\gamma =0},K_{2})\) contains one solution, this is also the unique solution of \( VI(F^{\gamma =0},K_{2})\).
This does not happen when \(\gamma _{l}^{N/S}\neq 0\) and \(\gamma _{l}^{N}\neq \gamma _{l}^{S}\) because the translations operated on the problems are now different. In other words:
respectively for the TSON and TSOS. As a consequence, the solution set can admit several solutions. However, from conditions (193) and (194), one immediately deduces that \( \lambda^{N} _{l}=\lambda _{l}=\lambda^{S} _{l}\) when \(\gamma_{l}^{N/S}=0\) and that
□
Appendix J: Proof of Proposition 8
The proof is parallel to that of Proposition 6 (see Appendix I).
Rights and permissions
About this article
Cite this article
Oggioni, G., Smeers, Y., Allevi, E. et al. A Generalized Nash Equilibrium Model of Market Coupling in the European Power System. Netw Spat Econ 12, 503–560 (2012). https://doi.org/10.1007/s11067-011-9166-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11067-011-9166-7
Keywords
- Generalized Nash Equilibrium
- Quasi-Variational Inequalities
- Market coupling
- Counter-trading
- European electricity market