1 Introduction

Spatial equilibrium problems are usually utilized for describing complex systems when the distributed spatial location of their elements must be taken into account. In particular, these problems appeared to be very suitable for modeling various complex competitive economic systems; see e.g. Harker (1985), Nagurney (1999) and references therein. Rather recently, the necessity to make essential transformations in energy sectors discovered many new challenges; see e.g. Ilic et al. (1998), Zaccour (1998), Alanne and Saari (2006). For this reason, new kinds of spatial models devised to overcome difficulties related to deregulating and restructuring energy sectors have received considerable attention; see e.g. Wei and Smeers (1999), Metzler et al. (2003), Nagurney and Matsypura (2006) and references therein. Since most parts of the energy sector are attributed to natural monopolies, perfect competition seems a strong assumption there and most models are based upon imperfect competition assumptions, hence, represent non-cooperative game problems. As a result, these models are formulated as Nash–Cournot non-cooperative games, variational inequalities, or optimization problems with equilibrium constraints. They appeared suitable for the situation where any explicit regulation of the energy market can be neglected. At the same time, the situation where a state permits mass privatization in the energy sector, but keeps certain tools for influence in this field, deserves a separate consideration. Usually, the auction market mechanisms are utilized in this case; see e.g. Anderson and Philpott (2002), Beraldi et al. (2004) and references therein. Note that the general auction models are mainly formulated as non-cooperative game problems; see e.g. Weber (1985). Hence, rather complex behavior of separate markets (participants) and the presence of network capacity and balance constraints may again lead to very complicated mathematical problems such as global optimization problems with equilibrium constraints or mixed integer programming problems, which have usually a great number of variables.

In this paper, we develop the approach to modeling auction markets, which was proposed in Konnov (2006, 2007a, b), where variational inequality models of separate auction markets with general price functions were described, i.e. these models allow for rather complex behavior of traders and buyers. The first goal of the paper is to suggest rather simple variational inequality problems for modeling a system of spatially distributed auction markets joined by transmission lines in a network subject to joint capacity and balance constraints, with taking the account behavior of participants within each auction market. Clearly, this task is essentially more complicated in comparison with that of a separate auction market. The second goal of the paper is to develop efficient methods for investigation and solution of spatial auction market problems via the presented variational inequality models.

In this paper, we propose several equivalent formulations of the above problem, some of them involving algorithmically defined mappings. Being based on these properties, we propose iterative solution methods, which reflect decomposition schemes adjusted essentially to peculiarities of the structure of the problem and to possible large dimensionality. We illustrate work of the methods by computational results.

2 Single auctions of a homogeneous commodity

We first investigate properties of a single auction market of a homogeneous commodity. Denote by I and J the index sets of traders and buyers at this auction. For each i ∈ I, the i-th trader chooses some offer value x i in his capacity segment [0, α i ] and has a price function g i (x i ). Similarly, for each j ∈ J, the j-th buyer chooses some bid value y j in his capacity segment [0, β j ] and has a price function h j (x j ). Therefore, the prices of participants may depend on offer/bid values. Denote by u the value of external excess demand for this market. That is, u reflects the excess demand of external economic agents who do not participate explicitly in the auction process, but agree with its price. Then we can define the feasible set of offer/bid values

$$\displaystyle D=\left\{ (x, y) \ \vrule \ \begin{array}{c} \sum \limits_{i \in I} x_{i} - \sum \limits_{j \in J} y_{j} - u = 0; \\ x_{i} \in [0, \alpha _{i}], i \in I, y_{j} \in [0, \beta _{j}], j \in J \end{array} \right\},$$

where x = (x i ) i ∈ I , y = (y j ) j ∈ J . The solution of the auction problem consists in finding a feasible volume vector (x *, y *) ∈ D and a number p * such that

$$g_{i}(x_{i}^{*}) \left\{ \begin{array}{ll} \geq p^{*} \quad & \ \ \mbox{if} \quad x^{*}_{i} = 0, \\ =p^{*} \quad & \ \ \mbox{if} \quad x^{*}_{i} \in (0, \alpha _{i}), \\ \leq p^{*} \quad & \ \ \mbox{if} \quad x^{*}_{i}=\alpha _{i}, \end{array} \right. \quad i \in I,$$
(1)

and

$$h_{j}(y_{j}^{*}) \left\{ \begin{array}{ll} \leq p^{*} \quad & \ \ \mbox{if} \quad y^{*}_{j} = 0, \\ =p^{*} \quad & \ \ \mbox{if} \quad y^{*}_{j} \in (0, \beta _{j}), \\ \geq p^{*} \quad & \ \ \mbox{if} \quad y^{*}_{j}=\beta _{j}, \end{array} \right. \quad j \in J;$$
(2)

where p * is the auction clearing price. That is, zero offer (bid) values correspond to traders (buyers) whose prices are greater (less) than the auction price, and the maximal offer (bid) values correspond to traders (buyers) whose prices are less (greater) than the auction price. The prices of other participants are equal to the auction price and their values may be arbitrary within their capacity bounds, but should be subordinated to the balance equation.

In Konnov (2006) (see also Konnov 2007a, b), the following strong relation between the above auction market problem and a variational inequality was established.

Proposition 1

  1. (a)

    If (x *, y *, p *) satisfies Eqs. (1) and (2) and (x *, y *) ∈ D, then (x *, y *) solves the variational inequality: Find (x *, y *) ∈ D such that

    $$\sum \limits_{i \in I} g_{i} \left(x^{*}_{i}\right) \left(x_{i} - x_{i}^{*}\right) - \sum \limits_{j \in J} h_{j} \big(y^{*}_{j}\big) \big(y_{j} - y_{j}^{*}\big) \geq 0 \quad \forall (x, y) \in D.$$
    (3)
  2. (b)

    If a pair (x *, y *) solves the problem in Eq. (3), then there exists p * such that (x *, y *, p *) satisfies Eqs. (1) and (2).

Moreover, it was also noticed that the set of possible auction prices p * in Eqs. (1) and (2) coincides with the set of Lagrange multipliers corresponding to the balance constraint

$$\sum \limits_{i \in I} x_{i}-\sum \limits_{j \in J} y_{j}-u=0.$$

Thus, we can associate to each value of u the set of the corresponding auction prices, denoted by P(u). Clearly, P(u) need not be a singleton in general and we thus obtain the multivalued inverse excess supply mapping for the auction market since u is also the excess supply from the market. In order to obtain additional properties of this mapping, we utilize monotonicity properties of the functions g i and − h j , which seem rather natural. In fact, from Eq. (1) we conclude that if the i-th trader announces a price g i  = g i (x i ) and an offer x i , then he agrees to sell any smaller volume with the same price, hence any smaller volume is not associated with a greater price, and the function g i is monotone. Similarly, it follows from Eq. (2) that if the j-th buyer announces a price h j  = h j (y j ) and a bid y j , then he agrees to purchase any smaller volume with the same price, hence any smaller volume is not associated with a smaller price, and the function − h j is monotone.

For this reason we can suppose that all the functions g i , i ∈ I and − h j , j ∈ J are continuous and monotone. Then we can define convex differentiable functions μ i : [0, α i ]→ℝ, i ∈ I and concave differentiable functions η j : [0, β j ]→ℝ, j ∈ J such that

$$\mu '_{i} (x_{i})=g_{i} (x_{i}) \ \mbox{and} \ \eta '_{j} (y_{j}) = h_{j} (y_{j}).$$
(4)

Therefore, the variational inequality in Eq. (3) is replaced with the convex optimization problem:

$$\begin{array}{lll}&&\mbox{ minimize} \quad \sum \limits_{i \in I} \mu _{i} (x_{i}) - \sum \limits_{j \in J} \eta_{j} (y_{j}) \nonumber\\ &&\mbox{subject to} \ (x, y) \in D. \end{array}$$
(5)

Since the cost function in Eq. (5) is nothing but the difference between the sold and paid amounts within the market, which can be treated as the negative profit of the auction manager, the problem in Eq. (5) maximizes this profit subject to the balance and participants’ capacity constraints.

Proposition 2

If Eq. (4) holds, then under the above assumptions Eqs. (3) and (5) are equivalent.

It also follows that P(u) is nothing but the solution set of the dual optimization problem of Eq. (5) and we can utilize the usual perturbation analysis. Let us define the perturbation function φ(u), which determines the optimal value in Eq. (5) dependent of the perturbation u. Then (see e.g. Sukharev et al. 1986, Chapter 6 and Minoux 1989, Chapter 6) φ is a convex function, u ↦ P(u) is a maximal monotone mapping, and P(u) is the subdifferential of φ at u.

This result allows us to determine the inverse mapping U(p) = P  − 1(u), i.e.

$$U(p)=\left\{ u \ | \ p \in P(u) \right\}.$$

It is also the subdifferential mapping of the function ψ(p) = φ *(p), which is conjugate for φ (see e.g. Aubin 1984, Corollary 4.1). Observe that the computation of values of U(p) is easier in comparison with P(u). In fact, given a number p * = p, we should find offer/bid values \(x^{*}_{i}\) and \(y^{*}_{j}\) separately from Eqs. (1), (2) and after set

$$U(p)=\sum \limits_{i \in I} x_{i}^{*} - \sum \limits_{j \in J} y_{j}^{*}.$$

Clearly, p ↦ U(p) is the excess supply mapping of the market and it is multi-valued in general since Eqs. (1) and (2) admit many solutions. These properties of the mappings P and U can be used in creating more general spatial auction market models.

3 Spatial equilibrium models

Let us consider the model of n spatially distributed markets of a homogeneous commodity, which are joined by two-directional links in a network. For each k-th auction market, we denote by I k and J k the index sets of traders and buyers, respectively. Also, each i-th trader chooses his offer value x i  ∈ [0, α i ] and has a price function g i (x i ), i ∈ I k . Similarly, each j-th buyer chooses his bid value y j  ∈ [0, β j ] and has a price function h j (y j ), j ∈ J k . Let u k denotes the value of the external excess demand and simultaneously the internal excess supply for the k-th market, then we can define the feasible offer/bid volume set for this market:

$$\displaystyle D_{(k)}(u_{k}) =\left\{ \left( {x_{(k)}, y_{(k)}} \right) \ \vrule \ \begin{array}{c} \sum \limits_{i \in I_{k}} x_{i} - \sum \limits_{j \in J_{k}} y_{j}-u_{k}=0, \\ x_{i} \in [0,\alpha _{i}], i \in I_{k}; \ y_{j} \in [0, \beta _{j}], j \in J_{k} \end{array} \right\},$$

where \(x_{(k)}=(x_{i})_{i \in I_{k}}\), \(y_{(k)}=(y_{j})_{j \in J_{k}}\). Given a value u k , the solution of the k-th auction problem consists in finding a feasible pair of vectors \((x_{(k)}^{*}, y_{(k)}^{*}) \in D_{(k)}(u_{k})\) and a number \(p^{*}_{k}\) such that

$$g_{i}(x_{i}^{*}) \left\{ \begin{array}{ll} \geq p^{*}_{k} \quad &\ \ \ \mbox{if} \quad x^{*}_{i} = 0, \\ =p^{*}_{k} \quad &\ \ \ \mbox{if} \quad x^{*}_{i} \in (0, \alpha _{i}), \\ \leq p^{*}_{k} \quad &\ \ \ \mbox{if} \quad x^{*}_{i}=\alpha _{i}, \end{array} \right. \quad i \in I_{k};$$
(6)

and

$$h_{j}(y_{j}^{*}) \left\{ \begin{array}{ll} \leq p^{*}_{k} \quad &\ \ \ \mbox{if} \quad y^{*}_{j} = 0, \\ =p^{*}_{k} \quad &\ \ \ \mbox{if} \quad y^{*}_{j} \in (0, \beta _{j}), \\ \geq p^{*}_{k} \quad &\ \ \ \mbox{if} \quad y^{*}_{j}=\beta _{j}, \end{array} \right. \quad j \in J_{k};$$
(7)

where \(p_{k}^{*}\) is the auction clearing price. This problem was investigated in the previous section. In what follows, we will utilize the following assumption on the price functions.

(A1)

The functions g i , i ∈ I k and − h j , j ∈ J k , k = 1,...,n are monotone and continuous.

From (A1) we in particular obtain that there exist convex continuously differentiable functions μ i : [0, α i ]→ℝ, i ∈ I k and η j : [0, β j ]→ℝ, j ∈ J k such that Eq. (4) holds for k = 1,...,n. Now, combining Propositions 1 and 2, we obtain the same equivalence result.

Proposition 3

Let assumption (A1) hold.

  1. (a)

    If \((x^{*}_{(k)}, y^{*}_{(k)}, p^{*}_{k})\) satisfies Eqs. (6) and (7) and \((x^{*}_{(k)}, y^{*}_{(k)}) \in D_{(k)} (u_{k})\) , then \((x^{*}_{(k)}, y^{*}_{(k)})\) solves the variational inequality

    $$\sum \limits_{i \in I_{k}} g_{i}\left(x_{i}^{*}\right) \left(x_{i}-x_{i}^{*}\right) - \sum \limits_{j \in J_{k}} h_{j}\big(y_{j}^{*}\big) \big(y_{j}-y_{j}^{*}\big) \geq 0 \quad \forall (x_{(k)}, y_{(k)}) \in D_{(k)} (u_{k})$$
    (8)

    and the equivalent convex optimization problem:

    $$\begin{array}{lll}&&\mbox{{\rm minimize}} \quad \sum \limits_{i \in I_{k}} \mu _{i} (x_{i}) -\sum \limits_{j \in J_{k}} \eta _{j} (y_{j}) \nonumber\\ [2pt] &&\mbox{\rm subject to} \ (x_{(k)}, y_{(k)}) \in D_{(k)} (u_{k}). \end{array}$$
    (9)
  2. (b)

    If \((x^{*}_{(k)}, y^{*}_{(k)})\) solves the problem in Eq. (8) (or Eq. (9)), then there exists \(p^{*}_{k}\) such that \((x^{*}_{(k)}, y^{*}_{(k)}, p^{*}_{k})\) satisfies Eqs. (6) and (7).

Moreover, if we denote by \(\varphi _{k}(u_{k}^{*})\) the optimal value in Eq. (9), then the function φ k is convex and its subdifferential at u k coincides with the set of all the auction clearing prices P k (u k ) obtained from Eqs. (6) and (7), i.e.,

$$\partial \varphi _{k} (u_{k})=P_{k} (u_{k}),$$

hence the mapping u k ↦ P k (u k ) is maximal monotone.

We now turn to writing general equilibrium conditions for the network of auction markets. Denote by \(\mathcal{A}\) the set of all the links (arcs) joining the markets. Let f a denote the commodity flow along arc a = (k, l) and let [γ′ a , γ′′ a ] be the segment of feasible flows, where γ′ a  ≤ 0, γ′′ a  ≥ 0 and the negative value of f a indicates the reverse direction of the flow. For a given node k, we denote by \(\mathcal{A}^{+}_{k}\) and \(\mathcal{A}^{-}_{k}\) the sets of incoming and outgoing arcs at k. Next c a (f a ) denotes the cost of shipment of one unit of commodity along arc \(a \in \mathcal{A}\). By using the mappings P k we can write the usual spatial equilibrium conditions as follows: Find u * ∈ ℝn, f * ∈ F such that

$$\begin{array}{rll} \displaystyle \exists p^{*}_{k} &\in& P_{k} (u^{*}_{k}), \ k=1,\dots,n; \nonumber\\ [2pt] \displaystyle \left( c_{a}\left(f^{*}_{a}\right)+p^{*}_{k}-p^{*}_{l}\right) \left(f_{a}-f^{*}_{a}\right) &\geq& 0 \quad \forall f_{a} \in \left[\gamma '_{a}, \gamma ''_{a}\right], a \in \mathcal{A}; \nonumber\\ [2pt] \displaystyle \sum \limits_{a \in \mathcal{A}^{-}_{k}} f^{*}_{a} - \sum \limits_{a \in \mathcal{A}^{+}_{k}} f^{*}_{a} - u^{*}_{k}&=&0; \end{array}$$
(10)

where \(u^{*}=(u^{*}_{1},\dots,u^{*}_{n})\), \(f^{*}=(f^{*}_{a})_{a \in \mathcal{A}}\), \(F=\prod \limits_{a \in \mathcal{A}} [\gamma '_{a}, \gamma ''_{a}]\); see e.g. Harker (1985), Nagurney (1999), and Konnov (2007b). These relations reflect the absence of profit from shipment of commodity between each pair of nodes and the flow balance at each node. The above problem can be also converted in the usual variational inequality format.

Proposition 4

The problem in Eq. (10) is equivalent to the variational inequality: Find (f *, u *) ∈ V and \(p^{*}_{k} \in P_{k}(u^{*}_{k})\) , k = 1,...,n such that

$$\begin{array}{c} \displaystyle \sum \limits_{a \in \mathcal{A}} c_{a} (f^{*}_{a}) \left(f_{a}-f^{*}_{a}\right)+ \sum \limits_{k=1}^{n} p^{*}_{k} \left(u_{k}-u^{*}_{k}\right) \geq 0 \quad \forall (f, u) \in V, \end{array}$$
(11)

where

$$V=\left\{ (f, u) \in F\times \mathbb{R}^{n} \ \vrule \ \sum \limits_{a \in \mathcal{A}^{-}_{k}} f_{a} - \sum \limits_{a \in \mathcal{A}^{+}_{k}} f_{a}-u_{k}=0, \quad k=1,\dots,n \right\} .$$

Proof

Writing the necessary and sufficient optimality conditions for Eq. (11) (see e.g. Konnov 2007b, Proposition 11.7), we obtain

$$\begin{array}{rll}\left(c_{a}\left(f_{a}^{*}\right)+\lambda _{k}-\lambda _{l}\right) \left(f_{a}-f^{*}_{a}\right) &\geq& 0 \quad \forall f_{a} \in \left[\gamma '_{a}, \gamma ''_{a}\right], \ a=(k, l) \in \mathcal{A}; \\ p^{*}_{k}-\lambda _{k}=0, p^{*}_{k} &\in& P_{k} \left(u^{*}_{k}\right), \quad k=1, \dots,n; \\ \sum \limits_{a \in \mathcal{A}^{-}_{k}} f_{a}^{*} - \sum \limits_{a \in \mathcal{A}^{+}_{k}} f_{a}^{*} - u^{*}_{k}&=&0, \quad k=1,\dots,n; \end{array}$$

for f * ∈ F, u * ∈ ℝn and some numbers λ k , k = 1, ..., n. But these relations are equivalent to Eq. (10), as desired. □

We introduce the following natural assumptions on transmission costs.

(A2)

The functions \(c_{a}, a \in \mathcal{A}\) are monotone and continuous.

Then there exist convex continuously differentiable functions σ a :[γ′ a , γ′′ a ] → ℝ, \(a \in \mathcal{A}\) such that

$$\sigma '_{a} (f_{a})=c_{a}(f_{a}),$$

and Eq. (11) becomes a variational inequality problem with monotone integrable mappings. Therefore (see e.g. Sukharev et al. 1986, and Minoux 1989), Eq. (11) is equivalent to a convex nondifferentiable optimization problem, as the following proposition states.

Proposition 5

Let assumptions (A1) and (A2) hold. Then Eq. (11) is equivalent to the optimization problem:

$$\begin{array}{lll} &&\mbox{{\rm minimize}} \quad \sum \limits_{a \in \mathcal{A}} \sigma _{a} (f_{a})+\sum \limits_{k=1}^{n} \varphi _{k} (u_{k}) \nonumber\\ &&\mbox{\rm subject to} \ (f, u) \in V. \end{array}$$
(12)

It follows that we can apply the well known convex nonsmooth optimization methods (see e.g. Shor 1979 and Kiwiel 1985) in order to find a solution of the spatial auction market problem above. The corresponding iterative subgradient schemes for Eq. (12) can be viewed as certain two-level decomposition methods (see e.g. Shor 1979 and Minoux 1989) where network flows are upper level variables, offer/bid volumes are lower level variables, and excess supplies are interface variables.

Equation (10) represents the so-called quantity formulation of the spatial equilibrium problem. By using the excess supply mapping U k (p k ) we can write the so-called price formulation: Find vectors p * ∈ ℝ, f * ∈ F such that

$$\begin{array}{rll}\displaystyle \exists u^{*}_{k} &\in& U_{k}\left(p^{*}_{k}\right), \ k=1, \dots, n; \nonumber\\ [3pt] \left(c_{a}\left(f^{*}_{a}\right)+p^{*}_{k}-p^{*}_{l}\right) \left(f_{a}-f^{*}_{a}\right) &\geq& 0 \quad \forall f_{a} \in \left[f'_{a}, f''_{a}\right], a \in \mathcal{A};\nonumber\\ [3pt] \sum \limits_{a \in \mathcal{A}^{-}_{k}} f_{a}^{*}-\sum \limits_{a \in \mathcal{A}^{+}_{k}} f^{*}_{a}-u^{*}_{k}&=&0, \quad k=1, \dots, n; \end{array}$$
(13)

where \(p^{*}=(p^{*}_{1}, \dots, p^{*}_{n})\). Since

$$U_{k}(p_{k})=P^{-1}_{k}(u_{k}),$$

we have the equivalence result.

Proposition 6

Equations (10) and (13) are equivalent.

However, taking into account the result of Section 2 and assumptions (A1) and (A2), we can reduce Eq. (13) to a saddle point problem. In fact, let us consider the bifunction

$$\displaystyle M(f, p)= \sum \limits_{a \in \mathcal{A}} \sigma _{a} (f_{a})+\sum \limits_{k=1}^{n} p_{k} \left({ \sum \limits_{a \in \mathcal{A}^{-}_{k}} f_{a}-\sum \limits_{a \in \mathcal{A}^{+}_{k}} f_{a}} \right) - \sum \limits_{k=1}^{n} \psi _{k} (p_{k}),$$
(14)

where \(U_{k}(p_{k})=\partial \psi _{k}(p_{k})\), i.e. \(\psi _{k}(p_{k})=\varphi _{k}^{*}(p_{k})\). Clearly, under (A1) and (A2), the function M is convex in f and concave in p. Next, we can consider the saddle point problem: Find (f *, p *) ∈ F × ℝn such that

$$\displaystyle M\left(f^{*}, p\right) \leq M\left(f^{*}, p^{*}\right) \leq M\left(f, p^{*}\right) \quad \forall f \in F, \forall p \in \mathbb{R}^{n};$$
(15)

when Eq. (13) gives the necessary and sufficient optimality conditions for this problem.

Proposition 7

Let assumptions (A1) and (A2) hold. Then Eqs. (13) and (14)–(15) are equivalent.

Therefore, the price formulation leads to the convex–concave nonsmooth saddle point problem, which can be also solved with certain iterative methods; see e.g. Shor (1979) and Minoux (1989). Again we then obtain two-level decomposition schemes where prices serve as interface variables between levels.

However, both the formulations yield nonsmoothness and high dimensionality due to the presence of network flow variables, which can cause certain difficulties in creating rapidly convergent iterative sequences. For this reason, decomposition schemes without nonsmooth functions would have certain advantages.

4 Constrained spatial auction market problem

In order to construct a general spatial auction market model, we collect optimality conditions from both the network and market levels. Set \(x=(x_{i})_{i \in I_{k}, k=1, \dots, n}; y=(y_{j})_{j \in J_{k}, k=1, \dots, n}\);

$$X=\prod \limits_{k=1}^{n} \prod \limits_{i \in I_{k}} [0, \alpha _{i}] \quad \mbox{and} \quad Y= \prod \limits_{k=1}^{n} \prod \limits_{j \in J_{k}} [0, \beta _{j}].$$

The problem is to find a collection (x *, y *, f *, p *, u *) ∈ X × Y × F × ℝn × ℝn such that Eqs. (6) and (7) hold true for k = 1, ..., n, and also

$$\sum \limits_{i \in I_{k}} x_{i}^{*}-\sum \limits_{j \in J_{k}} y^{*}_{j}-u^{*}_{k}=0 \quad \mbox{for} \ \ \ k=1, \dots, n; $$
(16)
$$\sum \limits_{a \in \mathcal{A}^{-}_{k}} f_{a}^{*}-\sum \limits_{a \in \mathcal{A}_{k}^{+}} f^{*}_{a}-u^{*}_{k}=0 \quad \mbox{for} \ \ \ k=1, \dots, n; $$
(17)
$$c_{a}\left(f^{*}_{a}\right)+p^{*}_{k}-p^{*}_{l} \left\{ \begin{array}{ll} \geq 0 \quad & \ \ \ \mbox{if} \quad f^{*}_{a}=\gamma '_{a}, \\[8pt] =0 \quad & \ \ \ \mbox{if} \quad f^{*}_{a} \in \left(\gamma '_{a}, \gamma ''_{a}\right), \\[8pt] \leq 0 \quad & \ \ \ \mbox{if} \quad f^{*}_{a}=\gamma '' _{a}, \end{array} \right. \quad a=(k, l) \in \mathcal{A};$$
(18)

(cf. Eqs. (10), (13)). Comparing all the formulations, we obtain the common equivalence result.

Proposition 8

The problem of finding (x *, y *, f *, p *, u *) satisfying Eqs. (16), (17) and (18) and Eqs. (6) and (7) for k = 1, ..., n, is equivalent to Eq. (10) and also to Eq. (13).

Observe that Eq. (17) implies the total material balance equation

$$\sum \limits_{k=1}^{n} u^{*}_{k}=\sum \limits_{k=1}^{n}\left[ {\sum \limits_{a \in \mathcal{A}^{-}_{k}} f_{a}^{*}-\sum \limits_{a \in \mathcal{A}_{k}^{+}} f^{*}_{a}} \right]=0,$$

which can be in principle added to Eqs. (16), (17) and (18). We now intend to present a simpler formulation of spatial auction problems. Set

$$W=\left\{ \begin{array}{l} (x, y, f) \\ \in X\times Y\times F \end{array} \ \vrule \ \begin{array}{l} \left( \sum \limits_{a \in \mathcal{A}_{k}^{-}} f_{a} -\sum \limits_{a \in \mathcal{A}_{k}^{+}}f_{a}\right) \\ - \left(\sum \limits_{i \in I_{k}} x_{i}-\sum \limits_{j \in J_{k}} y_{j}\right)=0, \quad k=1,\dots, n \end{array} \right\}$$

and consider the problem of finding a triplet (x *, y *, f *) ∈ W such that

$$\begin{array}{lll} &&{\kern-7pt} \sum \limits_{k=1}^{n} \left[ {\sum \limits_{i \in I_{k}} g_{i}\left(x_{i}^{*}\right)\left(x_{i}-x_{i}^{*}\right)- \sum \limits_{j \in J_{k}} h_{j}\left(y_{i}^{*}\right)\left(y_{j}-y_{j}^{*}\right) } \right] \nonumber\\ &&{\kern3pt} +\, \sum \limits_{a \in \mathcal{A}} c_{a}\left(f^{*}_{a}\right) \left(f_{a}-f_{a}^{*}\right)\geq 0 \quad \forall (x, y, f) \in W. \end{array}$$
(19)

Theorem 1

  1. (a)

    If (x *, y *, f *) solves Eq. (19), there exist numbers \(p^{*}_{k}\) and \(u^{*}_{k}, k=1, \dots, n\) such that (x *, y *, f *, p *, u *) satisfies Eqs. (16), (17) and (18) and Eqs. (6) and (7) for k = 1, ..., n.

  2. (b)

    If (x *, y *, f *, p *, u *) satisfies Eqs. (16), (17) and (18) and Eqs. (6) and (7) for k = 1, ..., n, then (x *, y *, f *) is a solution of Eq. (19).

Proof

First of all we write the Karush–Kuhn–Tucker optimality conditions for Eq. (19) (see e.g. Konnov 2007b, Proposition 11.7):

$$(x^{*}, y^{*}, f^{*}, p^{*}) \in X\times Y\times F\times \mathbb{R}^{n},$$
$$\begin{array}{lll} &&{\kern-7pt} \sum \limits_{k=1}^{n} \left[ {\sum \limits_{i \in I_{k}} g_{i}\left(x_{i}^{*}\right)(x_{i}-x_{i}^{*})- \sum \limits_{j \in J_{k}} h_{j}\left(y_{i}^{*}\right)\left(y_{j}-y_{j}^{*}\right) } \right]\nonumber\\ [3pt] &&\;\,{\kern1pc}{\kern-7pt} + \sum \limits_{a \in \mathcal{A}} c_{a}\left(f^{*}_{a}\right) \left(f_{a}-f_{a}^{*}\right) + \sum \limits_{k=1}^{n} p^{*}_{k} \left[ \sum \limits_{a \in \mathcal{A}_{k}^{-}}\left(f_{a}-f_{a}^{*}\right)- \sum \limits_{a \in \mathcal{A}_{k}^{+}}\left(f_{a}-f_{a}^{*}\right) \right.\nonumber\\ &&\qquad\qquad\qquad{\kern12.2pc} \left. - \sum \limits_{i \in I_{k}} \left(x_{i}-x_{i}^{*}\right)+\sum \limits_{j \in J_{k}} \left(y_{j}-y_{j}^{*}\right) \right] \geq 0\nonumber\\ &&\;\,{\kern1pc} {\kern-7pt}\forall (x, y, f) \in X\times Y\times F; \end{array}$$
(20)

and

$$\left( {\sum \limits_{a \in \mathcal{A}_{k}^{-}} f_{a}^{*}-\sum \limits_{a \in \mathcal{A}_{k}^{+}} f_{a}^{*}} \right) - \left( {\sum \limits_{i \in I_{k}} x_{i}^{*}-\sum \limits_{j \in J_{k}} y_{i}^{*} } \right) =0, \quad k=1, \dots, n.$$
(21)

That is, if (x *, y *, f *) solves Eq. (19), then there exists p * ∈ ℝn such that Eqs. (20) and (21) hold true. Conversely, if (x *, y *, f *, p *) satisfies Eqs. (20) and (21), then (x *, y *, f *) is a solution of Eq. (19). Thus, we should show the equivalence between Eqs. (6) and (7), (16) and (18) and (20) and (21). Note that Eq. (20) can be replaced with the following system of partial variational inequalities:

$$\begin{array}{rll} \left(g_{i}(x^{*}_{i})-p_{k}^{*}\right) \left(x_{i}-x_{i}^{*}\right) &\geq& 0 \quad \forall x_{i} \in [0, \alpha _{i}], \ i \in I_{k}, k=1, \dots, n; \nonumber\\ \left(p^{*}_{k}-h_{j}(y_{j}^{*})\right) \left(y_{j}-y_{j}^{*}\right) &\geq& 0 \quad \forall y_{j} \in [0, \beta _{j}], \ j \in J_{k}, k=1, \dots, n; \nonumber\\ \left( c_{a}(f_{a}^{*})+ p_{k}^{*}-p_{l}^{*}\right) \left(f_{a}-f_{a}^{*}\right) &\geq& 0 \quad \forall f_{a} \in \left[\gamma '_{a}, \gamma ''_{a}\right], \forall a =(k, l) \in \mathcal{A}. \end{array}$$
(22)

However, Eq. (22) is equivalent to Eqs. (6) and (7) for k = 1, ..., n and Eq. (18). Next, Eqs. (16) and (17) clearly give Eq. (21), whereas Eq. (21) allows us to find \(u_{k}^{*}, k=1, \dots, n\) from Eqs. (16) and (17) then must hold. The proof is complete. □

So, we can solve the variational inequality of Eq. (19) instead of the system Eqs. (6) and (7), (16), (17) and (18). Again, the numbers \(p_{k}^{*}\) here are precisely the Lagrange multiplies of the balance constraints in Eq. (21). Under assumptions (A1) and (A2) we can derive the equivalence to the convex optimization problem:

$$\begin{array}{lll} &&\mbox{{\rm minimize}} \quad \sum \limits_{k=1}^{n} \left[ \sum \limits_{i \in I_{k}} \mu _{i} (x_{i})- \sum \limits_{j \in J_{k}} \eta _{j} (y_{j}) \right] +\sum \limits_{a \in \mathcal{A}} \sigma _{a} (f_{a}) \nonumber\\ [3pt] &&\mbox{\rm subject to} \ (x, y, f) \in W, \end{array}$$
(23)

where μ i :[0, α i ] → ℝ, i ∈ I k , − η j :[0, β j ] → ℝ, j ∈ J k , k = 1, ..., n, and σ a :[γ′ a , γ′′ a ] → ℝ, \( a \in \mathcal{A}\), are convex differentiable functions such that

$$\mu '_{i} (x_{i})=g_{i}(x_{i}), \eta '_{j}(y_{j})=h_{j}(y_{j}), \sigma '_{a}(f_{a})=c_{a}(f_{a});$$
(24)

since Eq. (19) then represents the necessary and sufficient optimality conditions for the problem in Eq. (23).

Proposition 9

Suppose that assumptions (A1) and (A2) hold. Then Eqs. (19) and (23) are equivalent, where the functions μ i , η j , and σ a are defined in Eq. (24).

Observe that Eq. (23) maximizes the profit of the manager of the spatially distributed auction market system subject to the material balance and capacity constraints, with taking into account the transmission costs (cf. Eq. (5)).

Remark 1

We chose the network with two-directional edges as one of possible presentations of the spatial problems, which is more suitable for implementation in solution methods. Of course, all the above results remain true for some other representations, say, for graphs with one-directional arcs, where one edge is replaced by two arcs.

5 Dual decomposition methods

In the previous section we showed that the general spatial auction market problem is reduced to the variational inequality of Eq. (19) or to the convex optimization problem of Eq. (23). Therefore, we can in principle utilize a great number of the corresponding iterative methods (see e.g. Facchinei and Pang 2003; Konnov 2007b; Minoux 1989; Polyak 1983; and Sukharev et al. 1986) to find a solution. However, the problem has a decomposable structure and we are interested in applying methods which can take into account this peculiarity. More precisely, the dual type methods seem rather efficient since they allow us to find explicitly the auction clearing prices as well. One of the most known is the Uzawa method (Arrow et al. 1958), Chapter 10, which can be treated as the subgradient ascent method for the dual problem:

$$\begin{array}{lll} &&\mbox{maximize} \quad \Psi (p) \nonumber\\ &&\mbox{subject to} \ p \in \mathbb{R}^{n}, \end{array}$$
(25)

where

$$\begin{array}{lll}\Psi (p)&=& \min \limits_{ (x, y, f) \in X\times Y\times F } \left\{ \sum \limits_{k=1}^{n} \left( \sum \limits_{i \in I_{k}} \mu _{i} (x_{i})- \sum \limits_{j \in J_{k}} \eta _{j} (y_{j}) \right) \right.\nonumber\\ &&\qquad\quad{\kern5.1pc} +\sum \limits_{a \in \mathcal{A}} \sigma _{a} (f_{a}) +\sum \limits_{k=1}^{n} p_{k} \left( \sum \limits_{a \in \mathcal{A}_{k}^{-}} f_{a} -\sum \limits_{a \in \mathcal{A}_{k}^{+}} f_{a} \right) \nonumber\\ &&\qquad\quad{\kern5.1pc}\left. - \left( \sum \limits_{i \in I_{k}} x_{i}-\sum \limits_{j \in J_{k}} y_{j} \right) \right\} . \end{array}$$
(26)

Finding a solution in Eq. (26) is very simple since it decomposes into a number of one-dimensional optimization problems. However, the function Ψ may be nonsmooth if the functions μ i , − η j , and σ a are non strictly convex. The well-known way to overcome this drawback consists in replacing the usual Lagrangian in Eq. (26) with an extended one. Then an analogue of Eq. (25) becomes a smooth optimization problem, but the decomposable structure is destroyed and the inner problem is not decomposed into one-dimensional ones; see e.g. Polyak (1983) and Minoux (1989).

For this reason, the combination of the proximal point method (Martinet 1970; Rockafellar 1976) and the dual Uzawa type method seems rather suitable. In fact, the proximal point method replaces the initial problem in Eq. (23) by a sequence of regularized problems, so that, at the s-th iteration, we solve the dual regularized problem

$$\begin{array}{lll} &&\mbox{maximize} \quad \Psi_{s} (p) \nonumber\\ &&\mbox{subject to} \ p \in \mathbb{R}^{n}, \end{array}$$
(27)

where

$$\begin{array}{lll}\Psi_{s} (p) &=& \min \limits_{ (x, y, f) \in X\times Y\times F} \left\{ \sum \limits_{k=1}^{n} \left[ \sum \limits_{i \in I_{k}} \left(\mu_{i} (x_{i})+0.5\lambda _{s}\left(x_{i}-x_{i}^{s-1}\right)^{2}\right) \right. \right.\nonumber\\ &&\qquad\quad\;\;{\kern7pc} \left. - \sum \limits_{j \in J_{k}} \left( \eta _{j} (y_{j})-0.5\lambda_{s}\left(y_{j}-y_{j}^{s-1}\right)^{2}\right) \right]\nonumber\\ &&\quad\qquad{\kern5.1pc}+\sum \limits_{a \in \mathcal{A}} \left[ \sigma _{a} (f_{a})+0.5\lambda _{s}\left(f_{a}-f_{a}^{s-1}\right)^{2} \right] \nonumber\\ &&\quad\qquad{\kern5.1pc}\left. +\sum \limits_{k=1}^{n} p_{k} \left[ \left( \sum \limits_{a \in \mathcal{A}_{k}^{-}} f_{a}-\sum \limits_{a \in \mathcal{A}_{k}^{+}} f_{a} \right) - \left( \sum \limits_{i \in I_{k}} x_{i}-\sum \limits_{j \in J_{k}} y_{j} \right) \right] \right\} \nonumber\\ &=& \sum \limits_{k=1}^{n}\left[ \sum \limits_{i \in I_{k}} \min \limits_{x_{i} \in [0, \alpha _{i}]} \left(\mu _{i}(x_{i})+0.5\lambda_{s}\left(x_{i}-x_{i}^{s-1}\right)^{2}-p_{k}x_{i}\right)\right. \nonumber\\ &&\;\;{\kern1.9pc} \left. -\sum \limits_{j \in J_{k}} \max \limits_{y_{j} \in [0, \beta_{j}]} \left(\eta _{j}(y_{j})-0.5\lambda _{s}\left(y_{j}-y_{j}^{s-1}\right)^{2}-p_{k}y_{j}\right) \right]\nonumber\\ &&+\sum \limits_{a=(k, l) \in \mathcal{A}} \min \limits_{f_{a} \in [\gamma'_{a}, \gamma ''_{a}]} \left( \sigma _{a}(f_{a})+0.5\lambda_{s} \left(f_{a}-f_{a}^{s-1}\right)^{2}+ (p_{k}-p_{l})f_{a} \right). \end{array}$$
(28)

Again, the inner problem in Eq. (28) decomposes into simple one dimensional problems, but the function Ψ s in Eq. (21) is now differentiable and concave if (A1) and (A2) are fulfilled.

In fact, if (x s(p), y s(p), f s(p)) denotes the solution triplet of the inner problem in Eq. (28), then

$$\displaystyle \frac{\partial \Psi _{s}(p)}{\partial p_{k}} = \left( {\sum \limits_{a \in \mathcal{A}_{k}^{-}} f_{a}^{s}(p)- \sum \limits_{a \in \mathcal{A}_{k}^{+}} f_{a}^{s}(p) } \right) -\left( {\sum \limits_{i \in I_{k}} x_{i}^{s}(p)-\sum \limits_{j \in J_{k}} y_{j}^{s}(p) } \right)$$

for k = 1, ..., n. Since Eq. (27) is an unconstrained differentiable maximization problem, we can apply one of the conjugate gradient methods (see e.g. Polyak 1983) for faster convergence. Next, in the case where all the functions are affine, the proximal point method above finds a solution in a finite number of iterations; see Polyak and Tretyakov (1974), Bertsekas (1975). At the same time, we observe that this combined proximal-dual approach includes an additional iteration level, requires a careful selection of the regularization parameter λ s and accuracies of solving the problems in Eqs. (27), (28) and of the linesearch procedure in the conjugate gradient method.

6 Alternating direction method

The idea of the alternating direction method consists in combining the Douglas–Rachford splitting method, which was proposed for systems of linear equations (Douglas and Rachford 1956) and further extended to inclusions (Lions and Mercier 1979), and the augmented Lagrangian method for constrained optimization problems; see Gabay and Mercier (1976), Eckstein and Bertsekas (1992). Being applied to the inclusion

$$0 \in P(x)+Q(x),$$
(29)

where P and Q are maximal monotone operators, the Douglas–Rachford splitting method generates an iteration sequence { x k } in conformity with the rule

$$x^{k+1}=J^{\lambda}_{P} \circ \left(2J^{\lambda }_{Q}-I\right)x^{k}+\left(I-J^{\lambda }_{Q}\right)x^{k},$$
(30)

where I is the identity map, \(J^{\lambda }_{P}=(I+\lambda P)^{-1}\) is the resolvent operator, λ > 0 is an iteration parameter. If Eq. (29) is solvable, then iterations (Eq. 30) converge to a solution of Eq. (29) with any positive λ; see Lions and Mercier (1979), Theorem 1. The alternating direction method represents an adjustment of the above splitting method for special structured problems. Namely, being applied to the optimization problem

$$\begin{array}{lll} &&\mbox{minimize} \quad f_{1}(x)+f_{2}(y) \nonumber\\ &&\mbox{subject to} \ Ax-By=0, x \in X, y \in Y; \end{array}$$
(31)

where f 1 and f 2 are convex functions, A and B are some matrices, X and Y are convex and closed sets, this method is written as follows:

$$\left\{ \begin{array}{l} \displaystyle x^{k+1}=\mbox{argmin}_{x \in X} \left\{ f_{1}(x)+ \left\langle z^{k}, Ax \right\rangle +\frac{r}{2} \left\|Ax-By^{k}\right\|^{2} \right\} , \\[10pt] \displaystyle y^{k+1}=\mbox{argmin}_{y \in Y} \left\{ f_{2}(y)- \left\langle z^{k}, By \right\rangle +\frac{r}{2} \left\|Ax^{k+1}-By\right\|^{2} \right\} , \\[10pt] z^{k+1}=z^{k}+r \left[ Ax^{k+1}-By^{k+1} \right]; \end{array} \right.$$
(32)

where z is the vector of dual variables (multipliers) and r > 0 is the iteration parameter. If we write the augmented Lagrangian for the problem of Eq. (31):

$$M(x, y, z)=f_{1}(x)+f_{2}(y)+ \langle z, Ax-By \rangle +\frac{r}{2} \|Ax-By\|^{2},$$
(33)

then Eq. (32) corresponds to a modified multiplier method, where the first two relations define the (block) Gauss–Seidel iteration with respect to primal variables (x, y), whereas the third relation is the standard multiplier update rule. However, the penalty term in Eq. (33) again destroys the decomposable structure of the problem and this fact leads to certain difficulties in implementation of iterations in Eq. (32). In Eckstein and Fukushima (1994), it was proposed to enhance properties of the method by somewhat enlarging its dimensionality and splitting its constraints. Following this approach, we intend to propose an alternating direction method for the spatial auction market problem of form Eq. (23). To this end, we rewrite Eq. (23) briefly as follows:

$$\begin{array}{lll}&&\mbox{minimize} \quad \varphi (z) \nonumber\\ &&\mbox{subject to} \ Az=0, z \in Z; \end{array}$$
(34)

where z = (x, y, f), Z = X × Y × F, the matrix A has n rows and N columns, where N is the dimensionality of z. Set

$$w=\left(\tilde x, \tilde y, \tilde f\right) \quad \mbox{and} \quad q=\left(\bar x, \bar y, \bar f\right)$$

and write the equivalent representation of Eq. (34):

$$\begin{array}{lll} &&\mbox{minimize} \quad f_{1}(Aw)+f_{2}(z) \nonumber\\ &&\mbox{subject to} \ z=w; \end{array}$$
(35)

where

$$f_{1}(u)= \left\{ \begin{array}{ll} 0 \quad & \mbox{if} \quad u=0 \in \mathbb{R}^{n}, \\ +\infty \quad & \mbox{otherwise};\\ \end{array} \right.$$

and

$$f_{2}(z)= \left\{ \begin{array}{ll} \varphi (z) \quad & \mbox{if} \quad z \in Z, \\ +\infty \quad & \mbox{otherwise}.\\ \end{array} \right.$$

The method of Eq. (32) applied to the problem of Eq. (35) can be defined as follows. Starting from the initial point z 0 = (x 0, y 0, f 0) ∈ Z, construct sequences {z s}, {w s}, and {q s} in conformity with the rules:

$$\left\{ \begin{array}{l} \displaystyle w^{s+1}=\mbox{argmin}_{w \in \mathbb{R}^{N}} \left\{ f_{1}(Aw)+ \left\langle q^{s}, w \right\rangle + \frac{r}{2} \left\|w-z^{s}\right\|^{2} \right\} , \\[12pt] \displaystyle z^{s+1}=\mbox{argmin}_{z \in \mathbb{R}^{N}} \left\{ f_{2}(z)- \left\langle q^{s}, z \right\rangle +\frac{r}{2} \left\|w^{s+1}-z\right\|^{2} \right\} , \\[10pt] q^{s+1}=q^{s}+r\left(w^{s+1}-z^{s+1}\right); \end{array} \right.$$
(36)

with r > 0.

Clearly, updating q does not cause any difficulties. We now consider updating w and z in Eq. (36) in more detail.

First of all we note that the first problem in Eq. (36) is equivalent to the following:

$$\begin{array}{lll} &&\displaystyle \mbox{minimize} \quad \left\langle q^{s}, w \right\rangle + \frac{r}{2} \left\|w-z^{s}\right\|^{2} \nonumber\\ &&\displaystyle \mbox{subject to} \ Aw=0; \end{array}$$
(37)

whose solution can be found by the explicit formulas:

$$w^{s+1}=z^{s}+r^{-1}\left(A^{T}\lambda -q^{s}\right),$$

where

$$\lambda =\left(AA^{T}\right)^{-1}A\left(q^{s}-rz^{s}\right).$$

Note that AA T is an n × n matrix, which can be made non-degenerate by adding some artificial variables. For this reason, the problem of Eq. (37) can be resolvable rather easily.

In turn, the second problem in Eq. (36) is rewritten as follows:

$$\begin{array}{lll} &&\displaystyle \mbox{minimize} \quad \sum \limits_{k=1}^{n} \left[ \sum \limits_{i \in I_{k}} \mu _{i} (x_{i})- \sum \limits_{j \in J_{k}}\eta _{j} (y_{j}) \right] +\sum \limits_{a \in \mathcal{A}} \sigma _{a} (f_{a}) \\ &&\quad\;\;\;{\kern50pt} \displaystyle -\langle q^{s}, z \rangle + \displaystyle{\frac{r}{2}} \left\|w^{s+1}-z\right\|^{2}\\ &&\displaystyle \mbox{subject to} \ z \in Z. \end{array}$$

Clearly, this is a completely separable problem, which is equivalent to the series of the following one-dimensional problems:

$$\begin{array}{lll} && \displaystyle \mbox{minimize} \quad \mu _{i}(x_{i})-\bar x^{s}_{i}x_{i}+0.5r\left(x_{i}-\tilde x^{s+1}_{i}\right)^{2} \\[2pt] && \mbox{subject to} \ 0 \leq x_{i} \leq \alpha _{i} \quad \mbox{for} \ i \in I_{k}, k=1,\dots, n; \\[2pt] &&\displaystyle \mbox{minimize} \quad -\eta _{j}(y_{j})-\bar y^{s}_{j}y_{j}+0.5r\left(y_{j}-\tilde y^{s+1}_{j}\right)^{2} \\[2pt] && \mbox{subject to} \ 0 \leq y_{j} \leq \beta _{j} \quad \mbox{for} \ j \in J_{k}, k=1, \dots, n; \\[2pt] &&\displaystyle \mbox{minimize} \quad \sigma _{a}(f_{a})-\bar f^{s}_{a}f_{a}+0.5r\left(f_{a}-\tilde f^{s+1}_{a}\right)^{2}\\[2pt] && \mbox{subject to} \ \gamma'_{a} \leq f_{a} \leq \gamma ''_{a} \quad \mbox{for} \ a \in \mathcal{A}. \end{array}$$

Under assumptions (A1) and (A2) these problems have unique solutions which can be found very easily.

After obtaining a solution of the problem in Eq. (23), the auction clearing prices are found from Eqs. (6), (7), and (18).

7 Computational results

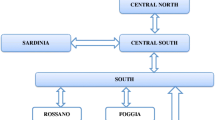
In order to check the performance of the above methods we implemented them in Delphi with double precision arithmetic and carried out several series of computational experiments. More precisely, we select five examples of spatial auction market problems with different topology structures. Since their data files are very bulky, we only outline here their basic parameters. The dimensionalities are given in Table 1. The data in Examples 1 and 2 were taken from real electricity markets. The topologies of the graphs in Examples 1–3 are trees, whereas the graphs in Examples 4 and 5 involve cycles. In all the examples, the prices were fixed and all the links were supposed to be costless. For instance, the graph of Example 5 is given in Fig. 1. The numbers of participants in this example were distributed as follows:

  1. (i)

    traders (6, 6, 5, 5, 6, 4, 5, 4, 4, 5, 6, 6, 5, 5, 6, 4, 5, 4, 4, 5),

  2. (ii)

    buyers (6, 6, 5, 6, 6, 6, 3, 4, 4, 3, 6, 6, 5, 6, 6, 6, 3, 4, 4, 3).

The fixed prices were taken in the segment [40, 80], all the minimal offer/bid bounds were set to be zero, the maximal offer/bid bounds were taken in the segment [100, 1,500].

Table 1 n is the number of markets (nodes), m is the total number of traders, l is the total number of buyers, N is the total number of edges
Full size table
Fig. 1
figure 1

Example 5: topology with edge capacities

Full size image

In all the cases, we took the zero starting point. Since a comparatively low accuracy is sufficient for application, we utilized the accuracy values δ = 0.1 and δ = 0.01 for both the methods.

First we tested the combined proximal point and dual conjugate gradient method (PCG for short), described in Section 5. We chose the usual Polyak–Polak–Ribière variant of the conjugate gradient method; see e.g. Polyak (1983). We fixed the stepsize λ s  ≡ 0.2 and chose the norm of violations of conditions Eqs. (20) and (21) as accuracy measure. The results are given in Table 2.

Table 2 itprox is the number of proximal iterations, iter is the total number of the conjugate gradient method iterations, – indicates that the total number of iterations exceeds the maximal value = 1,500
Full size table

Next we tested the alternating direction method (ADM for short) described in Section 6. Here we chose the value

$$\max \left\{ { \left\|w^{s+1}-w^{s}\right\|, \left\|z^{s+1}-z^{s}\right\|, \left\|w^{s+1}-z^{s+1}\right\|} \right\}$$

as accuracy measure. The results are given in Table 3.

Table 3 iter is the total number of iterations
Full size table

In all the cases, the processor solution time did not exceed 1 s. In general, the results of both the methods were satisfactory for application. They gave us the optimal offer/bid values for each market as well as the optimal commodity flows along arcs. Besides, (PCG) yielded directly all the auction clearing prices. As to (ADM), they were obtained easily from Eqs. (6), (7), and (18), as indicated in the end of Section 6. Also, the presence of cycles in the system topology did not cause any difficulties. At the same time, we noticed that (PCG) required more careful tuning of parameters such as the stepsize and the accuracies of linesearches and solutions of the inner problem in Eq. (27), even for the same test problem with different values of δ. Managing (ADM) appeared to be simpler.

8 Conclusions

In this paper, we suggested a new model of a system of spatially distributed auction markets joined by transmission lines with joint capacity and balance constraints and with rather complex behavior of traders and buyers within each auction market. Namely, we showed that this model was formulated as a simple variational inequality problem. Besides, we proposed several equivalent formulations of the above problem as non-smooth convex optimization or convex–concave saddle point ones. This enables us to apply the well-developed tools for investigation and solution of spatial auction market problems. In particular, we proposed two iterative solution methods, namely, the combined dual-proximal and modified alternating direction ones, which preserved the decomposable structure of the problem and can be used in the case of its possible large dimensionality. They gave us the optimal commodity flows and offer/bid values for each market as well as all the auction clearing prices. The computational results confirmed rather rapid convergence and applicability of both the methods.

Of course, this approach admits further extensions and modifications. The author hopes to consider them in some forthcoming works.