A Relaxation Approach for Estimating Origin–Destination Trip Tables

Abstract

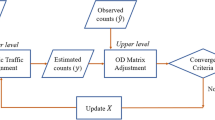
The problem of estimating origin-destination travel demands from partial observations of traffic conditions has often been formulated as a network design problem (NDP) with a bi-level structure. The upper level problem in such a formulation minimizes a distance metric between measured and estimated traffic conditions, and the lower level enforces user-equilibrium traffic conditions in the network. Since bi-level problems are usually challenging to solve numerically, especially for large-scale networks, we proposed, in an earlier effort (Nie et al., Transp Res, 39B:497–518, 2005), a decoupling scheme that transforms the O–D estimation problem into a single-level optimization problem. In this paper, a novel formulation is proposed to relax the user equilibrium conditions while taking users’ route choice behavior into account. This relaxation approach allows the development of efficient solution procedures that can handle large-scale problems, and makes the integration of other inputs, such as path travel times and historical O–Ds rather straightforward. An algorithm based on column generation is devised to solve the relaxed formulation and its convergence is proved. Using a benchmark example, we compare the estimation results obtained from bi-level, decoupled and relaxed formulations, and conduct various sensitivity analysis. A large example is also provided to illustrate the efficiency of the relaxation method.

1 Introduction

Knowing where and when people start their trips and where they are heading to is one of the fundamental issues in transportation research. The success of building and operating an efficient urban transportation system (urban planning, travel forecasting and real-time traffic control/management, to name a few) relies on a sound understanding of the spatial and temporal patterns of travel demands. Due to the difficulty of directly measuring O–D travel demands, estimating them from limited observations of traffic conditions on the road network has been attempted by numerous researchers in the past three decades. This paper deals with the estimation of static O–D demands, which concerns trips made over a relatively long time period within which the traffic condition is assumed to be in a steady state.

Consider a traffic network represented as a graph G(N, A) where N and A are the sets of nodes and links, respectively. Let R be the set of origins and S be the set of destinations. Underlying the O-D estimation problem is the following measurement equation:

$$\Delta q = \bar x$$

(1)

where

q :

is an o × 1 vector of travel demands to be estimated;

$\bar x$ :

is an m × 1 vector of measured traffic counts

Δ :

is an m × o assignment matrix whose entry represents the proportion of trips between a given O–D pair using a given link.

The problem of static O–D estimation (SODE), in its simplest form, is to solve the system 1 for q according to a given rule for determining the assignment matrix Δ. Generally, Eq. 1 is underdetermined and thus does not yield a unique solution. To resolve the problem, additional information should be supplied which includes but is not limited to:

• A partial or complete historical O–D table, which is usually established from existing survey data.

• Supplemented flow counts, including those made on cordon (or screen) lines and turning counts at intersections.

• Vehicle identification data that provides link-to-link traffic counts or fractions.

• Path travel times obtained from probe vehicles.

In this research, both historical O–D information and observed paths travel times are considered as inputs in addition to traffic counts. We do not consider the other two data sources because they can be treated in a similar fashion as traffic counts.

When congestion effects are unimportant, the assignment matrix Δ may be exogenously specified. This is known as the proportional-assignment approach (cf. Chapter 12, Ortuzar and Willumsen 2001). This category includes gravity models (e.g., Low 1972), information minimizing (Van Zuylen and Willumsen 1980), entropy maximizing (Willumsen 1981) and generalized least squares (Cascetta 1984). The proportional-assignment methods assume that users’ route choices are given and independent of the estimation process. This assumption causes an inconsistency issue in congested networks, because the predetermined assignment matrix may not be replicated when the estimated O–D table is assigned onto the network according to some route choice assumptions. A conventional way to resolve this inconsistency is to introduce a traffic assignment component into the estimation problem (see, e.g., Nguyen 1977; Gur et al. 1980; LeBlanc and Farhangian 1982; Nguyen 1984; Fisk 1984, 1988; Yang et al. 1992; Yang 1995).

A SODE problem combined with traffic assignment falls into a general class of network design problems (NDP) involving the interaction of two groups of decision makers: network designers (known collectively as the leader) and network users (known collectively as the follower). For the SODE problem, solving q from Eq. 1 is interpreted as the leader problem whereas the follower problem is to determine Δ from an assignment model based on the decision of the leader problem (i.e., the estimated O–D table). How Δ is determined depends on the assumptions about users’ route choice behavior. The most embraced behavioral assumption, known as Wardrop’s first principle (Wardrop 1952), states that every user chooses the least cost path(s) which produces the user-equilibrium (UE) flow pattern.

Due to the embedded UE conditions, this class of network design problems is usually difficult to tackle from both analytical and computational perspectives. Various heuristic algorithms have been proposed to produce acceptable solutions for real-size problems. Most existing algorithms fall into one of four categories:

• Iterative optimization-assignment algorithms (Yang et al. 1992; Allsop 1974; Gartner et al 1980).

• Sensitivity-based algorithms (Yang 1995).

• Global search algorithms (Abdulaal and LeBlanc 1979; Friesz et al. 1992, 1993).

• Algorithms based on mathematical program with equilibrium constraints (e.g., Tan et al. 1979; Lim 2002)

Most of the aforementioned NDP algorithms share two major limitations: they may not attain global optimums and they have to solve the UE traffic assignment problem iteratively. The second shortcoming substantially limits the practical value of this approach where traffic assignment could not be efficiently solved, such as in the dynamic case in which the lack of differentiability makes the solution notoriously difficult. On the other hand, observed traffic flow patterns may not strictly satisfy UE conditions in reality. Above all, the behavioral assumptions that yield UE are too ideal to be realistic. What is more, the performance of a real traffic system is influenced by many stochastic factors that are not modeled or not adequately modeled by the UE models. This suggests that imposing strict UE conditions in the SODE problem might be unnecessary and even inappropriate in practice.

Motivated by the above observations, this paper formulates SODE as a one-level problem without strictly enforcing the UE conditions. This formulation bypasses the bi-level structure and its associated analytical and numerical difficulties, and is amenable to more powerful solution methods. Path flows, rather than O–D demands themselves, are employed as solution variables because the mapping from path flows to link counts does not depend on a traffic assignment procedure. The use of path flows as solution variables for the static O–D estimation problem was first seen in Sherali et al. (1994). Obviously, O−D demands can be easily derived from path flows.

Using path flows, the system 1 can be rewritten as:

$${\mathbf{Pf}} = \bar x$$

(2)

where

f :

is a vector of used path flows; and

P :

is a path–link incidence matrix representing the assignment relationship.

In an earlier work, Nie et al. (2005) proposed a decoupled formulation based on Eq. 2 in which paths used at UE (hence P) are determined exogenously using a K-shortest path ranking procedure. The approach of Nie et al. (2005) avoids the bi-level structure but requires all traffic counts to be available and travelers strictly adhere to the UE principle. This strong assumption is relaxed in this paper. The formulation to be proposed intends to identify a set of path flows that would replicate available observations as closely as possible when loaded onto the network. Users’ responses to traffic conditions are taken into account in the process of identifying the path set. Namely, whether or not a path is “selected” depends on its combined potential of improving the match of observations and satisfying users’ travel preferences.

In Section 2 the decoupled O–D estimation formulation is reviewed and a relaxed formulation without route choice is briefly discussed. Sections 3 and 4 present the relaxed formulation with route choice and its solution algorithms respectively. Numerical results are discussed in Section 5.

2 The decoupled formulation

Let us denote the vector of UE link flow volumes as x _e, the vector of observed traffic counts as $\overline x$ and the vector of estimated traffic counts as $\hat x$. A path flow pattern corresponding to x _e and its estimate are denoted as f _e and ${\hat f}$, respectively. Each f _e corresponds to a UE path set $K_e = \cup K_{rs}^e ,\forall r,s$, where $K_{rs}^e$ is a set of paths used at UE for the O−D pair rs.

Nie et al. (2005) showed that a best linear unbiased estimator for f _e can be obtained by solving the following decoupled problem 3, if (1) travellers adhere to the Wardrop’s first principle so that $\overline x$ is a measurement of UE link volumes x _{e ,} (2) traffic counts are available on all links and subject to no measurement errors, and (3) active constraints (f = 0) can be ignored.

$$\min 0.5\left( {{\mathbf{P}}_{\mathbf{e}} {\mathbf{f}} - \bar x} \right)^T {\mathbf{T}}^{ - 1} \left( {{\mathbf{P}}_{\mathbf{e}} {\mathbf{f}} - \bar x} \right) + 0.5\left( {{\mathbf{M}}_{\mathbf{e}} {\mathbf{f}} - \bar q} \right)^T {\mathbf{S}}^{ - 1} \left( {{\mathbf{M}}_{\mathbf{e}} {\mathbf{f}} - \bar q} \right){\text{ subject to }}{\mathbf{f}} \geqslant 0$$

(3)

where

P _e :

is a path-link incidence matrix corresponding to K _e ;

M _e :

is the OD-path incidence matrix corresponding to K _e ;

$\bar q$ :

is a vector of historical O–D demands;

T :

is the covariance matrix associated with ${\mathbf{\bar x}}$; and

S :

is the covariance matrix associated with $\bar q$.

This formulation, which determines P _e and M _e independently according to UE conditions from a K-shortest path ranking (KSPR) procedure, require that all links are measured and the measurements are without errors. While these assumptions allowed us to study the analytical properties of the formulated problem and answered interesting questions such as estimation efficiency and biases, they do seriously limit the practical value of the method since in reality neither can one measure at all road locations nor can one measure traffic flow with no errors. To relax these assumptions, we first put aside the equilibrium conditions by including all paths into the formulation. Then problem 3 is relaxed as follows:

$$\min \,0.5\left( {Pf - \bar x} \right)^T T^{ - 1} \left( {Pf - \bar x} \right) + 0.5\left( {Mf - \bar q} \right)^T S^{ - 1} \left( {Mf - \bar q} \right)\;{\text{subject}}\;{\text{to}}:f \geqslant 0$$

(4)

where f is a vector of flows on all simple (i.e., loop-free) paths, and P and M are corresponding path-link incidence and path-OD incidence matrices, respectively. Unlike Eq. 3, this problem includes flows on all paths as solution variables regardless whether the paths belong to K _e or not. As such, the violation of equilibrium constraints is expected because non-UE paths may receive positive flows during the estimation process. We have the following results (see Nie 2006 for proofs).

Theorem 1

An optimal solution to problem4provides a linear unbiased estimator for the UE path flowsf _e .

Theorem 2

The estimator given by problem4 is always equally or less efficient compared to that obtained from problem3.

3 The relaxed formulation with route choice

Theorem 2 indicates that the over-specification is the cause of the inefficiency of the estimator derived from the relaxed problem 4. Obviously, the more non-UE paths are included, the less efficient the estimator would be. In real networks where the number of non-UE paths is overwhelming, problem 4 may lead to fairly poor estimates. It is important, therefore, to discourage the use of non-UE paths so that the over-specification can be controlled to some extent. Since non-UE paths usually have higher costs than UE paths, a natural way of achieving this is to add a proper cost-related term into the objective function of Eq. 4. Physically, this term takes users’ route choice behavior (i.e., their preference for shorter paths) into account and thus prevents flows from dispersing over all paths.

Now the relaxed SODE problem 4 is reformulated as follows¹:

$$\min z\left( f \right) = 0.5w_x \left( {Pf - \bar x} \right)^2 + 0.5w_q \left( {Mf - \bar q} \right)^2 + \frac{1}{\theta }\sum\limits_a {\int_0^{P_a f} {\tau _a \left( w \right)dw} } $$

(5)

subject to

$${\mathbf{Pf}} = {\mathbf{x}},\,{\mathbf{P}} = \left[ {\begin{array}{*{20}r} \hfill {P_1 }\hfill \cdots \hfill {P_a }\hfill \cdots \hfill {P_n } \\ \end{array} } \right]^T $$

(6)

$${\mathbf{f}} \geqslant 0$$

(7)

where

τ _a (.):

is a convex and strictly increasing function of link volume x _a; and

w_x>0 and w_q>0:

are relative confidence scalars associated with traffic counts and the historical O–D demands, respectively.

The third term in the objective function is a scaled Beckmann’s objective function used in the UE traffic assignment problem (Beckmann et al. 1956). θ is a positive scalar called dispersion parameter. The added Beckmann term in the objective function penalizes traffic flow on non-UE paths, which helps reduce the loss of estimation efficiency caused by non-UE paths. Note that the resulting flow pattern is less “dispersed” for smaller θ because more flows are concentrated on low-cost paths. In this sense θ is similar to the dispersion parameter used in the logit traffic assignment model (Fisk 1980), from which its name is borrowed. The scalars w _x and w _q reflect our confidence in the accuracy of the measurements and can be easily set according to our knowledge of the accuracy of the corresponding measurements. Determining a proper value for the dispersion parameter θ, howeve, is a tricky problem. With the Beckmann term, flows are discouraged from not only paths with higher costs, but indeed any path with a positive cost. Obviously, if θ goes to zero, the relaxed estimation problem will produce f = 0 as the optimum. Thus, θ should not be set too small in order to avoid an underestimation. On the other hand, a very large θ is not desirable as well. As θ gets larger, the relative preference for low-cost paths diminishes, and the efficiency of the resulting estimator may degenerate because of the inclusion of more non-UE paths. It is difficult to establish a theoretical bound for a “proper” θ because it depends on a problem’s specific setting. A few heuristics for selecting a proper θ are suggested in Section 5.1.2. The objective function z(f) in Eq. 5 is convex with respect to f because it is the sum of three convex functions (note that the two quadratic terms of z(f) are surely convex and the Beckmann term is also convex; see Sheffi 1985). Since it is defined on a nonnegative orthant, the above relaxed SODE problem is a convex program, which implies that any local minimum would be a global minimum. However, the optimal path solution of problems 5, 6, and 7 is not unique in general.

We now turn to the optimality condition of the relaxed SODE problem. For any given f ≥ 0, $\bar x > 0$ and $\bar q > 0$, the deviation on path k ∈ K _rs is defined as

$$d_{rs}^k = w_x \mathop \sum \limits_a \delta _{rs}^{ak} dx_a + w_q dq_{rs} $$

(8)

where

$$dx_a = \left\{ {\begin{array}{*{20}c} {\bar x_a - \Sigma _r \Sigma _s \Sigma _k \delta _{rs}^{ak} f_{rs}^k }{a \in A_o } \\ {\text{0}}{{\text{otherwise}}} \\ \end{array} } \right.$$

(9)

$$dq_{rs} = \left\{ {\begin{array}{*{20}c} {\bar q_{rs} - \Sigma _k f_{rs}^k }{{\text{if historical}}\;{\text{demand}}\;{\text{is}}\;{\text{given}}\;{\text{for}}\;{\text{the}}\;{\text{O - D}}\;{\text{pair}}\;{rs}} \\ 0{{\text{otherwise}}} \\ \end{array} } \right.;$$

(10)

$$ \delta ^{{a,\,k}}_{{rs}} = \left\{ {\begin{array}{*{20}l} {1 \hfill} & {{{\text{if path }}k{\text{ connecting O - D pair rs uses link }}a} \hfill} \\ {0 \hfill} & {{{\text{otherwise}}} \hfill} \\ \end{array} } \right.; $$

(11)

$\overline x _a$ :

is the traffic count on link a;

$\overline q _{rs}$ :

is the historical demand for O–D pair rs;

$f_{rs}^k$ :

is the flow on path k ∈ K _rs ; and

A _o :

is a set of links on which traffic counts are available.

The path deviations function ${\mathbf{d}}\left( \cdot \right) = \left[ { \ldots ,\,d_{rs}^k , \ldots } \right]^T :\;R_ + ^{\left| K \right|} \mapsto R^{\left| K \right|}$ is a well-defined mapping.

Proposition 1

The path deviation function ${\mathbf{d}}\left( \cdot \right)$ is linear, continuous and monotone.

Proof

Note that ${\mathbf{d}}\left( \cdot \right)$ can be written in matrix form as

$${\mathbf{d}}\left( {\mathbf{f}} \right) = {\mathbf{P}}^T w_x \left( {\overline {\mathbf{x}} - {\mathbf{Pf}}} \right) + {\mathbf{M}}^T w_q \left( {\overline {\mathbf{q}} - {\mathbf{Mf}}} \right)$$

(12)

The RHS of Eq. 12 is clearly linear in f. Continuity and monotonicity then follow from linearity.

The cost on path k ∈ K _rs is denoted as $c_{rs}^k = \sum {_a \delta _{rs}^k \tau _a \left( {P_a f} \right)}$ (P _a is defined in Eq. 6), and we define ${\mathbf{c}}\left( \cdot \right) = \left[ { \ldots ,\,c_{rs}^k , \ldots } \right]^T :\;\;R_ + ^{\left| K \right|} \mapsto R^{\left| K \right|}$ as the path cost function.

The following theorem states the optimality conditions of the relaxed SODE problem.

Theorem 3

${\mathbf{f}} \in R_ + ^{\left| K \right|}$is an optimal solution to problems5, 6, and7 if and only if$\forall r \in R,\,s \in S,\,k \in K$

$$ \left\{ {\begin{array}{*{20}l} {{f^{k}_{{rs}} {\left( {c^{k}_{{rs}} - \theta d^{k}_{{rs}} } \right)} = 0} \hfill} \\ {{c^{k}_{{rs}} \geqslant \theta d^{k}_{{rs}} ,\,f^{k}_{{rs}} \geqslant 0} \hfill} \\ \end{array} } \right. $$

(13)

Proof

Applying the KKT conditions, f solves the nonlinear optimization programs 5, 6, and 7 if and only if

$$\begin{array}{*{20}r}\hfill {\left\langle {\nabla z\left( {\text{f}} \right),{\text{f}}} \right\rangle = 0} \\\hfill {\nabla z\left( {\text{f}} \right) \geqslant 0} \\\hfill {{\text{f}} \geqslant {\text{0}}} \\\end{array} $$

Using Eq. 12, we have

$$\nabla z_k \left( f \right) = w_x P^T \left( {Pf - \overline x } \right) + w_q M^T \left( {Mf - \overline q } \right) + \frac{1}{{\text{ $ \theta $ }}}c\left( f \right) = \frac{1}{{\text{ $ \theta $ }}}c\left( f \right) - d\left( f \right)$$

Replacing $\nabla z\left( {\mathbf{f}} \right)$ in the above KKT conditions with this expression, and noting that the dot product of $\nabla z\left( {\mathbf{f}} \right)$ and f is zero $\Leftrightarrow \nabla z_k \left( {\mathbf{f}} \right)f^k = 0,\forall k$, we get the optimality conditions.

Remark 1

A path flow pattern that perfectly replicates all available observations (i.e., d(f) = 0) is not an optimal solution since path deviations must be positive to equilibrate path costs at optimum. The existence of path deviation provides a route choice mechanism for distinguishing paths of different costs. From the optimality conditions we see that to equilibrate a path of higher cost requires a larger deviation to be imposed than for paths of lower costs. Therefore, assigning more flows onto the lower cost paths helps reduce the overall deviations (hence better objective function values). Certainly individual paths with higher costs may be equilibrated without necessarily increasing the total system deviation. Nonetheless, the above mechanism works collectively to impose route differentiation.

Remark 2

Paths bid for flows against each other based on their costs, and such a competition is not confined within each O–D pair (as in traffic assignment problems). As a consequence, O–D pairs with shorter average travel times may be assigned more flows than those with longer average travel times. This is somewhat similar to the gravity trip distribution model that always assigns more flows to O–D pairs having smaller friction factors. If such an effect is considered a bias, historical O–D information may help reduce the preference for O–D pairs with smaller travel times (costs) between them, should the historical O–D trip table contain reliable information on the spatial distribution of traffic demand.

Remark 3

When θ is so small that the maximum possible deviation is not large enough to equilibrate the minimum possible path cost, the estimated path flows will approach nil. On the other hand, a large θ favors a solution that provides small total deviations to satisfy the equilibrium conditions. This often means using more paths and thus increasing the chances of having those high-cost paths in the solution.

The relaxed SODE problem can be further extended to incorporate travel times on certain paths measured by probe vehicles. Such information is useful because traffic counts often fail to reflect the demand level in over-saturated situations (note that loop detectors cannot measure flow beyond capacity).

Let $\overline K$ denote the set of paths for which average travel costs (times) are measured, and $\overline {\mathbf{c}}$ a vector of measured travel costs. To account for the cost observations, another quadratic term is added into the objective function as follows:

$$\min z\left( f \right) = 0.5w_x \left( {pf - \bar x} \right)^2 + 0.5w_q \left( {Mf - \bar q} \right)^2 + 0.5w_p s_p \sum\limits_{k_ \in \bar K} {\left[ {c_{rs}^k \left( f \right) - \bar c_{rs}^k } \right]} ^2 + \frac{1}{\theta }\sum\limits_a {\int_0^{P_a f} {\tau _a \left( w \right)dw} } $$

(14)

subject to Eqs. 6 and 7.

Here w _p  > 0 is the relative confidence parameter associated with path cost observations, and s _p is a positive scalar to balance the weight of cost and flow deviations.

To derive the optimality condition, we need to obtain the gradient of the path cost term. Let $z_p \left( {\mathbf{f}} \right) = w_p s_p \sum {_{k \in \bar K} } \left[ {c_{rs}^k \left( {\mathbf{f}} \right) - \bar c_{rs}^k } \right]^2$, we then have

$$\frac{{\partial z_p \left( f \right)}}{{\partial f_{rs}^{k\prime } }} = w_p s_p \sum\limits_{k \in K} {\frac{{\partial c_{rs}^k \left( f \right)}}{{\partial f_{rs}^{k\prime } }}\left[ {c_{rs}^k \left( f \right) - \overline c _{rs}^k } \right],\forall k\prime \in \overline K } $$

where

$$\frac{{\partial c_{rs}^k \left( f \right)}}{{\partial f_{rs}^{k\prime } }} = \sum\limits_a {\delta _{rs}^{ka} \delta _{rs}^{k\prime a} \frac{{d\tau _a \left( {x_a = P_a f} \right)}}{{dx_a }}} $$

To be consistent with our earlier formulations we now redefine the path deviation $d_{rs}^k$ as follows:

$$d_{rs}^k = w_x \mathop \sum \limits_a \delta _{rs}^{ak} dx_a + w_q dq_{rs} + w_p s_p dc_{rs}^k $$

(15)

where

$$dc_{rs}^k = \mathop \sum \limits_{k \in \overline K } \frac{{\partial c_{rs}^k \left( {\mathbf{f}} \right)}}{{\partial f_{rs}^{k\prime } }}\left[ {\overline c _{rs}^k - c_{rs}^k \left( {\mathbf{f}} \right)} \right]$$

The matrix form of the path deviation function in Eq. 12 becomes:

$${\mathbf{d}}\left( {\mathbf{f}} \right) = {\mathbf{P}}^T w_x \left( {\overline {\mathbf{x}} - {\mathbf{Pf}}} \right) + {\mathbf{M}}^T w_q \left( {\overline {\mathbf{q}} - {\mathbf{Mf}}} \right) + w_p s_p J_c \left( {\overline {\mathbf{c}} - {\mathbf{c}}} \right)$$

(16)

where J _c is the Jacobian matrix of c(f). Thus, the optimality conditions given in Theorem 3 still applies in this extended model provided that d(f) is defined by Eq. 16. We note that the use of the path deviation function provides a flexible framework to combine different observations together. The optimality condition is quite general and may be applied even when the estimation problem cannot be cast as a mathematical program (like in the dynamic case). However, z _p(f) is not necessarily a convex function with respect to f. Thus, obtaining a global optimum for this extended problem is difficult.

4 Solution algorithms

We shall first assume that a subset of paths has been selected to formulate the relaxed SODE problem, which is called a restricted master problem (RMP). Then a scheme is introduced in Section 4.2 to generate the collection of paths iteratively such that the original problem (i.e., the one containing all paths) is optimally solved.

4.1 Solve RMP

The restricted master problem of the relaxed SODE is defined on a nonnegative orthant. The class of algorithms based on the projected antigradient direction can take full advantage of such a simple constraint structure because projections can be performed very efficiently.

The gradient of the objective function with respect to $f_{rs}^k$ is given by

$$g_{rs}^k \equiv \frac{{\partial z\left( {\mathbf{f}} \right)}}{{\partial f_{rs}^k }} = \frac{1}{\theta }c_{rs}^k - d_{rs}^k $$

(17)

where $d_{rs}^k$ is defined in Eq. (15). The projected anti-gradient direction $\widetilde{\mathbf{g}} = \left[ { \ldots ,\,e_{rs}^k , \ldots } \right]$ is expressed by

$$\overline g = \prod _{R_n^ + } \left( { - g} \right),$$

where ${\mathbf{g}} = \left[ { \ldots ,\,g_{rs}^k , \ldots } \right]$. That is,

$$\tilde g_{rs}^k = \left\{ {\begin{array}{*{20}c} 0{{\text{if}}\;{\text{g}}_{rs}^k > 0\;{\text{and}}\,f_{{\text{rs}}}^{\text{k}} = 0} \\ { - g_{rs}^k }{{\text{otherwise}}} \\ \end{array} } \right.$$

(18)

$\widetilde{\mathbf{g}}$ itself provides a natural candidate for the descent search direction e. Another possible option for generating a search direction is to use the conjugate gradient, which updates the search direction at iteration i, eⁱ, by

$${\mathbf{e}}^i = \widetilde{\mathbf{g}}^i + \rho _i {\mathbf{e}}^{i - 1} $$

(19)

The scalar ρ _i is called a deflection parameter and may be computed by (Sherali and Park 2001)

$$\rho _i = \frac{{\left\| {\widetilde{\mathbf{g}}^i } \right\|^2 }}{{\left\| {\widetilde{\mathbf{g}}^{i - 1} } \right\|^2 }}$$

(20)

We proceed to derive the optimal step size λ along the search direction given by e. This equates to solving the following one-dimensional optimization problem

$$\mathop {\min }\limits_\lambda ^ z\left( {{\mathbf{f}} + \lambda {\mathbf{e}}} \right){\text{ subject to: }}{\mathbf{f}} \geqslant 0$$

(21)

The gradient of z(f + λ e) with respect to λ is

$$\frac{{\partial z\left( {{\mathbf{f}} + \lambda {\mathbf{e}}} \right)}}{{\partial \lambda }} = \left\langle {\frac{{\partial z\left( {{\mathbf{f}} + \lambda {\mathbf{e}}} \right)}}{{\partial \left( {{\mathbf{f}} + \lambda {\mathbf{e}}} \right)}},\,{\mathbf{e}}} \right\rangle = \left\langle {\frac{1}{\theta }{\mathbf{c}}\left( {{\mathbf{f}} + \lambda {\mathbf{e}}} \right) - {\mathbf{d}}\left( {{\mathbf{f}} + \lambda {\mathbf{e}}} \right),\,{\mathbf{e}}} \right\rangle $$

(22)

where ${\mathbf{d}}\left( \cdot \right)$ and ${\mathbf{c}}\left( \cdot \right)$ are the path deviation and cost functions defined before. Clearly, the optimal step size is the one such that

$$\frac{{\partial z\left( {{\mathbf{f}} + \lambda {\mathbf{e}}} \right)}}{{\partial \lambda }} = 0$$

In general, an iterative procedure is needed to solve for the step size. We adopt a bisection method (cf. Sheffi 1985).

We are now ready to summarize the projected antigradient (PAG) algorithm:

4.1.1 Algorithm PAG

• Step 0. Initialization: set i = 0, f ⁱ = 0, ρ _i  = 0.

• Step 1. Evaluate the projected antigradient $\widetilde{\mathbf{g}}$ using Eq. 18. If $\left\| {\widetilde{\mathbf{g}}} \right\|_2 \leqslant \varepsilon _1$, terminate the procedure; otherwise, update the search direction e ⁱ using Eq. 19. To use the conjugate gradient strategy, calculate ρ _i using Eq. 20.

• Step 2. Obtain an optimal step size from a line search. To use the conjugate gradient strategy, go to step 3 to update ρ; otherwise go to step 4.

• Step 3. If $\left| {\lambda - \lambda _{\max } } \right| < \varepsilon _2$ (i.e., the obtained step size equals the maximum allowed value), set ρ _i  = 0.

• Step 4. Compute the new solution ${\mathbf{f}}^{i + 1} = {\mathbf{f}}^i + \lambda {\mathbf{e}}^i$. If $\left\| {{\mathbf{f}}^{i + 1} - {\mathbf{f}}^i } \right\|_2 < \varepsilon _3$, terminate the procedure; otherwise, set $i = i + 1$, and go to step 1.

4.2 Column generation

This section shows how a column generation scheme can be adopted to iteratively build the restricted master problem (RMP). Assume that a restricted set of paths K ^r is given and the optimal solution f ^r is obtained by solving the corresponding RMP. We concern ourselves with the following question: among the paths currently excluded from K ^r, which one should be included to optimally solve the original problem? According to the optimality conditions, an unused path may be a candidate if it satisfies the following condition.

$$c_{rs}^k - \theta d_{rs}^k < 0$$

Intuitively, the above condition presents a violation to the optimality condition. To achieve as much improvement of the objective function as possible, the unused path which violates the optimality condition the most should be added into K ^r. In other words, we want to solve the following minimization problem in search of such paths.

$${\text{Find}}\;{\text{path}}\;k \in {K \mathord{\left/ {\vphantom {K {K^r }}} \right. \kern-\nulldelimiterspace} {K^r }},{\text{such}}\;{\text{that}}\;k = argmin\left\{ {c_{rs}^k \left( {f^r } \right) - \theta d_{rs}^k \left. {\left( {f^r } \right)} \right|c_{rs}^k \left( {f^r } \right) < \theta d_{rs}^k \left( {f^r } \right)} \right\}$$

This minimization problem can be solved using the following minimum-cost path algorithm (MCPA).

4.2.1 Algorithm MCPA

• Step 0. Set the general cost on each link a using

  $$\mu _a = \frac{1}{\theta }\tau _a - w_x dx_a $$

where τ _a is link travel time and dx _a is defined in Eq. 9.

• Step 1. Find the minimum cost path $k_{rs}^ *$ for each O–D pair rs using μ _a as arc weights. Denote the minimum cost as $\pi _{rs}^ *$.

• Step 2. Find the path $k_1^ * = {\mathbf{argmin}}\left\{ {\pi _{rs}^ * + \left. {w_q dq_{rs} } \right|\forall r,\,s} \right\}$, where dq _rs is defined in Eq. 10. Set σ ₁ as the minimum general cost associated with $k_1^ *$.

If observed path traversal times are not used

$${\text{If}}\,\sigma _1 < 0,\;{\text{return}}\;k_1^* ;\;{\text{otherwise}}\;{\text{return}}\;{\text{NULL}};$$

Otherwise, go to step 3.

• Step 3. Find $k_2^ * = {\mathbf{argmin}}\left\{ {\tfrac{1}{\theta }c_{rs}^k - \left. {d_{rs}^k } \right|k \in \overline K } \right\}$, where $d_{rs}^k$ is defined in Eq. 15. Set σ ₂ as the minimum general cost associated with $k_2^ *$.

If σ ₁ > σ ₂

$$if\;\sigma _2 < 0,\;{\text{return}}\quad {\text{;}}\;k_2^* \;{\text{otherwise}},\;{\text{return}}\;{\text{NULL}}{\text{.}}$$

Otherwise

$${\text{if }}\sigma _1 < 0,{\text{ return }};{\text{ }}k_1^* \;{\text{otherwise}},{\text{ return NULL}}.$$

Remark 4

If negative cycles do not exist, the shortest path tree problem can be solved in polynomial time. If there are negative cycles (which is very likely to occur in our problem since link weights can be negative), the shortest path problem is NP-complete and thus may not be solved efficiently. Sherali et al. (1994) devised an approximate method which transforms the shortest path problem into a minimum cost network flow problem with bounded link capacities. A simpler but coarser approximation is to force all negative link weights to zero in sep 2 to eliminate negative cycles. Another alternative is to avoid column generation by creating a subset of K-shortest paths before hand. For large-scale problems, the use of these heuristics might be justified.

Remark 5

The algorithm MCPA generates only one path (with the minimum general cost in all paths) during each iteration. This scheme is inefficient if the optimal path set contains a large number of paths. As an alternative, new paths can be generated for each O–D pair for each iteration. Note that when this strategy is employed, Step 3 in Algorithm MCPA can be ignored because $dq_{rs}$ is identical for the same O–D pair. The all-OD-at-a-time strategy is an approximation and has a mixed effect on the overall convergence of the column generation. On the one hand, it accelerates the construction of a near-optimal path set. On the other hand, however, the strategy may result in undesirable oscillations within the neighborhood of the optimum. Intuitively a better strategy would be to use the approximate method to get to a near-optimum quickly, and then switch to the exact method for fine tuning. The column generation algorithm for solving the relaxed SODE problem is summarized in the following.

4.2.2 Algorithm column generation

• Step 0. Initialization. Set i = 0 and the estimated O–D matrix ${\mathbf{q}}^i = \overline {\mathbf{q}}$. Initialize link flow vector x ⁱ according to

  $$x_a = \left\{ {\begin{array}{*{20}c} {\bar x_a }{a \in A_o } \\ 0{a \in {A \mathord{\left/ {\vphantom {A {A_o }}} \right. \kern-\nulldelimiterspace} {A_o }}} \\ \end{array} } \right.$$

If the historical O–D information q is available and of good quality, $x_a ,\,a \in {A \mathord{\left/ {\vphantom {A {A_o }}} \right. \kern-\nulldelimiterspace} {A_o }}$ may also be approximated by assigning q (e.g., based on user-equilibrium principle) onto the network.

• Step 1. Update path set. If i = 0, generate a shortest path for each O–D pair using as the weight on link a. This forms an initial restricted path set K ^r; otherwise, call Algorithm MCPA to get the minimum cost paths k*. If $k \ne {\text{NULL}}$,² update $K^r = K^r \cup k^ *$; otherwise, terminate the procedure and the current f ⁱ is the optimal solution. Set $i = i + 1$, go to step 2;

• Step 2. Call algorithm PAG to solve the restricted master problem for f ⁱ.

• Step 3. Update link volume $x_a^i$, link traversal time $\tau _a^i$ and estimated O–D table q ⁱ based on f ⁱ. Remove all paths whose flows equal to zero from K ^r. Go to step 1.

Theorem 4

Algorithm column generation converges to the optimal solution of the relaxed SODE problem.

Proof

When RMP is solved successfully (step 2), the optimality conditions are satisfied for all paths contained in K ^r. We only need to check unused paths. If for all unused paths we have $c_{rs}^k \geqslant \theta d_{rs}^k$, then the optimality condition 13 is completely satisfied. Whenever $c_{rs}^k < \theta d_{rs}^k$ is detected and so the corresponding path need to be included into K ^r, we claim that the improvement of the objective function is ensured. To see this, note that the entry of the gradient corresponding to the new path, $\tfrac{{\partial z}}{{\partial f_{rs}^k }} = c_{rs}^k - \theta d_{rs}^k$, is negative. Denote the current path vector as f ⁱ and the one with the newly generated path f ^{i  + 1}. The direction derivative along ${\mathbf{f}}^{i + 1} - {\mathbf{f}}^i = \left[ {0, \ldots ,\,f_{rs}^k ,\,0, \ldots } \right]^T$ is ${\left\langle {\nabla z{\left( {f^{i} } \right)},f^{{i + 1}} - f^{i} } \right\rangle } < 0$

That is, assigning a sufficiently small flow onto the new path always decreases the objective function. As the objective function is continuously improved when new paths are included, the convergence of the algorithm is ensured.

5 Numerical examples

To establish a benchmark for the various formulations and solution algorithms proposed in this paper, we first employ a small network studied in Yang (1995). A larger example is reported in Section 5.2. In all cases, the link performance function is the BPR function

$$\tau _a = \tau _a^0 \left[ {1 + \alpha \left( {\frac{{X_a }}{{C_a }}} \right)^\beta } \right]$$

where C _a is the capacity of link a and $\tau _a^0$ is its free flow travel time. $\alpha$ and $\beta$ are parameters taking values of 0.15 and 4 respectively in this study.

5.1 Yang’s network

The topology of the network and the synthesized “true” O–D demand table are given in Fig. 1. The capacity C _a and free flow travel time $\tau _a^0$ of each link can be found in Table 4 of Yang (1995). Let $A_o = \left\{ {1,\,3,\,9} \right\}$, and the “true” and “observed” traffic counts are

$$ {\left[ {\begin{array}{*{20}c} {{x^{e}_{1} }} \\ {{x^{e}_{3} }} \\ {{x^{e}_{9} }} \\ \end{array} } \right]} = {\left[ {\begin{array}{*{20}c} {{222.58}} \\ {{187.50}} \\ {{262.42}} \\ \end{array} } \right]},\,{\left[ {\begin{array}{*{20}c} {{\overline{x} _{1} }} \\ {{\overline{x} _{3} }} \\ {{\overline{x} _{9} }} \\ \end{array} } \right]} = {\left[ {\begin{array}{*{20}c} {{215}} \\ {{190}} \\ {{265}} \\ \end{array} } \right]} $$

Fig. 1

The example network and “true” O–D table

Note that the “true” traffic counts are obtained from a static UE traffic assignment and “observed” ones are generated by perturbing the “true” counts. For the purpose of demonstration, the following parameters are used:

$$w_x = 1.0,w_q = 1.0,w_p = 2.0,s_p = 192.86$$

In using these parameters, we set the same confidence level for traffic counts and historical O–D tables, and a higher confidence for path travel time observations (if they are available). The value of s _p is set such that the magnitude of the path cost term in the objective function is roughly in the same order as the other two terms.

5.1.1 Basic results

In this section, we provide preliminary testing results of the decoupled and the relaxed SODE problems. For comparison purposes, the result from the conventional bi-level model is also presented. Note that our implementation of the bi-level model employs path flows as solution variables. As a result, the formulation is slightly different than the one shown in Yang (1995). Particularly, ours takes the following form

$$\begin{aligned}& \quad {\text{The}}\;{\text{Leader}}\;{\text{Problem:minw}}_{\text{x}} \left( {Pf - \overline x } \right)^2 + w_q \left( {f - U^T \overline q } \right)^2 ,{\text{subject}}\;{\text{to:}}f \geqslant {\text{0}} \\& {\text{The}}\;{\text{Follower}}\;{\text{Problem:}}\left( {P,U} \right) = \Gamma \left( q \right),q = Mf \\ \end{aligned} $$

Here $\Gamma \left( \cdot \right)$ represents the UE assignment, and P and U are the path-link incidence matrix and path-OD usage matrix, respectively. U plays a similar role as the influence factor matrix in Yang (1995), i.e., carrying over the equilibrium path usage from the follower problem to the leader problem. Note that the dimension of U equals that of M ^T (M is the path-OD incidence matrix). An iterative optimization-assignment method is employed to solve this bi-level formulation.

The decoupled SODE problem is formulated as in Eq. 3 but the covariance matrices T and S are simplified as

$$T = w_x I,S = w_q I$$

where I is an identity matrix with proper dimensions. For the relaxed SODE problem solved in this subsection, the term associated with observed path costs is excluded. Moreover, the dispersion parameter θ is set as 0.05. Due to the small size of the problem, the relaxed SODE problem is solved by enumerating all paths. We shall compare different column generation strategies later.

The estimated O–D tables and corresponding path flows for two different historical O–D tables are reported in Tables 1 and 2. r _t in the tables denotes the root mean squared error (RMSE) of an estimated O–D table ${\hat q}$, i.e.,

$$r_t = \sqrt {\frac{{\Sigma _r \Sigma _s \left( {q_{rs} - \widehat{q_{rs} }} \right)^2 }}{o}} $$

(24)

Table 1 Estimated result: random historical O–D table

Table 2 Estimated result: down-scaled historical O–D table

where q _rs is the “true” O–D demand between the O–D pair rs, and o is the number of O–D pairs. r _t measures the distance between the estimated and “true” O–D tables. g _e measures the violation of the user equilibrium conditions of the estimated path flow pattern, i.e.,

$$g_e = \sum\limits_r {\sum\limits_s {\left( {\frac{{\Sigma _k \hat f_{rs}^k \left( {\hat c_{rs}^k - \hat \pi _{rs} } \right)}}{{\hat q_{rs} }}} \right)} } $$

(25)

where $\hat \pi _{rs}$ is the estimated minimum travel time (cost) between O–D pair rs, $\hat f_{rs}^k$ and $\hat c_{rs}^k$ are the estimated path flow and time (cost) respectively.

In both cases, the two approximate methods produced O–D estimates comparable to the bi-level method. For the first case (Table 1), none of the three methods achieved significant improvements, apparently because the historical O–D table is already close to the true one. The bi-level method provided the best performance with about 5% RMSE improvement.³ For the second case (Table 2), all three methods achieved about 50% RMSE improvement over the down-scaled historical O–D table. The decoupled method obtained the smallest r _t in this case.

As expected, the estimated path flow patterns obtained by the bi-level method best satisfied the UE conditions in both cases (g _e is the smallest). Although the decoupled method only assigned positive flows to UE paths, the resulting path flow pattern produced considerable violations of UE conditions. This is not a surprise since the travel times are only used in the decoupled method for identifying UE paths externally. The relaxed method obtained a path flow pattern relatively similar to that of the bi-level method. Although the relaxed method assigned a small amount of flow to path 11 (which does not actually belong to K ^e) in both cases, it obtained a path flow pattern more similar to that of the bi-level method and achieved a much smaller g _e compared to the decoupled method. Apparently, the scaled Beckman function helps push the estimated flow pattern to approach the UE flow pattern. Interestingly, although the path flow pattern obtained by the decoupled problem is far from equilibrium, the corresponding O–D estimate (Table 2) is the closest to the true O–D table. This observation seems to indicate that a solution better observing equilibrium conditions does not necessarily correspond to better O–D estimates.

5.1.2 The effect of θ

We proceed to examine the impact of the dispersion parameter θ, which determines the weight of the Beckman term in the relaxed SODE problem. The historical O–D table used hereafter is the one reported in Table 2. As shown in Fig. 2, when 1/θ increases from 0.001 to 0.5, the resulting path flow pattern more and more conforms to the UE conditions (with less g _e ). This confirms the role of the Beckman term in steering the estimated path flow solution toward a UE solution.

Fig. 2

The impact of the dispersion parameter

On the other hand, the estimated O–D table tends to move further away from the true O–D table as 1/θ increases. As discussed before, the Beckman term will discourage flows from not only paths with higher costs but indeed all paths with positive costs. As a result, a large 1/θ will lead to significant underestimation and hence large r _t . Figure 2 shows that the change of r _t is not sensitive to θ in the range of [20, 1,000], whereas the equilibrium gap was significantly improved as θ decreases from 1,000 to 20. For this example, θ = 20 seems to provide a proper tradeoff between equilibrium and underestimation. To some extent θ reflects the traveler’s sensitivity to the congestion level, and thus may be correlated with the dispersion parameter in the logit traffic assignment model (Fisk 1980). If a dispersion parameter has been calibrated with real data for the logit assignment model, it may also be employed in the relaxed SODE problem. If no calibrated results exist, θ can be selected such that the magnitude of the Beckman term roughly equals that of all deviation terms as a whole.

5.1.3 Using observed path travel times

In real applications reliable historical O–D demand information is often not available. We show in this subsection that observed path travel times can be a good alternative input under such a circumstance.

Results with and without observed path costs are compared in Table 3. When neither historical O–D information nor path costs are available, the estimated O–D table significantly deviated from the true one (r _t is about 90). Particularly, the demand for O–D pairs 2 and 3 is heavily underestimated whereas the demand for O–D pairs 2–4 is heavily overestimated. The quality of the estimated O–D table was significantly improved as observed costs on path 1, 8, 12 and 13 were brought into the estimation, as shown in the table. Not only was r _t reduced by 2/3, but also the uneven demand distribution among O–D pairs 2 and 3 and 2–4 was fixed. Moreover, the equilibrium gap was substantially improved (from 6.2 to 2.2).

Table 3 Estimation results with and without observed path costs

5.1.4 Different path generation strategies

So far all the relaxed SODE problems have been solved by path enumeration. We now examine three path generation strategies and see how they affect estimation accuracy and convergence.

• Strategy I: the path generation strategy described in Algorithm MCPA.

• Strategy II: force negative link costs to zero to avoid negative cycles, as described in Remark 4 in Section 4.2.

• Strategy III: generate one path for each O–D pair in each iteration to reduce the total number of iterations, as described in Remark 5 in Section 4.2.

Table 4 compares the estimated O–D tables and path flows obtained from the three different strategies to those obtained from path enumeration. As expected, strategy I produced an estimated O–D table identical to that from path enumeration. Interestingly, the estimated path flows from Strategy I do not completely agree with the path enumeration case. This illustrates multiple optimums of the relaxed SODE problem in terms of path flows. Both strategies II and III failed to identify path 8 as one of equilibrium paths, even though the failure apparently came from different reasons. The resulting path flow pattern is significantly different than the path enumeration case and subject to much higher violation of equilibrium conditions. However, note that the O–D table estimated from these two simplified strategies is actually “better” than the one obtained from Strategy I in terms of r _t . This contradiction reinforces the comment we made in Section 5.1.1.

Table 4 Estimation results associated with different path generation strategies

Figure 3 compares the convergence process of the three strategies. Starting from an initial set of four paths, strategy I spent about six main iterations to identify the optimal solution which uses eight paths. The final objective function value is identical to the path enumeration case. Strategy II took four main iterations and ended up with an optimal set of six paths. Yet it did not achieve the true optimal objective function value. Obviously, some critical paths were missed from the path search as negative costs were screened out. Strategy III spent only three iterations to converge, but also got stuck before the true optimality was attained. In a nutshell, the approximated column generation strategies may substantially reduce the total number of iterations (hence computational overhead), but usually not converge to true optimality. For large-scale problems it might be worthwhile to adopt these approximation schemes to improve the overall computational efficiency, particularly when negative cycles are prevalent.

Fig. 3

A comparison of different column generation strategies

5.1.5 Non-UE traffic counts

In this experiment, traffic counts are obtained from a non-UE traffic assignment, which first assigns 80% of traffic according to UE and then assigns the rest to the free-flow shortest paths. The assignment yields observed (small perturbation was applied) counts 200, 185, 290 for links 1, 3 and 9, respectively. Algorithmic parameters remain same as those specified in Section 5.1.1. Table 5 compares the estimation results from bi-level and relaxation approaches. As expected, the performance of the bi-level approach degrades substantially (compared to Table 2 where all settings are the same except traffic counts) when the underlying traffic distribution does not observe UE. On the contrary, the relaxation approach seems robust, providing OD estimates comparable to those obtained earlier (see Table 2 again). Considering that UE is an idealized condition that real world traffic may well deviate from, one should exercise caution when applying the bi-level approach to estimate O–D trip matrices, for the traffic counts used in the estimation may not come from a route choice process that satisfies UE.

Table 5 Estimated results based on non-UE traffic counts

5.2 A larger example

In this section we test the relaxation method over a larger network. Randomly created from a grid-network generator, the network has 400 links, 140 nodes, and 380 O–D pairs carrying 78799.43 trips in total. Traffic counts are produced from a static UE traffic assignment, and assumed to be available on all links with a v/c ratio higher than 0.5 (the number of links satisfying this condition is 139). Two different historical O–D demand tables are used. In case I, the table is produced by multiplying each entry in the “true” table by 1.2. In case II, the multiplier is a random variable following a uniform distribution between −0.75 to 1.25. The following parameters are employed in the calculation w _x = 1.0, w _q = 0.5, θ = 0.02. In addition to r _t, the indices adopted to measure the quality of the O–D estimates include

• Total demand captured (TDC): TDC measures the ratio of the total estimated demands to the total true demands, i.e.,

  $$TDC = \frac{{\Sigma _r \Sigma _s \hat q_{rs} }}{{\Sigma _r \Sigma _s q_{rs} }}$$

The best possible TDC is 1, which implies that the true total demands are perfectly captured.

• RMSE Improvement factor (RIF): RIF measure the ratio of the root mean square error of the estimated O–D table (with respect to the true O–D table) to that of the historical O–D table, i.e.,

  $$RIF = \frac{{RMSE\left( {\hat q,q} \right)}}{{RMSE\left( {\bar q,q} \right)}} = \sqrt {\frac{{\sum\nolimits_r {\sum\nolimits_s {\left( {\hat q_{{\text{rs}}} - {\text{q}}_{{\text{rs}}} } \right)^2 } } }}{{\sum\nolimits_r {\sum\nolimits_s {\left( {\bar q_{{\text{rs}}} - {\text{q}}_{{\text{rs}}} } \right)^2 } } }}} $$

• RMSE improvement ratio (RIR): RIR is the percentage of O–D pairs for which the estimated demand is “closer” to the true demand than the historical demand, i.e.,

  $$RIR = \frac{{\sum\nolimits_r {\sum\nolimits_s {n_{rs}^t } } }}{{m_a o}},n_{rs}^t = 1\;{\text{if}}\;\left| {\frac{{\hat q_{rs}^t - q_{rs}^t }}{{\bar q_{rs}^t - q_{rs}^t }}} \right| < 1,\;{\text{and}}\;{\text{0}}\;{\text{otherwise}}$$

Table 6 summarizes the results in two cases (each corresponds to a different historical O–D table) for both the relaxation and bi-level methods. Note that the column generation strategy is not employed in the relaxation method due to the likely existence of negative cycles. Instead, a predefined path set is formed using the first five shortest paths of each O–D pair. Interestingly, the bi-level method did not work well in this experiment. It only improved 3.4% of 380 O–D pairs in the first case and none in the second. A closer examination of the results indicates that the bi-level method has been trapped in the neighborhood of the historical O–D table. The symptom is that the estimated O–D table is very similar to the one used as the “target” while the link traffic counts are far from being well replicated (RMSEs of estimated link counts are 596.42 and 108.16 in cases I and II respectively). The relaxation method, however, did not seem to experience the same difficulties. As shown in Table 5, the relaxation method improved 67.7 and 36.6% of all O–D pairs in case I and II respectively, which is much better than the bi-level method. Note that the overall RMSE was improved only in the first case (${\text{RIF = 0}}{\text{.62 $<$ 1}}$). In the second case the overall RMSE was slightly increased (${\text{RIF}} = 1.17 > 1.0$) even though more than 1/3 of O–D pairs have an improved RMSE. Moreover, the link traffic counts were better replicated in the relaxation method (RMSEs of estimated link counts are about 2–5% of those obtained from the bi-level method).

Table 6 Estimation results for the large grid network

As for the computational efficiency, the bi-level method was terminated after five and two major iterations in cases I and II, consuming about 3 and 0.4 s of CPU time respectively. It should be pointed out that these small numbers of iterations might be caused by the aforementioned “traps” forbidding further progress. The relaxation method, on the other hand, spent 5,000 iterations (the maximum allowed number of iterations) in both cases (approximately equal to 35 to 40 s CPU time) to achieve a satisfactory convergence. The seemingly slow convergence of the relaxation method is partly due to the redundant paths included in the solution set. As observed, a large amount of iterations were needed to clear flows on those paths. Second but more important, the step size along the anti-gradient direction tends to be rather small in order to observe the feasibility, particularly when the solution gets into the neighborhood of the optimal solution. A more suitable nonlinear program solver might significantly accelerate the convergence of the relaxation method. Finally, the computational expense per iteration of the bi-level method is roughly 20 to 40 times higher than that of the relaxation method in this case. As this extra effort is tied to solving the equilibrium problem, it increases with the size of the problem and the difficulty of finding equilibrium solutions. As a result, the relaxation method might outperform the bi-level method computationally for large size problems in which finding good equilibrium solutions is time-consuming.

6 Conclusions

Conventional formulations for the O–D estimation problems have a bi-level structure which poses both analytical and computational difficulties. Such a bi-level formulation is particularly problematic when applied in the dynamic context when an efficient solution procedure does not exist to perform traffic assignment—the lower level problem. This study proposes a strategy which relaxes the equilibrium conditions but still takes users’ route choice behavior into account. The relaxation strategy intends to discourage the use of non-equilibrium paths by incorporating the Beckmann’s cost function into the objective. In addition to traffic counts, the relaxed formulation can incorporate other observations such as historical O–D information and path travel times measured from probe vehicles. We proposed a solution procedure based on column generation for the relaxed formulation and proved its convergence.

Using a benchmark example, we compared the estimation results obtained from bi-level, decoupled and relaxed formulations. Our sensitivity analysis confirmed the role of the Beckman term in steering the estimated path solution toward a UE solution and demonstrated how such a role is affected by the dispersion parameter. The results also showed that using observed path travel times helped improve the estimation quality, in the absence of good historical O–D information. A larger example was also tested to demonstrate the efficiency of the relaxation method.

Applying the relaxation strategy to the dynamic O–D estimation problem is an immediate next step and an on-going research. Other directions for further investigations include to consider other behavioral assumptions such as stochastic user equilibrium, and to develop a proper calibration procedure for the dispersion parameter.