$S^{p}$-Almost Periodic Solutions of Clifford-Valued Fuzzy Cellular Neural Networks with Time-Varying Delays

Abstract

In this paper, we consider Clifford-valued fuzzy cellular neural networks with time-varying delays. In order to avoid the inconvenience caused by the non-commutativity of the multiplication of Clifford numbers, we first decompose the considered n-dimensional Clifford-valued systems into $2^{m}n$-dimensional real-valued systems. Then by using the Banach fixed point theorem and a proof by contradiction, we establish sufficient conditions ensuring the existence, the uniqueness and the global exponential stability of $S^{p}$-almost periodic solutions for the considered neural networks. Finally, we give an example to illustrate the effectiveness of the obtained results. Our results are new even when the considered neural networks degenerates to real-valued, complex-valued and quaternion-valued neural networks.

1 Introduction

Fuzzy cellular neural networks are a class of neural networks that combine fuzzy operations (fuzzy AND and fuzzy OR) with cellular neural networks [1, 2]. They have been found many applications in various fields such as physics, chemistry, biology, economics, sociology, medicine and meteorology [3,4,5,6]. Since all of these applications are related to their dynamics, their various dynamic behaviors are heavily studied [7,8,9,10,11,12,13,14,15,16,17]. For example, in [7], the existence and global attractivity of a unique almost periodic solution for a class of fuzzy cellular neural networks with multi-proportional delays was investigated by applying contraction mapping fixed point theorem and differential inequality techniques, in [8], the existence and exponential stability of almost periodic solutions for a class of fuzzy cellular neural networks with time-varying delays was studied by the almost periodic function theory and differential inequality techniques, in [10], the global exponential convergence of T-S fuzzy complex-valued neural networks with time-varying delays and impulsive effects is discussed by employing Lyapunov functional method and matrix inequality technique, in [11], the existence and global exponential stability of periodic solutions of quaternion-valued fuzzy cellular neural networks with time-varying delays was established by using the Schauder fixed point theorem and by constructing an appropriate Lyapunov function.

Clifford-valued neural networks are a kind of neural networks whose state variables, connection weights and external inputs are Clifford numbers. They are generalizations of real-valued, complex-valued and quaternion-valued neural networks. They have been proved to be superior to real-valued, complex-valued and quaternion-valued neural networks in dealing with high-dimensional data, multi-level data and spatial geometric transformation [18, 19]. However, due to the fact that the multiplication of Clifford numbers does not satisfy the commutative law, the current research on the dynamics of Clifford-valued neural networks is still rare [20,21,22,23,24]. For example, in [20], authors studied the existence of anti-periodic solutions for a class of Clifford-valued inertial Cohen–Grossberg networks by a coincidence degree theory and constructing a suitable Lyapunov functional, in [22], authors investigated the stability of Clifford-valued recurrent neural networks with time delays in terms of a linear matrix inequality, in [23], authors considered the global asymptotic almost periodic synchronization of Clifford-valued cellular neural networks with discrete delays based on the Banach fixed point theorem and Lyapunov functional method.

Periodic oscillation, almost periodic oscillation and stability of solutions are important dynamic characteristics of dynamic systems. Therefore, the periodic and almost periodic oscillations, and the stability of solutions of differential equations, neural network systems, ecosystems and physical systems have been extensively studied [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47]. The almost periodicity is a generalization of the periodicity, which was invented by Bohr [48, 49]. The concept of Bohr’s almost periodic functions has attracted wide attention of mathematicians since it was put forward, which has led to various extensions and variants of the concept. However, Bohr’s almost periodic functions are defined on the class of uniformly continuous functions. Stepanov [50] proposed a weaker concept of almost periodic functions in Bohr’s sense, while Stepanov’s almost periodic function may be discontinuous. For more details on Stepanov almost periodic functions, see [51, 52]. But until today, there is no research on the existence and stability of $S^p$-almost periodic solutions of fuzzy cellular neural networks with time-varying delays. This is an interesting and valuable question.

Motivated by the above discussion, in this paper, we consider the following Clifford-valued fuzzy cellular neural network with time-varying delays:

$$\begin{aligned} x'_{i}(t)= & {} -a_{i}(t)x_{i}(t)+ \sum \limits _{j=1}^{n}b_{ij}(t)f_{j}\big (x_{j}(t)\big )+ \sum \limits _{j=1}^{n}d_{ij}(t)\mu _{j}(t)\nonumber \\&+\,\bigwedge \limits _{j=1}^{n}\alpha _{ij}(t)g_{j}\big (x_{j}(t-\tau _{ij}(t))\big ) +\bigvee \limits _{j=1}^{n}\beta _{ij}(t)g_{j}\big (x_{j}(t-\tau _{ij}(t))\big )\nonumber \\&+\,\bigwedge \limits _{j=1}^{n}T_{ij}(t)\mu _{j}(t)+ \bigvee \limits _{j=1}^{n}S_{ij}(t)\mu _{j}(t)+I_{i}(t), \end{aligned}$$

(1)

where $i\in \{1,2,\ldots ,n\}=:I$, ${\mathcal {A}}$ is a Clifford algebra, n is the number of neurons in layers; $x_{i}(t)\in {\mathcal {A}}$, $\mu _{i}(t)\in {\mathcal {A}}$ and $I_{i}(t)\in {\mathcal {A}}$ are the state, input and bias of the ith neuron, respectively; $a_{i}>0$ represents the rate with which the ith neuron will reset its potential to the resting state in isolation when they are disconnected from the network and the external inputs at time t, $\alpha _{ij}(t)\in {\mathcal {A}}$, $\beta _{ij}(t)\in {\mathcal {A}}$, $T_{ij}(t)\in {\mathcal {A}}$, and $S_{ij}(t)\in {\mathcal {A}}$ are the elements of fuzzy feedback MIN template, fuzzy feedback MAX template, fuzzy feed forward MIN template and fuzzy feed forward MAX template, respectively; $b_{ij}(t)\in {\mathcal {A}}$ and $d_{ij}(t)\in {\mathcal {A}}$ are the elements of feedback template and feed forward template, $\bigwedge$,$\bigvee$ denote the fuzzy AND and fuzzy OR operations, respectively, which will be defined in the next section; $f_{j}$ and $g_{j}:{\mathcal {A}}\rightarrow {\mathcal {A}}$ are the activation functions; $\tau _{ij}(t)\ge 0$ corresponds to transmission delays at time t.

The initial conditions of system (1) are

$$\begin{aligned} x_{i}(s)=\varphi _{i}(s),\,\,\,\,s\in [-\tau ,0], \end{aligned}$$

where $\tau =\max \nolimits _{1\le i,j \le n}\{{\overline{\tau }}_{ij}\}$, $\varphi _{i} \in C([-\tau ,0],{\mathcal {A}})$, $i\in I$.

Our main aim of this paper is to study the existence and global stability of $S^{p}$-almost periodic solutions of system (1). As we mentioned that there is no research on the $S^p$-almost periodicity of fuzzy cellular neural networks with time-varying delays. Even when system (1) degenerates into real-valued, complex-valued, and quaternion-valued systems, the results of this paper are brand new.

The rest of the paper is organized as follows. In Sect. 2, we make some preparation. In Sect. 3, we state and prove the existence, the uniqueness and the global exponential stability of the $S^{p}$-almost periodic solution. In Sect. 4, we present an example to illustrate the effectiveness of the obtained results. In Sect. 5, we give a conclusion.

2 Preliminaries

The real Clifford algebra over ${\mathbb {R}}^{m}$ is defined as

$$\begin{aligned} {\mathcal {A}}=\bigg \{\sum _{A\subseteq \{1,2,\ldots ,m\}}a_Ae_A, a_A\in {\mathbb {R}} \bigg \}, \end{aligned}$$

where $e_A=e_{h_1}e_{h_2}\cdots e_{h_\nu }$ with $A=\{h_1,h_2,\ldots ,h_\nu \}, 1\le h_1<h_2<\cdots <h_\nu \le m.$ Moreover, $e_\emptyset =e_0=1$ and $e_{\{h\}}=e_h, h=1,2,\ldots ,m$ are called Clifford generators which satisfy the relations:

$$\begin{aligned} \left\{ \begin{array}{ll} e_\mu e_\nu +e_\nu e_\mu =0, &{}\quad \mu \ne \nu , \\ e_\mu ^2=-1, &{}\quad \mu = 1, 2,\ldots ,m. \\ \end{array}\right. \end{aligned}$$

For simplicity, when one element is the product of multiple Clifford generators, we will write its subscripts together. For example $e_1e_2=e_{12}$ and $e_3e_7e_4e_5=e_{3745}$. We define $\varLambda =\{\emptyset , 1,2,\ldots ,A,\ldots ,12\cdots m\},$ then it is easy to see that

$$\begin{aligned} {\mathcal {A}}=\bigg \{\sum _{A\in \varLambda }a^Ae_A, a_A\in {\mathbb {R}} \bigg \}. \end{aligned}$$

For every $x,y\in {\mathbb {R}}$, we define

$$\begin{aligned} x\bigwedge y=\left\{ \begin{array}{ll} x, &{}\quad \mathrm {if} \,\,x\le y,\\ y,&{}\quad \mathrm {if}\,\, x>y \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} x\bigvee y=\left\{ \begin{array}{ll} y,&{}\quad \mathrm {if} \,\,x\le y,\\ x,&{} \mathrm {if}\,\, x>y. \end{array}\right. \end{aligned}$$

For every $x=\sum \nolimits _{A\in \varLambda }x^Ae_A,y=\sum \nolimits _{A\in \varLambda }y^Ae_A\in {\mathcal {A}}$, we define $x\bigwedge y=\sum \nolimits _{A\in \varLambda }(x^A\bigwedge y^A)e_A$ and $x\bigwedge y=\sum \nolimits _{A\in \varLambda }(x^A\bigvee y^A)e_A$.

For any $x=\sum _Ax^{A}\in {\mathcal {A}}$, the principal involution of x is defined as

$$\begin{aligned} {\overline{x}}=\sum \limits _{A\in \varLambda }x^{A}{\overline{e}}_A, \end{aligned}$$

where ${\overline{e}}_A=(-1)^{\frac{n[A](n[A]+1)}{2}}e_A$, if $A=\emptyset$, then $n[A]=0$ and if $A=h_1h_2\cdots h_v\in \varLambda$, then $n[A]=v$.

It is easy to see that $e_A{\overline{e}}_A={\overline{e}}_Ae_A=1$ and ${\overline{xy}}={\overline{y}} {\overline{x}}$ for $A\in \varLambda , x, y\in {\mathcal {A}}$.

The derivative of function $z=\sum _{A}z^Ae_A:{\mathbb {R}}\rightarrow {\mathcal {A}}$ is given by ${\dot{z}}(t)=\sum _{A\in \varLambda }{\dot{z}}^A(t)e_A,$ where $z^A:{\mathbb {R}}\rightarrow {\mathbb {R}}$.

Due to the fact that $e_B{\overline{e}}_A=(-1)^{\frac{n[A](n[A]+1)}{2}}e_Be_A$, we can simplify and express $e_B{\overline{e}}_A=e_C$ or $e_B{\overline{e}}_A=-e_C$ with $e_C$ being some basis of Clifford algebra. For example, $e_{42}{\overline{e}}_{27}=-e_{42}e_{27}=-e_4e_2e_2e_7=e_4e_7=e_{47}$. So it is possible to find a unique corresponding basis $e_C$ for the given $e_B{\overline{e}}_A$. Define

$$\begin{aligned} n[B\cdot {\overline{A}}]=\left\{ \begin{array}{ll} 0, &{}\quad \mathrm {if}\,\, e_B{\overline{e}}_A=e_C,\\ 1,&{}\quad \mathrm {if}\,\, e_B{\overline{e}}_A=-e_C,\end{array}\right. \end{aligned}$$

then $e_B{\overline{e}}_A=(-1)^{n[B\cdot {\overline{A}}]}e_C$. In addition, for any $\varTheta \in {\mathcal {A}}$, define $\varTheta ^C$ satisfying $\varTheta ^{B\cdot {\overline{A}}}=(-1)^{n[B\cdot {\overline{A}}]}\varTheta ^C$ for $e_B{\overline{e}}_A=(-1)^{n[B\cdot {\overline{A}}]}e_C$. Therefore,

$$\begin{aligned} \varTheta ^{B\cdot {\overline{A}}}e_B{\overline{e}}_A=\varTheta ^{B\cdot {\overline{A}}}(-1)^{n[B\cdot {\overline{A}}]}e_C =(-1)^{n[B\cdot {\overline{A}}]}\varTheta ^C(-1)^{n[B\cdot {\overline{A}}]}e_C=\varTheta ^Ce_C \end{aligned}$$

and

$$\begin{aligned} \varTheta =\sum _{C\in \varLambda }\varTheta ^Ce_C\in {\mathcal {A}}. \end{aligned}$$

For example, for the second term in system (1), we have

$$\begin{aligned} \sum \limits _{j=1}^{n}b_{ij}(t)f_{j}\big (x_{j}(t)\big )= & {} \sum \limits _{j=1}^{n}\sum \limits _{C\in \varLambda }b^{C}_{ij}(t)e_{C}\sum \limits _{B\in \varLambda }f^{B}_{j}\big (x_{j}(t)\big )e_{B}\\= & {} \sum \limits _{j=1}^{n}\sum \limits _{A\in \varLambda }\sum \limits _{B\in \varLambda }(-1)^{n[A\cdot {\overline{B}}]}b^{A\cdot {\bar{B}}}_{ij}(t)(-1)^{n[A\cdot {\overline{B}}]}e_{A}{\overline{e}}_{B}f^{B}_{j}\big (x_{j}(t)\big )e_{B}\\= & {} \sum \limits _{j=1}^{n}(-1)^{2n[A\cdot {\overline{B}}]}\sum \limits _{A\in \varLambda }\sum \limits _{B\in \varLambda }b^{A\cdot {\bar{B}}}_{ij}(t)f^{B}_{j}\big (x_{j}(t)\big )e_{A}{\overline{e}}_{B}e_{B}\\= & {} \sum \limits _{j=1}^{n}\sum \limits _{A\in \varLambda }\sum \limits _{B\in \varLambda }b^{A\cdot {\bar{B}}}_{ij}(t)f^{B}_{j}\big (x_{j}(t)\big )e_{A},\,\, i\in I. \end{aligned}$$

To overcome the difficulty of the non-commutativity of the Clifford number’s multiplication, according to the above discussion, we can transform (1) into the following equivalent real-valued system:

$$\begin{aligned} {\dot{x}}^{A}_{i}(t)= & {} -a_{i}(t)x^{A}_{i}(t)+ \sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }b^{A\cdot {\overline{B}}}_{ij}(t)f^{B}_{j}\big (x_{j}(t)\big )+ \sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }d^{A\cdot {\overline{B}}}_{ij}(t)\mu ^{B}_{j}(t)\nonumber \\&+\bigwedge \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }\alpha ^{A\cdot {\overline{B}}}_{ij}(t)g^{B}_{j}(x_{j}(t-\tau _{ij}(t)))\nonumber \\&+\bigvee \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }\beta ^{A\cdot {\overline{B}}}_{ij}(t)g^{B}_{j}(x_{j}(t-\tau _{ij}(t)))\nonumber \\&+\bigwedge \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }T^{A\cdot {\overline{B}}}_{ij}(t)\mu ^{B}_{j}(t)+ \bigvee \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }S^{A\cdot {\overline{B}}}_{ij}(t)\mu ^{B}_{j}(t)+I^{A}_{i}(t),\,\, i\in I \end{aligned}$$

(2)

and

$$\begin{aligned} x^{A}_{i}(s)=\varphi ^{A}_i(s),\quad i\in I,\quad s\in [-\tau ,0], \end{aligned}$$

where

$$\begin{aligned} x_i(t)= & {} \sum \limits _{A\in \varLambda }x_i^A(t)e_A,\quad I_i(t)=\sum _{A\in \varLambda }I_i^A(t)e_A, \\ b_{ij}(t)= & {} \sum \limits _{C\in \varLambda }b_{ij}^C(t)e_C,\quad b_{ij}^{A\cdot {\bar{B}}}(t)=(-1)^{n[A\cdot {\bar{B}}]}b_{ij}^C(t), \\ d_{ij}(t)= & {} \sum \limits _{C\in \varLambda }d_{ij}^C(t)e_C,\quad d_{ij}^{A\cdot {\bar{B}}}(t)=(-1)^{n[A\cdot {\bar{B}}]}d_{ij}^C(t), \\ \alpha _{ij}(t)= & {} \sum \limits _{C\in \varLambda }\alpha _{ij}^C(t)e_C,\quad \alpha _{ij}^{A\cdot {\bar{B}}}(t)=(-1)^{n[A\cdot {\bar{B}}]}\alpha _{ij}^C(t), \\ \beta _{ij}(t)= & {} \sum \limits _{C\in \varLambda }\beta _{ij}^C(t)e_C,\quad \beta _{ij}^{A\cdot {\bar{B}}}(t)=(-1)^{n[A\cdot {\bar{B}}]}\beta _{ij}^C(t), \\ T_{ij}(t)= & {} \sum \limits _{C\in \varLambda }b_{ij}^C(t)e_C,\quad T_{ij}^{A\cdot {\bar{B}}}(t)=(-1)^{n[A\cdot {\bar{B}}]}T_{ij}^C(t), \\ S_{ij}(t)= & {} \sum \limits _{C\in \varLambda }S_{ij}^C(t)e_C,\quad S_{ij}^{A\cdot {\bar{B}}}(t)=(-1)^{n[A\cdot {\bar{B}}]}S_{ij}^C(t), \\ f_j(x_j(t-\tau _{ij}(t)))= & {} \sum \limits _{B\in \varLambda }f_j^B(x_j^{C_1}(t-\tau _{ij}(t)),x_j^{C_2}(t-\tau _{ij}(t)),\ldots , \\ x_j^{C_{2^m}}(t-\tau _{ij}(t)))e_B= & {} \sum \limits _{B\in \varLambda }f_j^B(x_j(t-\tau _{ij}(t)))e_B, \\ g_j(x_j(t))= & {} \sum \limits _{B\in \varLambda }g_j^B(x_j^{C_1}(t),x_j^{C_2}(t),\ldots ,x_j^{C_{2^m}}(t))e_B=\sum \limits _{B\in \varLambda }g_j^B(x_j(t))e_B, \end{aligned}$$

for $e_A{\overline{e}}_B=(-1)^{n[A\cdot {\overline{B}}]}e_C.$

Remark 1

If $x=(x_1^0,x_1^1,\ldots ,x_1^{1\cdot 2\cdot \cdots m}, x_2^0,x_2^1,\ldots ,x_2^{1\cdot 2\cdot \cdots m},\ldots ,x_n^0,x_n^1,\ldots , x_n^{1\cdot 2\cdot \cdots m})^T:=\{x^A_i\}$ is a solution to system (2), then $x=(x_1,\ldots ,x_n)^T$ must be a solution to (1), where $x_{i}=\sum \limits _{A\in \varLambda }x_i^Ae^A,\,\,i=1,2,\ldots ,n$, and vise versa.

Let $({\mathbb {X}},\Vert \cdot \Vert )$ be a Banach space and $BC({\mathbb {R}},{\mathbb {X}})$ be the set of all bounded continuous functions from ${\mathbb {R}}$ to ${\mathbb {X}}$.

Definition 1

[53] A function $f\in BC({\mathbb {R}},{\mathbb {X}})$ is said to be almost periodic if for every $\epsilon >0$ there exists a positive number $\ell$ such that every interval of length $\ell$ contains a number $\tau$ such that

$$\begin{aligned} \Vert f(t+\tau )-f(t)\Vert <\epsilon ,\quad t\in {\mathbb {R}}. \end{aligned}$$

The $\tau$ is called the $\epsilon$-almost period of f. Denote by $AP({\mathbb {R}},{\mathbb {X}})$ the set of all such functions.

Lemma 1

[53] For each $\epsilon >0$, a finite family of almost periodic functions has a common set of $\epsilon$-almost periods.

Definition 2

[53] Let $p\in [1,\infty )$. Denote by $L_{loc}^{p}({\mathbb {R}},{\mathbb {X}})$ the space of all functions from ${\mathbb {R}}$ into ${\mathbb {X}}$ which are locally p-integrable in the sense of Bochner-Lebesgue. A function $f\in L_{loc}^{p}({\mathbb {R}},{\mathbb {X}})$ is called $S^{p}$-bounded if

$$\begin{aligned} \Vert f\Vert _{S^{p}}=\sup _{t\in {\mathbb {R}}}\bigg (\int _{t}^{t+1}\Vert f(s)\Vert ^{p}\mathrm {d}s \bigg )^{\frac{1}{p}}<\infty . \end{aligned}$$

We denote by $L_{s}^{p}({\mathbb {R}},{\mathbb {X}})$ the set of all such functions.

Definition 3

[53] A function $f\in L_{s}^{p}({\mathbb {R}},{\mathbb {X}})$ is said to be $S^{p}$-almost periodic, if for every $\epsilon >0$ there exists $\ell >0$ such that every interval of length $\ell$ contains a number $\tau$ such that

$$\begin{aligned} \sup \limits _{t\in {\mathbb {R}}}\bigg [\int _{t}^{t+1}\Vert f(s+\tau )-f(s)\Vert ^{p}ds\bigg ]^{\frac{1}{p}}<\epsilon . \end{aligned}$$

We denote by $S^{p}AP({\mathbb {R}},{\mathbb {X}})$ the set of all such functions.

Definition 4

A function $f=\sum \nolimits _{i=1}^nf^Ae_A:{\mathbb {R}}\rightarrow {\mathcal {A}}$ is said to be $S^{p}$-almost periodic, if $f^A\in S^{p}AP({\mathbb {R}},{\mathbb {R}})$ for all $A\in \varLambda$.

Lemma 2

[53] $S^{p}AP({\mathbb {R}},{\mathbb {X}})$ is a Banach space with the norm

$$\begin{aligned} \Vert f\Vert _{S^{p}}=\sup _{t\in {\mathbb {R}}}\bigg (\int _{t}^{t+1}\Vert f(s)\Vert ^{p}\mathrm {d}s \bigg )^{\frac{1}{p}}. \end{aligned}$$

Lemma 3

[54] If $a\in AP({\mathbb {R}},{\mathbb {R}})$, and $f\in S^{p}AP({\mathbb {R}},{\mathbb {X}})$, then $af\in S^{p}AP({\mathbb {R}},{\mathbb {X}})$.

Lemma 4

[53] If $x\in S^{p}AP({\mathbb {R}},{\mathbb {X}})$ and $\tau \in AP({\mathbb {R}},{\mathbb {R}})$, then $x(\cdot -\tau (\cdot ))\in S^{p}AP({\mathbb {R}},{\mathbb {X}})$.

Similar to the proof of Lemma 3.7 in [53], one can prove

Lemma 5

Let $f\in C({\mathbb {X}},{\mathbb {X}})$ and satisfy the Lipschiz condition. If $g\in S^{p}AP({\mathbb {R}}, {\mathbb {X}})$, then $f(g(\cdot ))\in S^{p}AP({\mathbb {R}},{\mathbb {X}})$.

From the relevant results of [55], one can easily obtain that

Lemma 6

For $i=1,2,\ldots ,n, a_{i}\in BC({\mathbb {R}},{\mathbb {R}})$ with $\inf \nolimits _{t\in {\mathbb {R}}} a_{i}(t)>0$. If $f\in BC({\mathbb {R}},{\mathbb {R}}^n)$, then the linear system

$$\begin{aligned} x'(t)=A(t)x(t)+f(t) \end{aligned}$$

has a unique bounded solution

$$\begin{aligned} x(t)=\int _{-\infty }^{t} e^{\int ^{t}_{s}A(u)\mathrm {d}u}f(s)d s, \end{aligned}$$

where $A(t)=\mathrm {diag}(-a_{1}(t),-a_{2}(t),\dots ,-a_{n}(t))$.

Throughout the rest of this paper. For convenience, for a bounded and continuous function $f:{\mathbb {R}}\rightarrow {\mathbb {R}}$, we denote ${\underline{f}}=\inf \limits _{t\in {\mathbb {R}}}|f(t)|$ and ${\overline{f}}=\sup \limits _{t\in {\mathbb {R}}}|f(t)|.$

Before ending this section, we introduce the following lemma.

Lemma 7

[56] Suppose x and y are two states of system (2). Then we have

$$\begin{aligned} \Big |\bigwedge \limits _{j=1}^{n}\alpha _{ij}(t)f_{j}(x)-\bigwedge \limits _{j=1}^{n}\alpha _{ij}(t)f_{j}(y)\Big | \le \sum \limits _{j=1}^{n}|\alpha _{ij}(t)||f_{j}(x)-f_{j}(y)|,\quad i\in I,\\ \Big |\bigvee \limits _{j=1}^{n}\beta _{ij}(t)f_{j}(x)-\bigvee \limits _{j=1}^{n}\beta _{ij}(t)f_{j}(y)\Big | \le \sum \limits _{j=1}^{n}|\beta _{ij}(t)||f_{j}(x)-f_{j}(y)|,\quad i\in I. \end{aligned}$$

3 Main Results

In this section, we will establish some results for the existence, the uniqueness and the global exponential stability of $S^{p}$-almost periodic solutions of system (2).

Now, we let $D=\{x|x=\{x_i^A\}\in S^{p}AP({\mathbb {R}},{\mathbb {R}}^{2^{m}\cdot n})\}$ and equip it with the norm $\Vert x\Vert _{S^{p}}=\max \limits _{i\in I}\Big \{\max \limits _{A\in \varLambda }|x_{i}^{A}|_{S^{p}}\Big \}$, where $|x_{i}^{A}|_{S^{p}}=\sup \nolimits _{t\in {\mathbb {R}}}\Big (\int _{t}^{t+1}|x_{i}^{A}(s)|^{p}\mathrm {d}s \Big )^{\frac{1}{p}}.$ Then, we know that D is a Banach space. Let $\varphi _{0}=\{(\varphi _0)_{i}^{A}\}$, where $(\varphi _0)^{A}_{i}(t)=\int _{-\infty }^{t}e^{-\int ^{t}_{s}a_{i}(u)\mathrm {d}u} \Big (\sum \nolimits _{j=1}^{n}\sum \nolimits _{B\in \varLambda }d^{A\cdot {\overline{B}}}_{lh}(s)\mu ^{B}_{j}(s) +\bigwedge \limits _{h=1}^{n}\sum \limits _{B\in \varLambda }T^{A\cdot {\overline{B}}}_{ij}(s)\mu ^{B}_{j}(s) +\bigvee \limits _{h=1}^{n}\sum \limits _{B\in \varLambda } S^{A\cdot {\overline{B}}}_{ij}(s)\mu ^{B}_{j}(s)+I^{A}_{i}(s)\Big )\mathrm {d}s$, $i\in I, A\in \varLambda$ and r be a constant satisfying $r\ge \Vert \varphi _{0}\Vert _{S^{p}}$.

Throughout this paper, we assume that the following conditions hold:

$(H_{1})$:

Functions $a_{i}\in AP({\mathbb {R}},{\mathbb {R}}^{+})$, $\tau _{ij}\in AP({\mathbb {R}},{\mathbb {R}}^{+})$, $b_{ij}^{A\cdot {\overline{B}}}$, $\alpha _{ij}^{A\cdot {\overline{B}}}$, $\beta _{ij}^{A\cdot {\overline{B}}}$, $\mu ^{B}_{j}\in AP({\mathbb {R}},{\mathbb {R}})$ and $d_{ij}^{A\cdot {\overline{B}}}$, $I_{i}^{A},T_{ij}^{A\cdot {\overline{B}}}$, $S_{ij}^{A\cdot {\overline{B}}}\in S^{p}AP({\mathbb {R}},{\mathbb {R}})$, where $i,j\in I,A,B\in \varLambda$.

$(H_{2})$:

There exist positive constants ${L_j^f},{L_j^g}$ such that for any $u,v\in {\mathcal {A}}$, functions $f^{B}_{j},g^{B}_{j}\in C({\mathcal {A}},{\mathbb {R}})$ satisfying

$$\begin{aligned} |f^{B}_{j}(u)-f^{B}_{j}(v)|\le & {} L_j^f\sum \limits _{C\in \varLambda }|u^{C}-v^{C}|,\\ |g^{B}_{j}(u)-g^{B}_{j}(v)|\le & {} L_j^g\sum \limits _{C\in \varLambda }|u^{C}-v^{C}| \end{aligned}$$

and $f^{B}_{j}({\mathbf {0}})=g_{j}^{B}({\mathbf {0}})=0$, where $j\in I,A,B\in \varLambda .$

$(H_{3})$:

$\max \limits _{i\in I,A\in \varLambda }\bigg \{\Big (\frac{1}{p{\underline{a}}_{i}}\Big )^{1/p} Q^{A}_{i}\bigg \}=:\rho <1$, where $Q^{A}_{i}=\sum \limits _{j=1}^{n}2^{m}\bigg (\sum \limits _{B\in \varLambda }{\overline{b}}^{A\cdot {\overline{B}}}_{ij}{L_j^f}+\sum \limits _{B\in \varLambda }{\overline{\alpha }}^{A\cdot {\overline{B}}}_{ij}{L_j^g}+\sum \limits _{B\in \varLambda }{\overline{\beta }}^{A\cdot {\overline{B}}}_{ij}{L_j^g}\bigg ).$

Lemma 8

If $b_{j}\in S^{p}AP({\mathbb {R}},{\mathbb {R}})$ and $a_{ij}\in AP({\mathbb {R}},{\mathbb {R}})$, then $\bigwedge \nolimits _{j=1}^{n}a_{ij}(\cdot )b_{j}(\cdot )$, $\bigvee \nolimits _{j=1}^{n}a_{ij}(\cdot )b_{j}(\cdot )\in S^{p}AP({\mathbb {R}},{\mathbb {R}}), \,i\in I$.

Proof

Since $a_{ij}\in AP({\mathbb {R}},{\mathbb {R}})$ and $b_{j}\in S^{p}AP({\mathbb {R}},{\mathbb {R}})$, we have

$$\begin{aligned} \sup \limits _{t\in {\mathbb {R}}}|a_{ij}(t)|:=K_{ij}<\infty \quad \mathrm {and} \quad |b_{j}|_{S^p}:=K_{j}< \infty . \end{aligned}$$

Now, for given any $\epsilon _{ij},\,\epsilon _{j}>0$, let $\tau$ be a common almost period of $a_{ij}$ and $b_{j}$. By using Minkowski’s inequality, we have

$$\begin{aligned}&\sup \limits _{t\in {\mathbb {R}}}\bigg (\int ^{t+1}_{t} \Big |\bigwedge \limits _{j=1}^{n}a_{ij}(s+\tau )b_{j}(s+\tau )- \bigwedge \limits _{j=1}^{n}a_{ij}(s)b_{j}(s)\Big |^{p}\mathrm {d}s\bigg )^{1/p}\\&\quad \le \sup \limits _{t\in {\mathbb {R}}}\bigg (\int ^{t+1}_{t} \Big |\bigwedge \limits _{j=1}^{n}a_{ij}(s+\tau )b_{j}(s+\tau )- \bigwedge \limits _{j=1}^{n}a_{ij}(s)b_{j}(s+\tau )\Big |^{p}\mathrm {d}s\bigg )^{1/p}\\&\qquad +\sup \limits _{t\in {\mathbb {R}}}\bigg (\int ^{t+1}_{t} \Big |\bigwedge \limits _{j=1}^{n}a_{ij}(s)b_{j}(s+\tau )- \bigwedge \limits _{j=1}^{n}a_{ij}(s)b_{j}(s)\Big |^{p}\mathrm {d}s\bigg )^{1/p}\\&\quad \le \sup \limits _{t\in {\mathbb {R}}}\bigg [\int ^{t+1}_{t} \sum \limits _{j=1}^{n}|b_{j}(s+\tau )|^{p}|a_{ij}(s+\tau )-a_{ij}(s)|^{p}\mathrm {d}s\bigg ]^{1/p}\\&\qquad +\sup \limits _{t\in {\mathbb {R}}}\bigg [\int ^{t+1}_{t} \sum \limits _{j=1}^{n}|a_{ij}(s)|^{p}|b_{j}(s+\tau )-b_{j}(s)|^{p}\mathrm {d}s\bigg ]^{1/p}\\&\quad \le \sum \limits _{j=1}^{n}\big (K_{j}\epsilon _{ij}+K_{ij}\epsilon _{j}\big ),\quad i\in I, \end{aligned}$$

which implies

$$\begin{aligned} \bigwedge \limits _{j=1}^{n}b_{ij}(\cdot )a_{j}(\cdot )\in S^{p}AP({\mathbb {R}},{\mathbb {R}}),\,\, i\in I. \end{aligned}$$

Similarly, we can get

$$\begin{aligned} \bigvee \limits _{j=1}^{n}b_{ij}(\cdot )a_{j}(\cdot )\in S^{p}AP({\mathbb {R}},{\mathbb {R}}),\quad i\in I. \end{aligned}$$

$\square$

Theorem 1

Assume that $(H_{1})$-$(H_{3})$ hold, then system (2) has a unique $S^{p}$-almost periodic solution in the region $D^{*}=\{\varphi |\varphi \in D,\Vert \varphi -\varphi _{0}\Vert _{S^{p}}\le \frac{\rho r}{1-\rho }\}.$

Proof

For every $\varphi \in D$, we consider the linear differential equation system

$$\begin{aligned} {\dot{x}}^{A}_{i}(t)= & {} -a_{i}(t)x^{A}_{i}(t)+ \sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }b^{A\cdot {\overline{B}}}_{ij}(t)f^{B}_{j}\big (\varphi _{j}(t)\big )+ \sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }d^{A\cdot {\overline{B}}}_{ij}(t)\mu ^{B}_{j}(t)\nonumber \\&+\bigwedge \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }\alpha ^{A\cdot {\overline{B}}}_{ij}(t)g^{B}_{j}(\varphi _{j}(t-\tau _{ij}(t))) +\bigvee \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }\beta ^{A\cdot {\overline{B}}}_{ij}(t)\nonumber \\&\times g^{B}_{j}(\varphi _{j}(t-\tau _{ij}(t)))+\bigwedge \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }T^{A\cdot {\overline{B}}}_{ij}(t)\mu ^{B}_{j}(t)\nonumber \\&+\bigvee \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }S^{A\cdot {\overline{B}}}_{ij}(t)\mu ^{B}_{j}(t)+I^{A}_{i}(t),\quad i\in I. \end{aligned}$$

(3)

Combining $(H_{1})$ and Lemma 6, we deduce that system (3) has a unique bounded solution

$$\begin{aligned} (x^\varphi )_i^A(t)= & {} \int ^{t}_{-\infty }e^{-\int ^{t}_{s}a_{i}(u)\mathrm {d}u}\bigg [ \sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }b^{A\cdot {\overline{B}}}_{ij}(s)f^{B}_{j}\big (\varphi _{j}(s)\big )\nonumber \\&+\sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }d^{A\cdot {\overline{B}}}_{ij}(s)\mu ^{B}_{j}(s) +\bigwedge \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }\alpha ^{A\cdot {\overline{B}}}_{ij}(s)g^{B}_{j}(\varphi _{j}(s-\tau _{ij}(s)))\nonumber \\&+\bigvee \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }\beta ^{A\cdot {\overline{B}}}_{ij}(s)g^{B}_{j}(\varphi _{j}(s-\tau _{ij}(s)))\nonumber \\&+\bigwedge \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }T^{A\cdot {\overline{B}}}_{ij}(s)\mu ^{B}_{j}(s)+ \bigvee \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }S^{A\cdot {\overline{B}}}_{ij}(s)\mu ^{B}_{j}(s)+I^{A}_{i}(s)\bigg ]\mathrm {d}s\nonumber \\:= & {} \int ^{t}_{-\infty }e^{-\int ^{t}_{s}a_{i}(u)\mathrm {d}u} (\zeta _{\varphi })_{i}^{A}(s)\mathrm {d}s,\quad i\in I, A\in \varLambda . \end{aligned}$$

(4)

Now, we define a mapping $\varPhi :D^{*}\rightarrow D$ by setting $(\varPhi \varphi )(t)=\{(x^{\varphi })^A_i(t)\}$, $\forall \varphi \in D^{*}$. First, we show that the mapping $\varPhi$ is a self-mapping from $D^{*}$ to $D^{*}$. By $(H_{1})$ and Lemmas 3-5, we have $(\zeta _{\varphi })_{i}^{A}(t)\in S^{p}AP({\mathbb {R}},{\mathbb {R}})$. Let $\epsilon _{i} >0$, there exist $G_{i}>0$ and $\ell >0$ such that every interval of length $\ell$ contains a number $\tau$ such that

$$\begin{aligned}&\sup \limits _{t\in {\mathbb {R}}}\bigg [\int _{t}^{t+1}|(\zeta _{\varphi })_{i}^{A}(s)|^{p}ds\bigg ]^{\frac{1}{p}}<G_{i}, \end{aligned}$$

(5)

$$\begin{aligned}&\sup \limits _{t\in {\mathbb {R}}}\bigg [\int _{t}^{t+1}|(\zeta _{\varphi })_{i}^{A}(s+\tau ) -(\zeta _{\varphi })_{i}^{A}(s)|^{p}ds\bigg ]^{\frac{1}{p}}<\epsilon _{i} \end{aligned}$$

(6)

and

$$\begin{aligned} |a_{i}(t+\tau )-a_{i}(t)|<\epsilon _{i},\quad i\in I. \end{aligned}$$

By the Minkowski’s inequality and (4)–(6), we obtain

$$\begin{aligned}&\sup \limits _{t\in {\mathbb {R}}}\bigg [\int _{t}^{t+1}\Big |\int ^{w+\tau }_{-\infty }e^{-\int ^{w+\tau }_{s}a_{i}(u)\mathrm {d}u} (\zeta _{\varphi })_{i}^{A}(s)\mathrm {d}s\\&\qquad -\int ^{w}_{-\infty }e^{-\int ^{w}_{s}a_{i}(u)\mathrm {d}u} (\zeta _{\varphi })_{i}^{A}(s)\mathrm {d}s\Big |^{p}\mathrm {d}w\bigg ]^{\frac{1}{p}}\nonumber \\&\quad =\sup \limits _{t\in {\mathbb {R}}}\bigg [\int _{t}^{t+1}\Big |\int ^{w}_{-\infty } e^{-\int ^{w}_{s}a_{i}(u+\tau )\mathrm {d}u} (\zeta _{\varphi })_{i}^{A}(s+\tau )\mathrm {d}s\\&\qquad -\int ^{w}_{-\infty }e^{-\int ^{w}_{s}a_{i}(u)\mathrm {d}u} (\zeta _{\varphi })_{i}^{A}(s)\mathrm {d}s\Big |^{p}\mathrm {d}w\bigg ]^{\frac{1}{p}}\nonumber \\&\quad \le \sup \limits _{t\in {\mathbb {R}}}\bigg [\int _{t}^{t+1}\Big |\int ^{w}_{-\infty } e^{-\int ^{w}_{s}a_{i}(u)\mathrm {d}u} \big ((\zeta _{\varphi })_{i}^{A}(s+\tau )-(\zeta _{\varphi })_{i}^{A}(s)\big )\mathrm {d}s\Big |^{p} \mathrm {d}w\bigg ]^{\frac{1}{p}}\nonumber \\&\qquad +\, \sup \limits _{t\in {\mathbb {R}}}\bigg [\int _{t}^{t+1} \Big |\int ^{w}_{-\infty } e^{-\int ^{w}_{s}a_{i}(u+\tau )\mathrm {d}u} (\zeta _{\varphi })_{i}^{A}(s+\tau )\mathrm {d}s\nonumber \\&\qquad -\int ^{w}_{-\infty }e^{-\int ^{w}_{s}a_{i}(u)\mathrm {d}u} (\zeta _{\varphi })_{i}^{A}(s+\tau )\mathrm {d}s\Big |^{p}\mathrm {d}w\bigg ]^{\frac{1}{p}}\nonumber \\&\quad \le \sup \limits _{t\in {\mathbb {R}}}\bigg [\int _{t}^{t+1}\int ^{w}_{-\infty } e^{-\int ^{w}_{s}pa_{i}(u)\mathrm {d}u} \big |(\zeta _{\varphi })_{i}^{A}(s+\tau )-(\zeta _{\varphi })_{i}^{A}(s)\big |^{p}\mathrm {d}s \mathrm {d}w\bigg ]^{\frac{1}{p}}\nonumber \\&\qquad +\sup \limits _{t\in {\mathbb {R}}}\bigg [\int _{t}^{t+1} \Big |\int ^{w}_{-\infty } \Big (e^{-\int ^{w}_{s}a_{i}(u+\tau )\mathrm {d}u}\\&\qquad -e^{-\int ^{w}_{s}a_{i}(u)\mathrm {d}u}\Big ) (\zeta _{\varphi })_{i}^{A}(s+\tau )\mathrm {d}s\Big |^{p}\mathrm {d}w\bigg ]^{\frac{1}{p}}\nonumber \\&\quad \le \sup \limits _{t\in {\mathbb {R}}}\bigg [\int _{t}^{t+1}\int ^{w}_{-\infty } e^{-\int ^{w}_{s}pa_{i}(u)\mathrm {d}u} \big |(\zeta _{\varphi })_{i}^{A}(s+\tau )-(\zeta _{\varphi })_{i}^{A}(s)\big |^{p}\mathrm {d}s \mathrm {d}w\bigg ]^{\frac{1}{p}}\nonumber \\&\qquad +\sup \limits _{t\in {\mathbb {R}}}\bigg [\int _{t}^{t+1} \Big |\int ^{w}_{-\infty }e^{-{\underline{a}}_{i}(w-s)} \Big (\int ^{w}_{s}|a_{i}(u+\tau )\\&\qquad -a_{i}(u)|\mathrm {d}u\Big ) (\zeta _{\varphi })_{i}^{A}(s+\tau )\mathrm {d}s\Big |^{p}\mathrm {d}w\bigg ]^{\frac{1}{p}}\nonumber \\&\quad \le \sup \limits _{t\in {\mathbb {R}}}\bigg [\int ^{\infty }_{0} e^{-p{\underline{a}}_{i}\sigma }\int _{t}^{t+1} \big |(\zeta _{\varphi })_{i}^{A}(w-\sigma +\tau )-(\zeta _{\varphi })_{i}^{A}(w-\sigma )\big |^{p}\mathrm {d}w \mathrm {d}\sigma \bigg ]^{\frac{1}{p}}\nonumber \\&\qquad +\, \epsilon _{i}\sup \limits _{t\in {\mathbb {R}}}\bigg [\int _{t}^{t+1} \int ^{\infty }_{0}e^{-p{\underline{a}}_{i}\sigma }\sigma ^{p} |(\zeta _{\varphi })_{i}^{A}(w-\sigma +\tau )|^{p}\mathrm {d}\sigma \mathrm {d}w\bigg ]^{\frac{1}{p}}\nonumber \\&\quad <\epsilon _{i}(\frac{1}{p{\underline{a}}_{i}})^{1/p}+ \epsilon _{i}G_{i}\Big [\int ^{\infty }_{0}e^{-p{\underline{a}}_{i}\sigma }\sigma ^{p}\mathrm {d}\sigma \Big ]^{1/p}, \end{aligned}$$

where $\sigma =w-s$, $i\in I$, which implies that $(x^\varphi )^A_i\in S^{p}AP({\mathbb {R}}, {\mathbb {R}}), i\in I, A\in \varLambda$. Hence, $\varPhi D\subset S^{p}AP({\mathbb {R}}, {\mathbb {R}}^{2^{m}\cdot n})$. In addition, for any $\varphi \in D^*$, we have

$$\begin{aligned} \Vert \varphi \Vert _{S^{p}}\le \Vert \varphi -\varphi _{0}\Vert _{S^{p}}+\Vert \varphi _{0}\Vert _{S^{p}}\le \frac{\rho r}{1-\rho }+r=\frac{r}{1-\rho } \end{aligned}$$

and by the Minkowski’s inequality, we have

$$\begin{aligned}&|(\varPhi \varphi )^{A}_{i}-(\varphi _{0})^{A}_{i}|_{S^{p}}\\&\quad \le \sup \limits _{t\in {\mathbb {R}}}\bigg \{\bigg [\int ^{t+1}_{t}\bigg |\int ^{w}_{-\infty } e^{-\int ^{w}_{s}a_{i}(u)\mathrm {d}u}\bigg ( \sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }b^{A\cdot {\overline{B}}}_{ij}(s)\\&\qquad \times \, f^{B}_{j}\big (\varphi _{j}(s)\big )\bigg ) \mathrm {d}s\bigg |^{p}\mathrm {d}w\bigg ]^{1/p}\bigg \}+\bigg [\int ^{t+1}_{t}\bigg |\int ^{w}_{-\infty } e^{-\int ^{w}_{s}a_{i}(u)\mathrm {d}u}\bigg (\bigwedge \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }\alpha ^{A\cdot {\overline{B}}}_{ij}(s)\\&\qquad \times g^{B}_{j}(\varphi _{j}(s-\tau _{ij}(s)))\bigg ) \mathrm {d}s\bigg |^{p}\mathrm {d}w\bigg ]^{1/p} +\bigg [\int ^{t+1}_{t} \bigg |\int ^{w}_{-\infty }e^{-\int ^{w}_{s}a_{i}(u)\mathrm {d}u}\\&\qquad \times \bigg (\bigvee \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }\beta ^{A\cdot {\overline{B}}}_{ij}(s)g^{B}_{j}(\varphi _{j}(s-\tau _{ij}(s)))\bigg ) \mathrm {d}s\bigg |^{p}\mathrm {d}w\bigg ]^{1/p}\bigg \}\\&\quad \le \sup \limits _{t\in {\mathbb {R}}}\sum \limits _{j=1}^{n}\bigg \{\bigg [\int ^{t+1}_{t}\bigg |\int ^{w}_{-\infty } e^{-\int ^{w}_{s}a_{i}(u)\mathrm {d}u}\bigg (\sum \limits _{B\in \varLambda }{\overline{b}}^{A\cdot {\overline{B}}}_{ij}\\&\qquad \times f^{B}_{j}\big (\varphi _{j}(s)\big )\bigg ) \mathrm {d}s\bigg |^{p}\mathrm {d}w\bigg ]^{1/p}\bigg \}+\bigg [\int ^{t+1}_{t}\bigg |\int ^{w}_{-\infty } e^{-\int ^{w}_{s}a_{i}(u)\mathrm {d}u}\\&\qquad \times \bigg (\sum \limits _{B\in \varLambda }{\overline{\alpha }}^{A\cdot {\overline{B}}}_{ij} |g^{B}_{j}(\varphi _{j}(s-\tau _{ij}(s)))|\bigg ) \mathrm {d}s\bigg |^{p}\mathrm {d}w\bigg ]^{1/p}+\bigg [\int ^{t+1}_{t} \bigg |\int ^{w}_{-\infty }\nonumber \\&\qquad \times e^{-\int ^{w}_{s}a_{i}(u)\mathrm {d}u}\bigg (\sum \limits _{B\in \varLambda }{\overline{\beta }}^{A\cdot {\overline{B}}}_{ij}|g^{B}_{j}(\varphi _{j}(s-\tau _{ij}(s)))|\bigg ) \mathrm {d}s\bigg |^{p}\mathrm {d}w\bigg ]^{1/p}\bigg \}\\&\quad \le \sup \limits _{t\in {\mathbb {R}}}\sum \limits _{j=1}^{n}\bigg [\sum \limits _{B\in \varLambda }{\overline{b}}^{A\cdot {\overline{B}}}_{ij}{L_j^f}\sum _{C\in \varLambda }\bigg ( \int ^{t+1}_{t}\int ^{\infty }_{0} e^{-p{\underline{a}}_{i}\sigma }|\varphi ^{C}_{j}(w-\sigma )|^{p} \mathrm {d}\sigma \mathrm {d}w\bigg )^{1/p}\\&\qquad +\sum \limits _{B\in \varLambda }{\overline{\alpha }}^{A\cdot {\overline{B}}}_{ij} {L_j^g}\sum _{C\in \varLambda }\bigg (\int ^{t+1}_{t}\int ^{\infty }_{0} e^{-p{\underline{a}}_{i}\sigma }|\varphi ^{C}_{j}(w-\sigma \\&\qquad -\tau _{ij}(w-\sigma ))|^{p} \mathrm {d}\sigma \mathrm {d}w\bigg )^{1/p}+\sum \limits _{B\in \varLambda }{\overline{\beta }}^{A\cdot {\overline{B}}}_{ij}{L_j^g}\sum _{C\in \varLambda }\bigg (\int ^{t+1}_{t} \int ^{\infty }_{0} e^{-p{\underline{a}}_{i}\sigma }\\&\qquad \times |\varphi ^{C}_{j}(w-\sigma -\tau _{ij}(w-\sigma )))|^{p} \mathrm {d}\sigma \mathrm {d}w\bigg )^{1/p}\bigg ]\\&\quad \le \Big (\frac{1}{p{\underline{a}}_{i}}\Big )^{1/p}2^{m}\sum \limits _{j=1}^{n}\bigg (\sum \limits _{B\in \varLambda }{\overline{b}}^{A\cdot {\overline{B}}}_{ij}{L_j^f}+\sum \limits _{B\in \varLambda }{\overline{\alpha }}^{A\cdot {\overline{B}}}_{ij} {L_j^g}+\sum \limits _{B\in \varLambda }{\overline{\beta }}^{A\cdot {\overline{B}}}_{ij}{L_j^g}\bigg )\Vert \varphi \Vert _{S^{p}}\\&\quad \le \frac{\rho r}{1-\rho }, \end{aligned}$$

which implies that $\varPhi \varphi \in D^{*}$, so the mapping $\varPhi$ is a self-mapping from $D^{*}$ to $D^{*}$.

Next, we shall prove that $\varPhi$ is a contraction mapping. In fact, for any $\varphi ,\,\psi \in D^{*}, i\in I$, we have

$$\begin{aligned}&|(\varPhi \varphi )^{A}_{i}-(\varPhi \psi )^{A}_{i}|_{S^{p}}\\&\quad =\sup \limits _{t\in {\mathbb {R}}}\bigg \{\bigg [\int ^{t+1}_{t}\bigg |\int ^{w}_{-\infty } e^{-\int ^{w}_{s}a_{i}(u)\mathrm {d}u}\bigg ( \sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }b^{A\cdot {\overline{B}}}_{ij}(s)\big [f^{B}_{j}\big (\varphi _{j}(s)\big )-f^{B}_{j}\big (\psi _{j}(s)\big ]\big ) \\&\qquad +\bigwedge \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }\alpha ^{A\cdot {\overline{B}}}_{ij}(s) \times \big [g^{B}_{j}(\varphi _{j}(s-\tau _{ij}(s)))-g^{B}_{j}(\psi _{j}(s-\tau _{ij}(s)))\big ]\\&\qquad +\bigvee \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }\beta ^{A\cdot {\overline{B}}}_{ij}(s)\big [g^{B}_{j}(\varphi _{j}(s-\tau _{ij}(s))) -g^{B}_{j}(\psi _{j}(s-\tau _{ij}(s)))\big ]\bigg ) \mathrm {d}s\bigg |^{p}\mathrm {d}w\bigg ]^{1/p}\bigg \}\\&\quad \le \sup \limits _{t\in {\mathbb {R}}}\bigg \{\bigg [\int ^{t+1}_{t}\bigg |\int ^{w}_{-\infty } e^{-\int ^{w}_{s}a_{i}(u)\mathrm {d}u}\bigg ( \sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }b^{A\cdot {\overline{B}}}_{ij}(s) \big [f^{B}_{j}\big (\varphi _{j}(s)\big )\\&\qquad -f^{B}_{j}\big (\psi _{j}(s)\big )\big ]\bigg ) \mathrm {d}s\bigg |^{p}\mathrm {d}w\bigg ]^{1/p}\bigg \} +\bigg [\int ^{t+1}_{t}\bigg |\int ^{w}_{-\infty } e^{-\int ^{w}_{s}a_{i}(u)\mathrm {d}u}\\&\qquad \times \bigg (\bigwedge \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }\alpha ^{A\cdot {\overline{B}}}_{ij}(s)\big [g^{B}_{j}(\varphi _{j}(s-\tau _{ij}(s))) -g^{B}_{j}(\psi _{j}(s-\tau _{ij}(s)))\big ]\bigg ) \mathrm {d}s\bigg |^{p}\mathrm {d}w\bigg ]^{1/p}\\&\qquad +\bigg [\int ^{t+1}_{t} \bigg |\int ^{w}_{-\infty }e^{-\int ^{w}_{s}a_{i}(u)\mathrm {d}u} \bigg (\bigvee \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }\beta ^{A\cdot {\overline{B}}}_{ij}(s)\big [g^{B}_{j}(\varphi _{j}(s-\tau _{ij}(s)))\\&\qquad -g^{B}_{j}(\psi _{j}(s-\tau _{ij}(s)))\big ]\bigg ) \mathrm {d}s\bigg |^{p}\mathrm {d}w\bigg ]^{1/p}\bigg \}\\&\quad \le \sup \limits _{t\in {\mathbb {R}}}\sum \limits _{j=1}^{n}\bigg (\sum \limits _{B\in \varLambda }{\overline{b}}^{A\cdot {\overline{B}}}_{ij}{L_j^f}\sum _{C\in \varLambda }\bigg (\int ^{t+1}_{t}\int ^{\infty }_{0} e^{-p{\underline{a}}_{i}\sigma }| \varphi ^{C}_{j}(w-\sigma )\\&\qquad -\psi ^{C}_{j}(w-\sigma )|^{p} \mathrm {d}\sigma \mathrm {d}w\bigg )^{1/p}\\&\qquad +\sum \limits _{B\in \varLambda }{\overline{\alpha }}^{A\cdot {\overline{B}}}_{ij} {L_j^g}\sum _{C\in \varLambda }\bigg (\int ^{t+1}_{t}\int ^{\infty }_{0} e^{-p{\underline{a}}_{i}\sigma }|\varphi ^{C}_{j}(w-\sigma -\tau _{ij}(w-\sigma ))\\&\qquad -\psi ^{C}_{j}(w-\sigma -\tau _{ij}(w-\sigma ))|^{p} \mathrm {d}\sigma \mathrm {d}w\bigg )^{1/p}+\sum \limits _{B\in \varLambda }{\overline{\beta }}^{A\cdot {\overline{B}}}_{ij}{L_j^g}\\&\qquad \times \sum _{C\in \varLambda }\bigg (\int ^{t+1}_{t} \int ^{\infty }_{0}e^{-p{\underline{a}}_{i}\sigma } \times |\varphi ^{C}_{j}(w-\sigma -\tau _{ij}(w-\sigma )))\\&\qquad -\psi ^{C}_{j}(w-\sigma -\tau _{ij}(w-\sigma )))|^{p} \mathrm {d}\sigma \mathrm {d}w\bigg )^{1/p}\bigg ]\\&\quad \le \Big (\frac{1}{p{\underline{a}}_{i}}\Big )^{1/p}2^{m}\sum \limits _{j=1}^{n}\bigg (\sum \limits _{B\in \varLambda }{\overline{b}}^{A\cdot {\overline{B}}}_{ij}{L_j^f}+\sum \limits _{B\in \varLambda }{\overline{\alpha }}^{A\cdot {\overline{B}}}_{ij} {L_j^g}+\sum \limits _{B\in \varLambda }{\overline{\beta }}^{A\cdot {\overline{B}}}_{ij}{L_j^g}\bigg )\Vert \varphi -\psi \Vert _{S^{p}}, \end{aligned}$$

that is, we have

$$\begin{aligned}&\max \limits _{A\in \varLambda }|(\varPhi \varphi )^{A}_{i}-(\varPhi \psi )^{A}_{i}|_{S^{p}}\\&\quad \le \Big (\frac{1}{p{\underline{a}}_{i}}\Big )^{1/p}2^{m}\max \limits _{A\in \varLambda }\sum \limits _{j=1}^{n}\bigg (\sum \limits _{B\in \varLambda }{\overline{b}}^{A\cdot {\overline{B}}}_{ij}{L_j^f}\\&\qquad +\sum \limits _{B\in \varLambda }{\overline{\alpha }}^{A\cdot {\overline{B}}}_{ij} {L_j^g}+\sum \limits _{B\in \varLambda }{\overline{\beta }}^{A\cdot {\overline{B}}}_{ij}{L_j^g}\bigg )\Vert \varphi -\psi \Vert _{S^{p}}. \end{aligned}$$

Therefore,

$$\begin{aligned} \Vert \varPhi \varphi -\varPhi \psi \Vert _{S^{p}}\le \rho \Vert \varphi -\psi \Vert _{S^{p}}. \end{aligned}$$

Hence, $\varPhi$ is a contraction mapping. Thus, system (2) has a unique $S^{p}$-almost periodic solution in the region $D^{*}=\{\varphi \in D|\Vert \varphi -\varphi _{0}\Vert _{S^{p}}\le \frac{\rho r}{1-\rho }\}$. This completes the proof of Theorem 1. $\square$

Similar to the definitions about the global exponential stability of solutions given in [11, 12, 14, 20], we give the following definition.

Definition 5

Let $x=\{x_{i}^{A}\}$ be a $S^{p}$-almost periodic solution of system (2) with the initial value ${\overline{x}}=\{{\overline{x}}_{i}^{A}\}$. If there exist constants $\omega >0$ and $M>0$, for any solution $\varphi =\{\varphi _{i}^{A}\}$ of system (2) with initial value ${\overline{\varphi }}=\{{\overline{\varphi }}_{i}^{A}\}$ such that

$$\begin{aligned} \Vert x(t)-\varphi (t)\Vert \le M\Vert \varpi \Vert _{0}e^{-\omega t},\,\,\forall t>0, \end{aligned}$$

where

$$\begin{aligned} \Vert x(t)-\varphi (t)\Vert =\max _{i\in I}\Big \{\max \limits _{A\in \varLambda }|x^{A}_{i}(t)-\varphi ^{A}_{i}(t)|\Big \} \end{aligned}$$

and

$$\begin{aligned} \Vert \varpi \Vert _{0}=\max _{i\in I}\bigg \{\max \limits _{A\in \varLambda }\Big \{\sup _{s\in [-\tau ,0]}|{\overline{x}}^{A}_{i}(s)-{\overline{\varphi }}^{A}_{i}(s)|\Big \}\bigg \}. \end{aligned}$$

Then, x is said to be globally exponential stable.

Theorem 2

Assume that $(H_{1})$-$(H_{3})$ hold. Suppose further that

$(H_{4})$:

$\max \limits _{i\in I,A\in \varLambda }\bigg \{\frac{Q^{A}_{i}}{{\underline{a}}_{i}}\bigg \}<1,$

then system (2) has a unique $S^{p}$-almost periodic solution ${\bar{x}}(t)$ which is globally exponentially stable.

Proof

From Theorem 1, we see that system (2) has an $S^{p}$-almost periodic solution ${\overline{x}}=\{{\overline{x}}^A_i\}$ with initial value ${\overline{\varphi }}=\{{\overline{\varphi }}_{i}^{A}\}$. Suppose that $x=\{x_{i}^{A}\}$ is an arbitrary solution of system (2) with initial value $\varphi =\{\varphi _{i}^{A}\}$. Set $X=x-{\overline{x}}$, then, according to (2), we have

$$\begin{aligned} {\dot{X}}^{A}_{i}(t)= & {} -a_{i}(t)X^{A}_{i}(t)+\sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }b^{A\cdot {\overline{B}}}_{ij}(t)\big [f^{B}_{j}\big (x_{j}(t)\big )-f^{B}_{j} \big ({\overline{x}}_{j}(t)\big ]\big )\nonumber \\&+\bigwedge \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }\alpha ^{A\cdot {\overline{B}}}_{ij}(t) \times \big [g^{B}_{j}(x_{j}(t-\tau _{ij}(t)))-g^{B}_{j}({\overline{x}}_{j}(t-\tau _{ij}(t)))\big ]\nonumber \\&+\bigvee \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }\beta ^{A\cdot {\overline{B}}}_{ij}(t)\big [g^{B}_{j}(x_{j}(t-\tau _{ij}(t)))\nonumber \\&-g^{B}_{j}({\overline{x}}_{j}(s-\tau _{ij}(t)))\big ], i\in I, A\in \varLambda . \end{aligned}$$

(7)

For $i\in I$, we define functions $\varTheta _{i}(\theta )$ as follows:

$$\begin{aligned} \varTheta _{i}(\theta )= & {} {\underline{a}}_{i}-\theta -2^{m}\sum \limits _{j=1}^{n}\bigg (\sum \limits _{B\in \varLambda }{\overline{b}}^{A\cdot {\overline{B}}}_{ij} {L_j^f} +\sum \limits _{B\in \varLambda }{\overline{\alpha }}^{A\cdot {\overline{B}}}_{ij} {L_j^g}e^{\theta {\overline{\tau }}_{ij}}\\&+\sum \limits _{B\in \varLambda }{\overline{\beta }}^{A\cdot {\overline{B}}}_{ij} {L_j^g}e^{\theta {\overline{\tau }}_{ij}}\bigg ),\quad i\in I. \end{aligned}$$

By ($H_{4}$), for $i\in I$, we get

$$\begin{aligned} \varTheta _{i}(0)={\underline{a}}_{i}-Q_{i}>0. \end{aligned}$$

Since $\varTheta _{i}$ is continuous on $[0,+\infty )$ and $\varTheta _{i}(\theta ) \rightarrow -\infty$, as $\theta \rightarrow +\infty$, so there exist $\zeta _{i}$ such that $\varTheta _{i}(\zeta _{i})=0$ and $\varTheta _{i}(\theta )>0$ for $\theta \in (0,\zeta _{i})$, $i\in I$. By choosing $c=\min \nolimits _{i\in I}\{\zeta _{i}\}$, we have $\varTheta _{i}(c)\ge 0$, $i\in I$. So, we can choose a positive constant $0<\lambda <\min \big \{c,\min \nolimits _{i\in I}\{{\underline{a}}_{i}\}\big \}$ such that

$$\begin{aligned} \varTheta _{i}(\lambda )>0,\quad i\in I, \end{aligned}$$

which imply that

$$\begin{aligned} \frac{2^{m}}{{\underline{a}}_{i}-\lambda }\sum \limits _{j=1}^{n}\bigg (\sum \limits _{B\in \varLambda }{\overline{b}}^{A\cdot {\overline{B}}}_{ij} {L_j^f} +\sum \limits _{B\in \varLambda }{\overline{\alpha }}^{A\cdot {\overline{B}}}_{ij} {L_j^g}e^{\lambda {\overline{\tau }}_{ij}} +\sum \limits _{B\in \varLambda }{\overline{\beta }}^{A\cdot {\overline{B}}}_{ij} {L_j^g}e^{\lambda {\overline{\tau }}_{ij}}\bigg )<1, \end{aligned}$$

where $i\in I$.

Set $M=\max \limits _{i\in I}\{\frac{{\underline{a}}_{i}}{Q_{i}}\}$, then by ($H_{3}$), we have $M>1$. Thus,

$$\begin{aligned} \frac{1}{M} -\frac{1}{a_{i}-\lambda }2^{m}\sum \limits _{j=1}^{n}\bigg (\sum \limits _{B\in \varLambda }{\overline{b}}^{A\cdot {\overline{B}}}_{ij} {L_j^f}+\sum \limits _{B\in \varLambda }{\overline{\alpha }}^{A\cdot {\overline{B}}}_{ij} {L_j^g}e^{\lambda {\overline{\tau }}_{ij}}+\sum \limits _{B\in \varLambda }{\overline{\beta }}^{A\cdot {\overline{B}}}_{ij} {L_j^g}e^{\lambda {\overline{\tau }}_{ij}}\bigg )<0,\quad i\in I. \end{aligned}$$

Obviously, for any $\varepsilon >0$,

$$\begin{aligned} \Vert X(0)\Vert < \Vert \varpi \Vert _{0}+\varepsilon \end{aligned}$$

(8)

and

$$\begin{aligned} \Vert X(t)\Vert< (\Vert \varpi \Vert _{0}+\varepsilon )e^{-\lambda t}< M(\Vert \varpi \Vert _{0}+\varepsilon )e^{-\lambda t},\quad \forall \, t\in [-\tau ,0). \end{aligned}$$

(9)

We claim that

$$\begin{aligned} \Vert X(t)\Vert < M(\Vert \varpi \Vert _{0}+\varepsilon )e^{-\lambda t},\quad \forall \, t>0. \end{aligned}$$

(10)

If (10) is not true, then there must be some $t_{1}>0$ such that

$$\begin{aligned} \bigg \{\begin{array}{ll} \Vert X(t_{1})\Vert =M(\Vert \varpi \Vert _{0}+\varepsilon )e^{-\lambda t_{1}},\\ \Vert X(t)\Vert< M(\Vert \varpi \Vert _{0}+\varepsilon )e^{-\lambda t},\quad 0<t<t_{1}. \end{array} \end{aligned}$$

(11)

Multiplying the both sides of (7) by $e^{\int ^{t}_{0}a_{i}(u)\mathrm {d}u}$ and integrating over [0, t], we get

$$\begin{aligned} X^{A}_{i}(t)= & {} X^{A}_{i}(0)e^{-\int ^{t}_{0}a_{i}(u)\mathrm {d}u}+\int ^{t}_{0}e^{-\int ^{t}_{s}a_{i}(u)\mathrm {d}u} \bigg (\sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }b^{A\cdot {\overline{B}}}_{ij}(s)\big [f^{B}_{j}\big (x_{j}(s)\big )\\&-f^{B}_{j}\big ({\overline{x}}_{j}(s)\big )\big ] +\bigwedge \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }\alpha ^{A\cdot {\overline{B}}}_{ij}(s) \big [g^{B}_{j}(x_{j}(s-\tau _{ij}(s)))\\&-g^{B}_{j}({\overline{x}}_{j}(s-\tau _{ij}(s)))\big ] +\bigvee \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }\beta ^{A\cdot {\overline{B}}}_{ij}(s)\big [g^{B}_{j}(x_{j}(s-\tau _{ij}(s)))\\&-g^{B}_{j}({\overline{x}}_{j}(s-\tau _{ij}(s)))\big ]\bigg )\mathrm {d}s,\quad i\in I,A\in \varLambda . \end{aligned}$$

Thus, by $M>1$, (8), (9) and (11), we obtain

$$\begin{aligned}&|X^{A}_{i}(t_{1})|\\&\quad \le \bigg |X^{A}_{i}(0) e^{-\int ^{t_{1}}_{0}a_{i}(u)\mathrm {d}u}\bigg | +\bigg |\int ^{t_{1}}_{0}e^{-\int ^{t_{1}}_{s}a_{i}(u)\mathrm {d}u} \bigg ( \sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }{\overline{b}}^{A\cdot {\overline{B}}}_{ij} {L_j^f}\\&\qquad \times \sum \limits _{C\in \varLambda }|x^{C}_{j}(s)-{\overline{x}}^{C}_{j}(s)| +\sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }{\overline{\alpha }}^{A\cdot {\overline{B}}}_{ij} {L_j^g}\sum \limits _{C\in \varLambda }|x^{C}_{j}(s-\tau _{ij}(s))\\&\qquad -{\overline{x}}^{C}_{j}(s-\tau _{ij}(s))|+\sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }{\overline{\beta }}^{A\cdot {\overline{B}}}_{ij} {L_j^g}\\&\qquad \times \sum \limits _{C\in \varLambda }|x^{C}_{j}(s-\tau _{ij}(s))-{\overline{x}}^{C}_{j}(s-\tau _{ij}(s))|\bigg ) \mathrm {d}s\bigg |\\&\quad \le (\Vert \varpi \Vert _{0}+\varepsilon )e^{-{\underline{a}}_{i} t_{1}} +\int ^{t_{1}}_{0} e^{-\int ^{t_{1}}_{s}a_{i}(u)\mathrm {d}u}2^{m}\bigg (\sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }{\overline{b}}^{A\cdot {\overline{B}}}_{ij} {L_j^f}\\&\qquad +\sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }{\overline{\alpha }}^{A\cdot {\overline{B}}}_{ij} {L_j^g}e^{\lambda {\overline{\tau }}_{ij}} +\sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }{\overline{\beta }}^{A\cdot {\overline{B}}}_{ij} {L_j^g}e^{\lambda {\overline{\tau }}_{ij}}\bigg )M(\Vert \varpi \Vert _{0}+\varepsilon )e^{-\lambda s}\mathrm {d}s\\&\quad \le M(\Vert \varpi \Vert _{0}+\varepsilon )\bigg \{\frac{e^{-{\underline{a}}_{i} t_{1}}}{M} +\int ^{t_{1}}_{0} e^{-\int ^{t_{1}}_{s}(a_{i}(u)-\lambda )\mathrm {d}u}2^{m}e^{-\lambda t_{1}}\bigg (\sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }\\&\qquad \times {\overline{b}}^{A\cdot {\overline{B}}}_{ij} {L_j^f}+\sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }{\overline{\alpha }}^{A\cdot {\overline{B}}}_{ij} {L_j^g}e^{\lambda {\overline{\tau }}_{ij}} +\sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }{\overline{\beta }}^{A\cdot {\overline{B}}}_{ij} {L_j^g}e^{\lambda {\overline{\tau }}_{ij}}\bigg )\mathrm {d}s\bigg \}\\&\quad \le M(\Vert \varpi \Vert _{0}+\varepsilon )e^{-\lambda t_{1}}\bigg \{\frac{e^{(\lambda -{\underline{a}}_{i}) t_{1}}}{M} +\frac{1-e^{(\lambda -{\underline{a}}_{i})t_{1}}}{a_{i}-\lambda }2^{m}\bigg (\sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }{\overline{b}}^{A\cdot {\overline{B}}}_{ij} {L_j^f}\\&\qquad +\sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }{\overline{\alpha }}^{A\cdot {\overline{B}}}_{ij} {L_j^g}e^{\lambda {\overline{\tau }}_{ij}} +\sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }{\overline{\beta }}^{A\cdot {\overline{B}}}_{ij} {L_j^g}e^{\lambda {\overline{\tau }}_{ij}}\bigg )\bigg \}\nonumber \\&\quad \le M(\Vert \varpi \Vert _{0}+\varepsilon )e^{-\lambda t_{1}}\bigg \{\bigg [\frac{1}{M} -\frac{1}{a_{i}-\lambda }2^{m}\bigg (\sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }{\overline{b}}^{A\cdot {\overline{B}}}_{ij} {L_j^f}\nonumber \\&\qquad +\sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }{\overline{\alpha }}^{A\cdot {\overline{B}}}_{ij} {L_j^g}e^{\lambda {\overline{\tau }}_{ij}} +\sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }{\overline{\beta }}^{A\cdot {\overline{B}}}_{ij} {L_j^g}e^{\lambda {\overline{\tau }}_{ij}}\bigg )\bigg ]e^{(\lambda -{\underline{a}}_{i}) t_{1}}\\&\qquad +\frac{1}{a_{i}-\lambda }2^{m} \times \bigg (\sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }{\overline{b}}^{A\cdot {\overline{B}}}_{ij} {L_j^f}+\sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }{\overline{\alpha }}^{A\cdot {\overline{B}}}_{ij} {L_j^g}e^{\lambda {\overline{\tau }}_{ij}}\\&\qquad +\sum \limits _{j=1}^{n}\sum \limits _{B\in \varLambda }{\overline{\beta }}^{A\cdot {\overline{B}}}_{ij} {L_j^g}e^{\lambda {\overline{\tau }}_{ij}}\bigg )\bigg \}\\&\quad <M(\Vert \varpi \Vert _{0}+\varepsilon )e^{-\lambda t_{1}},\quad i\in I,A\in \varLambda , \end{aligned}$$

that is,

$$\begin{aligned} \Vert X(t_{1})\Vert <M(\Vert \varpi \Vert _{0}+\varepsilon )e^{-\lambda t_{1}}, \end{aligned}$$

which contradicts the first equation (11). Therefore, (10) holds. Letting $\varepsilon \rightarrow 0^{+}$ leads to

$$\begin{aligned} \Vert X(t)\Vert \le M\Vert \varpi \Vert _{0}e^{-\lambda t},\quad \forall \, t\in (0,+\infty ). \end{aligned}$$

Hence, the $S^{p}$-almost periodic solution of system (2) is globally exponentially stable. The proof of Theorem 2 is completed. $\square$

4 An Example

In this section, we give an example to illustrate the feasibility and effectiveness of our results obtained in Sects. 3 and 4.

Example 1

In System (1), let $n=m=2$. The coefficients are taken as follows:

$$\begin{aligned} a_{1}(t)= & {} 0.1+0.2|\cos \sqrt{3}t|,\quad a_{2}(t)=0.8+0.8|\sin 6t|,\quad f_{1}(x)=g_{1}(x)=\\&0.0025\Big (\big (|x^{0}+1|-|x^{2}-1|\big )e_{0}+e_{1}\sin \frac{\sqrt{2}}{2}\big (x^{1}+x^{12}\big ) -e_{2}\sin x^{2} \\&+\, e_{12}\tanh \big (x^{2}+x^{12}+x^{0}\big )\Big ),\quad f_{2}(x)=g_{2}(x)=\\&0.0025\Big (\frac{1}{2}\big (|x^{0}+1|-|x^{2}-1|\big )e_{0}+e_{1}\sin \frac{\sqrt{2}}{2}\big (x^{1}+x^{12}\big ) -e_{2}\sin x^{2}\\&+\, 2e_{12}\tanh \big (x^{2}+x^{12}+x^{0}\big )\Big ),\\ I_{1}(t)= & {} 0.2e_{0}\cos 9t+ (0.1+0.2\sin \sqrt{2}t)e_{1}+0.2 e_{2}\sin 2t+0.1 e_{12}\cos 4t,\\ I_{2}(t)= & {} 0.4e_{0}\cos 9t+ (0.1+0.2\sin \sqrt{2}t)e_{1}+0.2 e_{2}\sin 2t+0.1 e_{12}\cos 4t,\\ b_{11}(t)= & {} 0.4e_{0}\sin 2t+0.1 e_{1}\cos 3t+0.1 e_{2} \cos 6t+ 0.3 e_{12}\sin ^{2} 7t,\\ b_{12}(t)= & {} 0.4e_{0}\sin 2t+0.2 e_{1}\cos 3t+0.1 e_{2} \cos 6t+ 0.3 e_{12}\sin ^{2} 7t,\\ b_{21}(t)= & {} 0.4e_{0}\sin 2t+0.1 e_{1}\cos 3t+0.2 e_{2} \cos 6t+ 0.3 e_{12}\sin ^{2} 7t,\\ b_{22}(t)= & {} 0.4e_{0}\sin 2t+0.2 e_{1}\cos 3t+0.2 e_{2} \cos 6t+ 0.3 e_{12}\sin ^{2} 7t,\\ d_{11}(t)= & {} 0.1e_{0}\cos 3\sqrt{2}t+0.3 e_{1}\sin \sqrt{7}t+0.1e_{2}\cos 2t+0.1 e_{12}\sin \sqrt{2}t,\\ d_{12}(t)= & {} 0.1e_{0}\cos 3\sqrt{2}t+0.3 e_{1}\sin \sqrt{7}t+0.2e_{2}\cos 2t+0.1 e_{12}\sin \sqrt{2}t,\\ d_{21}(t)= & {} 0.2e_{0}\cos 3\sqrt{2}t+0.3 e_{1}\sin \sqrt{7}t+0.1e_{2}\cos 2t+0.1 e_{12}\sin \sqrt{2}t,\\ d_{22}(t)= & {} 0.2e_{0}\cos 3\sqrt{2}t+0.3 e_{1}\sin \sqrt{7}t+0.2e_{2}\cos 2t+0.1 e_{12}\sin \sqrt{2}t,\\ \alpha _{11}(t)= & {} 0.1e_{0}\cos 3t+0.2 e_{1}\sin 2t+0.2 e_{2}\sin 8t+ 0.1 e_{12}\sin ^{2} 2t,\\ \alpha _{12}(t)= & {} 0.2e_{0}\cos 3t+0.4 e_{1}\sin 2t+0.2 e_{2}\sin 8t+ 0.1 e_{12}\sin ^{2} 2t,\\ \alpha _{21}(t)= & {} 0.1e_{0}\cos 3t+0.2 e_{1}\sin 2t+0.2 e_{2}\sin 8t+ 0.1 e_{12}\sin ^{2} 2t,\\ \alpha _{22}(t)= & {} 0.2e_{0}\cos 3t+0.4 e_{1}\sin 2t+0.2 e_{2}\sin 8t+ 0.1 e_{12}\sin ^{2} 2t,\\ \beta _{11}(t)= & {} 0.3e_{0}\sin t+0.1 e_{1}\cos 2t+0.2 e_{2}\cos \sqrt{6}t+0.2e_{12}\sin 3t,\\ \beta _{12}(t)= & {} 0.3e_{0}\sin t+0.1 e_{1}\cos 2t+0.4 e_{2}\cos \sqrt{6}t+0.2e_{12}\sin 3t,\\ \beta _{21}(t)= & {} 0.3e_{0}\sin t+0.1 e_{1}\cos 2t+0.2 e_{2}\cos \sqrt{6}t+0.2e_{12}\sin 3t,\\ \beta _{22}(t)= & {} 0.3e_{0}\sin t+0.1 e_{1}\cos 2t+0.4 e_{2}\cos \sqrt{6}t+0.2e_{12}\sin 3t,\\ T_{11}(t)= & {} (0.2+0.1\sin 2t)e_{0}+0.1 e_{1}\cos ^{2} 2t+0.1 e_{2}\sin 5t+0.1 e_{12}\cos t,\\ T_{12}(t)= & {} (0.2+0.2\sin 2t)e_{0}+0.1 e_{1}\cos ^{2} 2t+0.1 e_{2}\sin 5t+0.1 e_{12}\cos t,\\ T_{21}(t)= & {} (0.2+0.1\sin 2t)e_{0}+0.1 e_{1}\cos ^{2} 2t+0.2 e_{2}\sin 5t+0.2 e_{12}\cos t,\\ T_{22}(t)= & {} (0.2+0.2\sin 2t)e_{0}+0.1 e_{1}\cos ^{2} 2t+0.2 e_{2}\sin 5t+0.2 e_{12}\cos t,\\ S_{11}(t)= & {} 0.1e_{0}\cos 5t+0.1 e_{1}\sin t+0.1 e_{2}2\cos 9t+0.2 e_{12}\sin t,\\ S_{12}(t)= & {} 0.1e_{0}\cos 5t+0.2 e_{1}\sin t+0.1 e_{2}2\cos 9t+0.2 e_{12}\sin t,\\ S_{21}(t)= & {} 0.1e_{0}\cos 5t+0.1 e_{1}\sin t+0.1 e_{2}2\cos 9t+0.4 e_{12}\sin t,\\ S_{22}(t)= & {} 0.1e_{0}\cos 5t+0.2 e_{1}\sin t+0.1 e_{2}2\cos 9t+0.4 e_{12}\sin t,\\ \mu _{1}(t)= & {} 0.1e_{0}\sin t+0.2 e_{1}\cos ^{2} t+0.2 e_{2}\cos 5t+0.1 e_{12}\sin \sqrt{3}t,\\ \mu _{2}(t)= & {} 0.1e_{0}\sin t+0.4 e_{1}\cos ^{2} t+0.2 e_{2}\cos 5t+0.1 e_{12}\sin \sqrt{3}t,\\ \tau _{11}(t)= & {} \tau _{12}(t)=\tau _{21}(t)=\tau _{22}(t)=\cos ^{2} \sqrt{3}t. \end{aligned}$$

By calculating, we have

$$\begin{aligned} L_{1}^f= & {} L^g_{1}=0.0025,\quad L_{2}^f=L^g_{2}=0.005,\quad {\overline{a}}_{1}=0.3,\quad {\overline{a}}_{2}=1.6,\\ {\underline{a}}_{1}= & {} 0.1,\quad {\underline{a}}_{2}=0.8,\quad {\overline{b}}_{11}^{0}=0.4,\quad {\overline{b}}_{11}^{1} ={\overline{b}}_{11}^{2}={\overline{b}}_{12}^{2}=0.1, \quad {\overline{b}}_{11}^{12}=0.3,\\ {\overline{b}}_{12}^{0}= & {} {\overline{b}}_{21}^{0}=0.4,\quad {\overline{b}}_{12}^{12}={\overline{b}}_{21}^{12}=0.3,\quad {\overline{b}}_{21}^{1}=0.1,\quad {\overline{b}}_{21}^{2}={\overline{b}}_{22}^{1} ={\overline{b}}_{22}^{2}=0.2,\\ {\overline{b}}_{22}^{0}= & {} 0.4,\quad {\overline{b}}_{22}^{12}= {\overline{d}}_{11}^{1}=0.3,\quad \quad {\overline{d}}_{12}^{1}=0.3, \quad {\overline{d}}_{12}^{2}= {\overline{d}}_{21}^{0}={\overline{b}}_{12}^{1}=0.2,\\ {\overline{d}}_{11}^{0}= & {} {\overline{d}}_{11}^{2}={\overline{d}}_{11}^{12}= {\overline{d}}_{12}^{0}={\overline{d}}_{12}^{12}={\overline{ d}}_{21}^{1}={\overline{d}}_{21}^{2} ={\overline{d}}_{21}^{12}=0.1,\\ {\overline{d}}_{22}^{0}= & {} {\overline{d}}_{22}^{2}=0.2, \quad {\overline{d}}_{22}^{1}=0.3,\quad {\overline{d}}_{22}^{12}=0.1, \quad {\overline{\tau }}_{11}={\overline{\tau }}_{12}={\overline{\tau }}_{21}= {\overline{\tau }}_{22}=1,\\ {\overline{\alpha }}_{11}^{0}= & {} {\overline{\alpha }}_{11}^{12}={\overline{\alpha }}_{12}^{12}=0.1,\quad {\overline{\alpha }}_{11}^{2}={\overline{\alpha }}_{11}^{1} ={\overline{\alpha }}_{12}^{0}={\overline{\alpha }}_{12}^{2}=0.2, {\overline{\alpha }}_{12}^{1}=0.4,\\ {\overline{\alpha }}_{21}^{0}= & {} 0.1, \quad {\overline{\alpha }}_{21}^{1}={\overline{\alpha }}_{21}^{2} ={\overline{\alpha }}_{22}^{2}={\overline{\alpha }}_{22}^{0}=0.2,\quad {\overline{\alpha }}_{21}^{12}={\overline{\alpha }}_{22}^{12}=0.1,\quad {\overline{\alpha }}_{22}^{1}=0.4,\\ {\overline{\beta }}_{11}^{0}= & {} {\overline{\beta }}_{21}^{0}={\overline{\beta }}_{12}^{0} ={\overline{\beta }}_{22}^{0}=0.3, \quad {\overline{\beta }}_{11}^{1}={\overline{\beta }}_{12}^{1}={\overline{\beta }}_{21}^{1} ={\overline{\beta }}_{22}^{1}=0.1,\\ {\overline{\beta }}_{12}^{2}= & {} {\overline{\beta }}_{22}^{2}=0.4,\quad {\overline{\beta }}_{11}^{2}={\overline{\beta }}_{21}^{2}= {\overline{\beta }}_{12}^{12}={\overline{\beta }}_{11}^{12}= {\overline{\beta }}_{21}^{12}={\overline{\beta }}_{22}^{12}=0.2. \end{aligned}$$

Take $p=3$, it is easy to verify that condition $(H_{1})$ and $(H_2)$ are satisfied. By a simple calculation, we have

$$\begin{aligned}&Q^{0}_{1}=Q^{1}_{1}=Q^{2}_{1}=Q^{12}_{1}=0.056,\quad Q^{0}_{2}=Q^{1}_{2}=Q^{2}_{2}=Q^{12}_{2}=0.106,\\&\max \limits _{A\in \varLambda }\bigg \{\Big (\frac{1}{3{\underline{a}}_{1}}\Big )^{1/3}Q^{A}_{1}, \Big (\frac{1}{3{\underline{a}}_{2}}\Big )^{1/3}Q^{A}_{2}\bigg \}=0.0792<1,\\&\max \limits _{A\in \varLambda }\bigg \{\frac{1}{{\underline{a}}_{1}}Q^{A}_{1}, \frac{1}{{\underline{a}}_{2}}Q^{A}_{2}\bigg \}=0.56<1, \end{aligned}$$

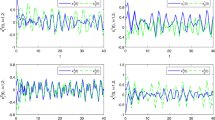
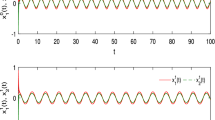
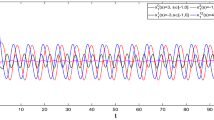
which implies that conditions $(H_{3})$ and $(H_{4})$ are also satisfied. Therefore, according to Theorem 2, (1) has a unique $S^{3}$-almost periodic solution, which is globally exponentially stable (see Figs. 1, 2, 3).

Fig. 1

Curves of $x_{i}^{0}(t)$ and $x_{i}^{1}(t)$, $i=1,2$

Fig. 2

Curves of $x_{i}^{2}(t)$ and $x_{i}^{12}(t)$, $i=1,2$

Fig. 3

Curves of $x^{0}(t)$, $x^{1}(t)$, $x^{2}(t)$ and $x^{12}(t)$ in 3-dimensional space for stable case

Remark 2

For all we know, this is the first paper to study the existence and global exponential stability of $S^{p}$-almost periodic solutions for Clifford-valued fuzzy cellular neural networks with time-varying delays. No known results can lead to the conclusion of Example 1.

5 Conclusion

In this paper, we have investigated the existence and exponential stability of $S^{p}$-almost periodic solutions for a class of Clifford-valued neural networks with time-varying delays. As far as we know, this is the first time to study the $S^{p}$-almost periodicity for Clifford-valued neural networks with time-varying delays. Our results are new even when the considered neural networks degenerates to real-valued, complex-valued and quaternion-valued neural networks. Our method of this paper can be applied to study other types of Clifford-valued neural networks, such as recurrent neural networks, BAM neural networks, SICNNs, Cohen–Grossberg neural networks and so on.