1 Introduction

In standard machine learning, both training and test data are assumed to be drawn from the same distribution. However, this assumption turns out unrealistic for lots of real-world problems, which could cause performance degradation for testing. For example, in visual recognition task, test images may differ from training ones due to changes in backgrounds, sensors, viewpoints, etc. To address this issue, domain adaptation has been proposed in quest of adapting the models built in one domain (source domain) to serve another different but related domain (target domain), in such a way that the learned models perform well in the target domain.

In DA problems, the dataset from the source domain and the dataset from the target domain usually follow different distributions. To narrow the difference, the first thing is to appropriately evaluate the distribution discrepancy across domains for most DA models. Many candidate statistical distances, such as the Kullback–Leibler divergence [5], the Bregman divergence [33], the Wasserstein distance [32] and the maximum mean discrepancy (MMD) [11], can be used to achieve this purpose. MMD is one of the most widely used distances and it is designed to evaluate the distance between the kernel mean embedding of distributions in a reproducing kernel Hilbert space (RKHS). MMD possesses a decent theoretical property, i.e., characteristic kernels establish MMD as metrics on the space of probability distributions [9, 11, 34]. Due to its non-parametric form and its theoretical properties, MMD has attracted widespread attention from the DA community.

Much progress has been made in an effort to explore MMD and thereby obtain transferrable knowledge from the source domain. Theoretically, the characteristic kernel is the natural choice for MMD. However, in specific applications, non-characteristic counterparts might be more appropriate than characteristic ones [3]. Several MMD-based DA methods employ non-characteristic kernels (such as the linear kernel [16, 20, 25] and the polynomial kernel [1, 2]) or the non-kernel linear transformation [14,15,16, 20, 37] to cope with domain shift. Despite the state-of-the-art performance achieved by the non-characteristic kernel based methods, in this paper we point out that there is still much room to improve these current methods. To be specific, with a deep insight into the recent MMD methods, we can come to the conclusion that the non-characteristic kernel based MMD could lose some statistical information that is important for DA.

To capture more information about distributions, this paper designs a new distribution metric termed the maximum mean and covariance discrepancy (MMCD). This metric is designed to address both the first- and second-order statistical information in the RKHS. Specifically, MMCD is comprised of MMD and our proposed maximum covariance discrepancy (MCD). MCD evaluates the Hilbert–Schmidt norm of the difference between covariance operators such that it addresses the second-order statistics in the RKHS. Since MMCD unites MCD and MMD, MMCD is able to simultaneously consider the first- and second-order statistics in the RKHS. Thus, when the non-characteristic kernel is used, MMCD has the ability to capture more information about distributions than MMD does. This point will be analyzed in Sects. 3.2 and 3.3.

To verify the efficacy of MMCD, we propose an unsupervised DA method that is based on MMCD (McDA) in the joint distribution adaptation (JDA) paradigm [20]. JDA has been chosen because it jointly adapts both the marginal and conditional distributions across domains. It is not easy to optimize McDA due to its non-convex term. To address this issue, we approximate the non-convex term with its convex upper bound, thereby yielding a closed-form solution to each sub-problem. Experiments in cross-domain image classification on two datasets (PIE and Office-Caltech) show the effectiveness of McDA in the JDA paradigm when compared with the baseline methods, which implies the efficacy of MMCD.

The rest of this paper is organized as follows. Section 2 reviews the related works. Section 3 introduces the proposed maximum mean and covariance discrepancy. Section 4 details the MMCD based unsupervised DA model McDA, along with an optimization algorithm to solve it. In Sect. 5, we report the performance of McDA on two benchmark datasets. Finally, Sect. 6 concludes the paper.

2 Related Work

Domain adaptation (DA) has been widely studied in extensive literatures [26, 27]. DA can be categorized into two groups supervised DA and unsupervised DA according to whether or not the data in the target domain is labeled [4, 6, 25, 38, 40]. In this paper, we focus on the unsupervised setting. To tackle the unsupervised DA problem, many methods has been proposed including sample reweighting [17], projection learning [25] and subspace alignment [8, 36]. Among them, a popular way is to learn the domain-invariant representation which minimize the distribution discrepancy across domains. Notably, two methods of measuring the distribution discrepancy have been widely adopted in DA models: maximum mean discrepancy (MMD) metric [11] and the explicit order-wise distance between distributions.

As a representative metric used to measure distribution discrepancy, MMD has been widely used in DA methods. For instance, Pan et al. [25] developed transfer component analysis (TCA) to learn invariant features across domains in the reproducing kernel Hilbert space (RKHS). To investigate the benefits of conditional distributions, Long et al. [20] constructed a joint distribution adaptation (JDA) paradigm which adopted MMD in order to jointly evaluate the marginal and conditional distribution differences across domains. JDA yielded the state-of-the-art classification performance. Recently, Hsieh et al. [15] generalized JDA in order to tackle heterogeneous DA problems. Later, the closest common space learning [16] was proposed to deal with imbalanced cross-domain data problem in the frame of JDA. With advances in deep learning, MMD-based deep models have also made great success in adaptation performance across domains. Long et al. [19] proposed a deep adaptation network architecture, in which a multiple-kernel MMD was utilized in order to match cross-domain distributions of multiple task-specific CNN layers, so as to boost the transferability of deep features. Recently, Long et al. [21] have proposed a new DA method to be used in deep networks, i.e., residual transfer networks, which was able to jointly learn both adaptive classifiers and transferable features. To be different, Our MMCD explores both the first- and second-order statistics in the RKHS.

In addition to MMD-based models, recent work has explicitly matched the order-wise statistics of cross-domain distributions, thereby taking the statistics of distributions into account. For example, Sun et al. [35] proposed an efficient unsupervised DA method, which they designated as correlation alignment, to align the covariance matrix of the source and target distributions. Jiang et al. [18] proposed to use the second moment matching so as to learn the domain-invariant feature. Zong et al. [41] took a different approach which explores both the least-square regression and mean–covariance feature matching in order to enhance the performance of cross-corpus speech emotion recognition. Zellinger et al. [39] took a step forward to explore higher order moment which learns domain-invariant representations by means of explicitly order-wise moment matching. Different from the above mentioned methods which all study in the original feature space, our MMCD, however, explores the higher order statistics in the RKHS by using the kernel trick.

It is noted that MMCD is related to the work of [22] which embeds distributions in a finite dimensional feature space, and matches the mean and covariance feature statistics in order to train generative adversarial networks. The proposed MMCD differs from this approach in two ways. Firstly, MMCD function set is from the RKHS which is infinitely dimensional in the setting of PSD kernels. In comparison, the function set used by [22] is parameterized by a finite-dimensional CNN. Secondly, MCD can be represented as the Hilbert–Schmidt norm. By contrast, the covariance matching in [22] is related to the nuclear norm. Besides, we notice that the empirical estimator of squared MCD has similar form to that from [28, 29]. However, they are different in three aspects. Firstly, MCD is defined in the frame of integral probability metrics [24] and can be regarded as the second-order generation of MMD, while [28] uses the empirical estimator of squared MCD directly. Secondly, MCD serves as distribution metric, while [28] uses covariance operators as image representation. Thirdly, this paper unites both MMD and MCD as MMCD to measure the distribution discrepancy.

3 Maximum Mean and Covariance Discrepancy

This section will introduce the maximum covariance discrepancy (MCD) and its joint variant the maximum mean and covariance discrepancy (MMCD). In addition, several theoretical analyses will be provided. At first, we introduce the notations that are used throughout this section.

Let \(\mathcal{H}\) be a reproducing kernel Hilbert space (RKHS) over X with associated kernel \(k\left( { \cdot , \cdot } \right) \), whose canonical feature map is \(\phi \left( x \right) = k\left( {x, \cdot } \right) \) for \(x \in X\). Let x and y be random variables defined on X, we assume \(x\sim p\) and \(y\sim q\), where \(x\sim p\) indicates x follows distribution p. The notation \({E_{x\sim p}}\) denotes the expectation with respect to p, and we abbreviate \({E_{x\sim p}}\) and \({E_{x\sim q}}\) to \({E_x}\) and \({E_y}\) respectively when there is no ambiguity. Following [12], when given \(f,g \in \mathcal{H}\), the tensor product operator \(f \otimes g{:}\,\mathcal{H} \rightarrow \mathcal{H}\) is defined as \(\left( {f \otimes g} \right) h = f{\left\langle {g,h} \right\rangle _\mathcal{H}}\) for all \(h \in H\), where \( \otimes \) denotes the tensor product. Based on the tensor product operator and probability distributions, the centered covariance operator \(C{:}\,\mathcal{H} \rightarrow \mathcal{H}\) associated with the distribution p has the definition \(C\left[ p \right] = {E_{x\sim p}}\left[ {\phi \left( x \right) \otimes \phi \left( x \right) } \right] - {E_{x\sim p}}\left[ {\phi \left( x \right) } \right] \otimes {E_{x\sim p}}\left[ {\phi \left( x \right) } \right] \). At last, we make two assumptions in our paper. First, we assume the kernel \(k\left( { \cdot , \cdot } \right) \) to be bounded, which makes the covariance operator bounded and the mean embedding of distributions in \(\mathcal{H}\) exists [11]. Second, we assume \(\mathcal{H}\) to be separable such that the basis of \(\mathcal{H}\) is finite or countably infinite.

3.1 Definition

With the assumptions and notations above, we define the MCD in Definition 1.

Definition 1

The maximum covariance discrepancy (MCD) is defined as

$$\begin{aligned} {\mathop {\mathrm{MCD}}\nolimits } \left[ {p,q,\mathcal{H}} \right] = \mathop {\sup }\limits _{\left\| a \right\| \le 1} \sum \limits _{i,j \in I} {{a_{ij}}\left( {{\mathop {\mathrm{cov}}} \left[ {{e_i}\left( x \right) ,{e_j}\left( x \right) } \right] - {\mathop {\mathrm{cov}}} \left[ {{e_i}\left( y \right) ,{e_j}\left( y \right) } \right] } \right) }, \end{aligned}$$
(1)

where \(\left\{ {{e_i}|i \in I} \right\} \) is an orthogonal basis of \(\mathcal{H}\), \(\left\| a \right\| = {(\sum \nolimits _{i,j \in I} {a_{ij}^2} )^{1/2}}\), and the notation \({\mathop {\mathrm{cov}}} \) has the following formula: \({\mathop {\mathrm{cov}}} \left[ {{e_i}\left( x \right) ,{e_j}\left( x \right) } \right] = {E_x}\left[ {{e_i}\left( x \right) {e_j}\left( x \right) } \right] - {E_x}\left[ {{e_i}\left( x \right) } \right] {E_x}\left[ {{e_j}\left( x \right) } \right] \).

Next, we show that the (1) can be associated with the Hilbert–Schmidt norm with the following lemma:

Lemma 1

$$\begin{aligned} {\mathop {\mathrm{MCD}}\nolimits } \left[ {p,q,\mathcal{H}} \right] = {\left\| {C\left[ p \right] - C\left[ q \right] } \right\| _{{\mathrm{HS}}}}, \end{aligned}$$
(2)

where \({\left\| {} \right\| _{{\mathrm{HS}}}}\) denotes the Hilbert–Schmidt norm of the vectors in \({\mathrm{HS}}\left( \mathcal{H} \right) \), which is the Hilbert space of Hilbert–Schmidt operators mapping from \(\mathcal{H}\) to \(\mathcal{H}\).

Proof

By using the reproducing property of the kernel k, we have

$$\begin{aligned}&\sum \limits _{i,j \in I} {{a_{ij}}\left( {{E_x}\left[ {{e_i}\left( x \right) {e_j}\left( x \right) } \right] - {E_x}\left[ {{e_i}\left( x \right) } \right] {E_x}\left[ {{e_j}\left( x \right) } \right] } \right) }\nonumber \\&\quad = {\left\langle {\sum \nolimits _{i,j \in I} {{a_{ij}}{e_i} \otimes {e_j}} ,C\left[ p \right] } \right\rangle _{{\mathrm{HS}}}}. \end{aligned}$$
(3)

Similarly, we also have

$$\begin{aligned}&\sum \limits _{i,j \in I} {{a_{ij}}\left( {{E_y}\left[ {{e_i}\left( y \right) {e_j}\left( y \right) } \right] - {E_y}\left[ {{e_i}\left( y \right) } \right] {E_y}\left[ {{e_j}\left( y \right) } \right] } \right) } \nonumber \\&\quad = {\left\langle {\sum \nolimits _{i,j \in I} {{a_{ij}}{e_i} \otimes {e_j}} ,C\left[ q \right] } \right\rangle _{{\mathrm{HS}}}}. \end{aligned}$$
(4)

In terms of (3) and (4), we have

$$\begin{aligned} {\mathop {\mathrm{MCD}}\nolimits } \left[ {p,q,\mathcal{H}} \right]= & {} \mathop {\sup }\limits _{\left\| a \right\| \le 1} {\left\langle {\sum \nolimits _{i,j \in I} {{a_{ij}}{e_i} \otimes {e_j}} ,C\left[ p \right] - C\left[ q \right] } \right\rangle _{{\mathrm{HS}}}}\nonumber \\= & {} \mathop {\sup }\limits _{h \in \mathcal{H} \otimes \mathcal{H},\;{{\left\| h \right\| }_{\mathcal{H} \otimes \mathcal{H}}} \le 1} {\left\langle {{h^*},C\left[ p \right] - C\left[ q \right] } \right\rangle _{{\mathrm{HS}}}}\nonumber \\= & {} \mathop {\sup }\limits _{h \in \mathcal{H} \otimes \mathcal{H},\;{{\left\| {{h^*}} \right\| }_{{\mathrm{HS}}}} \le 1} {\left\langle {{h^*},C\left[ p \right] - C\left[ q \right] } \right\rangle _{{\mathrm{HS}}}}\nonumber \\= & {} {\left\| {C\left[ p \right] - C\left[ q \right] } \right\| _{{\mathrm{HS}}}}, \end{aligned}$$
(5)

where \({h^*}\) denotes the tensor product operator of h which belongs to the tensor product space \(\mathcal{H} \otimes \mathcal{H}\). Since \(\left\{ {{e_i}|i \in I} \right\} \) is the orthogonal basis of \(\mathcal{H}\), \(\left\{ {{e_i} \otimes {e_j}|i,j \in I} \right\} \) consists of the orthogonal basis of \(\mathcal{H} \otimes \mathcal{H}\). Thus, the second equality holds. The third equality follows from the following fact:

$$\begin{aligned} \left\| {{h^*}} \right\| _{{\mathrm{HS}}}^2= & {} {\left\langle {\sum \nolimits _{i,j \in I} {{a_{ij}}{e_i} \otimes {e_j}} ,\sum \nolimits _{i,j \in I} {{a_{ij}}{e_i} \otimes {e_j}} } \right\rangle _{\mathrm{HS}}}\nonumber \\= & {} \sum \limits _{i,j \in I} {{a_{ij}}} \sum \limits _{m,n \in I} {{a_{mn}}} {\left\langle {{e_i} \otimes {e_j},{e_m} \otimes {e_n}} \right\rangle _{\mathrm{HS}}}\nonumber \\= & {} \sum \limits _{i,j \in I} {{a_{ij}}} \sum \limits _{m,n \in I} {{a_{mn}}} {\left\langle {{e_i},{e_m}} \right\rangle _\mathcal{H}}{\left\langle {{e_j},{e_n}} \right\rangle _\mathcal{H}}\nonumber \\= & {} \sum \limits _{i,j \in I} {a_{ij}^2} \nonumber \\= & {} \left\| h \right\| _{\mathcal{H} \otimes \mathcal{H}}^2. \end{aligned}$$
(6)

\(\square \)

To compute it, we express MCD as the expansion formula with respect to kernel functions, using the following lemma:

Lemma 2

The squared MCD terms of kernel functions is

$$\begin{aligned}&{{\mathop {\mathrm{MCD}}\nolimits } ^2}\left[ {p,q,\mathcal{H}} \right] = {E_{x,x'}}\left[ {{k^2}\left( {x,x'} \right) } \right] - 2{E_x}\left[ {E_{x'}^2\left[ {k\left( {x,x'} \right) } \right] } \right] \nonumber \\&\quad +\,E_{x,x'}^2\left[ {k\left( {x,x'} \right) } \right] - 2{E_{x,y}}\left[ {{k^2}\left( {x,y} \right) } \right] + 2{E_x}\left[ {E_y^2\left[ {k\left( {x,y} \right) } \right] } \right] \nonumber \\&\quad +\,2{E_y}\left[ {E_x^2\left[ {k\left( {x,y} \right) } \right] } \right] - 2E_{x,y}^2\left[ {k\left( {x,y} \right) } \right] + {E_{y,y'}}\left[ {{k^2}\left( {y,y'} \right) } \right] \nonumber \\&\quad -\,2{E_y}\left[ {E_{y'}^2\left[ {k\left( {y,y'} \right) } \right] } \right] + E_{y,y'}^2\left[ {k\left( {y,y'} \right) } \right] , \end{aligned}$$
(7)

where \(x'\) and \(y'\) are independent copy of x and y, with the same distribution, respectively.

Given the limited observations \(X = \left\{ {{x_1},\ldots ,{x_n}} \right\} \) and \(Y = \left\{ {{y_1},\ldots ,{y_m}} \right\} \) sampled from p and q, and based on Lemma 2 and statistical theory, an empirical estimator of squared MCD can be given by

$$\begin{aligned} {\widehat{{\mathop {\mathrm{MCD}}\nolimits } }^2}\left[ {X,Y,\mathcal{H}} \right]= & {} \frac{1}{{{n^2}}}tr\left( {{K_{XX}}{L_n}{K_{XX}}{L_n}} \right) \nonumber \\&- \frac{2}{{nm}}tr\left( {{K_{XY}}{L_m}K_{XY}^T{L_n}} \right) + \frac{1}{{{m^2}}}tr\left( {{K_{YY}}{L_m}{K_{YY}}{L_m}} \right) , \end{aligned}$$
(8)

where \({({K_{XX}})_{ij}} = k({x_i},{x_j})\), \({({K_{XY}})_{ij}} = k({x_i},{y_j})\), \({({K_{YY}})_{ij}} = k({y_i},{y_j})\), and \({L_n} = {I_n} - {\frac{1}{n}}1_n^T{1_n}\) wherein \({I_n}\) is the identity matrix of size n, and \({1_n}\) is the vector of ones with length n. This can be notated as, \({L_m} = {I_m} - {\frac{1}{m}}1_m^T{1_m}\). To be concise, we can rewrite (8) as the elegant formula

$$\begin{aligned} {\widehat{\mathrm{MCD}}^2}\left[ {X,Y,\mathcal{H}} \right] = tr\left( {KZKZ} \right) , \end{aligned}$$
(9)

where

$$\begin{aligned} K = \left[ {\begin{array}{*{20}{c}} {{K_{XX}}}&{}\quad {{K_{XY}}}\\ {{K_{YX}}}&{}\quad {{K_{YY}}}\end{array} } \right] , \end{aligned}$$
(10)

and

$$\begin{aligned} {Z_{ij}} = \left\{ \begin{array}{llll} \frac{1}{n} - \frac{1}{{{n^2}}},&{}\quad i = j,{x_i} \in X\\ - \frac{1}{{{n^2}}},&{}\quad i \ne j,{x_i} \in X,{x_j} \in X\\ \frac{1}{{{m^2}}} - \frac{1}{m},&{}\quad i = j,{x_i} \in Y\\ \frac{1}{{{m^2}}},&{}\quad i \ne j,{x_i} \in Y,{x_j} \in Y\\ 0,&{}\quad otherwise.\; \end{array} \right. \end{aligned}$$
(11)

Moreover, we can also yield another equivalent representation of (8), as follows:

$$\begin{aligned} \left\| {\frac{1}{n}\phi \left( X \right) {L_n}\phi {{\left( X \right) }^T} - \frac{1}{m}\phi \left( Y \right) {L_m}\phi {{\left( Y \right) }^T}} \right\| _{\mathrm{HS}}^2, \end{aligned}$$
(12)

where \(k\left( {x,y} \right) = \phi {\left( x \right) ^T}\phi \left( y \right) \), wherein \(\phi \left( X \right) = \left[ {\phi \left( {{x_1}} \right) ,\ldots ,\phi \left( {{x_n}} \right) } \right] \) and \(\phi \left( Y \right) = \left[ {\phi \left( {{y_1}} \right) ,\ldots ,\phi \left( {{y_m}} \right) } \right] \). This form will be utilized in the later section.

Now, we unite MMD and MCD into a joint metric, namely maximum mean and covariance discrepancy (MMCD) in order to capture more statistical information from data distributions.

Definition 2

The maximum mean and covariance discrepancy (MMCD) is defined as

$$\begin{aligned} {\mathrm{MMCD}}\left[ {p,q,\mathcal{H}} \right] = {\left( {\left\| {\mu \left[ p \right] - \mu \left[ q \right] } \right\| _\mathcal{H}^2 + \beta \left\| {C\left[ p \right] - C\left[ q \right] } \right\| _{{{\mathrm{HS}}}}^2} \right) ^{1/2}}, \end{aligned}$$
(13)

where \(\mu \left[ p \right] = {E_x}\left[ {\phi \left( x \right) } \right] \) and \(\beta \) is a non-negative parameter.

According to this definition, MMCD can be proven as a distribution metric when the associate kernel of \(\mathcal{H}\) is characteristic. This property can be established by Theorem 1.

Theorem 1

Let the associated kernel of \(\mathcal{H}\) be characteristic. Then \({\mathrm{MMCD}}\left[ {p,q,\mathcal{H}} \right] = 0\) if and only if \(p = q\). Moreover, \({\mathrm{MMCD}}\left[ {p,q,\mathcal{H}} \right] \) is a metric on the space of probability distribution.

Proof

According to [7], a metric d should satisfy four properties: non-negativity, \(d(p, q)=0 \Leftrightarrow p=q\), symmetry and triangle inequality. Apparently, MMCD is non-negative due to the non-negativity of the norm. For the necessity and sufficiency of the second property, first, under the condition \(p = q\), \({\mathop {\mathrm{MMCD}}\nolimits } \left[ {p,q,\mathcal{H}} \right] = 0\); conversely, \(p = q\) can be deduced according to the definition of characteristic kernel [9] and \({\mathop {\mathrm{MMD}}\nolimits } \left[ {p,q,\mathcal{H}} \right] = 0\). As a side assertion, it is easy to verify that \({\mathop {\mathrm{MMCD}}\nolimits } \left[ {p,q,\mathcal{H}} \right] = {\mathop {\mathrm{MMCD}}\nolimits } \left[ {q,p,\mathcal{H}} \right] \) which demonstrates the symmetric property of MMCD. The only property left to prove is the triangle inequality. First, we need to prove that the \({\mathrm{MCD}}\) meets this property. Let \({{\mathrm{d}}_{ij}}\left( {x,y} \right) = {\mathop {\mathrm{cov}}} [ {{e_i}\left( x \right) ,{e_j}\left( x \right) } ] - {\mathop {\mathrm{cov}}} [ {{e_i}\left( y \right) ,{e_j}\left( y \right) } ]\), and then we have

$$\begin{aligned}&{\mathop {\mathrm{MCD}}\nolimits } \left[ {p,r,\mathcal{H}} \right] + {\mathop {\mathrm{MCD}}\nolimits } \left[ {r,q,\mathcal{H}} \right] \nonumber \\&\quad = \mathop {\sup }\limits _{\left\| a \right\| \le 1} \left( {\sum \limits _{i,j \in I} {{a_{ij}}{{\mathrm{d}}_{ij}}\left( {x,z} \right) } } \right) + \mathop {\sup }\limits _{\left\| a \right\| \le 1} \left( {\sum \limits _{i,j \in I} {{a_{ij}}{{\mathrm{d}}_{ij}}\left( {z,y} \right) } } \right) \nonumber \\&\quad \ge \mathop {\sup }\limits _{\left\| a \right\| \le 1} \left( {\sum \limits _{i,j \in I} {{a_{ij}}{{\mathrm{d}}_{ij}}\left( {x,z} \right) } + \sum \limits _{i,j \in I} {{a_{ij}}{{\mathrm{d}}_{ij}}\left( {z,y} \right) } } \right) \nonumber \\&\quad = \mathop {\sup }\limits _{\left\| a \right\| \le 1} \left( {\sum \limits _{i,j \in I} {{a_{ij}}{{\mathrm{d}}_{ij}}\left( {x,y} \right) } } \right) \nonumber \\&\quad = {\mathop {\mathrm{MCD}}\nolimits } \left[ {p,q,\mathcal{H}} \right] , \end{aligned}$$
(14)

where \(z\sim r\). Next, we prove the triangle inequality holds for the \({\mathrm{MMCD}}\). To simplify the notation, let \({\mathop {\mathrm{M}}\nolimits } \left[ {p,q} \right] = {\mathop {\mathrm{MMD}}\nolimits } \left[ {p,q,\mathcal{H}} \right] \), \(\mathrm{C}\left[ {p,q} \right] = {\mathop {\mathrm{MCD}}\nolimits } \left[ {p,q,\mathcal{H}} \right] \) and \(\mathrm{MC}\left[ {p,q} \right] = {\mathop {\mathrm{MMCD}}\nolimits } \left[ {p,q,\mathcal{H}} \right] \), and then we have

$$\begin{aligned} {\mathrm{MC}^2}\left[ {p,q} \right]= & {} {\mathrm{M}^2}\left[ {p,q} \right] + \beta {\mathrm{C}^2}\left[ {p,q} \right] \nonumber \\\le & {} {\left( {\mathrm{M}\left[ {p,r} \right] + \mathrm{M}\left[ {r,q} \right] } \right) ^2} + \beta {\left( {\mathrm{C}\left[ {p,r} \right] + \mathrm{C}\left[ {r,q} \right] } \right) ^2}\nonumber \\= & {} {\mathrm{M}^2}\left[ {p,r} \right] + \beta {\mathrm{C}^2}\left[ {p,r} \right] + {\mathrm{M}^2}\left[ {r,q} \right] + \beta {\mathrm{C}^2}\left[ {r,q} \right] \nonumber \\&\quad +\,2\left( {\mathrm{M}\left[ {p,r} \right] \mathrm{M}\left[ {r,q} \right] + \sqrt{\beta }\mathrm{C}\left[ {p,r} \right] \sqrt{\beta }\mathrm{C}\left[ {r,q} \right] } \right) \nonumber \\\le & {} {\mathrm{M}^2}\left[ {p,r} \right] + \beta {\mathrm{C}^2}\left[ {p,r} \right] + {\mathrm{M}^2}\left[ {r,q} \right] + \beta {\mathrm{C}^2}\left[ {r,q} \right] \nonumber \\&\quad +\,2{\left( {{\mathrm{M}^2}\left[ {p,r} \right] + \beta \mathrm{C}\left[ {p,r} \right] } \right) ^{1/2}}{\left( {{\mathrm{M}^2}\left[ {r,q} \right] + \beta \mathrm{C}\left[ {r,q} \right] } \right) ^{1/2}}\nonumber \\= & {} {\left( {\mathrm{MC}\left[ {p,r} \right] + \mathrm{MC}\left[ {r,q} \right] } \right) ^2}, \end{aligned}$$
(15)

where the first inequality holds because both \({\mathrm{MMD}}\) and \({\mathrm{MCD}}\) meet the triangle inequality, and the second inequality holds from the Cauchy–Schwarz inequality. Taking the square root of both sides, there holds \({\mathop {\mathrm{MMCD}}\nolimits } \left[ {p,q} \right] \le {\mathop {\mathrm{MMCD}}\nolimits } \left[ {p,r} \right] + {\mathop {\mathrm{MMCD}}\nolimits } \left[ {r,q} \right] \). Obviously, \({\mathrm{MMCD}}\) meets the metric definition, and is, therefore, a metric. \(\square \)

In fact, while Theorem 1 relies on the condition that the kernel is characteristic, even if the condition does not hold, MMCD is still a pseudo-metric. According to (9) and [11], the empirical estimator of the squared MMCD can be given by

$$\begin{aligned} {{\widehat{\mathrm{MMCD}}}^2}\left[ {p,q,\mathcal{H}} \right] = tr\left( {KM} \right) + \beta tr\left( {KZKZ} \right) , \end{aligned}$$
(16)

and

$$\begin{aligned} {\widehat{\mathrm{MMCD}}}^2\left[ {p,q,\mathcal{H}} \right]= & {} \left\| {\frac{1}{n}\phi \left( X \right) {1_n} - \frac{1}{m}\phi \left( Y \right) {1_m}} \right\| _\mathcal{H}^2\nonumber \\&+\,\beta \left\| {\frac{1}{n}\phi \left( X \right) {H_n}\phi {{\left( X \right) }^T} - \frac{1}{m}\phi \left( Y \right) {H_m}\phi {{\left( Y \right) }^T}} \right\| _{{\mathrm{HS}}}^2, \end{aligned}$$
(17)

where

$$\begin{aligned} {M_{ij}} = \left\{ \begin{array}{lll} \frac{1}{{n^2}},&{}\quad {x_i},{x_j} \in X\\ \frac{1}{{m^2}},&{}\quad {x_i},{x_j} \in Y\\ - \frac{{ 1}}{{{n}{m}}},&{}\quad otherwise. \end{array} \right. \end{aligned}$$
(18)

3.2 Explicit Representation of MMCD

As stated above, we have defined MMCD as the (pseudo-) metric of distributions. However, it is not easy to understand what specific information about the distribution is captured by MMCD. Towards this goal, we deduce the explicit representation of MMCD with the polynomial kernel and the linear kernel to illustrate the mechanism of MMCD.

We first introduce the explicit representation of MMCD associated with the polynomial kernel with a specific degree d, i.e., \(k\left( {x,y} \right) = {( {x^T{y} + c} )^d}\). According to the explicit feature map of the polynomial kernel [23, 31], MMCD can be explicitly written as

$$\begin{aligned}&\mathrm{MMCD}{^2}\left[ {p,q} \right] = \left\| {E\left[ {{W_p}} \right] - E\left[ {{W_q}} \right] } \right\| _2^2\nonumber \\&\quad +\,\beta \left\| {E\left[ {{W_p}W_p^T} \right] - E\left[ {{W_p}} \right] E\left[ {W_p} \right] ^T - \left( {E\left[ {{W_q}W_q^T} \right] - E\left[ {{W_q}} \right] E\left[ {W_q} \right] ^T} \right) } \right\| _F^2,\qquad \quad \end{aligned}$$
(19)

where

$$\begin{aligned} {W_p} = {\left[ {\sqrt{{c^{d - 1}}C_d^1} vec{{( { \otimes ^1x} )}^T},\ldots ,\sqrt{{c^{d - i}}C_d^i} vec{{( { \otimes ^ix} )}^T},\ldots ,\sqrt{{c^{0}}C_d^d} vec{{( { \otimes ^dx} )}^T}} \right] ^T},\qquad \end{aligned}$$
(20)

and \(C_d^i\) denotes the binomial coefficient, vec() converts the matrix into a column vector, and \( \otimes ^ix \) denotes the ith order tensor product of x, wherein \(x \sim p\).

By setting \(d=1\), (19) becomes

$$\begin{aligned} {\mathrm{MMCD}}^2\left[ {p,q} \right]= & {} \left\| {E\left[ x \right] - E\left[ y \right] } \right\| _2^2\nonumber \\&\quad +\,\beta \left\| {E\left[ {x{x^T}} \right] - E\left[ x \right] E{{\left[ x \right] }^T} - \left( {E\left[ {y{y^T}} \right] - E\left[ y \right] E{{\left[ y \right] }^T}} \right) } \right\| _F^2,\nonumber \\ \end{aligned}$$
(21)

where \(x \sim p\) and \(y \sim q\). Given limited X and Y sampled from p and q, respectively, there is

$$\begin{aligned} {\widehat{\mathrm{MMCD}}}^2\left[ {p,q} \right] = \left\| {{\mu _p} - {\mu _q}} \right\| _2^2 + \beta \left\| {{\varSigma _p} - {\varSigma _q}} \right\| _F^2, \end{aligned}$$
(22)

where \({\mu _p} = \frac{1}{n}X{1_n}\) and \({\varSigma _p} = \frac{1}{n}X{H_n}{X^T}\) are mean vector and covariance matrix of X, respectively. Specially, when \(c=0\), the polynomial kernel becomes the linear kernel \(k\left( {x,y} \right) = x^T{y}\). Accordingly, (21) is exactly the explicit representation of MMCD with the linear kernel, and (22) is still the corresponding empirical estimator. As a result, both (21) and (22) show that MMD and MCD of MMCD measures the difference between means and covariances of distributions, respectively, when the polynomial kernel with degree \(d=1\) or the linear kernel is adopted.

Moreover, by setting \(d = 2\), there is

$$\begin{aligned} {W_p} = {\left[ {\sqrt{2c} vec{{\left( {x{x^T}} \right) }^T},{x^T}} \right] ^T}. \end{aligned}$$
(23)

Combination of (19) with (23) shows that the MMD term of MMCD measures the difference between both the first and second raw moments of two distributions, whereas the MCD term measures the difference between covariances of up to the second raw moment of two distributions. An analogy for setting \(d>2\) means that the MCD term can capture higher order statistical information. From the statistical perspective, more insights into MCD remain to be further investigated in the future work.

3.3 Toy Examples

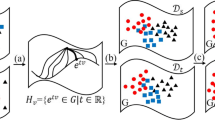
To clarify the efficacy of MMCD, which fuses both first- and second-order statistics in the RKHS, we illustrate two toy examples in Fig. 1a, b. We synthesize two groups of data points which follow different distributions in the two-dimensional space. Then, we fix one group of data points (in blue) and adjust the points from the other group (in red) by minimizing the values of MMD, MCD and MMCD via the gradient descent algorithm. Two types of kernels, that is, the linear kernel (Fig. 1a) and the polynomial kernel with \(d=2\) and \(c=1\) (Fig. 1b), are adopted. For concise, the details of computing their gradients are left in “Appendix A”.

Fig. 1
figure 1

Two toy examples for comparison of MMD, MCD and MMCD on the synthetic data. a Blue and red points are sampled from two Gaussian distributions whose both the mean and covariance are different, and the linear kernel is used, b blue points are sampled from a complicated distribution with the zero mean (0, 0), while red points are sampled from a Gaussian distribution with the mean (0, 1). The polynomial kernel with degree two is used therein. (Color figure online)

Full size image

From Fig. 1a, through the distribution matching of MMD, the means of the red and blue points are almost identical, but the corresponding spread of these data points has different shapes. That is, MMD cannot match the covariances of two distributions. But, for MCD, the result is reversed, namely, the covariances of two groups of data points appear to be similar, but the corresponding means of these data points keep invariant as before and still differ from each other. Notably, after MMCD performs the distribution matching over two groups of data points, the distribution regions of both the red and blue points overlap highly. This is because MMCD simultaneously takes both mean and covariance differences into consideration, while either MMD or MCD could singly consider one aspect where the linear kernel is used.

Figure 1b displays, for the complicated distribution, the distribution matching results of MMD, MCD and MMCD, when the polynomial kernel with degree two is equipped. In this case, MMD induces different spread shapes, which corresponds to the high-order statistics. Meanwhile, it can be verified that the mean of the red data points is above that of the blue points which is zero. Thus, both MMD and MCD fail to make two distributions matched in this example. By using MMCD, the red and blue points become highly overlapped. This implies the efficacy of MMCD which explores both first- and second-order statistics in the RKHS, as compared to MMD and MCD. Hence, in contrast with MMD and MCD, MMCD has the promising potential of matching data distributions across domains for domain adaptation. More empirical analyses about the efficacy of MMCD in domain adaptation are shown in experiments.

4 Domain Adaptation Via MMCD

In this section, we apply the MMCD to unsupervised domain adaptation problem to verify the efficacy of MMCD. Unsupervised domain adaptation is still very challenging, as there is no supervised knowledge of target domains. Recently, joint distribution adaptation (JDA) [20] has been proven a promising domain adaptation method which matches both marginal and conditional distributions. JDA adopts MMD as the distance measurement of distributions; however, in the case of non-characteristic kernels, MMD based JDA loses the high-order statistical information. As mentioned in the previous section, MMCD has a better chance to capture more information about distributions than MMD. We thus substitute our MMCD for MMD in the frame of JDA to produce a new unsupervised domain adaptation method called McDA. In the subsection, we first introduce the problem formulation and notation, and then propose the McDA.

4.1 Problem Formulation and Notations

Given the dataset \({D_s} = \left\{ {{x_1},\ldots ,{x_{{n_s}}}} \right\} \) in the source domain with labels \({y_1},\ldots ,{y_{{n_s}}}\) and the unlabeled dataset \({D_t} = \left\{ {{x_{{n_s} + 1}},\ldots ,{x_{{n_s} + {n_t}}}} \right\} \) in the target domain under the assumption that both the marginal and conditional probability distributions in two domains are different, i.e., \({P_s}\left( {{x_s}} \right) \ne {P_t}\left( {{x_t}} \right) \) and \({P_s}\left( {{y_s}|{x_s}} \right) \ne {P_t}\left( {{y_t}|{x_t}} \right) \). We will adapt both marginal and conditional distributions in order to train a robust classifier on target dataset by leveraging the labeled source dataset.

For clarity, we now summarize several commonly used notations. The source and target data are denoted as \({X_s} = \left[ {{x_1},\ldots ,{x_{{n_s}}}} \right] \) and \({X_t} = \left[ {{x_{{n_s} + 1}},\ldots ,{x_{{n_s} + {n_t}}}} \right] \), respectively, and, for brevity, \(X = \left[ {{X_s},{X_t}} \right] \). The centeralized matrix \({L_n}\) is defined as \({L_n} = {I_n} - \frac{1}{n}1_n^T{1_n}\), where \({I_n}\) is the identity matrix of size n, and \({1_n}\) is the vector of ones with length n.

Since our model McDA is based on the JDA paradigm, it is necessary to review it before our text. JDA is to adapt both marginal and conditional distributions across domains by minimizing the following objective:

$$\begin{aligned} \mathop {\min }\limits _\phi {\left\| {E\left[ {\phi \left( {{x_s}} \right) } \right] - E\left[ {\phi \left( {{x_t}} \right) } \right] } \right\| ^2} + {\left\| {E\left[ {{y_s}|\phi \left( {{x_s}} \right) } \right] - E\left[ {{y_s}|\phi \left( {{x_s}} \right) } \right] } \right\| ^2}. \end{aligned}$$
(24)

According to [20], \(\phi \) can serve as a linear transformation, or a non-linear feature map associated with the kernel. The property of MMD still is an open problem when substituting its feature map for linear transformation. Then we roughly regard the terms of (24) as the estimation of the generalized MMD whose feature map can be replaced with any arbitrary maps. Thus, following [20], we obtain two variants of our McDA according to the used feature maps: the linear transformation and the kernel feature map.

4.2 McDA

For the first variant of McDA, we adopt the linear transformation denoted by a matrix \(A \in {R^{m \times k}}\) to MMCD. According to (17), the distance between marginal distributions across domains can be converted into

$$\begin{aligned}&\left\| {\frac{1}{{{n_s}}}{A^T}{X_s}{1_{{n_s}}} - \frac{1}{{{n_t}}}{A^T}{X_t}{1_{{n_t}}}} \right\| _2^2 + \beta \left\| {\frac{1}{{{n_s}}}{A^T}{X_s}{L_{{n_s}}}X_s^TA - \frac{1}{{{n_t}}}{A^T}{X_t}{L_{{n_t}}}X_t^TA} \right\| _F^2\nonumber \\&\quad = tr\left( {{A^T}X{M_0}{X^T}A} \right) + \beta \left\| {{A^T}X{Z_0}{X^T}A} \right\| _F^2, \end{aligned}$$
(25)

where \({M_0}\) is defined as:

$$\begin{aligned} {\left( {{M_0}} \right) _{ij}} = \left\{ \begin{array}{lll} \frac{1}{{n_s^2}},&{}\quad {x_i},{x_j} \in {D_s}\\ \frac{1}{{n_t^2}},&{}\quad {x_i},{x_j} \in {D_t}\\ -\frac{{ 1}}{{{n_s}{n_t}}},&{}\quad otherwise, \end{array} \right. \end{aligned}$$
(26)

and \({Z_0}\), termed as the MCD matrix, is defined as:

$$\begin{aligned} {\left( {{Z_0}} \right) _{ij}} = \left\{ \begin{array}{llll} \frac{1}{{{n_s}}} - \frac{1}{{n_s^2}},&{}\quad i = j,{x_i} \in {D_s}\\ - \frac{1}{{n_s^2}},&{}\quad i \ne j,{x_i} \in {D_s},{x_j} \in {D_s}\\ \frac{1}{{n_t^2}} - \frac{1}{{{n_t}}},&{}\quad i = j,{x_i} \in {D_t}\\ \frac{1}{{n_t^2}},&{}\quad i \ne j,{x_i} \in {D_t},{x_j} \in {D_t}\;\\ 0,&{}\quad otherwise. \end{array} \right. \end{aligned}$$
(27)

Similarly, the discrepancy between conditional distributions across transformed domains can be cast as:

$$\begin{aligned} tr\left( {{A^T}X{M_c}{X^T}A} \right) + \beta \left\| {{A^T}X{Z_c}{X^T}A} \right\| _F^2, \end{aligned}$$
(28)

where \(c \in \left\{ {1,\ldots ,C} \right\} \), and \({M_c}\) is

$$\begin{aligned} {\left( {{M_c}} \right) _{ij}} = \left\{ \begin{array}{llll} \frac{1}{{n_{s,c}^2}},&{}\quad {x_i} \in {D_{s,c}},{x_j} \in {D_{s,c}}\\ \frac{1}{{n_{t,c}^2}},&{}\quad {x_i} \in {D_{t,c}},{x_j} \in {D_{t,c}}\\ - \frac{{1}}{{{n_{s,c}}{n_{t,c}}}},&{}\quad \left\{ \begin{array}{ll}{x_i} \in {D_{s,c}},{x_j} \in {D_{t,c}}\\ {x_j} \in {D_{s,c}},{x_i} \in {D_{t,c}} \end{array} \right. \\ 0,&{}\quad otherwise, \end{array} \right. \end{aligned}$$
(29)

wherein \({D_{s,c}}\left( {{D_{t,c}}} \right) = \left\{ {{x_i}|{x_i} \in {D_s}\left( {{D_t}} \right) ,{y_i} = c} \right\} \) and \({n_{s,c}}\left( {{n_{t,c}}} \right) = \left| {{D_{s,c}}\left( {{D_{t,c}}} \right) } \right| \), while \({Z_c}\) is defined as

$$\begin{aligned} {\left( {{Z_c}} \right) _{ij}} = \left\{ \begin{array}{llll} \frac{1}{{{n_{s,c}}}} - \frac{1}{{n_{s,c}^2}},&{}\quad i = j,{x_i} \in {D_{s,c}}\\ - \frac{1}{{n_{s,c}^2}},&{}\quad i \ne j,{x_i} \in {D_{s,c}},{x_j} \in {D_{s,c}}\\ \frac{1}{{n_{t,c}^2}} - \frac{1}{{{n_{t,c}}}},&{}\quad i = j,{x_i} \in {D_{t,c}}\\ \frac{1}{{n_{t,c}^2}},&{}\quad i \ne j,{x_i} \in {D_{t,c}},{x_j} \in {D_{t,c}}\\ 0,&{}\quad otherwise. \end{array} \right. \end{aligned}$$
(30)

By combining (25) and (28) and denoting \(H = {L_{{n_s} + {n_t}}}\), we can obtain the overall objective function as follows:

$$\begin{aligned} \mathop {\min }\limits _{{A^T}XH{X^T}A = I} \sum \limits _{c = 0}^C {tr\left( {{A^T}X{M_c}{X^T}A} \right) } + \beta \sum \limits _{c = 0}^C {\left\| {{A^T}X{Z_c}{X^T}A} \right\| _F^2} + \lambda \left\| A \right\| _F^2, \end{aligned}$$
(31)

where I is the identity matrix of size k, a constraint is imposed to avoid yielding a trivial solution and the parameter \(\lambda \) remains (31) as a well-defined optimization problem.

For the second variant of McDA, we, however, adopt the kernel feature map \(\varphi {:}\,x \rightarrow \varphi \left( x \right) \) to MMCD. Let the kernel matrix \(K = \varphi {(X)^T}\varphi (X)\). The MMCD-based distance of both marginal and conditional cross-domain distributions is defined as:

$$\begin{aligned} \sum \limits _{c = 0}^C {tr\left( {K{M_c}} \right) } + \beta \sum \limits _{c = 0}^C {tr\left( {K{Z_c}K{Z_c}} \right) }. \end{aligned}$$
(32)

Following [25], we employ the empirical kernel mapping \(K = (K{K^{ - 1/2}})({K^{ - 1/2}}K)\) and further introduce the low dimensional transformation in order to obtain \({\tilde{K}} = (K{K^{ - 1/2}}{\tilde{A}})({{\tilde{A}}^T}{K^{ - 1/2}}K) = KA{A^T}K\), where \(A = {K^{ - 1/2}}{\tilde{A}}\). Thus, substituting \({\tilde{K}}\) into (32) leads to the following minimization problem

$$\begin{aligned} \mathop {\min }\limits _{{A^T}KH{K^T}A = I} \sum \limits _{c = 0}^C {tr\left( {{A^T}K{M_c}{K^T}A} \right) } + \beta \sum \limits _{c = 0}^C {\left\| {{A^T}K{Z_c}{K^T}A} \right\| _F^2} + \lambda \left\| A \right\| _F^2. \end{aligned}$$
(33)

4.3 Optimization Algorithm

Both (31) and (33) possess similar optimization problems; hence, only the optimization algorithm for (31) is provided here. Obviously, (31) is non-convex with the variable A and hard to optimize, as it contains a non-convex fourth-order term which is the second term of (31). In [20, 25], the optimization problem have the closed-form solution by solving a generalized eigen-decomposition problem. To preserve this property, we can approximate the fourth-order term in (31) with its convex upper bound by using the following theorem:

Theorem 2

The following inequality holds

$$\begin{aligned} \sum \limits _{c = 0}^C {\left\| {{A^T}X{Z_c}{X^T}A} \right\| _F^2} \le \sigma k\sum \limits _{c = 0}^C {\left\| {{A^T}X{Z_c}{X^T}} \right\| _F^2}, \end{aligned}$$
(34)

where k is the reduced dimensionality and \(\sigma = {\left\| {{{(XH{X^T})}^{ - 1/2}}} \right\| ^2}\).

Proof

$$\begin{aligned} \sum \limits _{c = 0}^C {\left\| {{A^T}X{Z_c}{X^T}A} \right\| _F^2}= & {} \sum \limits _{c = 0}^C {\left\| {{A^T}X{Z_c}{X^T}{{\left( {XH{X^T}} \right) }^{ - 1/2}}{{\left( {XH{X^T}} \right) }^{1/2}}A} \right\| _F^2} \nonumber \\\le & {} \sum \limits _{c = 0}^C {\left\| {{A^T}X{Z_c}{X^T}{{\left( {XH{X^T}} \right) }^{ - 1/2}}} \right\| _F^2\left\| {{{\left( {XH{X^T}} \right) }^{1/2}}A} \right\| _F^2} \nonumber \\= & {} k\sum \limits _{c = 0}^C {\left\| {{A^T}X{Z_c}{X^T}{{\left( {XH{X^T}} \right) }^{ - 1/2}}} \right\| _F^2} \nonumber \\\le & {} k\sum \limits _{c = 0}^C {\left\| {{A^T}X{Z_c}{X^T}} \right\| _F^2\left\| {{{\left( {XH{X^T}} \right) }^{ - 1/2}}} \right\| _F^2} \nonumber \\= & {} k\sigma \sum \limits _{c = 0}^C {\left\| {{A^T}X{Z_c}{X^T}} \right\| _F^2}. \end{aligned}$$
(35)

The first equation holds because \(XH{X^T}\) is semi-definite positive, while the second and forth inequalities follow the Cauchy–Schwarz inequality. In terms of the constraint of (31), \(k = Tr\left( {{A^T}XH{X^T}A} \right) = Tr\left( {{I_k}} \right) \). \(\square \)

According to Theorem 2, we absorb the constant of (34) in order to obtain the convex objective of (31), as follows:

$$\begin{aligned} \mathop {\min }\limits _{{A^T}XH{X^T}A = I} \sum \limits _{c = 0}^C {tr\left( {{A^T}X{M_c}{X^T}A} \right) } + \beta \sum \limits _{c = 0}^C {\left\| {{A^T}X{Z_c}{X^T}} \right\| _F^2} + \lambda \left\| A \right\| _F^2. \end{aligned}$$
(36)

Then, we derive the Lagrange function of (36), as follows:

$$\begin{aligned}&tr\left( {A^T}\left( X\sum \limits _{c = 0}^C {{M_c}} {X^T} + \beta \sum \limits _{c = 0}^C {X{Z_c}{X^T}X{Z_c}{X^T}} + \lambda I\right) A\right) \nonumber \\&\quad +\,tr((I - {A^T}XH{X^T}A)\varPhi ), \end{aligned}$$
(37)

where the diagonal matrix \(\varPhi \) denotes the Lagrange multipliers. By setting the derivative of (37) over A to zero, we can obtain the following generalized eigenvalue decomposition problem:

$$\begin{aligned} \left( X\sum \limits _{c = 0}^C {{M_c}} {X^T} + \beta \sum \limits _{c = 0}^C {X{Z_c}{X^T}X{Z_c}{X^T}} + \lambda I\right) A = XH{X^T}\varPhi . \end{aligned}$$
(38)
figure a

Following the JDA paradigm [20], we learn the transformation matrix via (38) and can then project all the samples to a low-dimensional subspace. Based on the labeled source data, we can train a specific classifier to assign pseudo-labels to the samples of the target domain, and then repeat the procedure above until convergence. The overall procedure of McDA is summarized in Algorithm 1.

5 Experiments

This section is to verify the effectiveness of McDA by comparing its classification performance against the baseline methods on two benchmark datasets including PIE and Office-Caltech.

5.1 Datasets

The PIE dataset contains face images of size 32x32 from 68 individuals with different poses, illuminations and expressions. Following [20], We evaluate our method using five subsets from the PIE face dataset. Each subset corresponds to a different pose, e.g. P1 (left), P2 (upward), P3 (downward), P4 (frontal) and P5 (right). We then construct 20 cross-domain datasets via a pairwise combination of subsets, i.e., P1 \(\rightarrow \) P2, P1 \(\rightarrow \) P3, \( \ldots \), P5 \(\rightarrow \) P4. Since the source and target face images from each cross-domain dataset have different poses, they will follow different distributions.

Office-Caltech is a widely used dataset for domain adaptation which contains four domains: A (Amazon), W (Webcam), D (DSLR) and C (Caltech-256) [13, 30]. The SURF feature is extracted for each image before being converted into histograms over an 800-bin codebook clustered by k-means on the Amazon database. We construct 12 cross-domain datasets by pairwise combination of the four domains, i.e., \(\hbox {C}\rightarrow \hbox {A}\), \(\hbox {C}\rightarrow \hbox {W}\), \( \ldots \), \(\hbox {D}\rightarrow \hbox {W}\). Several sample images from PIE and Office-Caltech datasets are illustrated in Fig. 2.

Fig. 2
figure 2

Sample images from a PIE and b Office-Caltech datasets

Full size image

5.2 Cross-Domain Image Classification

We compare McDA with five typical and related baseline methods including nearest neighbor classifier (NN), principal component analysis (PCA), correlation alignment (CA) [35], transfer component analysis (TCA) [25], geodesic flow kernel (GFK) [10], and joint domain adaptation (JDA) [20]. As suggested by [10, 20], NN serves as the base classifier for both McDA and compared methods.

We follow the evaluation protocol of [20] for both benchmark datasets. In order to give a fair comparison, we also give the candidate ranges for the parameters used in the compared methods. Both TCA and JDA have a regularization parameter, and its candidate values are as follows: {0.001, 0.01, 0.1, 1, 10, 100}. For McDA, it is rather expensive to search all the possible parameter combinations for the best average accuracy. Since McDA shares the reduced dimensionality k and the regularization parameter \(\lambda \) with JDA, we directly set \(\lambda \) in McDA to the specific value at which JDA achieves its best accuracy and then search the other parameter \(\beta \) from {0.001, 0.01, 0.1, 1, 10, 100} at each k. We further empirically set the number of iterations N in McDA to 10 to guarantee convergence. For the compared subspace learning methods, the subspace dimensionality ranges from {10, 20, \(\ldots \), 200}. For TCA, JDA and McDA, we apply the linear transformation for the PIE dataset and the linear kernel for the Office-Caltech dataset as suggested by [20]. We adopt the broadly used classification accuracy on target dataset as the evaluation metric.

Figure 3 shows the compared classification accuracy versus different subspace dimensionalities. For two benchmark datasets, McDA is superior to all the compared methods in all dimensionalities in terms of average accuracy. The average accuracy is defined as the mean of classification accuracy over different cross-domain datasets.

Fig. 3
figure 3

Average accuracy versus reduced dimensionalities on a PIE and b Office-Caltech datasets

Full size image
Table 1 Accuracy (%) on the PIE dataset
Full size table
Table 2 Accuracy (%) on the Office-Caltech dataset
Full size table

Table 1 illustrates the accuracy of facial image classification on 20 cross-domain datasets of the PIE dataset. The results of the experiment show that our method outperforms the baseline methods in quantity. Importantly, McDA exceeds the average accuracy of JDA by 9.7%. Table 2 reports object recognition accuracy when the Office-Caltech dataset is used. McDA also outweighs the baseline methods in most situations and its average accuracy is higher than those of the compared baseline methods. Based on the analysis above, the prominent performance of McDA implies the efficacy of the proposed MMCD.

5.3 Sensitivity Analysis

5.3.1 Kernel Choice

It is an open problem to choose suitable kernels for kernel-based learning methods. To investigate the effect of the kernels on the performance of McDA, we run McDA and the baseline JDA on two datasets by comparing various kernel and non-kernel based cases. For the kernel based cases, the linear kernel, the polynomial kernel of degree two \({( {x^T{y} + 1} )^2}\), the Gaussian kernel \(\exp ( { - \left\| {x - y} \right\| _2^2/{2\sigma ^2} } )\), and the exponential kernel \(\exp ( { - \left\| {x - y} \right\| _2/\sigma } )\) are used. For the non-kernel case, the linear transformation in the original space is performed. For both Gaussian and exponential kernels, \(\sigma \) is set to the median of pairwise distances between all the samples. For the PIE dataset, it is hard to perform the eigenvalue decomposition over the large kernel matrix for the sake of large sample sizes. A compromise solution is to construct a small dataset termed PIE-sub, which is a subset of the PIE dataset by randomly selecting 10 images from each class. As a result, each domain of PIE-sub consists of 680 images from 68 classes.

Table 3 shows that McDA consistently outperforms the baseline method JDA in all the cases. This implies that the MCD regularization term in McDA is beneficial for capturing more distribution information so as to promote the performance of domain adaptation in a variety of kernels. It is worth mentioning that in non-kernel condition the performance of McDA is also enhanced due to the presence of the MCD term.

Table 3 Average accuracy (%) versus different kernels on PIE-sub and Office-Caltech datasets
Full size table

5.3.2 Parameter Selection

Our McDA has two regularization parameters: \(\lambda \) which is to avoid the optimization problem to be ill-defined, and \(\beta \) which is to balance the importance of the MCD term. In order to analyze the effect of parameters on the performance, we vary \(\lambda \) and \(\beta \) from the range {\(10^{-3}\), \(10^{-2.5}\), ..., \(10^2\)} and run McDA on PIE and Office-Caltech datasets. The reduced dimensionality is set to the optimal value according to Fig. 3, i.e., \(k=90\) for PIE and \(k=20\) for Office-Caltech. Figure 4a shows that small values of \(\lambda \) and relatively big values of \(\beta \) for the PIE dataset help achieve high accuracy. This could result from both significant mean and covariance differences between source and target data distributions. It can be seen from Fig. 4b that the performance of McDA is relatively stable to the change of the values of \(\lambda \) and \(\beta \) in the area of \(\lambda \ge \beta \) on the Office-Caltech dataset. Hence, \(\lambda \in \left[ {0.001,1} \right] \) and \(\beta \in \left[ {0.01,10} \right] \) are suggested for accomplishing enhanced performance.

Fig. 4
figure 4

Average accuracy of McDA versus different parameter values on a PIE and b Office-Caltech datasets

Full size image

6 Conclusion

This paper proposes a new distribution metric namely maximum mean and covariance discrepancy (MMCD) which unites MMD with the proposed maximum covariance discrepancy (MCD). MMCD is able to capture more information about distributions compared to MMD. Based on MMCD, we developed a new domain adaptation method in the joint distribution adaptation paradigm. Experiments conducted on two benchmark datasets verify the effectiveness of our method, which implies the efficacy of MMCD. In the future, we plan to apply the MMCD to other domain adaptation methods and test them on various applications.