1 Introduction

In machine learning and pattern recognition, effectiveness of an approach or an algorithm is determined by the ability of modeling underlying distribution of observed data [38]. Finite mixture models have been extensively used for statistical modeling in machine learning and pattern recognition and have demonstrated their importance in many speech and image processing applications [33, 60]. Gaussian mixture model (GMM) is well renowned for data clustering. The parameters of GMM can be estimated effectively using expectation maximization (EM) algorithm by maximizing the log-likelihood function [10, 51]. The main problem associated with GMM is sensitivity to outliers [51]. Student’s-t mixture model (SMM) has been proposed in order to improve the robustness of Gaussian mixture model for statistical modeling [44, 56, 76]. In SMM, each component has one more parameter, called degree of freedom, as compared to GMM. Cauchy and Gaussian distributions are special cases of student’s-t distribution with degree of freedom 1 and \(\infty \), respectively [51]. There have been substantial growth in research for developing mixture models using generalized Gaussian distribution (GGD) [2,3,4, 13, 45]. This distribution has one extra parameter (shape parameter \(\lambda \)) than Gaussian distribution, which controls the tails of distribution. One problem associated with above mentioned mixture models is unbounded support range (\(-\,\infty \),\(+\,\infty \)) of their distributions [51]. It is observed that many real applications have their data within bounded support regions [21, 26, 43]. For speech processing applications, bounded Gaussian mixture model (BGMM) has been proposed in [26, 43]. The idea of bounded support mixture is adopted for GGMM and BGGMM has been proposed in [51], which provides a generalization for GMM, Laplace mixture model (LMM), GGMM and BGMM as special cases.

ICA mixture model has been proposed as an extension of Gaussian mixture model in [38, 39, 41]. ICA has been successfully applied to problems such as blind source separation and signal analysis describing its ability to model non-Gaussian statistical structures. If the source distributions are assumed to be Gaussian, it is equivalent to principle component analysis (PCA), which assumes that observed data is distributed as a multivariate Gaussian [38]. ICA generalize PCA by modeling the observed data with non-Gaussian distributions and goal is to linearly transform the data structures in such a way that variables after transformation are independent from each other [41]. One limitation in ICA is that it assumes the sources to be independent from each other. This assumption can be relaxed by employing a mixture model. The observed data can be categorized into several mutually exclusive classes by employing a mixture model [40], simply called an ICA mixture model. It can be generalized with the assumption that observed data in each class is produced by a linear combination of independent, non-Gaussian sources as in case of ICA [41]. Hence, in an ICA mixture model, it is assumed that observed data can be categorized into mutually exclusive classes and components of the model are generated by linear combination of independent sources [66]. Many variations of ICA mixture model have been proposed in the last few years [12, 48, 67, 68]. It has been extensively used for statistical modeling in a variety of applications that include segmentation, image enhancement and BSS [39, 41, 62]. In [52], ICA mixture model was proposed with adaptive source densities including generalized Gaussian and Student’s t distributions as special cases along with other forms of densities. In this paper, we are interested in extending the model presented in [38] with BGGD. In [51], BGGMM is formulated for univariate data which is extended here for multivariate data. The parameter estimation for proposed ICA mixture is adopted from [38, 41] using ICA and gradient ascent. The preliminary results obtained by applying the proposed ICA mixture are published in [6, 7]. In this paper we have extended the applications of ICA mixture in BSS and unsupervised keyword spotting frameworks for more insightful analysis.

Blind source separation has been applied to many signal processing and machine learning problems including speech enhancement, speech recognition, medical signal processing and telecommunications [41]. BSS is defined as a method which reconstruct the unknown sources of observed signals from an unknown mixture [11, 57, 72, 73]. BSS was formulated around 1982 and first related contributions appeared around 1985 in [5, 16, 27,28,29, 35]. The ICA was proposed as general framework for solving blind source separation problems based on statistical independence of the unknown sources in [34] and formalized for linear mixtures in [14, 15]. The limitations associated with ICA were controlled by ICA mixture as proposed in [37, 38] and successfully applied to BSS [8, 40, 41]. Research for the development of many new approaches for BSS is continued and many interesting algorithms and techniques have been developed [1, 24]. The Expectation-Maximization (EM) algorithm has also been applied to ICA in [32, 59]. In this paper, we have proposed BGGMM using ICA for the task of BSS. For the evaluation of proposed BSS framework, we have used signal-to-distortion ratio (SDR), signal-to-interference ratio (SIR), signal-to-artifact ratio (SAR) and perceptual evaluation of speech quality (PESQ). The detailed explanation of evaluation metrics is presented in [20, 49, 58, 74].

Automatic speech recognition (ASR) is considered as a nonlinear transformation from spoken words to text [61, 79], which requires large quantities of annotated data along with the language specific speech and text data, used for training complex statistical acoustic and language models [31, 78, 80]. Keyword spotting task has also been explored for many years and ASR is used to detect the occurrence of a specific keyword in speech data [70]. Keyword spotting is defined as an approach for speech understanding to detect specific keyword(s) that most likely express the intent of a speaker rather than recognition of a whole speech utterance [46]. Hidden Markov models based keyword spotting methods have been proposed widely for supervised and unsupervised settings [63, 64, 69, 71, 77]. Dynamic time warping has been used extensively for speech recognition and keyword spotting [17, 50, 53,54,55, 65, 81, 82]. The use of mixture model in automatic speech recognition and keyword spotting has demonstrated its effectiveness in unsupervised platforms and settings [42, 75]. We have proposed BGGMM with ICA in unsupervised keyword spotting and preliminary results are submitted in [6]. In many real time scenarios, speech signals are mixed with noise or other speech signal which reduces the intelligibility of signals in keyword spotting and speech recognition. In order to improve the detection rate in keyword spotting, speech signal can be pre-processed using BSS before being applied to the trained model for keyword detection or speech recognition. The proposed ICA mixture have demonstrated its effectiveness in BSS as described in Sect. 3.1 and we have proposed the same BSS framework as prepossessing to unsupervised keyword spotting presented in [6]. Due to mixing of speech utterances, two types of problems occur in keyword spotting. In the first case, target keyword will more likely not detected during the keyword spotting, whereas in second case target keyword will be detected in correct speech utterance but it will also get detected in other speech utterances as false alarm. These two problems are explained in detail in Sect. 3.2. In this paper, we have proposed BSS as pre-processing to unsupervised keyword spotting as an extension to the work submitted in [6].

The rest of the paper is organized as follows. Section 2 describes derivation of learning rules for proposed algorithm. In Sect. 3, application of ICA mixture model in BSS and unsupervised keyword spotting is presented with set of experiments and results. Section 4 presents the conclusions and future perspectives.

2 Bounded Generalized Gaussian Mixture Model with ICA

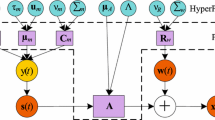
In this section, BGGMM with ICA is proposed for statistical modeling. In an ICA mixture model, it is assumed that observed data come from a mixture model and it can be categorized into mutually exclusive classes which means that each class of the data is modeled via an ICA [38, 66]. Consider the case where input is a set of features of the data represented as \({\mathcal {X}}=({\vec {X}}_{1},\ldots ,{\vec {X}}_{N})\) and \({\vec {X}}_{i}\) is a D-dimensional random variable \({\vec {X}}_{i}=[X_{i1},\ldots ,X_{iD}]^T\). The \({\vec {X}}_{i}\) follows a K components mixture distribution if its probability function can be written as follows:

$$\begin{aligned} p({\vec {X}}_{i}|\Theta )=\sum _{j=1}^{K}p({\vec {X}}_{i}|{\xi }_{j})p_{j} \end{aligned}$$
(1)

provided that \(p_{j}\ge 0\) and \(\sum _{j=1}^{K}p_{j}=1\). In Eq. (1), \(p({\vec {X}}_{i}|{\xi }_{j})\) is probability density function, \(\xi _j\) represents the set of parameters defining jth component, \(p_j\) is mixing proportion, \(\Theta =(\xi _1,\ldots ,\xi _K,p_1,\ldots ,p_K)\) is complete set of parameters to characterize the mixture model and \(K\ge 1\) is number of components in the mixture model [18, 22, 47]. For an ICA mixture model, each data vector \({\vec {X}}_{i}\) can be represented as:

$$\begin{aligned} {\vec {X}}_{i}=\text {A}_{j}\vec {\text {s}}_{j,i}+\vec {\text {b}}_{j} \end{aligned}$$
(2)

where \(\text {A}_{j}\) is \(L\times D\) scalar matrix termed as basis functions, \(\vec {\text {s}}_{j,i}\) is D-dimensional source vector and \(\vec {\text {b}}_{j}\) is an L-dimensional bias vector for a particular mixture component j [38, 39, 41, 66,67,68]. In order to define the BGGD for a variable \({\vec {X}}\in {\mathbb {R}}\), it is required to provide an indicator function which introduces the boundary conditions. For each component (denoted by j), indicator function \(\text {H}({{{\vec {X}}}_i}|j)\) is defined with bounded support region (\(\Omega _{S_j}\)) for each component:

$$\begin{aligned} \text {H}({{{\vec {X}}}_i}|j)={\left\{ \begin{array}{ll} 1 &{}\quad \text {if}\quad {{\vec {X}}_i}\in \Omega _{S_j}\\ 0 &{}\quad \text {otherwise} \end{array}\right. } \end{aligned}$$
(3)

For BGGMM, \({\vec {X}}_{i}\) follows a K components mixture represented in Eq. (1), where \(p({\vec {X}}_{i}|\xi _{j})\) is multivariate BGGD as:

$$\begin{aligned} p({\vec {X_i}}|\xi _{j})=\frac{f_{ggd}({\vec {X_i}}|\xi _{j})\text {H}(\vec {X_i}|j)}{\int _{\Omega _{S_j}}f_{ggd}(\vec {\text {u}}|\xi _{j})d\text {u}} \end{aligned}$$
(4)

where term \(f_{ggd}(\vec {X_i}|\xi _{j})\) represents the multivariate generalized Gaussian distribution (GGD):

$$\begin{aligned} f_{ggd}({\vec {X_i}}|{\xi _j}) = \prod _{d=1}^{D}\frac{\lambda _{jd}{\sqrt{\frac{{\Gamma (3/\lambda _{jd})}}{{\Gamma (1/\lambda _{jd})}}}}}{2\sigma _{jd}\Gamma (1/\lambda _{jd})}\exp \left( -A(\lambda _{jd})\Big |\frac{X_{id}-\mu _{jd}}{\sigma _{jd}}\Big |^{\lambda _{jd}}\right) \end{aligned}$$
(5)

with

$$\begin{aligned} A(\lambda _{jd})=\left[ \frac{\Gamma (3/\lambda _{jd})}{\Gamma (1/\lambda _{jd})}\right] ^{\lambda _{jd}/2} \end{aligned}$$
(6)

The term \(\int _{\Omega _{S_j}}f_{ggd}(\vec {\text {u}}|\xi _{j})d\text {u}\) is normalization constant that indicates the share of \(f_{ggd}(\vec {X_i}|\xi _{j})\) which belongs to the support region. Note that \({\xi _j=\left\{ \vec {\mu }_{j},\vec {\sigma }_{j},\vec {\lambda }_{j},\text {A}_{j},\vec {\text {b}}_{j}\right\} }\) is the set of parameters defining jth component, where \(\vec {\mu }_{j}=({\mu }_{j1},\ldots ,{\mu }_{jD})\), \(\vec {\sigma }_{j}=(\sigma _{j1},\ldots ,\sigma _{jD})\), \(\vec {\lambda }_{j}=(\lambda _{j1},\ldots ,\lambda _{jD})\), \(\text {A}_{j}=({\text {a}}_{1},\ldots ,{\text {a}}_{L})\) and \(\vec {\text {b}}_{j}=({\text {b}}_{j1},\ldots ,{\text {b}}_{jD})\) are the mean, standard deviation, shape parameters, basis functions and bias vector, respectively. The vectors representing mean, standard deviation, shape parameters and bias are D-dimensional for each component of the mixture model, whereas the basis functions for each component has L number of linear combination with each linear combination being D-dimensional. For simplicity, number of linear combinations (L) is considered to be equal to the number of sources (D) in each observation which makes basis functions a \(D\times D\) scalar matrix. With a mixture of K BGGDs, the likelihood of data \({\mathcal {X}}\) can be defined as:

$$\begin{aligned} p({\mathcal {X}}|\Theta )=\prod _{i=1}^{N}\sum _{j=1}^{K}p({\vec {X}}_{i}|{\xi }_{j})p_{j} \end{aligned}$$
(7)

where complete set of parameters of the ICA mixture model having K classes is defined by \(\Theta =(\vec {\mu }_{1},\ldots ,\vec {\mu }_{K},\vec \sigma _{1},\ldots ,\vec \sigma _{K},\vec \lambda _{1},\ldots ,\vec \lambda _{K},{\text {A}}_{1},\ldots ,{\text {A}}_{K},\vec {\text {b}}_{1},\ldots ,\vec {\text {b}}_{K},p_{1},\ldots ,p_{K})\). We introduce the stochastic indicator \({\mathcal {Z}}=\{\vec {Z}_1,\ldots ,\vec {Z}_N\}\), where \(\vec {Z}_{i}=(Z_{i1},\ldots ,Z_{iK})\) is the label of each observation, such that \(Z_{ij}\in \left\{ 0,1\right\} \), \(\sum _{j=1}^{K}Z_{ij}=1\). The role of these variables is to encode membership of each observation for a relative component of the mixture model. In other words, \(Z_{ij}\), the unobserved variable in each indicator vector equals to 1 if \({\vec {X}}_i\) belongs to class j and 0, otherwise [10, 18, 19]. The complete data likelihood is:

$$\begin{aligned} p({\mathcal {X}},{\mathcal {Z}}|\Theta )=\prod _{i=1}^{N}\prod _{j=1}^{K}\left( p({\vec {X}}_{i}|{\xi }_{j})p_{j}\right) ^{Z_{ij}} \end{aligned}$$
(8)

For instance, if we consider that number of mixture components is known, then parameter estimation requires the maximization of log-likelihood function:

$$\begin{aligned} {{\mathcal {L}}}(\Theta ,{\mathcal {Z}},{\mathcal {X}})=\sum _{i=1}^{N}\sum _{j=1}^{K}{Z_{ij}}\log \left( p({\vec {X}}_{i}|{\xi }_{j})p_{j}\right) \end{aligned}$$
(9)

By replacing each \(Z_{ij}\) with its expectation, defined as posterior probability that the ith observation belongs to jth component of the mixture model we obtain:

$$\begin{aligned} {\hat{Z}}_{ij}=p(j|{\vec {X}}_{i})=\frac{p({\vec {X}}_{i}|{\xi }_{j})p_{j}}{\sum _{j=1}^{K}p({\vec {X}}_{i}|{\xi }_{j})p_{j}} \end{aligned}$$
(10)

2.1 Parameters Estimation

In a mixture model, parameters include mixing proportions and parameters of the distribution whereas in case of ICA mixture model each vector of the data is represented as in Eq. (2), which also necessitates the estimation of basis functions and bias vectors. The basis functions and bias vectors are further adopted to compute the sources in ICA model. For the parameters mean, standard deviation and mixing proportions, maximization of log-likelihood is obtained by setting the gradient of log-likelihood (with respect to each parameter) to zero. The maximization of log-likelihood for the shape parameters, basis functions and bias vector is performed by employing standard ICA model and gradient ascent. Using Eq. (10), each observation can be labeled to one or zero for a particular component of the mixture model which can be further applied to maximize the complete data log-likelihood with respect to parameters of ICA mixture model. The gradient of log-likelihood with respect to parameters of each component is computed as following:

$$\begin{aligned} \nabla _{\Theta _j}{{\mathcal {L}}}(\Theta ,{\mathcal {Z}},{\mathcal {X}})=\nabla _{\Theta _j}\sum _{i=1}^{N}\sum _{j=1}^{K}{Z_{ij}}\log \left( p({\vec {X}}_{i}|{\xi }_{j})p_{j}\right) \end{aligned}$$
(11)

The \(\nabla _{\Theta _j}\) represents here the gradient with respect to \(p_j\), \(\vec {\mu }_{j}\), \(\vec {\sigma }_{j}\), \(\vec {\lambda }_{j}\), \({\text {A}}_{j}\) and \(\vec {\text {b}}_{j}\). Eq. (11) can be written as:

$$\begin{aligned}&\nabla _{\Theta _j}{{\mathcal {L}}}(\Theta ,{\mathcal {Z}},{\mathcal {X}})\nonumber \\&\quad =\nabla _{\Theta _j}\sum _{i=1}^{N}\sum _{j=1}^{K}Z_{ij} \times \left\{ \log p_j+\log f_{ggd}(\vec {X_i}|{\xi }_{j})+\log \text {H}(\vec {X_i}|j)-\log {\int _{\Omega _{S_j}}f_{ggd}(\vec {\text {u}}|\xi _{j})d{\text {u}}} \right\} \end{aligned}$$
(12)

2.1.1 Estimation of Mixing Parameter, Mean and Standard Deviation

The mixing parameter can be estimated by taking the gradient of complete data log-likelihood with respect to \(p_j\). In order to ensure the constraints \(p_j>0\) and \(\sum _{j=1}^{M}p_j=1\), a Lagrange multiplier is introduced while estimating \(p_j\). Thus, the augmented log-likelihood function can be expressed by:

$$\begin{aligned} \Phi (\Theta ,{\mathcal {Z}},{\mathcal {X}},\Lambda )= \sum _{i=1}^{N}\sum _{j=1}^{K}Z_{ij}\log \left( p({\vec {X}}_{i}|{\xi }_{j})p_{j}\right) +\Lambda \left( 1-\sum _{j=1}^{K}p_j\right) \end{aligned}$$
(13)

where \(\Lambda \) is the Lagrange multiplier. Taking the gradient of augmented log-likelihood function with respect to \(p_j\), we get the estimated value of \(p_j\) as:

$$\begin{aligned} {\hat{p}}_{j}=\frac{1}{N}\sum _{i=1}^{N}p(j| {\vec {X}}_{i}) \end{aligned}$$
(14)

where \(p(j| {\vec {X}}_{i})\) is the posterior probability. The mean \(\mu _j\) can be estimated by maximizing the log-likelihood with respect to \(\mu _j\). The estimated mean \({\hat{\mu }}_{jd}\) for \(d=1,\ldots ,D\) is given by:

$$\begin{aligned} {\hat{\mu }}_{jd}&=\frac{1}{\sum _{i=1}^{N}{\hat{Z}}_{ij}\Big |X_{id}-\mu _{jd}\Big |^{(\lambda _{jd}-2)}}\sum _{i=1}^{N}{\hat{Z}}_{ij} \left\{ \left[ \Big |X_{id}-\mu _{jd}\Big |^{(\lambda _{jd}-2)}X_{id}\right] \right. \nonumber \\&\left. \quad -\,\left[ \frac{\int _{\Omega _{S_j}}f_{ggd}({\text {u}}|\xi _{j})\text {sign}\left( \text {u}-\mu _{jd}\right) {\Big |\text {u}-\mu _{jd}\Big |^{\lambda _{jd}-1}}d{\text {u}}}{ {\int _{\Omega _{S_j}}f_{ggd}({\text {u}}|\xi _{j})d{\text {u}}}}\right] \right\} \end{aligned}$$
(15)

Note that, in Eq. (15), the term \(\int _{\Omega _{S_j}}f_{ggd}({\text {u}}|\xi _{j})\text {sign}\left( \text {u}-\mu _{jd}\right) {\Big |\text {u}-\mu _{jd}\Big |^{\lambda _{jd}-1}}d{\text {u}}\) is the expectation of function \(\text {sign}\left( \text {u}-\mu _{jd}\right) {\Big |\text {u}-\mu _{jd}\Big |^{\lambda _{jd}-1}}\) under the probability distribution \(f_{ggd}({\text {u}}|\xi _{j})\) [10, 21, 51], which can be approximated as:

$$\begin{aligned}&\int _{\Omega _{S_j}}f_{ggd}({\text {u}}|\xi _{j})\text {sign}\left( \text {u}-\mu _{jd}\right) {\Big |\text {u}-\mu _{jd}\Big |^{\lambda _{jd}-1}}d{\text {u}} \nonumber \\&\quad \approx \frac{1}{M}\sum _{m=1}^{M}\text {sign}(\mu _{jd}-{s_{j}}_{md})\big |\mu _{jd}-{s_{j}}_{md}\big |^{\lambda _{jd}-1}\text {H}({s_{j}}_{md}|{j}) \end{aligned}$$
(16)

where \(s_{m_{jd}}\sim f_{ggd}({\text {u}}|\xi _{j})\) is a set of random variables drawn from generalized Gaussian distribution for particular component of the mixture model j. The set of data with random variables have M vectors with D dimensions. M is a large integer chosen to generate the set of random variables. Similarly, the term \(\int _{\Omega _{S_j}}f_{ggd}({\text {u}}|{\xi }_{j})d{\text {u}}\) in Eq. (15) can be approximated as:

$$\begin{aligned} \int _{\Omega _{S_j}}f_{ggd}({\text {u}}|{\xi }_{j})d{\text {u}}\approx \frac{1}{M}\sum _{m=1}^{M}\text {H}(s_{m_{jd}}|j) \end{aligned}$$
(17)

From Eqs. (16) and (17), \(\hat{\mu _j}\) can be written as:

$$\begin{aligned} {\hat{\mu }}_{jd}&=\frac{1}{\sum _{i=1}^{N}{\hat{Z}}_{ij}\Big |X_{id}-\mu _{jd}\Big |^{(\lambda _{jd}-2)}}\sum _{i=1}^{N}{\hat{Z}}_{ij} \left\{ \left[ \Big |X_{id}-\mu _{jd}\Big |^{(\lambda _{jd}-2)}X_{id}\right] \right. \nonumber \\&\quad \left. -\left[ \frac{\sum _{m=1}^{M}\text {sign}(\mu _{jd}-{s_{j}}_{md})\big |\mu _{jd}-{s_{j}}_{md}\big |^{\lambda _{jd}-1}\text {H}({s_{j}}_{md}|{j})}{\sum _{m=1}^{M}\text {H}({s_{j}}_{md}|{j})}\right] \right\} \end{aligned}$$
(18)

with \(i={1,\ldots ,N}\), \(j={1,\ldots ,K}\), \(d={1,\ldots ,D}\) and \(m={1,\ldots ,M}\). The standard deviation \(\sigma _j\) can be estimated by maximizing the log-likelihood with respect to \(\sigma _j\). The estimated standard deviation \({\hat{\sigma }}_{jd}\) for \(d=1,\ldots ,D\) is given as:

$$\begin{aligned} {\hat{\sigma }}_{jd}=\left( \frac{\sum _{i=1}^{N}{\hat{Z}}_{ij}\left[ A(\lambda _{jd})\big |X_{id}-\mu _{jd}\big |^{\lambda _{jd}}\lambda _{jd}\right] }{\sum _{i=1}^{N}{\hat{Z}}_{ij}\left\{ 1+\left[ \frac{{\int _{\partial _{\Omega _j}}f_{ggd}({\text {u}}|\xi _{j})\left\{ -1+A(\lambda _{jd})\big |X_{id}-\mu _{jd}\big |^{\lambda _{jd}}\lambda _{jd}(\sigma _{jd})^{-\lambda _{jd}}\right\} d{\text {u}}}}{ {\int _{\Omega _{S_j}}f_{ggd}({\text {u}}|\xi _{j})d{\text {u}}}}\right] \right\} }\right) ^{1/\lambda _{jd}} \end{aligned}$$
(19)

Similar to Eq. (16), in Eq. (19) the term \(\int _{\Omega _{S_j}}f_{ggd}({\text {u}}|\xi _{j})(-1+A(\lambda _{jd}) \big |X_{id}-\mu _{jd}\big |^{\lambda _{jd}}\lambda _{jd}(\sigma _{jd})^{-\lambda _{jd}})d{\text {u}}\) can be approximated as:

$$\begin{aligned}&\int _{\Omega _{S_j}}f_{ggd}({\text {u}}|\xi _{j})(-1+A(\lambda _{jd})\big |X_{id}-\mu _{jd}\big |^{\lambda _{jd}}\lambda _{jd}(\sigma _{jd})^{-\lambda _{jd}})d{\text {u}}\nonumber \\&\quad \approx \frac{1}{M}\sum _{m=1}^{M}(-1+\lambda _{jd}A(\lambda _{jd})\big |s_{mjd}-\mu _{jd}\big |^{\lambda _{jd}}(\sigma _{jd})^{-\lambda _{jd}}) \text {H}(s_{mjd}|{j}) \end{aligned}$$
(20)

From Eqs. (20) and (17), \(\hat{\sigma _j}\) can be written as:

$$\begin{aligned} {\hat{\sigma }}_{jd}=\left( \frac{\sum _{i=1}^{N}{\hat{Z}}_{ij}\left[ A(\lambda _{jd})\big |X_{id}-\mu _{jd}\big |^{\lambda _{jd}}\lambda _{jd}\right] }{\sum _{i=1}^{N}{\hat{Z}}_{ij}\left\{ 1+\left[ \frac{\sum _{m=1}^{M}(-1+\lambda _{jd}A(\lambda _{jd})\big |s_{mjd}-\mu _{jd}\big |^{\lambda _{jd}}(\sigma _{jd})^{-\lambda _{jd}}) \text {H}(s_{mjd}|{j})}{\sum _{m=1}^{M}\text {H}(s_{mjd}|{j})}\right] \right\} }\right) ^{1/\lambda _{jd}} \end{aligned}$$
(21)

with \(i={1,\ldots ,N}\), \(j={1,\ldots ,K}\), \(d={1,\ldots ,D}\) and \(m={1,\ldots ,M}\).

2.1.2 Parameter Estimation using ICA and Gradient Ascent

For parameter estimation using ICA and gradient ascent, zero mean and unit variance is assumed which is fundamental assumption of the source in ICA. The parameters estimated using ICA with gradient ascent include basis functions, bias vector and shape parameters. The gradient of complete data log-likelihood for the parameters of each class is given below:

$$\begin{aligned} \nabla _{\Theta _j}{{\mathcal {L}}}(\Theta ,{\mathcal {Z}},{\mathcal {X}})=\sum _{i=1}^{N}\sum _{j=1}^{K}p(j|{\vec {X}}_{i})\nabla _{\Theta _j}\log \left( p({\vec {X}}_{i}|{\xi }_{j})p_{j}\right) \end{aligned}$$
(22)

The \(\nabla _{\Theta _j}\) represents here the gradient with respect to basis function, bias vector and shape parameter.

$$\begin{aligned} \nabla _{\Theta _j}{{\mathcal {L}}}(\Theta ,{\mathcal {Z}},{\mathcal {X}})=\sum _{i=1}^{N}\sum _{j=1}^{K}p(j|{\vec {X}}_{i})\left( \nabla _{\Theta _j}\log p({\vec {X}}_{i}|{\xi }_{j})+\nabla _{\Theta _j}\log p_{j}\right) \end{aligned}$$
(23)

The term \(\nabla _{\Theta _j}\log p_{j}\) will become zero while taking gradient with respect to basis functions, bias vector and shape parameter which will lead us to :

$$\begin{aligned} \nabla _{\Theta _j}{{\mathcal {L}}}(\Theta ,{\mathcal {Z}},{\mathcal {X}})=\sum _{i=1}^{N}\sum _{j=1}^{K}p(j|{\vec {X}}_{i})\left( \nabla _{\Theta _j}\log p({\vec {X}}_{i}|{\xi }_{j})\right) \end{aligned}$$
(24)

The class log-likelihood \(\log p({\vec {X}}_{i}|{\xi }_{j})\) in Eq. (24) can be estimated using standard ICA model as follows:

$$\begin{aligned} \log p({\vec {X}}_{i}|{\xi }_{j}) =\log \frac{p(\vec {\text {s}}_{j,i})}{\big |\text {det}{\text {A}_{j}}\big |} \end{aligned}$$
(25)

The source can be computed by applying estimated basis function and bias vector in the above equation and log-likelihood of the standard ICA model will become:

$$\begin{aligned} \log p({\vec {X}}_{i}|{\xi }_{j})=\log p({\text {A}_{j}}^{-1}({\vec {X}}_{i}-\vec {\text {b}}_{j}))-\log \big |\text {det}{\text {A}_{j}}\big | \end{aligned}$$
(26)

(a) Basis Functions Estimation The adaptation of basis functions for each component of ICA mixture is performed by maximizing the log-likelihood with respect to basis functions \({\text {A}_{j}}\) for each component of mixture model:

$$\begin{aligned} \nabla _{\text {A}_{j}}{{\mathcal {L}}}(\Theta ,{\mathcal {Z}},{\mathcal {X}})=\sum _{i=1}^{N}p(j|{\vec {X}}_{i})\nabla _{\text {A}_{j}}\log p({\vec {X}}_{i}|{\xi }_{j}) \end{aligned}$$
(27)

The adaptation performed by the gradient ascent with respect to basis functions is given as:

$$\begin{aligned} \Delta {\text {A}_{j}}\propto p(j| {\vec {X}}_{i})\frac{\partial }{\partial {\text {A}_{j}}}\log p({\vec {X}}_{i}|{\xi }_{j}) \end{aligned}$$
(28)

The derivative in Eq. (28) can be computed using derivations given in standard ICA learning algorithm [41].

$$\begin{aligned} \frac{\partial }{\partial {\text {A}_{j}}}\log p({\vec {X}}_{i}|{\xi }_{j}) ={\text {A}_{j}}\left[ \text {I}-2\tanh (\vec {\text {s}}_{j,i})\vec {\text {s}}_{j,i}^{T}\right] \end{aligned}$$
(29)

By using the standard ICA model for log-likelihood, we get:

$$\begin{aligned} \Delta {\text {A}_{j}}\propto p(j|{\vec {X}}_{i}){\text {A}_{j}}\left[ \text {I}-2\tanh (\vec {\text {s}}_{j,i})\vec {\text {s}}_{j,i}^{T}\right] \end{aligned}$$
(30)

In adaptation of basis functions, the gradient of component of mixture model with respect to basis functions is weighted by \(p(j|{\vec {X}}_{i})\). An estimate of basis functions using gradient ascent is as follows:

$$\begin{aligned} {\hat{\text {A}}_{j}}={\text {A}_{j}}+\alpha \left( p(j|{\vec {X}}_{i}){\text {A}_{j}}\left[ \text {I}-2\tanh (\vec {\text {s}}_{j,i})\vec {\text {s}}_{j,i}^{T}\right] \right) \end{aligned}$$
(31)

where \(\alpha \) is step size and source is represented as:

$$\begin{aligned} \vec {\text {s}}_{j,i}={\text {A}_{j}}^{-1}(\vec {X_{i}}-\vec {\text {b}}_{j}) \end{aligned}$$
(32)

(b) Bias Vectors Estimation The adaptation of bias vector can be performed for each component of the mixture model by using the Eq. (24).

$$\begin{aligned} \nabla _{{\text {b}}_{jd}}{{\mathcal {L}}}(\Theta ,{\mathcal {Z}},{\mathcal {X}})=\sum _{i=1}^{N}p(j|{\vec {X}}_{i})\nabla _{{\text {b}}_{jd}}\log p({\vec {X}}_{i}|{\xi }_{j}) \end{aligned}$$
(33)

The gradient ascent is used for adaptation, with gradient of the component density with respect to bias term \({\text {b}}_{jd}\) for each component of the mixture model:

$$\begin{aligned} \Delta {\text {b}_{jd}}\propto p(j|{\vec {X}}_{i})\frac{\partial }{\partial {\text {b}_{jd}}}\log p({\vec {X}}_{i}|{\xi }_{j}) \end{aligned}$$
(34)

The Eq. (26) can be applied in Eq. (34) to adapt the bias term:

$$\begin{aligned} \Delta {\text {b}_{jd}}\propto p(j|{\vec {X}}_{i})\frac{\partial }{\partial {\text {b}_{jd}}}\left[ \log p({{\text {A}_{j}}}^{-1}({\vec {X}}_{i}-\vec {b}_{j}))-\log \big |\text {det}{\text {A}_{j}}\big |\right] \end{aligned}$$
(35)

An approximate method can also be applied for the adaptation of bias vectors instead of applying gradient. For approximate method, maximum likelihood estimate must satisfy the following condition:

$$\begin{aligned} \sum _{i=1}^{N}p(j|{\vec {X}}_{i})\nabla _{{\Theta }_{j}}\log p({\vec {X}}_{i}|{{\hat{\xi }}}_{j})=0 \end{aligned}$$
(36)

The bias term \(\text {b}_{jd}\) can be adapted as follows:

$$\begin{aligned} \nabla _{\text {b}_{jd}}{{\mathcal {L}}}(\Theta ,{\mathcal {Z}},{\mathcal {X}})=0,~~\Rightarrow ~~\sum _{i=1}^{N}p(j|{\vec {X}}_{i})\nabla _{\text {b}_{jd}}\log p({\vec {X}}_{i}|{\xi }_{j})=0 \end{aligned}$$
(37)

By substituting Eq. (26) into Eq. (37), it is clear that gradient of the \(\log p({{\text {A}_{j}}}^{-1}({\vec {X}}_{i}-\vec {\text {b}}_{j}))\) must be zero as given in Eq. (38).

$$\begin{aligned} \nabla _{\text {b}_{jd}}\log p({\text {A}_{j}}^{-1}({\vec {X}}_{i}-\vec {\text {b}}_{j}))=0 \end{aligned}$$
(38)

In adaptation of bias vector, if we assume that we have a large amount of data and prior probability distribution function of the source is differentiable and symmetric, then the \(\log p({\text {A}_{j}}^{-1}({\vec {X}}_{i}-\vec {\text {b}}_{j}))\) will be symmetric as well and the bias vector \(\vec {\text {b}}_j\) will be approximated by the weighted average of data samples as:

$$\begin{aligned} \vec {\text {b}}_{j}=\frac{\sum _{i=1}^{N}\vec {X_i}p(j| {\vec {X}}_{i})}{\sum _{i=1}^{N}p(j| {\vec {X}}_{i})} \end{aligned}$$
(39)

(c) Shape Parameter Estimation For estimation of parameters in ICA mixture model, unit variance and zero mean is assumed. For the purpose of estimation of shape parameter, same assumption is adopted and the problem will become estimation of shape parameter from data. The gradient ascent is used to estimate the shape parameter by maximizing log-likelihood:

$$\begin{aligned} \nabla _{{\lambda }_{jd}}{{\mathcal {L}}}(\Theta ,{\mathcal {Z}},{\mathcal {X}})=\sum _{i=1}^{N}p(j|{\vec {X}}_{i})\nabla _{{\lambda }_{jd}}\log p({\vec {X}}_{i}|{\xi }_{j}) \end{aligned}$$
(40)

The gradient ascent is used for adaptation, with gradient of the component density with respect to shape parameter vector \({\lambda }_{jd}\) for each component of the mixture model.

$$\begin{aligned} \Delta {\lambda }_{jd}\propto p(j|{\vec {X}}_{i})\frac{\partial }{\partial {\lambda }_{jd}}\log p({\vec {X}}_{i}|{\xi }_{j}) \end{aligned}$$
(41)

In adaptation of shape parameter \(\lambda _{jd}\), gradient of component of the mixture model with respect to shape parameter is weighted by \(p(j|{\vec {X}}_{i})\). An estimate of shape parameter using gradient ascent is as follows:

$$\begin{aligned} {\hat{\lambda }}_{jd}={\lambda }_{jd}+\alpha \left( p(j|{\vec {X}}_{i})\frac{\partial }{\partial {\lambda }_{jd}}\log p({\vec {X}}_{i}|{\xi }_{j})\right) \end{aligned}$$
(42)

The estimation of shape parameter in an ICA mixture model is discussed in [38] and the term \(\frac{\partial }{\partial {\lambda }_{jd}}\log p({\vec {X}}_{i}|{\xi }_{j})\) is computed with the assumption of unit variance and zero mean as follows:

$$\begin{aligned} \frac{\partial }{\partial {\lambda }_{jd}}\log p({X}_{id}|{\xi _{j}})&=\frac{\partial }{\partial {\lambda }_{jd}}\log \left[ \frac{f_{ggd}({X}_{id}|{\xi _{j}})\text {H}({X}_{id}|{j})}{\int _{\Omega _{S_j}}f_{ggd}({{\text {u}}}|{\xi _{j}})d\text {u}}\right] \nonumber \\&={h({X}_{id}|{\xi _{j}})}-\frac{\int _{\Omega _{S_j}}f_{ggd}(\text {u}|{\xi _{j}})h(\text {u}|{\xi _{j}})d\text {u}}{\int _{\Omega _{S_j}}f_{ggd}(\text {u}|{\xi _{j}})d\text {u}} \end{aligned}$$
(43)

where the term \({h({X}_{id}|{\xi _{j}})}\) is represented as:

$$\begin{aligned} {h({X}_{id}|{\xi _{j}})}&=\frac{\partial }{\partial {\lambda }_{jd}}\log {f_{ggd}({X}_{id}|{\xi _{j}})}\nonumber \\&=\left[ \frac{1}{\lambda _{jd}}+\frac{3}{2\lambda _{jd}}\left[ \Psi (1/\lambda _{jd})-\Psi (3/\lambda _{jd})\right] \right] -A(\lambda _{jd})\Big |{X_{id}}\Big |^{\lambda _{jd}}\log \Big |{X_{id}}\Big |\nonumber \\&\quad -\,A(\lambda _{jd})\left( \frac{1}{2}\log \frac{\Gamma (3/\lambda _{jd})}{\Gamma (1/\lambda _{jd})}+\frac{1}{2\lambda _{jd}}\left[ \Psi (1/\lambda _{jd})-3\Psi (3/\lambda _{jd})\right] \right) \Big |{X_{id}}\Big |^{\lambda _{jd}} \end{aligned}$$
(44)

The term \(h(\text {u}|{\xi _{j}})\) also follows computation presented in Eq. (44). The term \(\int _{\Omega _{S_j}} f_{ggd}(\text {u}|{\xi _{j}})h(\text {u}|{\xi _{j}})d\text {u}\) can be approximated similar to Eq. (16).

$$\begin{aligned} \int _{\Omega _{S_j}}f_{ggd}(\text {u}|{\xi _{j}})h(\text {u}|{\xi _{j}})d\text {u}\approx \frac{1}{M}\sum _{m=1}^{M}h({s_{j}}_{md}|{\xi _{j}})\text {H}({s_{j}}_{md}|{j}) \end{aligned}$$
(45)

The estimation of shape parameter can be expressed as follows:

$$\begin{aligned} {\hat{\lambda }}_{jd}={\lambda }_{jd}+\alpha \left[ p(j|{\vec {X}}_{i})\left\{ {h({X}_{id}|{\xi _{j}})}-\frac{\sum _{m=1}^{M}h({s_{j}}_{md}|{\xi _{j}})\text {H}({s_{j}}_{md}|{j})}{\sum _{m=1}^{M}\text {H}({s_{j}}_{md}|{j})}\right\} \right] \end{aligned}$$
(46)

The complete learning procedure for BGGMM with ICA is given in Algorithm 1, where \(t_{min}\) is minimum threshold used to examine convergence criteria in each iteration.

figure a

3 Experiments and Results

The proposed algorithm is applied to BSS and unsupervised keyword spotting and experimental results are presented in the following subsections.

3.1 Blind Source Separation

3.1.1 Design of Experiments

In this subsection, experimental framework for BSS is described. It uses ICA mixture model for statistical learning as described in Sect. 2. In BSS, basis functions are estimated using ICA mixture model which is further applied to separate mixed signals. We have estimated basis functions \(2\times 2\), \(3\times 3\), \(4\times 4\) and \(5\times 5\) to compute 2, 3, 4 and 5 sources in separate experiments. In order to validate this BSS framework, TIMIT, TSP and NOIZEUS speech corpora are adopted during the experiments [23, 30, 36]. For BSS, only speech signal after linear mixing are observed. No prior information about basis functions is utilized during the source separation. BSS framework is evaluated using subjective and objective measures. Subjective analysis consists of speech signals before and after the source separation. Objective analysis consists of SDR, SIR, SAR and PESQ. Objective measures SDR, SIR and SAR are measured in dB and PESQ score lies in the range \(-0.5\) to 4.5. Further details on objective measures can be found in [20, 49, 74]. This framework is also implemented using ICA in order to compare and examine the validity of statistical learning of ICA mixture model in BSS. ICA used in this work is implemented using Infomax [9].

Table 1 Objective measure for separation of 2 speech signals
Full size table
Table 2 Objective measure for separation of 3 speech signals
Full size table

3.1.2 Experimental Results

Blind source separation based on ICA mixture model is validated using TIMIT, TSP and NOIZEUS speech corpora. We have conducted 4 experiments to compute 2, 3, 4 and 5 speech sources from this BSS framework. For the recovery of 2, 3, 4 and 5 speech sources, we have taken linear mixture of 2, 3, 4 and 5 sources, respectively, from each database and performed blind source separation by employing BGGMM using ICA. Once the sources are recovered, objective analysis is performed on sources to examine quality of recovered speech signals and viability of ICA mixture model in BSS. Objective measures include SDR, SIR, SAR and PESQ analysis. SDR is a measure of distortion in output signal and it is defined as ratio between energy of clean signal and distortion and it is measured in dB. SIR is the ratio of target signal prower to the interference signal. It measures the amount of undesired interference still present after BSS and it is measured in dB. SAR measures the quality after source separation in terms of absence of artificial noise and measured in dB. PESQ is an objective assessment tool which correlates well with subjective listening scores [20, 49, 74]. The experiments are repeated 10 times with different linear speech mixtures of 2 and 3 sources from each database and average of objective measures is computed. In BSS for reconstruction of 4 and 5 sources, the experiments are repeated 10 times for TIMIT, 30 and 10 times for TSP and 7 and 6 times (due to the limitation of database) for NOIZEUS speech corpus, respectively and average of the objective measures is computed. For the case of TSP database with 4 sources, initially we repeated the experiment 10 times, but the effectiveness of our approach was not clear. We ran the same experiment for another set of 20 mixtures of 4 sources and averaged over all of 30 mixtures. We have performed same analysis using ICA in order to have a comparison of proposed BSS framework. The objective measures after the recovery of speech source signals are given in Tables 1, 2, 3 and 4. From the objective measures, it is observed that ICA mixture model outperforms the ICA in a relative setting of BSS for 2, 3, 4 and 5 sources for all databases. We do not have any permutation ambiguity while recovering 2 sources. In case of 3, 4 and 5 sources, permutation ambiguity is present and it is higher while recovering higher number of sources. The speech signals before mixing, after mixing and after BSS are shown in Figs. 1 and 2, where we have plotted the signals in the same order as they are before mixing in order to present a clear comparison to the reader.

Table 3 Objective measure for separation of 4 speech signals
Full size table
Table 4 Objective measure for separation of 5 speech signals
Full size table
Fig. 1
figure 1

Blind source separation with 2 signals

Full size image
Fig. 2
figure 2

Blind source separation with 3 signals

Full size image

From the above experiments on BSS using BGGMM using ICA, it is observed that ICA mixture model performs better as compared to ICA. It is also observed that rate of this improvement becomes slower when we increase the number linear mixtures in source separation.

3.2 Blind Source Separation as Preprocessing to Keyword Spotting

In this subsection, proposed framework for BSS as pre-processing to unsupervised keyword spotting using an ICA mixture is presented. In real time applications, detection rate of speech recognition and keyword spotting is badly affected by mixing of speech signals with noise or other speech signals. It is also possible to intentionally mix the speech signal with noise or some other speech utterances to reduce or some times completely eliminate the chances of getting spotted by keyword spotting systems. In many security application of keyword spotting, it becomes critically important to use BSS as pre-processing when we are interested to spot particular keywords and we do not want to lose any piece of information.

Fig. 3
figure 3

Blind source separation as pre-processing to unsupervised keyword spotting via an ICA mixture model

Full size image

An unsupervised keyword spotting framework via segmental DTW on Gaussian posteriorgrams was presented in [80]. However, instead of using independently trained phonetic recognizer or GMM, an ICA mixture was proposed for training the model and generation of posteriorgram in [6]. The training process involves directly modeling the speech without any transcription information using the proposed ICA mixture model. The trained model was further used to decode the keyword examples and test utterances in posteriorgrams. Segmental DTW was used to compare the posteriorgrams between keyword examples and the test utterances. The distortion scores were ranked for the most reliable warping path to achieve keyword detection [25, 80]. The detailed description on the keyword spotting is provided in [6, 80]. In the experimental setup presented in [6], parameters of keyword spotting framework were chosen exactly the same as given in [80], in order to have fair comparison of keyword detection results. ICA mixture model has demonstrated its viability and effectiveness in Keyword spotting framework based on detection rate presented in [6]. Experiments were performed on TIMIT speech corpus and a list of 10 keywords was selected to test the trained model for keyword spotting. In this framework same keyword spotting based on ICA mixture is adopted.

We have extended BSS framework presented in Sect. 3.1 and proposed as pre-processing for keyword spotting when the speech utterances with target keywords are mixed with noise or other speech utterances. The training phase of this proposed framework will remain same as presented in [6]. In order to examine the performance of keyword spotting framework, BSS is applied on test data to recover the speech signals. Once source separation is achieved through BSS via ICA mixture, the recovered signals can be applied to trained model for keyword detection. The proposed framework is shown in Fig. 3, which is inspired by [79]. Two types of problems occur in keyword spotting, when source mixing between speech utterances exist at initial stage during the testing. In the first case, if a speech utterance with a particular keyword is mixed with another speech utterance(s) and an overlap of a word exist in the second utterance(s) on same place as the particular keyword in first utterance. In this case, keyword will be mixed with the word of second utterance and it will more likely not detected during the keyword spotting. In second case, if a silent patch of speech exist in second utterance at the same place as keyword in the first speech utterance, it will be detected in the first speech utterance during keyword spotting. But it will also get detected in the second utterance which is a false alarm because keyword actually do not exist in the second speech utterance. These issues are addressed by proposing BSS as pre-processing to keyword spotting.

3.2.1 Design of Experiment

In this subsection, experimental framework and detection results for BSS based keyword spotting are presented. For keyword spotting, we have adopted the framework proposed in [6], and for the pre-processing stage, blind source separation framework presented in Sect. 3.1 is adopted. In both frameworks, ICA mixture is employed for statistical modeling and estimation of basis functions. In the training phase, speech data dedicated for training is used directly for statistical modeling without any transcription information. Once the model is trained, it can be used further to decode the keyword examples and test utterances into posteriorgrams. In this framework, it is assumed that test data is mixed with noise or other speech signals which requires the application of BSS before generation of posteriorgrams by employing the trained model. In order to perform pre-processing through BSS, we have created mixtures of 2, 3, 4 and 5 speech signals on test data. TIMIT speech corpus is employed during the modeling of keyword spotting framework and validation of the said framework is performed through the selected part of test data after being processed through BSS [23]. The speech signals processed through BSS are further applied to the trained model for generation of posteriorgrams. Segmental DTW is employed to compare the posteriorgrams for test utterances and keyword examples. Mel frequency cepstral coefficients (MFCCs) are used as features for in this framework.

3.2.2 Experimental Framework and Results

The BSS based keyword spotting framework is evaluated on TIMIT speech corpus. The TIMIT speech corpus is composed of 6300 speech utterances which contains 4620 speech utterances for training and 1680 speech utterances for testing. In this work, keyword spotting framework is modeled by all of the training data. For testing, speech utterances with target keywords and without target keywords were selected. The speech utterances with target keywords were mixed with the speech utterances without target keywords, for creating a mixture of 2, 3, 4, and 5 speech files. In these mixtures only one speech utterance have target keyword while rest of the speech utterances have no target keyword. Voice activity detection and feature extraction is applied directly before the modeling during training. For testing, feature extraction is applied after the test data is being processed through blind source separation. For feature extraction, each speech utterance is segmented into frames of 25 ms with a window shifting of 10 ms, where each frame is represented by 13 MFCCs. In order to initialize the parameters of ICA mixture during the training, K-Means is applied for mean, standard deviation and mixing weight whereas shape parameter is set to 2 for each component of mixture model. During the training for Keyword spotting, number of components of ICA mixture is set to be 50 as in [6, 80]. The smoothing factor, segmental DTW adjustment window size and score weighing factor are chosen to be 0.00001, 6 and 0.5, respectively as in [6, 80]. The keyword “Year” is uttered 177 times in the test part of dataset but in these experiments only 20 speech utterances with this keyword were selected, because rest of the keywords are uttered less than 20 times in the test data. For the testing, 10-keyword set presented in [6, 80] is adopted and given in Table 5.

Table 5 TIMIT 10 keyword list used in [6, 80]
Full size table

For the evaluation of keyword detection, three different evaluation matrices reported in [6, 25, 80] are examined, which are defined as: (1) the average precision for top 10 utterance hits termed as P@10, (2) the average precision for top N utterance hits termed as P@N, where N is equal to the number of occurrences of each keyword in the test data, (3) the average equal error rate (EER), where false acceptance rate is equal to false rejection rate. It is assumed that test data is affected by source mixing and it needs to be processed through BSS before applying to the trained model for generation of posteriorgrams. In order to validated the effectiveness of BSS as pre-processing, a new test data from the selected part of test data from TIMIT speech corpus is created. The purpose of this new dataset is to create the mixtures of \(2\times 2\), \(3\times 3\), \(4\times 4\) and \(5\times 5\) with speech utterances having target keywords and having no target keywords. In each mixture, one speech utterance have the target keyword while rest of them do not have target keyword. For example, in the case of keyword “age”, all the 10 speech utterances with this keyword are taken and each utterance is mixed with another speech utterance with no target keyword for creating a mixture of \(2\times 2\). For mixture of \(3\times 3\), each speech utterance of target keyword is mixed with 2 more utterances having no target keyword. For the keyword “age”, with mixtures of \(2\times 2\), we have 20 speech utterances in total (10 of them have target keyword and 10 have no target keyword), whereas with mixtures of \(3\times 3\), we have 30 speech utterances in total (10 of them have target keyword and 20 have no target keyword). All mixtures for the keywords given in Table 5 were created in the same fashion as discussed before. During the whole experiment, 100 speech utterances with no target keywords from the Table 5 and all the speech utterances with target keywords were selected and used according to the requirement for creating the mixture of speech data for each keyword. The next stage is to apply BSS and then adopt trained ICA mixture to generate posteriorgrams. BSS is performed by ICA mixture and same framework is adopted for BSS as discussed in Sect. 3.1. Table 6 indicates the performance of keyword detection before and after BSS, for different number of keyword examples based on P@N, P@N and EER.

For P@10 evaluation, 4 keywords from Table 5 are considered because only they have occurred more than 10 times both in the training and test part of dataset. For P@N and EER evaluations, with one keyword example experiment, all the keywords from the Table 5 were used. For P@N and EER evaluations, with 5 keyword examples experiment, 8 keywords were used because they have occurred more than 5 times in the training set. For P@N and EER evaluations, with 10 keyword examples experiment, only 5 keywords were used because they have occurred more than 10 times in the training set. The average precision for each keyword is calculated first and then mean of average precisions of all keywords for P@10 or P@N was computed. The EER for each keyword was computed based on false acceptance rate (FAR) and false rejection rate (FRR). The EER mentioned in Table 6 is the average of EER for all keywords used for that particular case [6, 80]. Table 6 indicates considerable improvement in the evaluation matrices after being processed through BSS for \(2\times 2\) and \(3\times 3\) mixtures in comparison to the case when no BSS was applied. There is also improvement for \(4\times 4\) and \(5\times 5\) mixtures as compared to the case when no BSS was applied, but the trend of improvement is slow as compared to the \(2\times 2\) and \(3\times 3\) mixtures.

Table 6 Evaluation matrix with BSS and without BSS
Full size table

The results for average precisions (P@10 and P@N) are very close to each other, because utterance of available keywords in the test data is very close to 10 in most of the case. It is also important to note that only 4 keywords are present more than 10 times in both training and testing and hence P@10 was computed only for 4 keywords from the list given in Table 5. However for P@N, most of the keywords were used for computations, so it more effective for examining the viability of this framework. It is also observed that trend of improvement is higher when going from one keyword example to 5 keyword examples, whereas it is slow from 5 to 10 keyword examples. If we compare the results presented in this paper with the results presented in frameworks when no source mixing is considered, there is a lot of room for improvement. However comparison of keyword spotting with BSS and keyword spotting without BSS indicates the effectiveness of this framework in keyword spotting when speech signals are affected by mixing. It is also observed that the problem of false alarm due to mixing of sources is more severe in computing the detection rate for keyword spotting, which actually reduces the overall performance of keyword spotting. In many security applications, it is necessarily important to find the particular keywords because they are further used to detect particular speakers. If false alarm occur and even correct speaker is also detected, it will increase the number of possibilities to find the particular speaker. In the other case, when keyword is mixed with the words of other speech utterances and it is more likely not detected during the keyword spotting, it can increase the chances of completely losing a particular information. It is important when it is mixed intentionally to hide the particular information (keyword) which is critical to security. The experiments performed in this work only include the mixing of speech utterances. This framework needs to be extended for keyword spotting when speech utterances are mixed with noise. This experiment can be further extended with a larger vocabulary database by having more number of keyword examples.

4 Conclusion

In this paper, BGGMM with ICA is proposed as a model for statistical learning, which is further proposed in BSS and unsupervised keyword spotting to validate the effectiveness of algorithm. The proposed algorithm is a multivariate ICA mixture model which adopt EM and gradient ascent methods for parameter estimation. This algorithm handles the limitations associated with ICA which assumes that sources are independent from each other. In ICA mixture model, it is assumed that data come from a mixture model and it can be categorized into mutually exclusive classes with an ICA. The proposed model has demonstrated its success through presented applications. BSS adopts TIMIT, TSP and NOIZEUS speech corpora for the validation and performance measures are computed using SDR, SIR,SAR and PESQ. From the experiments in BSS, it is observed that ICA mixture model performs better as compared to ICA. It is also observed that rate of this improvement becomes slower when we increase the number linear mixtures in source separation. BSS is further proposed as pre-processing to unsupervised keyword spotting, by employing ICA mixture model, when speech utterances having target keywords are affected by mixing of noise or other keywords. The experiments are performed by employing TIMIT speech corpus to train the ICA mixture for keyword spotting and then selecting the part of test data for creating a mixture of 2, 3, 4 and 5 speech signals to perform the blind source separation before the keyword spotting. The purpose of creating these mixtures of speech utterances with target keyword and with no target keyword is to validate the effectiveness of proposed framework. The keyword detection results are presented before and after the test data being processed through blind source separation. The keyword detection results based on average precision (P@10 and P@N), and EER validate the effectiveness of proposed framework when speech utterances with target keywords are affected by mixing. The experiments have shown significant improvement in the detection of keywords when mixed speech signals are processed through BSS via an ICA mixture. From the application of proposed algorithm in blind source separation and unsupervised keyword spotting, ICA mixture model has validated its effectiveness in statistical modeling.