A Time–Frequency Domain Blind Source Separation Method for Underdetermined Instantaneous Mixtures

Abstract

We propose a new method for underdetermined blind source separation based on the time–frequency domain. First, we extract the time–frequency points that are occupied by a single source, and then, we use clustering methods to estimate the mixture matrix A. Second, we use the parallel factor (PARAFAC), which is based on nonnegative tensor factorization, to synthesize the estimated source. Simulations using mixtures of audio and speech signals show that this approach yields good performance.

1 Introduction

Blind source separation (BSS) is a method that reconstructs N unknown sources of M observed signals from an unknown mixture. In this paper, we consider an instantaneous mixture system. Let A be the $M\times N$ mixing matrix, then the observations can be written as $x(t)=As(t)$, where $x(t)=[x_1 (t),x_2 (t),\ldots x_M (t)]$ and $s(t)=[s_1 (t),s_2 (t),\ldots s_N (t)]^{T}$. Our investigation considers the underdetermined case, where there are more sources than observations $(N>M)$.

BSS based on the instantaneous mixtures model has been extensively studied since the first papers by Herault and Jutten [25–27]. The early classical BSS method is based on independent component analysis (ICA) theory [10]. The classic ICA theory can only separate stationary non-Gaussian signals. Because of these limitations, it is difficult to apply it to real signals, such as audio signals. Some authors [5, 14, 15, 28, 36, 37] have proposed different approaches to enhance the classical ICA theory. These methods have better performance than classical ICA methods for nonstationary signals. However, these approaches [5, 28, 36, 37] cannot be applied to the underdetermined case. Many notable works for the underdetermined case have been published in recent years [1–3, 6, 7, 17, 22, 23, 29, 30, 32, 33, 38, 40, 41, 46, 47]. The basic assumption of these studies is that the mixed signals are sparse in the time–frequency domain. A signal is said to be sparse when it is zero or nearly zero more than might be expected from its variance. A notable sparse-based method called DUET was developed for delay and attenuation mixtures [29, 40]. The DUET algorithm requires W-disjoint orthogonal signals or approximate W-disjoint orthogonal signals [41, 46] in the time–frequency domain. In fact, the DUET algorithm is a ratio matrix (RM) method that uses clustering by an RM to accomplish source separation. Many well-known algorithms rely on the RM method, such as the SAFIA algorithm [3], the TIFROM algorithm [1], Abdeldjalil Aïssa-El-Bey et al.’s algorithm [2], Yuanqing Li et al.’s algorithm [13], and SangGyun Kim et al.’s algorithm [30]. In [6], Adel Belouchrani et al. presented an overview of source separation in the time–frequency domain.

Two methods have been widely used to make the signal sparse: the short-time Fourier transform (STFT) method [29, 41, 46] and the Wigner–Ville distribution (WVD) method [2, 5]. We use the WVD to represent the time–frequency spectrum to estimate the mixing matrix and the STFT for signals synthesis. The proposed underdetermined BSS algorithm in this paper is based on a two-stage approach. In the first stage, we estimate the mixture matrix using a RM in the time–frequency domain on the spatial Wigner–Ville spectrum. The second stage is the synthesis of the signals: We use a method combining the minimum mean square error (MMSE) and the parallel factor (PARAFAC) technique to reconstruct the estimated sources. PARAFAC is a multilinear algebra tool for tensor decomposition in a sum of rank-1 tensors. PARAFAC is a multidimensional method originating from psychometrics [24] that has slowly found its way into various disciplines. A good overview of the tensor decomposition can be found in [31]. PARAFAC is also a powerful tool for BSS [4, 8, 11, 13, 18, 20–23, 34, 35, 42, 45]. Recently, Pierre Comon provided a good overview of BSS and tensor decomposition in [12]. BSS based on nonnegative tensor factorization can be found in [8, 18, 20, 21, 35]. Nonnegative tensor factorization is a decomposition method for multidimensional data, in which all elements are nonnegative. As shown in [13, 34], the traditional application of the tensor decomposition technique to BSS is limited to restricted numbers of microphones and mixed sources: The number of sources $N$ and the number of observed mixtures $M$ must satisfy $N\le 2M-2$. However, the application of nonnegative tensor factorization to BSS is not restricted by the number of microphones and mixed sources. We therefore use a nonnegative PARAFAC model for source synthesis in this paper. The authors of [45] have proposed a time–frequency analysis based on the WVD together with the PARAFAC algorithm to separate electroencephalographic data.

There are many differences between the algorithm proposed in this paper and that in [45]. First, the PARAFAC model in [45] is based on the time–frequency domain with the WVD, while the PARAFAC model in this paper is based on the time–frequency domain with a STFT. Second, our PARAFAC model is different from the one in [45] because it has nonnegative elements. Thus, our PARAFAC model is not restricted by the number of microphones and mixed sources for BSS. Finally, the algorithm in this paper is a two-stage technique: We use time–frequency representation with the WVD to estimate the mixing matrix in the first stage, and the second stage is the source recovery with the nonnegative PARAFAC model.

This paper is organized as follows. In Sect. 2, we describe how the mixing matrix is estimated using the time–frequency ratio of the spatial Wigner–Ville spectrum. Then, we synthesize the estimated sources using MMSE and the PARAFAC method in Sect. 3. Section 4 provides the simulation results, and Sect. 5 draws various conclusions from this investigation.

2 Mixing Matrix Estimation

2.1 Spatial Time–Frequency Distributions

The WVD of $x(t)$ is defined as:

$$\begin{aligned} D_{xx}^{WV} (t,f)=\int \limits _{-\infty }^{+\infty } {x(t+\tau /2)x^{H}(t-\tau /2)} \mathrm{e}^{-j2\pi f\tau }\mathrm{d}\tau , \end{aligned}$$

(1)

where $t$ and $f$ represent the time index and the frequency index, respectively. The signal $x(t)$ of Cohen’s class of spatial time–frequency distributions (STFD) is written as [9]:

$$\begin{aligned} D_{xx} (t,f)=\int \limits _{-\infty }^{+\infty } {\int \limits _{-\infty }^{+\infty } {\phi (u-t,v-f)D_{xx}^{WV} (t,f)\mathrm{d}u\mathrm{d}v} } , \end{aligned}$$

(2)

where $\phi (u,v)$ is the kernel function of both the time and lag variables. In this paper, we assume that $\iint {\phi (t,f)\hbox {d}t\hbox {d\!}f=1}$. Under the linear instantaneous mixing model of $x(t)=As(t)$, the STFD of $x(t)$ becomes:

$$\begin{aligned} D_{xx} (t,f)=AD_{ss} (t,f)A^{H}. \end{aligned}$$

(3)

We note that $D_{xx} (t,f)$ is an $M\times M$ matrix, whereas $D_{ss} (t,f)$ is an $N\times N$ matrix.

2.2 Selecting a Single Source Active in the Time–Frequency Plane

If we assume that two signals $x_1$ and $x_2$ share the same frequency $f_0$ at the time $t_0$, then the cross-time–frequency distribution (cross-TFD) between $x_1$ and $x_2$ at $(t_0, f_0)$ is nonzero. Hence, if $D_{x_1 x_1 } (t_0 ,f_0)$ and $D_{x_2 x_2 } (t_0 ,f_0)$ are nonzero, it is likely $D_{x_1 x_2 } (t_0 ,f_0)$ and $D_{x_2 x_1 } (t_0 ,f_0)$ are nonzero. Therefore, if $D_{xx} (t,f)$ is diagonal, it is likely that it has only one nonzero diagonal entry [9]. The proposed algorithm is based on single autoterms (SATs) theory [19]; we can detect the points of single-source occupancy in every time–frequency plane by SATs. In this paper, we use a mask-TFD to compute the SATs. We define the mask-TFD as $D_{xx}^\mathrm{mask} (t,f)=D_{xx} (t,f)*X(t,f)$, where $X(t,f)$ is the matrix of a STFT with $x$, as the same process in [19]; the mask-SATs satisfy:

$$\begin{aligned} \left\{ {{\begin{array}{l} {C(t,f)\approx \frac{\max \left| {\mathrm{eig}(D_{xx}^\mathrm{mask} (t,f))} \right| }{\sum {\left| {\mathrm{eig}(D_{xx}^\mathrm{mask} (t,f))} \right| } }} \\ {\left\| {\mathrm{Grad}_C (t,f)} \right\| _2 \le \varepsilon _\mathrm{Grad} } \\ {H_C (t,f)<0} \\ \end{array} }} \right. , \end{aligned}$$

(4)

where $\mathrm{eig}(D_{xx}^\mathrm{mask} (t,f))$ denote the eigenvalues of $D_{xx}^\mathrm{mask} (t,f)$, and $\mathrm{Grad}_C (t,f)$ and $H_C (t,f)$ are the gradient function and the Hessian matrix of $C(t,f)$, respectively.

2.3 Mixing Matrix Estimation Using the Time–Frequency Ratio

If we assume that there exist two observations, $x_1 =[x_1 (t_1 )\ldots x_1 (t_{T_0 } )]^{T}$ and $x_2 =[x_2 (t_1 ) \ldots x_2 (t_{T_0 } )]^{T}$, and the two observations are mixed from $N$ sources, $s_1 \ldots s_n \ldots s_N$ and $s_n =[s_n (t_1 ) \ldots s_n (t_{T_0 } )]^{T}$, then we can compute the mask-TFDs for $x_1 (t)$ and $x_2 (t)$. They become:

$$\begin{aligned} D_{x_1 x_1 }^\mathrm{mask} (t,f)= & {} \sum \limits _n {D_{s_n s_n }^\mathrm{mask} (t,f)a_{1n}^{2}a_{1n}^H }\end{aligned}$$

(5)

$$\begin{aligned} D_{x_2 x_2 }^\mathrm{mask} (t,f)= & {} \sum \limits _n {D_{s_n s_n }^\mathrm{mask} (t,f)a_{2n}^{2}a_{2n}^H } . \end{aligned}$$

(6)

If we have extracted all the time–frequency points that are occupied by a single source via (4), and if furthermore we assume that $s_n$ occupies frequency $f_0$ at time $t_0$, then (5) and (6) become:

$$\begin{aligned} D_{x_1 x_1 }^\mathrm{mask} (t_0 ,f_0 )= & {} D_{s_n s_n }^\mathrm{mask} (t_0 ,f_0 )a_{1n}^{2}a_{1n}^H\end{aligned}$$

(7)

$$\begin{aligned} D_{x_2 x_2 }^\mathrm{mask} (t_0 ,f_0 )= & {} D_{s_n s_n }^\mathrm{mask} (t_0 ,f_0 )a_{2n}^{2}a_{2n}^H . \end{aligned}$$

(8)

Then, it follows that $\frac{D_{x_1 x_1 }^\mathrm{mask} (t_0 ,f_0 )}{D_{x_2 x_2 }^\mathrm{mask} (t_0 ,f_0 )}=\frac{D_{s_n s_n }^\mathrm{mask} (t_0 ,f_0 )a_{1n} a_{1n}^H }{D_{s_n s_n }^\mathrm{mask} (t_0 ,f_0 )a_{2n} a_{2n}^H }=\frac{a_{1n}^{2}*a_{1n}^H }{a_{2n}^{2}*a_{2n}^H }$. For the general case of $M$ observations and if we define a vector, $D_{xx}^{\prime } (t_0 ,f_0 )=[D_{x_1 x_1 }^\mathrm{mask} (t_0 ,f_0 ),\ldots ,D_{x_M x_M }^\mathrm{mask} (t_0 ,f_0 )]^{T}$, then we can obtain a ratio vector:

$$\begin{aligned} \frac{D_{xx}^{\prime } (t_0 ,f_0 )}{D_{x_1 x_1 }^\mathrm{mask} (t_0 ,f_0 )}=\left[ 1,\frac{a_{2n}^{2}*a_{2n}^H }{a_{1n}^{2}*a_{1n}^H },\ldots ,\frac{a_{Mn}^{2}*a_{Mn}^H }{a_{1n}^{2}*a_{1n}^H }\right] ^{T}. \end{aligned}$$

(9)

We denote the set of the above ratio as $C_{s_n}$ for $n=1,\ldots ,N$. Then, we can apply a clustering method to estimate the mixing matrix combining SATs and (9). We assume that the mixtures are normalized to have unit $l_2$-norm. We denote the $n$th column vector of $A$ as $a_n$, which is estimated as follows:

$$\begin{aligned} \hat{a}_n =\frac{1}{\left| {C_{s_n } } \right| }\sum \limits _{[t,f]\in C_{s_n } } {D_{xx}^{\prime } (t,f)} , \end{aligned}$$

(10)

where $\left| {C_{s_n } } \right|$ denotes the number of the points in the class for $n=1,\ldots ,N$.

3 Source Synthesis

Nonnegative tensor factorization (NTF) of multichannel spectrograms under the PARAFAC structure has been widely applied to BSS of multichannel signals [18, 20, 21]. In this paper, we use the IS-NTF method [18] to synthesize sources. First, we apply the STFT to time-domain observations $x(t)$; we further assume that $s(t,f)$ obeys the following distribution [18]:

$$\begin{aligned} \left\{ {{\begin{array}{l} {x_m (t,f)=\sum \limits _n {a_{mn} s_n^m (t,f)} } \\ {s_n^m (t,f)\sim N_\mathrm{c} (0|w_{fn} h_{tn} )} \\ \end{array} }} \right. , \end{aligned}$$

(11)

where $m$ is the number of observations, $n$ is the mixed-source index, $N_\mathrm{c}$ denotes the complex Gaussian distribution subject to $N_\mathrm{c} (x|u,\Sigma )=|\pi \Sigma |^{-1}\exp -(x-u)^{H}\Sigma ^{-1}(x-u)$, $w_{fn}$ is the $(f,n)$th element of matrix $W$ (its size is $F\times N$), and $h_{tn}$ is the $(t,n)$th element of matrix $H$ (its size is $T\times N$). Set $V=|X|^{2}$ and $Q=|A|^{2}$, where $X$ is the time–frequency matrix with elements $x(t,f)$. We note that (11) is equivalent to $\mathop {\min }\limits _{Q,W,H}\sum \nolimits _{mft} {d_{IS} (v_{mft} | \hat{{v}}_{mft})}$, where $Q,W,H\ge 0$, $d_{IS} (x|y)=\frac{x}{y}-\log \frac{x}{y}-1$. Then, we can obtain [18]:

$$\begin{aligned} W= & {} W \cdot \frac{\left\langle {G_{-} ,QoH} \right\rangle _{\{1,3\},\{1,2\}} }{\left\langle {G_{+} ,QoH}\right\rangle _{\{1,3\},\{1,2\}} }\end{aligned}$$

(12)

$$\begin{aligned} H= & {} H \cdot \frac{ \left\langle {G_- ,QoW}\right\rangle _{\{1,2\},\{1,2\}} }{ \left\langle {G_+ ,QoW}\right\rangle _{\{1,2\},\{1,2\}} }, \end{aligned}$$

(13)

where $G$ is the $M\times F\times T$ derivatives tensor with $g_{mft} =d^{{\prime }}(v_{mft} |\tilde{v}_{mft})$ and $\left\langle {A,B}\right\rangle _{\{1,\ldots ,M\},\{1,\ldots ,M\}} =\sum \limits _{i_1 }^{I_1 } {\ldots \sum \limits _{i_M }^{I_M } {a_{i_1 ,\ldots ,i_{M,} j_1 ,\ldots ,j_N } b_{i_1 ,\ldots ,i_{M,} k_1 ,\ldots ,k_O }}}$. Then, we can obtain the MMSE reconstruction as:

$$\begin{aligned} s_n^m (t,f)=\frac{a_{\textit{mn}}^2 w_{\textit{fn}} h_{\textit{fn}} }{\sum \nolimits _n {a_{\textit{mn}}^2 w_{\textit{fn}} h_{\textit{fn}} }}x_m (t,f). \end{aligned}$$

(14)

Finally, applying the inverse STFT to $s_n^m (t,f)$, we can obtain the time-domain source. Our source separation route is distinct from the method in [18, 20]. Our algorithm has two stages. The first is to estimate the mixing matrix. Then, source reconstruction is the inverse problem in the second stage. We fix the mixing matrix in the source reconstruction stage, which is equivalent to fixing $Q$ in (12) and (13).

4 Simulation

To show the validity of our technique of mixing matrix estimation, we conducted four experiments for mixing matrices of orders $2\, \times \,3$, $2\,\times \,4$, $3\,\times \,4$, and $3\,\times \,6$. For each order of the mixing matrix, we used random values. Each experiment was run 30 times. We used two methods to select the single signal active in the time–frequency plane: traditional SATs and mask-SATs, and we set $\varepsilon _\mathrm{Grad}$ randomly in the range $0.005\le \varepsilon _\mathrm{Grad} \le 0.05$. The mixing sources used in the experiments were music signals and speech. The length of the STFT was 1024, the window overlap was 0.5, and all signals were sampled at 16 kHz with a sample length of 160,000.

The performance of the mixing matrix estimation was evaluated using the normalized mean square error (NMSE), which is defined in [39]:

$$\begin{aligned} \mathrm{{NMSE}}=10\log \left( \frac{\sum \nolimits _{\textit{mn}} {(\hat{{a}}_{\textit{mn}} -a_{\textit{mn}} )^{2}} }{\sum \nolimits _{\textit{mn}} {a_{\textit{mn}}^2 } }\right) , \end{aligned}$$

(15)

where $\hat{{a}}_{\textit{mn}}$ is the $(m,n)$th element of the estimated mixing matrix, and $a_{\textit{mn}}$ is the $(m,n)$th element of the mixing matrix. Smaller NMSEs indicate better performance.

We must note that matrix $A_\mathrm{{TFD}}$ was obtained similarly to $A_{\text{ mask-TFD }}$. The only difference is that in (4), $D_{xx}^\mathrm{{mask}} (t,f)$ is replaced by $D_{xx} (t,f)$. To show the validity of our method, we compared it with the LI-TIFROM algorithm in [1] and the method in [39], as shown in Fig. 1. We see that the mask-TFD algorithm achieves a better mixing matrix estimation than that in [39]. The performance of the algorithm in [39] is better than that of the LI-TIFROM and TFD algorithms. As pointed out in [16], the TIFROM algorithm requires at least two adjacent windows in the time–frequency domain for each source to ensure the degree of sparsity needed. If this condition is not satisfied, the TIFROM algorithm cannot find the single-source points and thus cannot estimate the mixing matrix correctly. This is why the performance of the TIFROM algorithm is not very good in Fig. 1.

Fig. 1

Comparison of proposed algorithm with that in [1] and [39]

For the source synthesis stage, we performed two simulation experiments using $2 \times 3$ and $3 \times 4$ mixing matrices. The sources were taken from the Signal Separation Evaluation Campaign (SiSEC 2008) [43]. We used some “development data” from the “underdetermined speech and music mixtures task”:

• 1. For the music sources including drums: a linear instantaneous stereo mixture (with positive mixing coefficients) of two drum sources and one bass line.

• 2. For the nonpercussive music sources: a linear instantaneous stereo mixture (with positive mixing coefficients) of one rhythmic acoustic guitar, one electric lead guitar, and one bass line.

• 3. Four female sources.

The original mixing matrix of data 1 and data 2 had positive coefficients: $A_\mathrm{nodrum} =\left[ {{\begin{array}{ccc} {0.4937}&{}\quad {0.6025}&{}\quad {0.8488} \\ {0.7900}&{}\quad {0.6575}&{}\quad {0.4232} \\ \end{array} }} \right]$ and $A_\mathrm{wdrum} =\left[ {{\begin{array}{ccc} {0.5846}&{}\quad {0.7135}&{}\quad {1.0053} \\ {0.9356}&{}\quad {0.7786}&{}\quad {0.5012} \\ \end{array} }} \right]$. For the four female sources, we used the original mixing matrix:

$A_\mathrm{female} =\left[ {{\begin{array}{cccc} {0.6547}&{}\quad {0.6516}&{}\quad {0.8830}&{}\quad {-0.5571} \\ {0.3780}&{}\quad {-0.5923}&{}\quad {0.3532}&{}\quad {0.7428} \\ {-0.6547}&{}\quad {0.4739}&{}\quad {0.3091}&{}\quad {0.3714} \\ \end{array} }} \right]$. We used the proposed mask-TFD algorithm to estimate the three matrixes: $A_\mathrm{nodrum}$, $A_\mathrm{wdrum}$, and $A_\mathrm{female}$. The results of the estimations are $A_\mathrm{nodrum}^e =\left[ {\begin{array}{ccc} 0.5345 &{}\quad 0.5739 &{}\quad 0.8318 \\ 0.7836 &{}\quad 0.6825 &{}\quad 0.4194 \\ \end{array}} \right]$, $A_\mathrm{wdrum}^e =\left[ {\begin{array}{ccc} 0.5595 &{}\quad 0.7480 &{}\quad 1.0053 \\ 0.8957 &{}\quad 0.8109 &{}\quad 0.5012 \\ \end{array}} \right]$, and

$A_\mathrm{female}^e =\left[ {{\begin{array}{llll} {0.6472}&{}\quad {0.6500}&{}\quad {0.8715}&{}\quad {-0.5601} \\ {0.4010}&{}\quad {-0.6013}&{}\quad {0.3541}&{}\quad {0.7626} \\ {-0.6936}&{}\quad {0.4732}&{}\quad {0.2987}&{}\quad {0.3619} \\ \end{array} }} \right]$. The NMSEs of $A_\mathrm{nodrum}^e$, $A_\mathrm{wdrum}^e$, and $A_\mathrm{female}^e$ are –35.10, –50.88, and –33.90 dB, respectively.

To measure the performance, we decompose an estimated source image as [44]:

$$\begin{aligned} \hat{{s}}_{\textit{mn}}^\mathrm{img} (t)=s_{\textit{mn}}^\mathrm{img} (t)+e_{\textit{mn}}^\mathrm{spat} (t)+e_{\textit{mn}}^{\mathrm{interf}} (t)+e_{\textit{mn}}^\mathrm{artif} (t), \end{aligned}$$

(16)

where $s_{\textit{mn}}^\mathrm{img} (t)$ is the true source image, and $e_{\textit{mn}}^\mathrm{spat} (t)$, $e_{\textit{mn}}^{\mathrm{interf}} (t)$, and $e_{\textit{mn}}^\mathrm{artif} (t)$ are distinct error components representing spatial (or filtering) distortion, interference, and artifacts, respectively. As performance measures, we use the source to distortion ratio (SDR):

$$\begin{aligned} \mathrm{SDR}_n =10\log _{10} \frac{\sum \nolimits _{m=1}^M {\sum \nolimits _t {s_{\textit{mn}}^\mathrm{img} (t)^{2}} } }{\sum \nolimits _{m=1}^M {\sum \nolimits _t {\left( e_{\textit{mn}}^\mathrm{spat} (t)+e_{\textit{mn}}^\mathrm{interf} (t)+e_{\textit{mn}}^\mathrm{artif} (t)\right) ^{2}} } }, \end{aligned}$$

(17)

the source image to spatial distortion ratio (ISR):

$$\begin{aligned} \mathrm{ISR}_n =10\log _{10} \frac{\sum \nolimits _{m=1}^M {\sum \nolimits _t {s_{\textit{mn}}^\mathrm{img} (t)^{2}} } }{\sum \nolimits _{m=1}^M {\sum \nolimits _t {e_{\textit{mn}}^\mathrm{spat} (t)^{2}} } }, \end{aligned}$$

(18)

the source to interference ratio (SIR):

$$\begin{aligned} \mathrm{SIR}_n =10\log _{10} \frac{\sum \nolimits _{m=1}^M {\sum \nolimits _t {\left( s_{mn}^\mathrm{img} (t)+e_{mn}^{ \mathrm spat} (t)\right) ^{2}} } }{\sum \nolimits _{m=1}^M {\sum \nolimits _t {e_{mn}^\mathrm{interf} (t)^{2}} } }, \end{aligned}$$

(19)

and the sources to artifacts ratio (SAR):

$$\begin{aligned} \mathrm{SAR}_n =10\log _{10} \frac{\sum \nolimits _{m=1}^M {\sum \nolimits _t {\left( s_{mn}^\mathrm{img} (t)+e_{mn}^\mathrm{spat} (t)+e_{mn}^\mathrm{interf} (t)\right) ^{2}} } }{\sum \nolimits _{m=1}^M {\sum \nolimits _t {e_{mn}^\mathrm{artif} (t)^{2}} } }. \end{aligned}$$

(20)

Higher values indicate better results for SDR, ISR, SIR, and SAR. We note that in the MMSE method, we do not reconstruct the single-channel sources but their multichannel contribution to the multichannel data.

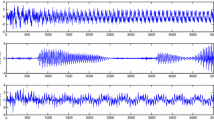
Figure 3 shows the three estimated signals with IS-MMSE. The two mixed signals in Fig. 3 are obtained using the three original source signals in Fig. 2 with mixing matrix $A_\mathrm{nodrum}$. Figure 5 shows the three estimated signals with IS-MMSE. The two mixed signals in Fig. 5 are obtained using the three original source signals in Fig. 4 with mixing matrix $A_\mathrm{wdrum}$ (we use $A^{\text{ mask-TFD }}$ in the IS-MMSE algorithm).

Fig. 2

Three original source signals with hi-hat, drums, and bass

Fig. 3

Three estimated signals with IS-MMSE

Fig. 4

Three original source signals with lead guitar, rhythm guitar, and bass

Fig. 5

Two mixed signals with lead guitar, rhythm guitar, and bass separated by IS-MMSE

Figure 6 shows the performance of the PARAFAC algorithm [18] and mask-TFD with PARAFAC in three examples with music, audio, and speech sources. As shown in Fig. 6, neither the method reported in [18] nor mask-TFD with PARAFAC yields good performance for the nonpercussive music sources. This may be because the number of single signals active in the time–frequency plane is very small. The performances of mask-TFD with the PARAFAC algorithm are better than that of the PARAFAC algorithm reported in [18] in all cases. As shown in [18, 35], the performance of the nonnegative PARAFAC model is heavily related to its initialization. If the initialization is poor, then it is difficult for the nonnegative PARAFAC algorithm to achieve global convergence. In fact, the first stage of mask-TFD with PARAFAC is the initialization of the nonnegative PARAFAC algorithm.

Fig. 6

Performance of the PARAFAC algorithm [18] and mask-TFD with PARAFAC in three examples (two microphones and three sources with no drums, two microphones and three sources with drums, and three microphones mixed with four female sources)

5 Conclusion

We have proposed a two-stage approach to solve the underdetermined instantaneous BSS problem. We used a cluster method for single time–frequency active points in the mixing matrix estimation stage. Methods using joint diagonalization [5, 19] are not suitable for underdetermined mixtures. In this paper, we have used a new cluster method for underdetermined mixing matrix estimation and then applied NTF to the source synthesis. Numerical simulations have illustrated the effectiveness of the new approach for the audio nonstationary signals of the Signal Separation Evaluation Campaign (SiSEC 2008) public data.