1 Introduction

Auto-encoder (AE) which is also often called Autoassociator [1,2,3] is a very classical type of neural network. It learns an encoder function from input to representation and a decoder function back from representation to input space, such that the reconstruction (composition of encoder and decoder) is good for training examples. As a result, the learned representation is supposed to retain as much as information of the input. Due to the particular structure, AEs were classically used as a non-linear dimensionality reduction or data compression technique in information processing applications such as speech recognition [4] and image compression [5].

In the modern applications AEs are also employed in a so called over-complete setting to extract a number of features larger than the input dimension, yielding a much higher dimensional representation. To avoid simple identity function, some tricks are used by adding prior constraints on the weights matrices or the hidden unit activations. The simplest form is a regularized AE with weight-decay that favors small \(L_2\) norm of the weight matrix [6]. Jia et al. [7] proposes a Laplacian AE which regularizes the learned hidden representations to have the locality-preserving property. Sparsity of the representation can also ensure meaningful representation, Le et al. [8] employs KL divergence to penalize the deviation of the expected activation of hidden units from a pre-given small target. Jiang et al. [9] ensures sparsity representations by adding \(L_1\) regularization to penalize non-zeros activations. Liu et al. [10] incorporates both Hessian regularization and sparsity constraints into the hidden units and proposes Hessian regularized sparse AE. Besides, Glorot et al. [11] uses the rectified function to replace the traditional sigmoid funtion as the activation function which also encourages sparsity of the representations.

Deep learning has drawn higher and higher interest since deep belief network (DBN) was proposed in 2006 [12]. Compared to the building block restricted Boltzmann machines (RBMs) used in DBN, AE is easier to learn and can achieve similar representations. As a result, Stacked Auto Encoders with AEs as building blocks have also become a widely used deep network. In such deep models, the decoder processes are abandoned and only the encoder processes are stacked to form deep networks [13,14,15]. The key idea in deep learning is the use of an additional unsupervised criterion to guide the learning at each layer. A proper unsupervised criteria may lead to much better solution, therefore some variants of AE that can detect important structure in the input patterns have been proposed. De-noising auto-encoder (DAE) in [16] and contractive auto-encoder (CAE) in [17] are both designed to learn robust representations of the input but through different methods. The DAE takes a corrupted version of original training data as input and demands the reconstruction through the DAE to be a clean version which can not only avoid simple identity mapping but also extract useful features. On the other hand, CAE encourages the hidden representations to be robust to slight transformation of the input by adding a Frobenius norm of the Jacobian matrix of the encoder activations with respect to the input. Besides, Rifai et al. [18] combines CAE with DAE and proposes contractive de-noising auto-encoder (CDAE), which is robust to both the original input and the learned feature. These variants of basic AE have also been used to build deep networks. Chen et al. [19] adds a nonnegativity constraint on the weight matrices of sparse AE and proposed a nonnegativity-constrained AE which can detect part-based representation of data.

In all of the above applications, AE and its variants are firstly trained in an unsupervised manner to detect the statistical structure of input data. Then, they are used in one of two ways: either as a preprocessing of the input data by replacing it with the representation given by the hidden layer, or an initialization for a feed-forward neural network with the parameters. In both cases, AE and its variants are trained without using any label information so that the learned models are blind to the nature of the supervised tasks that need to be solved and provide no guarantees that the information extracted by hidden layers will be useful. In order to take full advantage of the label information during representation learning, some discriminative AEs have also been proposed in recent years. Hosseiniasl et al. [20] utilizes the label information by considering the label as a part of the output and adding a logistic loss function term to penalize the classification error. Rolfe and Lecun [21] introduces a discriminative AEs for small targets detection, in which the learned manifold satisfying the constraint that the positive data should be better reconstructed than the negative data. Razakarivony and Jurie [22] introduces a discriminative AEs for small targets detection, in which the learned manifold satisfying the constraint that the positive data should be better reconstructed than the negative data by adding a hinge loss regularization. Lee et al. [23] extends the probabilistic linear discriminative analysis (PLDA) to a nonlinear version by replacing the linear mapping with AE for speaker verification. Liu et al. [24] proposes a large margin AE (LMAE) which boosts the discriminability by enforcing different class samples to be large marginally distributed in hidden feature space.

In this paper, we dedicate to the problem of training AE with label information and detecting discriminative representations which are suitable for classification problems. Naturally, we can concatenate the data and corresponding labels as the input of AE. But this method is unfriendly to test data as test data does not have labels. In order to avoid this problem, we employ the similar skill used in [25] where the model is designed to manage the case that both modalities are available in training while only one modality is available in testing for multi-modal learning. In [25], the proposed bimodal deep AE(BDAE) is trained in a de-noising manner, where an augmented but noisy dataset with additional examples that have only a single-modality is taken as input but both modalities are required to be reconstructed. Inspired by BDAE, we treat the data and corresponding label like two modalities in [25], take an augmented but noisy dataset as input and reconstruct both the data and label. To be exact, one-third of the training data has only data as input, while another one-third of the data has only label as input, and the last one-third of the data has both data and label as input. Different from what does in [25], a hyper-parameter is added to adjust the ratios between the data reconstruction and label reconstruction. We denote the proposed model as Supervised-AE (Sv-AE), in which the detection of hidden representations is guided by data and label information simultaneously. Consequently, the representations learned by Sv-AE are not only reconstructive but also discriminative.

The rest of this paper is organized as follows. In Sect. 2, we present the related models and learning algorithms. In Sect. 3, we describe the proposed Sv-AE, its relationship with other models and the learning algorithms. In Sect. 4, the performance comparison between Sv-AE and other algorithms are conducted over some frequently used data sets. In Sect. 5, we give a conclusion of this paper and discuss future work.

2 Autoencoder (AE)

2.1 Basic AE

Autoencoder was introduced in the late 80s [1, 2] which was considered as a dimensionality reduction technique. It is formed by two parts, an encoder and a decoder. The encoder takes an input x and maps it to a hidden representation h through a deterministic mapping and then the latent representation h is mapped back into a reconstruction z of the same shape as x by the decoder. Its typical form can be expressed by following formulas:

$$\begin{aligned} h&=s(Wx+b) \end{aligned}$$
(1)
$$\begin{aligned} z&=s(W'h+b') \end{aligned}$$
(2)

where s is a non-linear activation function, such as sigmoid function or rectified function [12]. The encoder and decoder are parameterized by weight matrix W and \(W'\) respectively. b and \(b'\) are biases vectors. AE can be divided into two kinds (tied-weight and untied-weight) depends on whether \(W=W'\) or not.

The training of AE is a optimization problem that the parameters \(\theta =(W,W',b,b')\) are optimized such that the average reconstruction error on a training set of examples \(D_n\) is minimized. The corresponding objective function can be represented as following:

$$\begin{aligned} J_{AE}(\theta )=\frac{1}{n}\sum _{x\in D_n} L(x,z) \end{aligned}$$
(3)

where L represents the type of cost function, the most frequently used one is squared error or cross-entropy error.

2.2 Denoising AE

DAE [17] is a very simple variant of basic AE described above. The main idea is to train a network that can reconstruct a clean input from a corrupted version of it. Firstly, the initial input x is corrupted into \(\tilde{x}\) by a stochastic mapping and then the corrupted input \(\tilde{x}\) is mapped, like the basic AE, to a hidden representation from which we get a reconstruction z as approximate as clean data x. The corresponding procedure can be expressed as following:

$$\begin{aligned}&\tilde{x}\sim q_D(\tilde{x}|x),h=s(W\tilde{x}+b) \end{aligned}$$
(4)
$$\begin{aligned}&z=s(W'h+b') \end{aligned}$$
(5)

The corruption processes can be chosen based on the data type. If the input data is continuous and real valued, Gaussian noise \(\tilde{x}|x\sim N(x,\sigma ^2 I)\) is an appropriate choice. The salt-and-pepper noise where a fraction v of the elements of x is set to their minimum or maximum possible value is suitable for input data which is interpretable as binary or near binary. Besides, the masking noise where a fraction v of the elements of x is forced to 0 is also frequently used.

The parameters are trained to minimize the average reconstruction error over a training set, that is, to have z as close as possible to the uncorrupted input x, seem to be the same as the training target of basic AE and the only difference is that z is a deterministic function of \(\tilde{x}\) instead of x. It thus forces the network to extract useful features that will constitute better higher level representation.

Both the basic AE and DAE described above are studied in an unsupervised manner which results in that the learned representations are blind to label information which would be a disadvantage in classification problems. In the next part, we change the network architecture slightly and introduce label information during representation learning and obtain a more powerful representation extractor Sv-AE, in which the learned representations are both reconstructive but also discriminative.

Fig. 1
figure 1

Illustration of the proposed model. a Preprocessing of input, b Sv-AE

Full size image

3 Supervised Auto-encoder

3.1 Proposed Model

In this section, we describe the proposed Sv-AE specifically. In order to take label information into account during feature detection in AE, one of the most straightforward idea is training an AE over the concatenated data and label. Although this approach can learn features using both data and the corresponding label information, but it is not appropriate as it can’t handle test data that are not accompanied with labels. A suitable learning model must be able to deal with both training data and testing data.

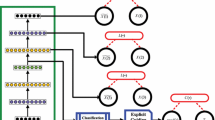
In order to satisfy such a requirement, we consider the skill used in [25]. The training data is divided into three parts, one third training data has only attribute data and zero labels, another one third training data has only label input and attribute part are zeros, the last one third data has both original data and label input. By training the network in such a method, the learned hidden representation can not only retain the structure information of data but also integrate the class information. Besides, when given the data, we can infer the corresponding label from the learned network, and when given the label, we can reconstruct the corresponding data. The structure of this model can be showed in Fig. 1b. Given a training data \(x=(x_1,\ldots ,x_D )\) and label vector \(y=(y_1,\ldots ,y_D )\), where \(y_i\) has only one non-zero element and \(y_{ic}=1\) denotes example \(x_i\) belong to class c. The input is firstly preprocessed as described above, and the obtained input is denoted as \(z=(\tilde{x},\tilde{y})\), the encoder process of Sv-AE can be expressed as following:

$$\begin{aligned} h=s(W\tilde{x}+U\tilde{y}+b) \end{aligned}$$
(6)

and the decoder process is added with a label reconstruction requirement:

$$\begin{aligned}&v=s(W'h+b') \end{aligned}$$
(7)
$$\begin{aligned}&l=g(U'h+c) \end{aligned}$$
(8)

where the active function s and the network parameters \(\left\{ W,W^{'},b,b^{'}\right\} \) are similar as described in basic AE. In this paper, we use sigmoid active function that \(s(a)=\frac{1}{1+exp(-a)}\) and an untied training form without the requirement of \(W'=W^{T}\). Besides, \(\left\{ U,U^{'},c\right\} \) are new parameters that are used to leverage label information, l denotes the distribution of training data x belongs to each class, and the exact expression of l is:

$$\begin{aligned} l_i=\frac{exp\left( \sum _j U_{ji}h_j+c_j\right) }{\sum _k exp\left( \sum _j U_{jk}h_j+c_k\right) } \end{aligned}$$
(9)

\(l_i\) denotes the probability of data x belongs to class i.

The model is trained by optimizing the following objective function:

$$\begin{aligned} J_{Sv-AE}(\theta )=\frac{1}{n}\sum _{x\in D_n} L_1(y,l)+\lambda \frac{1}{n}\sum _{x\in D_n} L_2(x,v) \end{aligned}$$
(10)

where \(L_1\) and \(L_2\) denote the reconstruction error of label and data respectively. \(\lambda \) is a hyper-parameter that controls the trade-off between data reconstruction and label reconstruction. Based on the definition of y and l, here we adopt \(L_1\) as the cross-entropy loss that \(L_1(a,b)=-\sum _i a_i*log(b_i)\). The form of \(L_2\) can vary depending on the type of input data. For inputs with values in [0,1] we use the cross entropy loss \(L_2(a,b)=-\left( \sum _i (a_i*log(b_i)+(1-a_i)*log(1-b_i))\right) \), and for other types of inputs, we use the most frequently used squared error \(L_2(a,b)={\left\| a-b\right\| }^2\).

As described in part II, DAE is a variant of AE that encourages robust features by reconstructing the uncorrupted input from a corrupted version of the original input. It’s easy to find that the proposed model can be viewed as a special DAE where the original input is the concatenate data and label vector and the data is corrupted by setting one third of the label parts to be zeros and another one third of data parts to be zeros.

3.2 Model Learning

Just like basic AE, the proposed model can be trained as an optimization problem that minimizes objective function \(J_{Sv-AE} (\theta )\) with respect to parameters \(\theta =\left\{ W,W',U,U',b,b',c\right\} \). The key step of model learning is computing the partial derivatives. We will compute the partial derivatives in light of back-propagation algorithm. Firstly, we introduce three marks \(\delta ^{(1)}\), \(\delta ^{(2)}\) and \(\delta ^{(3)}\) to denote the input of hidden layer, data reconstruction layer and label reconstruction layer respectively. That is \(\delta ^{(1)}=W\tilde{x}+U\tilde{y}+b\), \(\delta ^{(2) }=W'h+b'\), \(\delta ^{(3)}=Uh+c\). Then we compute the derivatives of discriminative term:

Taking the marks described above into Eq. (9),we have:

$$\begin{aligned} l_k=\frac{exp(\delta _k^{(3)})}{\sum _i{exp(\delta _i^{(3)})}} \end{aligned}$$
(11)

and the discriminative term in the objective function turns into:

$$\begin{aligned} L_1(y,l)&=-\sum _k y_k*log{l_k} \nonumber \\&=-\sum _k y_k*\delta _k^{(3)}+\sum _k y_k*log\left( \sum _iexp(\delta _i^{(3)})\right) \end{aligned}$$
(12)

The derivative of discriminative term \(L_1\) with respect to \(\delta ^{(3)}\) is:

$$\begin{aligned} \frac{\partial L_1(y,l)}{\partial \delta _k^{(3)}}&=-\,y_k+\sum _i y_i*\frac{exp(\delta _k^{(3)})}{\sum _iexp(\delta _i^{(3)})}\nonumber \\&=-\,y_k+l_k*\sum _i y_i=l_k-y_k \end{aligned}$$
(13)

Based on the chain rule, we can get the derivatives of discriminative term \(L_1\) with respect to the weight \(U'\):

$$\begin{aligned} \frac{\partial L_1(y,l)}{\partial U'_{jk}}&=\sum _i \frac{\partial L_1(y,l)}{\partial \delta _i^{(3)}}*\frac{\partial \delta _i^{(3)}}{\partial U'_{jk}} \nonumber \\&=\frac{\partial L_1(y,l)}{\partial \delta _k^{(3)}}*\frac{\partial \delta _k^{(3)}}{\partial U'_{jk}}=\frac{\partial L_1(y,l)}{\partial \delta _k^{(3)}}*h_j \end{aligned}$$
(14)

and the derivatives with respect to bias c:

$$\begin{aligned} \frac{\partial L_1(y,l)}{\partial c_k}&=\sum _i \frac{\partial L_1(y,l)}{\partial \delta _i^{(3)}}*\frac{\partial \delta _i^{(3)}}{\partial c_k} \nonumber \\&=\frac{\partial L_1(y,l)}{\partial \delta _k^{(3)}}*\frac{\partial \delta _k^{(3)}}{\partial c_k}=\frac{\partial L_1(y,l)}{\partial \delta _k^{(3)}} \end{aligned}$$
(15)

Furthermore,we can get the derivative of discriminative term \(L_1\) with respect to \(\delta ^{(1)}\):

$$\begin{aligned} \frac{\partial L_1(y,l)}{\partial \delta _j^{(1)}}&=\sum _k\frac{\partial L_1(y,l)}{\partial \delta _k^{(3)}}*\frac{\partial \delta _k^{(3)}}{\partial \delta _j{(3)}} \nonumber \\&=\sum _k\left( \frac{\partial L_1(y,l)}{\partial \delta _k^{(3)}}*\sum _l\left( \frac{\partial \delta _k^{(3)}}{\partial h_l}*\frac{\partial h_l}{\partial \delta _j^{(1)}}\right) \right) \nonumber \\&=\sum _k\left( \frac{\partial L_1(y,l)}{\partial \delta _k^{(3)}}*\frac{\partial \delta _k^{(3)}}{\partial h_j}*\frac{\partial h_j}{\partial \delta _j^{(1)}}\right) \nonumber \\&=\sum _k\frac{\partial L_1(y,l)}{\partial \delta _k^{(3)}}*U'_{jk}*h_j*(1-h_j) \end{aligned}$$
(16)

And then the derivatives with respect to parameters of the first layer can be expressed as following:

$$\begin{aligned} \frac{\partial L_1(y,l)}{\partial W_{ij}}&=\sum _p \frac{\partial L_1(y,l)}{\partial \delta _p^{(1)}}*\frac{\partial \delta _p^{(1)}}{\partial W_{ij}} \nonumber \\&=\frac{\partial L_1(y,l)}{\partial \delta _j^{(1)}}*\frac{\partial \delta _j^{(1)}}{\partial W_{ij}}=\frac{\partial L_1(y,l)}{\partial \delta _j^{(1)}}*x_i \end{aligned}$$
(17)
$$\begin{aligned} \frac{\partial L_1(y,l)}{\partial b_j}&=\sum _p \frac{\partial L_1(y,l)}{\partial \delta _p^{(1)}}*\frac{\partial \delta _p^{(1)}}{\partial b_j} \nonumber \\&=\frac{\partial L_1(y,l)}{\partial \delta _j^{(1)}}*\frac{\partial \delta _j^{(1)}}{\partial b_j}=\frac{\partial L_1(y,l)}{\partial \delta _j^{(1)}} \end{aligned}$$
(18)

Using the same steps,we can get the derivatives of reconstructive term \(L_2\) with respect to related parameters:

$$\begin{aligned}&\displaystyle \frac{\partial L_2(x,v)}{\partial \delta _q^{(2)}} =v_q-x_q \end{aligned}$$
(19)
$$\begin{aligned}&\displaystyle \frac{\partial L_2(x,v)}{\partial W_{jq}^{'}} =\frac{\partial L_2(x,v)}{\partial \delta _q^{(2)}}*h_j \end{aligned}$$
(20)
$$\begin{aligned}&\displaystyle \frac{\partial L_2(x,v)}{\partial b_q^{'}}=\frac{\partial L_2(x,v)}{\partial \delta _q^{(2)}} \end{aligned}$$
(21)
$$\begin{aligned}&\displaystyle \frac{\partial L_2(x,v)}{\partial \delta _j^{(1)}}=\sum _q \left( \frac{\partial L_2(x,)}{\partial \delta _q^{(2)}}*W_{jq}^{'}\right) *h_j*(1-h_j) \end{aligned}$$
(22)
$$\begin{aligned}&\displaystyle \frac{\partial L_2(x,v)}{\partial W_{ij}}=\frac{\partial L_2(x,v)}{\partial \delta _j^{(1)}}*\tilde{x}_i \end{aligned}$$
(23)
$$\begin{aligned}&\displaystyle \frac{\partial L_2(x,v)}{\partial U_{kj}}=\frac{\partial L_2(x,v)}{\partial \delta _j^{(1)}}*\tilde{y}_k \end{aligned}$$
(24)
$$\begin{aligned}&\displaystyle \frac{\partial L_2(x,v)}{\partial b_j}=\frac{\partial L_2(x,v)}{\partial \delta _j^{(1)}} \end{aligned}$$
(25)

And the derivatives of the whole objective function is a linear combination of discriminative derivatives and reconstructive derivatives:

$$\begin{aligned} \frac{\partial J_{Sv-AE}}{\partial \theta }=\frac{1}{n}\sum _x \frac{\partial L_1(y,l)}{\partial \theta }+\lambda \frac{1}{n}\sum _x \frac{\partial L_2(x,v)}{\partial \theta } \end{aligned}$$
(26)

With the partial derivatives derived above, the learning procedure of Sv-AE can be expressed in Algorithm 1.

figure a

4 Experiments and Results

In this section, the performances of proposed Sv-AE are evaluated and compared with some benchmark classification algorithms on a wide range of classification tasks, such as classification of UCI datasets, character recognition and document classification.

4.1 Classification of UCI Datasets

Eleven data sets from the UCI repository [26] are used to test the performance of the algorithms. The characteristics of these data sets are summarized in Table 1. As done in the [27], USPST(B) data set is a binary classification task created from USPST by grouping the first five digits as Class 1 and the last five digits as Class 2, COIL20(B) data set is a binary classification task created from COIL20 by grouping the first ten objects as Class 1 and the last ten objects as Class 2. The training sets and testing sets are divided randomly with the set sizes fixed as Table 1 shows. The random data partitions are repeated 20 times and we show average classification error and standard deviation of different algorithms on each data set.

Table 1 Details of the UCI datasets
Full size table

The proposed method is compared with the following six baseline algorithms.

  1. (1)

    SVM: libsvm toolbox is used.

  2. (2)

    NNnet: a single hidden layer feed-forward network (SLFN) that are trained by back-propagation.

  3. (3)

    ELM [28]: a SLFN with random hidden units.

  4. (4)

    AE \(+\) BP: a NNnet that the weight matrix is initialized by a basic AE.

  5. (5)

    Nt \(+\) SVM: the hidden representations learned by NNnet are used to train a SVM classifier.

  6. (6)

    AE \(+\) SVM: the hidden representations learned by AE are used to train a SVM classifier.

For NNnet, ELM and AE, the number of hidden units are fixed to 50 for the first 9 data sets and 200 for the last 2 data sets. The learning rate and iterative steps are adjusted based on experimental experience for the proposed method and other compared methods. Libsvm toolbox is used to train SVM classifiers and the best hyper parameters are selected via cross validation. In the proposed model, the hyper-parameter \(\lambda \) is varied among \(\{10^{-6},10^{-5},\ldots ,10^6\}\), and we evaluate the testing error for all of the 13 cases, then the lowest one is chosen as the final testing error. Besides, in Sv-AE and AE, we use sigmoid decoder function and cross-entropy loss error if the input data belongs to [0,1], identity function and mean square error for other cases.

Table 2 Performance comparison on UCI datasets (classification error %)
Full size table

Table 2 shows the testing performance of the proposed Sv-AE and other benchmark methods described above on all of the eleven UCI data sets. It can be seen that Sv-AE outperforms all the other algorithms on most of the data sets except for Iris. On Iris dataset, AE \(+\) BP performs best and Sv-AE is second best that still better than Nt \(+\) SVM and AE \(+\) SVM. From Table 1 we can see that Iris dataset has only 4 attributes which is very small, this may be the reason why Sv-AE is slightly worse than AE \(+\) BP. The result indicates that the features learned by Sv-AE is better than the discriminative only representations learned by NNnet and reconstructive only representations learned by basic AE when managing classification tasks. Learning both reconstructive and discriminative features will improve the classification accuracy.

4.2 Character Recognition

In this part, we use more complicated data set with character images to verify the learning performance of Sv-AE. The Mixed National Institute of Standards and Technology (MNIST) handwriting data set and two variations (MNIST-basic and MNIST-BI) are used. MNIST consists of 60,000 training images and 10,000 testing images of digits 0–9 with \(28\times 28\) pixels in gray-scale. MNIST-basic is a different partition version of MNIST and MNIST-BI is more complicated by adding background images to MNIST digit. Both of them consist of 12,000 training images and 50,000 testing images. Figure 2 gives an illustration of MNIST-basic and MNIST-BI.

Fig. 2
figure 2

Illustration of datasets. a MNIST-basic, b MNIST-BI

Full size image

Firstly, we give an intuitional compare of the supervised representation learned by Sv-AE and the traditional unsupervised feature learned by basic-AE by showing the receptive fields learned on MNIST dataset. The receptive fields (the columns of the weight matrix W) learned by the Sv-AE and Basic AE are displayed in Fig. 3 and it can be helpful for us to understand the discriminative power of the corresponding models. The results show that the filters learned by basic AE have no recognizable structure, looking entirely random while the filters learned by Sv-AE are spatially localized stroke detectors which are much meaningful.

Fig. 3
figure 3

Comparison of the filters learned by basic-AE and Sv-AE. a filters learned by Sv-AE, b filters learned by basic-AE

Full size image

Besides, we take experiments on MNIST-basic and MNIST-BI datasets to verify the classification ability of the learned hidden representations by showing the classification accuracy. We also provide the performance of SVM, regular neural network, a neural network initialized by basic AE, AE \(+\) SVM and NNnet \(+\) SVM. The results show that Sv-AE can achieve higher classification accuracy than other algorithms on both training set and testing set. The discriminability of the learned representations by Sv-AE has been proved once again (Table 3).

Table 3 Classification accuracy on MNIST-basic and MNIST-BI
Full size table

After the training of Sv-AE, we can use the network to reconstruct corresponding data when given the label vector. As MNIST data has 10 classes, the label vector have 10 possible values, that is \((1,0\ldots ,0)\ldots (0,\ldots ,0,1)\). From such label vector, the reconstructed data for MNIST-basic and MNIST-BI are shown in Fig. 4. We can see that the reconstructed data only retain the structure information of digits and the backgrounds in MNIST-BI are filtered out.

Fig. 4
figure 4

Data reconstructed from the label vectors via Sv-AE. a MNIST-basic, b MNIST-BI

Full size image

4.3 Document Classification

We also evaluate the proposed models on the problem of document classification with 20 Newsgroups dataset. The 20 Newsgroups dataset consists of 18,774 posts from 20 different newsgroups. Some of the newsgroups are very closely related to each other, while others are highly unrelated. The 11,269 training posts and 7,505 testing posts are collected at different times that it is more reflective of a practical application. In our experiment, the training set was divided into a smaller training set and a validation set, with 10,000 and 1269 examples respectively. After removing stop-words and stemming, the most frequently used 5000 words in the training set were used to represent the documents.

Table 4 reports the classification accuracy of each algorithm. The results indicate that Sv-AE still performs better than NN-net and AE \(+\) BP which demonstrate the superiority of representations leaned by the proposed model.

Table 4 Classification accuracy on 20 newsgroups
Full size table

In order to get a better understanding of how the Sv-AE solves this classification problem, we give a look of the similarity matrix S of weights connected to each class neurons indicating different newsgroups. S is calculated by function \(S(U)=sigmoid(U^{T}U)\), \(S_{ij}\) can reflect the similarity between class i and class j to some degree, and the smaller of \(S_{ij}\) the less similar of class i and class j. The matrix is shown in Fig. 5, we see that S is not diagonal but more like block diagonal, which means that Sv-AE doesn’t use strictly non-overlapping sets of neurons for different newsgroups, but shares some of those neurons for newsgroups that are semantically related. We see that the Sv-AE tends to share neurons represent the same topics such as computer (comp.*) and science (sci.*), or secondary topics such as sports (rec.sports.*) and politics (talk.politics.*).

Fig. 5
figure 5

Similarity matrix of the newsgroup weights vector \(U_{.j}\)

Full size image

5 Conclusion

In this paper, we proposed a novel model Sv-AE which takes concatenate but noisy data and label as input and reconstructs both data and label. By doing this, the Sv-AE can take use of label information during representation extraction. Experiments on UCI datasets, MNIST and 20 newsgroups have shown that the representations extracted by our proposed model are more discriminative. It can achieve higher classification precision when be used to train a SVM classifier. Future work will extend this supervised model to a semi-supervised variant of AE. Currently the model is used as a shallow classifier, but it can also be used to build deep architectures which we will go on research in the future.